An Ensemble Model Based on Machine Learning Methods and Data Preprocessing for Short-Term Electric Load Forecasting
Abstract
:1. Introduction
2. Methodology
2.1. Empirical Mode Decomposition
2.2. Variational Mode Decomposition
2.3. The DE-ELM Model
2.3.1. Extreme Learning Machine
2.3.2. Differential Evolution Algorithm
2.3.3. The DE-ELM Model
2.4. The VMD-DE-ELM Forecasting Model
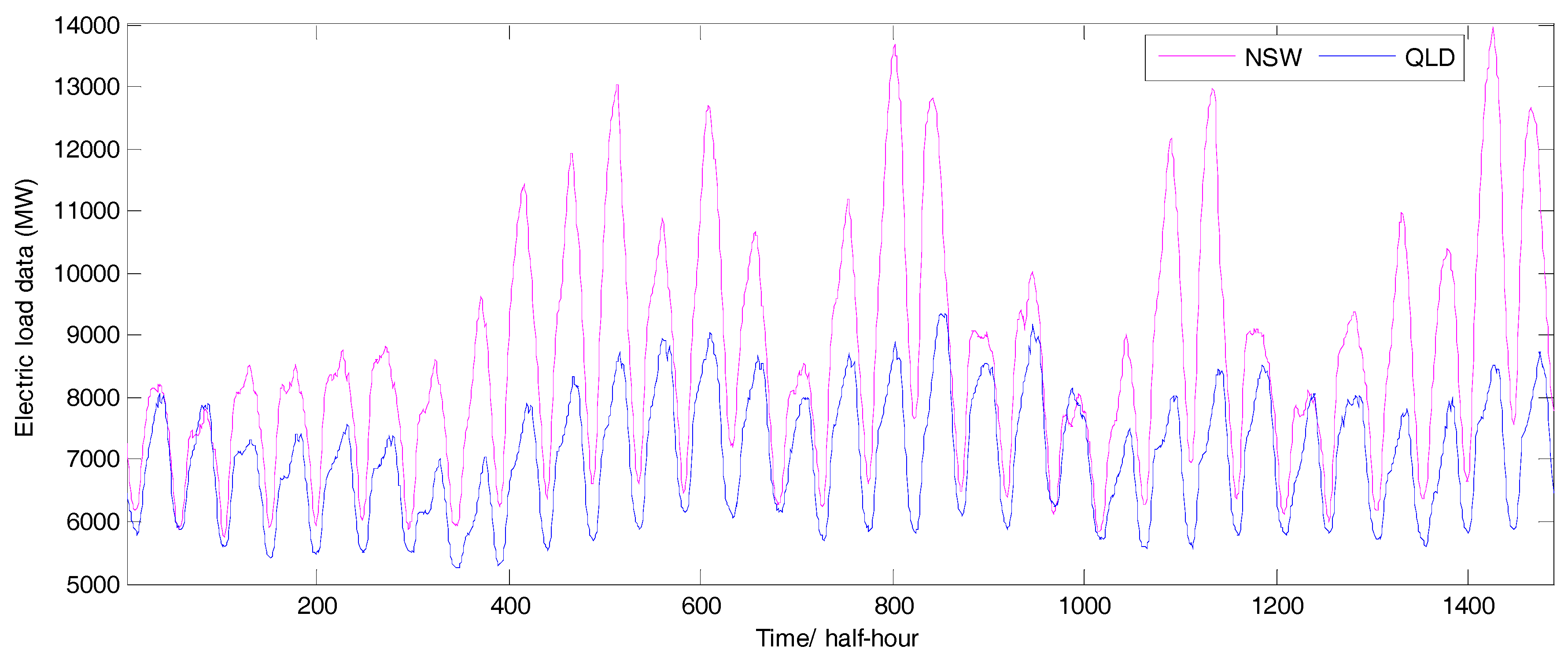
3. Data Description and Preprocessing
4. Empirical Study
4.1. Performance Criteria of Forecasting Accuracy
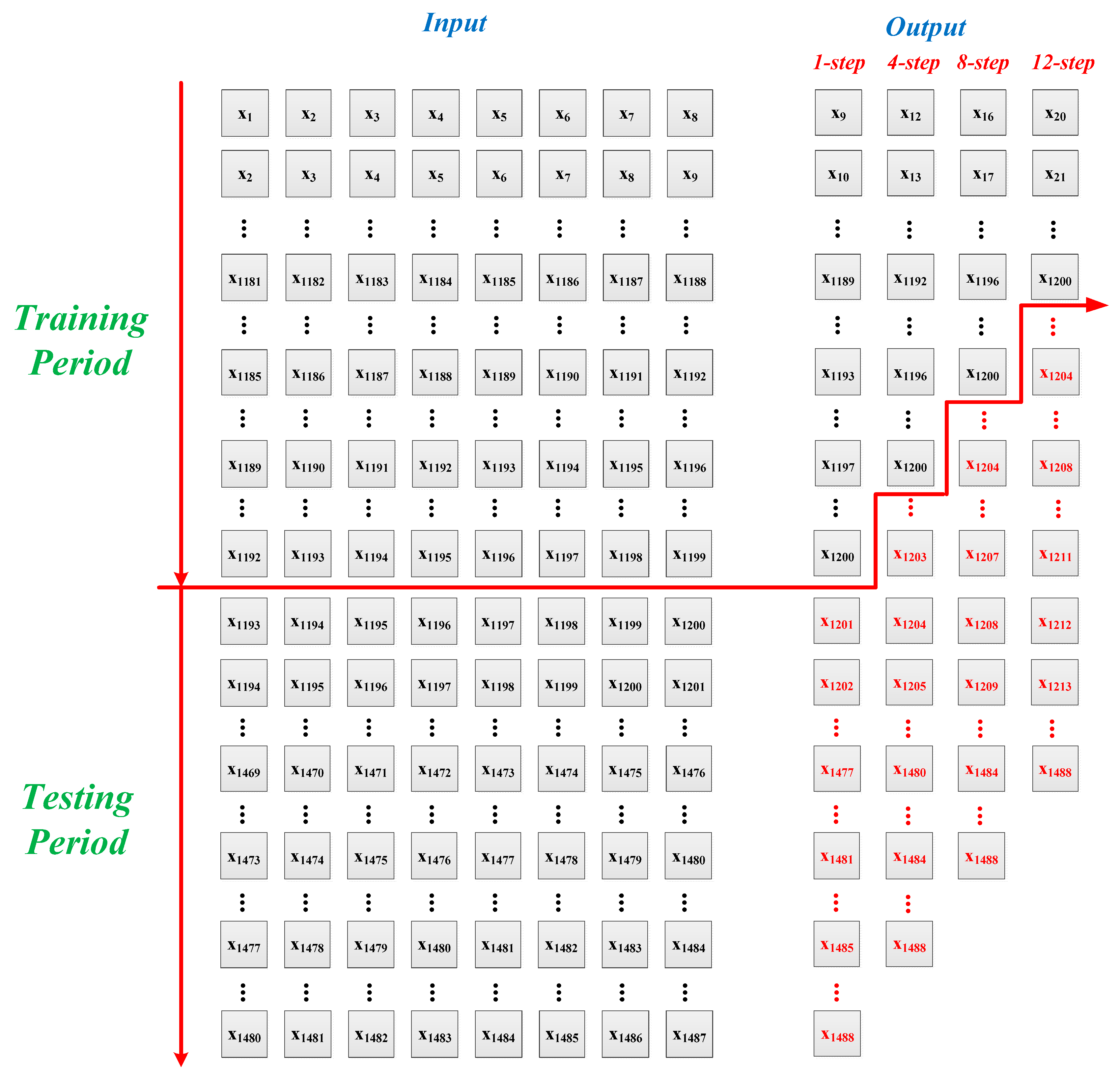
4.2. Multi-Step Ahead Electric Load Forecasting in NSW
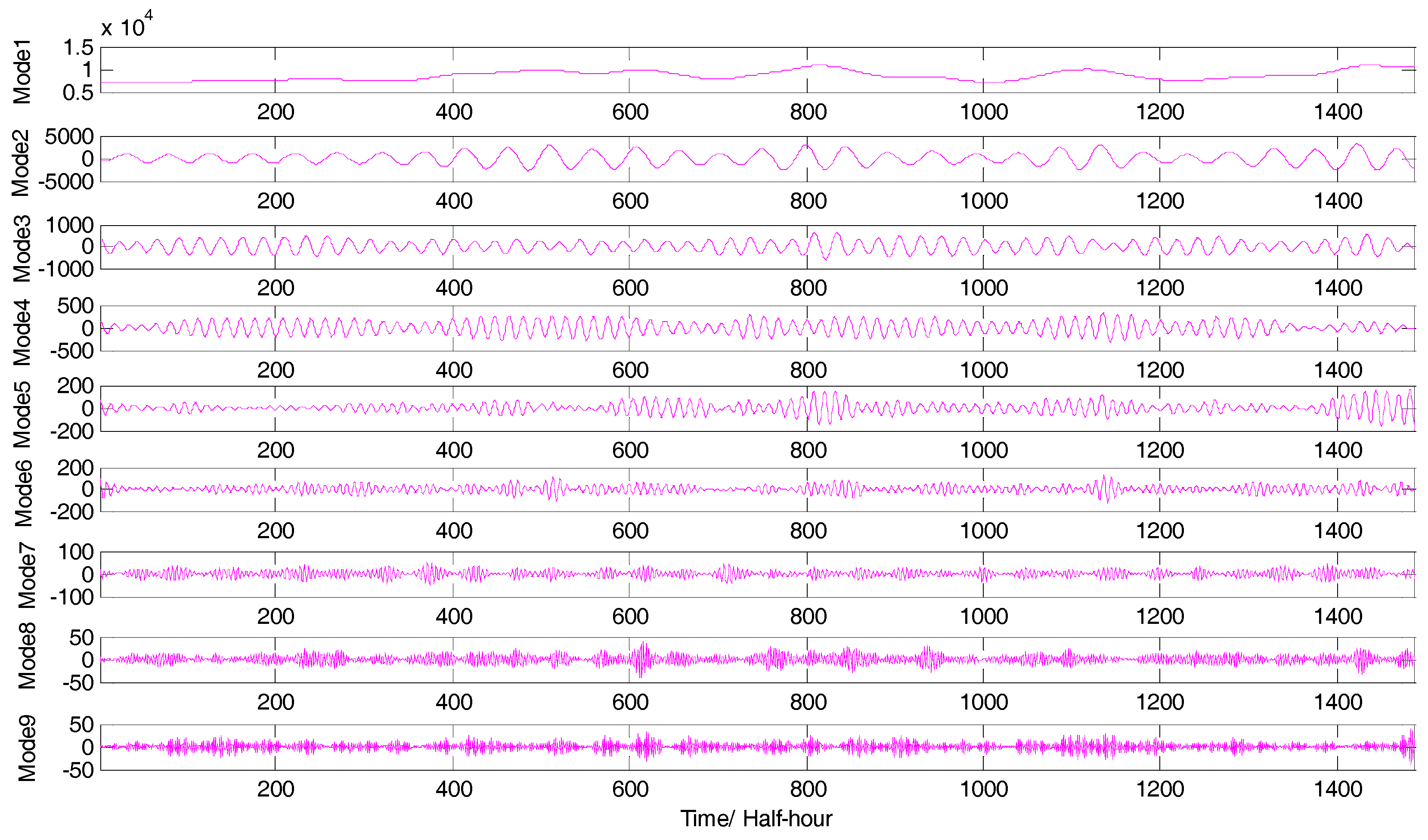
4.2.1. Data Preprocessing of the Original Electric Load Series
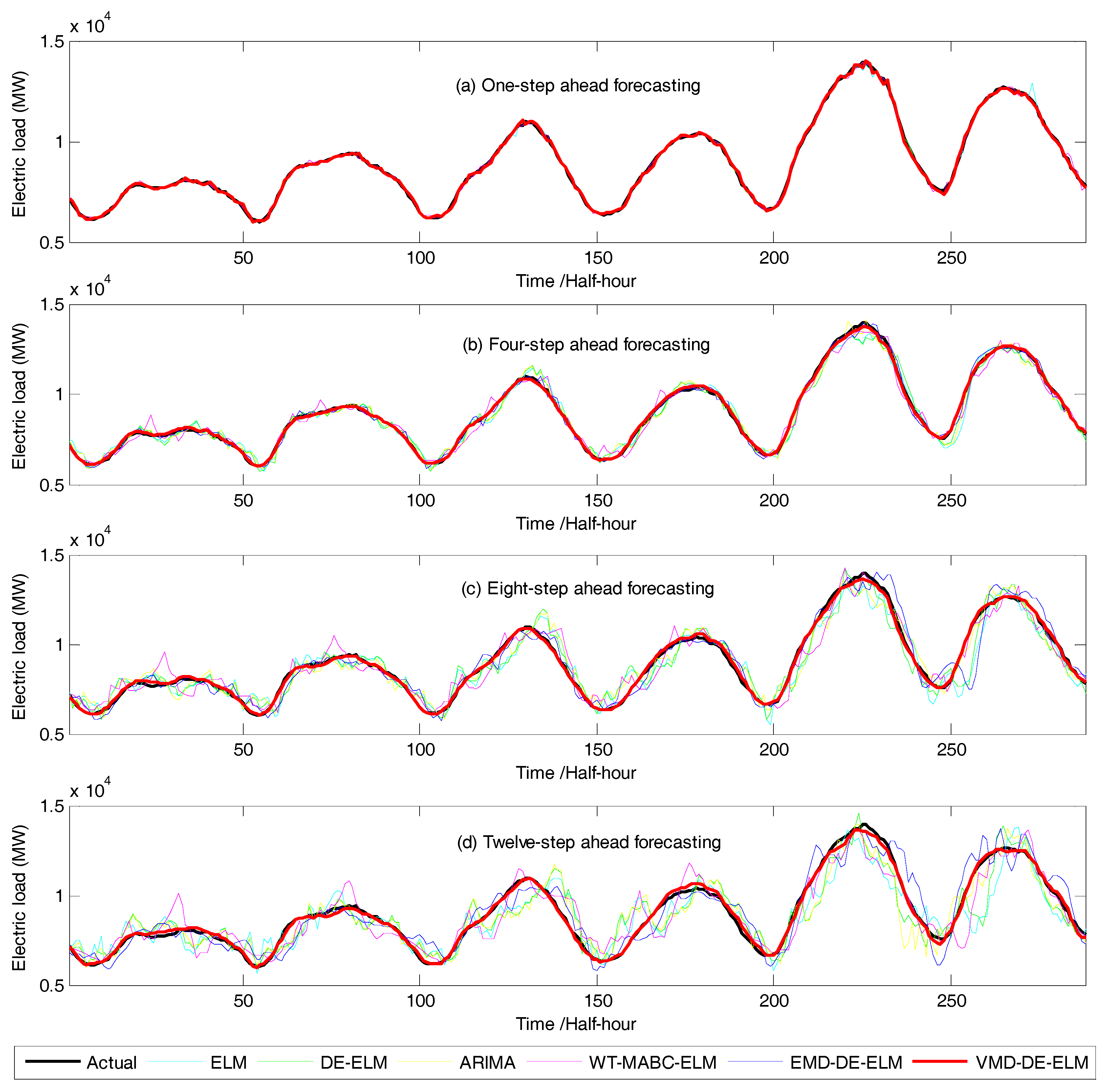
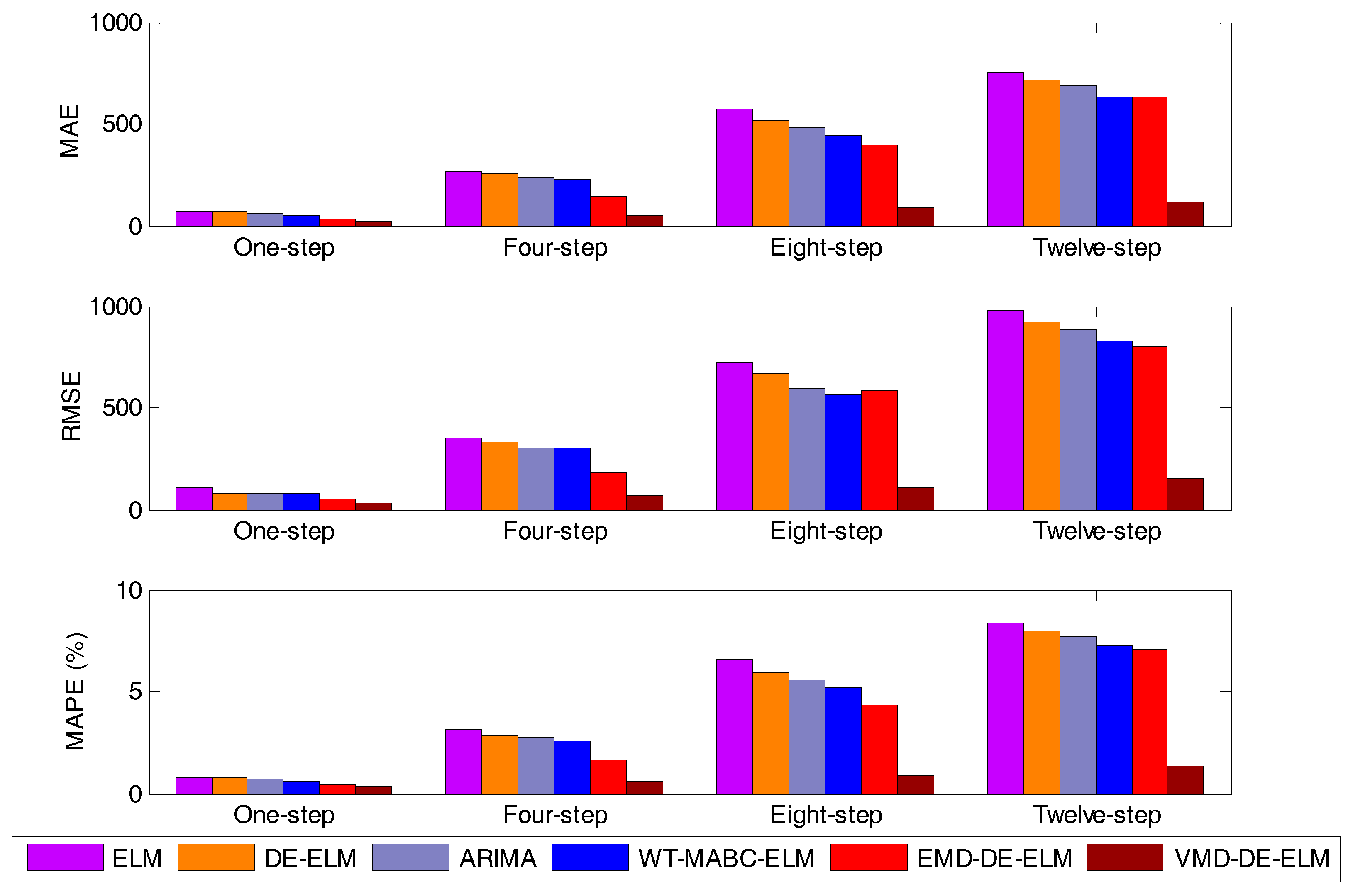
4.2.2. Forecasting Results, Comparative Analysis and Discussion
4.3. Multi-Step Ahead Electric Load Forecasting in QLD
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| VMD | Variational mode decomposition |
| EMD | Empirical mode decomposition |
| EEMD | Ensemble empirical mode decomposition |
| FEEMD | Fast ensemble empirical mode decomposition |
| IMF | Intrinsic mode function |
| WPT | Wavelet packet transform |
| WT | Wavelet transform |
| ARMA | Auto-regressive moving average |
| ARIMA | Auto-regressive integrated moving average |
| GARCH | Generalized autoregressive conditional heteroskedasticity |
| VAR | Vector auto-regression |
| ANN | Artificial neural network |
| SVM | Support vector machine |
| LSSVM | Least square support vector machine |
| ELM | Extreme learning machine |
| DE | Differential evolution |
| PSO | Particle swarm optimization |
| SA | Simulated annealing |
| ABC | Artificial bee colony |
| MABC | Modified artificial bee colony |
| SOM | Self-organizing maps |
| PSR | Phase space reconstruction |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| NSW | New south wales |
| QLD | Queensland |
References
- Abosedra, S.; Dah, A.; Ghosh, S. Electricity consumption and economic growth, the case of Lebanon. Appl. Energy 2009, 86, 429–432. [Google Scholar] [CrossRef]
- Adam, N.R.B.; Elahee, M.K.; Dauhoo, M.Z. Forecasting peak electricity demand in Mauritius using the non-homogeneous Gompertz diffusion process. Energy 2013, 36, 6763–6769. [Google Scholar] [CrossRef]
- Kavaklioglu, K.; Ceylan, H.; Ozturk, H.K.; Canyurt, O.E. Modeling and prediction of Turkey’s electricity consumption using Artificial Neural Networks. Energy Convers. Manag. 2009, 50, 2719–2727. [Google Scholar] [CrossRef]
- Chase, R.B.; Jacobs, F.R.; Aquilano, N.J. Operations Management for Competitive Advantage; McGraw-Hill/Irwin: New York, NY, USA, 2001. [Google Scholar]
- He, K.J.; Yu, L.A.; Tang, L. Electricity price forecasting with a BED (Bivariate EMD Denoising) methodology. Energy 2015, 91, 601–609. [Google Scholar] [CrossRef]
- Lei, M.; Luan, S.J.; Jiang, C.W.; Liu, H.L.; Zhang, Y. A review on the forecasting of wind speed and generated power. Renew. Sustain. Energy. Rev. 2009, 13, 915–920. [Google Scholar] [CrossRef]
- Pappas, S.S.; Ekonomou, L.; Karampelas, P.; Karamousantas, D.C.; Katsikas, S.K.; Chatzarakis, G.E.; Skafidas, P.D. Electricity demand load forecasting of the Hellenic power system using an ARMA model. Electr. Power Syst. Res. 2010, 80, 256–264. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Kavousi-Fard, F. A new hybrid correction method for short-term load forecasting based on ARIMA, SVR and CSA. J. Exp. Theor. Artif. Intell. 2013, 25, 559–574. [Google Scholar] [CrossRef]
- Takiyar, S.; Upadhyay, K.G.; Singh, V. Fuzzy ARTMAP and GARCH-based hybrid model aided with wavelet transform for short-term electricity load forecasting. Energy Sci. Eng. 2016, 4, 14–22. [Google Scholar] [CrossRef]
- Garcia-Ascanio, C.; Mate, C. Electric power demand forecasting using interval time series: A comparison between VAR and iMLP. Energy Policy 2010, 38, 715–725. [Google Scholar] [CrossRef]
- Takeda, H.; Tamura, Y.; Sato, S. Using the ensemble Kalman filter for electricity load forecasting and analysis. Energy 2016, 104, 184–198. [Google Scholar] [CrossRef]
- Yolcu, U.; Egrioglu, E.; Aladag, C.H. A new linear and nonlinear artificial neural network model for time series forecasting. Decis. Support Syst. 2013, 54, 1340–1347. [Google Scholar] [CrossRef]
- Gutierrez-Corea, F.V.; Manso-Callejo, M.A.; Moreno-Regidor, M.P.; Manrique-Sancho, M.T. Forecasting short-term solar irradiance based on artificial neural networks and data from neighboring meteorological stations. Sol. Energy 2016, 134, 119–131. [Google Scholar] [CrossRef]
- Li, S.; Wang, P.; Goel, L. Short-term load forecasting by wavelet transform and evolutionary extreme learning machine. Electr. Power Syst. Res. 2015, 122, 96–103. [Google Scholar] [CrossRef]
- Zhou, J.Y.; Jing, S.; Gong, L. Fine tuning support vector machines for short-term wind speed forecasting. Energy Convers. Manag. 2011, 52, 1990–1998. [Google Scholar] [CrossRef]
- Chen, T.T.; Lee, S.J. A weighted LSSVM based learning system for time series forecasting. Inf. Sci. 2015, 299, 99–116. [Google Scholar] [CrossRef]
- Liu, H.; Shi, J. Applying ARMA-GARCH approaches to forecasting short-term electricity prices. Energy Econ. 2013, 37, 152–166. [Google Scholar] [CrossRef]
- Voyant, C.; Muselli, M.; Paoli, C.; Nivet, M. Numerical weather prediction (NWP) and hybrid ARMA/ANN model to predict global radiation. Energy 2012, 39, 341–355. [Google Scholar] [CrossRef]
- Ismail, S.; Shabri, A.; Samsudin, R. A hybrid model of self-organizing maps (SOM) and least square support vector machine (LSSVM) for time-series forecasting. Expert Syst. Appl. 2011, 38, 10574–10578. [Google Scholar] [CrossRef]
- Liu, D.; Niu, D.X.; Wang, H.; Fan, L.L. Short-term wind speed forecasting using wavelet transform and support vector machines optimized by genetic algorithm. Renew. Energy 2014, 62, 592–597. [Google Scholar] [CrossRef]
- Wang, J.Z.; Wang, Y.; Jiang, P. The study and application of a novel hybrid forecasting model—A case study of wind speed forecasting in China. Appl. Energy 2015, 143, 472–488. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, H.; Wang, Z.H.; Li, J. A preliminary study on time series forecast of fair-weather atmospheric electric field with WT-LSSVM method. J. Electrost. 2015, 75, 85–89. [Google Scholar] [CrossRef]
- Wang, D.Y.; Luo, H.Y.; Grunder, O.; Lin, Y.B.; Guo, H.H. Multi-step ahead electricity price forecasting using a hybrid model based on two-layer decomposition technique and BP neural network optimized by firefly algorithm. Appl. Energy 2017, 190, 390–407. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Cincotti, S.; Gallo, G.; Ponta, L.; Raberto, M. Modelling and forecasting of electricity spot-prices: Computational intelligence vs classical econometrics. AI Commun. 2014, 27, 301–314. [Google Scholar]
- Amjady, N.; Keynia, F. Day ahead price forecasting of electricity markets by a mixed data model and hybrid forecast method. Int. J. Electr. Power 2008, 30, 533–546. [Google Scholar] [CrossRef]
- Abdoos, A.A. A new intelligent method based on combination of VMD and ELM for short term wind power forecasting. Neurocomputing 2016, 203, 111–120. [Google Scholar] [CrossRef]
- Lahmiri, S. A variational mode decompoisition approach for analysis and forecasting of economic and financial time series. Expert Syst. Appl. 2016, 55, 268–273. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary Time Series Analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, M.C.; Qu, W.; Long, S.R.; Shen, Z. Application of Hilbert-Huang Transform to Non-stationary Financial Time Series Analysis. Appl. Stoch. Model. Bus. Ind. 2003, 19, 245–268. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 985–990. [Google Scholar]
- Storn, R.; Price, K. Differential evolution: A simple and efficient adaptive scheme for global optimization over continuous spaces. J. Glob. Optim. 1995, 23, 341–359. [Google Scholar]
- Australian Energy Market Operator (AEMO). Available online: www.aemo.com.au (accessed on May 2017).
- Taieb, S.B.; Bontempi, G.; Atiya, A.F.; Sorjamaa, A. A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition. Expert Syst. Appl. 2011, 39, 7067–7083. [Google Scholar] [CrossRef]
- Wang, S.X.; Zhang, N.; Wu, L.; Wang, Y.M. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]

| Site | Descriptive Statistics | ||||||
|---|---|---|---|---|---|---|---|
| N | Mean | Standard Deviation | Minimum Value | Maximum Value | Coefficient of Skewness | Coefficient of Kurtosis | |
| NSW | 1488 | 8588.11 | 1812.13 | 5767.31 | 13947.70 | 0.786 | 0.024 |
| QLD | 1488 | 7025.13 | 964.55 | 5254.92 | 9357.09 | 0.171 | −0.989 |
| Prediction Horizon | Index | ELM | DE-ELM | ARIMA | WT-MABC-ELM | EMD-DE-ELM | VMD-DE-ELM |
|---|---|---|---|---|---|---|---|
| One-step ahead | MAE | 74.477 | 66.385 | 64.283 | 51.991 | 33.652 | 26.809 |
| RMSE | 111.127 | 83.838 | 83.691 | 78.671 | 47.185 | 34.212 | |
| MAPE (%) | 0.826 | 0.765 | 0.729 | 0.595 | 0.399 | 0.306 | |
| Four-step ahead | MAE | 268.927 | 253.366 | 236.422 | 227.829 | 142.189 | 54.471 |
| RMSE | 350.613 | 329.449 | 303.286 | 302.815 | 184.695 | 71.585 | |
| MAPE (%) | 3.090 | 2.876 | 2.731 | 2.588 | 1.616 | 0.590 | |
| Eight-step ahead | MAE | 571.469 | 523.137 | 480.196 | 443.308 | 393.016 | 84.301 |
| RMSE | 724.253 | 665.499 | 592.378 | 569.010 | 587.119 | 109.534 | |
| MAPE (%) | 6.546 | 5.946 | 5.549 | 5.147 | 4.364 | 0.918 | |
| Twelve-step ahead | MAE | 753.415 | 718.724 | 684.807 | 633.498 | 626.593 | 116.900 |
| RMSE | 975.893 | 918.407 | 880.956 | 831.308 | 797.494 | 152.374 | |
| MAPE (%) | 8.341 | 7.949 | 7.717 | 7.206 | 7.061 | 1.311 |
| Prediction Horizon | Index (%) | DF | ||||
|---|---|---|---|---|---|---|
| VMD-DE-ELM | VMD-DE-ELM | VMD-DE-ELM | VMD-DE-ELM | DE-ELM | ||
| vs. | vs. | vs. | vs. | vs. | ||
| ARIMA | EMD-DE-ELM | WT-MABC-ELM | DE-ELM | ELM | ||
| One-step ahead | MAE | 58.30 | 20.33 | 48.44 | 59.62 | 10.87 |
| RMSE | 59.12 | 27.49 | 56.51 | 59.19 | 24.56 | |
| MAPE | 58.02 | 23.31 | 48.57 | 60.00 | 7.38 | |
| Four-step ahead | MAE | 76.96 | 61.69 | 76.09 | 78.50 | 5.79 |
| RMSE | 76.40 | 61.24 | 76.36 | 78.27 | 6.04 | |
| MAPE | 78.40 | 63.49 | 77.20 | 79.49 | 6.93 | |
| Eight-step ahead | MAE | 82.44 | 78.55 | 80.98 | 83.89 | 8.46 |
| RMSE | 81.51 | 81.34 | 80.75 | 83.54 | 8.11 | |
| MAPE | 83.46 | 78.96 | 82.16 | 84.56 | 9.17 | |
| Twelve-step ahead | MAE | 82.93 | 81.34 | 81.55 | 83.74 | 4.60 |
| RMSE | 82.70 | 80.89 | 81.67 | 83.41 | 5.89 | |
| MAPE | 83.01 | 81.43 | 81.81 | 83.51 | 4.70 | |
| Prediction Horizon | Index | ELM | DE-ELM | ARIMA | WT-MABC-ELM | EMD-DE-ELM | VMD-DE-ELM |
|---|---|---|---|---|---|---|---|
| One-step ahead | MAE | 54.319 | 52.142 | 47.230 | 36.690 | 26.595 | 24.257 |
| RMSE | 72.347 | 67.914 | 62.768 | 45.993 | 34.996 | 30.673 | |
| MAPE (%) | 0.766 | 0.742 | 0.673 | 0.537 | 0.377 | 0.346 | |
| Four-step ahead | MAE | 185.559 | 165.310 | 154.155 | 132.181 | 96.670 | 33.801 |
| RMSE | 236.005 | 209.209 | 204.769 | 171.577 | 134.903 | 43.935 | |
| MAPE (%) | 2.620 | 2.345 | 2.178 | 1.884 | 1.395 | 0.476 | |
| Eight-step ahead | MAE | 369.909 | 327.546 | 293.851 | 253.762 | 239.131 | 50.352 |
| RMSE | 475.637 | 433.910 | 391.159 | 329.213 | 328.414 | 67.260 | |
| MAPE (%) | 5.281 | 4.688 | 4.151 | 3.579 | 3.454 | 0.703 | |
| Twelve-step ahead | MAE | 506.554 | 490.289 | 480.470 | 419.567 | 394.999 | 78.343 |
| RMSE | 643.787 | 629.534 | 627.282 | 559.602 | 513.964 | 99.880 | |
| MAPE (%) | 7.289 | 7.034 | 6.888 | 5.936 | 5.821 | 1.099 |
| Prediction Horizon | Index (%) | DF | ||||
|---|---|---|---|---|---|---|
| VMD-DE-ELM | VMD-DE-ELM | VMD-DE-ELM | VMD-DE-ELM | DE-ELM | ||
| vs. | vs. | vs. | vs. | vs. | ||
| ARIMA | EMD-DE-ELM | WT-MABC-ELM | DE-ELM | ELM | ||
| One-step ahead | MAE | 48.64 | 8.79 | 33.89 | 53.48 | 4.01 |
| RMSE | 51.13 | 12.35 | 33.31 | 54.84 | 6.13 | |
| MAPE | 48.59 | 8.22 | 35.57 | 53.37 | 3.13 | |
| Four-step ahead | MAE | 78.07 | 65.03 | 74.43 | 79.55 | 10.91 |
| RMSE | 78.54 | 67.43 | 74.39 | 79.00 | 11.35 | |
| MAPE | 78.15 | 65.88 | 74.73 | 79.70 | 10.50 | |
| Eight-step ahead | MAE | 82.86 | 78.94 | 80.16 | 84.63 | 11.45 |
| RMSE | 82.80 | 79.52 | 79.57 | 84.50 | 8.77 | |
| MAPE | 83.06 | 79.65 | 80.36 | 85.00 | 11.23 | |
| Twelve-step ahead | MAE | 83.69 | 80.17 | 81.33 | 84.02 | 3.21 |
| RMSE | 84.08 | 80.57 | 82.15 | 84.13 | 2.21 | |
| MAPE | 84.04 | 81.12 | 81.49 | 84.38 | 3.50 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Luo, H.; Wang, D.; Guo, H.; Zhu, K. An Ensemble Model Based on Machine Learning Methods and Data Preprocessing for Short-Term Electric Load Forecasting. Energies 2017, 10, 1186. https://doi.org/10.3390/en10081186
Lin Y, Luo H, Wang D, Guo H, Zhu K. An Ensemble Model Based on Machine Learning Methods and Data Preprocessing for Short-Term Electric Load Forecasting. Energies. 2017; 10(8):1186. https://doi.org/10.3390/en10081186
Chicago/Turabian StyleLin, Yanbing, Hongyuan Luo, Deyun Wang, Haixiang Guo, and Kejun Zhu. 2017. "An Ensemble Model Based on Machine Learning Methods and Data Preprocessing for Short-Term Electric Load Forecasting" Energies 10, no. 8: 1186. https://doi.org/10.3390/en10081186
APA StyleLin, Y., Luo, H., Wang, D., Guo, H., & Zhu, K. (2017). An Ensemble Model Based on Machine Learning Methods and Data Preprocessing for Short-Term Electric Load Forecasting. Energies, 10(8), 1186. https://doi.org/10.3390/en10081186




