Proposal of Physical-Statistical Model of Thermal Aging Respecting Threshold Value
Abstract
:1. Introduction
1.1. Example of Statistical Access
1.2. Use of Physical and Mathematical Models
- Mechanical aging models [34].
1.3. Thermal Aging Models
1.4. Electrical Aging Models
2. Physical-Statistical Model of Thermal Aging Respecting Threshold Value (Thermal Aging Model Respecting the Threshold (TAMRT))
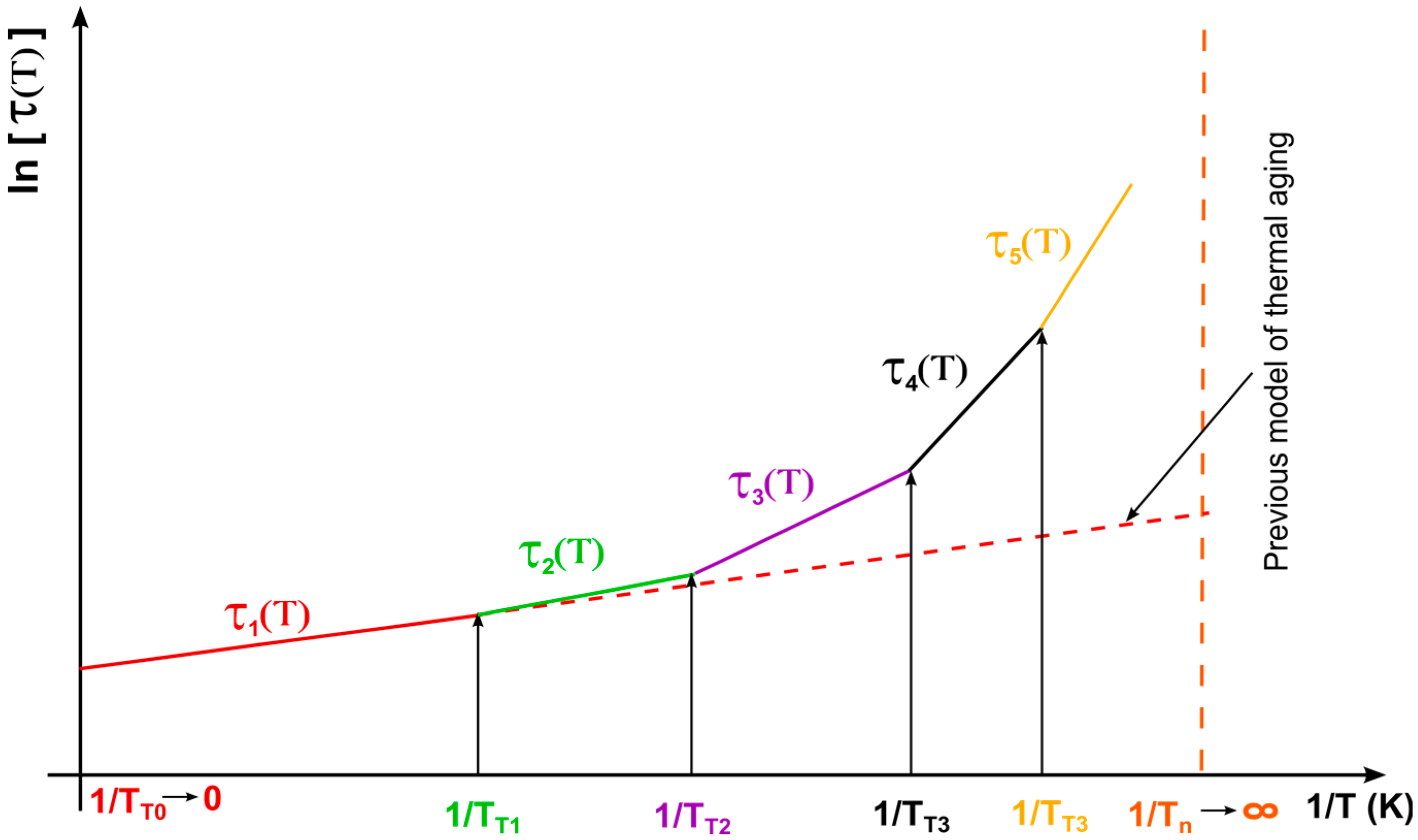
2.1. Model Suggestion
2.2. Determining the Threshold Value TT Using a Probabilistic Model
3. Experimental Verification of Proposed Model
Procedure for Establishing the Probabilistic Model for Validation of Experimental Data
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. List of Variables and Constants
| β | shape parameter of Weibull distribution |
| η | scale parameter of Weibull distribution |
| Γ(z) | Gamma function |
| τ (h) | lifetime |
| A (h), B (K−1) | material constants |
| k (s−1) | reaction rate |
| T (K) | absolute temperature |
| A* (s−1) | pre-exponential factor or frequency factor |
| Ea (J∙mol−1) | activation energy of thermal process |
| R (J∙K−1∙mol−1) | universal gas constant, which has the value 8.3144598 J∙K−1∙mol−1 |
| a (h) | reciprocal value of the pre-exponential factor A* |
| E (kV∙mm−1) | intensity of the electric field |
| k (kV−1∙mm∙h), N | material constants |
| b (kV−1∙mm), c* (h) | material constants |
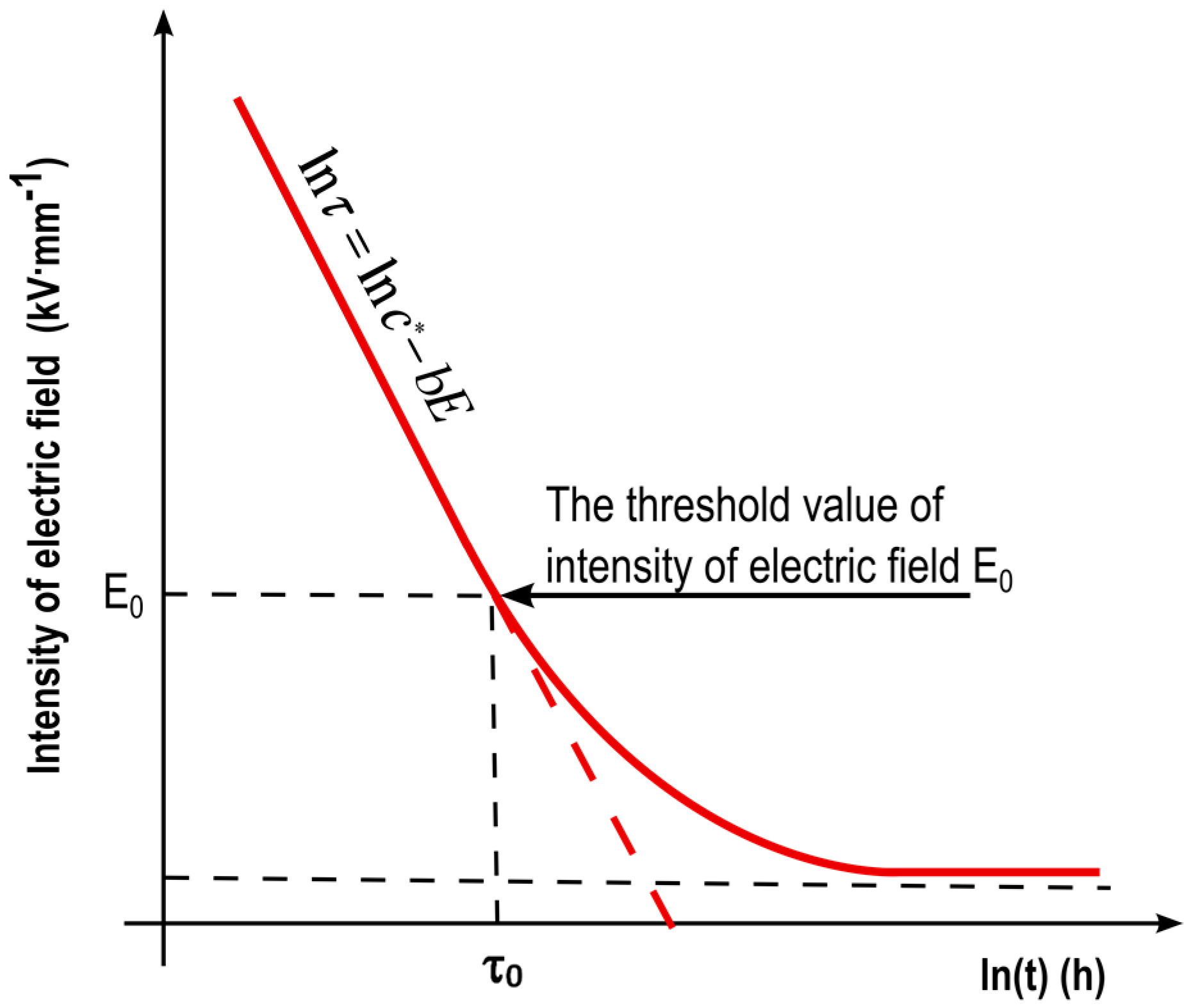
| τ0 (h) | lifetime of the insulation system for threshold value |
| E0 (kV∙mm−1) | threshold value of the intensity of the electric field |
| X1 (kV−1∙mm), X2 (kV∙mm−1∙h) | material constants |
| Ean (J∙mol−1) | activation energies of thermal processes which define partial degradation mechanisms and characterize aging electrical insulating system at intervals of extreme temperatures TT1 up to TTn |
| TTn (K) | extreme of the temperature intervals that define partial degradation mechanisms |
| τi (h) | lifetime of the insulation system in the temperature range |
| Ki | partial correction parameter of new model for preservation of condition |
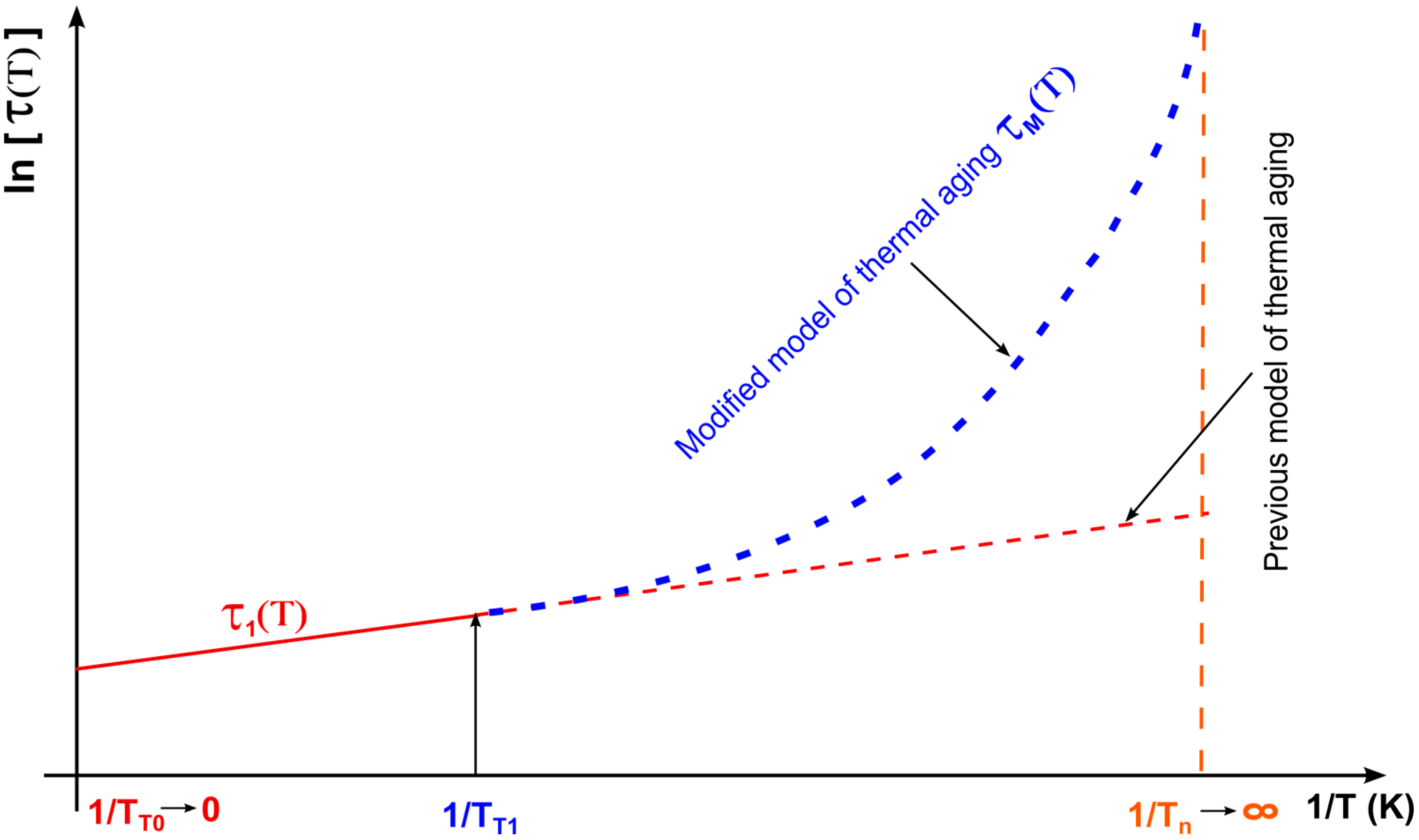
| τM (h) | modified model of thermal aging in range of temperature T ∈ (0,TT1) |
| D (K) | material constant, which is characterized by synergistic effect of partial degradation mechanisms |
| TT1 (K) | threshold value of the degradation factor of the new model |
| KM | correction parameter of modified model for preservation of condition |
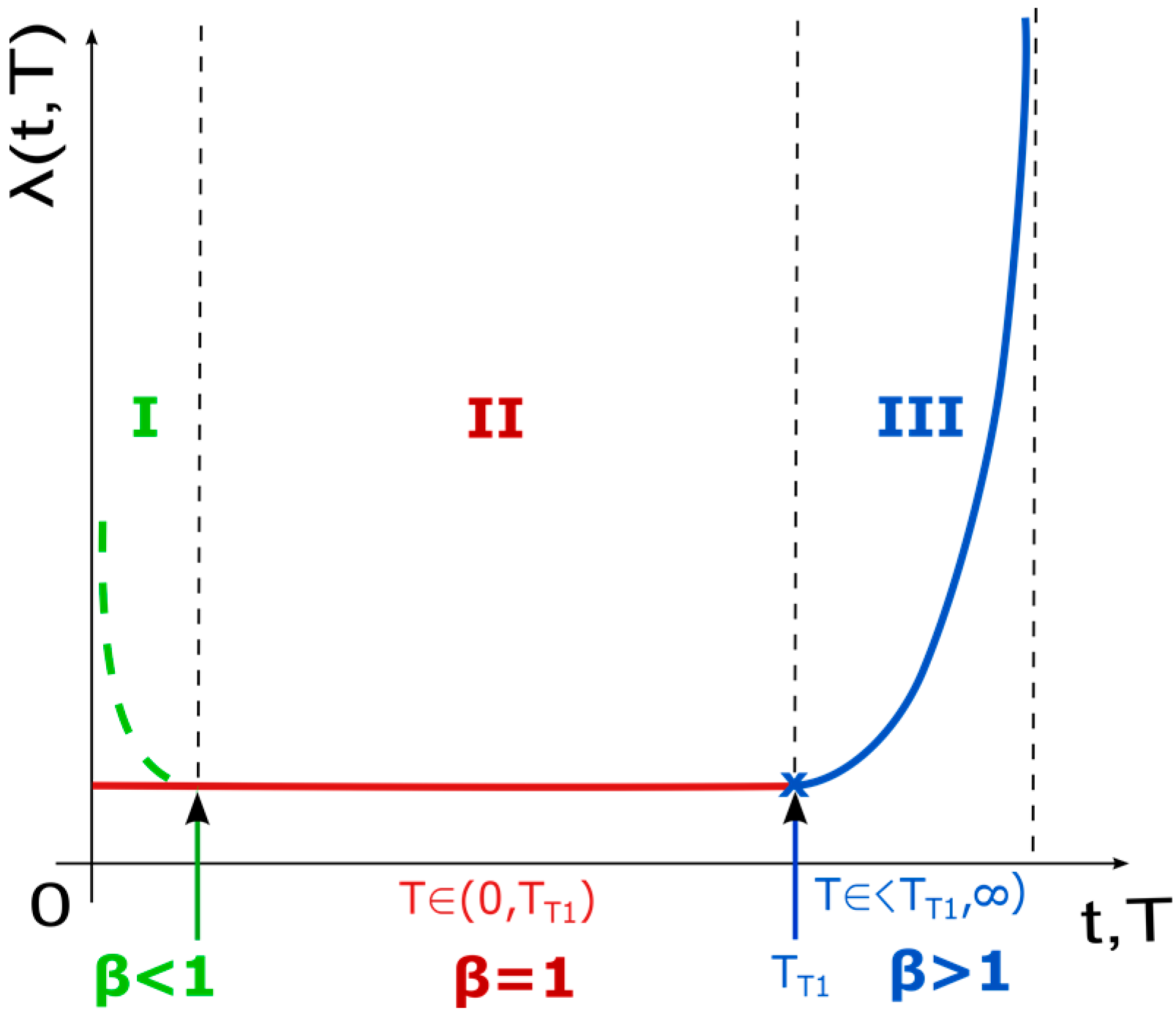
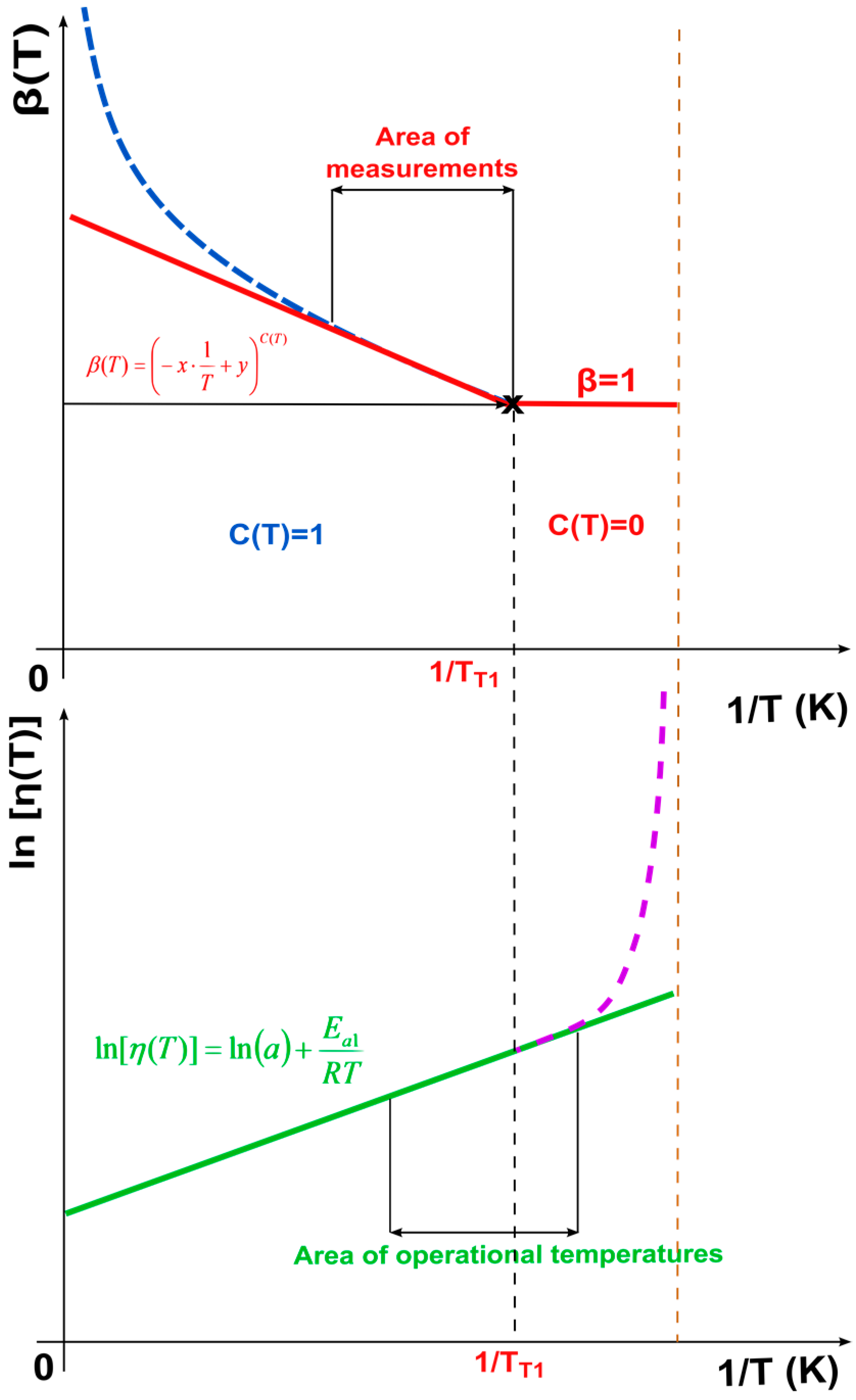
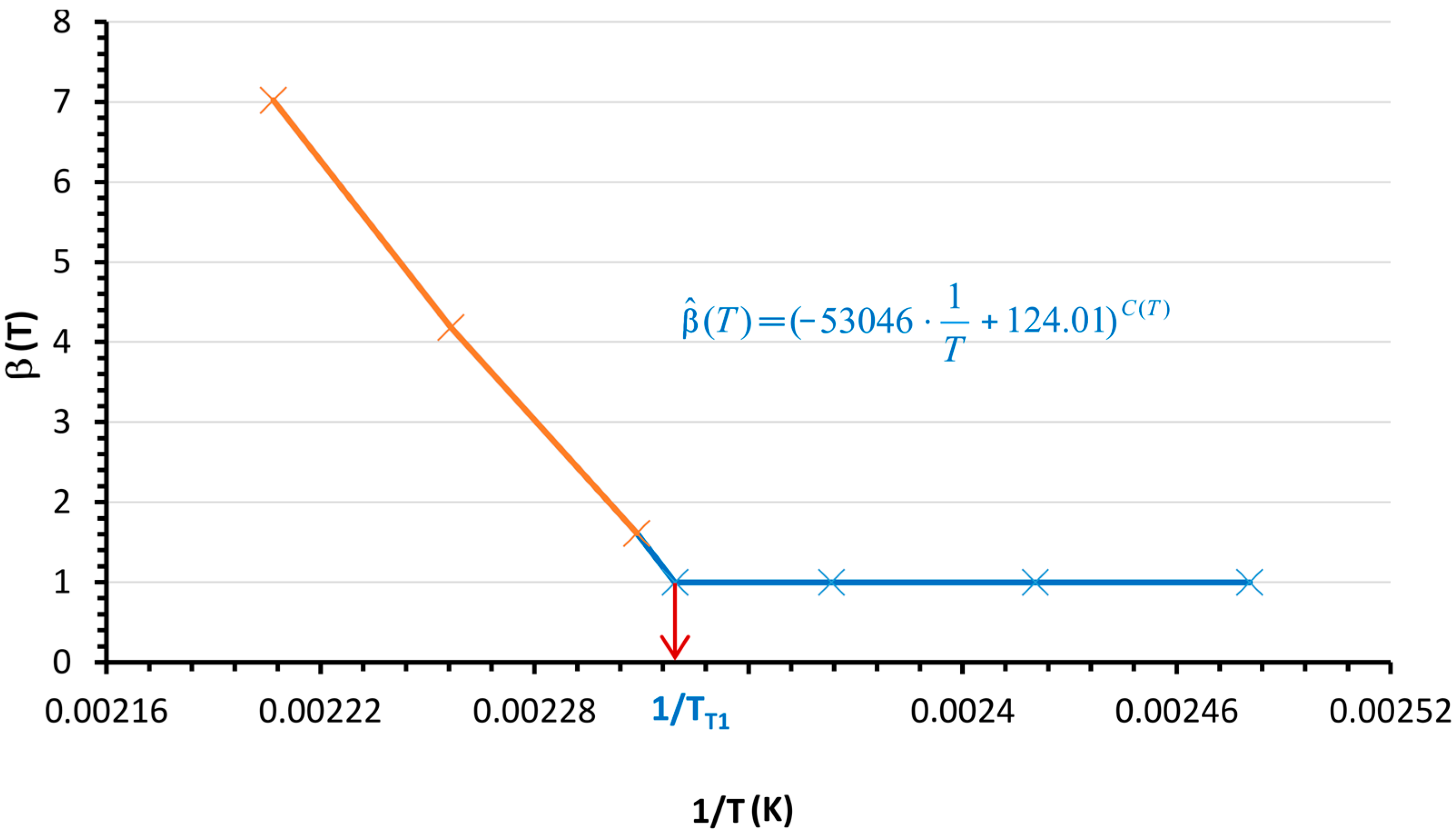
| B(T) and C(T) | functions defining the threshold value of the effect of the degradation factor TT1 depending on the temperature T, for which you apply B(T) = 0; C(T) = 1 for T ∈ 〈TT1,∞) and B(T = 0 for T ∈ (0,TT1). |
| β(T) | function of the shape parameter of Weibull distribution depending on the temperature T (K) |
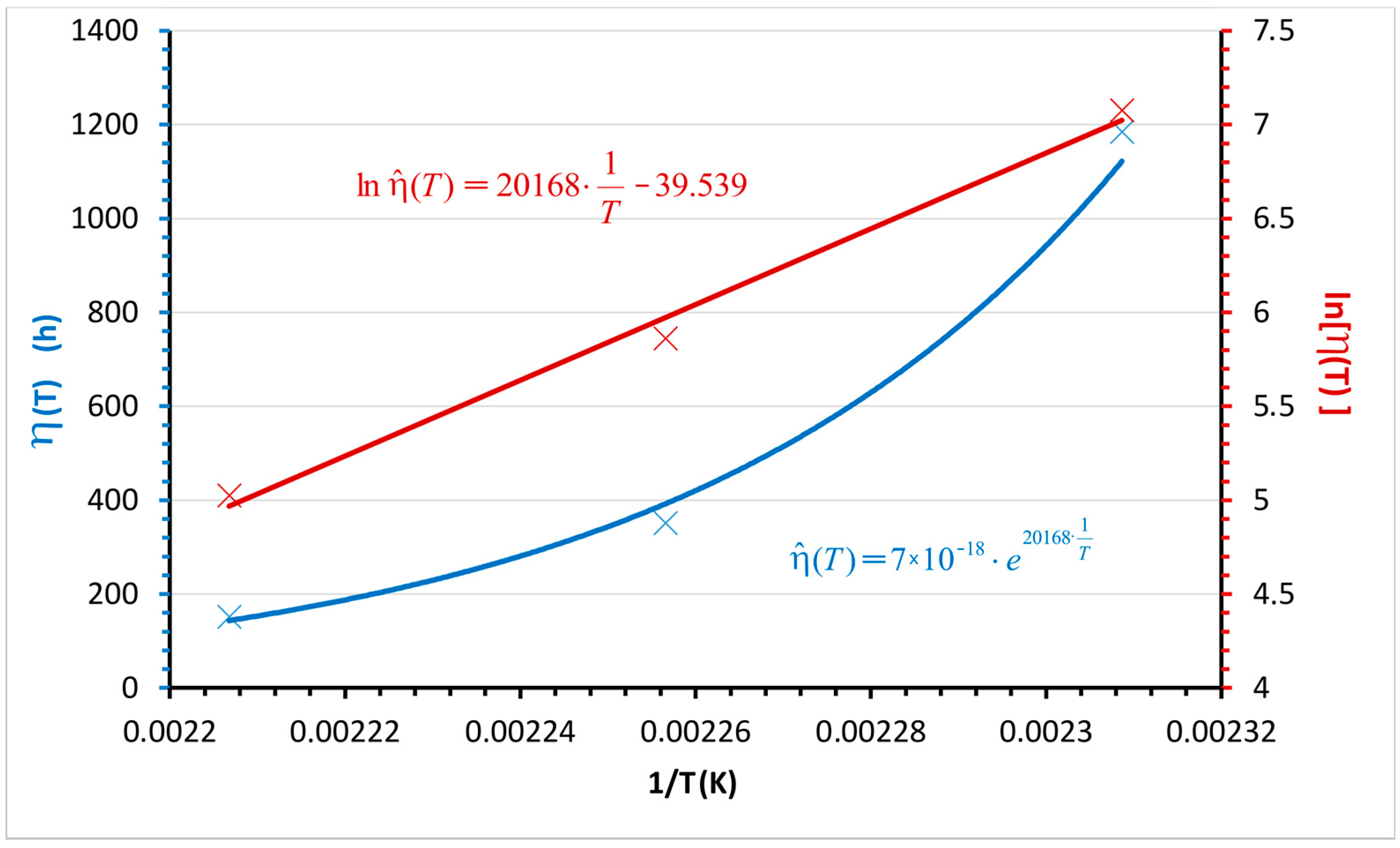
| η(T) (h) | function of the scale parameter of Weibull distribution depending on the temperature T (K) |
| t (h) | time to failure of insulation system |
| F(t,T) | distribution function which depend on time to failure t and temperature T (K) |
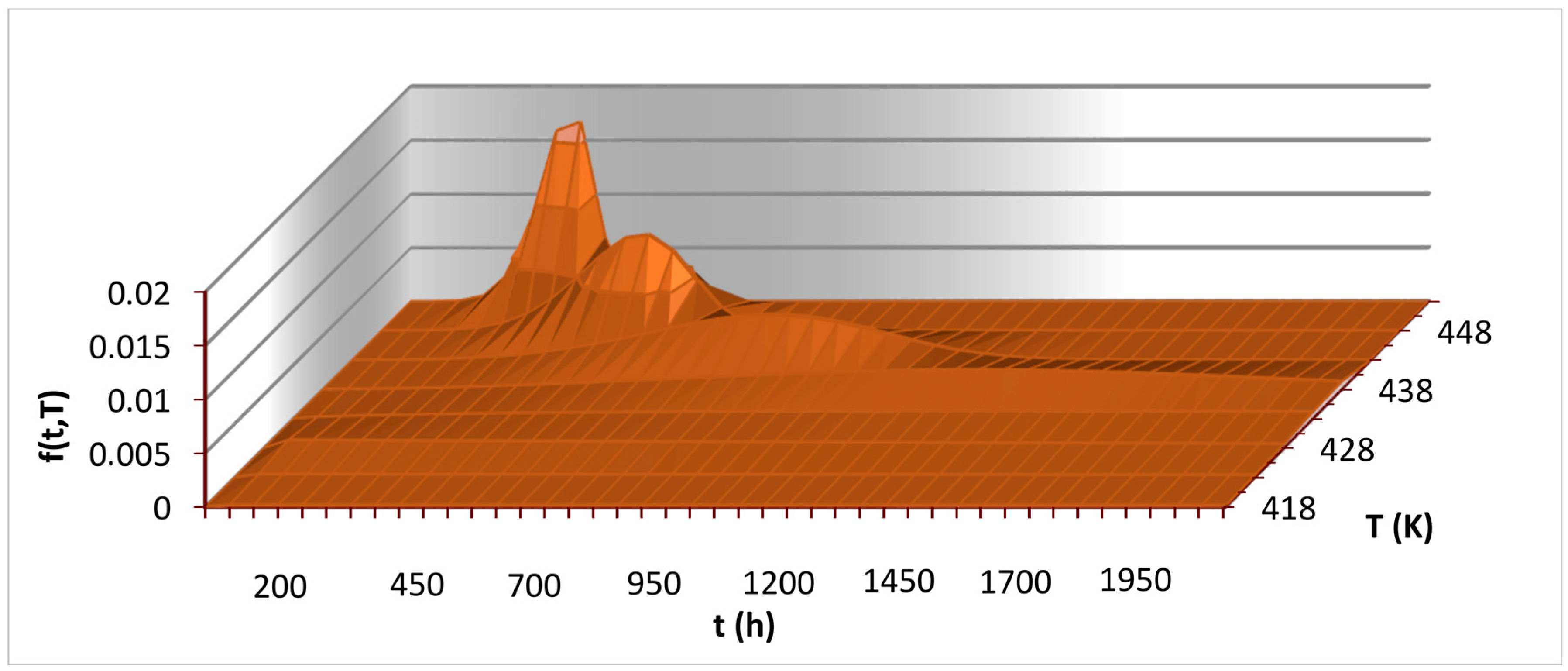
| f(t,T) | probability density which depend on time to failure t (h) and temperature T (K) |
| λ(t,T) | intensity of failures which depend on time to failure t (h) and temperature T (K) |
| (K) | estimation of threshold value of the effect of degradation factor |
| Ep (kV·mm−1) | dielectric strength |
Appendix A.2. Functions B(T) a C(T)
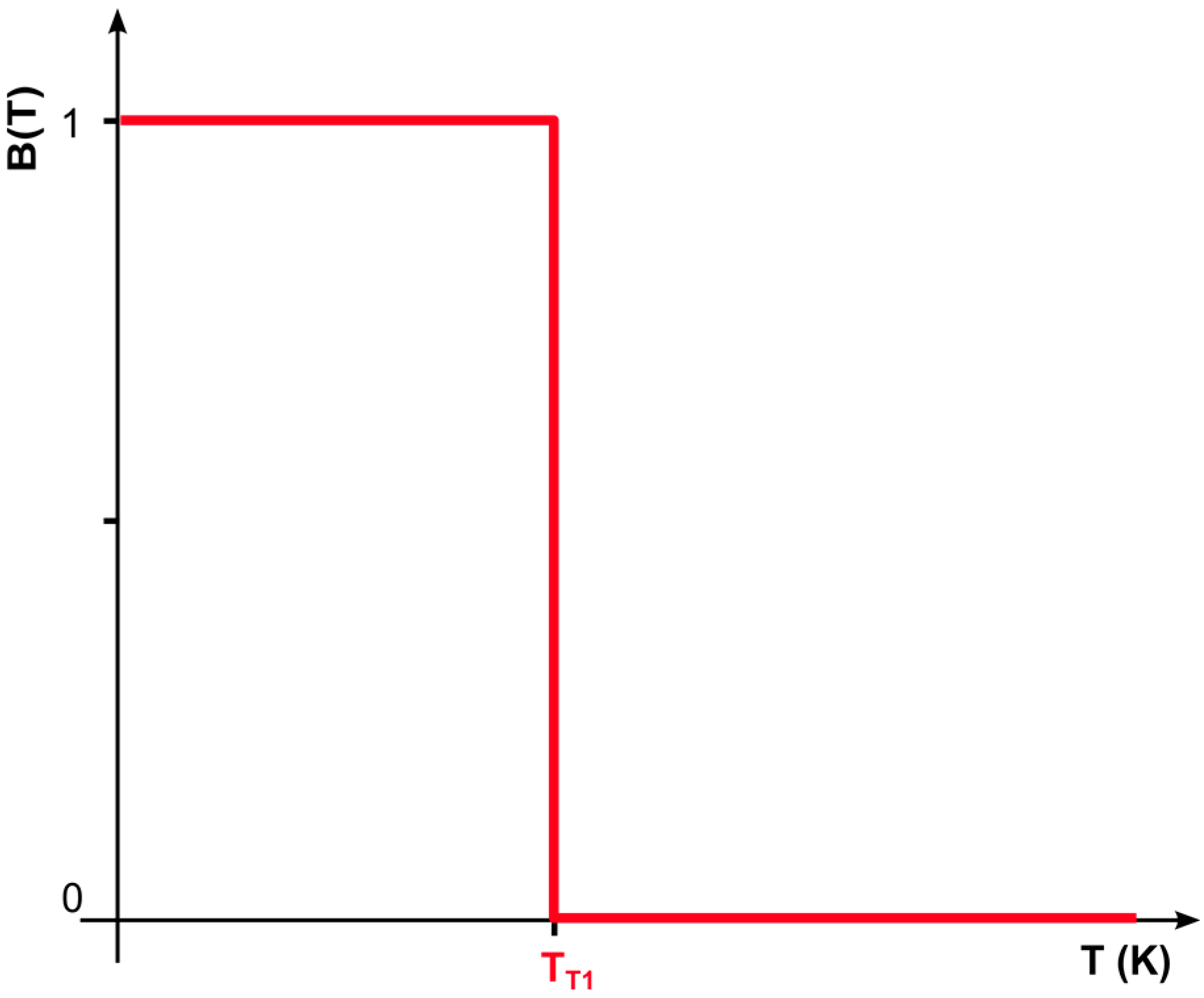
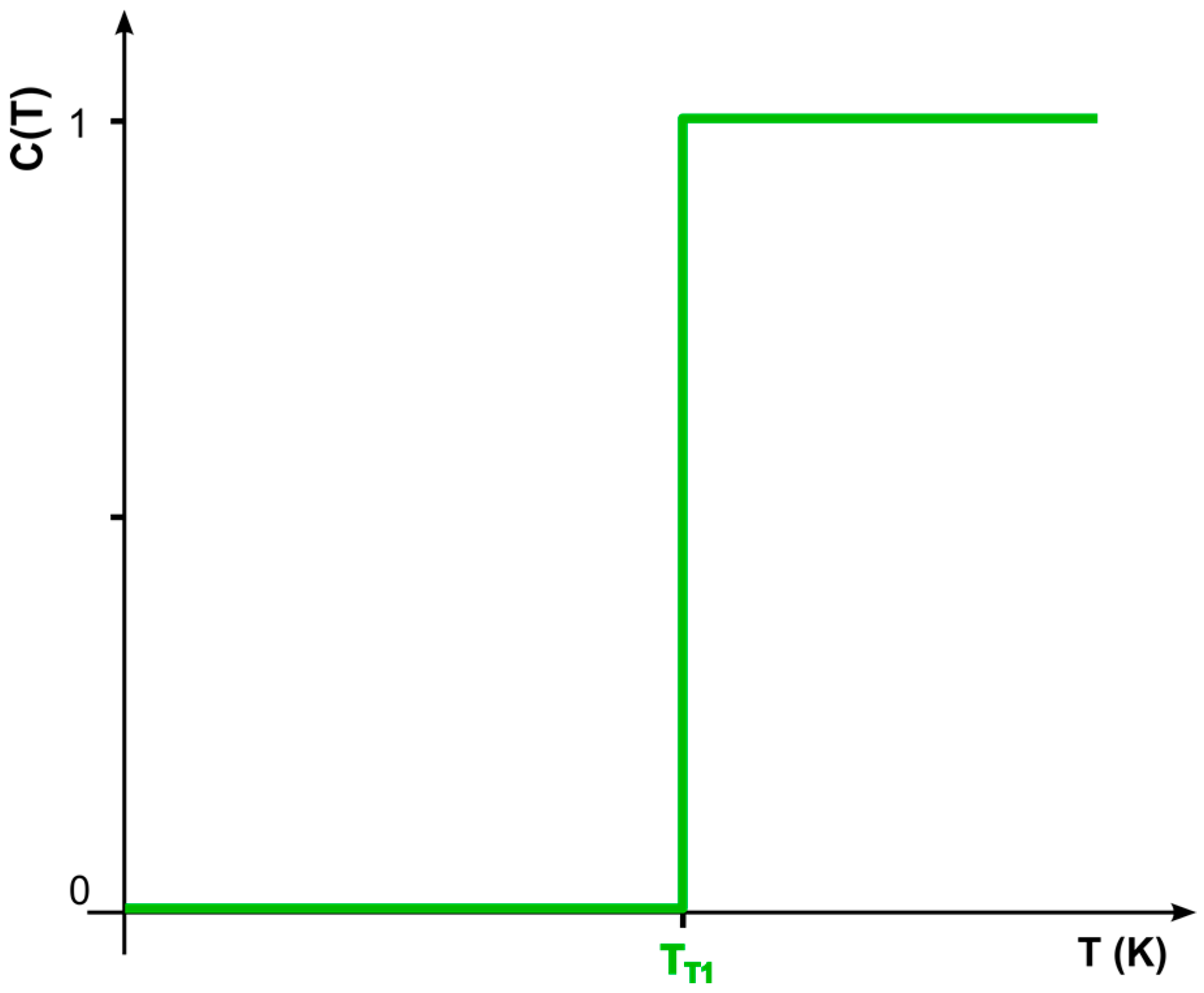
Appendix A.3. The D Constant Defining the Synergistic Effect of Partial Degradation Mechanisms

Appendix A.4. Deriving the Resulting Equation for Estimating the Constant D Defining the Synergistic Effect of the Partial Degradation Mechanisms
References
- Feilat, E.A.; Grzybowski, S.; Knight, P. Accelerated aging of high voltage encapsulated transformers for electronics applications. In Proceedings of the 6th International Conference on Properties and Applications of Dielectric Materials, Xi’an, China, 21–26 June 2000; Volume 1, pp. 209–212. [Google Scholar] [CrossRef]
- Lundgaard, L.E.; Hansen, W.; Linhjell, D.; Painter, T.J. Aging of oil-impregnated paper in power transformers. IEEE Trans. Power Deliv. 2004, 19, 230–239. [Google Scholar] [CrossRef]
- Montanari, G.C.; Simoni, L. Aging phenomenology and modeling. IEEE Trans. Electr. Insul. 1993, 28, 755–776. [Google Scholar] [CrossRef]
- Chinh, D.; Parpal, J.L.; Crine, J.P. Electrical aging of extruded dielectric cables: Review of existing theories and data. IEEE Trans. Dielectr. Electr. Insul. 1996, 3, 237–247. [Google Scholar] [CrossRef]
- Augood, D.R. Dielectric aging—Overview & comment. In Proceedings of the 1978 IEEE International Conference on Electrical Insulation, Philadelphia, PA, USA, 7–9 June 1978; pp. 17–21. [Google Scholar] [CrossRef]
- Whitman, L.C.; Doigan, P. Calculation of life characteristics of insulation. Trans. Am. Inst. Electr. Eng. Part I Commun. Electron. 1954, 73, 193–198. [Google Scholar] [CrossRef]
- Moonesan, M.S.; Jayaram, S.; Cherney, E.; Omranipour, R.; Haq, S.U. Analysis of times-to-failure of various turn insulations of form-wound coils under PWM voltage waveform. In Proceedings of the Electrical Insulation Conference (EIC), Ottawa, ON, Canada, 2–5 June 2013; pp. 187–190. [Google Scholar] [CrossRef]
- Stone, G.C.; Lawless, J.F. The Application of Weibull Statistics to Insulation Aging Tests. IEEE Trans. Electr. Insul. 1979, EI-14, 233–239. [Google Scholar] [CrossRef]
- IEEE. Guide for the Statistical Analysis of Electrical Insulation Voltage Endurance Data; ANSI/IEEE Std 930-1987; The Institute of Electrical and Electronics Engineers, Inc.: New York City, NY, USA, 1987; pp. 1–36. [Google Scholar] [CrossRef]
- Wichmann, A.; Gruenewald, P. Influence of dielectric stress concentration on voltage endurance of epoxy-mica generator insulation. In Proceedings of the 1976 IEEE International Conference on Electrical Insulation, Montreal, QC, Canada, 14–16 June 1976; pp. 88–92. [Google Scholar] [CrossRef]
- Meyer, H. Voltage endurance of electrical insulation. In Proceedings of the 1967 Seventh Electrical Insulation Conference, Chicago, IL, USA, 15–19 October 1967; pp. 268–271. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, T.; Bai, Y.; Ding, X. Wang, Y. Effects of accelerated repetitive impulse voltage aging on performance of model stator insulation of wind turbine generator. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1506–1515. [Google Scholar] [CrossRef]
- Dakin, T.W.; Studniarz, S.A. The Voltage Endurance of Cast Epoxy Resins. In Proceedings of the IEEE International Symposium on Electrical Insulation, Philadelphia, PA, USA, 12–14 June 1978; pp. 216–221. [Google Scholar] [CrossRef]
- Ruijin, L.; Chao, T.; Lijun, Y.; Huanchao, C. Thermal aging studies on cellulose insulation paper of power transformer using AFM. In Proceedings of the 2006 IEEE 8th International Conference on Properties & Applications of Dielectric Materials, Bali, Indonesia, 26–30 June 2006; pp. 722–725. [Google Scholar] [CrossRef]
- Han, S.; Li, Q.; Li, C.; Yan, J. Electrical and mechanical properties of the oil-paper insulation under stress of the hot spot temperature. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 179–185. [Google Scholar] [CrossRef]
- Jandial, A.P.; Spade, R.L. A study of the effects of long term exposure to rated operating temperature upon electrical properties of lead wire insulations. In Proceedings of the 1967 Seventh Electrical Insulation Conference, Chicago, IL, USA, 15–19 October 1967; pp. 226–231. [Google Scholar] [CrossRef]
- Pradhan, A.K.; Chatterjee, B.; Chakravorti, S. Effect of temperature on frequency dependent dielectric parameters of oil-paper insulation under non-sinusoidal excitation. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 653–661. [Google Scholar] [CrossRef]
- Heyda, P.G. Theoretical aspects of mechanical stresses in a paper-lapped cable insulation. Proc. Inst. Electr. Eng. 1967, 114, 1507–1510. [Google Scholar] [CrossRef]
- Wilk, D.J. Radiation effects on epoxy insulation system versus silicone system for rotating equipment applications. In Proceedings of the 1971 EIC 10th Electrical Insulation Conference, Chicago, IL, USA, 20–23 September 1971; pp. 202–204. [Google Scholar] [CrossRef]
- Melcher, J.; Deben, Y.; Arlt, G. Dielectric effects of moisture in polyimide. IEEE Trans. Electr. Insul. 1989, 24, 31–38. [Google Scholar] [CrossRef]
- Stone, G. Electrical Insulation for Rotating Machnies; Wiley: Piscataway, NJ, USA, 2004; ISBN 0-471-44506-1. [Google Scholar]
- Mentlik, V.; Hornak, J.; Trnka, P.; Harvanek, L. Effects of individual chemical cleaning detergents on conditions of winding surface. In Proceedings of the 2016 IEEE International on Dielectrics, Montpellier, France, 3–7 July 2016; pp. 768–771. [Google Scholar] [CrossRef]
- Trnka, P.; Soucek, J.; Hornak, J.; Totzauer, P. EIS aging estimation and threshold values. In Proceedings of the 2016 IEEE International Conference on High Voltage Engineering and Application, Chengdu, China, 19–22 September 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Montanari, G.C.; Cacciari, M. A probabilistic life model for insulating materials showing electrical thresholds. IEEE Trans. Electr. Insul. 1989, 24, 127–134. [Google Scholar] [CrossRef]
- Souček, J.; Trnka, P. A new statistical-physical model to the description of aging of electroinsulating systems. In Proceedings of the 2014 15th International Scientific Conference on Electric Power Engineering, Brno, Czech Republic, 12–14 May 2014; pp. 463–466. [Google Scholar] [CrossRef]
- Crine, J.-P.; Parpal, J.-L.; Dang, C. A new approach to the electric aging of dielectrics. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena, Leesburg, VA, USA, 29 October–2 November 1989; pp. 161–167. [Google Scholar] [CrossRef]
- Dissado, L.A.; Mazzanti, G.; Montanari, G.C. Proposal of a space-charge life model for electrical polymeric insulation aged under AC voltage. In Proceedings of the 1998 IEEE International Symposium on Electrical Insulation, Arlington, VA, USA, 7–10 June 1998; Volume 2, pp. 595–598. [Google Scholar] [CrossRef]
- Dissado, L.A.; Mazzanti, G.; Montanari, G.C. The role of trapped space charges in the electrical aging of insulating materials. IEEE Trans. Dielectr. Electr. Insul. 1997, 4, 496–506. [Google Scholar] [CrossRef]
- Montanari, G.C.; Pattini, G. Thermal Endurance Evaluation of Insulating Materials: A Theoretical and Experimental Analysis. IEEE Trans. Electr. Insul. 1986, EI-21, 69–77. [Google Scholar] [CrossRef]
- Ramteke, P.K.; Ahirwar, A.K.; Shrestha, N.B.; Sanyasi Rao, V.V.S.; Vaze, K.K.; Ghosh, A.K. Thermal ageing predictions of polymeric insulation cables from Arrhenius plot using short-term test values. In Proceedings of the 2010 2nd International Conference on Reliability, Safety and Hazard (ICRESH), Mumbai, India, 14–16 December 2010; pp. 325–328. [Google Scholar] [CrossRef]
- Paloniemi, P. Theory of Equalization of Thermal Ageing Processes of Electrical Insulating Materials in Thermal Endurance Tests II: The Theory with Practical Approximations and Application Principles. IEEE Trans. Electr. Insul. 1981, EI-16, 7–17. [Google Scholar] [CrossRef]
- Montsinger, V.M. Loading Transformers by Temperature. Trans. Am. Inst. Electr. Eng. 1930, 49, 776–790. [Google Scholar] [CrossRef]
- Dakin, T.W. Electrical Insulation Deterioration Treated as a Chemical Rate Phenomenon. AIEE Trans. 1948, 67, 113–122. [Google Scholar] [CrossRef]
- Crine, J.-P.; David, E. Influence of mechanical stresses on some electrical properties of polymers. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena, St. Petersburg, Russia, 27–30 June 2005; pp. 71–74. [Google Scholar] [CrossRef]
- Cygan, P.; Laghari, J.R. A review of electrical and thermal multistress aging models. In Proceedings of the 1990 IEEE International Symposium on Electrical Insulation, Toronto, ON, Canada, 3–6 June 1990; pp. 15–20. [Google Scholar] [CrossRef]
- Gjerde, A.C. Multifactor ageing models—Origin and similarities. IEEE Electr. Insul. Mag. 1997, 13, 6–13. [Google Scholar] [CrossRef]
- Simoni, L. A General Approach to Endurance of Electrical Insulation under Temperature and Voltage. IEEE Trans. Electr. Insul. 1981, 16, 277–289. [Google Scholar] [CrossRef]
- Simoni, L. General Equation of the Decline in the Electric Strength for Combined Thermal and Electrical Stresses. IEEE Trans. Electr. Insul. 1984, 19, 45–52. [Google Scholar] [CrossRef]
- Ramu, T.S. On the Estimation of Life of Power Apparatus Insulation under Combined Electrical and Thermal Stress. IEEE Trans. Dielectr. Electr. Insul. 1985, EI-20, 70–78. [Google Scholar] [CrossRef]
- Fallou, B.; Burguiere, C.; Morel, J.F. First approach on multiple stress accelerated life testing of electrical insulation. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena, Whitehaven, PA, USA, 12–24 October 1979; pp. 621–628. [Google Scholar]
- Crine, J.-P. The compensation law and polymer aging and relaxations. In Proceedings of the Conference on Conduction and Breakdown in Solid Dielectrics, Trondheim, Norway, 3–6 June 1989; pp. 321–325. [Google Scholar] [CrossRef]
- Grzybowski, S.; Kota, N. Lifetime characteristics of magnet wires under multistress conditions. In Proceedings of the Conference on Electrical Insulation and Dielectric Phenomena, St. Petersburg, Russia, 27–30 June 2005; pp. 605–608. [Google Scholar] [CrossRef]
- Weibull Analysis; IEC 61649:2008; International Electrotechnical Commission: Geneva, Switzerland, 2008.
- Equipment Reliability Testing—Part 4: Statistical Procedures for Exponential Distribution—Point Estimates, Confidence Intervals, Prediction Intervals and Tolerance Intervals; IEC 60605-4:2001; International Electrotechnical Commission: Geneva, Switzerland, 2001.
- Kacecioglu, D. Reliability Engineering Handbook; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991; ISBN 978-0137723027. [Google Scholar]
- Gubner, J.A. Probability and Random Processes for Electrical and Computer Engineers; Cambridge University Press: Cambridge, UK, 2006; ISBN 978-0521864701. [Google Scholar]
- Lewis, P.A.W.; Orav, E.J. Simulation Methodology for Statisticians, Operations Analysts, and Engineers; Wadsworth & Brooks/Cole: Pacific Grove, CA, USA, 1989; ISBN 0534094503. [Google Scholar]
- Brown, R.E. Electric Power Distribution Reliability, 2nd ed.; Marcel Dekker: New York, NY, USA, 2009; ISBN 9780849375675. [Google Scholar]
- Electrical Insulation—Thermal Evaluation and Designation; IEC 60085:2007; International Electrotechnical Commission: Geneva, Switzerland, 2007.
- Badicu, L.V.; Dumitran, L.M.; Notingher, P.V.; Setnescu, R.; Setnescu, T. Mineral oil lifetime estimation using activation energy. In Proceedings of the 2011 IEEE International Conference on Dielectric Liquids, Trondheim, Norway, 26–30 June 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Li, Ch.; Tang, T.B. Isoconversion method for kinetic analysis of solid-state reactions from dynamic thermoanalytical data. J. Mater. Sci. 1999, 34, 3467–3470. [Google Scholar] [CrossRef]
- Electric Strength of Insulating Materials—Test Methods—Part 1: Tests at Power Frequencies; IEC 60243-1:2013; International Electrotechnical Commission: Geneva, Switzerland, 2013.
- Liu, H.; Wang, Y.; Yang, Y.; Liao, R.; Geng, Y.; Zhou, L. A Failure Probability Calculation Method for Power Equipment Based on Multi-Characteristic Parameters. Energies 2017, 10, 704. [Google Scholar] [CrossRef]
- Zhuang, Q.; Morshuis, P.H.F.; Chen, X.; Meijer, S.; Smit, J.J.; Xu, Z. Life prediction for epoxy resin insulated transformer windings through accelerated aging tests. In Proceedings of the 2010 10th IEEE International Conference on Solid Dielectrics, Potsdam, Germany, 4–9 July 2010; pp. 1–4. [Google Scholar] [CrossRef]

| i | Interval of Ti (K) | TTi (K) | (h) | (J∙mol−1) | Ki |
|---|---|---|---|---|---|
| 1 | |||||
| 2 | |||||
| 3 | |||||
| n | |||||
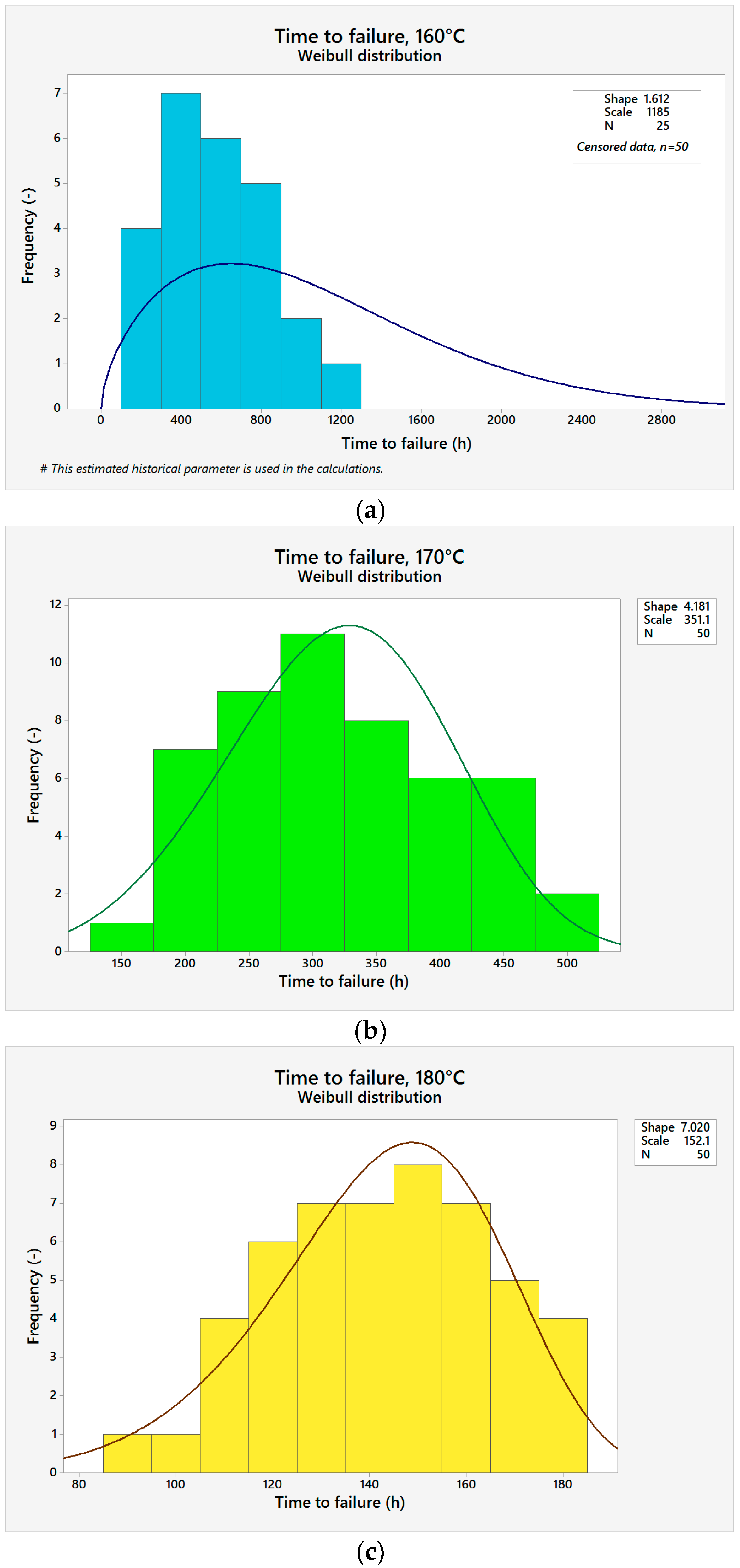
| Temperature (°C) | MLE | MLE (h) | Confidence Interval | Median Me (h) | MTTF (h) |
|---|---|---|---|---|---|
| 160 | 1.612 | 1184.643 | 0.95 | 944 | 1061.412 |
| 170 | 4.181 | 351.152 | 0.95 | 310 | 327.013 |
| 180 | 7.020 | 152.119 | 0.95 | 141 | 144.751 |
| Description | Function/Value of Parameter |
|---|---|
| Course estimation of | |
| Course estimation | |
| Threshold value (K) | 431.23 |
| Reciprocal value of pre-exponential factor α (h) | 7 × 10−18 |
| Activation energy Ea1 (J·mol−1) | 167,686.27 |
| Function for defining the threshold value of degradation factor C(T) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souček, J.; Trnka, P.; Hornak, J. Proposal of Physical-Statistical Model of Thermal Aging Respecting Threshold Value. Energies 2017, 10, 1120. https://doi.org/10.3390/en10081120
Souček J, Trnka P, Hornak J. Proposal of Physical-Statistical Model of Thermal Aging Respecting Threshold Value. Energies. 2017; 10(8):1120. https://doi.org/10.3390/en10081120
Chicago/Turabian StyleSouček, Jakub, Pavel Trnka, and Jaroslav Hornak. 2017. "Proposal of Physical-Statistical Model of Thermal Aging Respecting Threshold Value" Energies 10, no. 8: 1120. https://doi.org/10.3390/en10081120
APA StyleSouček, J., Trnka, P., & Hornak, J. (2017). Proposal of Physical-Statistical Model of Thermal Aging Respecting Threshold Value. Energies, 10(8), 1120. https://doi.org/10.3390/en10081120







