Optimal Dynamic Analysis of Electrical/Electronic Components in Wind Turbines
Abstract
1. Introduction
- Type A: Constant speed.
- -
- A0: WTs use passive stall control;
- -
- A1: WTs employ active stall control;
- -
- A2: WTs use a pitch control system, the most advanced technology used in larger WTs;
- Type B: Limited variable speed;
- Type C: Variable speed with partial-scale frequency converter. With DFIG (doubly fed induction generator);
- Type D: Variable speed with full-scale frequency converter:
- -
- DD: Direct-drive: Gearless and variable speed with full-scale frequency converter:
- o
- DDE: This type uses an electrically excited synchronous generator.
- o
- DDP: This group uses a permanent magnet synchronous generator, PMSG;
- -
- DI: Indirect-drive: Variable speed indirect drive with a full-scale power converter:
- o
- DI1P: It is the only configuration with a single-stage gearbox with PMSG;
- o
- DI3W: Three stages gearbox with a wound rotor synchronous generator;
- o
- DI3P: Three stages gearbox with PMSG;
- o
- DI3S: Three stages gearbox with squirrel-cage induction generator.
- Statistical methods.
- Trend analysis.
- Filtering methods.
- Time-domain analysis.
- Cepstrum analysis.
- Time synchronous averaging
- Fast-Fourier transform.
- Amplitude demodulation.
- Order analysis.
- Wavelet transforms.
- Hidden Markov models.
- Novel approaches.
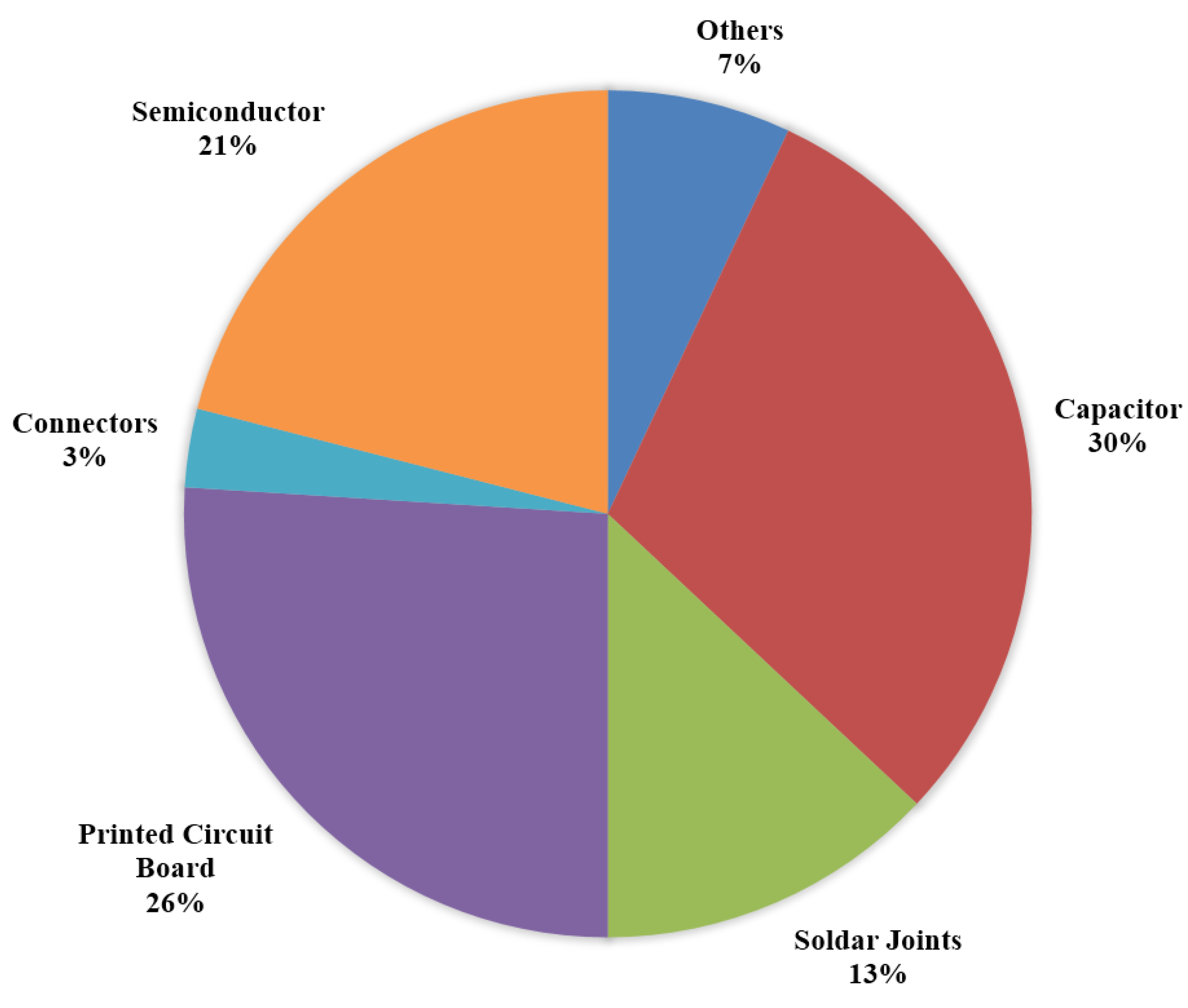
2. Electrical/Electronic Failures Analysis
- Calibration error
- Connection failure
- Electrical overload
- Electrical short
- Insulation failure
- Lightning strike
- Loss of power input
- Conducting debris
- Software design fault
- Electrical insulation
- Electrical failure
- Output inaccuracy
- Software fault
- Intermittent output
3. Reliability Analysis
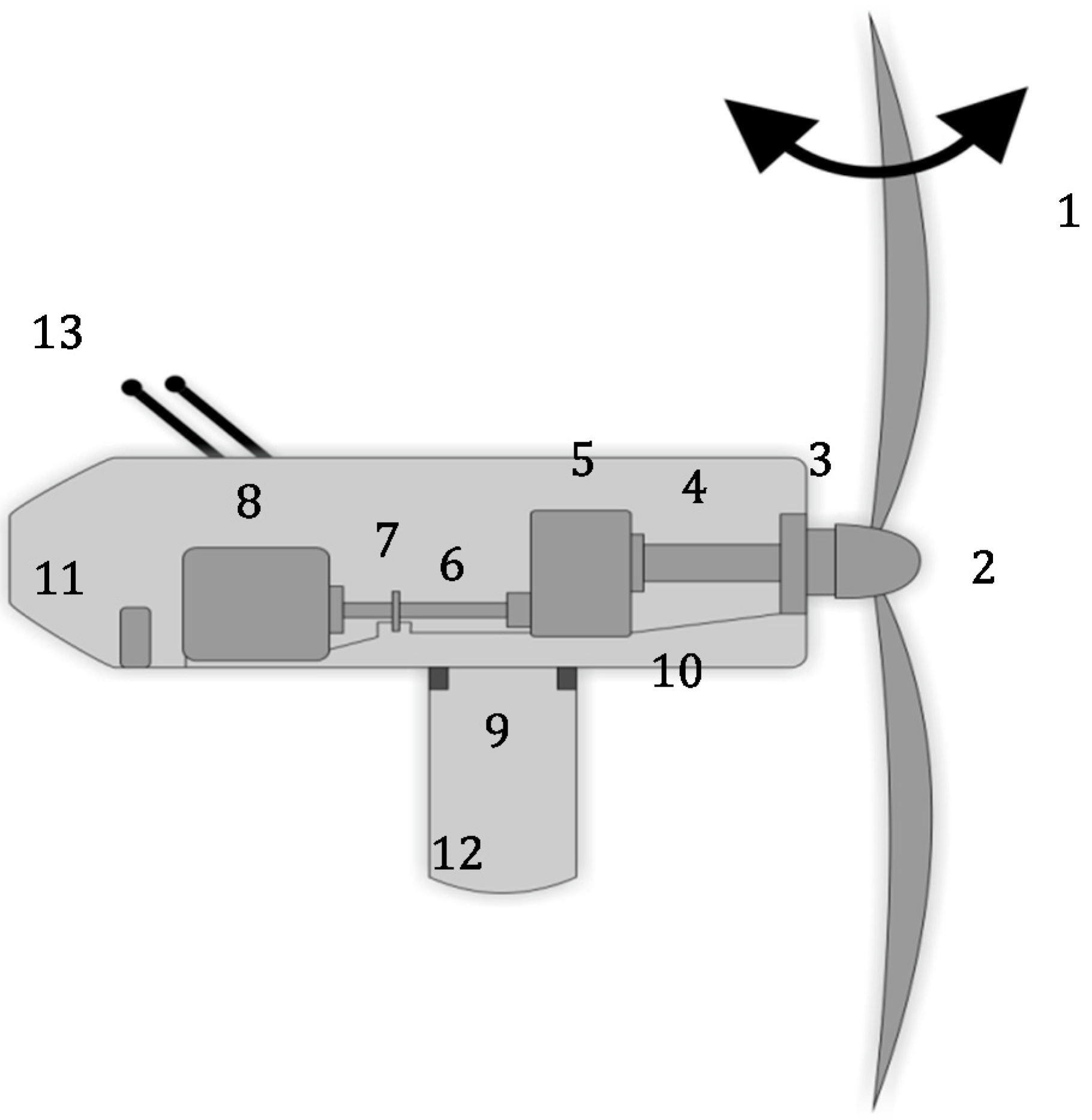
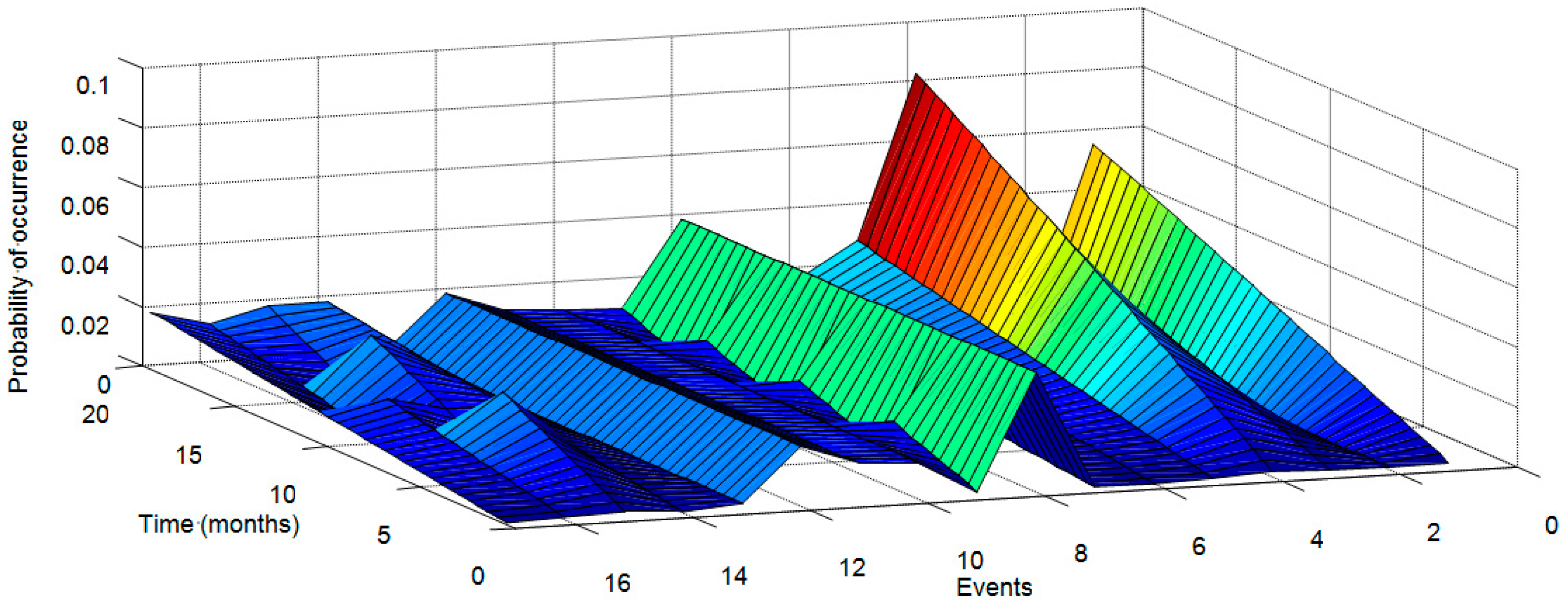
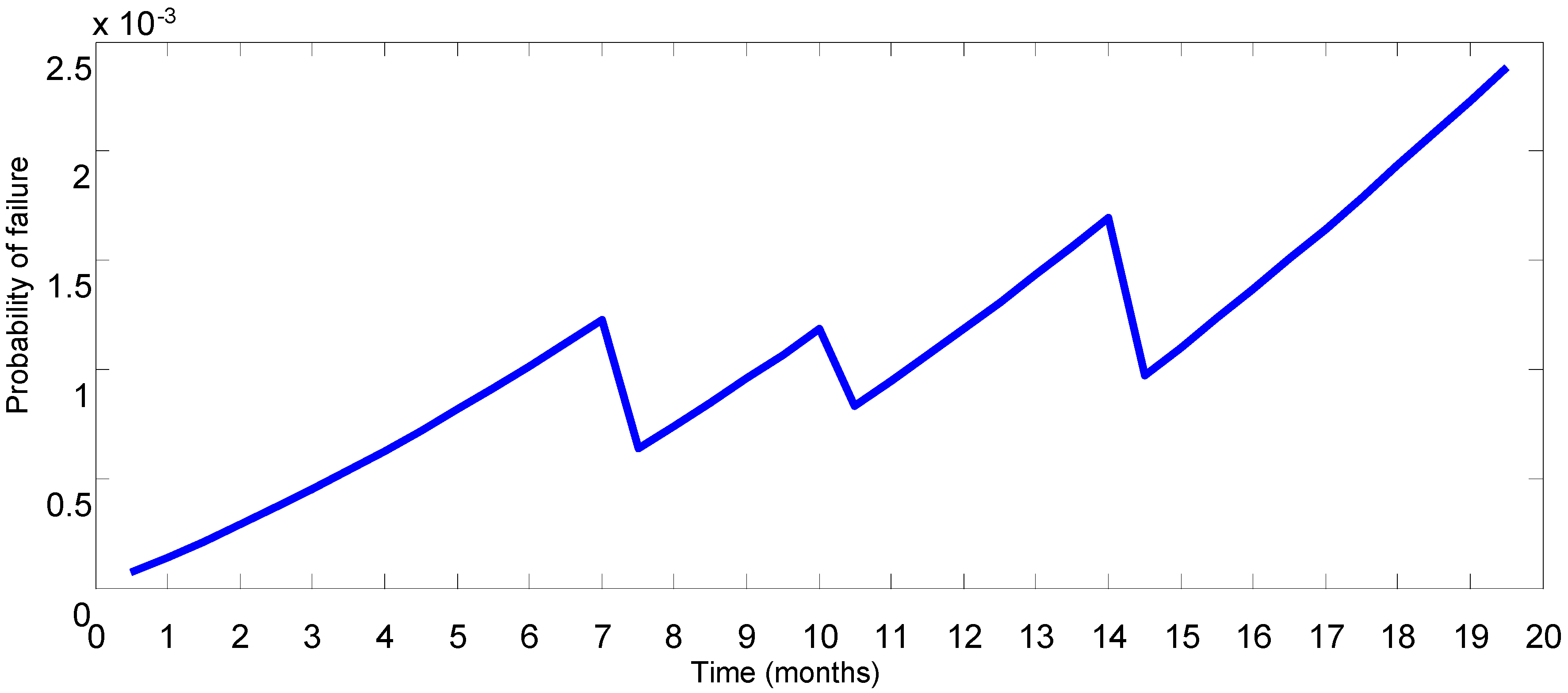
4. FT Dynamic Analysis for Converter, Generator, Electrical and Electronic Components
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BDD | Binary decision diagram |
| BFS | Breadth-first search |
| CMS | Condition monitoring system |
| CS | Cut-set |
| DFIG | Doubly fed induction generator |
| DFS | Depth-first search |
| FT | Fault tree |
| GWEC | Global wind energy council |
| IGBT | Insulated gate bipolar transistor |
| IM | Importance measure |
| O&M | Operation and maintenance |
| PFE | power feed equipment |
| PMSG | permanent magnet synchronous generator |
| PWM | pulse width modulation |
| SCADA | Supervisory control and data acquisition system |
| TDLR | Top-Down-Left-Right |
| WT | Wind turbine |
| 3L-NPC-BTB | Three-Level Neutral-Point Diode Clamped Back-To-Back |
| 2L-BTB | Two-level back-to-back voltage source converter |
| Formula Expressions | |
| CS | Cut-set |
| Qsys | Unavailability of the system |
| Probability of the event ‘ i’ over time | |
| probability rising velocity | |
| period size | |
| Constant | |
References
- Global Wind Energy Council (GWEC). Global Wind Report: Annual Market Update 2016. Available online: www.gwec.net (accessed on June 2017).
- Pérez, J.M.P.; Márquez, F.P.G.; Hernández, D.R. Economic viability analysis for icing blades detection in wind turbines. J. Clean. Prod. 2016, 135, 1150–1160. [Google Scholar] [CrossRef]
- Walford, C. Wind Turbine Reliability: Understanding and Minimizing Wind Turbine Operation and Maintenance Costs; Sandia Report, SAND2006-1100; Sandia National Laboratories: Albuquerque, NM, USA; Livermore, CA, USA, 2006. [Google Scholar]
- Novaes, G.; Araújoa, A.M.; Carvallo, P.A. Prognostic techniques applied to maintenance of wind turbines: A concise and specific review. Renew. Sustain. Energy Rev. 2017, in press. [Google Scholar]
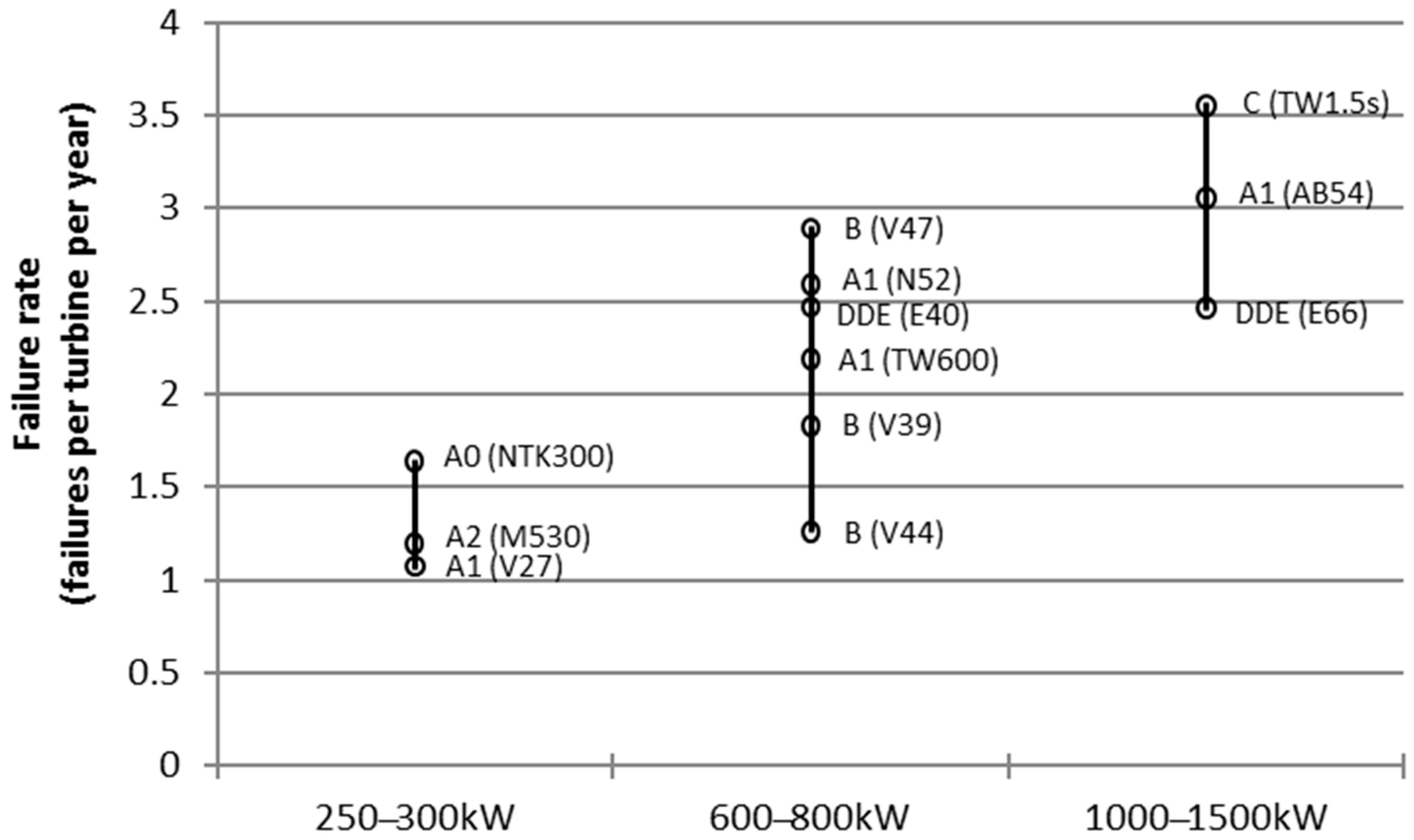
- Tavner, P.J.; van Bussel, G.J.W.; Koutoulakos, E. Reliability of Different Wind Turbine Concepts with Relevance to Offshore Application. In Proceedings of the European Wind Energy Conference, Brussels, Belgium, 31 March–3 April 2008. [Google Scholar]
- Anonymous. Managing the Wind: Reducing Kilowatt-Hour Costs with Condition Monitoring. Refocus 2005, 6, 48–51. [Google Scholar]
- Márquez, F.P.G.; Muñoz, J.M.C. A pattern recognition and data analysis method for maintenance management. Int. J. Syst. Sci. 2012, 43, 1014–1028. [Google Scholar] [CrossRef]
- Munoz, J.C.; Márquez, F.G.; Papaelias, M. Railroad inspection based on ACFM employing a non-uniform B-spline approach. Mech. Syst. Sign. Process. 2013, 40, 605–617. [Google Scholar] [CrossRef]
- Pliego, A.; Garcia, F.P.; Pinar, J.M. Optimal Maintenance Management of Offshore Wind Farms. Energies 2016, 9, 46. [Google Scholar] [CrossRef]
- De Novaes Pires, G.; Alencar, E.; Kraj, A. Remote Conditioning Monitoring System for a Hybrid Wind Diesel System-Application at Fernando de Naronha Island, Brasil. Available online: http://www.ontario-sea.org (accessed on 19 July 2010).
- Polinder, H.; Bang, D.J.; Li, H.; Chen, Z. Concept Report on Generator Topologies, Mechanical and Electromagnetic Optimization. Proj. UpWind 2007. [Google Scholar]
- Hansen, A.D.; Lov, F.; Blaabjerg, F.; Hansen, L.H. Review of contemporary wind turbine concepts and their market penetration. Wind Eng. 2004, 28, 247–263. [Google Scholar] [CrossRef]
- Hansen, A.D.; Hansen, L.H. Wind turbine concept market penetration over 10 years (1995–2004). Wind Energy 2007, 10, 81–97. [Google Scholar] [CrossRef]
- Li, H.; Chen, Z. Overview of different wind generator systems and their comparisons. Renew. Power Gener. IET 2008, 2, 123–138. [Google Scholar] [CrossRef]
- Argyriadis, K.; Rademakers, L.; Capellaro, K.; Ristow, M.; Hauptmann, S.; Kochmann, M.; Mouzakis, F. PROTEST (PROcedures for TESTing and measuring wind energy systems). In Deliverable D1: State-of-the-Art-Report; FP7-ENERGY-2007-1-RTD; University of Stuttgart: Stuttgart, Germany, 2009. [Google Scholar]
- Igarashi, T.; Hamada, H. Studies on the Vibration and Sound of Defective Roller Bearings (First report: Vibration of ball bearing with one defect). Bull. JSME 1982, 25, 994–1001. [Google Scholar] [CrossRef]
- Igarashi, T.; Yabe, S. Studies on the Vibration and Sound of Defective Roller Bearings (First report: Sound of ball bearing with one defect). Bull. JSME 1983, 26, 1791–1798. [Google Scholar] [CrossRef]
- Gómez, C.Q.; Ruiz, R.; Trapero, J.R.; Marquez, F.P.G. A novel approach to fault detection and diagnosis on wind turbines. Glob. NEST J. 2014, 16, 1029–1037. [Google Scholar]
- Nabati, E.G.; Thoben, K.D. Big Data Analytics in the Maintenance of Off-Shore Wind Turbines: A Study on Data Characteristics. In Dynamics in Logistics; Springer: Basel, Switzerland, 2017; pp. 131–140. [Google Scholar]
- Gómez, C.Q.; Marquez, F.P.G. A New Fault Location Approach for Acoustic Emission Techniques in Wind Turbines. Energies 2016, 9, 40. [Google Scholar] [CrossRef]
- Pedregal, D.J.; Garcia, F.P.; Roberts, C. An Algorithmic Approach for Maintenance Management. Ann. Oper. Res. 2009, 166, 109–124. [Google Scholar] [CrossRef]
- Marquez, F.P.G.; Pliego, A.; Lorente, J.; Trapero, J. A new ranking approach for Decision Making in Maintenance Management. In Proceedings of the Seventh International Conference on Management Science and Engineering Management, Philadelphia, PA, USA, 7–9 November 2013; Lecture Notes in Electrical Engineering. Springer: Berlin, Germany; pp. 27–38. [Google Scholar]
- Marquez, F.P.G.; Roberts, C.; Tobias, A. Railway Point Mechanisms: Condition Monitoring and Fault Detection. Proc. Inst. Mech. Eng. Part F 2010, 224, 35–44. [Google Scholar] [CrossRef]
- Marquez, F.P.G.; Pedregal, D.J.; Roberts, C. Time Series Methods Applied to Failure Prediction and Detection. Reliab. Eng. Syst. Saf. 2010, 95, 698–703. [Google Scholar]
- Ruiz, R.; Garcia, F.P.; Dimlaye, V. Maintenance management of wind turbines structures via MFCs and wavelet transforms. Renew. Sustain. Energy Rev. 2015, 48, 472–482. [Google Scholar]
- Levitin, G. Genetic Algorithms in Reliability Engineering. Reliab. Eng. Syst. Saf. 2006, 91, 975–976. [Google Scholar] [CrossRef]
- Development and Demonstration of a Novel Integrated Condition Monitoring System for Wind Turbines, NIMO Project. (NIMO, Ref.:FP7-ENERGY-2008-TREN-1: 239462). Available online: www.nimoproject.eu (accessed on 30 January 2012).
- Demonstration of Methods and Tools for the Optimisation of Operational Reliability of Large-Scale Industrial Wind Turbines, OPTIMUS Project. (OPTIMUS, Ref.: FP-7-Energy-2012-TREN-1: 322430). Available online: www.optimusproject.eu (accessed on 25 February 2014).
- McMillan, D.; Ault, G. Specification of reliability benchmarks for offshore wind farms. In Proceedings of the European Safety and Reliability, Valencia, Spain, 22–25 September 2008; CRC Press: Cleveland, OH, USA, 2008; pp. 22–25. [Google Scholar]
- Lu, B.; Li, Y.; Wu, X.; Yang, Z. A Review of Recent Advances in WT Condition Monitoring and Fault Diagnosis. In Proceedings of the Power Electronics and Machines in Wind Applications, Lincoln, NE, USA, 24–26 June 2009. [Google Scholar]
- Ciang, C.C.; Lee, J.R.; Bang, H.-J. Structural health monitoring for a WT system: A review of damage detection methods. Meas. Sci. Technol. 2008, 19, 22. [Google Scholar] [CrossRef]
- Hansena, D.; Michalke, G. Fault ride-through capability of DFIG wind turbines. Renew. Energy 2007, 32, 1594–1610. [Google Scholar] [CrossRef]
- Douglas, H.; Pillay, P.; Ziarani, A. Broken rotor bar detection in induction machines with transient operating speeds. IEEE Trans. Energy Convers. 2005, 20, 135–141. [Google Scholar] [CrossRef]
- Fischer, K.; Besnard, F.; Bertling, L. A Limited-Scope Reliability-Centred Maintenance Analysis of Wind Turbines. In Proceedings of the European Wind Energy Conference EWEA, Brussels, Belgium, 14–17 March 2011; pp. 89–93. [Google Scholar]
- Popa, L.M.; Jensen, B.B.; Ritchie, E.; Boldea, I. Condition monitoring of wind generators. In Proceedings of the Industry Applications Conference, 38th IAS Annual Meeting, Salt Lake City, UT, USA, 12–16 October 2003; pp. 1839–1846. [Google Scholar]
- Liu, W.; Tang, B.; Jiang, Y. Status and problems of WT structural health monitoring techniques in China. Renew. Energy 2010, 35, 1414–1418. [Google Scholar] [CrossRef]
- Wang, H.; Ma, K.; Blaabjerg, F. Design for reliability of power electronic systems. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 33–44. [Google Scholar]
- RELIAWIND Project. European Union’s Seventh Framework Programme for RTD (FP7). Available online: http://www.reliawind.eu/ (accessed on January 2014).
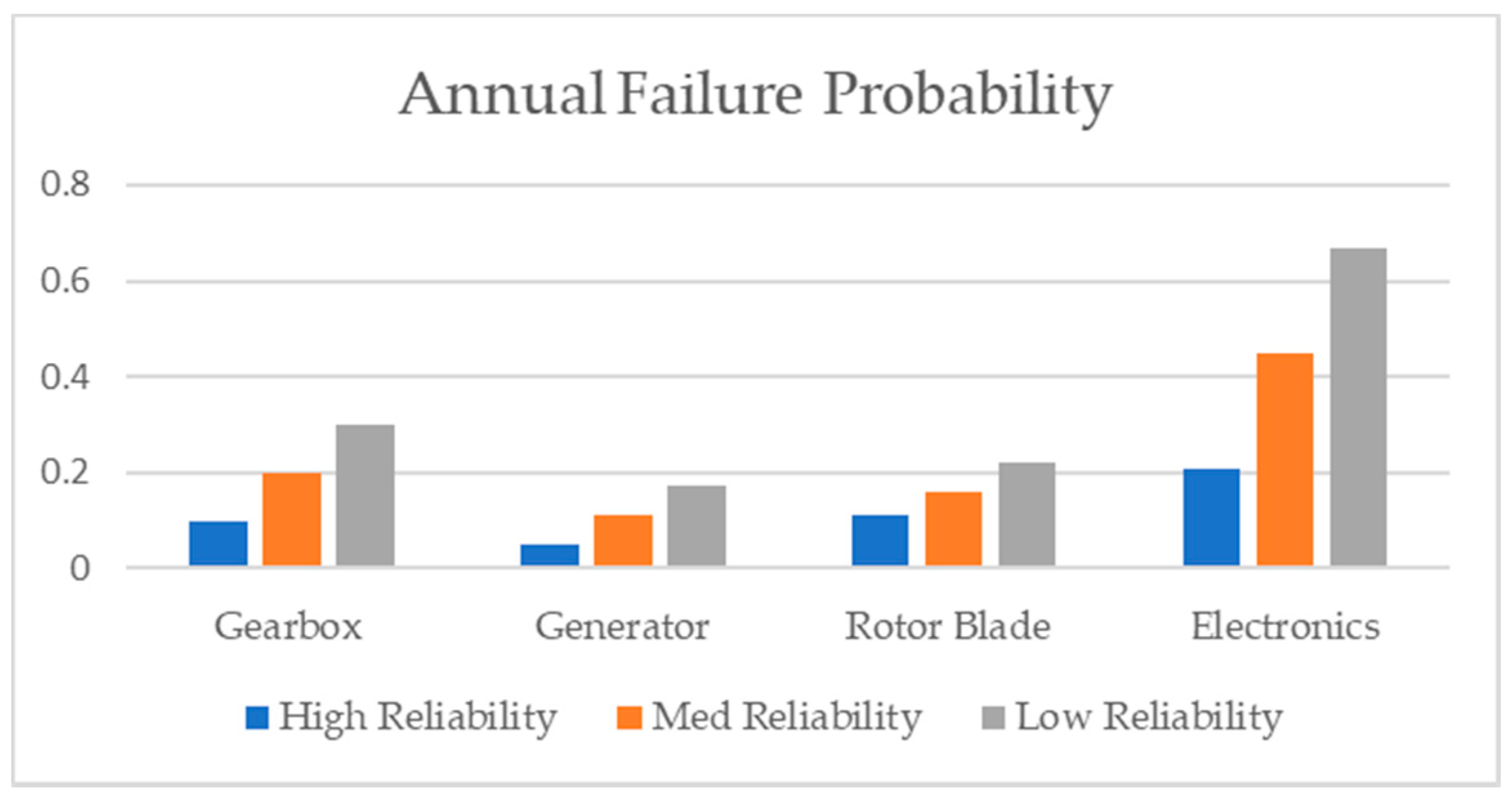
- Arabian-Hoseynabadi, H.; Oraee, H.; Tavner, P.J. Failure Modes and Effects Analysis (FMEA) for Wind Turbines. Int. J. Electr. Power Energy Syst. 2010, 32, 817–824. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. 2005–2008 Wind Turbines—Part 1: Design Requirements, 3rd ed.; IEC 61400-1; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- Schoen, R.R.; Lin, B.K.; Habetler, T.G.; Schlag, J.H.; Farag, S. An Unsupervised, On-Line System for Induction Motor Fault Detection Using Stator Current Monitoring. IEEE Trans. Ind. Appl. 1995, 31, 1280–1286. [Google Scholar] [CrossRef]
- Entezami, M.; Hillmansen, S.; Weston, P.; Papaelias, M. Fault detection and diagnosis within a wind turbine mechanical braking system using condition monitoring. Renew. Energy 2012, 47, 175–182. [Google Scholar] [CrossRef]
- Seo, D.C.; Lee, J.J. Damage detection of CFRP laminates using electrical resistance measurement and neural network. Compos. Struct. 1999, 47, 525–530. [Google Scholar] [CrossRef]
- Smith, B.M. Condition Monitoring by Thermography. NDT Int. 1978, 11, 121–122. [Google Scholar] [CrossRef]
- Gómez, C.Q.; Garcia, F.P.; Sanchez, J.M. Ice detection using thermal infrared radiometry on wind turbine blades. Measurement 2016, 93, 157–163. [Google Scholar] [CrossRef]
- Rumsey, M.A.; Musial, W. Application of Infrared Thermography Nondestructive Testing during Wind Turbine Blade Tests. J. Sol. Energy Eng. 2001, 123, 271. [Google Scholar] [CrossRef]
- Doliński, L.; Krawczuk, M. Damage detection in turbine wind blades by vibration based methods. In Proceedings of the 7th International Conference on Modern Practice in Stress and Vibration Analysis, Cambridge, UK, 8–10 September 2009. [Google Scholar]
- Blaabjerg, F.; Liserre, M.; Ma, K. Power electronics converters for wind turbine systems. IEEE Trans. Ind. Appl. 2012, 48, 708–719. [Google Scholar] [CrossRef]
- Alrifai, M.; Zribi, M.; Rayan, M. Feedback Linearization Controller for a Wind Energy Power System. Energies 2016, 9, 771. [Google Scholar] [CrossRef]
- Xu, P.; Shi, K.; Bu, F.; Zhao, D.; Fang, Z.; Liu, R.; Zhu, Y. A Vertical-Axis Off-Grid Squirrel-Cage Induction Generator Wind Power System. Energies 2016, 9, 822. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, T.; Ding, Z.; Li, C. The study of fuzzy proportional integral controllers based on improved particle swarm optimization for permanent magnet direct drive wind turbine converters. Energies 2016, 9, 343. [Google Scholar] [CrossRef]
- Masahiro, F.; Hisanori, F.; Bobuaki, K. Evaluation and Improvements of Boolean Comparison. In Method Based on Binary Decision Diagrams; Fujitsu Laboratories LTD: Hayes, UK, 1988. [Google Scholar]
- Lee, C.Y. Representation of switching circuits by binary-decision programs. Bell Syst. Tech. J. 1959, 38, 985–999. [Google Scholar] [CrossRef]
- Moret, B.M.E. Decision trees and diagrams. ACM Comput. Surv. 1982, 14, 413–416. [Google Scholar] [CrossRef]
- Pliego, A.; García, F.P.; Lev, B. Optimal decision-making via binary decision diagrams for investments under a risky environment. Int. J. Prod. Res. 2017, 55, 1–16. [Google Scholar]
- Stol, K.A. Disturbance tracking control and blade load mitigation for variable speed wind turbines. J. Sol. Energy Eng. 2003, 125, 396–401. [Google Scholar] [CrossRef]
- Bartlett, L.M. Progression of the Binary Decision Diagram Conversion Methods. In Proceedings of the 21st International System Safety Conference, Ottawa, ON, Canada, 4–8 August 2003; pp. 116–125. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 2nd ed.; Section 22.3: Depth-First Search; MIT Press: Cambridge, MA, USA; McGraw-Hill: New York, NY, USA, 2001; pp. 540–549. ISBN 0-262-03293-7. [Google Scholar]
- Jensen, R.; Veloso, M. OBDD-Based Universal Planning for Synchronized Agents in Non-Deterministic Domains. J. Artif. Intell. Res. 2000, 13, 189–226. [Google Scholar]
- Malik, S.; Wang, A.R.; Brayton, R.K.; Vincentelli, A.S. Logic Verification using Binary Decision Diagrams in Logic Synthesis Environment. In Proceedings of the IEEE International Conference on Computer Aided Design, ICCAD’88, Santa Clara, CA, USA, 7–10 November 1988; pp. 6–9. [Google Scholar]
- Xie, M.; Tan, K.C.; Goh, K.H.; Huang, X.R. Optimum Prioritisation and Resource Allocation Based on Fault Tree Analysis. Int. J. Qual. Reliab. Manag. 2000, 17, 189–199. [Google Scholar] [CrossRef]
- Birnbaum, Z.W. On the Importance of Different Components in a Multicomponent System; Academic Press: New York, NY, USA, 1969; pp. 581–592. [Google Scholar]
- Lambert, H.E. Measures of importance of events and cut sets. In Reliability and Fault Tree Analysis; SIAM: Philadelphia, PA, USA, 1975; pp. 77–100. [Google Scholar]
- Mankamo, T.; Pörn, K.; Holmberg, J. Uses of Risk Importance Measures; Technical Report, Research Notes 1245; Technical Research Centre of Finland: Espoo, Finland, 1991; ISBN 951-38-3877-3. ISSN 0358-5085. [Google Scholar]
- Swain, S.; Ray, P.K. Short circuit fault analysis in a grid connected DFIG based wind energy system with active crowbar protection circuit for ridethrough capability and power quality improvement. Int. J. Electr. Power Energy Syst. 2017, 84, 64–75. [Google Scholar] [CrossRef]
- Qiu, Y.; Jiang, H.; Feng, Y.; Cao, M.; Zhao, Y.; Li, D. A new fault diagnosis algorithm for PMSG wind turbine power converters under variable wind speed conditions. Energies 2016, 9, 548. [Google Scholar] [CrossRef]
- De Moura, E.P.; de Abreu Melo Junior, F.E.; Damasceno, F.F.R.; Figueiredo, L.C.C.; de Andrade, C.F.; de Almeida, M.S.; Rocha, P.A.C. Classification of imbalance levels in a scaled wind turbine through detrended fluctuation analysis of vibration signals. Renew. Energy 2016, 96, 993–1002. [Google Scholar]
- Faiz, J.; Moosavi, S.M.M. Eccentricity fault detection—From induction machines to DFIG—A review. Renew. Sustain. Energy Rev. 2016, 55, 169–179. [Google Scholar]
- Hameed, Z.; Hong, Y.S.; Cho, Y.M.; Ahn, S.H.; Song, C.K. Condition monitoring and fault detection of WTs and related algorithms: A review. Renew. Sustain. Energy Rev. 2009, 13, 1–39. [Google Scholar] [CrossRef]
- Wu, A.P.; Chapman, P.L. Simple expressions for optimal current waveforms for permanent-magnet synchronous machine drives. IEEE Trans. Energy Convers. 2005, 20, 151–157. [Google Scholar] [CrossRef]
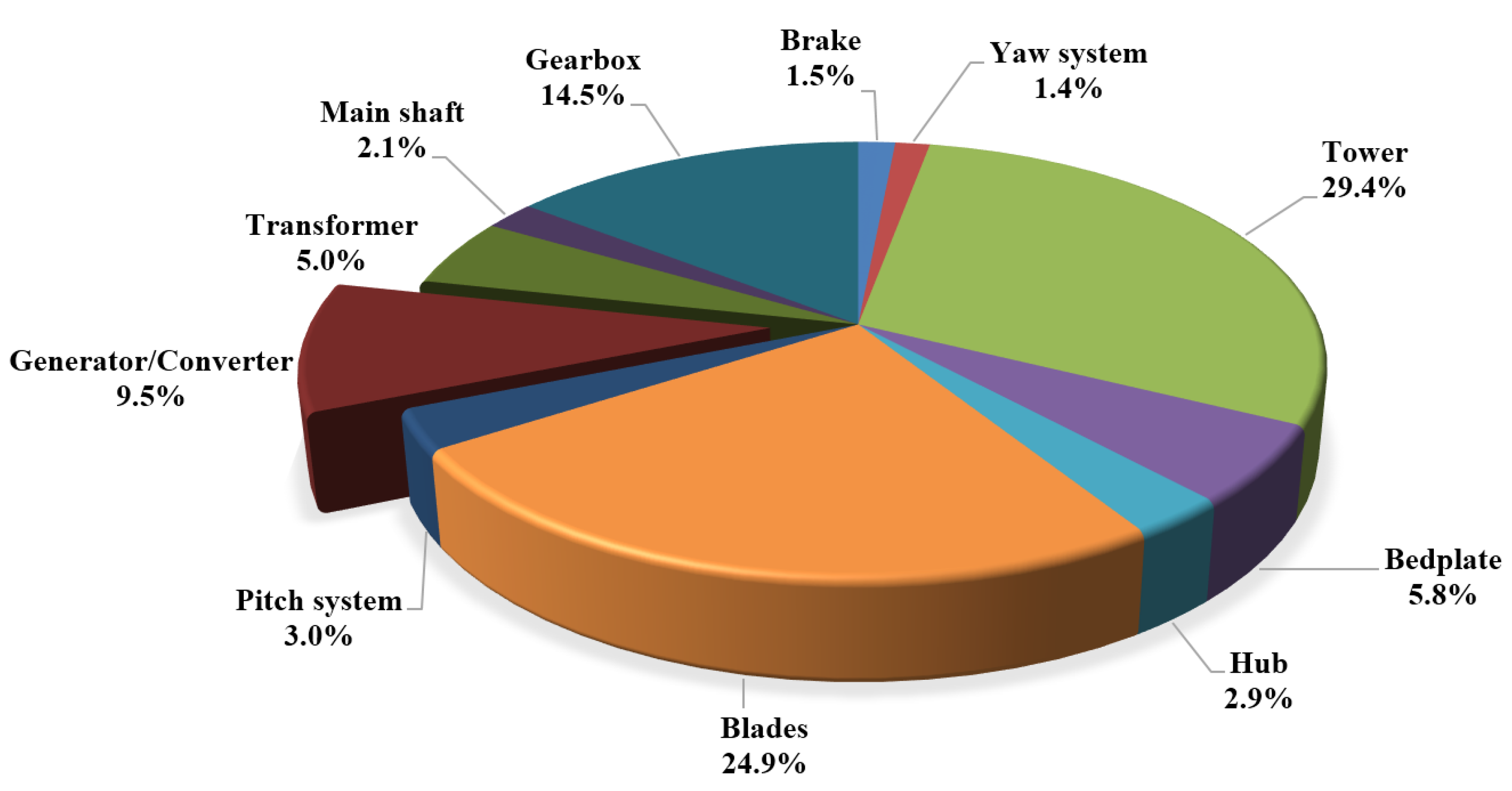
- Garcia, F.P.; Pinar, J.M.; Pliego, A.; Papaelias, M. Identification of critical components of wind turbines using FTA over time. Renew. Energy 2016, 85, 1178–1191. [Google Scholar]
- Pliego, A.; Garcia, F.P. A Novel Approach on Diagnostic and Prognostics in Railways: A Real Case Study. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2015, 230, 1440–1456. [Google Scholar] [CrossRef]

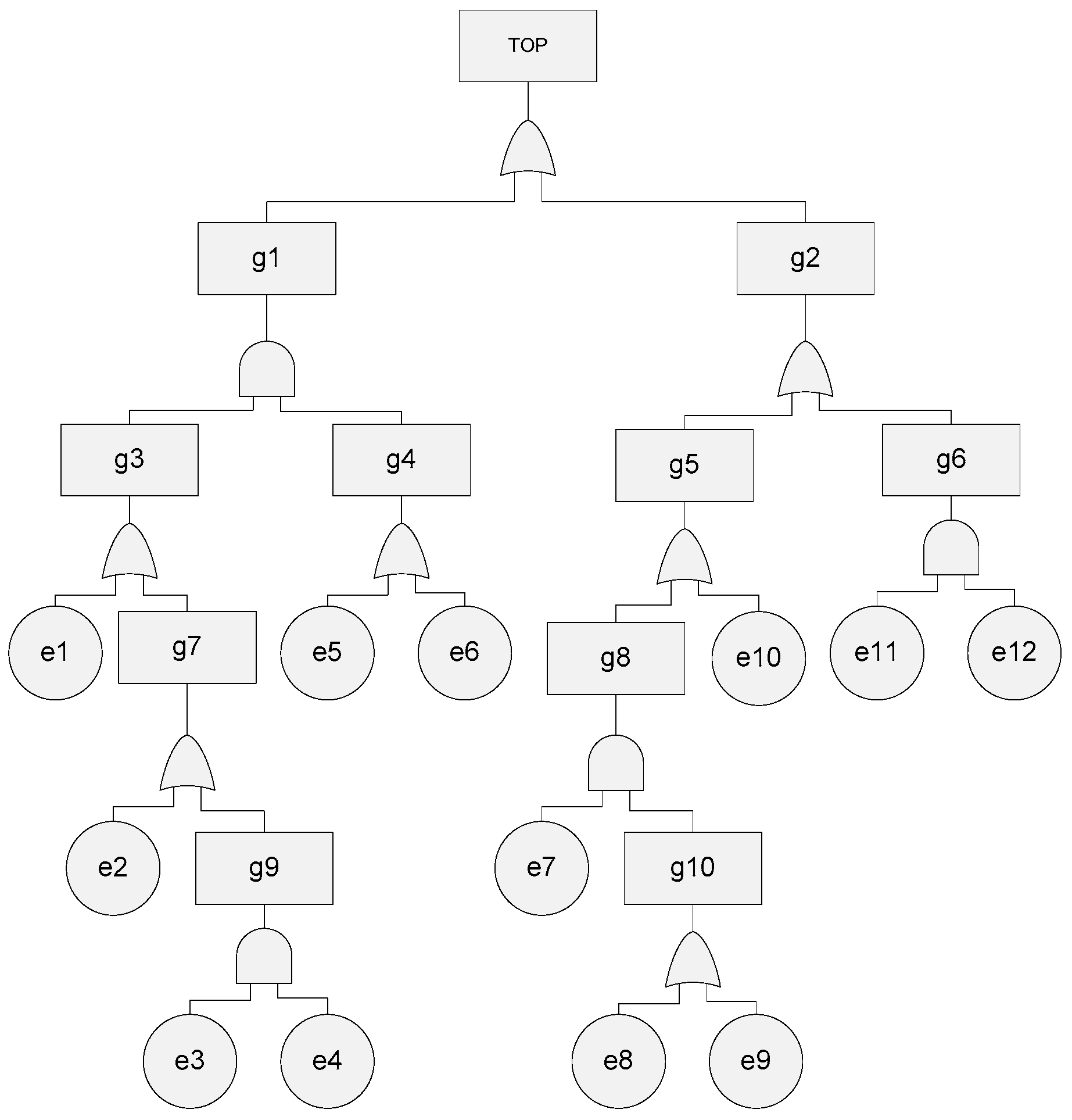

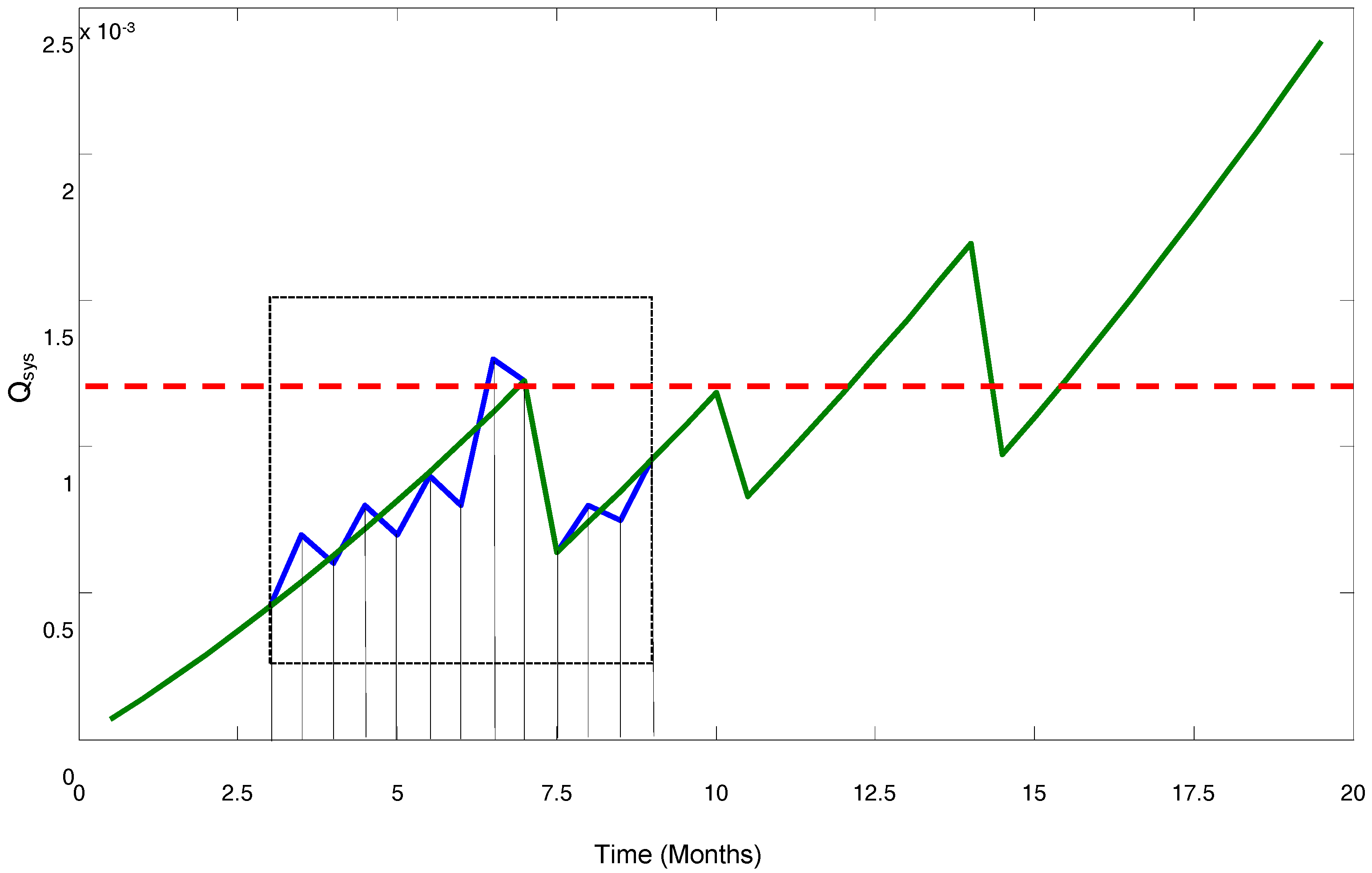
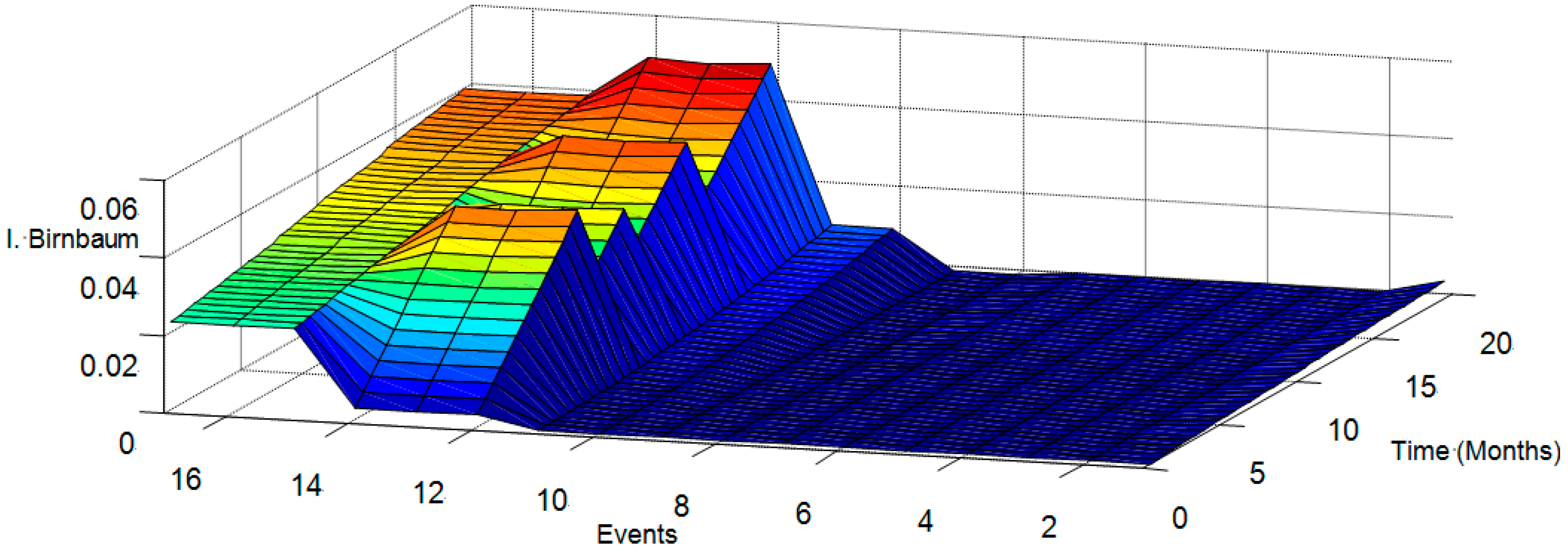

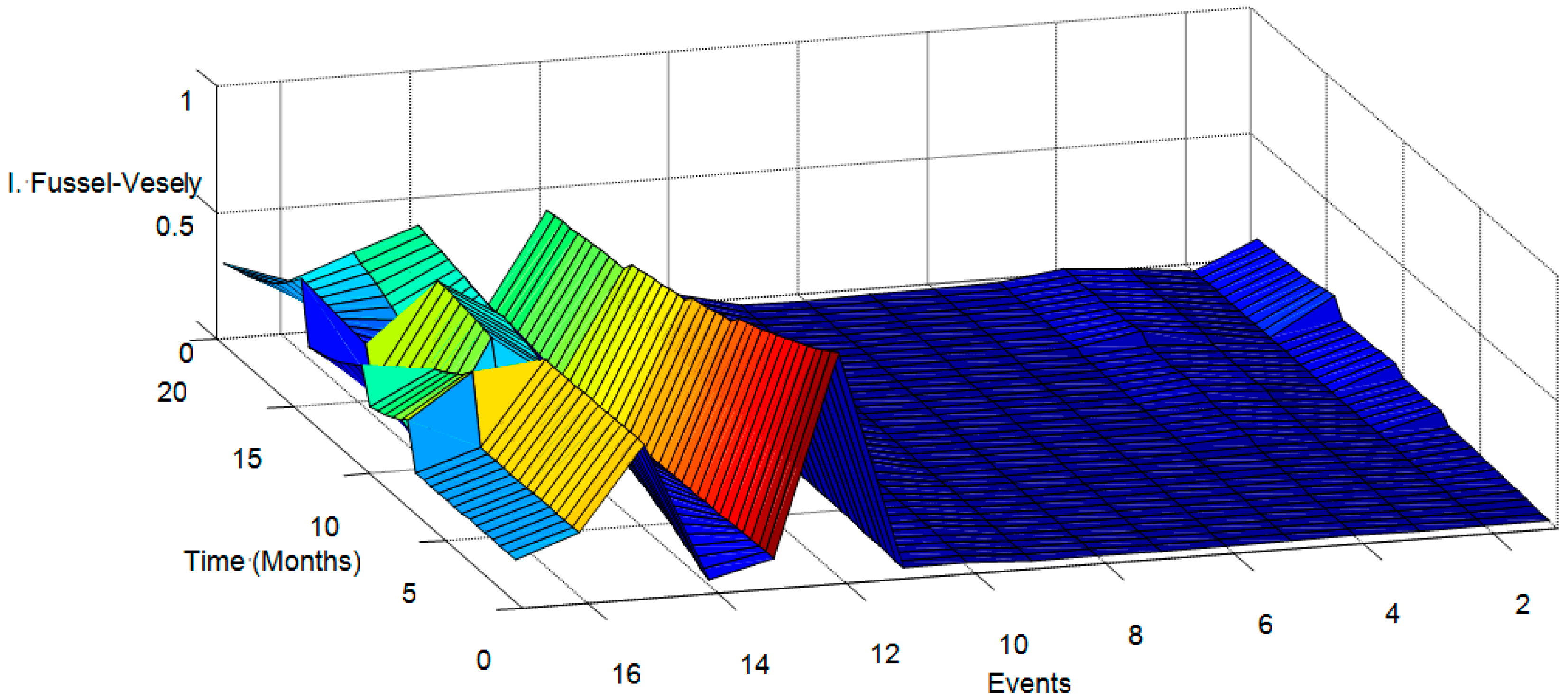
| Ranking Method | TLDR | DFS | BFS | Level | AND |
|---|---|---|---|---|---|
| Number of CS | 46 | 31 | 36 | 46 | 35 |
| Non-Basic Events | Basic Events | ||
|---|---|---|---|
| Critical Generator Failure | g001 | Abnormal Vibration G | e001 |
| Power electronics and electric controls failure | g002 | Cracks | e002 |
| Mechanical failure (generator) | g003 | Imbalance | e003 |
| Electrical failure (generator) | g004 | Asymmetry | e004 |
| Bearing generator failure | g005 | Air-Gap eccentricities | e005 |
| Rotor and stator failure | g006 | Broken bars | e006 |
| Bearing generator fault | g007 | Dynamic eccentricity | e007 |
| Rotor and stator fault | g008 | Sensor Tª error | e008 |
| Abnormal signals A | g009 | Temperature above limit | e009 |
| Overheating generator | g010 | Short circuit (generator) | e010 |
| Electrical fault (PE) | g011 | Open circuit (generator) | e011 |
| Mechanical fault (PE) | g012 | Short circuit (electronics) | e012 |
| Open circuit (electronics) | e013 | ||
| Gate drive circuit | e014 | ||
| Corrosion | e015 | ||
| Dirt | e016 | ||
| Terminals damage | e017 | ||
| Ranking Method | Number of CSs |
|---|---|
| TDLR | 99 |
| DFS | 171 |
| BFS | 171 |
| Level | 99 |
| AND | 99 |
| Event | Probability Model | Parameters |
|---|---|---|
| e001 | Exponential increasing | 𝜆 = 0.0030 months−1 |
| e002 | Constant | K = 0.0010 |
| e003 | Exponential increasing | 𝜆 = 0.0025 months−1 |
| e004 | Exponential increasing | 𝜆 = 0.0045 months−1 |
| e005 | Linear increasing | m = 0.0015 months−1 |
| e006 | Linear increasing | m = 0.0009 months−1 |
| e007 | Linear increasing | m = 0.0007 months−1 |
| e008 | Constant | K = 0.0040 |
| e009 | Periodic | 𝜆 = 0.0025 months−1, = 5 months |
| e010 | Constant | K = 0.0012 |
| e011 | Constant | K = 0.0013 |
| e012 | Constant | K = 0.0020 |
| e013 | Constant | K = 0.0021 |
| e014 | Linear increasing | m = 0.0010 months−1 |
| e015 | Periodic | 𝜆 = 0.0035 months−1, = 7 months |
| e016 | Periodic | 𝜆 = 0.0015 months−1, = 10 months |
| e017 | Linear increasing | m = 0.0010 months−1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García Márquez, F.P.; Pliego Marugán, A.; Pinar Pérez, J.M.; Hillmansen, S.; Papaelias, M. Optimal Dynamic Analysis of Electrical/Electronic Components in Wind Turbines. Energies 2017, 10, 1111. https://doi.org/10.3390/en10081111
García Márquez FP, Pliego Marugán A, Pinar Pérez JM, Hillmansen S, Papaelias M. Optimal Dynamic Analysis of Electrical/Electronic Components in Wind Turbines. Energies. 2017; 10(8):1111. https://doi.org/10.3390/en10081111
Chicago/Turabian StyleGarcía Márquez, Fausto Pedro, Alberto Pliego Marugán, Jesús María Pinar Pérez, Stuart Hillmansen, and Mayorkinos Papaelias. 2017. "Optimal Dynamic Analysis of Electrical/Electronic Components in Wind Turbines" Energies 10, no. 8: 1111. https://doi.org/10.3390/en10081111
APA StyleGarcía Márquez, F. P., Pliego Marugán, A., Pinar Pérez, J. M., Hillmansen, S., & Papaelias, M. (2017). Optimal Dynamic Analysis of Electrical/Electronic Components in Wind Turbines. Energies, 10(8), 1111. https://doi.org/10.3390/en10081111








