Linking the Power and Transport Sectors—Part 2: Modelling a Sector Coupling Scenario for Germany
Abstract
:1. Introduction
2. The METIS Package
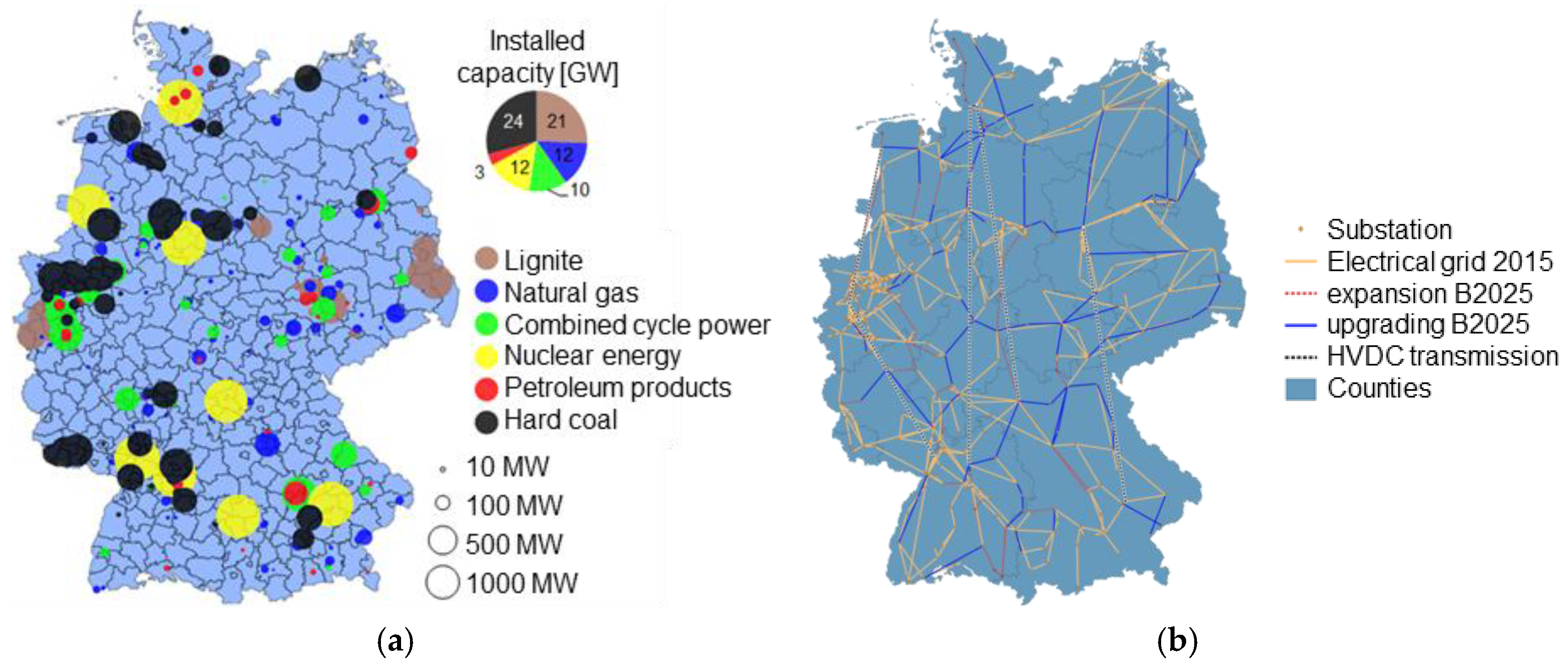
2.1. The Power Sector
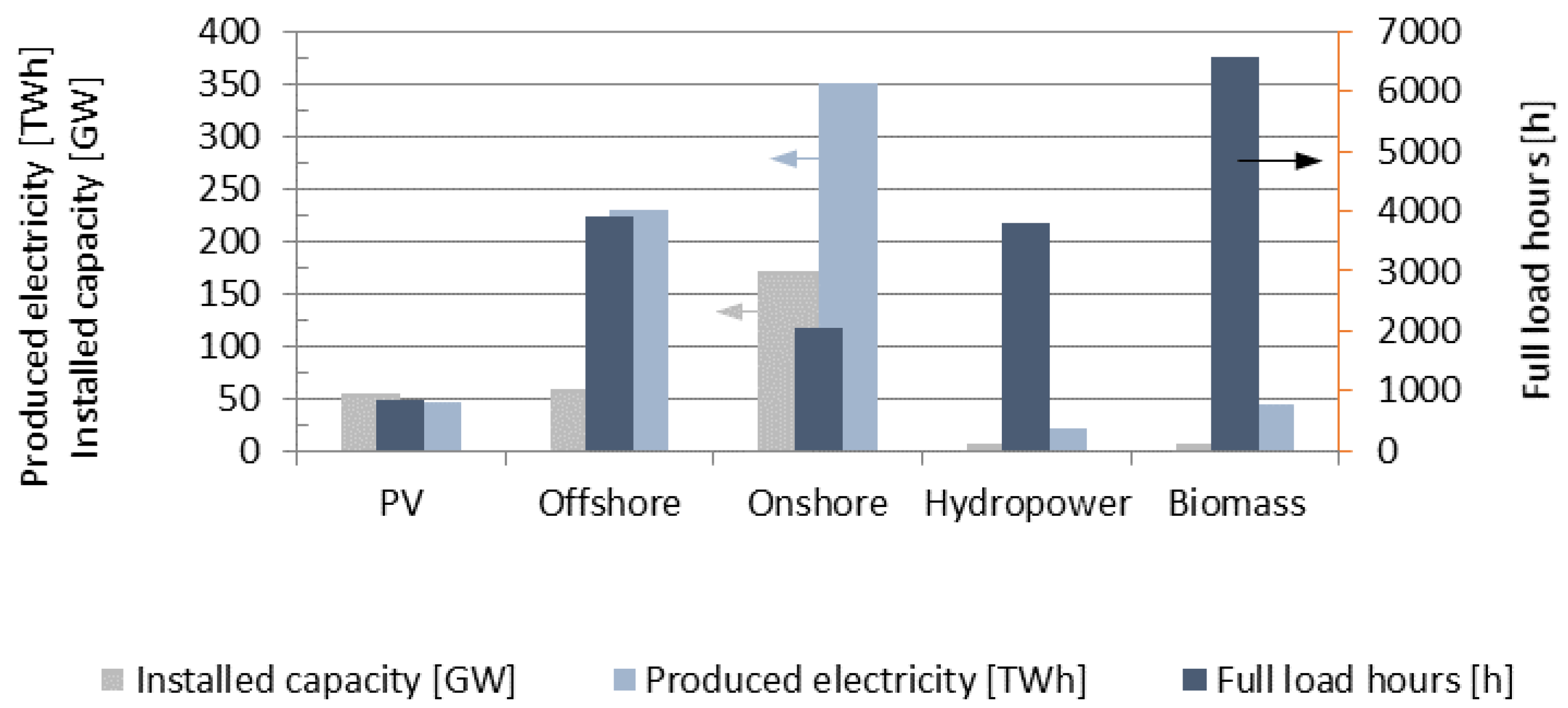
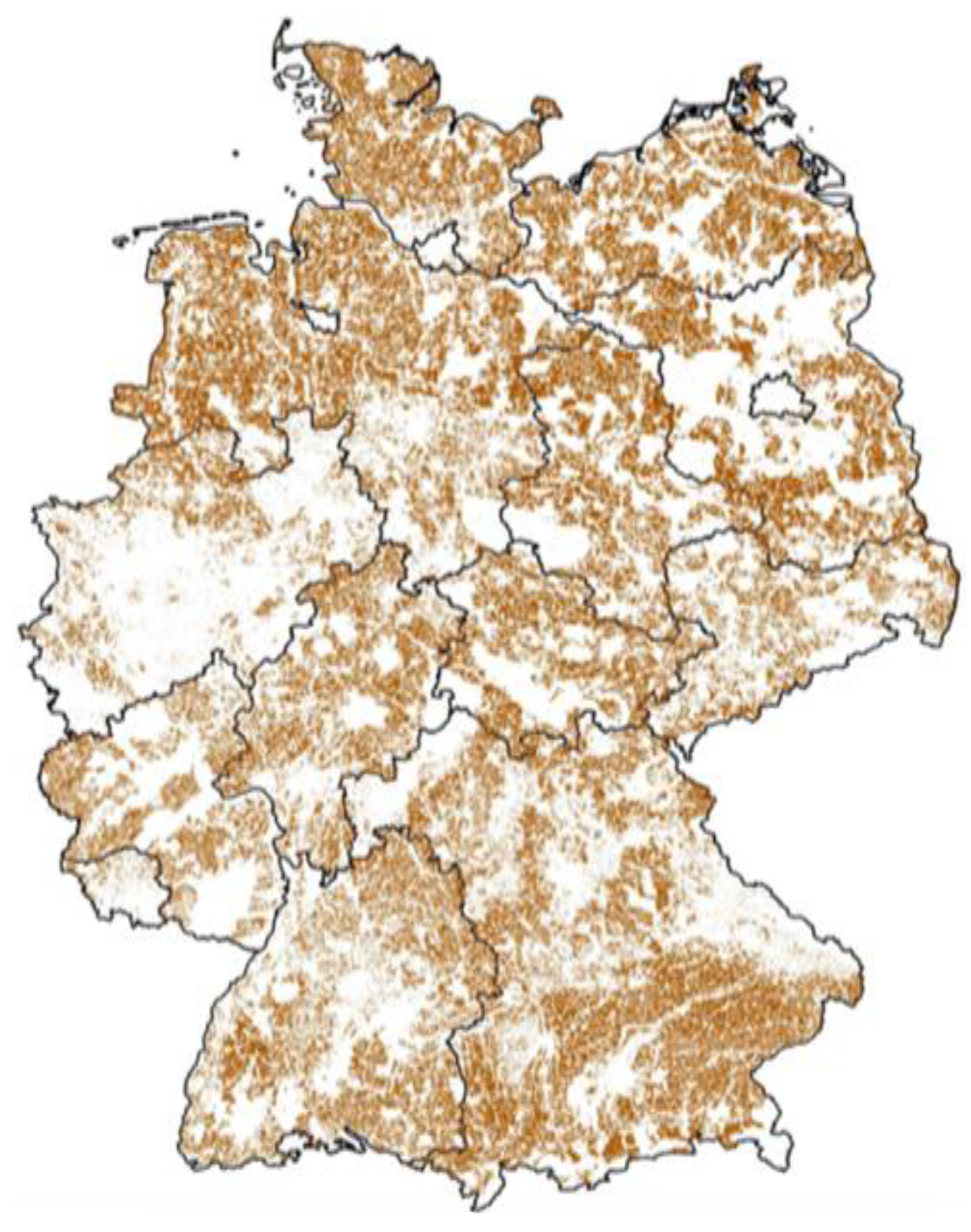
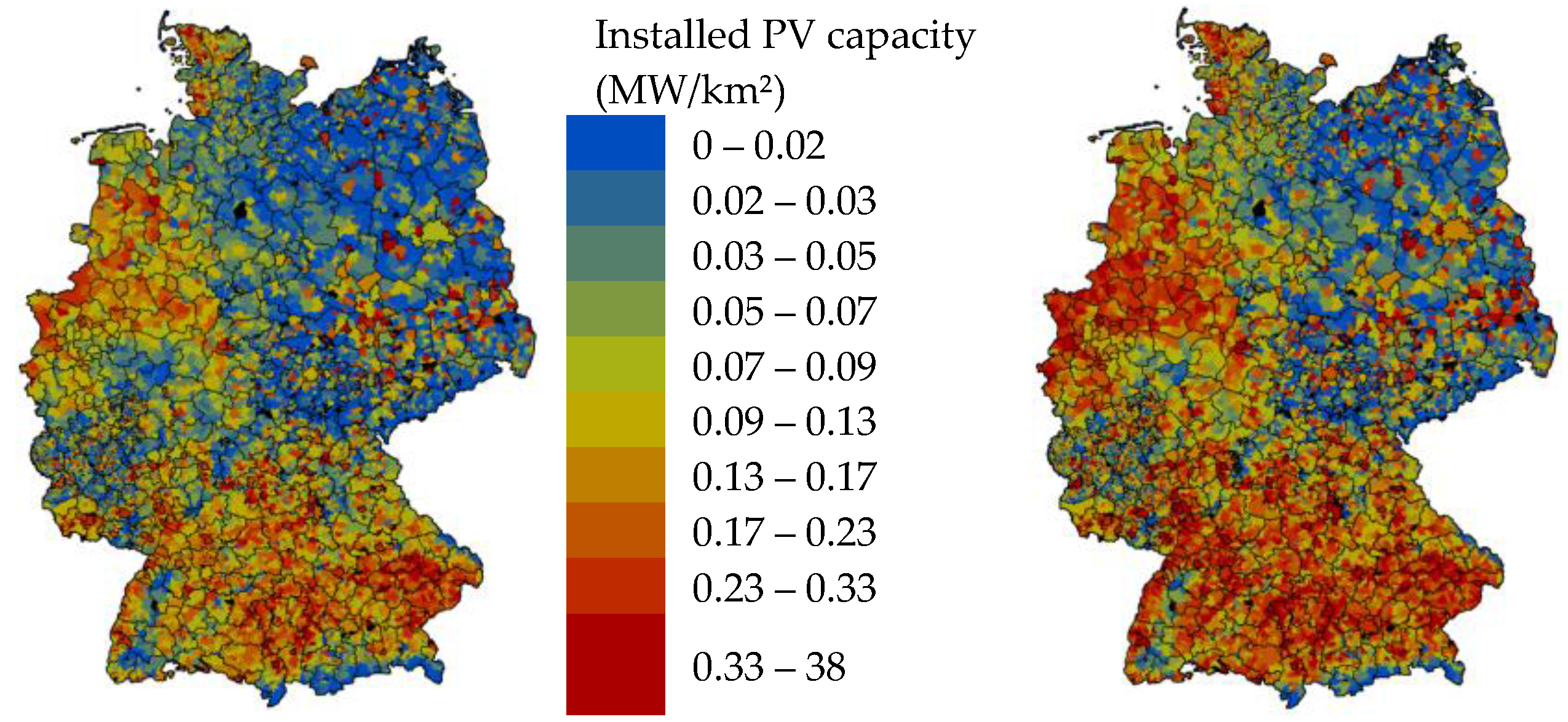
2.1.1. Renewable Capacity
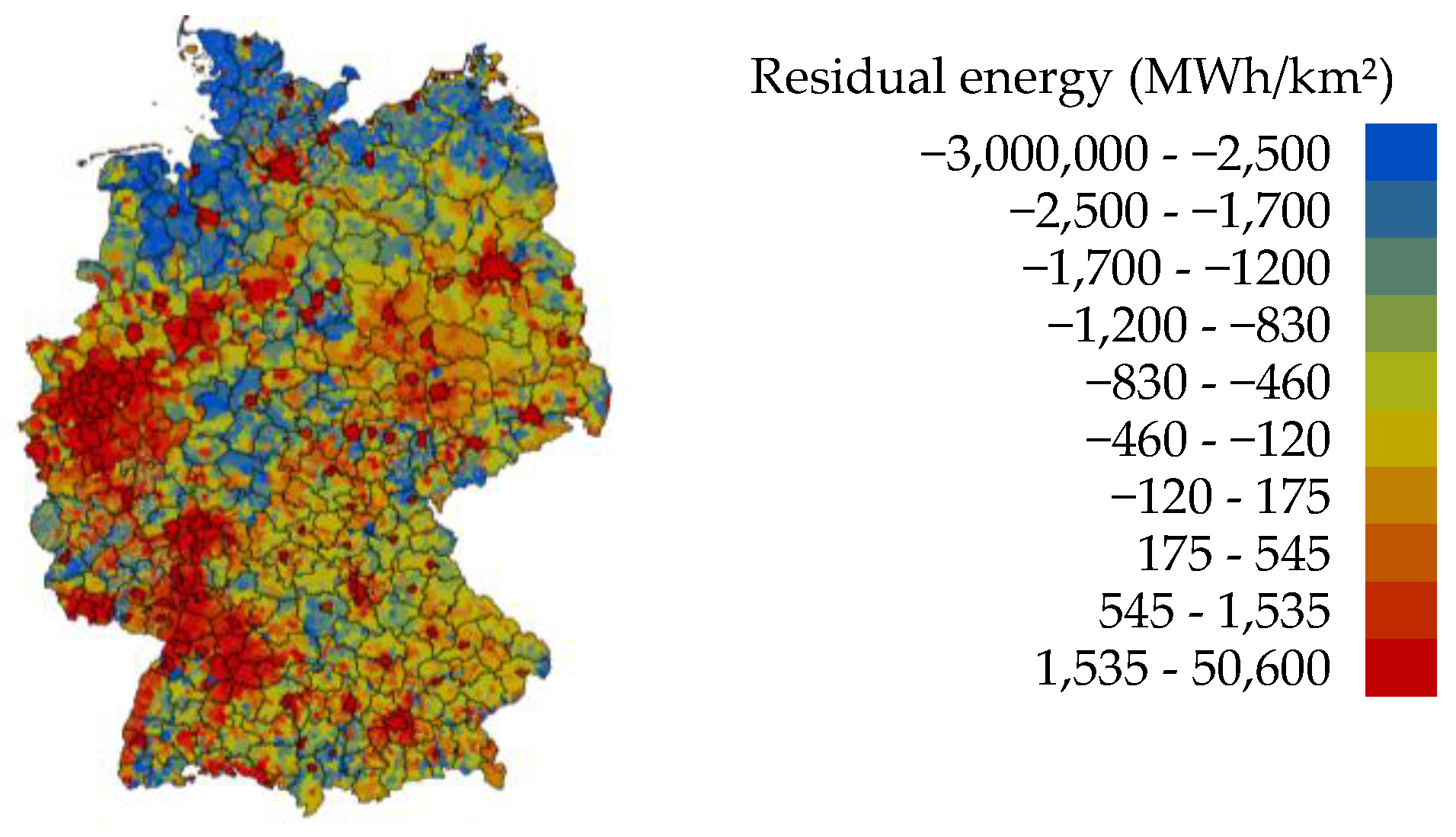
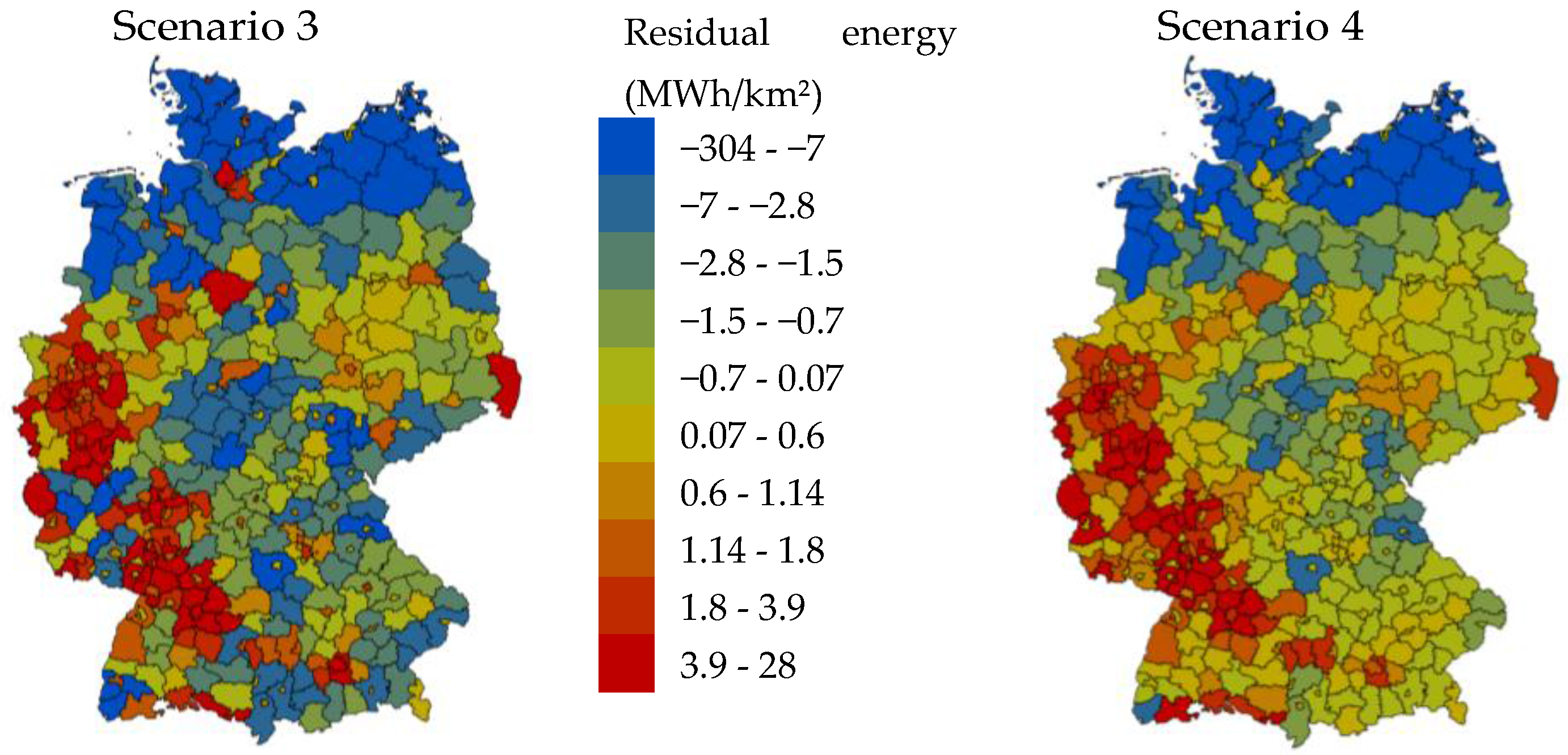
2.1.2. Residual Load
2.1.3. Power Trading and Conventional Dispatch
2.2. Transport Sector
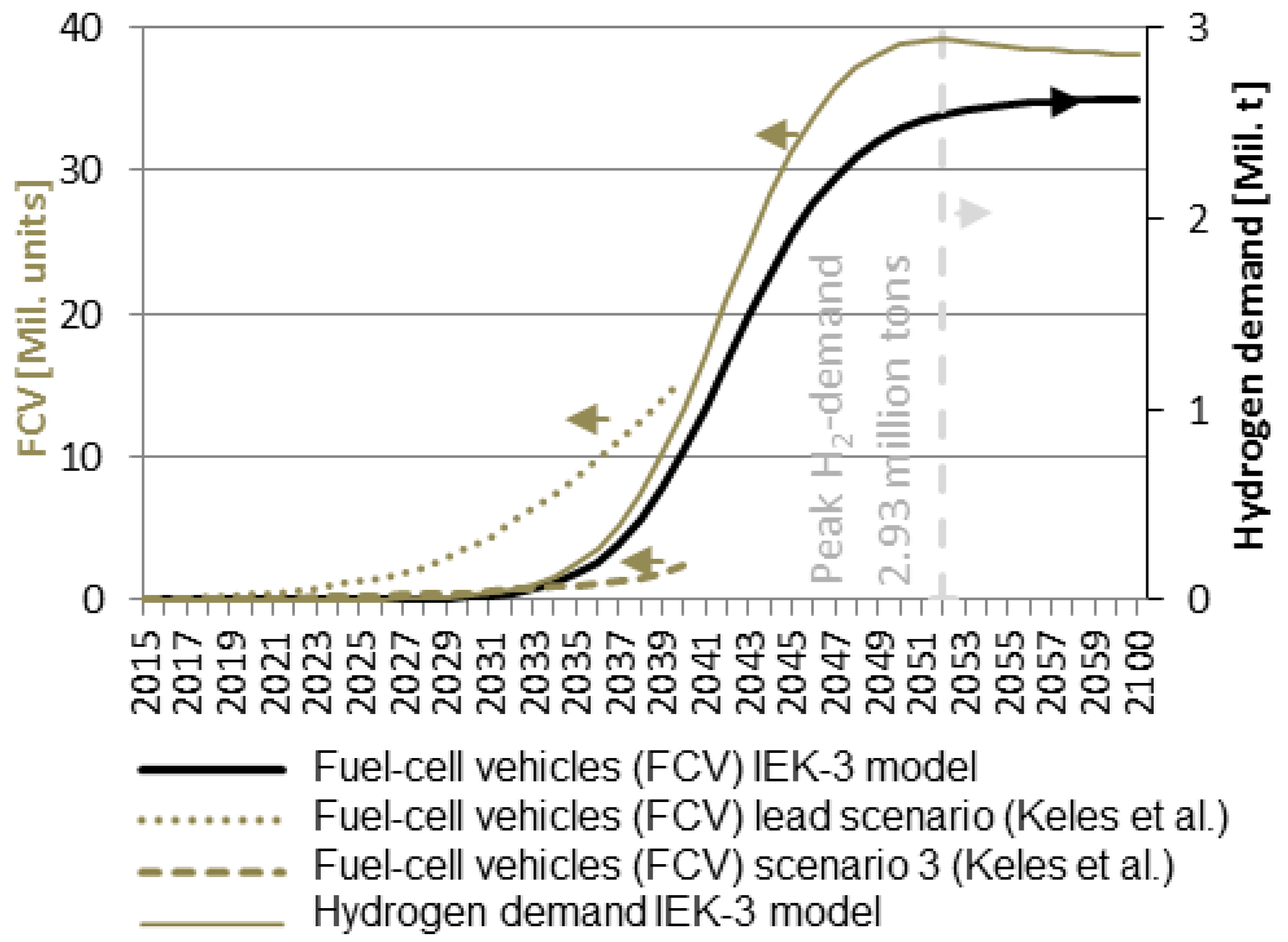
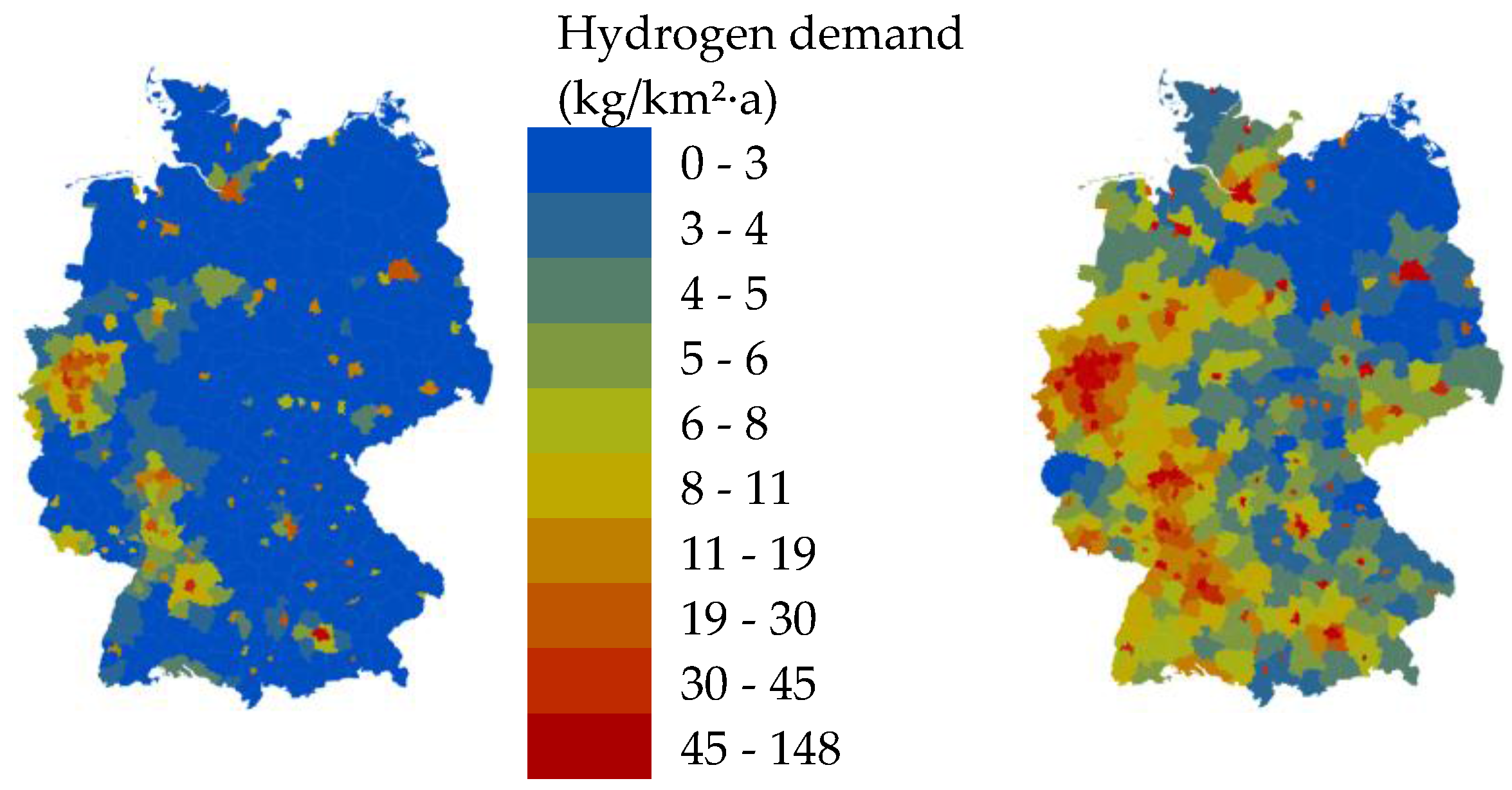
2.2.1. Hydrogen Demand 2050
- 500 hydrogen filling stations at the outset of the transformation in six metropolitan areas: the Ruhr area, Berlin, Hamburg, Munich, Stuttgart and Frankfurt.
- Consumers are willing to pay €2000 more for “green technology”, namely FCVs, over petrol- or diesel-driven cars
- No value added tax on FCVs in the beginning
- Tax-free hydrogen for up to 500,000 FCVs
- The same specific tax for hydrogen as for petrol and diesel for 1 million or more FCVs
- Population status
- Site-specific population density
- Obtainable private household income data per inhabitant
- Inhabitant-related motor car density
- Number of motor cars
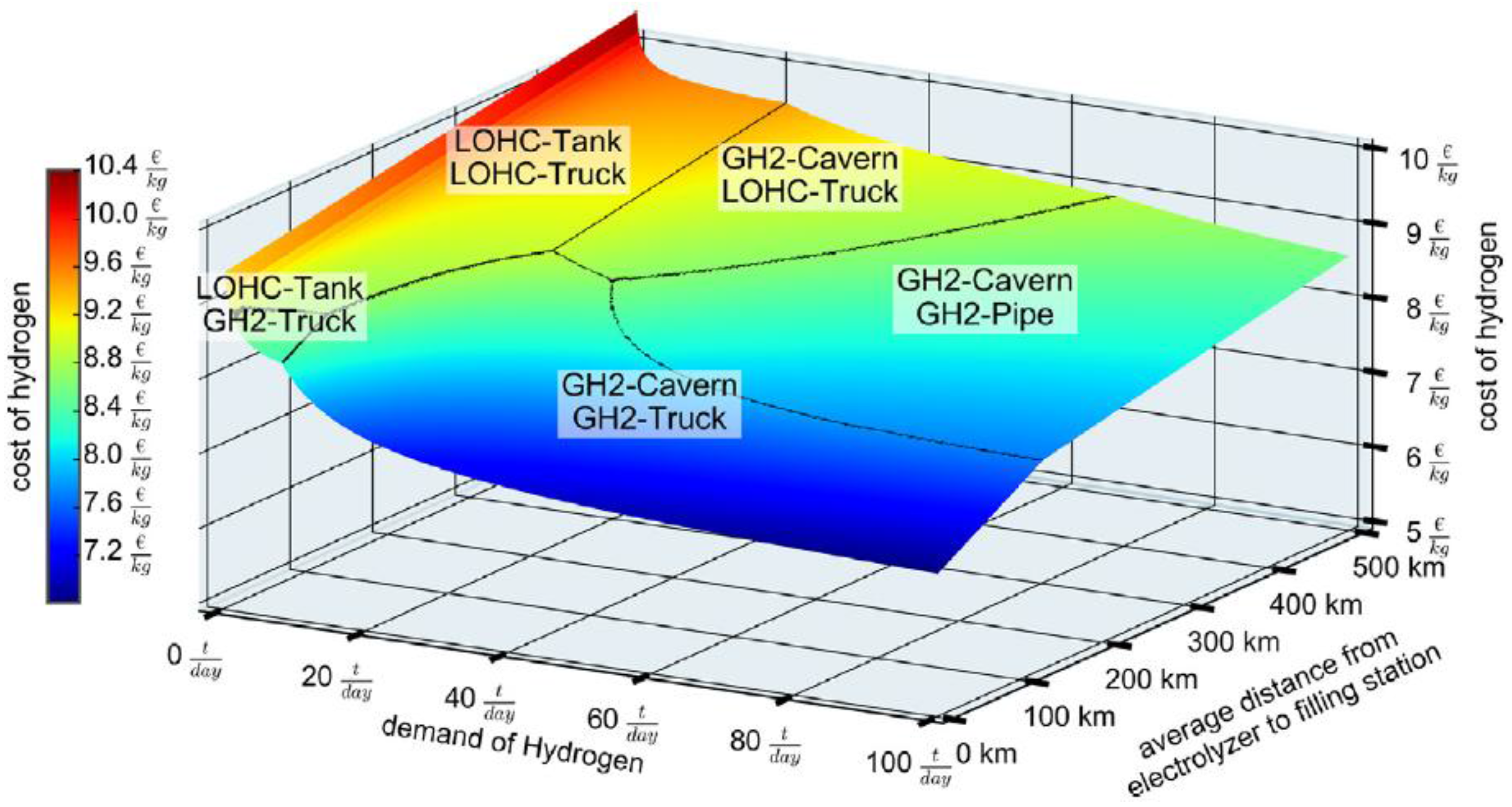
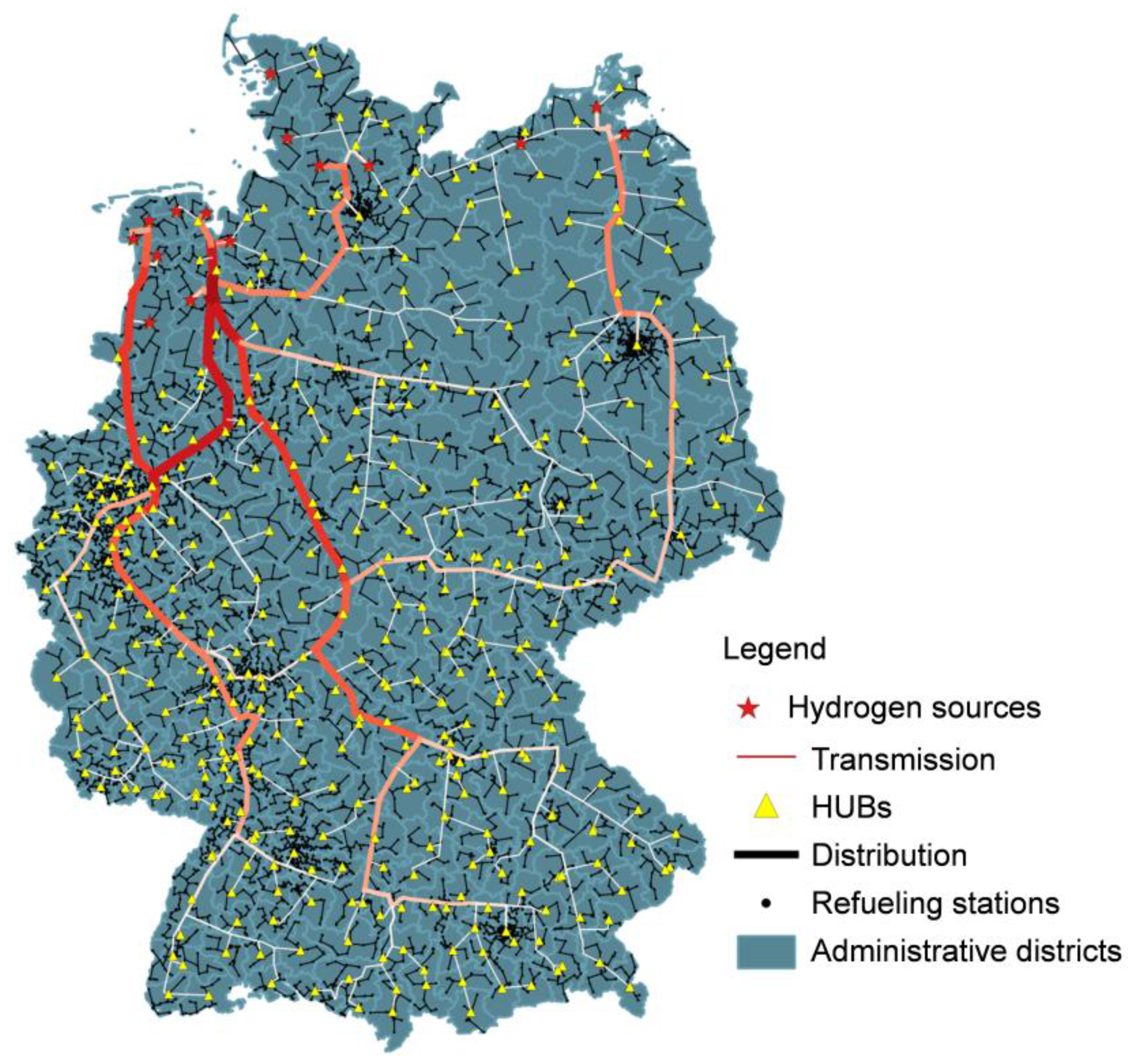
2.2.2. Hydrogen Transport
3. Results Analysis
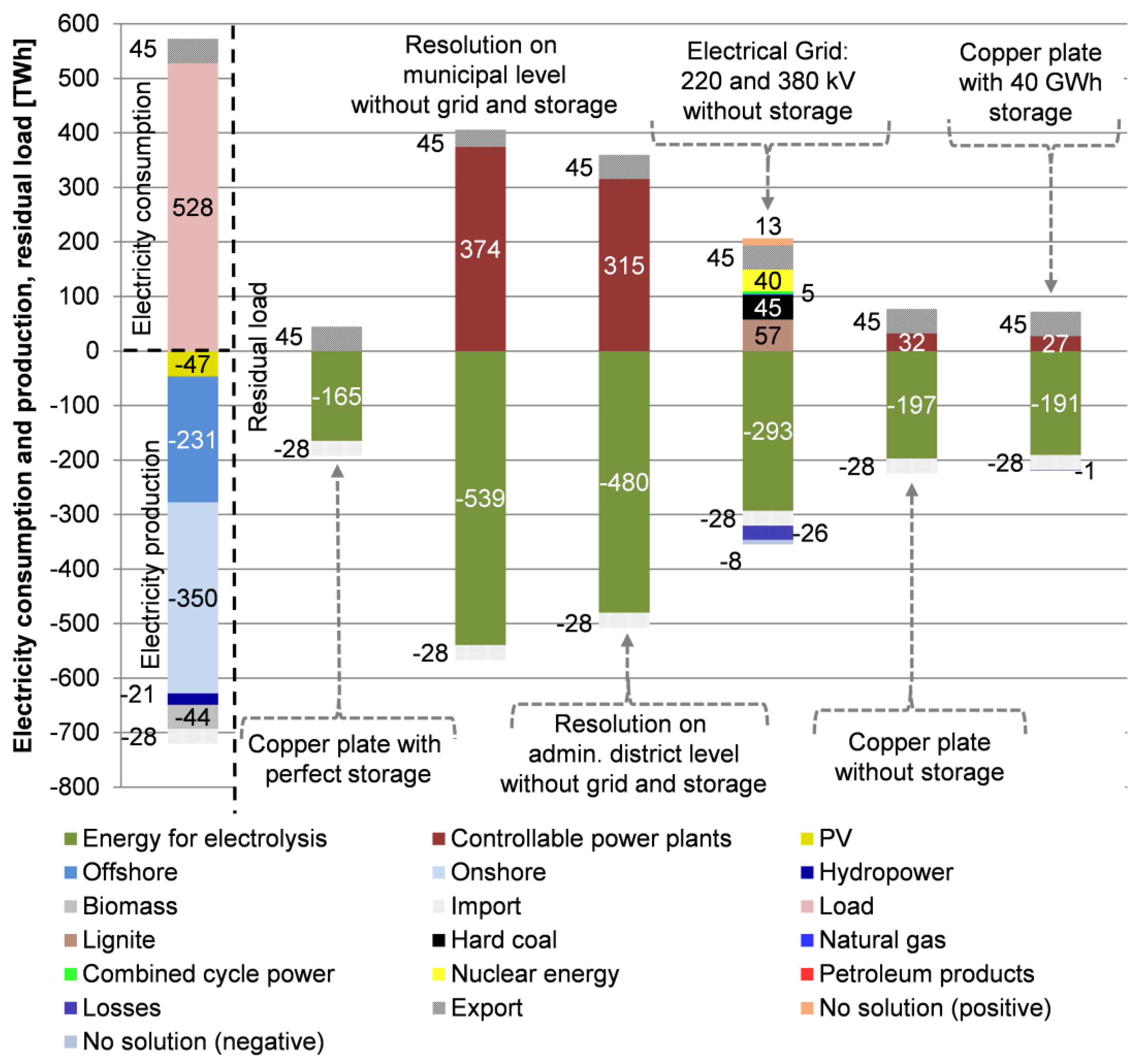
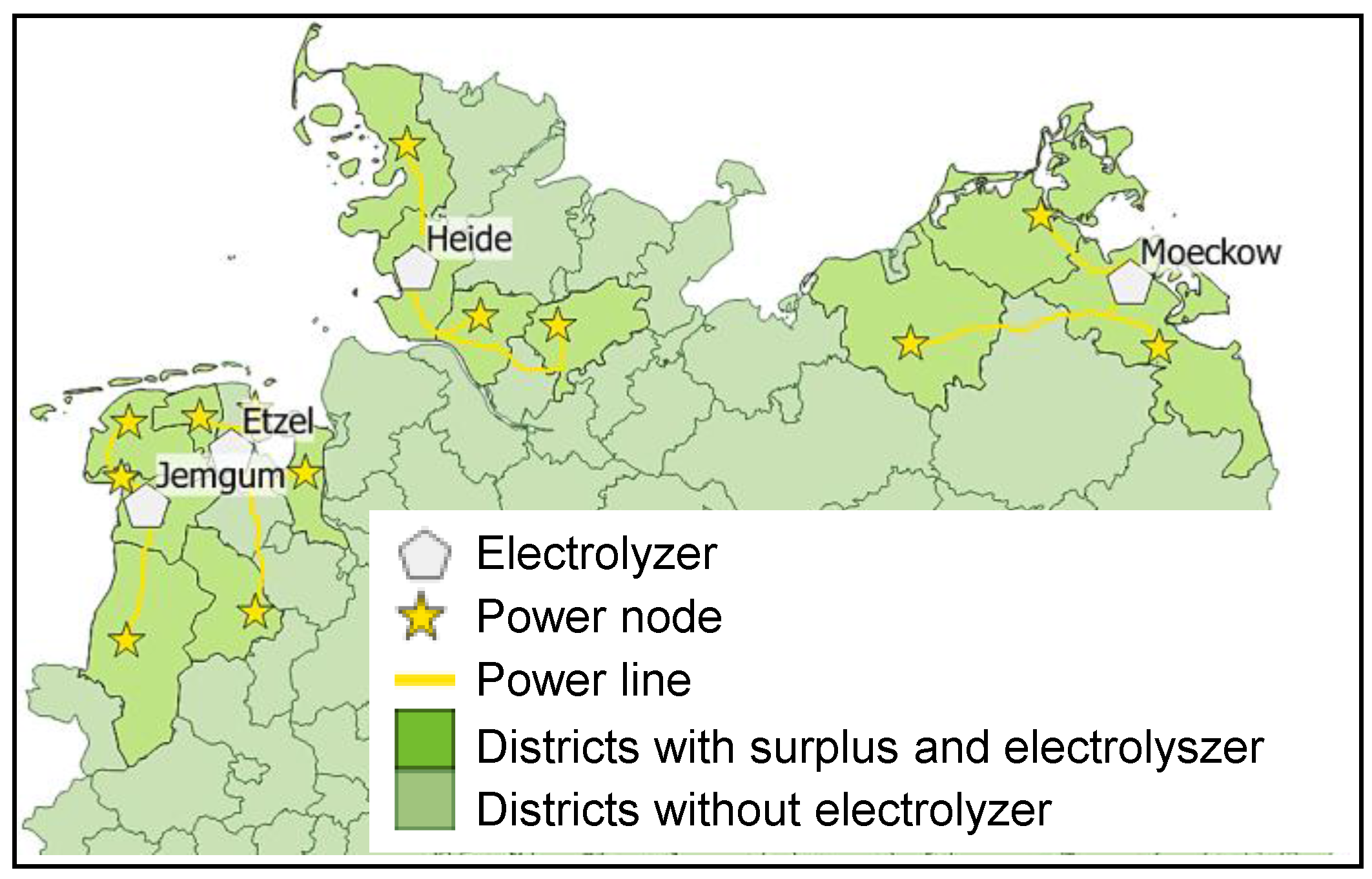
3.1. Surplus Analysis
- Copper plate (no grid limitations) and perfect storage systems (no storage losses or limitations)
- No electrical grid and no storage systems on the municipality level
- No electrical grid and no storage systems on the county level
- Current electrical grid (380 and 220 kV), no storage systems and current conventional power plants on the county level
- Copper plate (no grid limitations) and no storage systems
- Copper plate (no grid limitations) and 40 GWh of pumped storage hydropower stations (current situation in Germany)
- (1)
- 165 TWh
- (2)
- 539 TWh
- (3)
- 480 TWh
- (4)
- 293 TWh
- (5)
- 197 TWh
- (6)
- 191 TWh
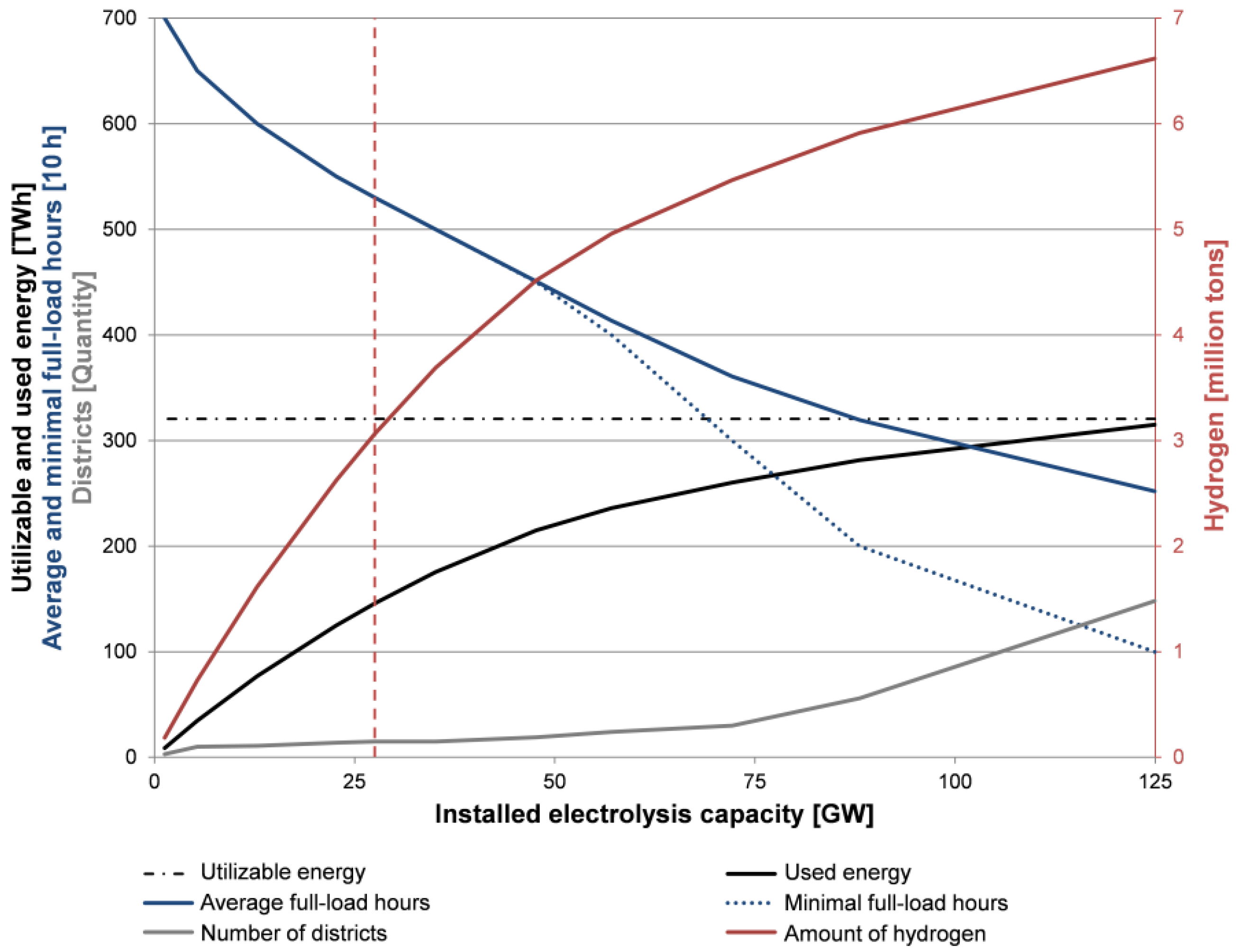
3.2. Utilization of the Surplus by Electrolysis
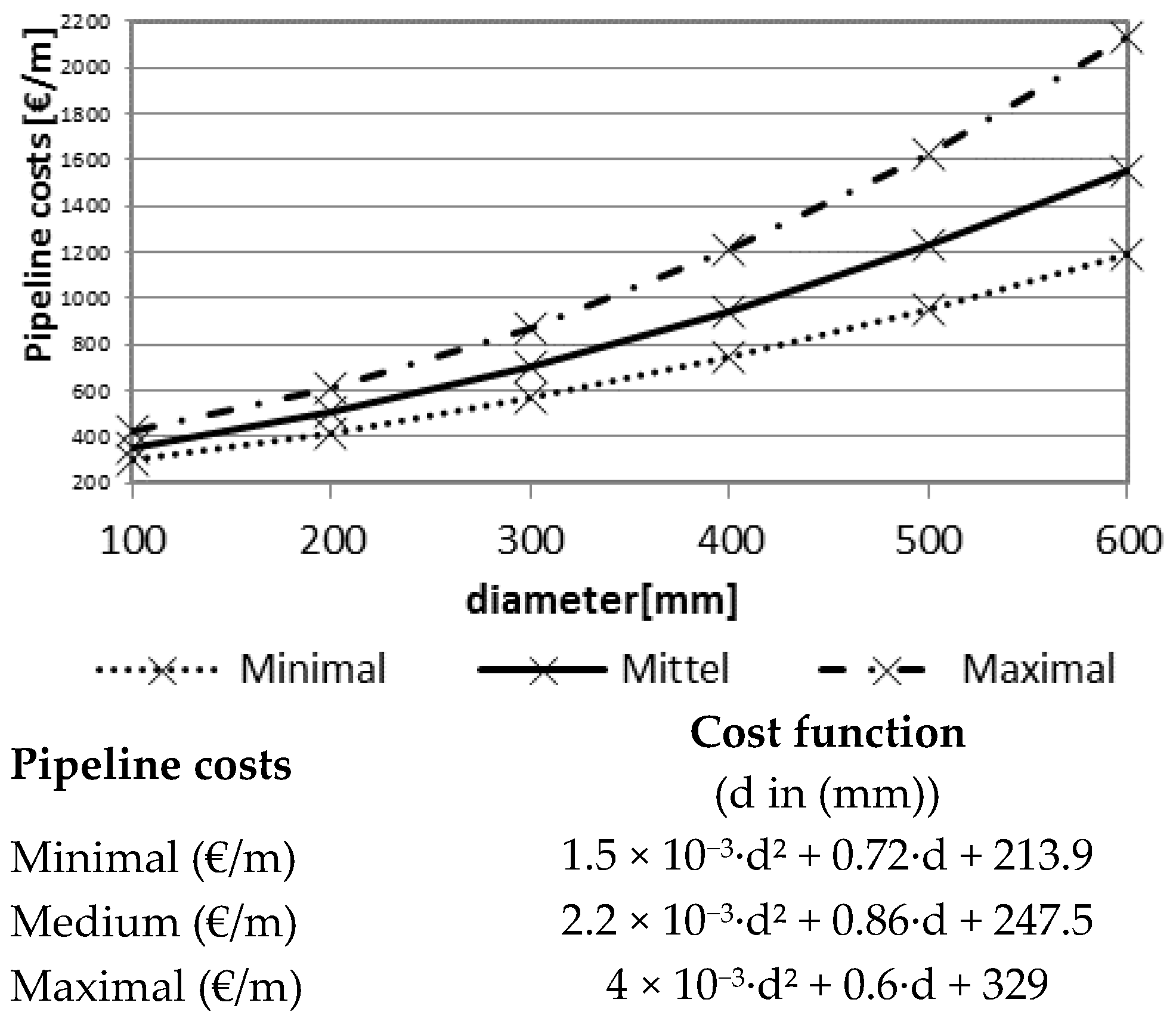
3.3. Hydrogen Pipeline Grid
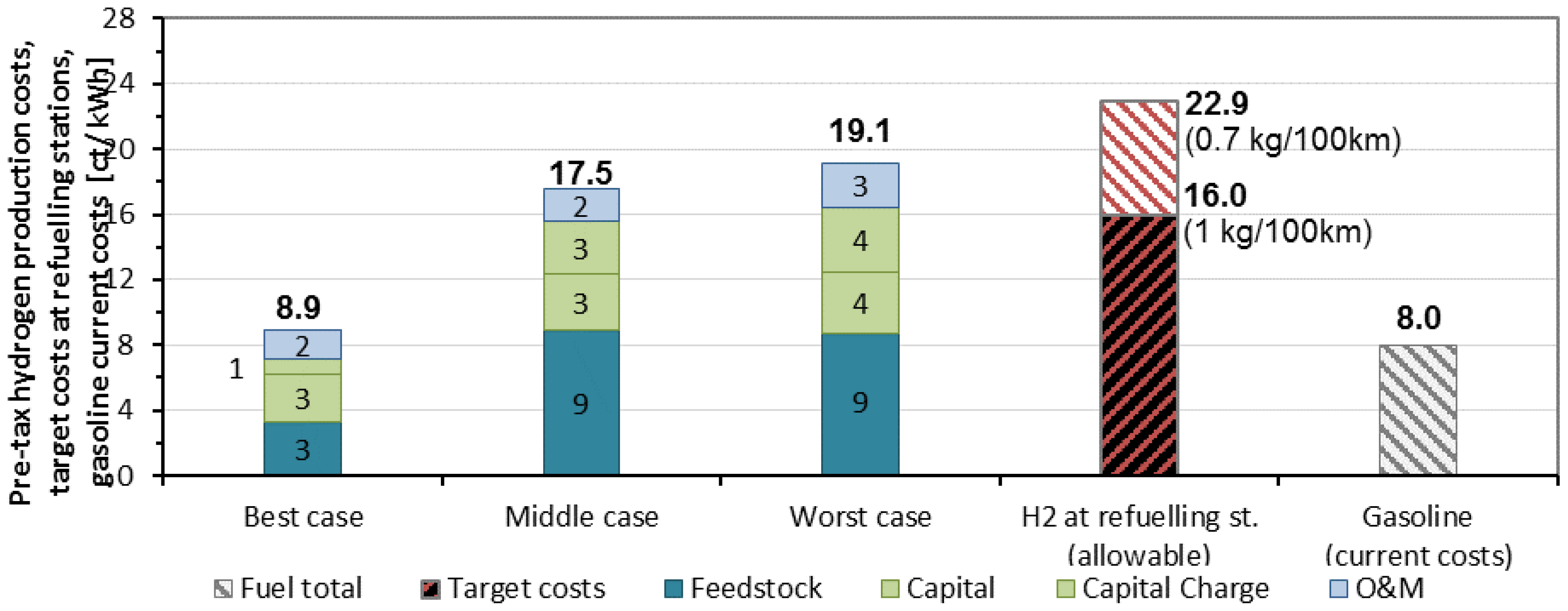
3.4. Economic Assessment
- Best case: Seasonal storage of 2.9 million tons of hydrogen at a cost of 2.7 billion €.
- Middle case: Storage of 2.9 million tons of hydrogen for 60 days at a cost of 8 billion €.
- Worst case: Storage of 5.4 million tons of hydrogen for 60 days at a cost of 15 billion €.
4. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Robinius, M.; Otto, A.; Heuser, P.; Welder, L.; Syranidis, K.; Ryberg, D.S.; Grube, T.; Markewitz, P.; Peters, R.; Stolten, D. Linking the power and transport sectors—Part 1: The principle of sector coupling. Energies 2017, 10, 956. [Google Scholar]
- Markewitz, P.; Kuckshinrichs, W.; Martinsen, D.; Hake, J.F. IKARUS—A fundamental concept for national GHG-mitigation strategies. Energy Convers. Manag. 1996, 37, 777–782. [Google Scholar] [CrossRef]
- Fraunhofer ISE. 100% Erneuerbare Energien für Strom und Wärme in Deutschland. 2012. Available online: http://www.ise.fraunhofer.de/de/veroeffentlichungen/veroeffentlichungen-pdf-dateien/studien-und-konzeptpapiere/studie-100-erneuerbare-energien-in-deutschland.pdf (accessed on 20 February 2017). (In German).
- Fraunhofer IWES. Geschäftsmodell Energiewende. Eine Antwort auf das “Die-Kosten-der-Energiewende”-Argument; IWES: Kassel Germany, 2014. (In German) [Google Scholar]
- Lunz, B.; Stöcker, P.; Eckstein, S.; Nebel, A.; Samadi, S.; Erlach, B.; Fischedick, M.; Elsner, P.; Sauer, D.U. Scenario-based comparative assessment of potential future electricity systems—A new methodological approach using Germany in 2050 as an example. Appl. Energy 2016, 171, 555–580. [Google Scholar] [CrossRef]
- Pfenninger, S.; Hawkes, A.; Keirstead, J. Energy systems modeling for twenty-first century energy challenges. Renew. Sustain. Energy Rev. 2014, 33, 74–86. [Google Scholar] [CrossRef]
- Guandalini, G.; Robinius, M.; Grube, T.; Campanari, S.; Stolten, D. Long-term power-to-gas potential from wind and solar power: A country analysis for Italy. Int. J. Hydrogen Energy 2017, 42, 13389–13406. [Google Scholar] [CrossRef]
- Varone, A.; Ferrari, M. Power to liquid and power to gas: An option for the German Energiewende. Renew. Sustain. Energy Rev. 2015, 45, 207–218. [Google Scholar] [CrossRef]
- Schemme, S.; Samsun, R.C.; Peters, R.; Stolten, D. Power-to-fuel as a key to sustainable transport systems—An analysis of diesel fuels produced from CO2 and renewable electricity. Fuel 2017, 205, 198–221. [Google Scholar] [CrossRef]
- Otto, A.; Robinius, M.; Grube, T.; Schiebahn, S.; Praktiknjo, A.; Stolten, D. Power-to-Steel: Reducing CO2 through the Integration of Renewable Energy and Hydrogen into the German Steel Industry. Energies 2017, 10, 451. [Google Scholar] [CrossRef]
- Nastasi, B.; Basso, G.L. Hydrogen to link heat and electricity in the transition towards future Smart Energy Systems. Energy 2016, 110, 5–22. [Google Scholar] [CrossRef]
- Grueger, F.; Möhrke, F.; Robinius, M.; Stolten, D. Early power to gas applications: Reducing wind farm forecast errors and providing secondary control reserve. Appl. Energy 2017, 192, 551–562. [Google Scholar] [CrossRef]
- Guandalini, G.; Campanari, S.; Romano, M.C. Power-to-gas plants and gas turbines for improved wind energy dispatchability: Energy and economic assessment. Appl. Energy 2015, 147, 117–130. [Google Scholar] [CrossRef]
- De Santoli, L.; Basso, G.L.; Bruschi, D. A small scale H2NG production plant in Italy: Techno-economic feasibility analysis and costs associated with carbon avoidance. Int. J. Hydrogen Energy 2014, 39, 6497–6517. [Google Scholar] [CrossRef]
- Basso, G.L.; Nastasi, B.; Garcia, D.A.; Cumo, F. How to handle the Hydrogen enriched Natural Gas blends in combustion efficiency measurement procedure of conventional and condensing boilers. Energy 2017, 123, 615–636. [Google Scholar] [CrossRef]
- Robinius, M. Strom- und Gasmarktdesign zur Versorgung des Deutschen Straßenverkehrs mit Wasserstoff. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2015. (In German). [Google Scholar]
- Robinius, M.; Stolten, D. Power-to-Gas: Quantifizierung lokaler Stromüberschüsse in Deutschland anhand unterschiedlicher Windenergie-Ausbaustufen. In Proceedings of the 9th Internationale Energiewirtschaftstagung, Wien, Austria, 20 February 2015. (In German). [Google Scholar]
- Ter Stein, F. Lokal und Temporär Aufgelöstes Strompreismodell in Deutschland. Master’s Thesis, RWTH-Aachen, Aachen, Germany, 2015. (In German). [Google Scholar]
- Terjung, L. Residuallastmodellierung zur Analyse eines Zonalen Strommarktmodells bei hohen Anteilen Erneuerbarer Energien. Bachelor’s Thesis, RWTH-Aachen, Aachen, Germany, 2015. (In German). [Google Scholar]
- Schiebahn, S.; Grube, T.; Robinius, M.; Tietze, V.; Kumar, B.; Stolten, D. Power to gas: Technological overview, systems analysis and economic assessment for a case study in Germany. Int. J. Hydrogen Energy 2015, 40, 4285–4294. [Google Scholar] [CrossRef]
- Tarrés, H.C. Determination of Potential Locations for Wind Turbines in Germany with Geospatial Information Systems. Bachelor’s Thesis, RWTH-Aachen, Aachen, Germany, 2014. [Google Scholar]
- Robinius, M.; ter Stein, F.; Schiebahn, S.; Stolten, D. Lastmodellierung und -visualisierung mittels Geoinformationssystemen. In Proceedings of the 13rd Symposium Energieinnovation, Graz, Austria, 12–14 February 2014. (In German). [Google Scholar]
- Robinius, M.; Rodriguez, R.A.; Kumar, B.; Andresen, G.B.; ter Stein, F.; Schiebahn, S.; Stolten, D. Optimal placement of electrolysers in a German power-to-gas infrastructure. In Proceedings of the 20th World Hydrogen Energy Conference (WHEC 2014), Gwangju, Korea, 15–20 June 2014. [Google Scholar]
- Franco, C.S.M. Estimation of the Technical Photovotaic Potential in Germany Using Geospatial Information System; RWTH-Aachen: Aachen, Germany, 2014. [Google Scholar]
- Tietze, V.; Stolten, D. Comparison of hydrogen and methane storage by means of a thermodynamic analysis. Int. J. Hydrogen Energy 2015, 40, 11530–11537. [Google Scholar] [CrossRef]
- Baufumé, S.; Grüger, F.; Grube, T.; Krieg, D.; Linssen, J.; Weber, M.; Hake, J.F.; Stolten, D. GIS-based scenario calculations for a nationwide German hydrogen pipeline infrastructure. Int. J. Hydrogen Energy 2013, 38, 3813–3829. [Google Scholar] [CrossRef]
- Robinius, M.; Stein, F.T.; Schwane, A.; Stolten, D. A Top-Down Spatially Resolved Electrical Load Model. Energies 2017, 10, 361. [Google Scholar] [CrossRef]
- Schiebahn, S.; Grube, T.; Robinius, M.; Otto, A.; Kumar, B.; Weber, M.; Stolten, D. Power to Gas. In Transition to Renewable Energy Systems; Stolten, D., Scherer, V., Eds.; Wiley-VCH: Hoboken, NJ, USA, 2013; pp. 813–849. [Google Scholar]
- Krieg, D. Konzept und Kosten eines Pipelinesystems zur Versorgung des deutschen Straßenverkehrs mit Wasserstoff. Ph.D. Thesis, Forschungszentrums Jülich, Jülich, Germany, 2012. (In German). [Google Scholar]
- ENTSO-E, Consumption Data. 2013. Available online: https://www.entsoe.eu/data/data-portal/consumption/ (accessed on 20 February 2017).
- Ter Stein, F. Regionale elektrische Lastmodellierung mittels Datenbank- und Geoinformationssystemen. Master’s Thesis, RWTH-Aachen, Aachen, Germany, 2014. (In German). [Google Scholar]
- Übertragungsnetzbetreiber. Netzentwicklungsplan Strom 2025 Offshore-Netzentwicklungsplan 2025 Version 2015; 2. Entwurf. 2016. Available online: https://www.netzentwicklungsplan.de/sites/default/files/paragraphs-files/NEP_ONEP_2025_2_Entwurf_Zahlen_Daten_Fakten.pdf (accessed on 20 February 2017). (In German).
- European Environment Agency. Corine Landcover 2006. Available online: https://www.eea.europa.eu/publications/COR0-landcover (accessed on 20 February 2017).
- European Topic Centre on Biological Diversity. EUNIS-sites: Common Database on Designated Areas. 2015. Available online: http://bd.eionet.europa.eu/activities/products/cdda (accessed on 20 February 2017).
- Geofabrik. Open Street Map. Available online: http://download.geofabrik.de/europe/germany.html (accessed on 20 February 2017).
- Adaramola, M.S.; Krogstad, P.Å. Experimental investigation of wake effects on wind turbine performance. Renew. Energy 2011, 36, 2078–2086. [Google Scholar] [CrossRef]
- Deutscher Wetterdienst. Winddaten für Deutschland. 2014. Available online: http://www.dwd.de/bvbw/appmanager/bvbw/dwdwwwDesktop?_nfpb=true&_pageLabel=_dwdwww_klima_umwelt_klimadaten_deutschland&_state=maximized&_windowLabel=T82002&T82002gsbDocumentPath=Navigation%252FOeffentlichkeit%252FKlima__Umwelt%252FKlimadaten%252Fkldaten__kostenfrei%252Fkldat__D__gebiete__wind__node.html%253F__nnn%253Dtrue (accessed on 20 February 2017). (In German).
- AG Energiebilanzen. Zeitreihen zur Entwicklung der erneuerbaren Energien in Deutschland; AG Energiebilanzen: Berlin, Germany, 2014. [Google Scholar]
- EnergyMap. Die Daten der EnergyMap zum Download. 2014. Available online: http://www.energymap.info/download.html (accessed on 20 February 2017).
- Quaschning, V. Systemtechnik einer klimaverträglichen Elektrizitätsversorgung in Deutschland für das 21. Jahrhundert; VDI-Verlag: Düsseldorf, Germany, 2000. (In German) [Google Scholar]
- Fraunhofer, I.W.E.S. Vorstudie zur Integration großer Anteile Photovoltaik in Die Elektrische Energieversorgung; IWES: Kassel, Germany, 2011. (In German) [Google Scholar]
- Lödl, M.; Kerber, G.; Witzmann, R.; Hoffmann, C.; Metzger, M. Abschätzung des Photovoltaik-Potenzials auf Dachflächen in Deutschland. In Proceedings of the Symposium Energieinnovation, Graz, Austria, 10–12 February 2010. (In German). [Google Scholar]
- Wesselak, V. Regenerative Energietechnik; Springer: Berlin/Heidelberg, Germany, 2013. (In German) [Google Scholar]
- Agora Energiewende. Agorameter-Dokumentation. 2014. Available online: http://www.agora-energiewende.de/fileadmin/downloads/sonstiges/Hintergrunddokumentation_Agora-Meter.pdf (accessed on 20 February 2017). (In German).
- Arbeitsgemeinschaft Energiebilanzen e.V. Energieverbrauch in Deutschland im Jahr 2013. Available online: www.ag-energiebilanzen.de/index.php?article_id=29&fileName=ageb_jahresbericht2013_20140317.pdf (accessed on 20 February 2017). (In German).
- Bundesnetzagentur. Kraftwerksliste 2013; Bundesnetzagentur: Bonn, Germany, 2013. [Google Scholar]
- Wend, A. Modellierung des Deutschen Strommarktes unter Verwendung der Residuallast; Institut für Brennstoffzellen, RWTH Aachen: Aachen, Germany, 2014. (In German) [Google Scholar]
- 50 Hertz Transmission GmbH. Lastflüsse. 2013. Available online: http://www.50hertz.com/de/Anschluss-Zugang/Engpassmanagement/Lastfluesse (accessed on 20 February 2017).
- Amprion GmbH. Berechnung von Regelblocküberschreitenden Übertragungskapazitäten zu Internationalen Partnernetzen; Amprion GmbH: Dortmund, Germany, 2012; p. 8. (In German) [Google Scholar]
- Amprion GmbH. Grenzüberschreitende Lastflüsse; Amprion GmbH: Dortmund, Germany, 2013. [Google Scholar]
- ENTSO-E. Exchange Data. 2014. Available online: https://www.entsoe.eu/data/data-portal/exchange/Pages/default.aspx (accessed on 20 February 2017).
- Nord Pool Spot. Historical Market Data. 2015. Available online: http://www.nordpoolspot.com/historical-market-data/ (accessed on 20 February 2017).
- Tennet TSO GmbH. Grenzüberschreitende Lastflüsse/abgestimmte Fahrpläne. 2015. Available online: https://www.tennettso.de/site/Transparenz/veroeffentlichungen/netzkennzahlen/grenzueberschreitende-lastfluesse (accessed on 20 February 2017). (In German).
- TransnetBW GmbH. Grenzüberschreitende Lastflüsse. 2015. Available online: http://www.transnetbw.de/de/kennzahlen/lastdaten/grenzueberschreitende-lastfluesse?app=last&activeTab=table&auswahl=day&date=10.03.2015&view=3&selectMonatDownload=15 (accessed on 20 February 2017). (In German).
- Übertragungsnetzbetreiber. Netzentwicklungsplan Strom 2014 zweiter Entwurf der Übertragungsnetzbetreiber; Übertragungsnetzbetreiber: Bonn, Germany, 2014; p. 137. (In German) [Google Scholar]
- Bystry, T. H2 mobility—Germany. In Proceedings of the H2Expo 2014, Hamburg, Germany, 23–26 September 2014. [Google Scholar]
- De Colvenaer, B. Fuel Cells and Hydrogen Joint Undertaking European Hydrogen Infrastructure Activities. In Proceedings of the H2Expo 2014, Hamburg, Germany, 23–26 September 2014. [Google Scholar]
- Ehret, O. Nationale initiativen für wasserstoff als marktnahe querschnittstechnologie; DBI-Fachforum ENERGIESPEICHER—HYBRIDNETZE: Berlin, Germany, 2012. (In German) [Google Scholar]
- GermanHy. Woher kommt der Wasserstoff in Deutschland bis 2050? GermanHy: Berlin, Germany, 2009. (In German) [Google Scholar]
- Höft, U. Lebenszykluskonzepte: Grundlage für das Strategische Marketing-und Technologiemanagement; Erich Schmidt Verlag GmbH & Co. KG: Berlin, Germany, 1992. (In German) [Google Scholar]
- Bundesministerium für Verkehr und digitale Infrastruktur. Verkehr in Zahlen 2014/2015; Bundesministerium für Verkehr und digitale Infrastruktur: Berlin, Germany, 2015. (In German) [Google Scholar]
- Fraunhofer ISI. Markthochlaufszenarien für Elektrofahrzeuge—Langfassung; Fraunhofer ISI: Karlsruhe, Germany, 2014. [Google Scholar]
- Kraftfahrt-Bundesamt. Kraftfahrzeugbestand nach Kraftfahrzeugarten; Kraftfahrt-Bundesamt: Flensburg, Germany, 2015. (In German) [Google Scholar]
- Toyota. Serien-Brennstoffzellenfahrzeug—Beste Effizienz am Markt. 2015. Available online: http://www.toyota.de/news/details-2015–43.json (accessed on 20 February 2017). (In German).
- Keles, D.; Wietschel, M.; Möst, D.; Rentz, O. Market penetration of fuel cell vehicles—Analysis based on agent behaviour. Int. J. Hydrogen Energy 2008, 33, 4444–4455. [Google Scholar] [CrossRef]
- Reuß, M.; Grube, T.; Robinius, M.; Preuster, P.; Wasserscheid, P.; Stolten, D. Seasonal storage and alternative carriers: A flexible hydrogen supply chain model. Appl. Energy 2017, 200, 290–302. [Google Scholar] [CrossRef]
- Grüger, F. Nachfrageorientierte Kapazitätsbestimmung einer Wasserstoffinfrastruktur für Deutschland. Master’s Thesis, RWTH Aachen, Aachen, Germany, 2011. (In German). [Google Scholar]
- Feck, T. Wasserstoff-Emissionen und ihre Auswirkungen auf den Arktischen Ozonverlust: Risikoanalyse einer globalen Wasserstoffwirtschaft; Forschungszentrum Jülich: Jülich, Germany, 2009. (In German) [Google Scholar]
- Bundesnetzagentur and Bundeskartellamt. Monitoringbericht 2013, 3. Auflage; Bundesnetzagentur and Bundeskartellamt: Bonn, Germany, 2014. (In German) [Google Scholar]
- Die Fernleitungsnetzbetreiber. Netzentwicklungsplan Gas 2015—Konsultationsdokument; Die Fernleitungsnetzbetreiber: Bonn, Germany, 2015. (In German) [Google Scholar]
- Stolten, D.; Grube, T.; Mergel, J. Beitrag Elektrochemischer Energietechnik zur Energiewende; VDI-Berichte: Düsseldorf, Germany, 2012. (In German) [Google Scholar]
- Südwest Presse. Daimler baut früher Autos mit Brennstoffzellen. 2011. Available online: http://www.swp.de/ulm/nachrichten/wirtschaft/Daimler-baut-frueher-Autos-mit-Brennstoffzellen;art4325,988215 (accessed on 20 February 2017). (In German).
- Geitmann, S. Wasserstoff und Brennstoffzellen: Die Technik von Morgen; Hydrogeit-Verlag: Oberkrämer, Germany, 2004. (In German) [Google Scholar]
- Geitmann, S. Energiewende 3.0: Mit Wasserstoff und Brennstoffzellen; Hydrogeit-Verlag: Oberkrämer, Germany, 2012. (In German) [Google Scholar]
- National Renewable Energy Lab. Hydrogen Station Cost Estimates—Comparing Hydrogen Station Cost Calculator Results with Other Recent Estimates; National Renewable Energy Lab: Golden, CO, USA, 2013.
- DOE Hydrogen and Fuel Cells Program Record. Hydrogen Production Cost from PEM Electrolysis; U.S. Department of Energy: Washington, DC, USA, 2014.
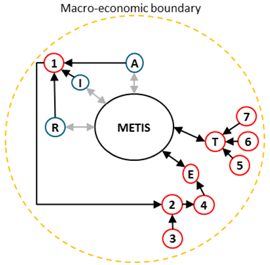 | Sub-Models | Considered Sectors | ||
| 1 | Electricity-Load-Model (ELM) [16,22,27] | T | Transport | |
| 2 | Regional Electricity Market Program (REMP) [16] | I | Industry, trade and commerce | |
| 3 | RES Potential Model [16,17] | R | Residential/households | |
| 4 | Electricity Grid Model [16] | A | Agriculture | |
| 5 | Hydrogen Pipeline Model [20,25,26,28,29] | E | Energy | |
| 6 | Hydrogen Demand Model [16] | |||
| 7 | Electrolysis Utilization Model [16] | |||
| Input-Data | Best Case | Middle Case | Worst Case |
|---|---|---|---|
| Electricity costs (ct/kWh) | 2.4 | 5.8 | 6 |
| Weighted average cost of capital (WACC) (%) | 3 | 8 | 8 |
| Electrolysis: | |||
| Investment costs (€/kW) | 446 | 500 | 500 |
| Efficiency (%) | 76 | 70 | 70 |
| Operating costs as a share of the investment costs (%) | 0.4 | 3 | 3 |
| Hydrogen Storage (Salt Caverns): | |||
| Size (TWh) | 15 | 48 | 90 |
| Costs (Bil. €) | 2.7 | 8 | 15 |
| Hydrogen Pipeline Grid: | |||
| Peak hydrogen demand (Mil. t) | 2.9 | 2.9 | 2.9 |
| Costs transmission pipeline (Bil. €) | 5.4 | 6.7 | 8.3 |
| Costs distribution pipeline (Bil. €) | 10.1 | 12 | 14.6 |
| Hydrogen Fuelling Station: | |||
| Costs per fuelling station (Mil. €) | 2 | 2 | 2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robinius, M.; Otto, A.; Syranidis, K.; Ryberg, D.S.; Heuser, P.; Welder, L.; Grube, T.; Markewitz, P.; Tietze, V.; Stolten, D. Linking the Power and Transport Sectors—Part 2: Modelling a Sector Coupling Scenario for Germany. Energies 2017, 10, 957. https://doi.org/10.3390/en10070957
Robinius M, Otto A, Syranidis K, Ryberg DS, Heuser P, Welder L, Grube T, Markewitz P, Tietze V, Stolten D. Linking the Power and Transport Sectors—Part 2: Modelling a Sector Coupling Scenario for Germany. Energies. 2017; 10(7):957. https://doi.org/10.3390/en10070957
Chicago/Turabian StyleRobinius, Martin, Alexander Otto, Konstantinos Syranidis, David S. Ryberg, Philipp Heuser, Lara Welder, Thomas Grube, Peter Markewitz, Vanessa Tietze, and Detlef Stolten. 2017. "Linking the Power and Transport Sectors—Part 2: Modelling a Sector Coupling Scenario for Germany" Energies 10, no. 7: 957. https://doi.org/10.3390/en10070957
APA StyleRobinius, M., Otto, A., Syranidis, K., Ryberg, D. S., Heuser, P., Welder, L., Grube, T., Markewitz, P., Tietze, V., & Stolten, D. (2017). Linking the Power and Transport Sectors—Part 2: Modelling a Sector Coupling Scenario for Germany. Energies, 10(7), 957. https://doi.org/10.3390/en10070957






