Complementary Power Control for Doubly Fed Induction Generator-Based Tidal Stream Turbine Generation Plants
Abstract
:1. Introduction
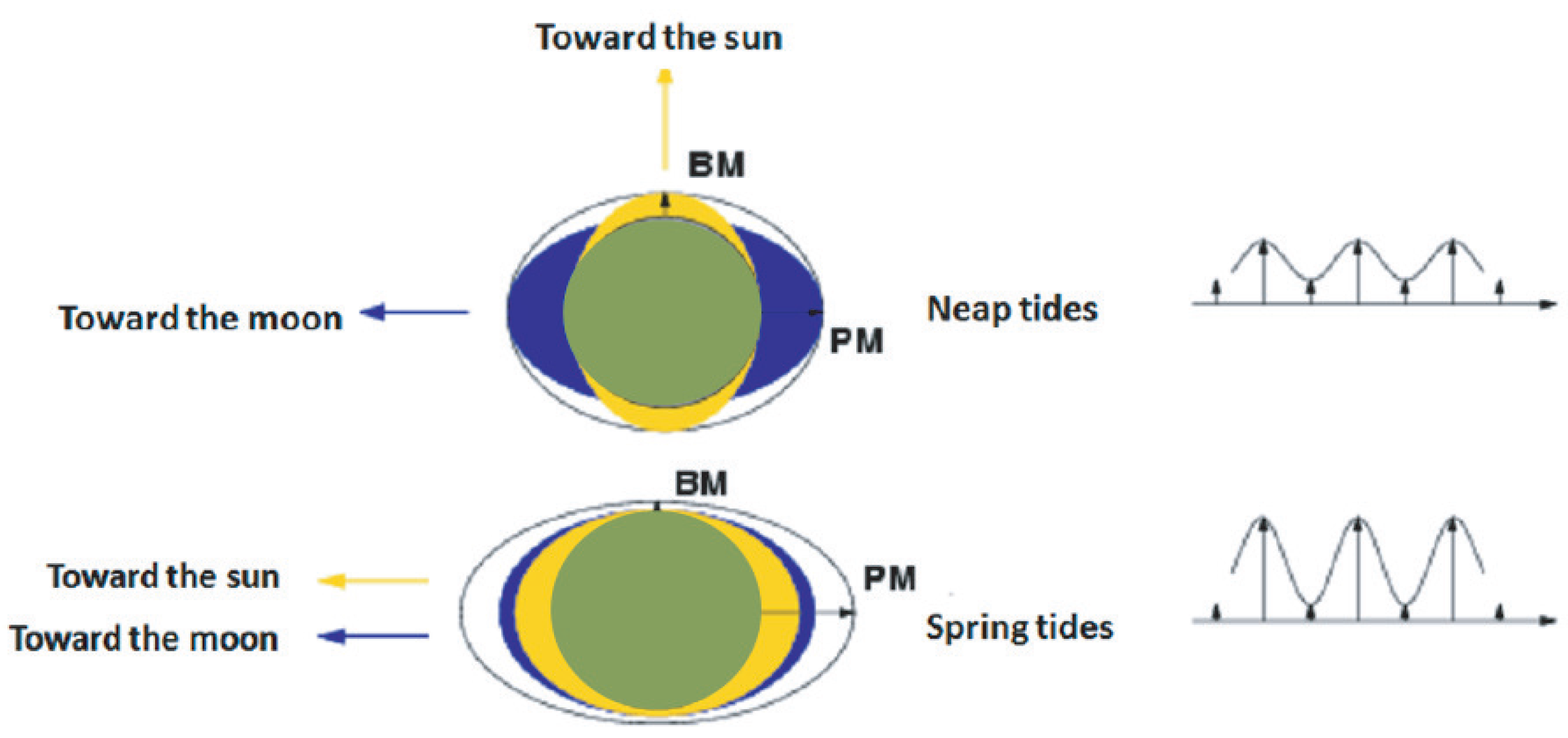
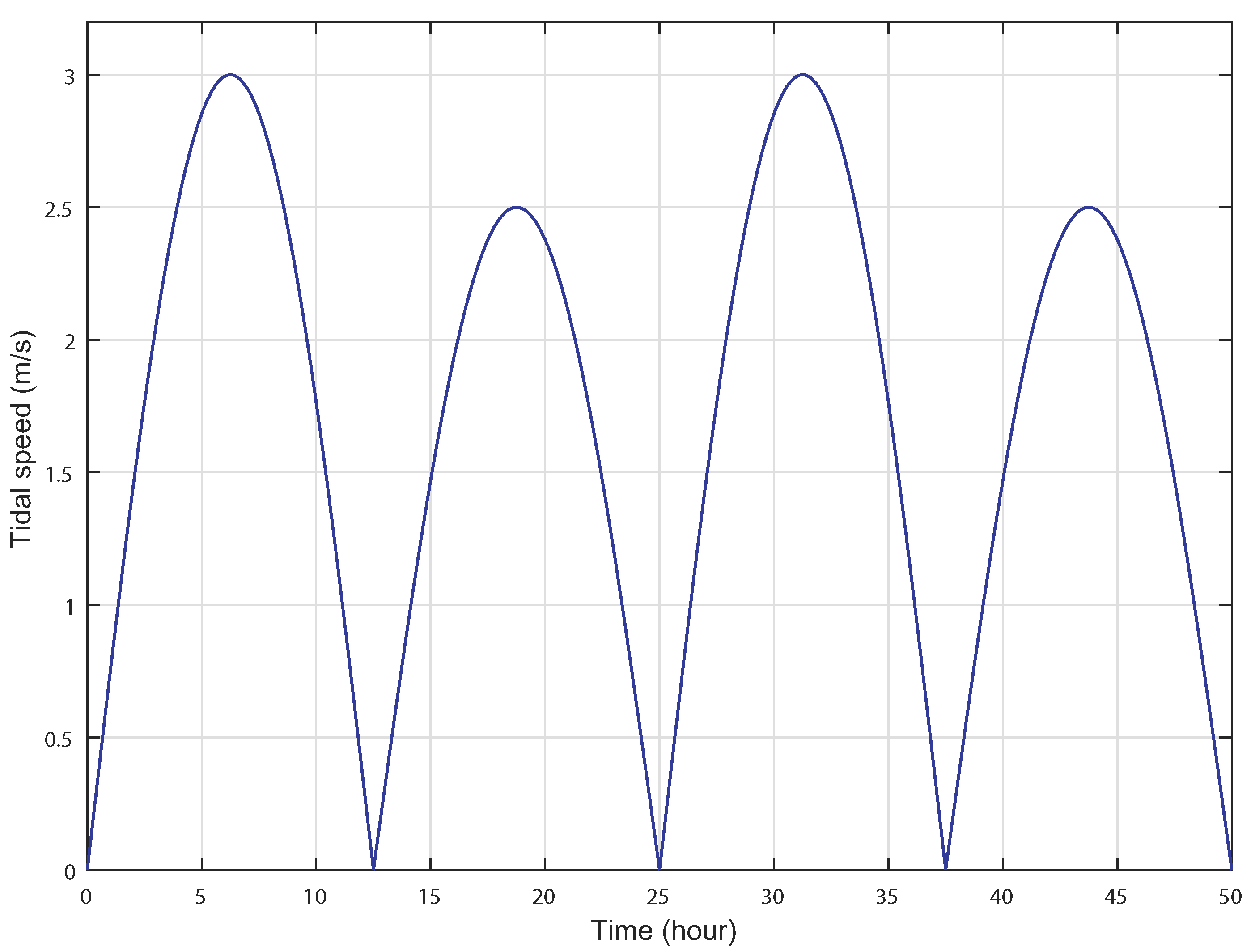
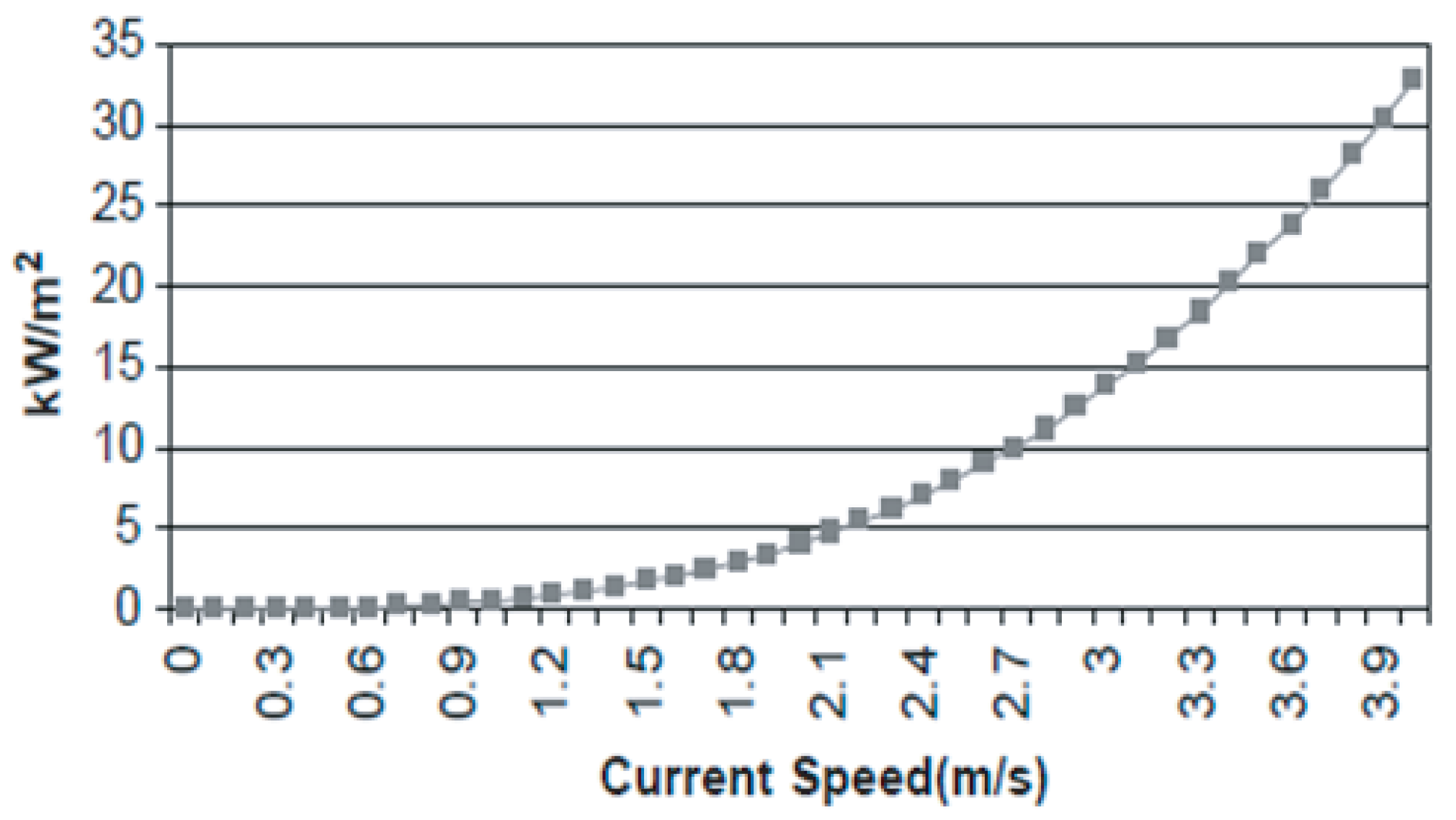
2. Background on Tidal Power
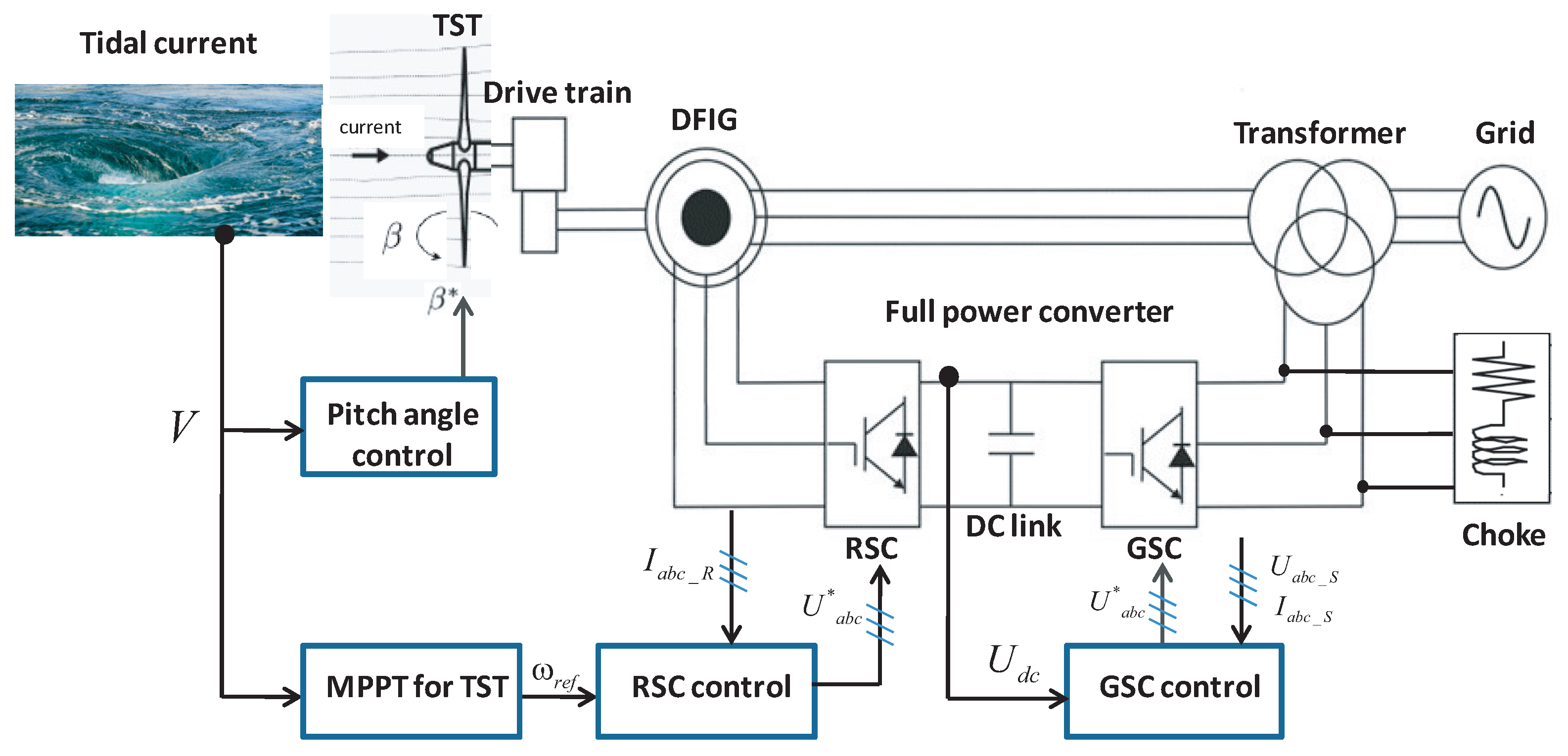
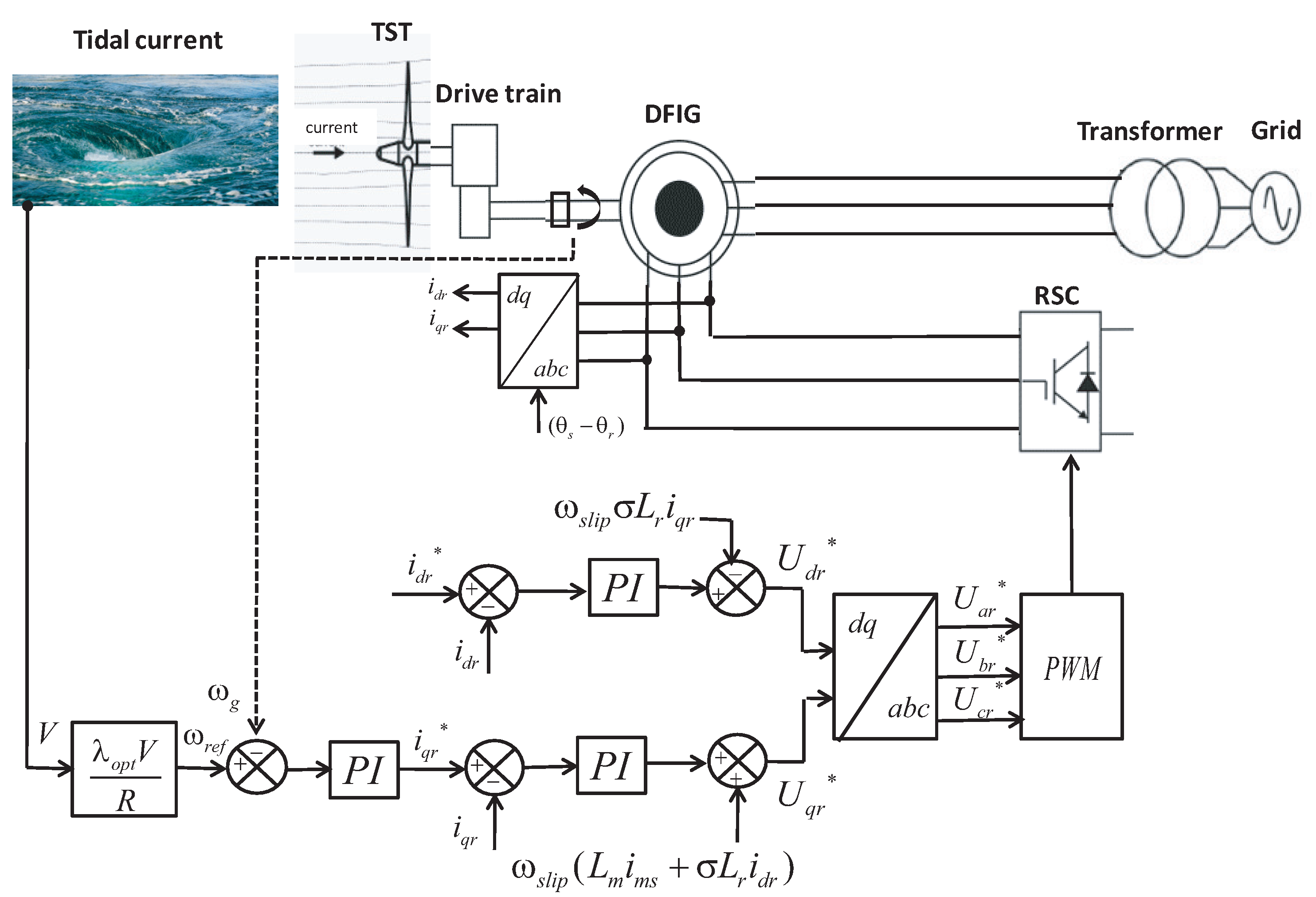
3. System Description
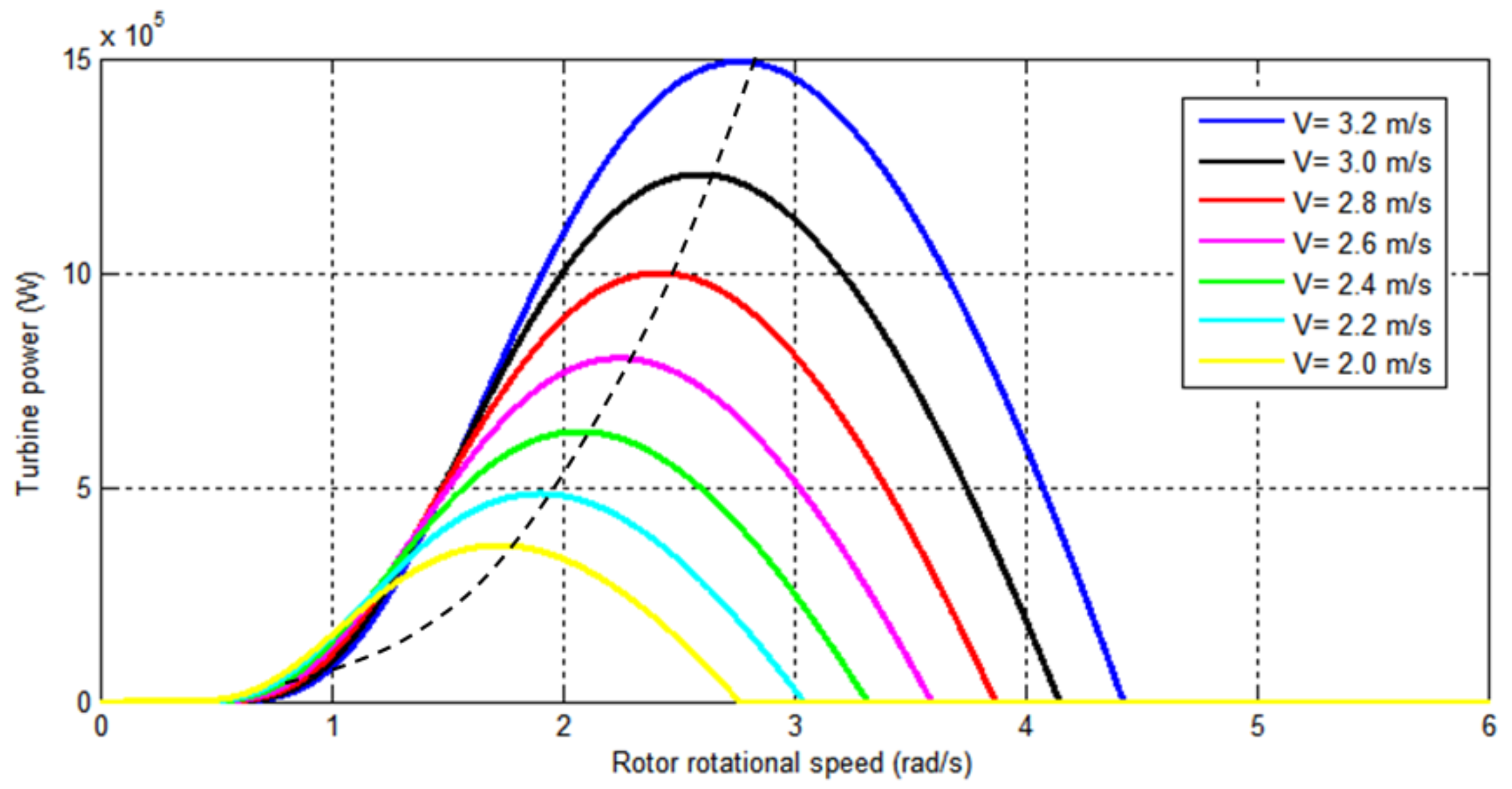
3.1. Hydrodynamic Turbine Model
3.2. Drive-Train Two-Mass Model
3.3. Doubly-Fed Induction Generator Model
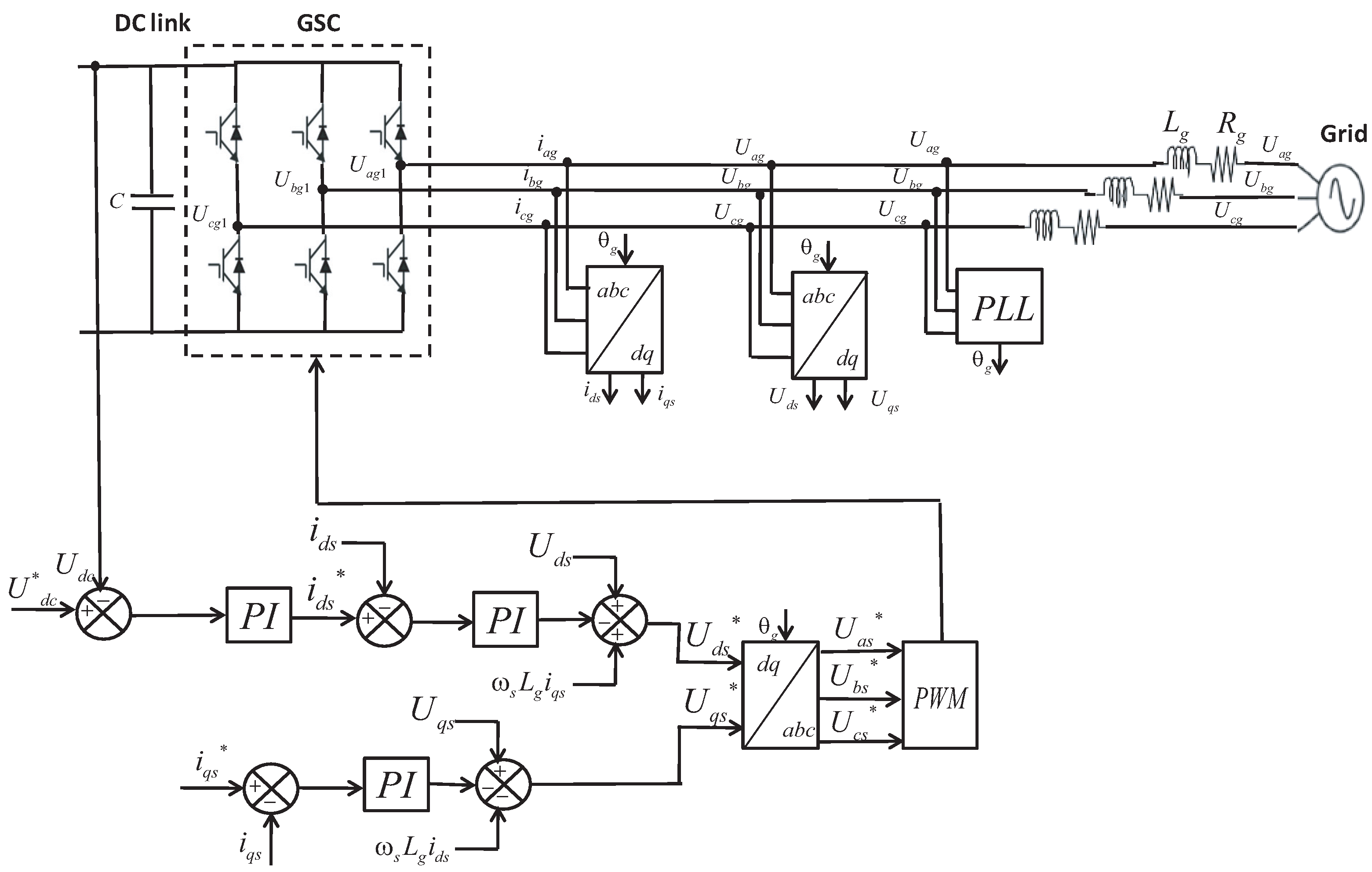
3.4. Back-To-Back Converters
4. Control Objectives and Strategies
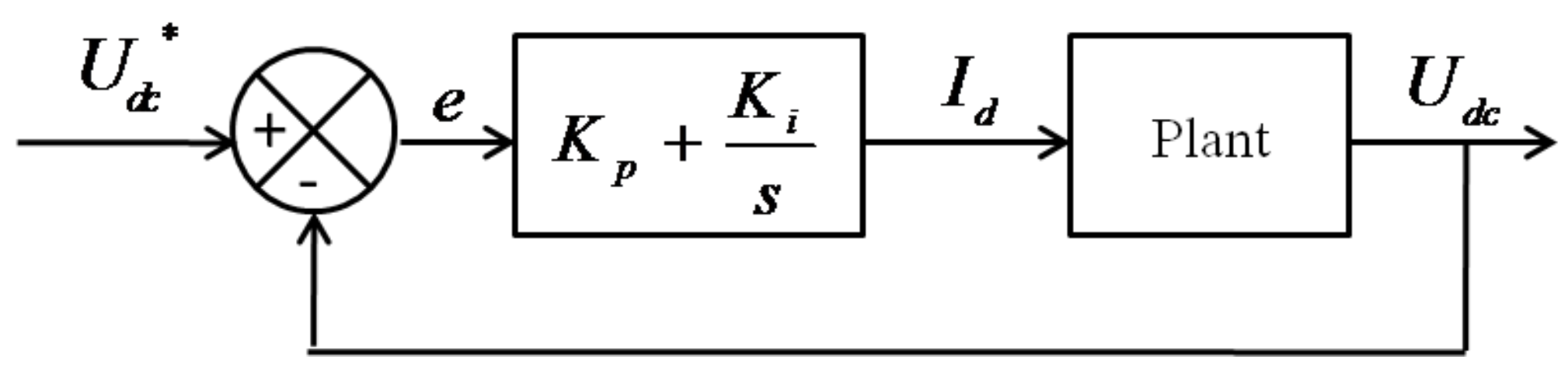
4.1. GSC DC-Link Control Design
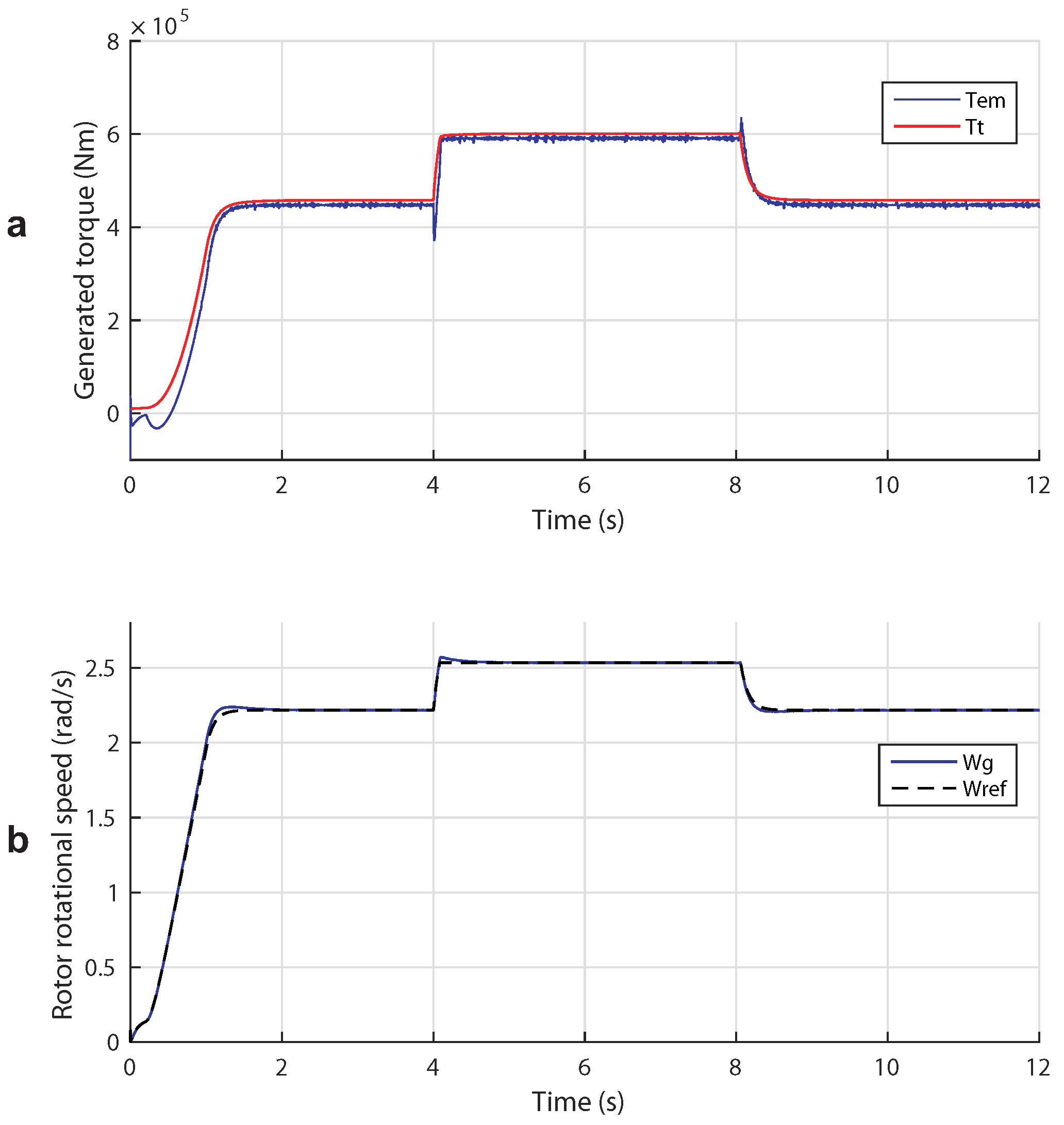
4.2. RSC Rotational Speed Control Design
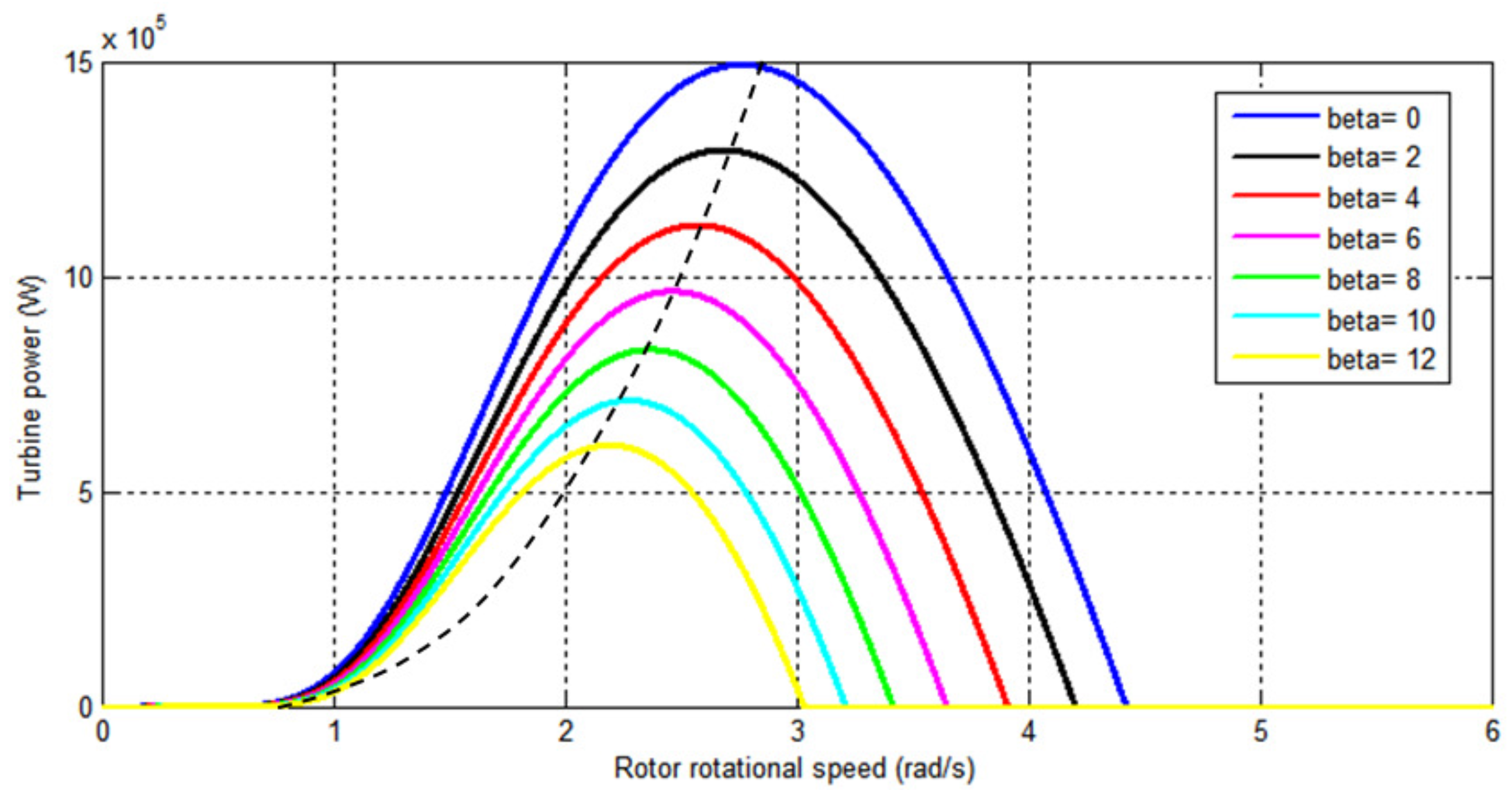
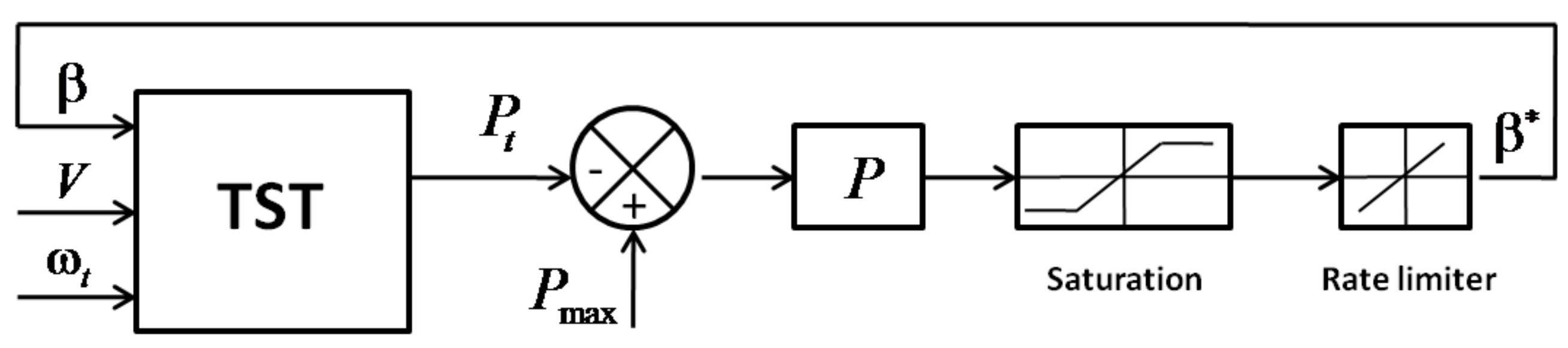
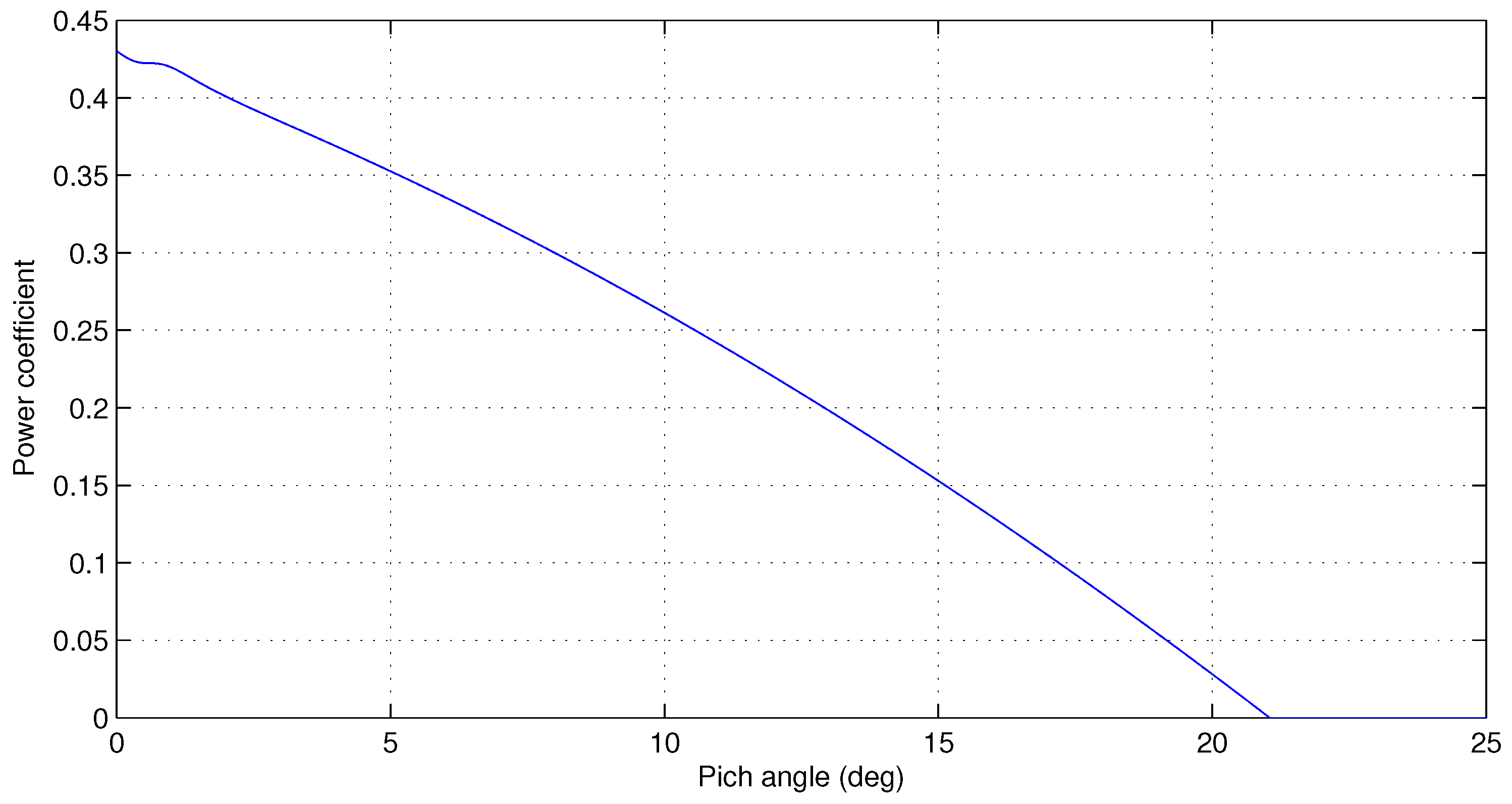
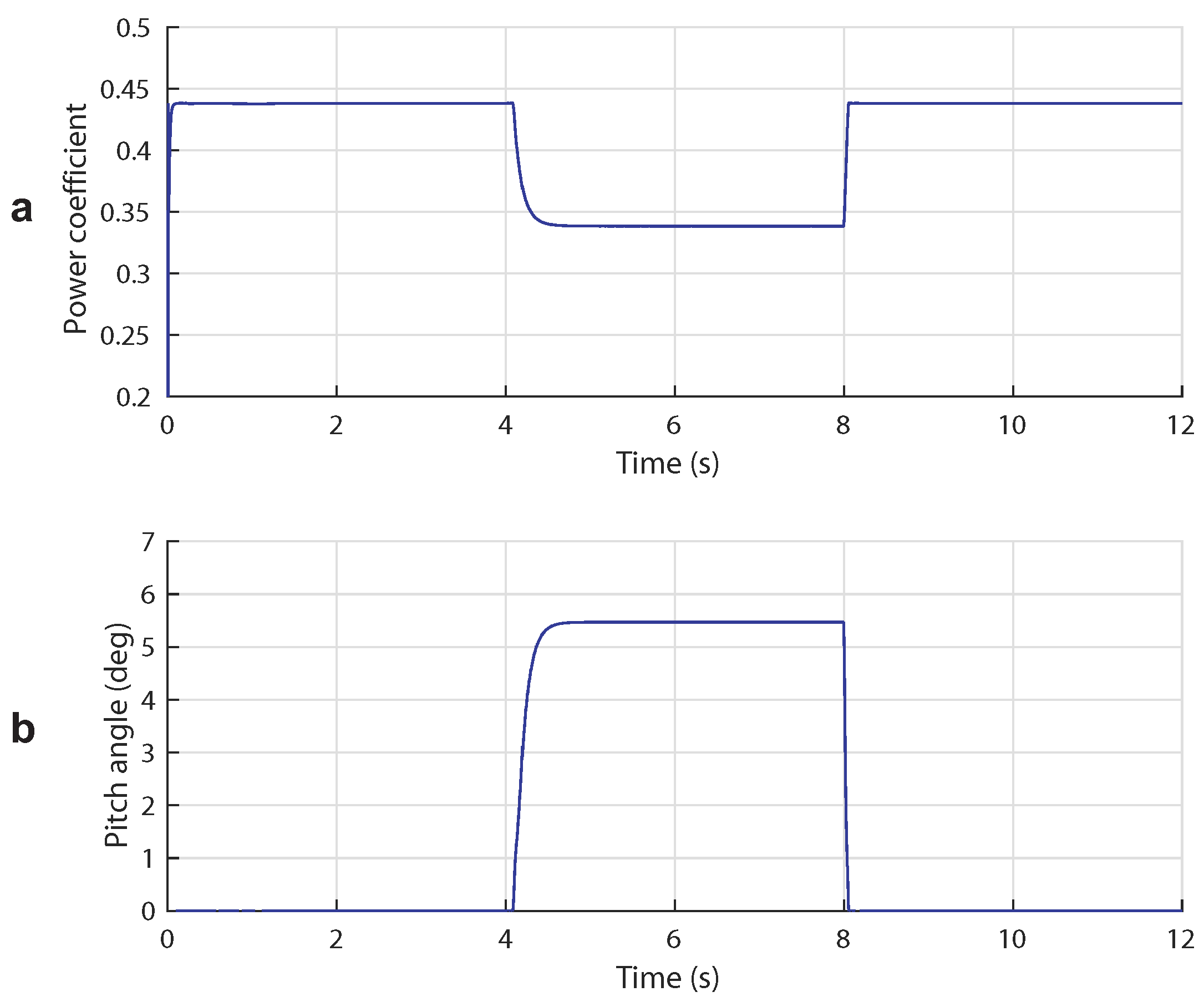
4.3. Pitch Angle Control
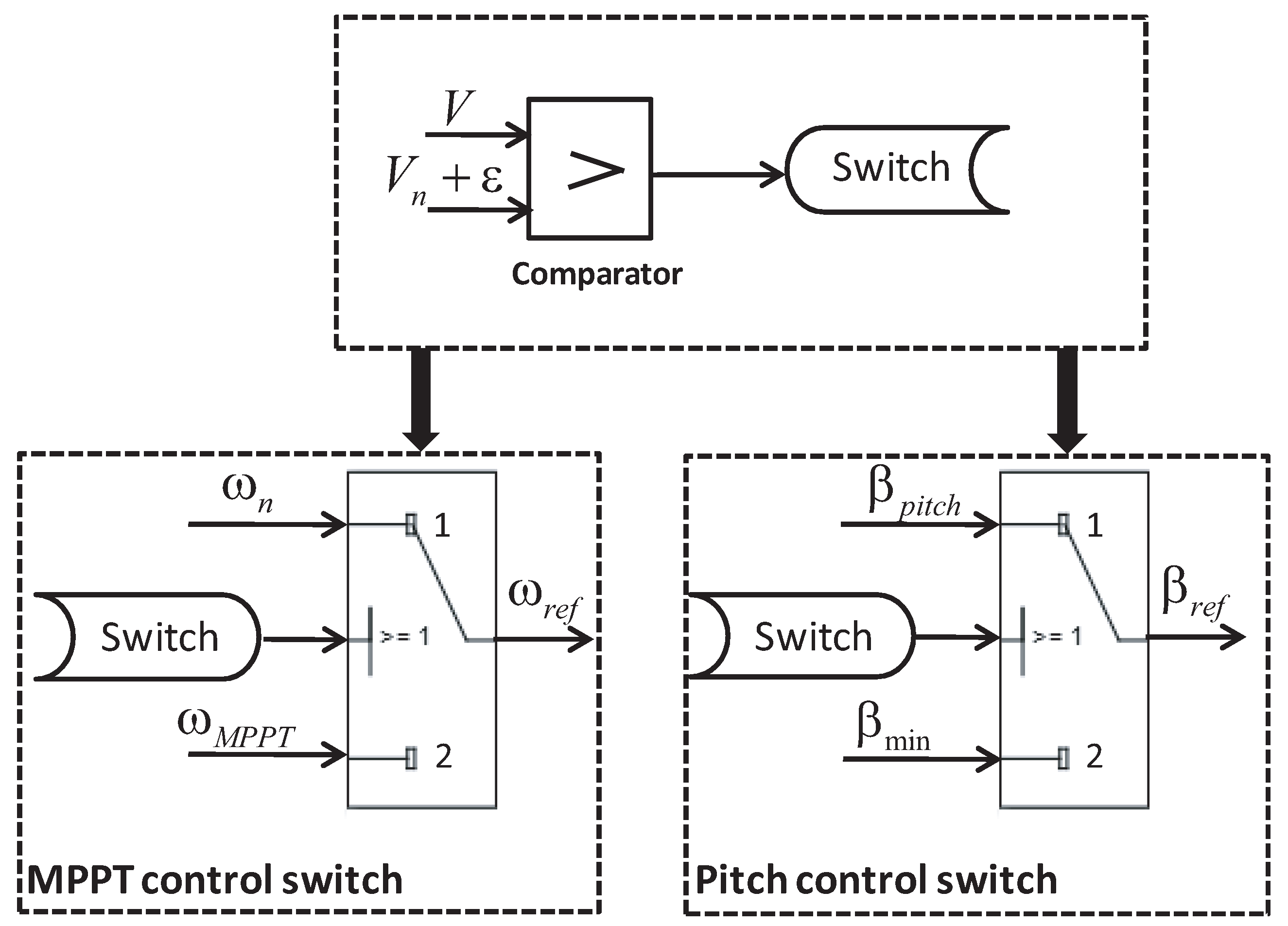
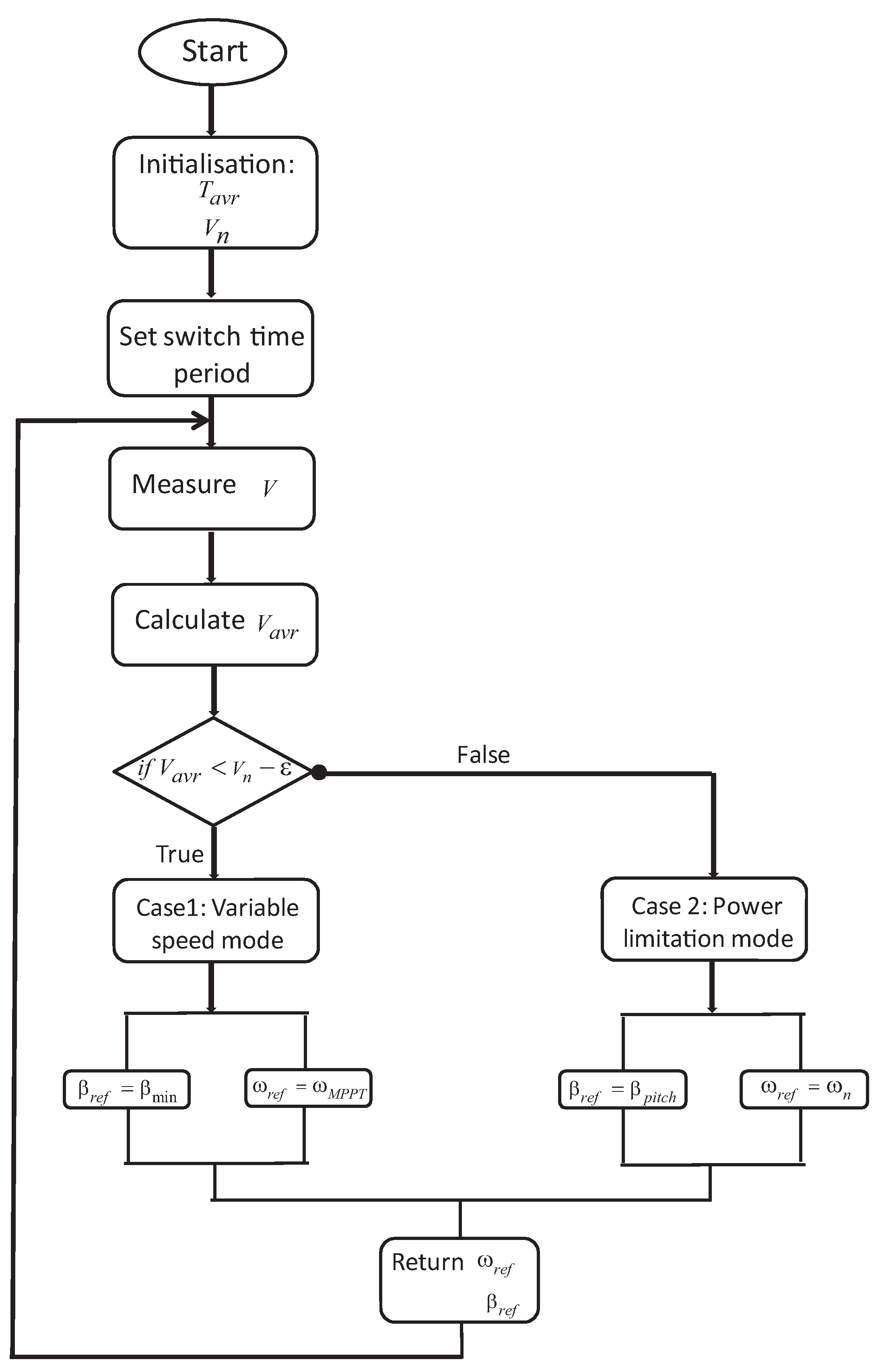
4.4. Complementary Control
5. Results and Discussion
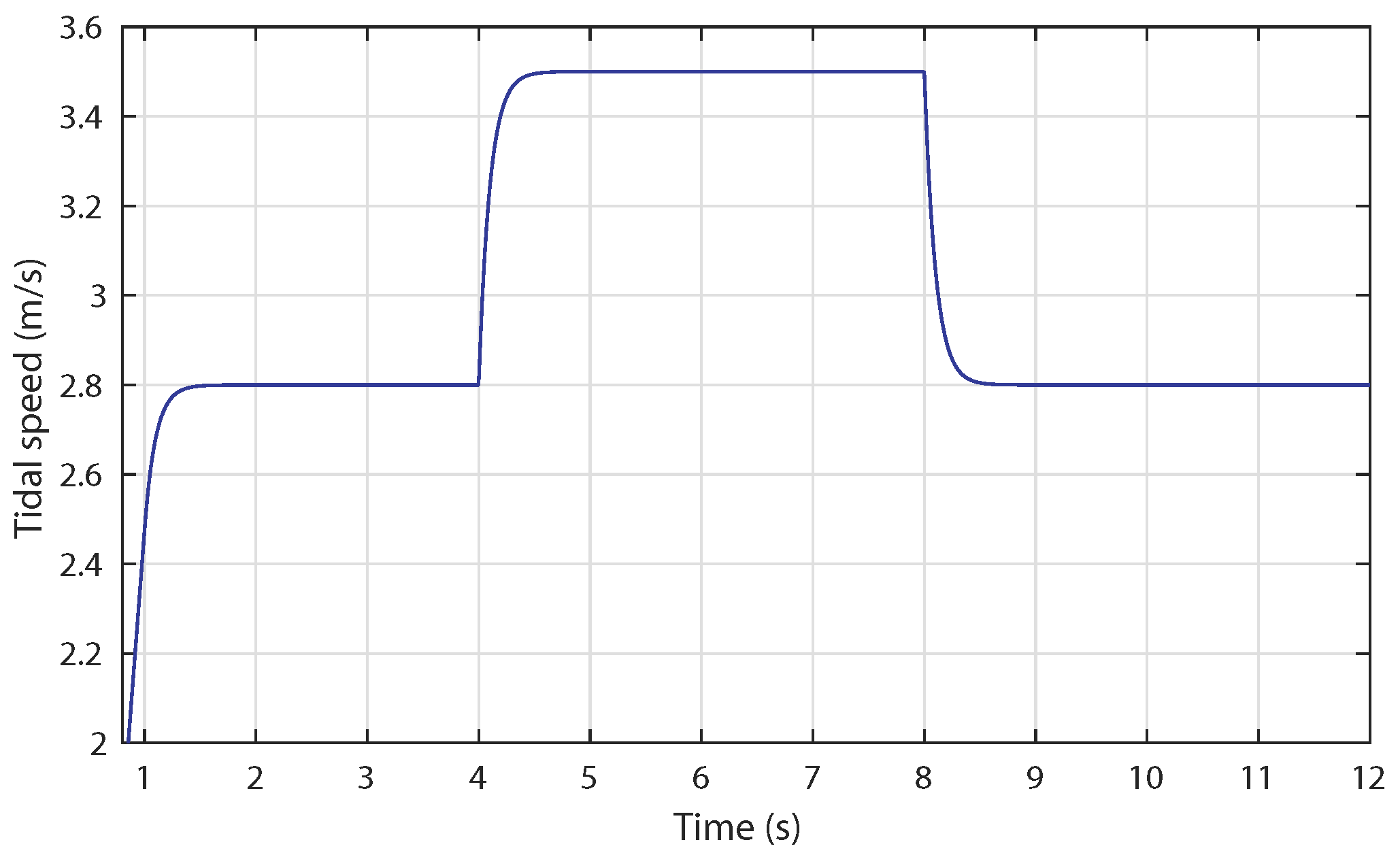
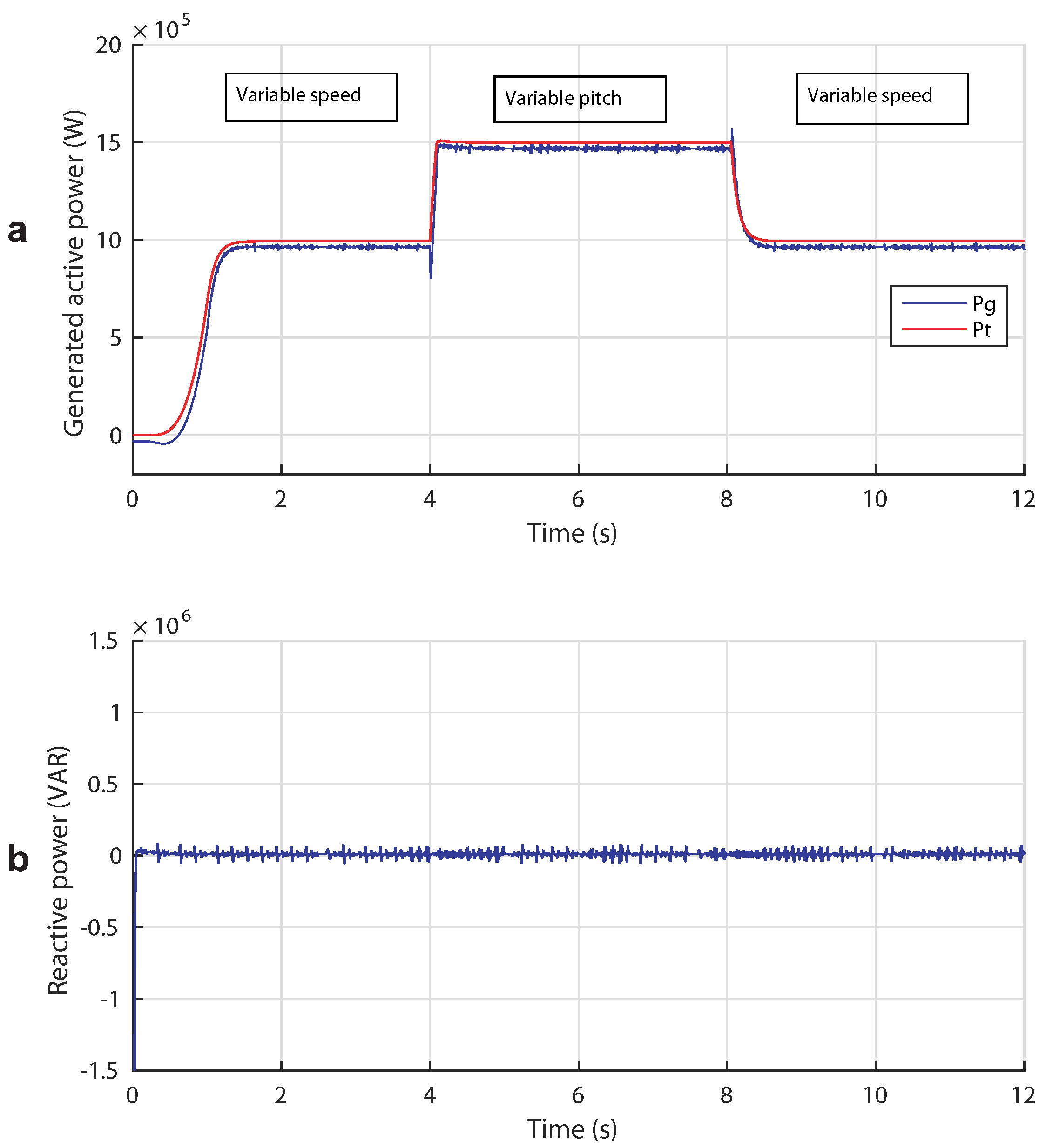
5.1. Case 1: Low Tidal Speed (Variable Speed Operation)
5.2. Case 2: High Tidal Speed (Power Limitation Mode)
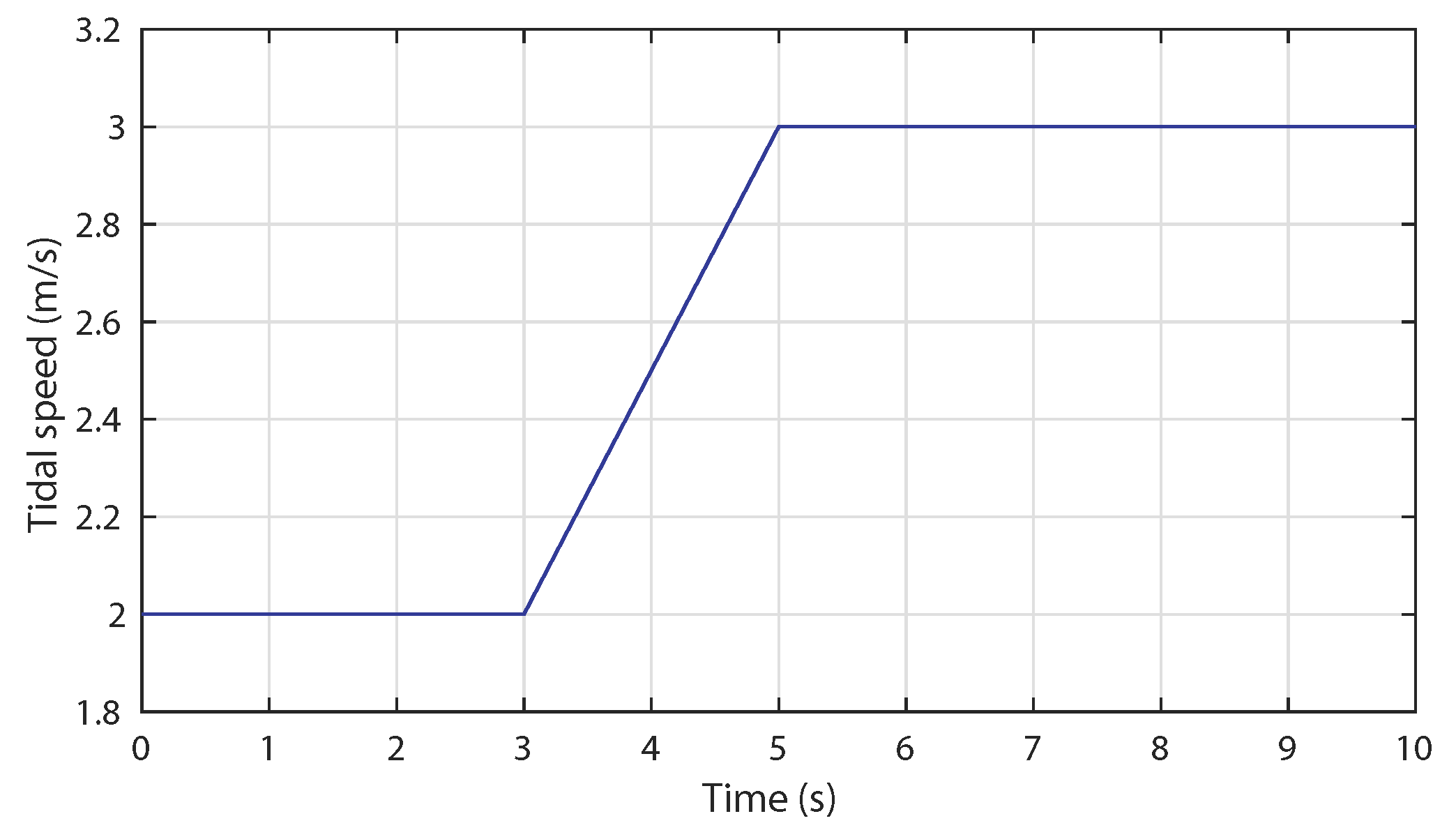
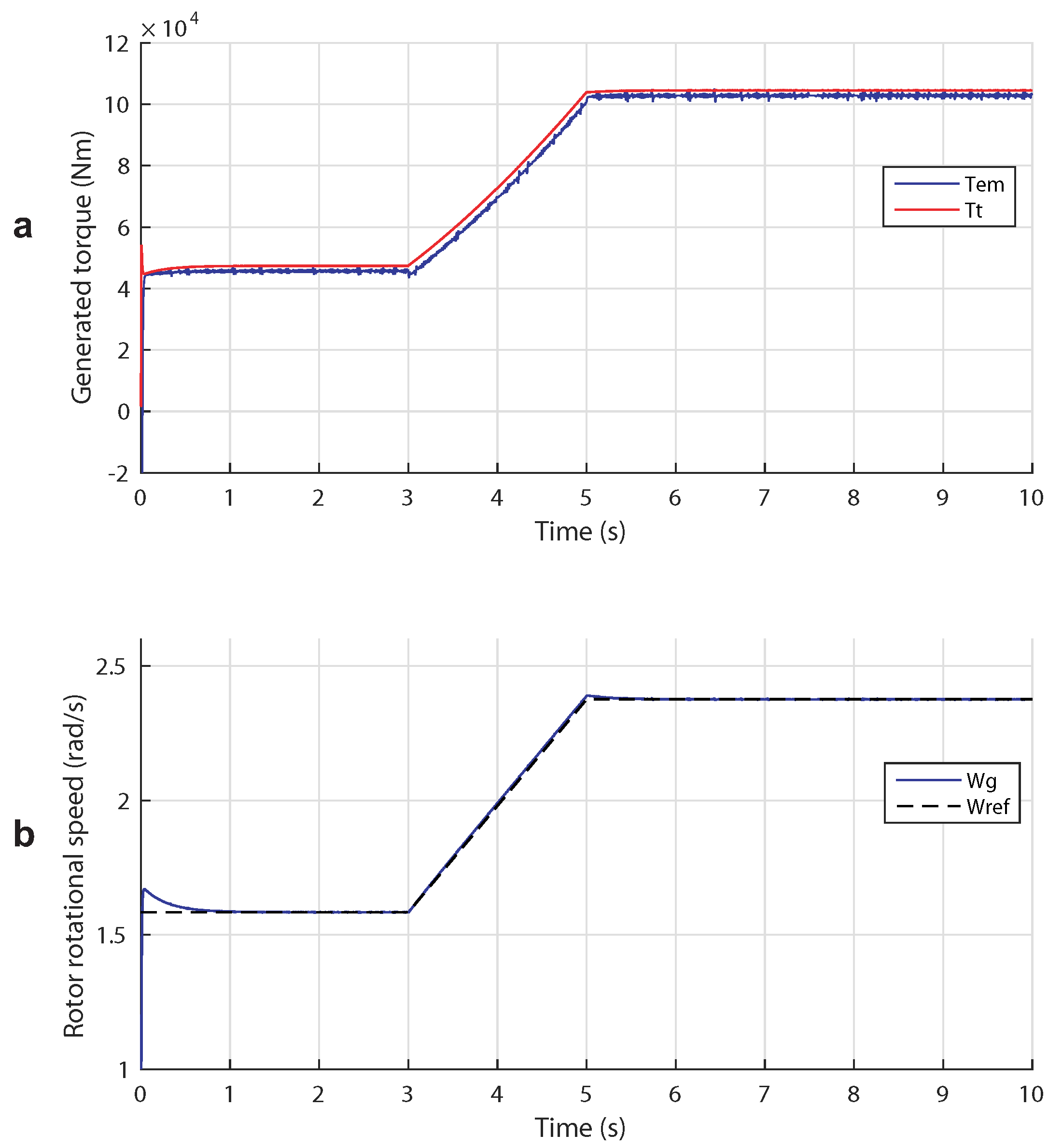
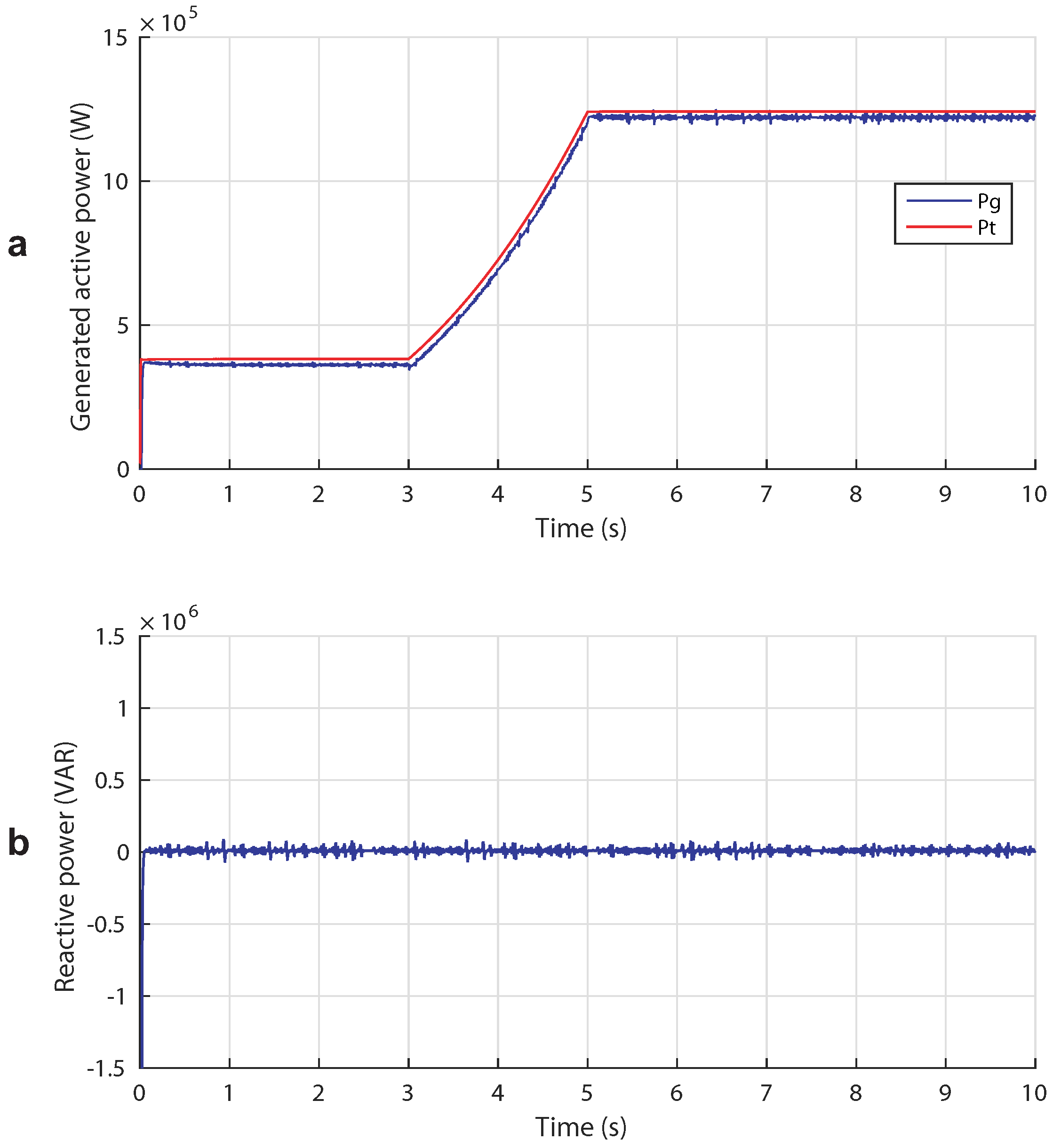
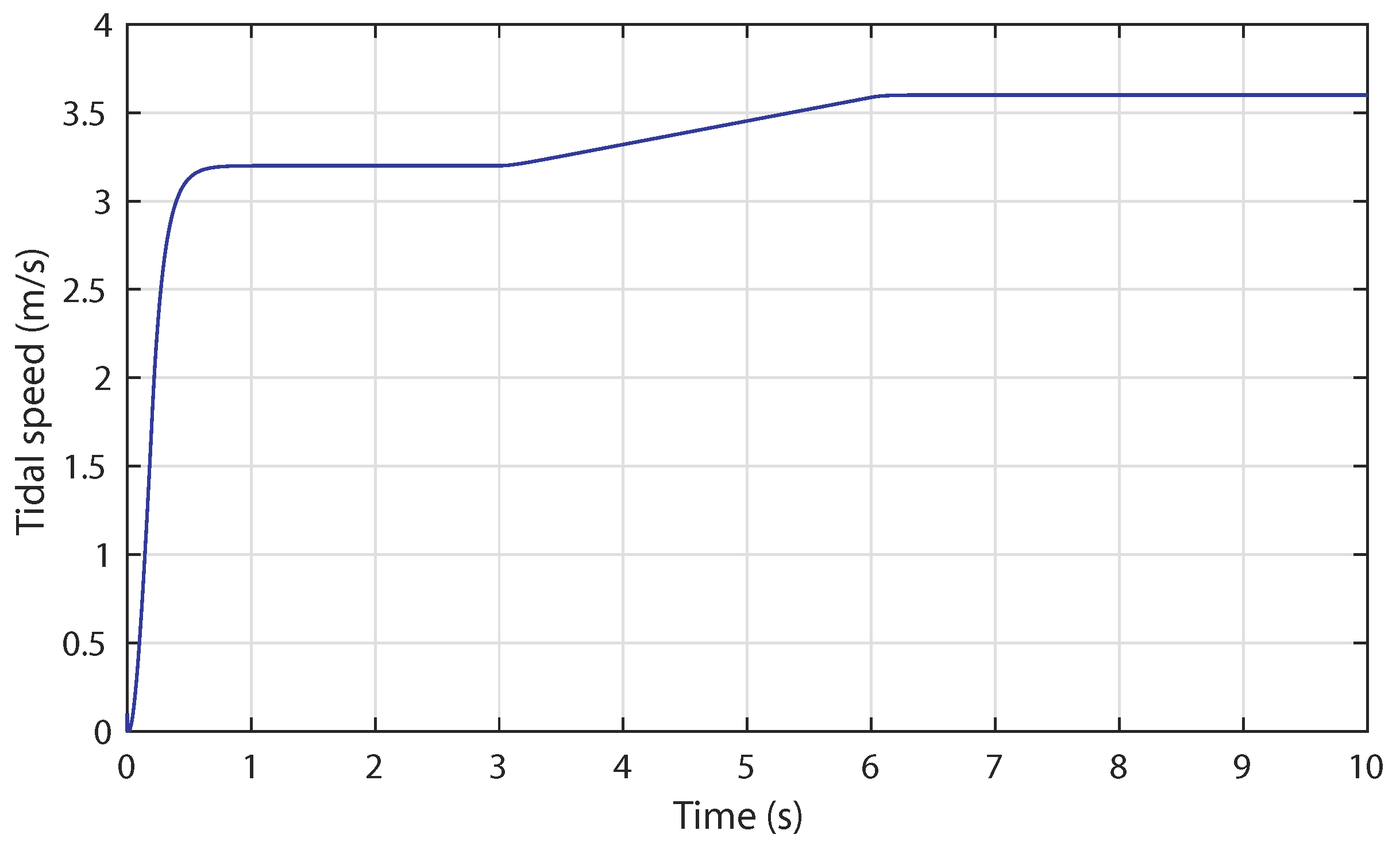
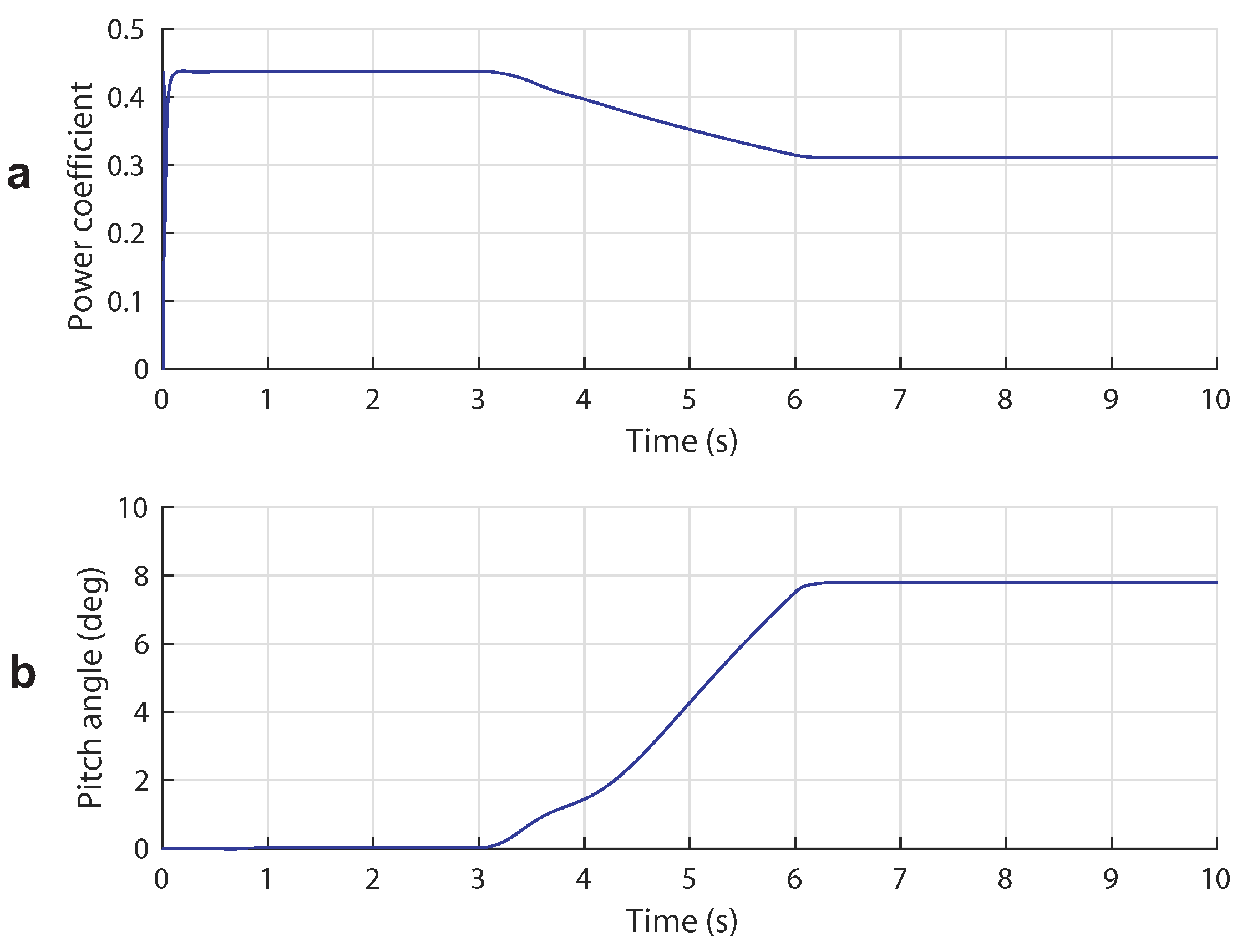
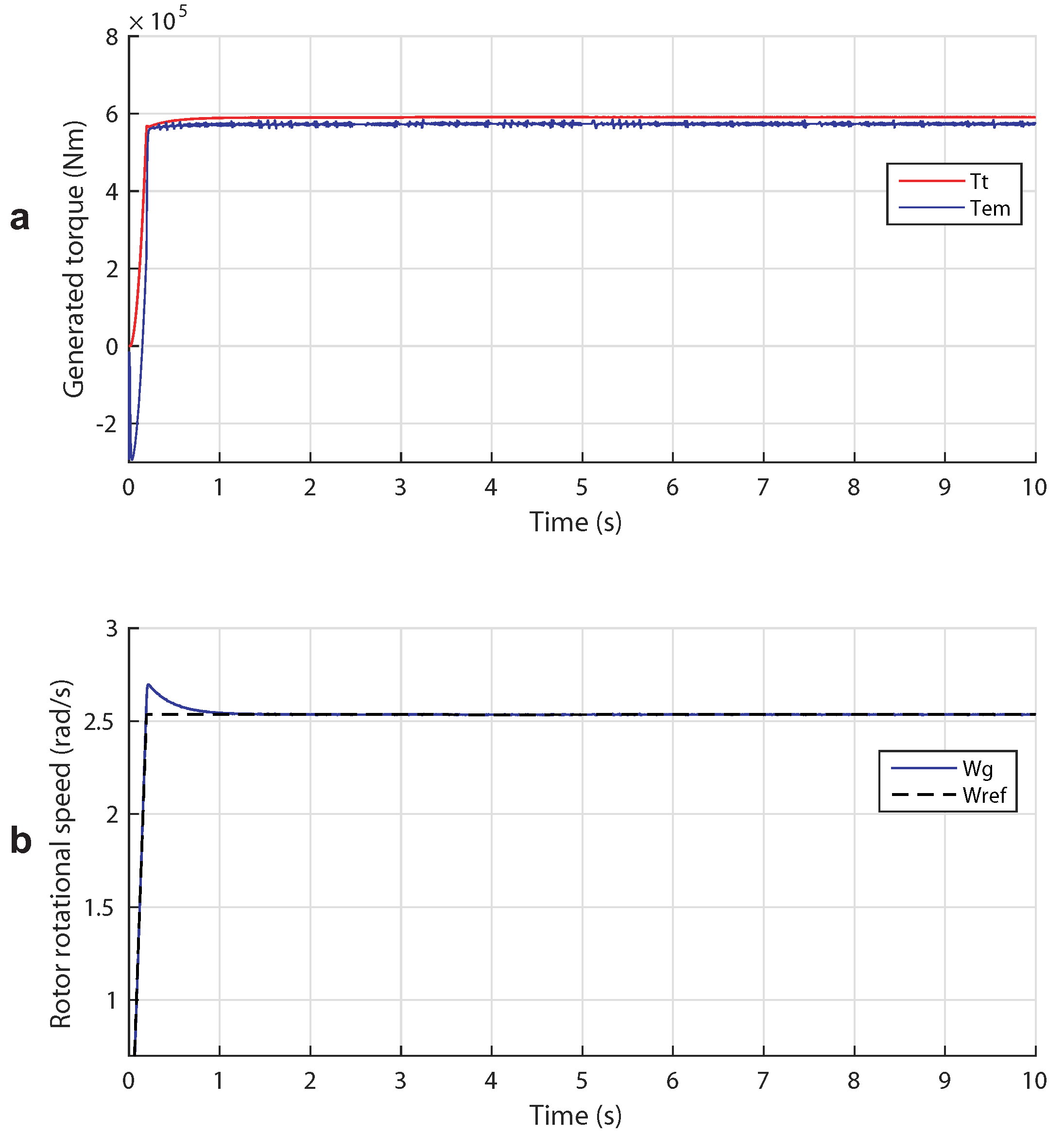
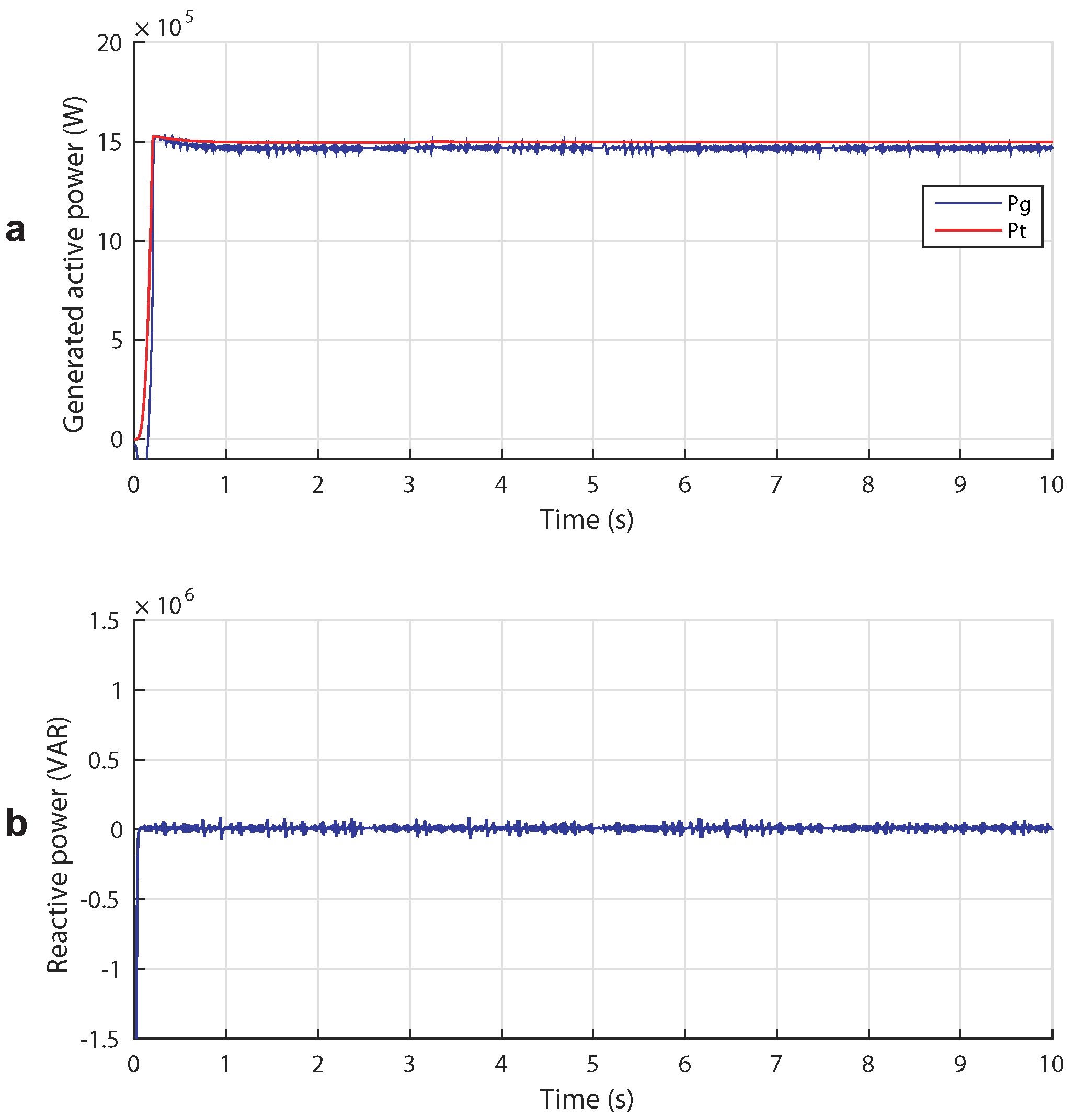
5.3. Case 3: Broad Tidal Speed Range (Complementary Control)
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kempener, R.; Neumann, F. IRENA Ocean Energy Tech Brief 3; Tidal Energy Technology Brief; IRENA: Abu Dhabi, UAE, 2014. [Google Scholar]
- Ocean Energy Forum. Draft Ocean Energy Strategic Roadmap Building Ocean Energy For Europe; Technical Report; European Commission: Brussels, Belgium, 2015. [Google Scholar]
- European Commission. Ocean Energy Europe and TP Ocean; Issue Paper on Ocean Energy Industry Response; European Commission: Brussels, Belgium, 2016. [Google Scholar]
- Hess, H.L.; Abdul Melek, N.A.; Muljadi, E. Power converter for wind turbine application. In Proceedings of the 2000 IEEE Power Engineering Society Summer Meeting, Washington, DC, USA, 16–20 July 2000; Volume 2, pp. 1275–1276. [Google Scholar]
- Blaabjerg, F.; Iov, F.; Terekes, T.; Teodorescu, R. Power electronics-key technology for renewable energy systems. In Proceedings of the 2011 2nd Power Electronics, Drive Systems and Technologies Conference (PEDSTC), Tehran, Iran, 16–17 February 2011; pp. 445–466. [Google Scholar]
- Zhou, D.; Blaabjerg, F.; Lau, M.; Tonnes, M. Optimized reactive power flow of DFIG power converters for better reliability performance considering grid codes. IEEE Trans. Ind. Electron. 2015, 62, 1552–1562. [Google Scholar] [CrossRef]
- Hu, J.; Nian, H.; Xu, H.; He, Y. Dynamic modeling and improved control of DFIG under distorted grid voltage conditions. IEEE Trans. Energy Convers. 2011, 26, 163–175. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Liserre, M.; Ma, K. Power Electronics Converters for Wind Turbine Systems. IEEE Trans. Ind. Appl. 2012, 48, 708–719. [Google Scholar] [CrossRef]
- Magagna, D.; Uihlein, A. 2014 JRC Ocean Energy Status Report; Joint Research Centre Institute for Energy and Transport: Luxembourg, 2015. [Google Scholar]
- Bae, Y.H.; Kim, K.O.; Choi, B.H. Lake Sihwa tidal power plant project. Ocean Eng. 2010, 37, 454–463. [Google Scholar] [CrossRef]
- Milne, I.A.; Sharma, R.N.; Flay, R.G.J.; Bickerto, S. The role of onset turbulence on tidal turbine blade loads. In Proceedings of the 17th Australasian Fluid Mechanics Conference, Auckland, New Zealand, 5–9 December 2010. [Google Scholar]
- Filipot, J.F.; Prevosto, M.; Maisondieu, C.; Le Boulluec, M.; Thomson, J. Wave and turbulence measurements at a tidal energy site. In Proceedings of the 2015 IEEE/OES Eleventh Current, Waves and Turbulence Measurement (CWTM), St Petersburg, FL, USA, 2–6 March 2015; pp. 1–9. [Google Scholar]
- Bouaziz, B.; Bacha, F.; Gasmi, M. Variable Switching Frequency Direct Power Control based on Sliding Mode approach for grid connected voltage source converters. In Proceedings of the 15th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Hammamet, Tunisia, 21–23 December 2014; pp. 878–883. [Google Scholar]
- Khaligh, A.; Onar, O.C. Energy Harvesting: Solar, Wind, and Ocean Energy Conversion Systems; CRC Press: Boca Raton, FL, USA, 2009; pp. 1–382. [Google Scholar]
- Benelghali, S.; Benbouzid, M.E.H.; Charpentier, J.F. Generator systems for marine current turbine applications: A comparative study. IEEE J. Ocean. Eng. 2012, 37, 554–563. [Google Scholar] [CrossRef]
- Jahromi, M.J.; Maswood, A.I.; Tseng, K.J. Design and evaluation of a new converter control strategy for near-shore tidal turbines. IEEE Trans. Ind. Electron. 2013, 60, 5648–5659. [Google Scholar] [CrossRef]
- Liu, C.; Xu, D.; Zhu, N.; Blaabjerg, F.; Chen, M. DC-voltage fluctuation elimination through a DC-capacitor current control for DFIG converters under unbalanced grid voltage conditions. IEEE Trans. Power Electron. 2013, 28, 3206–3218. [Google Scholar]
- Ben Elghali, S.E.; Benbouzid, M.E.H.; Charpentier, J.F. Modeling and Control of a Marine Current Turbine Driven Doubly-Fed Induction Generator. IET Renew. Power Gener. 2010, 4, 1–11. [Google Scholar] [CrossRef]
- Whitby, B.; Ugalde-Loo, C.E. Performance of Pitch and Stall Regulated Tidal Stream Turbines. IEEE Trans. Sustain. Energy 2014, 5, 64–72. [Google Scholar] [CrossRef]
- Wang, L.; Hsiung, C.T. Dynamic stability improvement of an integrated grid-connected offshore wind farm and marine-current farm using a STATCOM. IEEE Trans. Power Syst. 2011, 26, 690–698. [Google Scholar] [CrossRef]
- Kirke, B.K.; Lazauskas, L. Limitations of fixed pitch Darrieus hydrokinetic turbines and the challenge of variable pitch. Renew. Energy 2011, 36, 893–897. [Google Scholar] [CrossRef]
- Ben Elghali, S.E.; Balme, R.; Le Saux, K.; Benbouzid, M.E.H.; Charpentier, J.F.; Hauville, F. A Simulation Model for the Evaluation of the Electrical Power Potential Harnessed by a Marine Current Turbine. IEEE J. Ocean. Eng. 2007, 32, 786–797. [Google Scholar] [CrossRef]
- Ghefiri, K.; Bouallègue, S.; Haggège, J. Modeling and SIL simulation of a Tidal Stream Device for Marine Energy Conversion. In Proceedings of the 6th International Renew. Energy Congress (IREC) IEEE, Sousse, Tunisia, 24–26 March 2015; pp. 1–6. [Google Scholar]
- Ben Elghali, S.E.; Benbouzid, M.E.H.; Charpentier, J.F.; Tarek, A.A.; Munteanu, I. Experimental Validation of a Marine Current Turbine Simulator: Application to a Permanent Magnet Synchronous Generator-Based System Second-Order Sliding Mode Control. IEEE Trans. Ind. Electron. 2011, 58, 118–126. [Google Scholar] [CrossRef]
- Ben Elghali, S.E.; Benbouzid, M.E.H.; Charpentier, J.F. Marine Tidal Current Electric Power Generation Technology: State of the Art and Current Status. In Proceedings of the IEEE International Electric Machines and Drives Conference, Antalya, Turkey, 21–24 May 2007; Volume 2, pp. 1407–1412. [Google Scholar]
- Grifoll, M.; Fontan, A.; Ferrer, L.; Mader, J.; Gonzalez, M.; Espino, M. 3D hydrodynamic characterisation of a meso-tidal harbour: The case of Bilbao (northern Spain). Coast. Eng. 2009, 56, 907–918. [Google Scholar] [CrossRef]
- Hammons, T.J. Tidal power. Proc. IEEE 1993, 81, 419–433. [Google Scholar] [CrossRef]
- Bryden, I.G.; Grinsted, T.; Melville, G.T. Assessing the potential of a simple tidal channel to deliver useful energy. Appl. Ocean Res. 2004, 26, 198–204. [Google Scholar] [CrossRef]
- Bryden, I.G.; Couch, S.J. ME1-marine energy extraction: Tidal resource analysis. Renew. Energy 2006, 31, 133–139. [Google Scholar] [CrossRef]
- Myers, L.E.; Bahaj, A.S. Power output performance characteristics of a horizontal axis marine current turbine. Renew. Energy 2006, 31, 197–208. [Google Scholar] [CrossRef]
- Wang, L.; Li, C.N. Dynamic Stability Analysis of a Tidal Power Generation System Connected to an Onshore Distribution System. IEEE Trans. Energy. Convers. 2011, 26, 1191–1197. [Google Scholar] [CrossRef]
- Fernandez, L.M.; Jurado, F.; Saenz, J.R. Aggregated dynamic model for wind farms with doubly fed induction generator wind turbines. Renew. Energy 2008, 33, 129–140. [Google Scholar] [CrossRef]
- Alberdi, M.; Amundarain, M.; Garrido, A.J.; Garrido, I.; Casquero, O.; De la Sen, M. Complementary Control of Oscillating Water Column-Based Wave Energy Conversion Plants to Improve the Instantaneous Power Output. IEEE Trans. Energy Convers. 2011, 26, 1021–1032. [Google Scholar] [CrossRef]
- Amundarain, M.; Alberdi, M.; Garrido, A.J.; Garrido, I. Modeling and Simulation of Wave Energy Generation Plants: Output Power Control. IEEE Trans. Ind. Electron. 2011, 58, 105–117. [Google Scholar] [CrossRef]
- Carrasco, J.M.; Franquelo, L.G.; Bialasiewicz, J.T.; Galván, E.; Guisado, R.P.; Prats, M.A.M.; León, J.I.; Moreno-Alfonso, N. Power-electronic systems for the grid integration of renewable energy sources: A survey. IEEE Trans. Ind. Electron. 2006, 53, 1002–1016. [Google Scholar] [CrossRef]
- Pena, R.; Clare, J.C.; Asher, G.M. Doubly fed induction generator using back-to-back PWM converters and its application to variable speed wind-energy generation. IEE Proc. Electr. Power Appl. 1996, 143, 231–241. [Google Scholar] [CrossRef]
- Alberdi, M.; Amundarain, M.; Garrido, A.J.; Garrido, I.; Maseda, F.J. Fault-Ride-Through Capability of Oscillating-Water-Column-Based Wave-Power-Generation Plants Equipped With Doubly Fed Induction Generator and Airflow Control. IEEE Trans. Ind. Electron. 2011, 58, 1501–1517. [Google Scholar] [CrossRef]
- Alberdi, M.; Amundarain, M.; Garrido, A.J.; Garrido, I. Neural control for voltage dips ride-through of oscillating water column-based wave energy converter equipped with doubly-fed induction generator. Renew. Energy 2012, 48, 16–26. [Google Scholar] [CrossRef]
- Nunes, M.V.A.; Pecas, J.A.; Zurn, H.H.; Bezerra, U.H.; Almeida, R.G. Influence of the variable-speed wind generators in transient stability margin of the conventional generators integrated in electrical grids. IEEE Trans. Energy Convers. 2004, 19, 692–701. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of Control and Grid Synchronization for Distributed Power Generation Systems. IEEE Trans. Power Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Astrom, K.J.; Hagglund, T. PID Controllers: Theory, Design and Tuning, 2nd ed.; ISA: Research Triangle Park, NC, USA, 1995. [Google Scholar]
- Astrom, K.J.; Hagglund, T. Advanced PID Control; ISA-The Instrumentation, Systems and Automation Society: Research Triangle Park, NC, USA, 2006. [Google Scholar]
- Vilanova, R.; Visioli, A. PID Control in the Third Millennium; Springer: London, UK, 2012. [Google Scholar]
- Benelghali, S.; Benbouzid, M.; Charpentier, J.F.; Ahmed-Ali, T.; Gahery, J.M.; Denis, A. Modeling and MPPT Sensorless Control of a DFIG-Based Marine Current Turbine. In Proceedings of the 2008 18th International Conference on Electrical Machines (ICEM), Vilamoura, Portugal, 6–9 September 2008; Volume 2, pp. 1–6. [Google Scholar]
- Munteanu, I.; Bratcu, A.I.; Cutululis, N.A.; Ceanga, E. Optimal Control of Wind Energy Systems: Towards a Global Approach; Springer: London, UK, 2008; ISBN 978-1-84800-079-7. [Google Scholar]
- Multon, B. Marine Renewable Energy Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Harries, T.; Kwan, A.; Brammer, J.; Falconer, R. Physical testing of performance characteristics of a novel drag-driven vertical axis tidal stream turbine; with comparisons to a conventional Savonius. Int. J. Mar. Energy 2016, 14, 215–228. [Google Scholar] [CrossRef]
- Twining, E.; Holmes, D.G. Grid Current Regulation of a Three-Phase Voltage Source Inverter with an LCL Input Filter. IEEE Trans. Power Electron. 2003, 18, 888–895. [Google Scholar] [CrossRef]
- Slootweg, J.G.; Polinder, H.; Kling, W.L. Dynamic modelling of a wind turbine with doubly fed induction generator. In Proceedings of the 2001 IEEE Power Engineering Society Summer Meeting, Vancouver, BC, Canada, 15–19 July 2008; Volume 1, pp. 644–649. [Google Scholar]


| Turbine | Drive-Train | DFIG | Converter |
|---|---|---|---|
| = 1027 kg/m3 | = 3 s | = 1.5 MW | = 1150 V |
| m | s | V | C = 0.01 F |
| Nm/rad | = 50 Hz | ||
| Nms/rad | = 2.63 m | ||
| = 3.2 m/s | = 2.63 m | Choke | |
| = 0.168 mH | =0.595 m | ||
| = 0.133 mH | = 0.157 mH | ||
| = 5.474 mH | |||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghefiri, K.; Bouallègue, S.; Garrido, I.; Garrido, A.J.; Haggège, J. Complementary Power Control for Doubly Fed Induction Generator-Based Tidal Stream Turbine Generation Plants. Energies 2017, 10, 862. https://doi.org/10.3390/en10070862
Ghefiri K, Bouallègue S, Garrido I, Garrido AJ, Haggège J. Complementary Power Control for Doubly Fed Induction Generator-Based Tidal Stream Turbine Generation Plants. Energies. 2017; 10(7):862. https://doi.org/10.3390/en10070862
Chicago/Turabian StyleGhefiri, Khaoula, Soufiene Bouallègue, Izaskun Garrido, Aitor J. Garrido, and Joseph Haggège. 2017. "Complementary Power Control for Doubly Fed Induction Generator-Based Tidal Stream Turbine Generation Plants" Energies 10, no. 7: 862. https://doi.org/10.3390/en10070862
APA StyleGhefiri, K., Bouallègue, S., Garrido, I., Garrido, A. J., & Haggège, J. (2017). Complementary Power Control for Doubly Fed Induction Generator-Based Tidal Stream Turbine Generation Plants. Energies, 10(7), 862. https://doi.org/10.3390/en10070862







