Hydrodynamic Investigation of an Oscillating Buoy Wave Energy Converter Integrated into a Pile-Restrained Floating Breakwater
Abstract
:1. Introduction
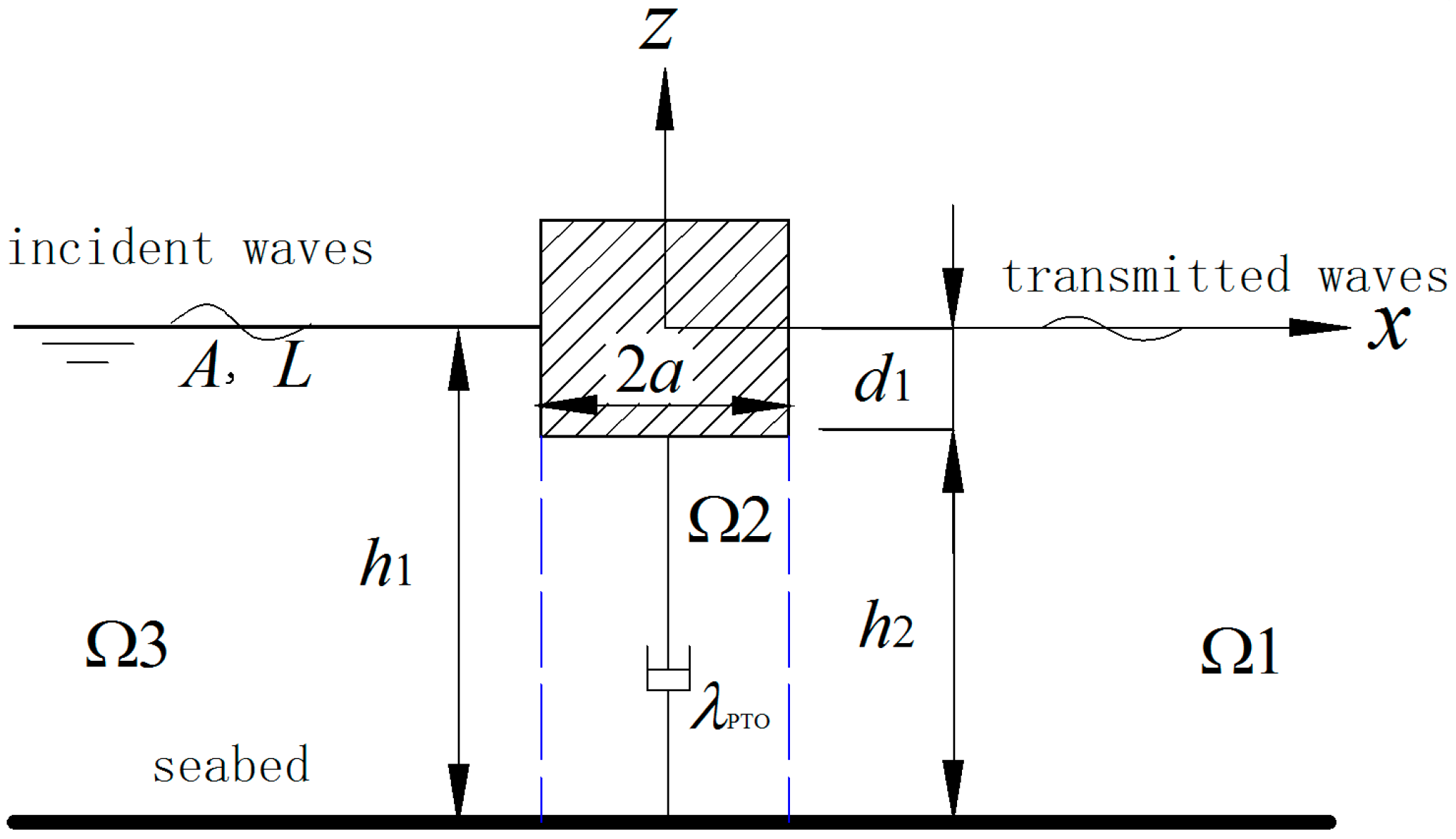
2. Formulas
3. Dimensional Analysis
4. Results and Discussion
4.1. Validation
4.2. Comparison of the Different Breakwater Systems
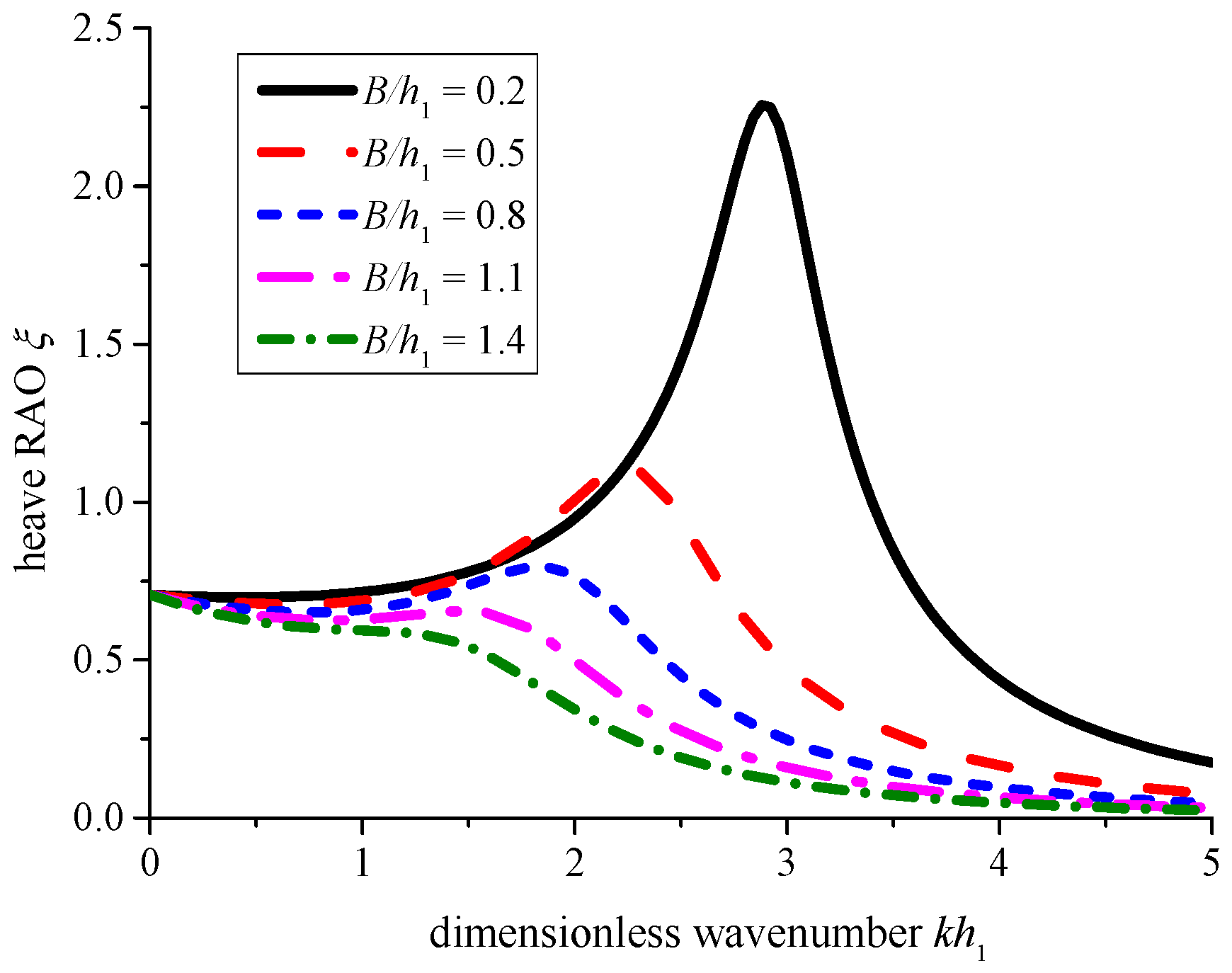
4.3. Effect of the Relative Breadth B/h1
4.4. Effect of the Relative Draft d1/h1
4.5. Effect of the PTO Damping
5. Conclusions
- (1)
- Compared with that of the free heave-motion breakwater, the wave attenuation performance of the breakwater is improved for the proposed integrated system.
- (2)
- For the system with the optimal PTO damping, the low threshold of the practical frequency region corresponds to the natural frequency.
- (3)
- With a decrease in the heave RAO of the breakwater, the transmission coefficient increases in the lower-frequency region, although a decreasing trend is initially observed, followed by an increasing trend in the middle-frequency region.
- (4)
- Due to the changing of the natural frequency, the effect of the relative breadth B/h1 and relative draft d1/h1 of the pontoon affect the performance of the system significantly. This shall be paid attention while such a system is designed.
- (5)
- The breakwater with the PTO damping of λPTO = 1.5–2λoptimal may give a broader frequency bandwidth with Kt < 0.5 and η > 20%. Fortunately, the transmission coefficient corresponding to the case with λPTO = 2λoptimal is slightly superior to that of the fixed breakwater.
- (6)
- The proposed system is theoretically proved to produce power effectively and, at the same time, the function of coastal protection can be comparable to that of the fixed breakwater.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- You, Y.G.; Zheng, Y.H.; Shen, Y.M.; Wu, B.J.; Liu, R. Wave energy study in China: Advancements and perspectives. China Ocean Eng. 2003, 17, 101–109. [Google Scholar]
- Falcão, A.F.d.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Ferro, B.D. Wave and tidal energy: Its emergence and the challenges it faces. Refocus 2006, 7, 46–48. [Google Scholar] [CrossRef]
- Lirn, T.C.; Wu, Y.C. J.; Chen, Y.J. Green performance criteria for sustainable ports in Asia. Int. J. Phys. Distrib. Logist. Manag. 2013, 43, 427–451. [Google Scholar] [CrossRef]
- Park, J.Y.; Yeo, G.T. An Evaluation of Greenness of major Korean ports: A Fuzzy Set Approach. Asian J. Shipp. Logist. 2012, 28, 67–82. [Google Scholar] [CrossRef]
- Mustapa, M.A.; Yaakob, O.B.; Ahmed, Y.M.; Rheem, C.; Koh, K.K.; Adnan, F.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- Contestabile, P.; Iuppa, C.; Lauro, E.D.; Cavallaro, L.; Andersen, T.L.; Vicinanza, D. Wave loadings acting on innovative rubble mound breakwater for overtopping wave energy conversion. Coast. Eng. 2017, 122, 60–74. [Google Scholar] [CrossRef]
- Iuppa, C.; Contestabile, P.; Cavallaro, L.; Foti, E.; Vicinanza, D. Hydraulic Performance of an Innovative Breakwater for Overtopping Wave Energy Conversion. Sustainability 2016, 8, 1226. [Google Scholar] [CrossRef]
- Takahashi, S.; Nakada, H.; Ohneda, H.; Shikamori, M. Wave power conversion by a prototype wave power extracting caisson in Sakata port. Coast. Eng. Proc. 1991, 1, 3440–3453. [Google Scholar]
- Arena, F.; Romolo, A.; Malara, G.; Ascanelli, A. On design and building of a U-OWC wave energy converter in the Mediterranean Sea: A case study. In Proceedings of the 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar]
- Yueh, C.Y.; Chuang, S.H. A boundary element model for a partially piston-type porous wave energy converter in gravity waves. Eng. Anal. Bound. Elements 2012, 36, 658–664. [Google Scholar] [CrossRef]
- McCartney, B.L. Floating breakwater design. J. Waterw. Port Coast. Ocean Eng. 1985, 111, 304–318. [Google Scholar] [CrossRef]
- He, F.; Huang, Z.H.; Law, W.K. An experimental study of a floating breakwater with asymmetric pneumatic chambers for wave energy extraction. Appl. Energy 2013, 106, 222–231. [Google Scholar] [CrossRef]
- Mendoza, E.; Silva, R.; Zanuttigh, B.; Angelelli, E.; Lykke Andersen, T.; Martinelli, L.; Ruol, P. Beach response to wave energy converter farms acting as coastal defense. Coast. Eng. 2014, 87, 97–111. [Google Scholar] [CrossRef]
- Chen, B.; Ning, D.Z.; Liu, C.Q.; Greated, C.A.; Kang, H.G. Wave energy extraction by horizontal floating cylinders perpendicular to wave propagation. Ocean Eng. 2016, 121, 112–122. [Google Scholar] [CrossRef]
- Martinelli, L.; Ruol, P.; Favaretto, C. Hybrid structure combining a wave energy converter and a floating breakwater. In Proceedings of the International Offshore and Polar Engineering Conference, Rhodes, Greece, 26 June–2 July 2016. [Google Scholar]
- Ning, D.Z.; Zhao, X.L.; Göteman, M.; Kang, H.G. Hydrodynamic performance of a pile-restrained WEC-type floating breakwater: An experimental study. Renew. Energy 2016, 95, 531–541. [Google Scholar] [CrossRef]
- Zheng, Y.H.; You, Y.G.; Shen, Y.M. On the radiation and diffraction of water waves by a rectangular buoy. Ocean Eng. 2004, 31, 1063–1082. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Sonin, A.A. The Physical Basis of Dimensional Analysis, 2nd ed.; MIT Department of Mechanical Engineering: Cambridge, MA, USA, 2001. [Google Scholar]
- Bódai, T.; Srinil, N. Performance analysis and optimization of a box-hull wave energy converter concept. Renew. Energy 2015, 81, 551–565. [Google Scholar] [CrossRef]
- Cao, F.S. The application of scaled boundary finite element method in potential flow theory. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2009. [Google Scholar]
- Isaacson, M.; Baldwin, J.; Bhat, S. Wave propagation past a pile-restrained floating breakwater. Int. J. Offshore Polar Eng. 1998, 8, 265–269. [Google Scholar]
- Mei, C.C. Hydrodynamic principles of wave power extraction. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2012, 370, 208–234. [Google Scholar] [CrossRef] [PubMed]
- Koutandos, E.; Prinos, P.; Gironella, X. Floating breakwaters under regular and irregular wave forcing: Reflection and transmission characteristics. J. Hydraul. Res. 2005, 43, 174–188. [Google Scholar] [CrossRef]
- Cheng, Z.S.; Yang, J.M.; Hu, Z.Q.; Xiao, L.F. Frequency/time domain modeling of a direct drive point absorber wave energy converter. Sci. China Phys. Mech. Astron. 2014, 57, 311–320. [Google Scholar] [CrossRef]
- Babarit, A.; Halsb, J.; Muliawan, M.J.; Kurniawan, A.; Moan, T.; Krokstad, J. Numerical benchmarking study of a selection of wave energy converters. Renew. Energy 2012, 41, 44–63. [Google Scholar] [CrossRef]

















| Dimensional Variables | Physical Unit | Nondimensional Variables |
|---|---|---|
| Water density, ρ | kg·m−3 | - |
| Gravitational acceleration, g | m·s−2 | - |
| Water depth, h1 | m | - |
| Incident wave amplitude, A | m | - |
| Wavenumber, k | m–1 | π1 = kh1 |
| Breadth, B | m | π2 = B/h1 |
| Draft, d1 | m | π3 = d1/h1 |
| PTO damping, λPTO | kg·s−1 | π4 = λPTO/λref |
| Response amplitude in heave, ζ | m | π5 = ζ/A |
| Outputted power, Pcapture | kg·m2·s−3 | πa = Pcapture/Pref |
| Reflected wave amplitude, Ar | m | πb = Ar/A |
| Transmitted wave amplitude, At, | m | πc = At/A |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Ning, D.; Zhang, C.; Kang, H. Hydrodynamic Investigation of an Oscillating Buoy Wave Energy Converter Integrated into a Pile-Restrained Floating Breakwater. Energies 2017, 10, 712. https://doi.org/10.3390/en10050712
Zhao X, Ning D, Zhang C, Kang H. Hydrodynamic Investigation of an Oscillating Buoy Wave Energy Converter Integrated into a Pile-Restrained Floating Breakwater. Energies. 2017; 10(5):712. https://doi.org/10.3390/en10050712
Chicago/Turabian StyleZhao, Xuanlie, Dezhi Ning, Chongwei Zhang, and Haigui Kang. 2017. "Hydrodynamic Investigation of an Oscillating Buoy Wave Energy Converter Integrated into a Pile-Restrained Floating Breakwater" Energies 10, no. 5: 712. https://doi.org/10.3390/en10050712
APA StyleZhao, X., Ning, D., Zhang, C., & Kang, H. (2017). Hydrodynamic Investigation of an Oscillating Buoy Wave Energy Converter Integrated into a Pile-Restrained Floating Breakwater. Energies, 10(5), 712. https://doi.org/10.3390/en10050712








