Multi-Objective Optimization of Hybrid Renewable Energy System Using an Enhanced Multi-Objective Evolutionary Algorithm
Abstract
:1. Introduction
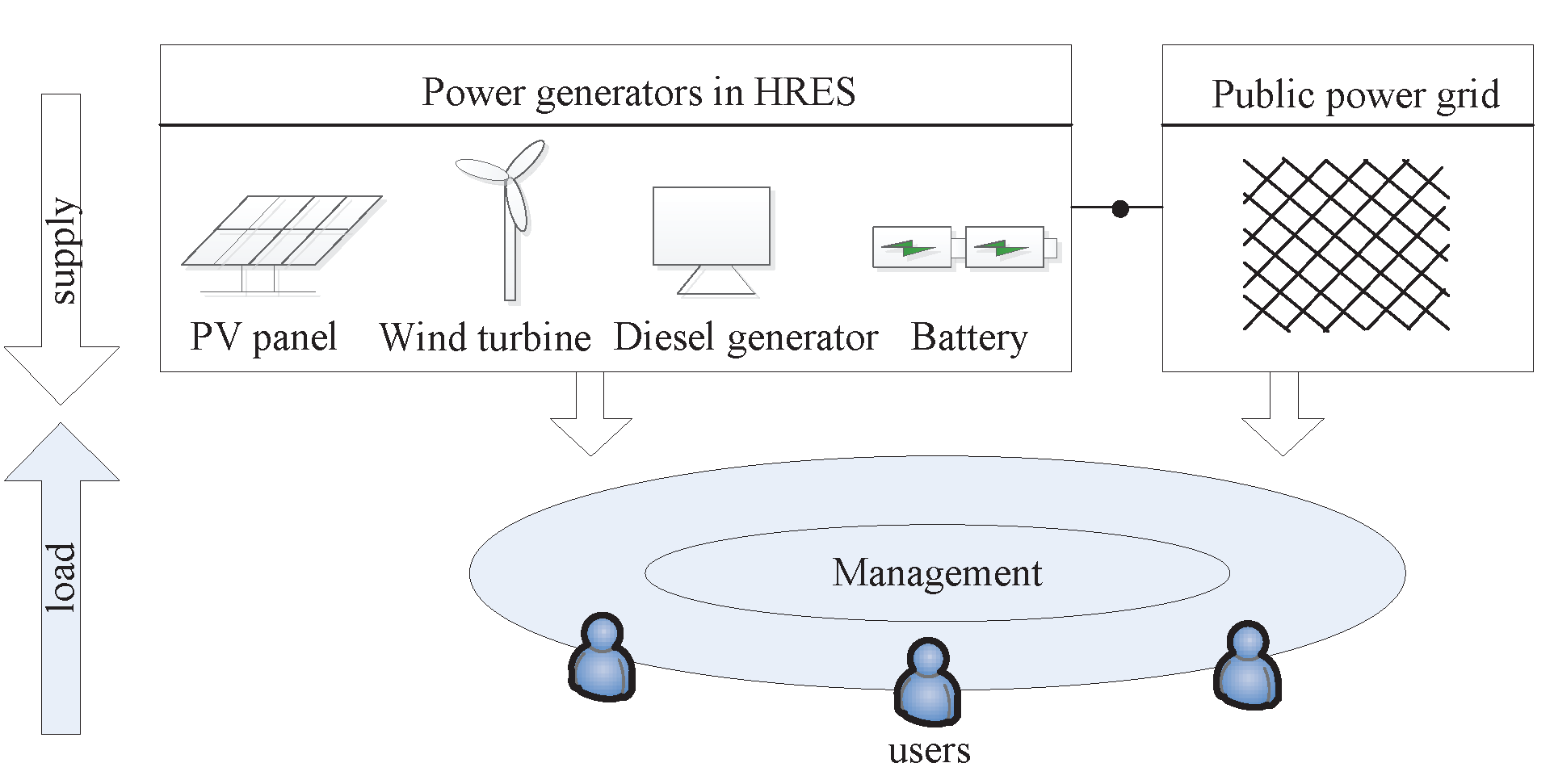
2. Mathematical Model of the HRES
2.1. Optimization Model
- Payment of purchasing and installing the PV panels, wind turbines, batteries, diesel generators, inverters and rectifiers, denoted as . Among them, the cost of the wind turbines includes that of the wind generator and the tower, and the expense in tower is positively related to its height.
- Cost of repair and maintenance of the devices, denoted as .
- Expenditure on the fuel consumed through the lifespan, denoted as , which is defined by unit price () multiplying the quantity of fuel consumption ().
- Cost of replacing the old batteries with the new ones, denoted as . It is calculated by where and are the unit price of a battery and the number of replacement, respectively.
- Cost/profit of exchanging power with the public power grid (positive for buying power and negative for selling power), denoted as .
2.2. Systematic Planning of Operation Mechanism
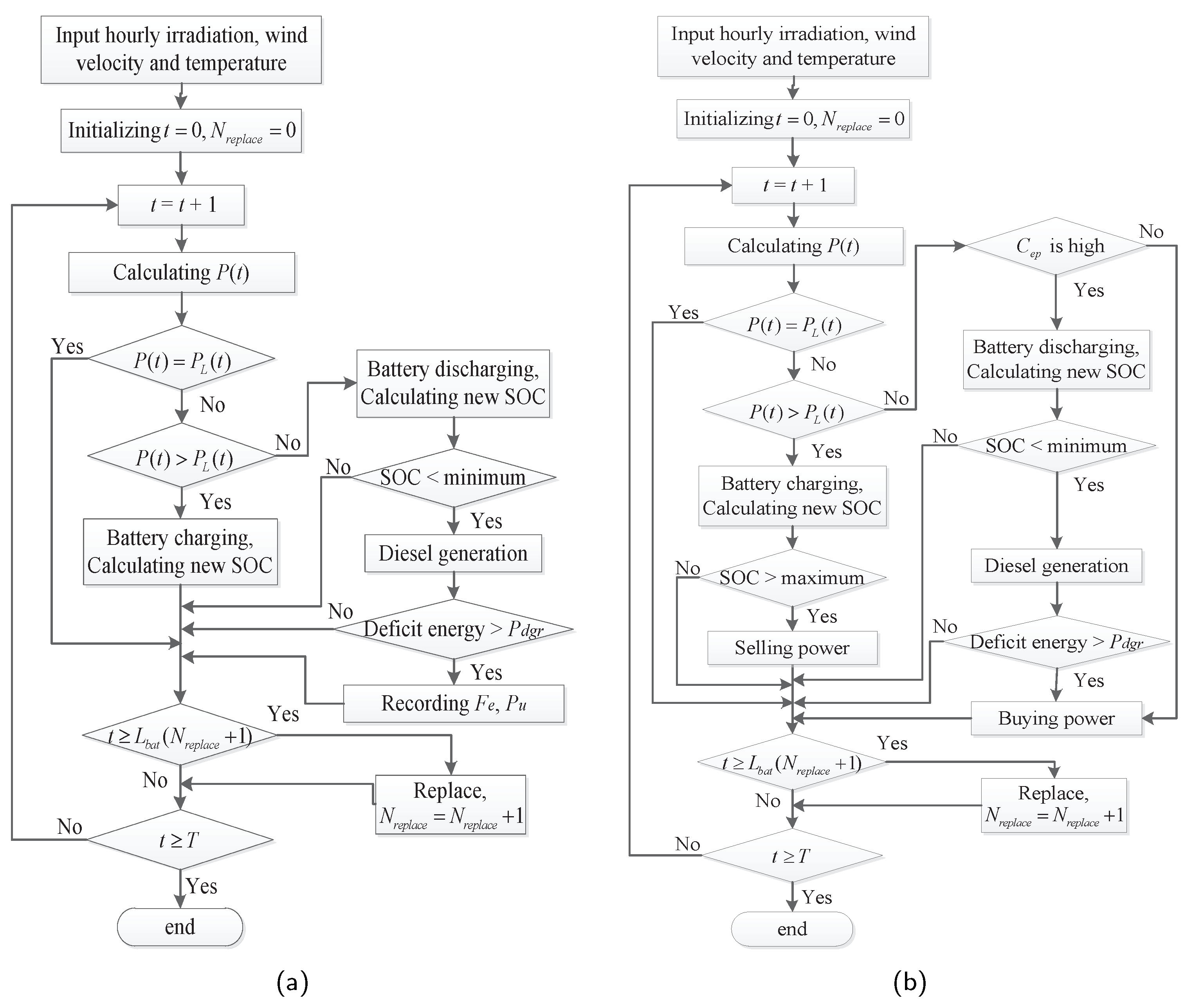
- Mode I: in this mode, the system is not connected to the power grid, thus the A module in Figure 2 is not considered. The energy produced by the PV panels and the wind turbines is directly provided for the direct-current (DC) load and flows to the alternating-current (AC) load through the inverter. If the provided energy exceeds the total demand (DC load plus AC load), the surplus energy will be saved in the battery storage after meeting the load. On the contrary, if it cannot satisfy the load demand, the batteries will discharge based on the . If there still exists unmet load, the diesel generators start as the emergency power-supply. Note that the power from the diesel generators is alternating current and the part used to supply DC load is converted by the AC-to-DC rectifier.
- Mode II: in this mode, when the produced renewable energy is more than the demanded quantity and the batteries have been charged to the maximum, the surplus energy will be sold to the power grid for the profit. On the contrary, if the produced energy cannot meet the load demand, the method of obtaining the supplement is determined by the electricity price (). Providing low , all of the deficit power will be bought from the public power grid and supplied to the load. On this condition, the B module does not operate. However, if the is high, first the battery storage and the diesel generators are used as supplement power. Once these devices still cannot cover the gap, the required power will be bought from the power grid. To describe it more clearly, the choosing strategy when the renewable energy is insufficient is shown in Algorithm 1.
| Algorithm 1: Decision strategy for the source of supplementing deficit energy in mode II. |
 |
3. Multi-Objective Optimization Using MOEA/D-LPBI
3.1. The Localized PBI Method
3.2. MOEA/D-LPBI
| Algorithm 2: MOEA/D-LPBI. |
 |
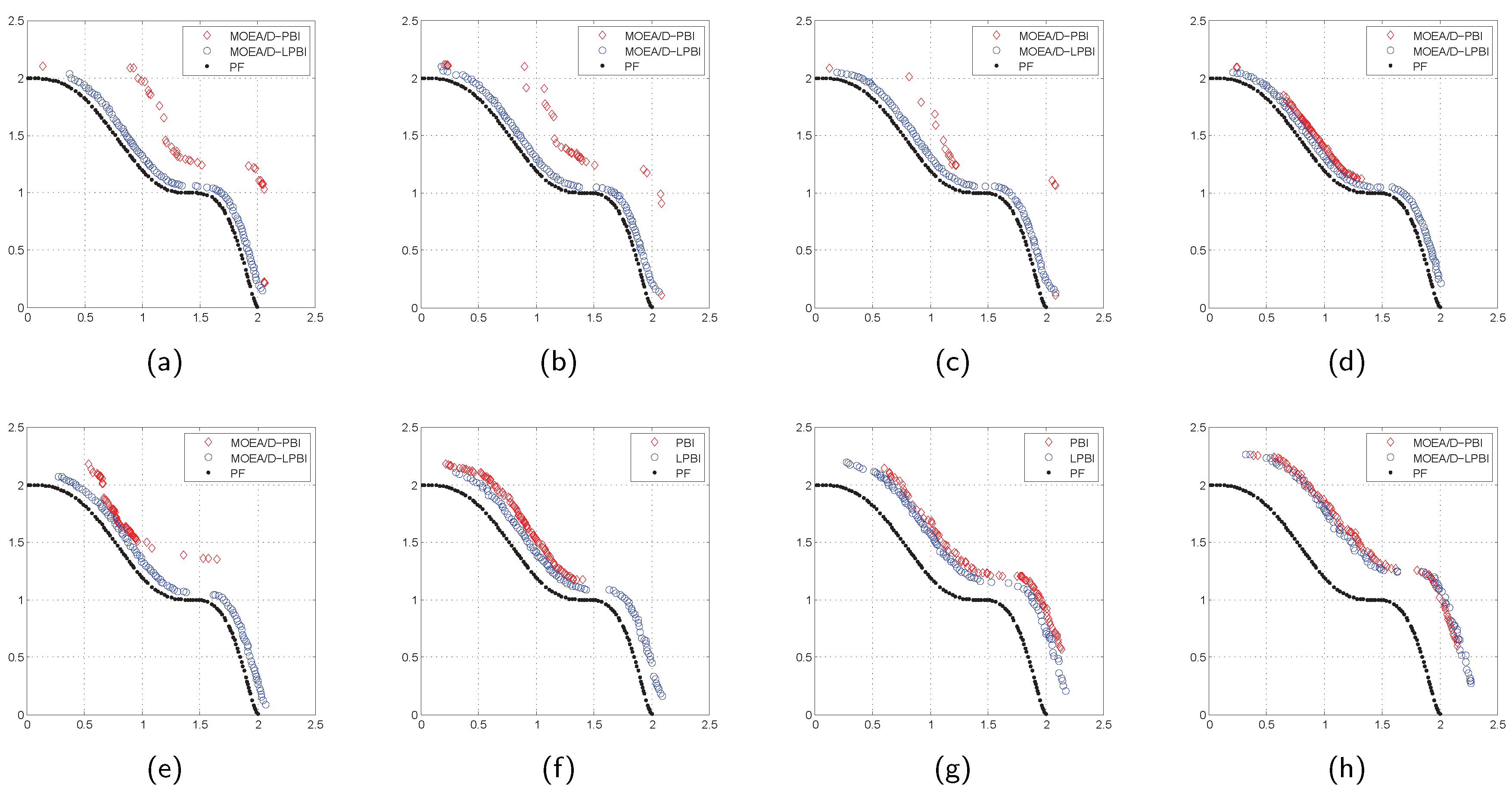
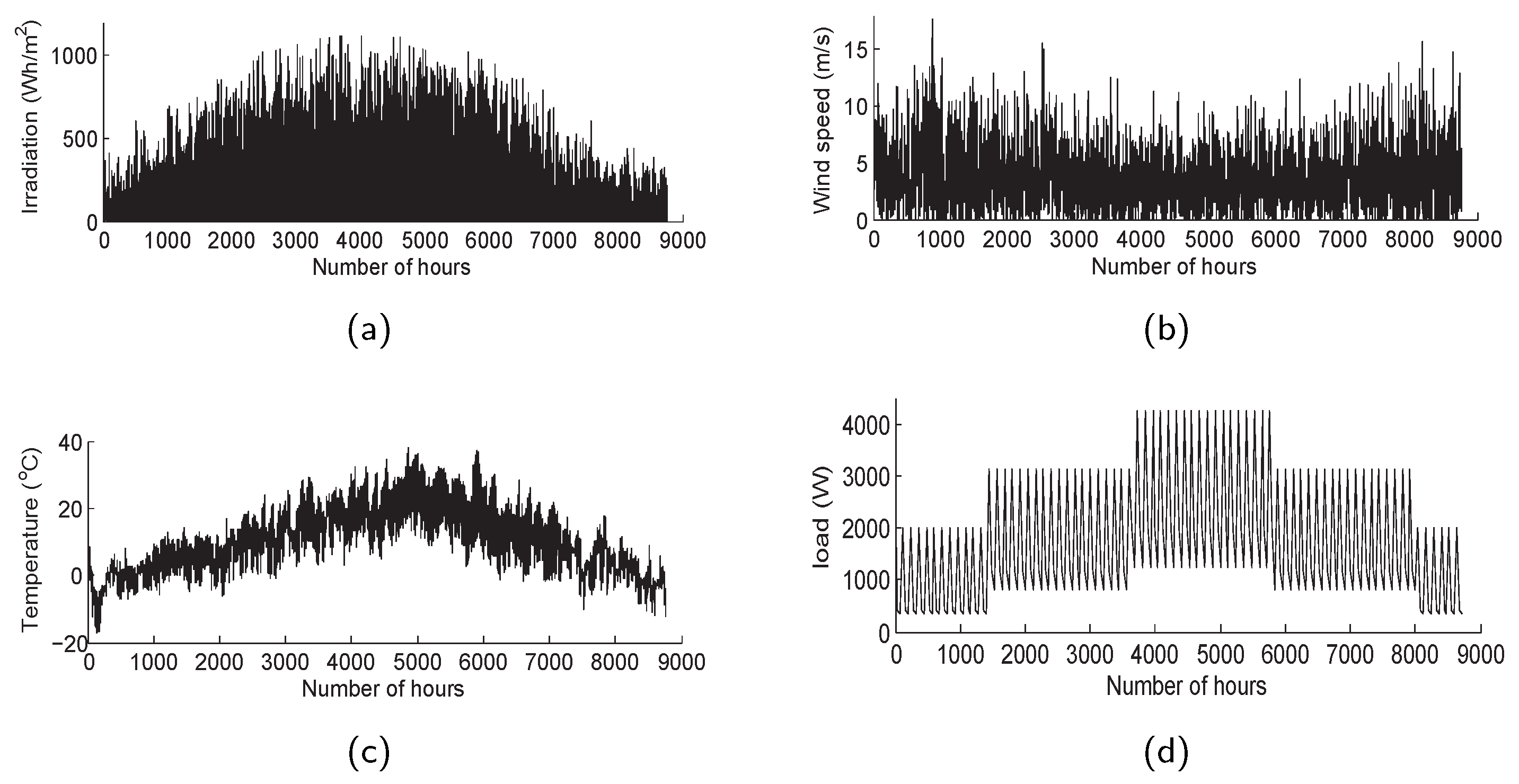
4. Experimental Results
- Algorithm runs: the maximum generation is set to 50.
- Individuals: the population size is N = 100. Each candidate solution consists of six variables in the form: [], which, respectively, represent the number of four main components, the height of the wind tower and the inclination angle of the tilted PV panel. Assuming that each PV string connects four units in series, the number of is a multiple of four.
- MOEA/D parameters: the neighbourhood size is set to be 10 and the probability of selecting in the neighbourhood is set as . In the reference algorithm, the replacement size is 2.
- Penalty values: the considered penalty values are .
- in mode I, if the decision maker prefers to meet the energy demand 100% and limit the emission within 250 kg, then one can set = 0% and . Then, the three filtered are shown in Table 5. Amongst these solutions, the one that produces the minimum cost is selected, i.e., the third one (in bold).
- in mode II, if the decision maker prefers to minimize the fuel emission and the utility of non-renewable energy, the solution having minimum and is selected, i.e., the first one (in bold). Additionally, it can be observed that the diesel generators are not used in this case.
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Zeng, J.; Li, M.; Liu, J.F.; Wu, J.; Ngan, H.W. Operational optimization of a stand-alone hybrid renewable energy generation system based on an improved genetic algorithm. In Proceedings of the 2010 IEEE Power and Energy Society General Meeting, Providence, RI, USA, 25–29 July 2010. [Google Scholar]
- Niknam, T.; Taheri, S.I.; Aghaei, J.; Tabatabaei, S.; Nayeripour, M. A modified honey bee mating optimization algorithm for multiobjective placement of renewable energy resources. Appl. Energy 2011, 88, 4817–4830. [Google Scholar] [CrossRef]
- Wang, R.; Fleming, P.J.; Purshouse, R.C. General framework for localised multi-objective evolutionary algorithms. Inf. Sci. 2014, 258, 29–53. [Google Scholar] [CrossRef]
- Fadaee, M.; Radzi, M.A.M. Multi-objective optimization of a stand-alone hybrid renewable energy system by using evolutionary algorithms: A review. Renew. Sustain. Energy Rev. 2012, 16, 3364–3369. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J.L. Design and control strategies of PV-Diesel systems using genetic algorithms. Sol. Energy 2005, 79, 33–46. [Google Scholar] [CrossRef]
- Dufo-López, R.; Contreras, J. Optimization of control strategies for stand-alone renewable energy systems with hydrogen storage. Renew. Energy 2007, 32, 1102–1126. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J.L. Multi-objective design of PV-wind-diesel–hydrogen–battery systems. Renew. Energy 2008, 33, 2559–2572. [Google Scholar] [CrossRef]
- Trivedi, M. Multi-Objective Generation Scheduling with Hybrid Energy Resources. Ph.D. Thesis, Department of Electrical Engineering, Clemson University, Clemson, SC, USA, 2007. [Google Scholar]
- Masoum, M.A.S.; Badejani, S.M.M.; Kalantar, M. Optimal placement of hybrid PV-wind systems using genetic algorithm. In Proceedings of the Innovative Smart Grid Technologies, Gaithersburg, MD, USA, 19–21 January 2010; pp. 1–5. [Google Scholar]
- Katsigiannis, Y.A.; Georgilakis, P.S.; Karapidakis, E.S. Multiobjective genetic algorithm solution to the optimum economic and environmental performance problem of small autonomous hybrid power systems with renewables. IET Renew. Power Gener. 2010, 4, 404–419. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muiltiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evolut. Comput. 2007, 2, 221–248. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evolut. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, F.; Zhang, T. Multi-objective optimal design of hybrid renewable energy systems using evolutionary algorithms. In Proceedings of the 2015 11th International Conference on Natural Computation (ICNC), Zhangjiajie, China, 15–17 August 2015; pp. 1196–1200. [Google Scholar]
- Myrzik, J.M.A.; Calais, M. String and module integrated inverters for single-phase grid connected photovoltaic systems—A review. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 2, p. 8. [Google Scholar]
- Fei, W. Research on Photovoltaic Grid-Connected Power System. Trans. China Electrotech. Soc. 2005, 20, 72–74, 91. [Google Scholar]
- Koutroulis, E.; Kolokotsa, D.; Potirakis, A.; Kalaitzakis, K. Methodology for optimal sizing of stand-alone photovoltaic/wind-generator systems using genetic algorithms. Sol. Energy 2006, 80, 1072–1088. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, R.; Zhang, T. Multi-objective optimal design of hybrid renewable energy systems using preference-inspired coevolutionary approach. Sol. Energy 2015, 118, 96–106. [Google Scholar] [CrossRef]
- Yang, H.; Lu, L.; Zhou, W. A novel optimization sizing model for hybrid solar-wind power generation system. Sol. Energy 2007, 81, 76–84. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, W.; Lu, L.; Fang, Z. Optimal sizing method for stand-alone hybrid solar–wind system with LPSP technology by using genetic algorithm. Sol. Energy 2008, 82, 354–367. [Google Scholar] [CrossRef]
- Wang, R.; Purshouse, R.C.; Fleming, P.J. Preference-inspired co-evolutionary algorithms using weight vectors. Eur. J. Oper. Res. 2015, 243, 423–441. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, Q.; Zhang, T. Decomposition based algorithms using Pareto adaptive scalarizing methods. IEEE Trans. Evolut. Comput. 2016, 20, 821–837. [Google Scholar] [CrossRef]
- Li, K.; Kwong, S.; Zhang, Q.; Deb, K. Interrelationship-Based Selection for Decomposition Multiobjective Optimization. IEEE Trans. Cybern. 2015, 45, 2076–2088. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, A.; Omidvar, M.N.; Li, X.; Deb, K. Sensitivity analysis of Penalty-based Boundary Intersection on aggregation-based EMO algorithms. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation, Sendai, Japan, 25–28 May 2015. [Google Scholar]
- Ishibuchi, H.; Akedo, N.; Nojima, Y. A study on the specification of a scalarizing function in MOEA/D for many-objective knapsack problems. In Learning and Intelligent Optimization; Springer: Berlin, Germany, 2013; pp. 231–246. [Google Scholar]
- Wang, R.; Ishibuchi, H.; Zhang, Y.; Zheng, X.; Zhang, T. On the effect of localized PBI method in MOEAD for multi-objective optimization. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence, Athens, Greece, 6–9 December 2016; pp. 647–650. [Google Scholar]
- Wang, R.; Zhou, Z.; Liao, T.; Zhang, T. Localized weighted sum method for many-objective optimization. IEEE Trans. Evolut. Comput. 2016, PP, 1. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Wang, R.; Purshouse, R.C.; Fleming, P.J. Preference-inspired Co-evolutionary Algorithms for Many-objective Optimisation. IEEE Trans. Evolut. Comput. 2013, 17, 474–494. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; Fonseca, V.G.D. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evolut. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D. Nonparametric Statistical Methods; Wiley-Interscience: Boston, MA, USA, 1999. [Google Scholar]
- Wang, R.; Purshouse, R.C.; Giagkiozis, I.; Fleming, P.J. The iPICEA-g: A new hybrid evolutionary multi-criteria decision making approach using the brushing technique. Eur. J. Oper. Res. 2015, 243, 442–453. [Google Scholar] [CrossRef]
- Wang, R.; Xiong, J.; Ishibuchi, H.; Wu, G.; Zhang, T. On the effect of reference point in MOEA/D for multi-objective optimization. Appl. Soft Comput. 2016, 58, 25–34. [Google Scholar] [CrossRef]


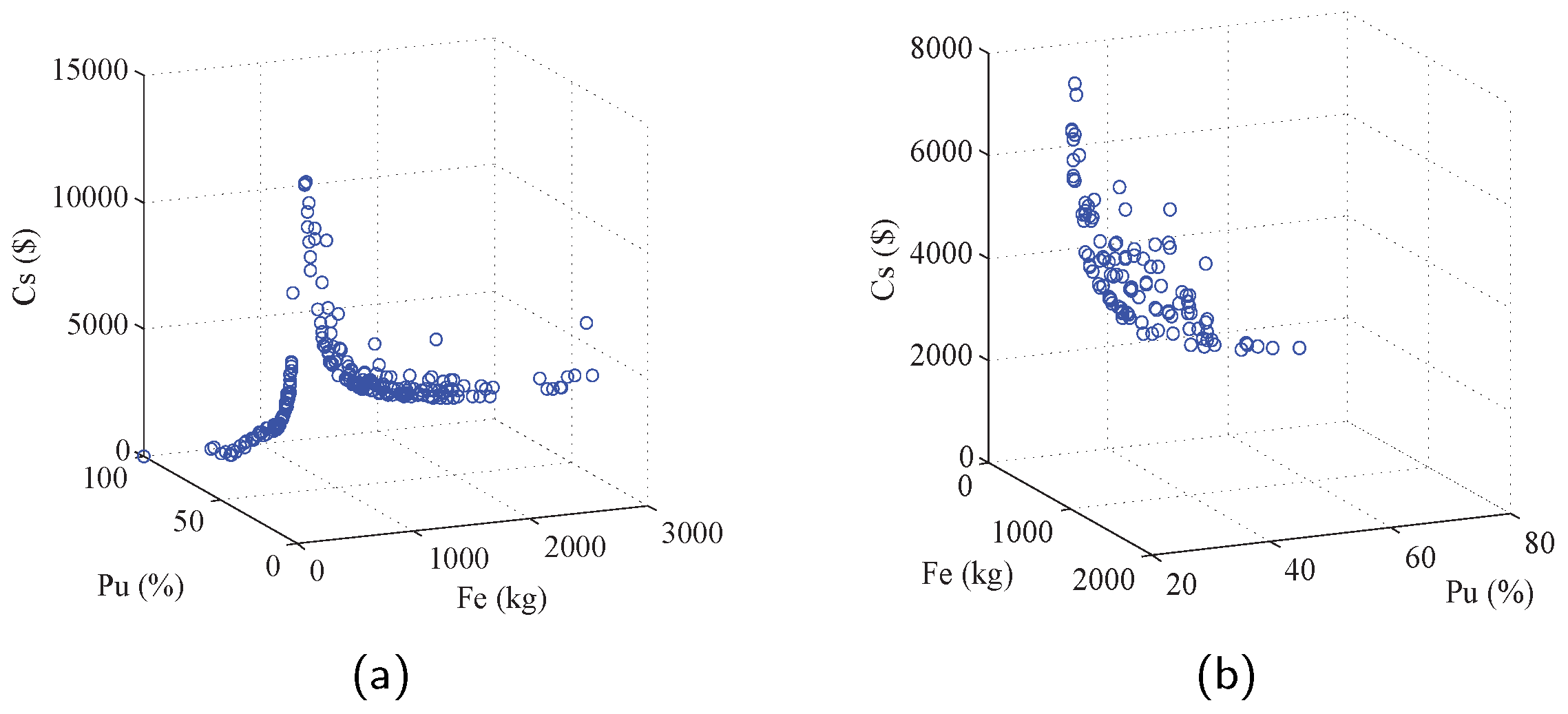

| Cost | PV Panel | Wind Turbine | Wind Tower | Battery | Diesel Generator | Inverter | Rectifier |
|---|---|---|---|---|---|---|---|
| ($) | 300 | 3000 | 250/m | 126 | 1514 | 240 | 225 |
| ($) | 30 | 50 | 2.5/m | 1.26 | 0.17/h | 12 | 8 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| 0.73 | 12.59 | 1 | |||
| (m/s) | 4 | (kW) | 1 | (kW) | 2 |
| (m/s) | 14 | 10 | (L/kWh) | 0.08 | |
| (m/s) | 20 | (Ah) | 100 | (L/kWh) | 0.25 |
| 0.4 | (V) | 12 | (kg/L) | 2.5 | |
| (kg/) | 1.29 | 0.2 | ($/L) | 1.2 |
| HRES | Algorithm | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| mode I | PBI | 0.921 | 0.903 | 0.907 | 0.710 | 0.569 | 0.694 | 0.723 | 0.704 |
| LPBI | 0.947 | 0.865 | 0.923 | 0.948 | 0.957 | 0.891 | 0.965 | 0.963 | |
| mode II | PBI | 0.622 | 0.621 | 0.646 | 0.616 | 0.620 | 0.559 | 0.632 | 0.585 |
| LPBI | 0.625 | 0.647 | 0.658 | 0.695 | 0.700 | 0.662 | 0.710 | 0.702 |
| HV | MOEA/D-LPBI | PICEA-g | MOEA/D-TE |
|---|---|---|---|
| mode I | 0.965 (0.089) | 0.892 (0.112) | 0.935 (0.127) |
| mode II | 0.710 (0.068) | 0.655 (0.077) | 0.681 (0.043) |
| Mode I | |||||||||
| Solution | (kg) | ($) | |||||||
| 1 | 28 | 17 | 30 | 5 | 21.605 | 58.545 | 109.404 | 0 | 13,324.550 |
| 2 | 28 | 18 | 30 | 8 | 14.546 | 59.662 | 151.846 | 0 | 12,345.850 |
| 3 | 28 | 12 | 28 | 7 | 19.081 | 48.441 | 219.842 | 0 | 10,186.780 |
| Mode II | |||||||||
| Solution | (kg) | ($) | |||||||
| 1 | 28 | 12 | 4 | 0 | 30 | 46.733 | 0 | 34.085 | 5733.406 |
| 2 | 28 | 11 | 4 | 0 | 30 | 49.870 | 0 | 34.243 | 5416.173 |
| 3 | 28 | 7 | 3 | 0 | 26.597 | 46.099 | 0 | 36.245 | 3903.858 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ming, M.; Wang, R.; Zha, Y.; Zhang, T. Multi-Objective Optimization of Hybrid Renewable Energy System Using an Enhanced Multi-Objective Evolutionary Algorithm. Energies 2017, 10, 674. https://doi.org/10.3390/en10050674
Ming M, Wang R, Zha Y, Zhang T. Multi-Objective Optimization of Hybrid Renewable Energy System Using an Enhanced Multi-Objective Evolutionary Algorithm. Energies. 2017; 10(5):674. https://doi.org/10.3390/en10050674
Chicago/Turabian StyleMing, Mengjun, Rui Wang, Yabing Zha, and Tao Zhang. 2017. "Multi-Objective Optimization of Hybrid Renewable Energy System Using an Enhanced Multi-Objective Evolutionary Algorithm" Energies 10, no. 5: 674. https://doi.org/10.3390/en10050674
APA StyleMing, M., Wang, R., Zha, Y., & Zhang, T. (2017). Multi-Objective Optimization of Hybrid Renewable Energy System Using an Enhanced Multi-Objective Evolutionary Algorithm. Energies, 10(5), 674. https://doi.org/10.3390/en10050674






