A Hybrid Dynamic System Assessment Methodology for Multi-Modal Transportation-Electrification
Abstract
:1. Introduction
1.1. The Emergence of Electrified Transportation
1.2. Infrastructure Considersations in Electrified Transportation
1.3. Original Contribution and Scope
1.4. Paper Outline
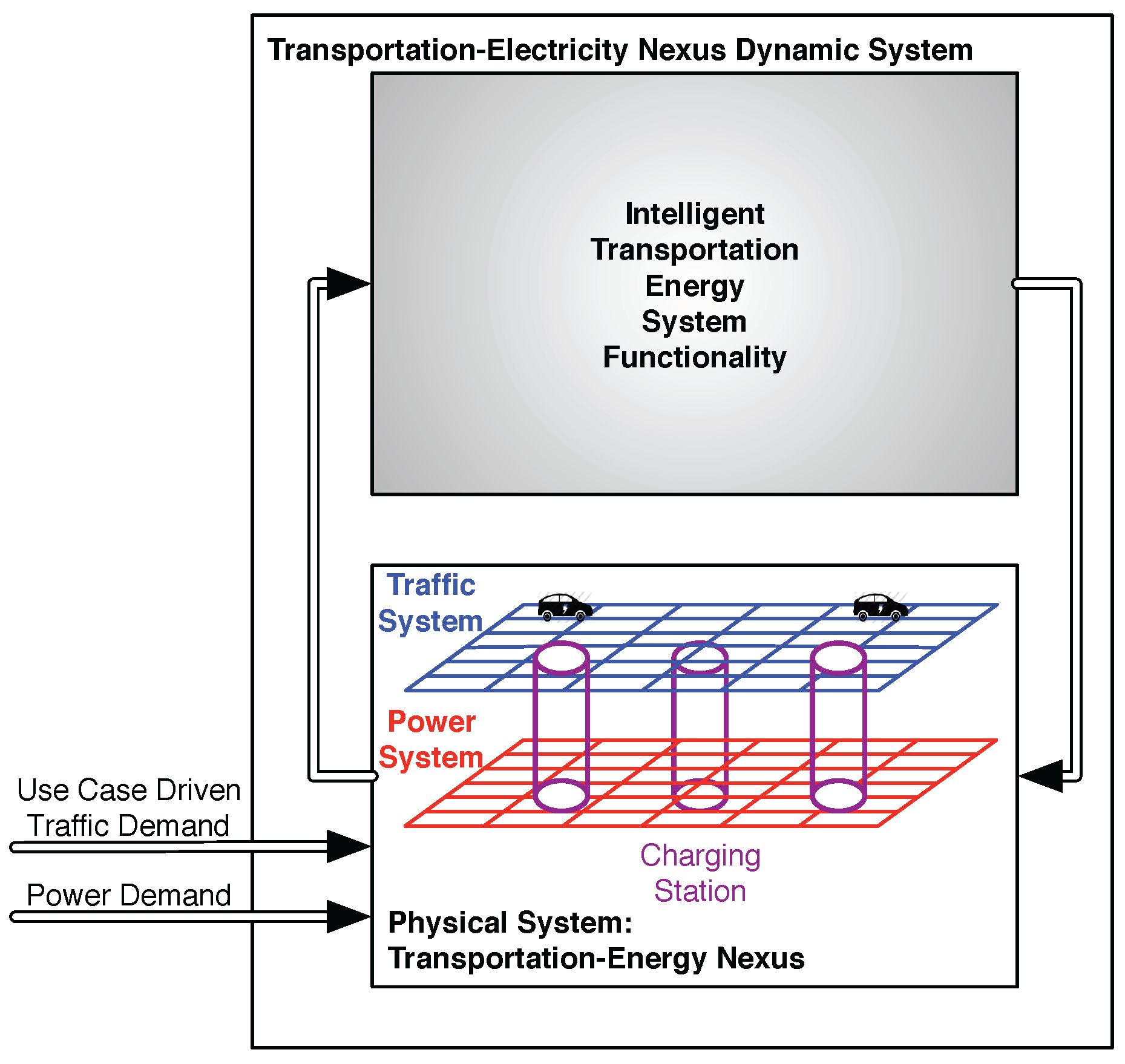
2. Transportation Electrification Assessment Methodology
2.1. Overview
- (1)
- Establish the TEN structure.
- (2)
- Establish the TEN behavior.
- (3)
- Establish the TEN ITES decision-making.
- (4)
- Assess the TEN performance by numerical simulation.
2.1.1. Methodology
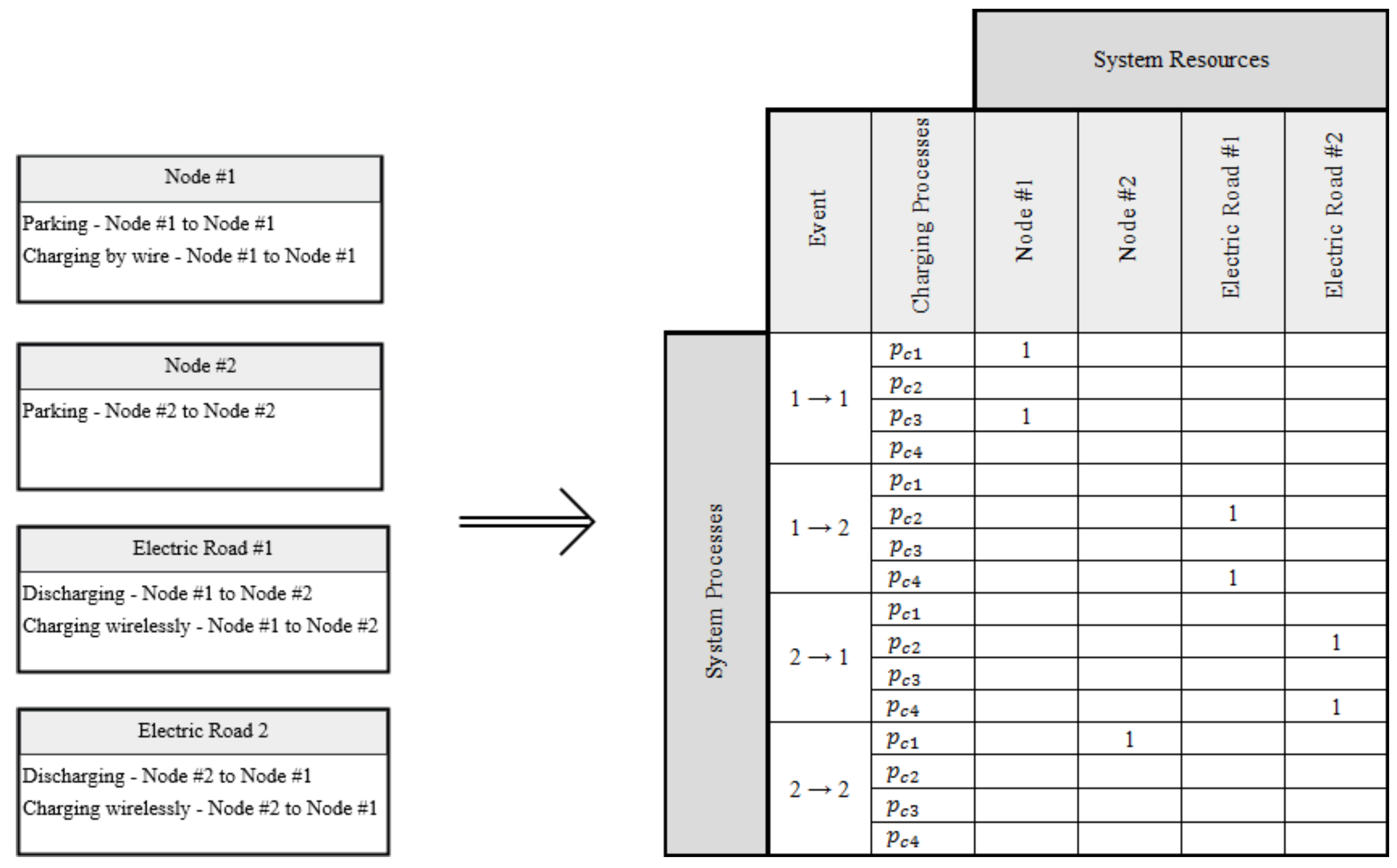
2.2. Establish TEN Structure
- —null charging does not change the EVs SOC.
- —discharge the EV SOC to the EV’s propulsion system.
- —charge the EV SOC by wire.
- —charge the EV SOC wirelessly.
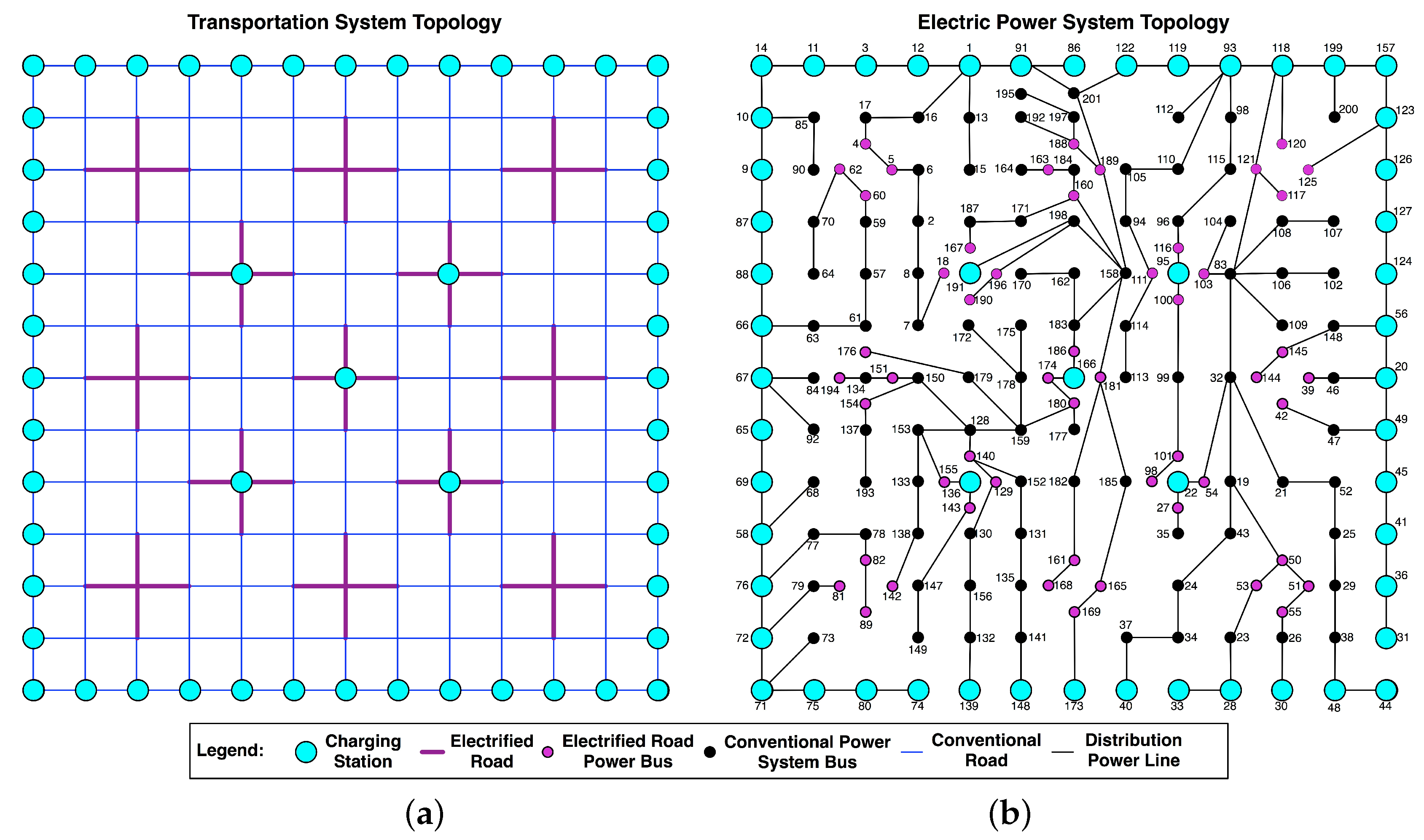
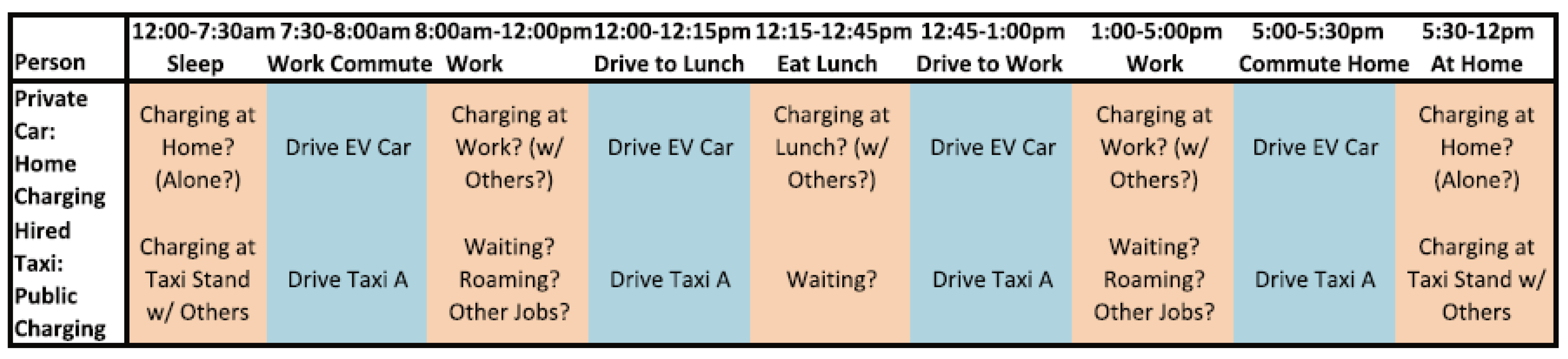
2.2.1. Symmetrica Example
2.3. Establish TEN Behavior
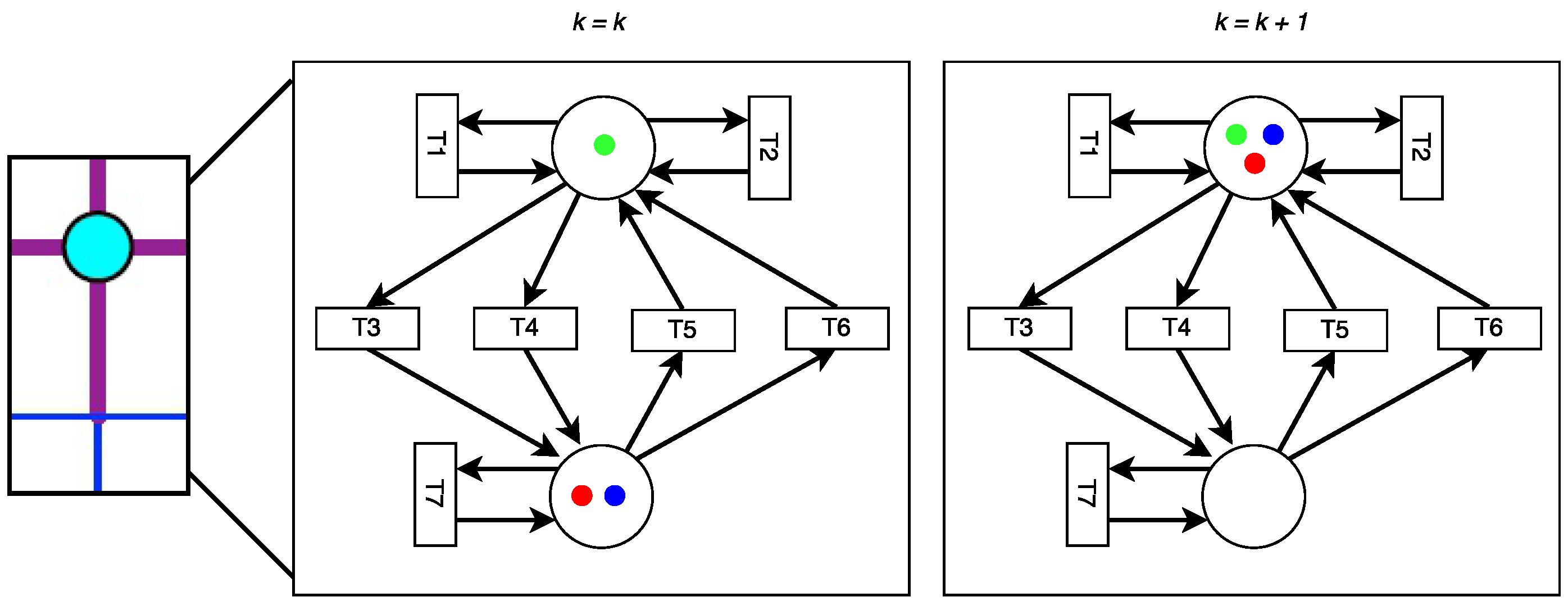
2.3.1. Methodology
- is the set of timed Petri net places. It represents transportation independent buffers (e.g., stations & intersections).
- is the set of timed Petri net discrete events. It represents the structural degrees of freedom (as defined in the previous section).
- is the set of arcs represented as the difference of two incidence matrices. It represents the logical relationship from the events to the places and from the places to the events.
- is the weighting function on the arcs. if and only if .
- is the timed Petri net discrete state vector for all discrete event times k.
- is the discrete state Petri-net transition function (Equation (7)).
- is a binary vehicle firing matrix for all discrete event times k.
- is a continuous-time state vector representing the kinematic and electric state of the TEN.
- is a set of invariant conditions [112] which associates a discrete state Q to an interval of X and within which X and must remain in order to also remain in the discrete state Q.
2.3.2. Symmetrica Example
2.4. Establish TEN Decision-Making
2.4.1. Methodology
2.4.2. Symmetrica Example
2.5. Assess the TEN Performance by Numerical Simulation
2.5.1. Methodology
3. Results: Symmetrica Test Case
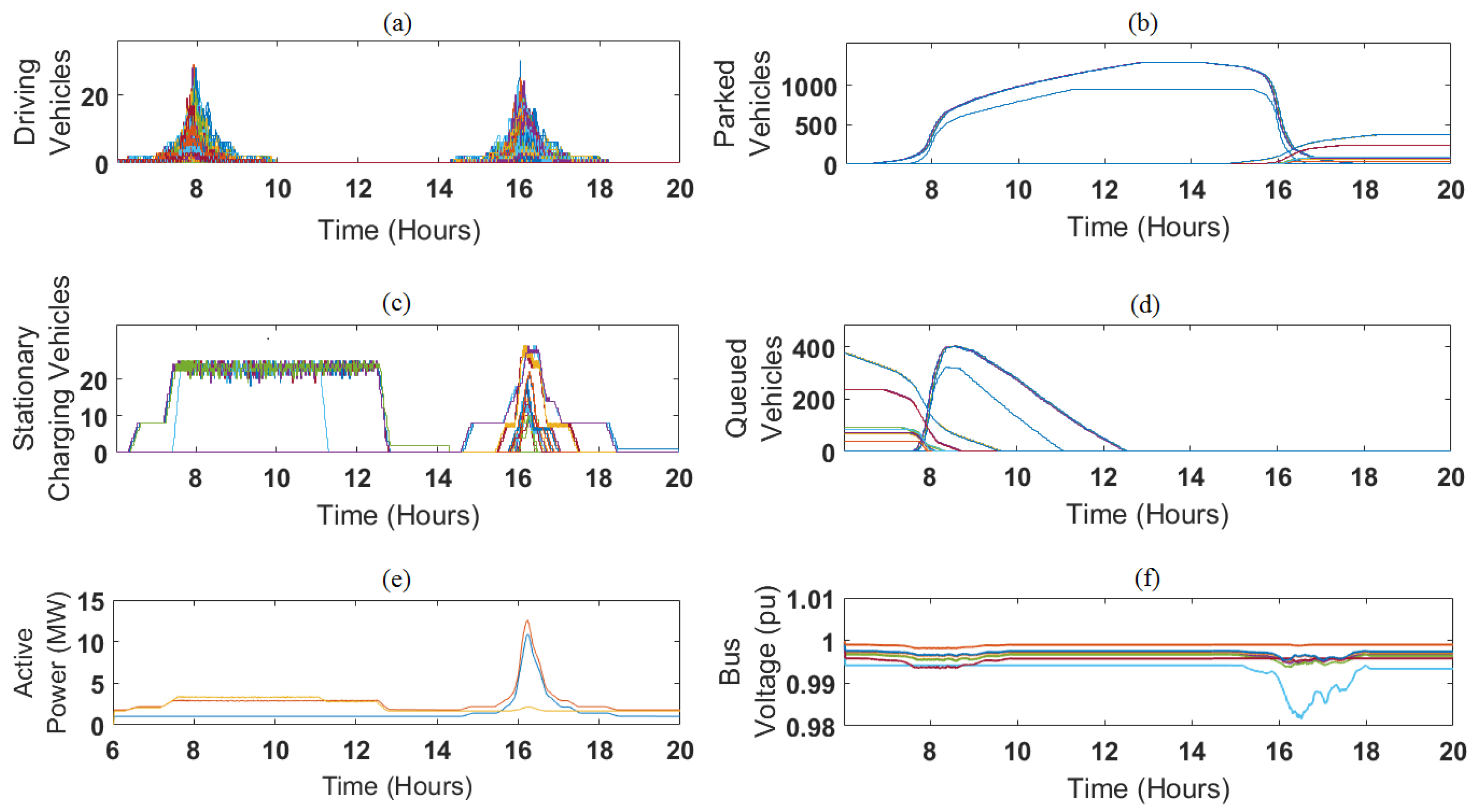
3.1. Performance Measures
3.2. Quantitative Results
4. Conclusions
Author Contributions
Conflicts of Interest
References
- International Energy Agency. World Energy Outlook 2016—Executive Summary; Technical Report; OECD/IEA: Paris, France, 2016. [Google Scholar]
- Pasaoglu, G.; Honselaar, M.; Thiel, C. Potential vehicle fleet CO2 reductions and cost implications for various vehicle technology deployment scenarios in Europe. Energy Policy 2012, 40, 404–421. [Google Scholar] [CrossRef]
- Anair, D.; Mahmassani, A. State of Charge: Electric Vehicles’ Global Warming Emissions and Fuel-Cost Savings across the United States; Technical Report; Union of Concerned Scientists, Citizens and Scientists for Environmental Solutions: Cambridge, MA, USA, 2012. [Google Scholar]
- Soylu, S. Electric Vehicles—The Benefits and Barriers; Intech Open Access Publisher: Rijeka, Croatia, 2011; pp. 1–252. [Google Scholar]
- Litman, T. Comprehensive Evaluation of Transport Energy Conservation and Emission Reduction Policies; Victoria Transport Policy Institute: Victoria, BC, Canada, 2012. [Google Scholar]
- Kassakian, J.G.; Schmalensee, R.; Desgroseilliers, G.; Heidel, T.D.; Afridi, K.; Farid, A.M.; Grochow, J.M.; Hogan, W.W.; Jacoby, H.D.; Kirtley, J.L.; et al. Chapter 5: The Impact of Distributed Generation and Electric Vehicles. In The Future of the Electric Grid: An Interdisciplinary MIT Study; MIT Press: Cambridge, MA, USA, 2011; pp. 109–126. [Google Scholar]
- Kempton, W.; Tomić, J. Vehicle-to-grid power implementation: From stabilizing the grid to supporting large-scale renewable energy. J. Power Sources 2005, 144, 280–294. [Google Scholar] [CrossRef]
- Sovacool, B.K.; Hirsh, R.F. Beyond batteries: An examination of the benefits and barriers to plug-in hybrid electric vehicles (PHEVs) and a vehicle-to-grid (V2G) transition. Energy Policy 2009, 37, 1095–1103. [Google Scholar] [CrossRef]
- Su, W.; Rahimi-eichi, H.; Zeng, W.; Chow, M.Y. A survey on the electrification of transportation in a smart grid environment. IEEE Trans. Ind. Inform. 2012, 8, 1–10. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, B.; Zhou, X.; Gao, Z.; Wu, Y.; Yin, J.; Xu, X. An overview on V2G strategies to impacts from EV integration into power system. In Proceedings of the 2016 Chinese IEEE Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2016. [Google Scholar]
- Gago, R.G.; Pinto, S.F.; Silva, J.F. G2V and V2G electric vehicle charger for smart grids. In Proceedings of the 2016 IEEE International Smart Cities Conference (ISC2), Trento, Italy, 12–15 September 2016. [Google Scholar]
- Carlsson, F.; Johansson-Stenman, O. Costs and benefits of electric vehicles: A 2010 perspective. J. Transp. Econ. Policy 2003, 37, 1–28. [Google Scholar]
- Li, Z.; Ouyang, M. The pricing of charging for electric vehicles in China—Dilemma and solution. Energy 2011, 36, 5765–5778. [Google Scholar] [CrossRef]
- Weiss, M.; Patel, M.K.; Junginger, M.; Perujo, A.; Bonnel, P.; Grootveld, G.V. On the electrification of road transport—Learning rates and price forecasts for hybrid-electric and battery-electric vehicles. Energy Policy 2012, 48, 374–393. [Google Scholar] [CrossRef]
- Sierzchula, W.; Bakker, S.; Maat, K.; van Wee, B. The competitive environment of electric vehicles: An analysis of prototype and production models. Environ. Innov. Soc. Trans. 2012, 2, 49–65. [Google Scholar] [CrossRef]
- Pesaran, A.A.; Markel, T.; Tataria, H.S.; Howell, D. Battery requirements for plug-in hybrid electric vehicles—Analysis and rationale. In Proceedings of the 2007 23rd International Electric Vehicle Symposium, Anaheim, CA, USA, 2–5 December 2007. [Google Scholar]
- Kromer, M.A.; Heywood, J.B. Electric Powertrains: Opportunities and Challenges in the U.S. Light-Duty Vehicle Fleet; Technical Report; Massachuseets Institute of Technology: Cambridge, MA, USA, 2007. [Google Scholar]
- Manzetti, S.; Mariasiu, F. Electric vehicle battery technologies: From present state to future systems. Renew. Sustain. Energy Rev. 2015, 51, 1004–1012. [Google Scholar] [CrossRef]
- Lukic, S.M.; Cao, J.; Bansal, R.C.; Rodriguez, F.; Emadi, A. Energy storage systems for automotive applications. IEEE Trans. Ind. Electron. 2008, 55, 2258–2267. [Google Scholar] [CrossRef]
- Vazquez, S.; Lukic, S.M.; Galvan, E.; Franquelo, L.G.; Carrasco, J.M. Energy storage systems for transport and grid applications. IEEE Trans. Ind. Electron. 2010, 57, 3881–3895. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S.; Wild, M. A review on electric vehicle battery modelling: From Lithium-ion toward Lithium–Sulphur. Renew. Sustain. Energy Rev. 2016, 56, 1008–1021. [Google Scholar] [CrossRef]
- Deutch, J.; Moniz, E. Electrification of the Transportation System; Technical Report; Massachusetts Institute of Technology: Cambridge, MA, USA, 2010. [Google Scholar]
- Markel, T. Plug-in electric vehicle infrastructure: A foundation for electrified transportation. In Proceedings of the 2010 MIT Energy Initiative Transportation Electrification Symposium, Cambridge, MA, USA, 8 April 2010. [Google Scholar]
- Nykvist, B.; Nilsson, M. Rapidly falling costs of battery packs for electric vehicles. Nat. Clim. Chang. 2015, 5, 329–332. [Google Scholar] [CrossRef]
- Hadhrami, M.A.; Viswanath, A.; Junaibi, R.A.; Farid, A.M.; Sgouridis, S. Evaluation of Electric Vehicle Adoption Potential in Abu Dhabi; Technical Report; Masdar Institute of Science and Technology: Abu Dhabi, UAE, 2013. [Google Scholar]
- Zheng, J.; Mehndiratta, S.; Guo, J.Y.; Liu, Z. Strategic policies and demonstration program of electric vehicle in China. Transp. Policy 2012, 19, 17–25. [Google Scholar] [CrossRef]
- Skippon, S.; Garwood, M. Responses to battery electric vehicles: UK consumer attitudes and attributions of symbolic meaning following direct experience to reduce psychological distance. Transp. Res. D Transp. Environ. 2011, 16, 525–531. [Google Scholar] [CrossRef]
- Ahman, M. Government policy and the development of electric vehicles in Japan. Energy Policy 2006, 34, 433–443. [Google Scholar] [CrossRef]
- Van Bree, B.; Verbong, G.; Kramer, G. A multi-level perspective on the introduction of hydrogen and battery-electric vehicles. Technol. Forecast. Soc. Chang. 2010, 77, 529–540. [Google Scholar] [CrossRef]
- Schellenberg, J.A.; Member, M.J.S. Electric Vehicle Forecast for a Large West Coast Utility. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]
- Yabe, K.; Shinoda, Y.; Seki, T.; Tanaka, H.; Akisawa, A. Market penetration speed and effects on CO2 reduction of electric vehicles and plug-in hybrid electric vehicles in Japan. Energy Policy 2012, 45, 529–540. [Google Scholar] [CrossRef]
- Burke, A. Present Status and Marketing Prospects of the Emerging Hybrid-Electric and Diesel Technologies to Reduce CO2 Emissions of New Light-Duty Vehicles in California; Institute of Transportation Studies: Davis, CA, USA, 2004. [Google Scholar]
- Parks, K.; Denholm, P.; Markel, T. Costs and Emissions Associated with Plug-In Hybrid Electric Vehicle Charging in the Xcel Energy Colorado Service Territory; Technical Report; National Renewable Energy Laboratory: Golden, CO, USA, 2007. [Google Scholar]
- Sikes, K.; Gross, T.; Lin, Z.; Sullivan, J.; Cleary, T.; Ward, J. Plug-In Hybrid Electric Vehicle Market Introduction Study Final Report; Technical Report; Sentech Inc.: Washington, DC, USA, 2010. [Google Scholar]
- Duvall, M.; Knipping, E. Environmental Assessment of Plug-In Hybrid Electric Vehicles; Technical Report; Electric Power Research Institute: Charlotte, NC, USA, 2007. [Google Scholar]
- Zhou, Y.; Wang, M.; Hao, H.; Johnson, L.; Wang, H. Plug-in electric vehicle market penetration and incentives: A global review. Mitig. Adapt. Strateg. Glob. Chang. 2015, 20, 777–795. [Google Scholar] [CrossRef]
- OCED-IEA-Anonymous. EV City Casebook: A Look at the Global Electric Vehicle Movement; Technical Report; Organisation for Economic Cooperation and Development/International Energy Agency: Paris, France, 2012. [Google Scholar]
- Tietge, U.; Mock, P.; Lutsey, N.; Campestrini, A. Comparison of Leading Electric Vehicle Policy and Deployment in Europe; International Council on Clean Transportation: Washington, DC, USA, 2016; Volume 49. [Google Scholar]
- U.S. Department of Transportation. Systems Engineering for Intelligent Transportation Systems: An Introduction for Transportation Professionals; Technical Report; U.S. Department of Transportation Federal Highway Administration Federal Transit Administration: Washington, DC, USA, 2007.
- TransCore. Integrating Intelligent Transportation Systems within the Transportation Planning Process; Technical Report; Federal Highway Administration: Washington, DC, USA, 1998.
- Meier, R.; Harrington, A.; Cahill, V. A Framework for Integrating Existing and Novel Intelligent Transportation Systems. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Vienna, Austria, 13–16 September 2005; pp. 650–655. [Google Scholar]
- Chowdhury, M.A.; Sadek, A.W. Fundamentals of Intelligent Transportation Systems Planning; Artech House: Boston, MA, USA, 2003; p. 190. [Google Scholar]
- Thill, J.C.; Rogova, G.; Yan, J. Evaluating benefits and costs of intelligent transportation systems elements from a planning perspective. Res. Transp. Econ. 2004, 8, 571–603. [Google Scholar] [CrossRef]
- Kanninen, B.J. Intelligent transportation systems: An economic and environmental policy assessment. Transp. Res. A Policy Pract. 1996, 30, 1–10. [Google Scholar] [CrossRef]
- He, J.; Zeng, Z.; Li, Z. Benefit evaluation framework of intelligent transportation systems. J. Transp. Syst. Eng. Inf. Technol. 2010, 10, 81–87. [Google Scholar] [CrossRef]
- Architecture-Development-Team. National Intelligent Transportation System Architecture: Executive Summary; Technical Report; Research and Innovation Technology Administration US Department of Transportation: Washington, DC, USA, 2012.
- Gómez-Expósito, A.; Conejo, A.J.; Cañizares, C. Electric Energy Systems: Analysis and Operation; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- PJM-ISO. PJM Manual 3A: Energy Management System (EMS) Model Updates and Quality Assurance (QA); Technical Report; PJM Division, Operations Support; Operations Planning Department: Norristown, PA, USA, 2011. [Google Scholar]
- Al Junaibi, R.; Viswanath, A.; Farid, A.M. Technical Feasibility Assessment of Electric Vehicles: An Abu Dhabi Example. In Proceedings of the 2nd IEEE International Conference on Connected Vehicles and Expo, Las Vegas, NV, USA, 2–6 December 2013. [Google Scholar]
- Farid, A.M. Electrified Transportation System Performance: Conventional vs. Online Electric Vehicles. In Electrification of Ground Transportation Systems for Environment and Energy Conservation; Suh, N.P., Cho, D.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; Chapter 22; pp. 1–25. [Google Scholar]
- Pointon, J. The Multi-Unit Dwelling Vehicle Charging Challenge. In Proceedings of the Electric Vehicles Virtual Summit 2012—The Smart Grid Observer, 13 September 2012; Volume 69. [Google Scholar]
- Junaibi, R.A. Technical Feasibility Assessment of Electric Vehicles in Abu Dhabi. Master’s Thesis, Masdar Institute of Science and Technology, Abu Dhabi, UAE, 2013. [Google Scholar]
- Pieltain Fernandez, L.; Roman, T.G.S.; Cossent, R.; Domingo, C.M.; Frias, P. Assessment of the Impact of Plug-in Electric Vehicles on Distribution Networks. IEEE Trans. Power Syst. 2011, 26, 206–213. [Google Scholar] [CrossRef]
- Lopes, J.A.P.; Soares, F.J.; Almeida, P.M.R. Integration of Electric Vehicles in the Electric Power System. Proc. IEEE 2011, 99, 168–183. [Google Scholar] [CrossRef]
- Qian, K.; Zhou, C.; Allan, M.; Yuan, Y. Modeling of Load Demand Due to EV Battery Charging in Distribution Systems. IEEE Trans. Power Syst. 2011, 26, 802–810. [Google Scholar] [CrossRef]
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The Impact of Charging Plug-In Hybrid Electric Vehicles on a Residential Distribution Grid. IEEE Trans. Power Syst. 2010, 25, 371–380. [Google Scholar] [CrossRef]
- Dyke, K.J.; Schofield, N.; Barnes, M. The Impact of Transport Electrification on Electrical Networks. IEEE Trans. Ind. Electron. 2010, 57, 3917–3926. [Google Scholar] [CrossRef]
- Galus, M.; Zima, M.; Andersson, G. On integration of plug-in hybrid electric vehicles into existing power system structures. Energy Policy 2010, 38, 6736–6745. [Google Scholar] [CrossRef]
- Galus, M.D.; Waraich, R.A.; Noembrini, F.; Steurs, K.; Georges, G.; Boulouchos, K.; Axhausen, K.W.; Andersson, G. Integrating Power Systems, Transport Systems and Vehicle Technology for Electric Mobility Impact Assessment and Efficient Control. IEEE Trans. Smart Grid 2012, 3, 934–949. [Google Scholar] [CrossRef]
- Perujo, A.; Ciuffo, B. The introduction of electric vehicles in the private fleet: Potential impact on the electric supply system and on the environment. A case study for the Province of Milan, Italy. Energy Policy 2010, 38, 4549–4561. [Google Scholar] [CrossRef]
- Soares, J.A.; Canizes, B.; Lobo, C.; Vale, Z.; Morais, H. Electric Vehicle Scenario Simulator Tool for Smart Grid Operators. Energies 2012, 5, 1881–1899. [Google Scholar] [CrossRef]
- Behr, P. MIT Panel Says a Charging Infrastructure May Be a Bigger Roadblock for Electric Vehicles Than Technology; Scientific American: New York, NY, USA, 2011; pp. 1–6. [Google Scholar]
- Farid, A.M. A Hybrid Dynamic System Model for Multi-Modal Transportation Electrification. IEEE Trans. Control Syst. Technol. 2017, 25, 940–951. [Google Scholar] [CrossRef]
- Lam, A.Y.; Leung, Y.W.; Chu, X. Electric vehicle charging station placement: Formulation, complexity, and solutions. IEEE Trans. Smart Grid 2014, 5, 2846–2856. [Google Scholar] [CrossRef]
- Palensky, P.; Dietrich, D. Demand Side Management: Demand Response, Intelligent Energy Systems, and Smart Loads. IEEE Trans. Ind. Inform. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Sortomme, E.; Hindi, M.M.; MacPherson, S.D.J.; Venkata, S.S. Coordinated Charging of Plug-In Hybrid Electric Vehicles to Minimize Distribution System Losses. IEEE Trans. Smart Grid 2011, 2, 198–205. [Google Scholar] [CrossRef]
- Saber, A.Y.; Venayagamoorthy, G.K. Plug-in Vehicles and Renewable Energy Sources for Cost and Emission Reductions. IEEE Trans. Ind. Electron. 2011, 58, 1229–1238. [Google Scholar] [CrossRef]
- Gan, L.; Topcu, U.; Low, S. Optimal decentralized protocol for electric vehicle charging. In Proceedings of the IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 5798–5804. [Google Scholar]
- Erol-Kantarci, M.; Sarker, J.H.; Mouftah, H.T. Quality of service in Plug-in Electric Vehicle charging infrastructure. In Proceedings of the 2012 IEEE International Electric Vehicle Conference (IEVC), Greenville, SC, USA, 4–8 March 2012. [Google Scholar]
- Ma, Z.; Callaway, D.; Hiskens, I. Optimal Charging Control for Plug-In Electric Vehicles. In Control and Optimization Methods for Electric Smart Grids; Springer: Berlin, Germany, 2012; pp. 259–273. [Google Scholar]
- Gong, Q.; Li, Y.; Peng, Z.R. Optimal Power Management of Plug-in HEV with Intelligent Transportation System. In Proceedings of the 2007 IEEE/ASME International Conference on Advanced intelligent Mechatronics, Zurich, Switzerland, 4–7 September 2007. [Google Scholar]
- Andersen, P.H.; Mathews, J.A.; Rask, M. Integrating private transport into renewable energy policy: The strategy of creating intelligent recharging grids for electric vehicles. Energy Policy 2009, 37, 2481–2486. [Google Scholar] [CrossRef]
- Falvo, M.C.; Lamedica, R.; Bartoni, R.; Maranzano, G. Energy management in metro-transit systems: An innovative proposal toward an integrated and sustainable urban mobility system including plug-in electric vehicles. Electr. Power Syst. Rese. 2011, 81, 2127–2138. [Google Scholar] [CrossRef]
- Richardson, D.B. Electric vehicles and the electric grid: A review of modeling approachces, Impacts, and renewable energy integration. Renew. Sustain. Energy Rev. 2013, 19, 247–254. [Google Scholar] [CrossRef]
- Junaibi, R.A.; Farid, A.M. A Method for the Technical Feasibility Assessment of Electrical Vehicle Penetration. In Proceedings of the 7th Annual IEEE System Conference (SysCon), Orlando, FL, USA, 15–18 April 2013. [Google Scholar]
- Farid, A.M. Symmetrica: Test Case for Transportation Electrification Research. Infrastruc. Complex. 2015, 2, 9. [Google Scholar] [CrossRef]
- Viswanath, A.; Farid, A.M. A Hybrid Dynamic System Model for the Assessment of Transportation Electrification. In Proceedings of the 2014 IEEE American Control Conference, Portland, OR, USA, 4–6 June 2014. [Google Scholar]
- Farid, A.M.; Jiang, B.; Muzhikyan, A.; Youcef-Toumi, K. The Need for Holistic Enterprise Control Assessment Methods for the Future Electricity Grid. Renew. Sustain. Energy Rev. 2015, 56, 669–685. [Google Scholar] [CrossRef]
- Brouwer, A.S.; van den Broek, M.; Seebregts, A.; Faaij, A. Impacts of large-scale Intermittent Renewable Energy Sources on electricity systems, and how these can be modeled. Renew. Sustain. Energy Rev. 2014, 33, 443–466. [Google Scholar] [CrossRef]
- Holttinen, H.; Milligan, M.; Ela, E.; Menemenlis, N.; Dobschinski, J.; Rawn, B.; Bessa, R.J.; Flynn, D.; Gomez-Lazaro, E.; Detlefsen, N.K. Methodologies to Determine Operating Reserves Due to Increased Wind Power. IEEE Trans. Sustain. Energy 2012, 3, 713–723. [Google Scholar] [CrossRef]
- Holttinen, H.; Orths, A.; Abilgaard, H.; van Hulle, F.; Kiviluoma, J.; Lange, B.; O’Malley, M.; Flynn, D.; Keane, A.; Dillon, J.; et al. IEA Wind Export Group Report on Recommended Practices Wind Integration Studies; Technical Report; International Energy Agency: Paris, France, 2013. [Google Scholar]
- Ela, E.; Milligan, M.; Parsons, B.; Lew, D.; Corbus, D. The evolution of wind power integration studies: Past, present, and future. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting (PES’09), Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Treiber, M.; Kesting, A. Traffic Flow Dynamics: Data, Models and Simulation; Springer: Heidelberg, Germany; New York, NY, USA, 2013; p. 503. [Google Scholar]
- Barcelo, J.; Kuwahara, M. Traffic Data Collection and Its Standardization; Springer: New York, NY, USA, 2008; p. 194. [Google Scholar]
- Zografos, K.G.; Androutsopoulos, K.N. Algorithms for Itinerary Planning in Multimodal Transportation Networks. IEEE Trans. Intell. Transp. Syst. 2008, 9, 175–184. [Google Scholar] [CrossRef]
- Pillac, V.; Gendreau, M.; Guéret, C.; Medaglia, A.L. A review of dynamic vehicle routing problems. Eur. J. Oper. Res. 2013, 225, 1–11. [Google Scholar] [CrossRef]
- Newman, M. Networks: An Introduction; OUP: Oxford, UK, 2009. [Google Scholar]
- Van Steen, M. Graph Theory and Complex Networks: An Introduction; Maarten van Steen: Enschede, The Netherlands, 2010; pp. 1–300. [Google Scholar]
- Lewis, T.G. Network Science: Theory and Applications; Wiley: Hoboken, NJ, USA, 2011; p. 512. [Google Scholar]
- Ip, W.H.; Wang, D. Resilience and Friability of Transportation Networks: Evaluation, Analysis and Optimization. IEEE Syst. J. 2011, 5, 189–198. [Google Scholar] [CrossRef]
- Zografos, K.G.; Androutsopoulos, K.N.; Spitadakis, V. Design and Assessment of an Online Passenger Information System for Integrated Multimodal Trip Planning. IEEE Trans. Intell. Transp. Syst. 2009, 10, 311–323. [Google Scholar] [CrossRef]
- Hame, L.; Hakula, H. Dynamic Journeying in Scheduled Networks. IEEE Trans. Intell. Transp. Syst. 2013, 14, 360–369. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- Ash, J.; Newth, D. Optimizing complex networks for resilience against cascading failure. Phys. A Stat. Mech. Appl. 2007, 380, 673–683. [Google Scholar] [CrossRef]
- Kivelä, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]
- Farid, A.M. Product Degrees of Freedom as Manufacturing System Reconfiguration Potential Measures. Int. Trans. Syst. Sci. Appl. 2008, 4, 227–242. [Google Scholar]
- Farid, A.M.; McFarlane, D.C. Production degrees of freedom as manufacturing system reconfiguration potential measures. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2008, 222, 1301–1314. [Google Scholar] [CrossRef]
- Farid, A.M. Static Resilience of Large Flexible Engineering Systems: Axiomatic Design Model and Measures. IEEE Syst. J. 2015, PP, 1–12. [Google Scholar] [CrossRef]
- Suh, N.P. Axiomatic Design: Advances and Applications; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- SE Handbook Working Group. Systems Engineering Handbook: A Guide for System Life Cycle Processes and Activities; International Council on Systems Engineering (INCOSE): San Diego, CA, USA, 2011; pp. 1–386. [Google Scholar]
- Friedenthal, S.; Moore, A.; Steiner, R. A Practical Guide to SysML: The Systems Modeling Language, 2nd ed.; Morgan Kaufmann: Burlington, MA, USA, 2011; p. 640. [Google Scholar]
- Ahn, S.; Kim, J.; Cho, D.-H. Wireless Power Transfer in On-Line Electric Vehicle. In Wireless Power Transfer, 2nd ed.; River Publishers: Aalborg, Denmark, 2012; p. 416. [Google Scholar]
- Jang, Y.J.; Ko, Y.D.; Jeong, S. Optimal design of the wireless charging electric vehicle. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012. [Google Scholar]
- Nam, P.; Suh, D.H.C. The On-line Electric Vehicle: Wireless Electric Ground Transportation Systems; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Ahn, S.; Suh, N.P.; Cho, D.H. The all-electric car you never plug in. In IEEE Spectrum; IEEE: Anaheim, CA, USA, 2013. [Google Scholar]
- Kim, J.; Kim, J.; Kong, S.; Kim, H.; Suh, I.S.; Suh, N.P.; Cho, D.H.; Kim, J.; Ahn, S. Coil design and shielding methods for a magnetic resonant wireless power transfer system. Proc. IEEE 2013, 101, 1332–1342. [Google Scholar] [CrossRef]
- Ramirez-Rosado, I.J.; Bernal-Agustin, J.L. Genetic algorithms applied to the design of large power distribution systems. IEEE Trans. Power Syst. 1998, 13, 696–703. [Google Scholar] [CrossRef]
- De Oliveira-De Jesus, P.M. Remuneration of Distributed Generation: A Holistic Approach. Ph.D. Thesis, Faculdade de Engharia Universidade de Porto, Porto, Portugal, 2007. [Google Scholar]
- Weilkiens, T. Systems Engineering with SysML/UML Modeling, Analysis, Design; Morgan Kaufmann: Burlington, MA, USA, 2007. [Google Scholar]
- Buede, D.M. The Engineering Design of Systems: Models and Methods, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; p. 516. [Google Scholar]
- Dori, D. Model-Based Systems Engineering with OPM and SysML; Springer: New York, NY, USA, 2015. [Google Scholar]
- Cassandras, C.G.; Lafortune, S. Introduction to Discrete Event Systems; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Popova-Zeugmann, L. Time and Petri Nets; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Reisig, W. Understanding Petri Nets; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Barcelo, J. Fundamentals of Traffic Simulation; Springer: New York, NY, USA, 2010; p. 440. [Google Scholar]
- Olstam, J.J.; Tapani, A. Comparison of Car-Following Models; VTI Meddelande 960A; Swedish National Road and Transport Research Institute: Linköping, Sweden, 2004; pp. 1–45. [Google Scholar]
- Brackstone, M.; McDonald, M. Car-following: A historical review. Tramsp. Res. Traffic Psychol. Behav. 1999, 2, 181–196. [Google Scholar] [CrossRef]
- Karabasoglu, O.; Michalek, J. Influence of driving patterns on life cycle cost and emissions of hybrid and plug-in electric vehicle powertrains. Energy Policy 2013, 60, 445–461. [Google Scholar] [CrossRef]
- Taniguchi, E.; Shimamoto, H. Intelligent transportation system based dynamic vehicle routing and scheduling with variable travel times. Transp. Res. C Emerg. Technol. 2004, 12, 235–250. [Google Scholar] [CrossRef]
- Bischoff, J.; Maciejewski, M. Agent-based simulation of electric taxicab fleets. Transp. Res. Procedia 2014, 4, 191–198. [Google Scholar] [CrossRef]
- Dijk, M.; Montalvo, C. Policy frames of Park-and-Ride in Europe. J. Transp. Geogr. 2011, 19, 1106–1119. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Gartner, N.H. Optimal traffic assignment with elastic demands: A review part I. Analysis framework. Transp. Sci. 1980, 14, 174–191. [Google Scholar] [CrossRef]
- Gartner, N.H. Optimal traffic assignment with elastic demands: A review part II. algorithmic approaches. Transp. Sci. 1980, 14, 192–208. [Google Scholar] [CrossRef]
- Janson, B.N. Dynamic traffic assignment for urban road networks. Transp. Res. B Methodol. 1991, 25, 143–161. [Google Scholar] [CrossRef]
- Malandrino, F.; Casetti, C.; Chiasserini, C.F.; Reineri, M. Where to get a charged EV battery: A route to follow as if it were your own advice. In Proceedings of the 2013 IEEE 5th International Symposium on Wireless Vehicular Communications (WiVeC), Dresden, Germany, 2–3 June 2013. [Google Scholar]
- Zhang, B.; Li, W.; Chen, T.; Su, W. A simulation platform for energy-efficient dynamic commuter transit using electric vehicles. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo Asia-Pacific (ITEC Asia-Pacific), Busan, Korea, 1–4 June 2016; pp. 812–817. [Google Scholar]
- Wei, W.; Mei, S.; Wu, L.; Shahidehpour, M.; Fang, Y. Optimal Traffic-Power Flow in Urban Electrified Transportation Networks. IEEE Trans. Smart Grid 2017, 8, 84–95. [Google Scholar] [CrossRef]
- Lu, F.; Hua, G. A location-sizing model for electric vehicle charging station deployment based on queuing theory. In Proceedings of the 2015 International Conference on Logistics, Informatics and Service Sciences (LISS), Barcelona, Spain, 27–29 July 2015. [Google Scholar]
- Muzhikyan, A.; Farid, A.M.; Youcef-Toumi, K. An Enterprise Control Assessment Method for Variable Energy Resource Induced Power System Imbalances Part 1: Methodology. IEEE Trans. Ind. Electron. 2015, 62, 2448–2458. [Google Scholar] [CrossRef]
- Muzhikyan, A.; Farid, A.M.; Youcef-Toumi, K. An Enterprise Control Assessment Method for Variable Energy Resource Induced Power System Imbalances Part 2: Results. IEEE Trans. Ind. Electron. 2015, 62, 2459–2467. [Google Scholar] [CrossRef]
- Muzhikyan, A.; Farid, A.M.; Youcef-Toumi, K. Relative Merits of Load Following Reserves and Energy Storage Market Integration Towards Power System Imbalances. Int. J. Electr. Power Energy Syst. 2016, 74, 222–229. [Google Scholar] [CrossRef]
- Muzhikyan, A.; Farid, A.M.; Youcef-Toumi, K. An a Priori Analytical Method for Determination of Operating Reserves Requirements. Int. J. Electr. Power Energy Syst. 2017, 86, 1–11. [Google Scholar] [CrossRef]
- Jiang, B.; Muzhikyan, A.; Farid, A.M.; Youcef-Toumi, K. Demand Side Management in Power Grid Enterprise Control—A Comparison of Industrial and Social Welfare Approaches. Appl. Energy 2016, 187, 833–846. [Google Scholar] [CrossRef]
- Duffey, C.K.; Stratford, R.P. Update of harmonic standard IEEE-519: IEEE recommended practices and requirements for harmonic control in electric power systems. IEEE Trans. Ind. Appl. 1989, 25, 1025–1034. [Google Scholar] [CrossRef]
|
| System | M | B | H | |||
|---|---|---|---|---|---|---|
| LFES | Transformation | Transportation | Holding | Transforming Resource | Independent Buffer | Transporting Resource |
| Transportation Systems | Entry & Exit | Transportation | Charging | Stations | Intersections | Roads & Lines |
| Power Grids | Generation & Consumption | Transmission | Voltage Level | Generators & Loads | Storage | Lines |
| Scenario | Quality of Service | Average Resource Utilization | Average EV Fleet Utilization | Average EV Fleet Availability | Effective EV Fleet Utilization |
|---|---|---|---|---|---|
| 50% Plug-In EVs | 82.6% | 2.7% | 2.8% | 86.0% | 3.3% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van der Wardt, T.J.T.; Farid, A.M. A Hybrid Dynamic System Assessment Methodology for Multi-Modal Transportation-Electrification. Energies 2017, 10, 653. https://doi.org/10.3390/en10050653
Van der Wardt TJT, Farid AM. A Hybrid Dynamic System Assessment Methodology for Multi-Modal Transportation-Electrification. Energies. 2017; 10(5):653. https://doi.org/10.3390/en10050653
Chicago/Turabian StyleVan der Wardt, Thomas J.T., and Amro M. Farid. 2017. "A Hybrid Dynamic System Assessment Methodology for Multi-Modal Transportation-Electrification" Energies 10, no. 5: 653. https://doi.org/10.3390/en10050653
APA StyleVan der Wardt, T. J. T., & Farid, A. M. (2017). A Hybrid Dynamic System Assessment Methodology for Multi-Modal Transportation-Electrification. Energies, 10(5), 653. https://doi.org/10.3390/en10050653






