1. Introduction
With the advent of more stringent regulations related to emissions, fuel economy, and global warming, as well as energy resource constraints, electrical, hybrid, and fuel-cell vehicles have attracted increasing attention from vehicle constructors, governments, and consumers [
1]. Electrical machines and drives are a key enabling technology for electrical, hybrid, and fuel cell vehicles [
2]. The fault diagnosis of rotating electrical machines has received an intense amount of research interest during the last 30 years [
3]. The failure of inverters is fatal in electric vehicles. Therefore, it is vital to adopt various algorithms to improve the diagnosis of the inverter faults. Timely maintenance and repair after a failure is very important to prevent a secondary failure, and to ensure the safe and reliable operation of the control system in electric vehicles.
Short-circuit faults and open circuit faults are the most common faults of insulated gate bipolar transistors (IGBTs) in power inverters [
4]. Short-circuit faults are generally protected by hardware for its short maintenance time which is generally less than 10 μs. When open circuit faults occur, the motor is still able to operate. A new secondary failure may occur if it is not detected in the meanwhile. During driving, these faults may reduce safety which is fatal for electric vehicles. Therefore, it is essential to detect the open circuit faults in time.
According to the classification of diagnostic signals, the existing diagnostic algorithms for IGBT open circuit faults can be broadly divided into the current-based diagnostic algorithms and the voltage-based diagnostic algorithms. Since the voltage source inverter outputs the voltage signals, the voltage-based diagnostic algorithms can quickly reflect the current status of the power switch and have a high reliability. Fast detection times can be achieved by using voltage-based algorithms [
5,
6,
7]. A very fast detection scheme is proposed for the conventional three-leg converter that minimizes the use of voltage sensors in [
8]. Faults and their locations are detected in less than 50 μs for the studied parameters.
However, additional voltage sensors may be required, which increases the drive costs and complexity. Furthermore, in order to avoid false alarms, some time-delay values must be correctly defined, which can be very difficult since they depend on several variables [
9]. Therefore, the voltage-based open circuit fault diagnostic algorithms are rarely used in electric vehicles. Current-based fault diagnostic algorithms do not need to add additional sensors. However, they have a certain response time constant because the current signal is a state parameter. Therefore, the current-based fault diagnostic algorithms are influenced by the system state and they have a certain time lag of detecting the faults.
For electric vehicles, in order to reduce the cost and complexity of the diagnostic system and ensure their safe and reliable operation, it is required to detect the open circuit faults as fast as possible while the diagnostic results need to be highly reliable without additional sensors [
10].
An open circuit fault diagnostic algorithm based on the Park’s vector center is proposed in [
11]. In this algorithm, open circuit faults are detected by calculating the position of the current trajectory’s midpoint, which is the average value of the AC current space vector over one period. An open circuit fault diagnosis algorithm based on Park’s vector slope is proposed in [
12]. The slope of the diameter of the current space vector trajectory is used to identify the faulty leg and the missing half-cycle of the current waveform is used to localize the faulty switch. In order to solve the drawback of being load dependent, a normalized DC current algorithm is proposed in [
13], which is an improvement over Park’s vector method. A modified normalized DC current algorithm is proposed in [
14]. To prevent multiple satisfactory conditions, a less restrictive method is employed to localize the faulty switch. A fault detection and the improved fault-tolerant control for an open fault in the five-phase inverter driving system is proposed in [
15]. A new fault diagnostic algorithm named the wind speed based normalized current trajectory is proposed and used to accurately detect and locate faulted IGBT in the circuit arms [
16]. A very fast and efficient field-programmable gate array (FPGA) based on the open circuit switch fault detection method associated to fault tolerant converter topology in DC-DC converters is proposed in [
17]. The detection time of the fault detection method is equal to or less than one switching period. Intelligent algorithms such as the clustering adaptive neuron fuzzy inference system [
18], fuzzy-based algorithm [
19], and wavelet transforms and neural network algorithms [
20] are also proposed. However, due to the complexity of the intelligent algorithm and the large amount of computation, it is not suitable for real-time applications.
The fault diagnostic algorithms are compared and analyzed for their effectiveness, resistivity against false alarms, detection time, implementation, and tuning effort [
21]. Among the open circuit fault algorithms, the modified normalized DC current algorithm is found to be very effective in detecting faults with a high resistivity to false alarms. In addition, it is independent of load variations. However, the modified normalized DC algorithm requires the discrete Fourier transform of the three-phase current, which may reduce the diagnostic detection speed.
The primary objective of this paper is to present a fast-acting diagnostic algorithm of IGBT open circuit faults for power inverters to improve the diagnostic detection speed, while ensuring the reliability of the diagnostic results in electric vehicles. The average of the difference between the actual three-phase current and the referential three-phase current values over one electrical period is used as the diagnostic variable. The three-phase referential current is obtained by transforming the target d-q axis current. In order to eliminate the diagnostic error caused by the load variations, the normalization method is adopted. Since the magnitude of the d-q axis current is the same as the magnitude of the three-phase current and is not affected by the signal acquisition, the average value of the d-q axis current amplitude over one electrical period is taken as the normalized referential value. In the parameter discretization process, the variable parameter moving average method (VPMAM) is used to automatically adjust the counting cycle according to the motor speed to be adapted to the fault diagnosis at different motor speeds. As only the three-phase current is used, the system does not need additional sensors, which is beneficial regarding the system complexity and cost. This algorithm has the advantages of fast detection speed and high resistivity against false alarms which are significantly essential for real-time control in electric vehicles.
MATLAB/SIMULINK (MathWorks, Natick, MA, USA) models are built to analyze the proposed algorithm. Furthermore, experiments are carried out to verify the algorithm.
3. Proposed Fault Diagnostic Algorithm
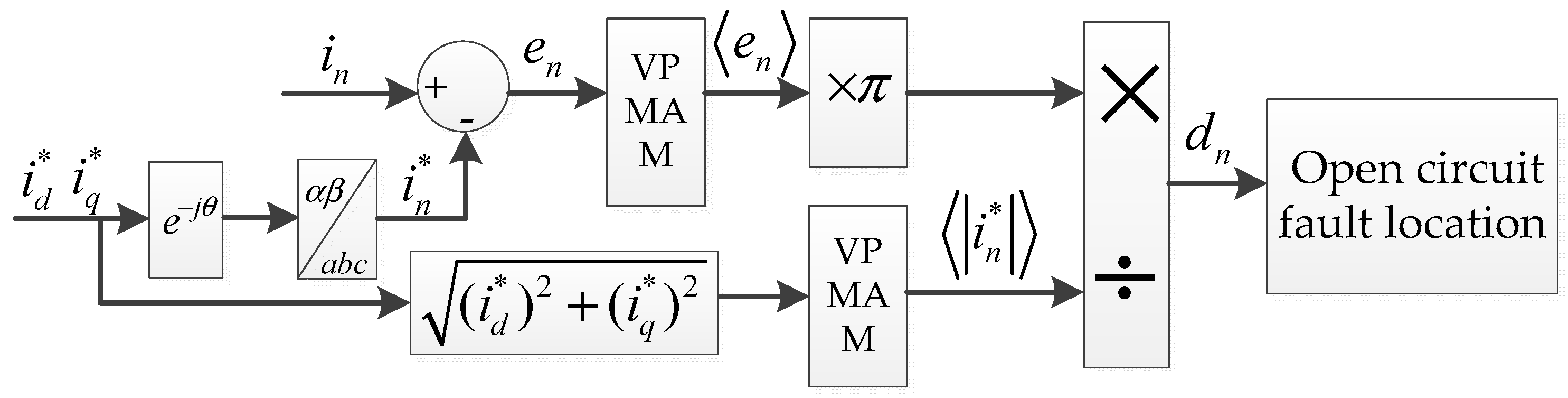
The proposed open circuit fault diagnostic algorithm is shown in
Figure 5.
The d-q axis current cannot be directly utilized for fault diagnosis because of the regulation of the current closed-loop. In this paper, the average of the difference between the actual three-phase current and the referential three-phase current values over one electrical period is used as the diagnostic variable. The three-phase referential current can be obtained from the target d-q axis current through the inverse Park transformation and inverse Clark transformation.
The average value of parameter
over one electrical period
can be expressed as follows:
The difference between the actual three-phase current and the referential three-phase current values can be expressed as follows:
To improve the reliability of the diagnostic system, the average value of
in one electrical period
is used as the diagnostic variable to reduce the misdiagnosis caused by the interference signal. The value of
is related to the magnitude of the phase current which represents the current load of the motor. In order to be independent of load variations, the normalization method is adopted. There are mainly three different normalized referential values: the first order harmonic coefficients of the three-phase current over one period [
14]; the magnitude of the
d-q axis current over one period [
11]; and the average absolute values of the three-phase current over one period [
9]. The first order harmonic coefficients usually require a large amount of computation due to the utilization of the discrete Fourier transform. The average absolute values of the three-phase current are affected by the noise of the signal acquisition and signal delay. Since the amplitude of the
d-q axis current is the same as the magnitude of the three-phase current and is not affected by the signal acquisition, the
time of average amplitude of the
d-q axis current over one period is used as the normalized referential value. Thus, the normalized diagnostic variables can be expressed as follows:
Ideally, the three-phase current is fully balanced which can be expressed as follows:
where
is the amplitude of the three-phase current,
is the initial phase, and
is the electrical angular velocity. If the current follows this well, the referential
d-q axis current can be expressed as follows:
where
is the angle between the stator current vector and the
d-axis.
The diagnostic variables can be obtained by substituting Equations (4) and (5) into Equations (1) and (3). Ideally,
closely follows
due to the current closed loop, and thus
is equal to zero. Actually,
is not equal to zero due to the acquisition error and noise. However, the average value of
over one period
is approximately equal to zero due to the randomness of error. Therefore,
is approximately equal to zero. When an open circuit fault occurs in T1, the upper half-bridge of phase A cannot output voltage. Therefore the output current of phase A in the first half of the period is zero, while the last half is normal. The output current of phase A can be expressed as follows:
Substituting Equation (6) into Equations (1) and (3), the diagnostic variable of phase A can be expressed as follows:
It can be similarly analyzed when the open circuit fault occurs in the other half-bridges. It can be proven that the value of the diagnostic variable
is approximately equal to 1 for an open circuit fault in the upper half-bridge and −1 for an open circuit fault in the lower half-bridge. Therefore, the open circuit fault can be located by identifying which diagnostic variable is beyond the threshold
, as shown in
Table 1.
Ideally, the values of the diagnostic variables are 0 and 1 in normal and faulty conditions, respectively. Therefore,
should be between 0 and 1. A smaller value of
can improve the diagnostic speed of the system, but may also lead to the possibility of misdiagnosis and vice versa. In order to improve the system response speed and diagnostic reliability, the selection for the value of
should consider the worst condition (usually a huge load variation) [
9]. The value of
should be as small as possible in the case of meeting the worst condition.
In the analysis above,
is defined as an analog parameter which needs to be discretized in the control process. The simple moving average method is commonly utilized to discretize the parameter. The simple moving average method averages a fixed number of data. It can be expressed as follows:
where
is the moving average value at k-time,
is the number of data,
is the control period, and
is the actual value at i-time before k-time.
is the average value of the discrete variables over an electrical period. However, the electrical period constantly changes with the motor speed. Therefore, the number of data used for the average cannot simply be a fixed value, it should vary with the electrical period synchronously. The VPMAM is obtained by replacing the parameter
of the simple moving average method with the parameter
which varies with the electrical period.
can be expressed as follows:
Thus, the VPMAM can be expressed as follows:
4. Simulation and Analysis
MATLAB/SIMULINK models are developed to examine the proposed algorithm. The permanent magnet synchronous motor (PMSM) is an attractive candidate for electric vehicles due to its advantage of high power density [
22]. A 75-kW PMSM for an electric vehicle is used in this paper, and its parameters are shown in
Table 2 [
23].
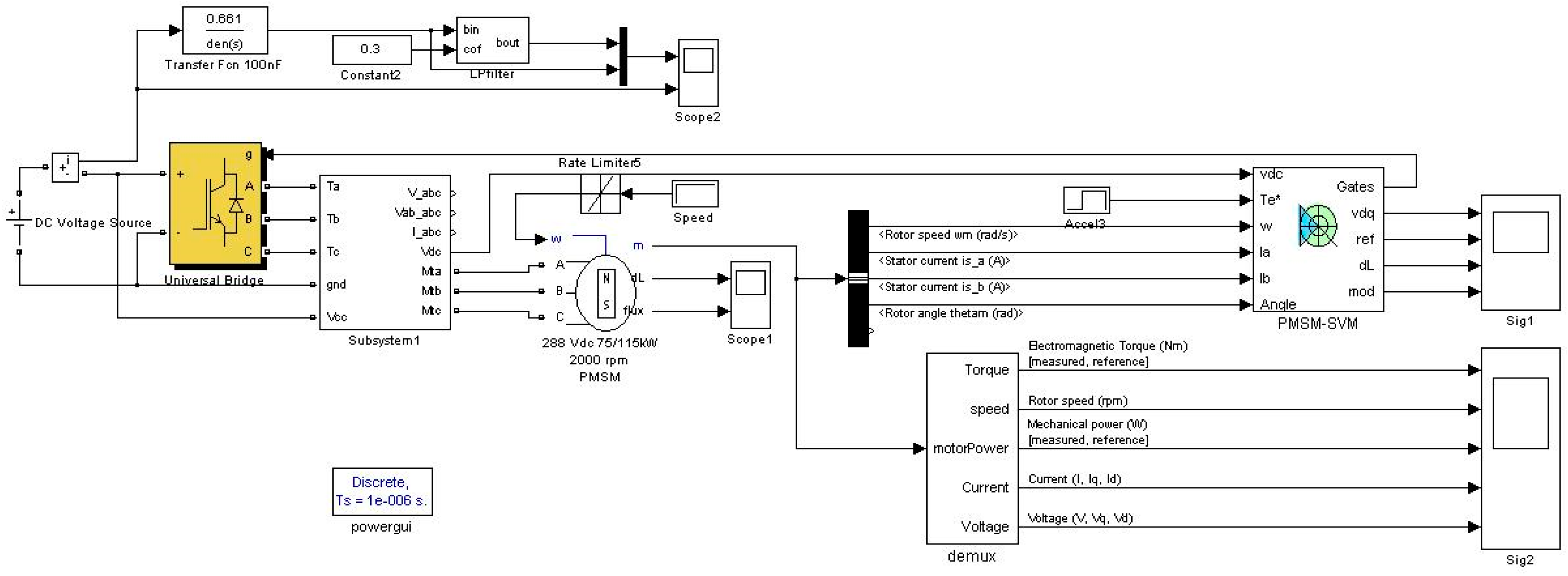
The simulation model is shown in
Figure 6.
As shown in
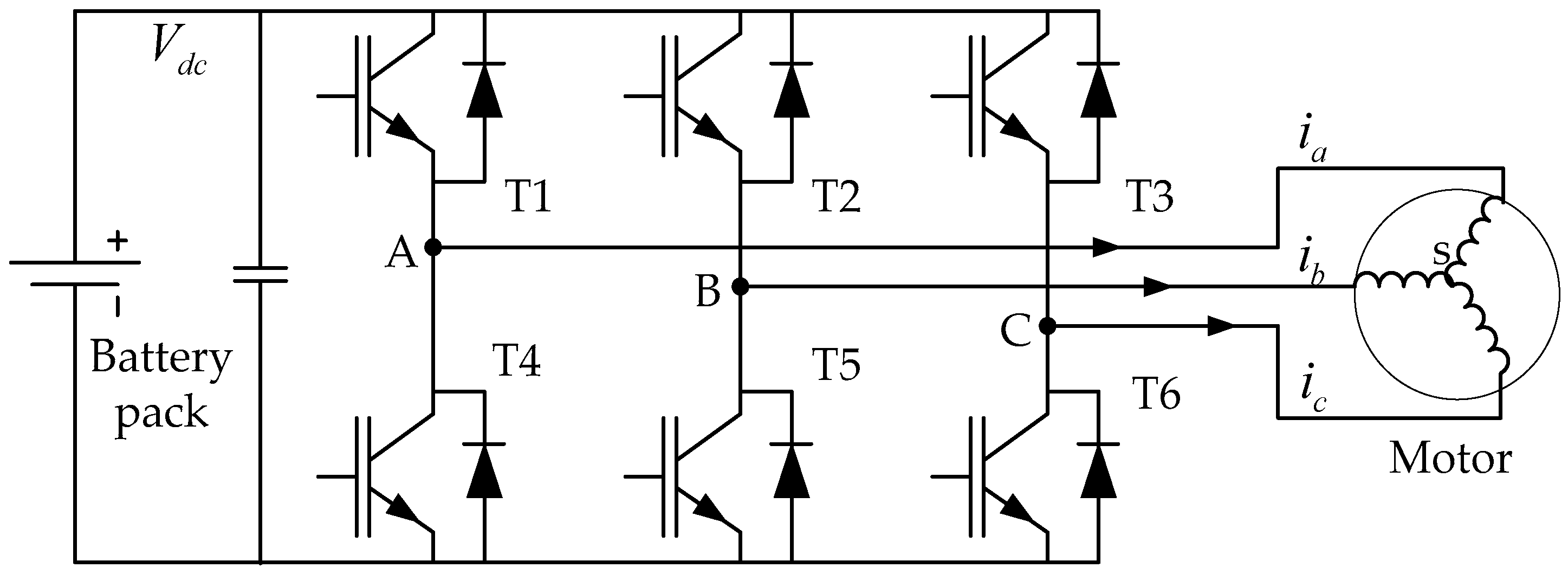
Figure 6, the simulation model includes the DC voltage source subsystem, the 75 kW PMSM subsystem, the universal bridge subsystem, and the PMSM-space vector modulation (PMSM-SVM) subsystem. Moreover, the proposed diagnostic algorithm is included in the PMSM-SVM subsystem. The pulse width modulation (PWM) frequency is set as 10 kHz and the proportional integral (PI) current regulating frequency is set as 20 kHz. The dead time and the voltage drop of the power device are ignored in the simulation. The IGBT open circuit faults are generated by removing the gate command signals of the required IGBTs.
In order to illustrate that the proposed algorithm is independent of load variations, low speed 600 rpm, rated speed 2000 rpm, and high speed 2800 rpm at rated torque conditions, rated speed at 10% rated torque, and sudden change of the load torque conditions are analyzed in this paper. Since the three phases are symmetrical, only the open circuit faults in phase A are analyzed.
4.1. Analysis of the Response
For convenience, the open circuit fault in the upper bridge of phase A is analyzed. Define
x as:
Assuming that the open circuit fault occurs when
, the diagnostic variable
changing with the rotor electrical angular degrees can be expressed as follows:
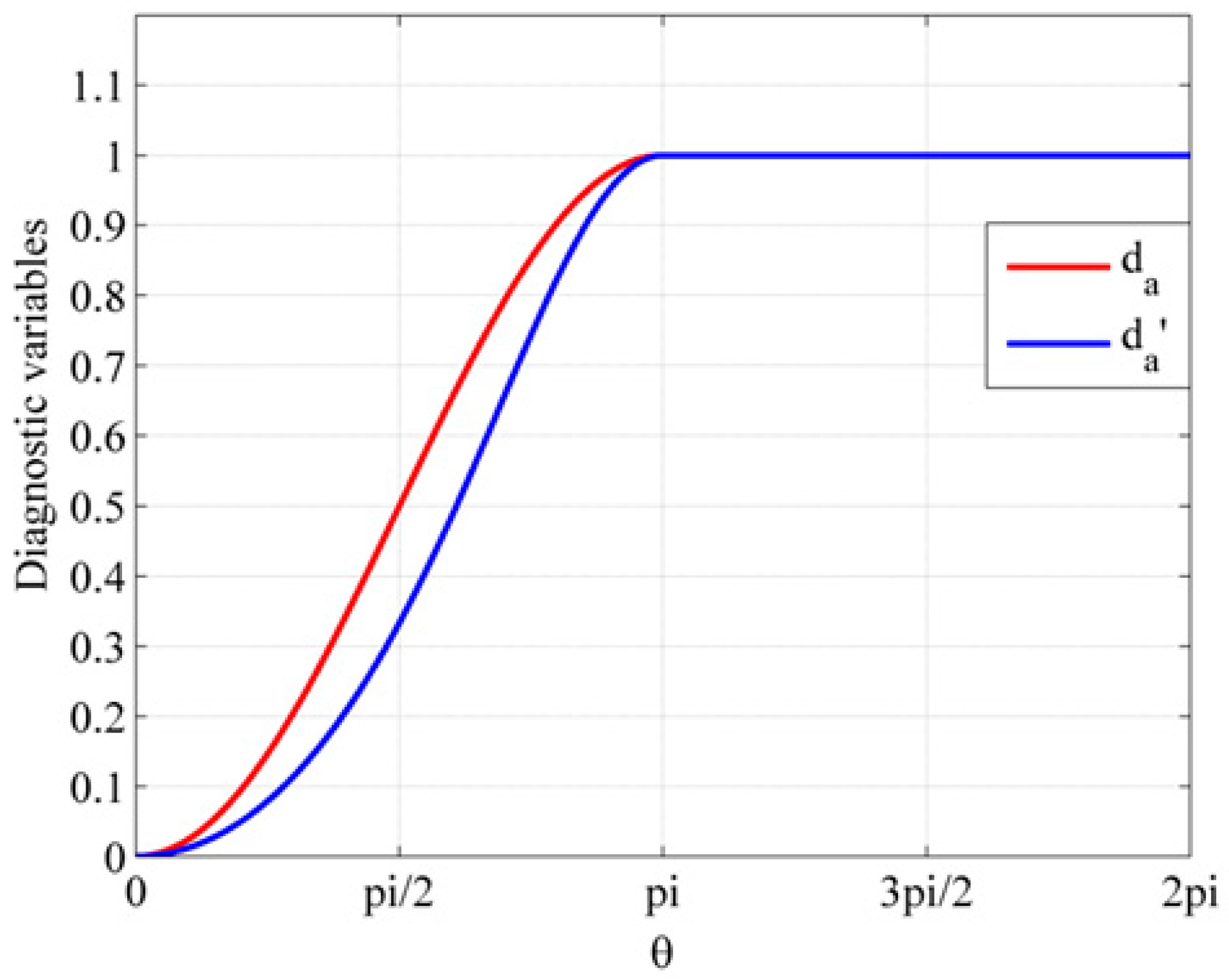
As shown in Equation (12), when , and when . The diagnostic variable can reach 0.5 in one quarter of the electrical period and can reach 1 in half of the electrical period after the failure. Therefore, the detection speed is fast.
If the average absolute value of the actual three-phase current over one electrical period is used as the normalized referential value [
9], the corresponding diagnostic variable
can be expressed as follows:
The two diagnostic variables with different normalized referential values varying with rotor electrical angular degrees are plotted in
Figure 7.
As shown in
Figure 7, although the two diagnostic variables achieve stability at the same time, the algorithm presented in this paper has a higher value of the diagnostic variable and a better response before achieving stability. In fact, a value smaller than 1 is often used as a threshold considering the response. Compared with the algorithm using the actual current as the normalized referential value, the proposed algorithm can not only avoid the interference errors caused by the actual current acquisition, but also detect the faults faster.
4.2. Analysis of the Diagnostic Algorithm under Different Speed and Torque Conditions
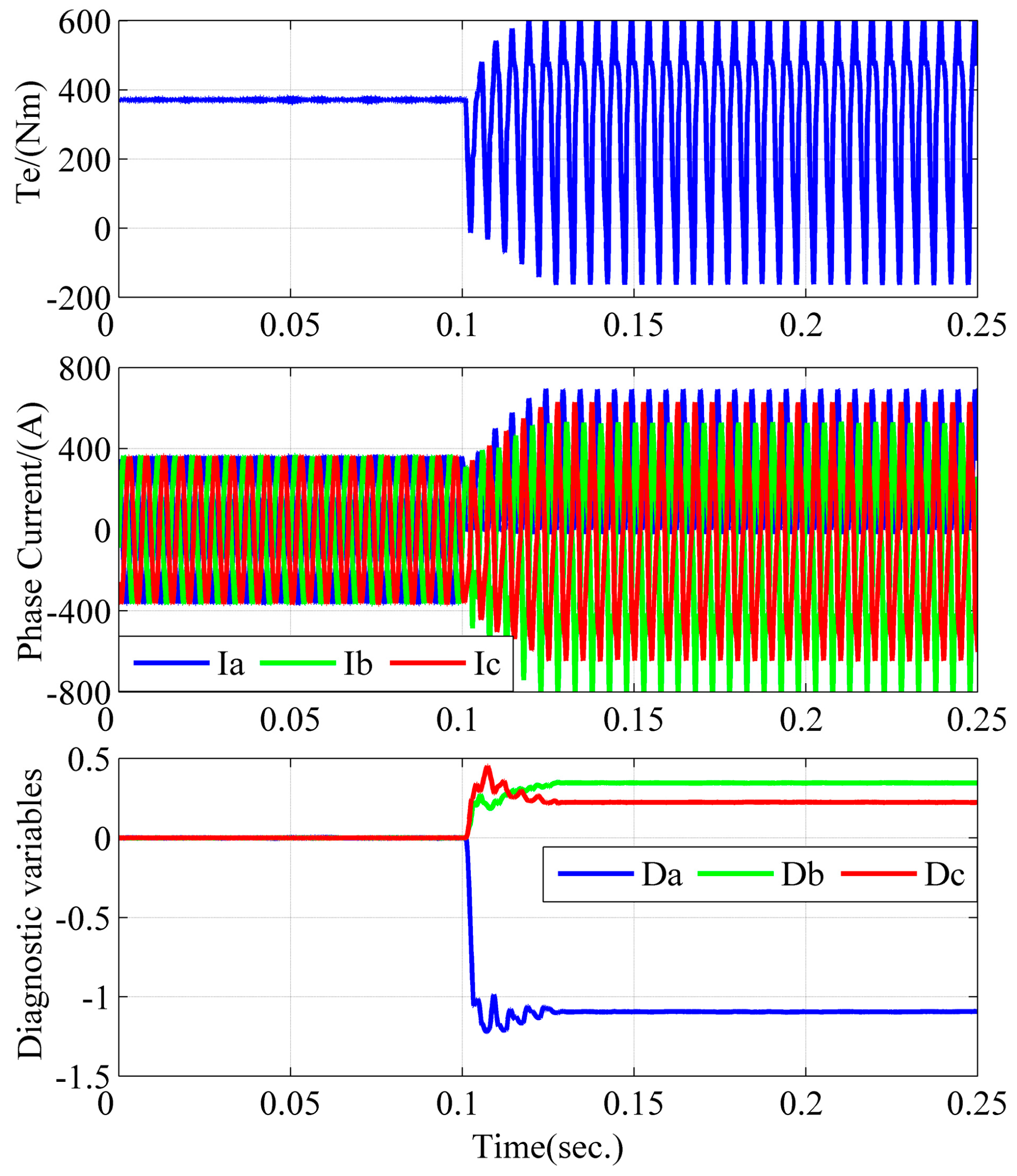
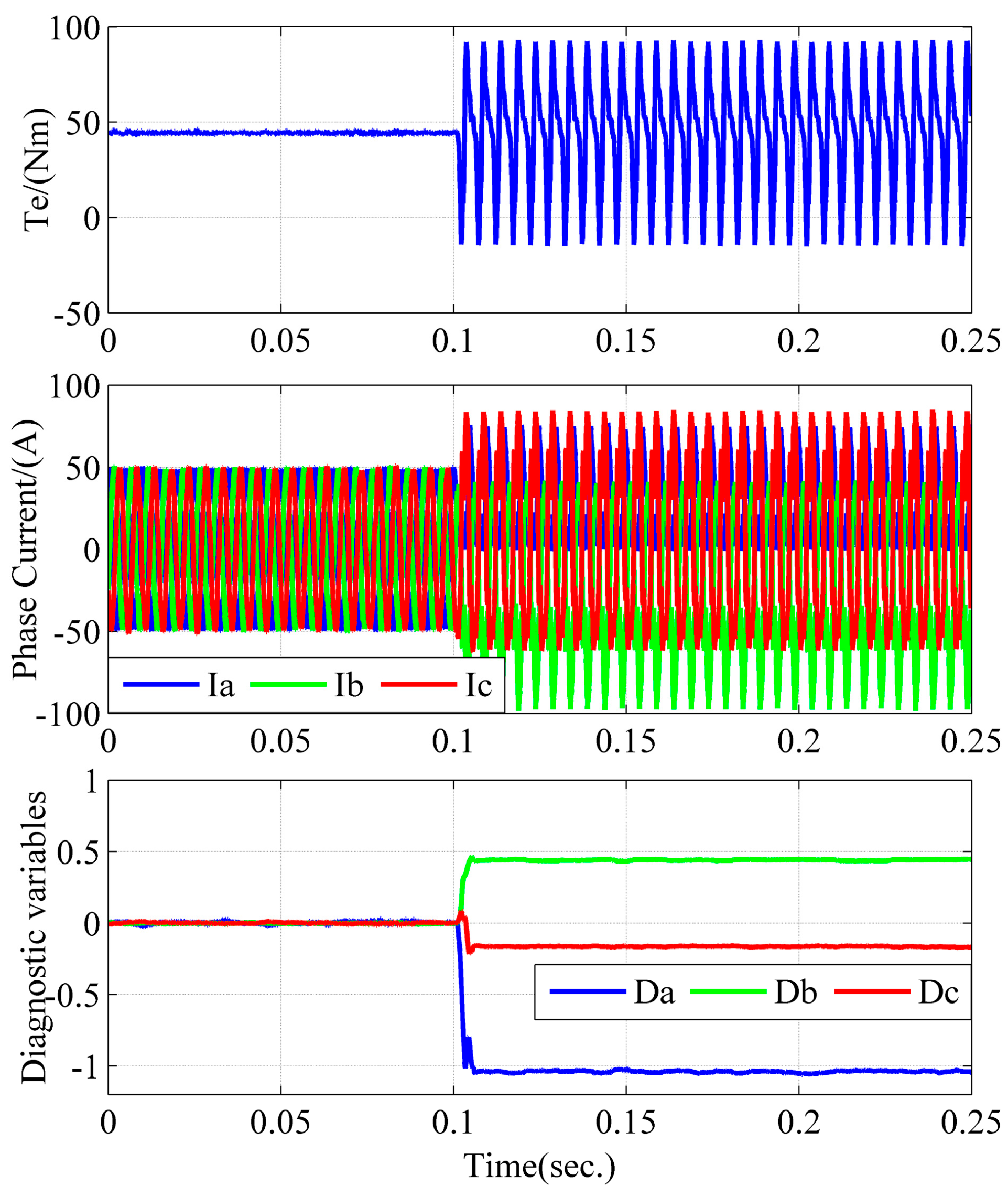
The simulation results when an open circuit fault occurs in T4 at 0.1 s at 2000 rpm/358 Nm and 2000 rpm/36 Nm are shown in
Figure 8 and
Figure 9. As shown in
Figure 8, at 2000 rpm/358 Nm, the output torque and current of the motor are stable and the diagnostic variable is around zero under normal conditions. When an open circuit fault occurs in T4, phase A can only output positive current, while the currents of phase B and phase C are distorted and fluctuate with the peak-to-peak value up to 1500 A. Furthermore, the output torque of the motor is unstable, the period of the torque ripple is the same as the period of the phase current, and the peak-to-peak value of the torque ripple is above 800 Nm. The diagnostic variables change rapidly after the open circuit fault occurs. The value of
decreases to approximately 1.05 (existing error due to the white noise during current sampling in the simulation) and the other two variables of
and
increase to approximately 0.34 and 0.22. Furthermore, when the current of phase A is in the upper half period at 0.1 s, the open circuit fault does not affect the actual current. When the current of phase A crosses zero at 0.1011 s, and since phase A cannot output negative voltage, the three-phase current starts to distort due to the open circuit fault. The value of
decreases to −0.5 and −1 at 0.1023 s (after 46% of the current period) and 0.1031 s (after 62% of the current period), respectively. At 2000 rpm/36 Nm, the stable value of the three diagnostic variables are −1, 0.44 and −0.16, respectively. The simulation results are similar to those at 2000 rpm/358 Nm except for the magnitude of the torque and current.
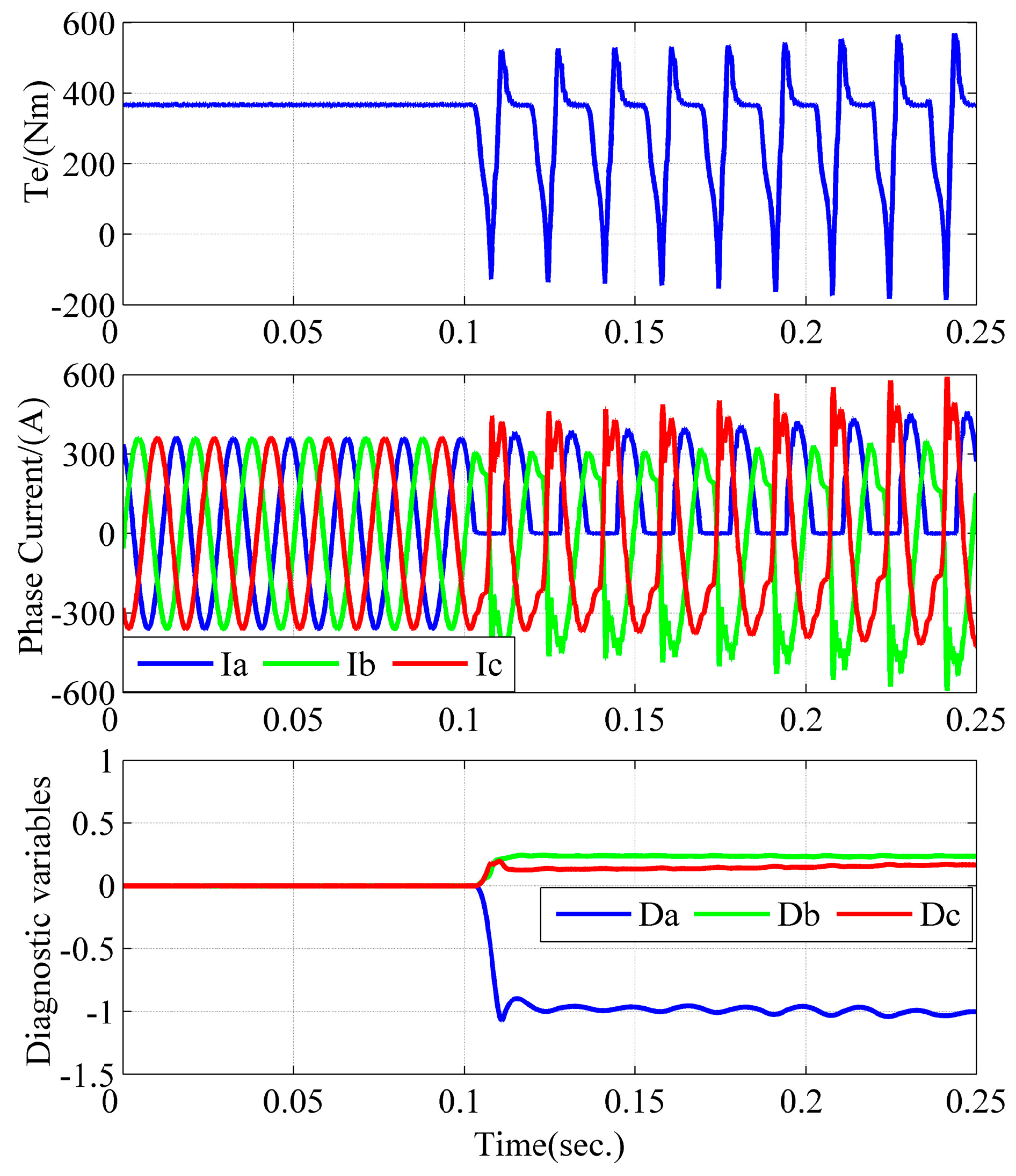
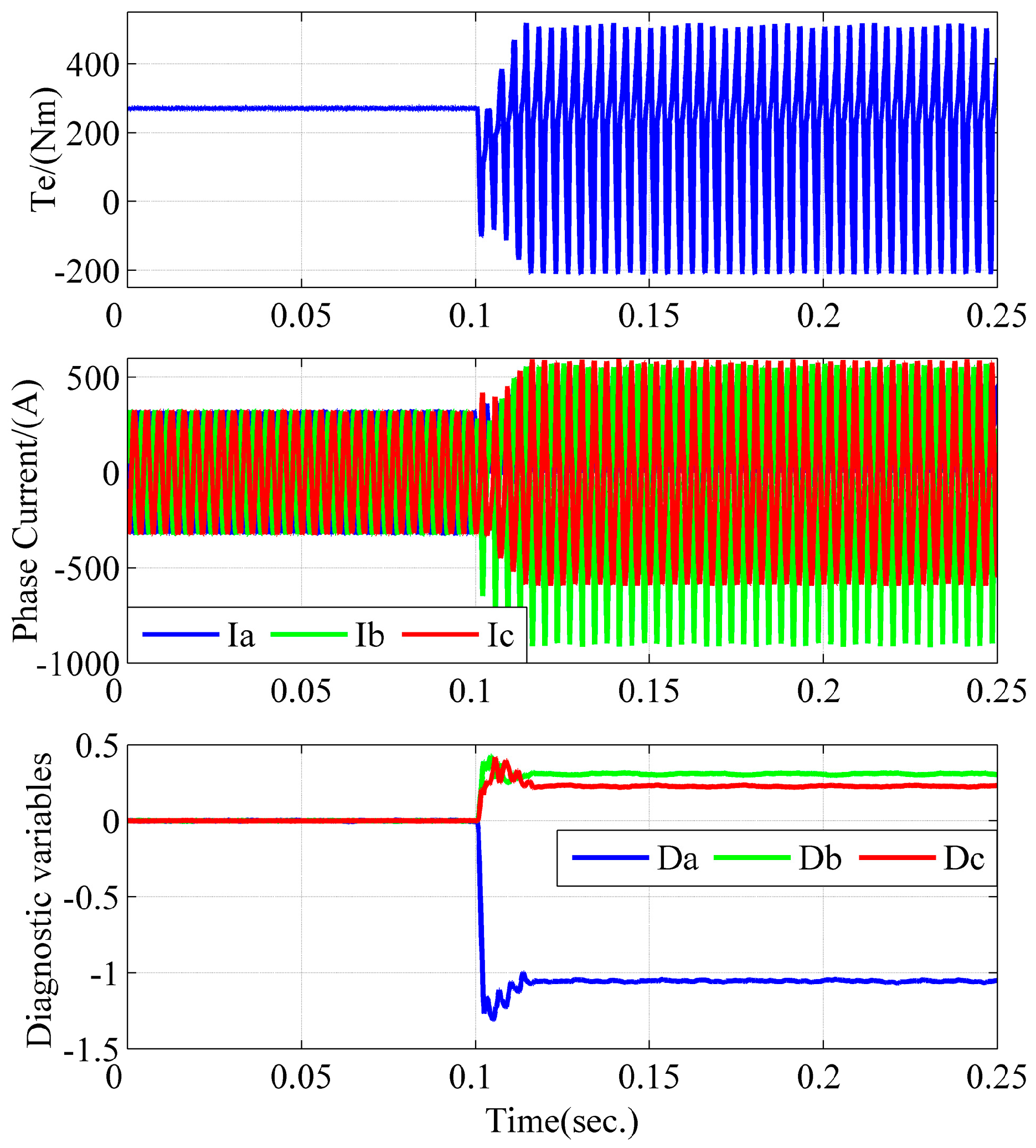
The simulation results when an open circuit fault occurs in T4 at 0.1 s at 600 rpm/358 Nm and 2800 rpm/256 Nm are shown in
Figure 10 and
Figure 11. As shown, the performance of the diagnostic algorithm at lower and higher speeds is consistent with that under rated condition. The open circuit fault can be detected accurately and the value of
is stable around −1. The simulation results show that the proposed algorithm is independent of load variations and has a good robustness.
4.3. Analysis of the Diagnostic Algorithm under a Sudden Change of Load Torque Conditions
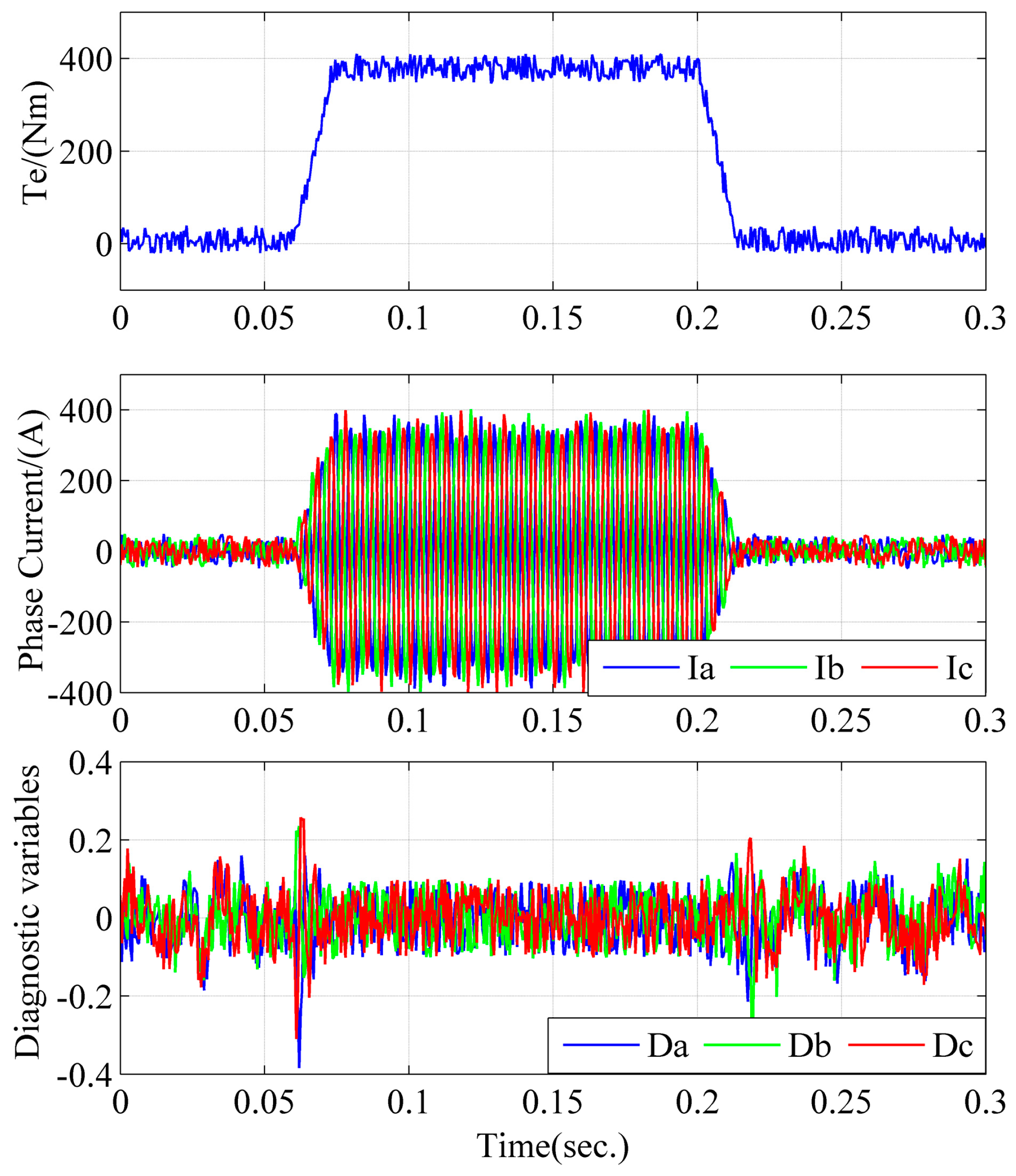
To illustrate the resistivity against false alarms of the proposed algorithm, a torque pulse from zero to the rated torque is applied to the motor at rated speed (2000 rpm), and the simulation results are shown in
Figure 12. When the load torque of the motor increases to the rated torque from zero at 0.01 s, the difference between the actual three-phase current and the referential three-phase current values is slightly increased, leading to the increase of the diagnostic variables. When the load torque of the motor decreases to zero from the rated torque at 0.05 s, the diagnostic variables also increase. However, as shown in
Figure 12, the amplitudes of the diagnostic variables are always smaller than 0.5 under normal conditions.
5. Experimental Results
The effectiveness of the proposed algorithm is tested experimentally with the PMSM as shown in
Table 2. The experimental setup basically comprises a PMSM coupled to a Siemens dynamometer (1GP5-280) (Siemens Aktiengesellschaft, Munich, Germany) test system, a LiFePO4 battery pack (288 V/180 Ah), a HBM torque meter (T40) (Hottinger Baldwin Messtechnik GmbH, Darmstadt, Germany) and an inverter developed internally. In the inverter, an Infineon six-pack IGBT (FS800R07A2E3) (Infineon Technologies AG, Neubiberg, Germany) is used as the power switches; a TI digital signal processor (TMS320F28335) (Texas Instruments Incorporated, Dallas, TX, USA) carries out the real-time algorithm; three LEM current sensors (HAH1DR 900-s) (LEM Switzerland SA, Genève, Switzerland) measure the stator phase current. The experimental bench is shown in
Figure 13.
The IGBT open circuit faults are controlled by the user by removing the gate command signals of the required IGBTs. The maximum implemented collector current of the IGBT used in the experiments is 800 A. Considering the reliability, the maximum amplitude of the phase current is limited to 600 A by the Altera complex programmable logic device (EPM240T100I5N) (Intel Corporation, Santa Clara, CA, USA). The three-phase current will be distorted in the fault state. It is difficult to obtain the experimental results at 2000 rpm/358 Nm and 2800 rpm/256 Nm because the distorted current will exceed the limited amplitude of the phase current. Therefore, the experiments are operated at 600 rpm/358 Nm and under a sudden change of the load torque conditions. The experimental results are shown in
Figure 14 and
Figure 15.
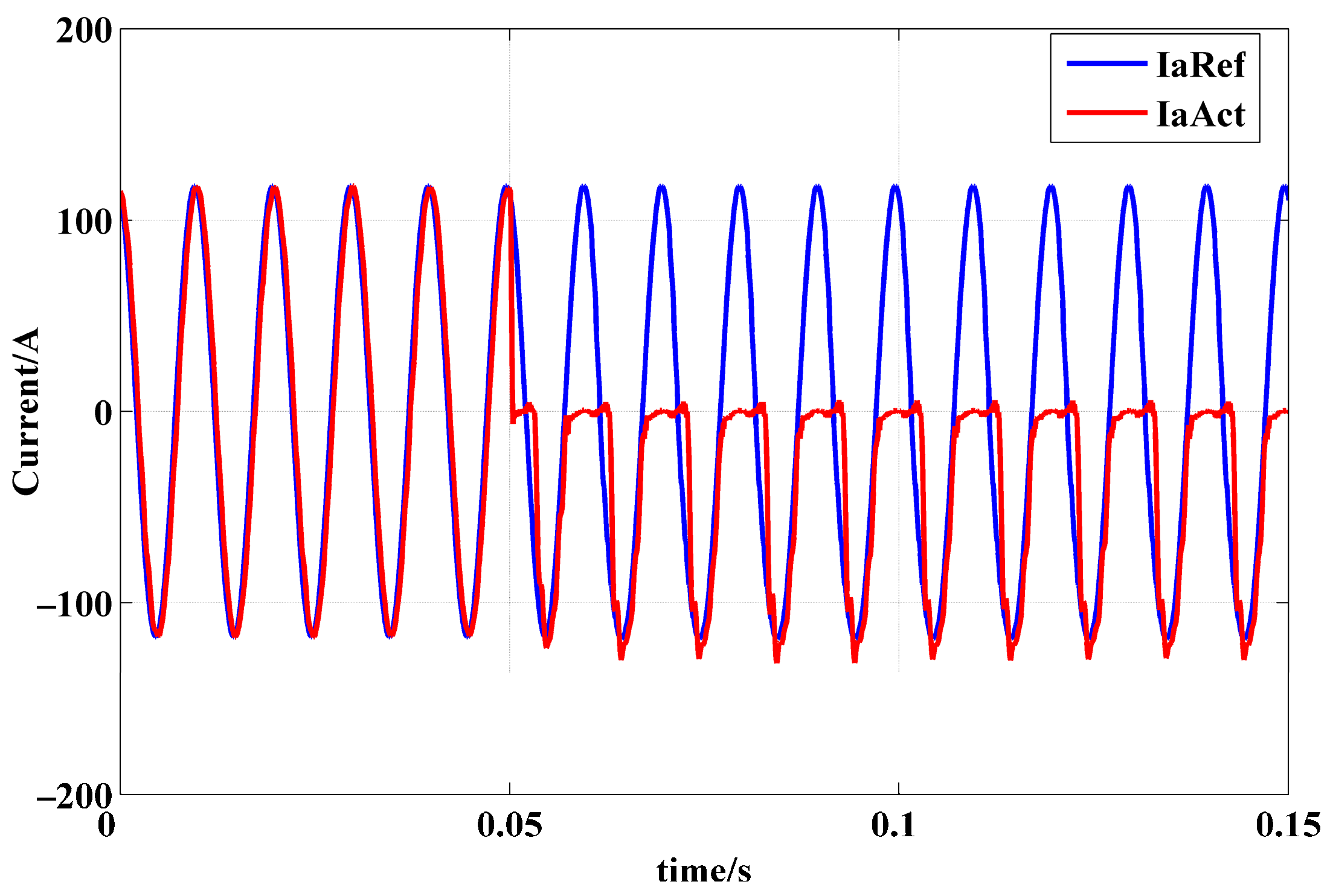
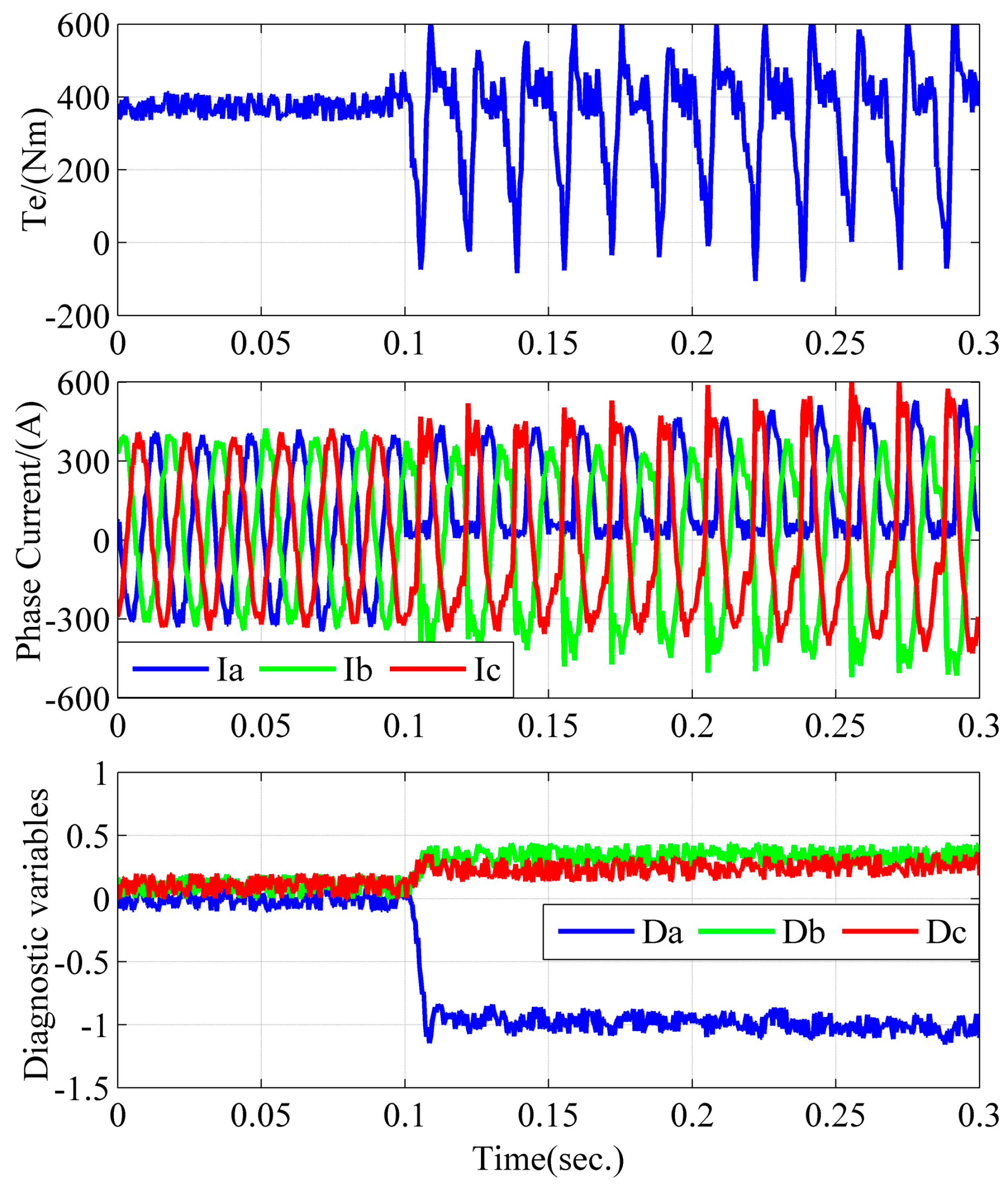
As shown in
Figure 14, at 600 rpm/358 Nm, the output torque and current of the motor are stable and the diagnostic variables are around zero under normal conditions. When an open circuit fault occurs in T4 at 0.1 s, phase A can only output positive current, while the currents of phase B and phase C are distorted and fluctuate with the peak-to-peak value up to 1200 A. Furthermore, the output torque of the motor is unstable, the period of the torque ripple is the same as the period of the phase current, and the peak-to-peak value of the torque ripple is above 700 Nm. The diagnostic variables change rapidly after the open circuit fault occurs. The value of
decreases to approximately −1 and the other two variables of
and
increase to approximately 0.41 and 0.32. Moreover, when the current of phase A is in the upper half period at 0.1 s, the open circuit fault does not affect the actual current immediately. When the current of phase A is crossing zero at 0.1021 s, and since phase A cannot output negative voltage, the three-phase current starts to distort due to the open circuit fault. The value of
decreases to −0.5 and −1 at 0.1045 s (after 27% of the current period) and 0.1047 s (after 28% of the current period), respectively.
To illustrate the resistivity against false alarms of the proposed algorithm, a torque pulse from zero to the rated torque is applied to the motor at rated speed (2000 rpm), and the experimental results are shown in
Figure 15. When the load torque of the motor increases to the rated torque from zero at 0.05 s, the difference between the actual three-phase current and the referential three-phase current values increases slightly, leading to the increase of the diagnostic variables. When the load torque of the motor decreases to zero from the rated torque at 0.2 s, the diagnostic variables also increase. However, as shown in
Figure 15, the amplitudes of the diagnostic variables are always smaller than 0.5 under normal conditions. Considering the response and reliability of the system, the threshold
is set to be 0.75.
As shown in
Figure 14 and
Figure 15, the output torque and the diagnostic variables have a certain lower harmonic. Under normal conditions, the three-phase current is not completely symmetrical, however, the trend is basically the same as that in the simulations. The reason of the deviation is that the simulation results do not take into account the dead-time effect of the switch, and the deviation and noise of the current and the position acquisition, resulting in the simulation results being better than the experimental results.
As shown in the simulation and experimental results, since the diagnostic variables are normalized, the thresholds are universal and can distinguish the open circuit faults accurately at different loads of the motor. Thus, this algorithm is independent of the load variations.
Typically, the detection speed of a current-based algorithm depends on the time instant of the fault occurrence [
24]. Specifically, if a fault occurs in the bottom IGBT and during the negative current half-cycle of the respective phase, the effect can be immediately seen since the current tends to be zero. Thus, the detection speed is relatively faster. However, if a fault occurs in the bottom IGBT and during the positive current half-cycle of the respective phase, the fault effects cannot be immediately seen and will just be seen at the next current half-cycle; hence, the fault can remain undetected for a period of time that exceeds half of the current fundamental period. Thus, the detection speed is relatively slower. An equivalent result is also verified for a fault in the top IGBT of the respective phase. Considering this, the best way to evaluate the detection speed is to obtain the detection time for a fault occurrence at different instants of the current period.
Table 3 summarizes the detection speed results, showing the minimum, average, and maximum detection times achieved by the different algorithms. The modified normalized DC current algorithm is selected to compare with the proposed algorithm in this paper. Among the open-circuit fault algorithms, the modified normalized DC current method is found to be very effective in detecting faults with a high resistivity to false alarms. In addition, it is independent of the load variations [
21]. Specifically, the minimum, average, and maximum detection times of the proposed algorithm are calculated according to the experimental results at 600 rpm/358 Nm.
As shown in
Table 3, the proposed algorithm presents a much faster detection speed than the modified normalized DC current algorithm.
6. Conclusions
In this paper, a fast-acting diagnostic algorithm of IGBT open circuit faults for power inverters in electric vehicles is presented. The common open circuit faults of an inverter are analyzed. When an open circuit fault occurs, the half-bridge of the inverter can only output positive or negative current, resulting in the difference between the actual three-phase current and the referential three-phase current values. Based on this difference, the diagnostic algorithm for open circuit faults is proposed, combined with the normalization method and the VPMAM.
The effectiveness of the algorithm is verified by both simulations and experiments. This algorithm is robust, independent of load variations, and has a high resistivity against false alarms. Since only the three-phase current of the motor is utilized for calculations in the time domain, the algorithm needs less implementation effort.
Compared with other similar diagnostic algorithms, the proposed algorithm is much faster. The results show that the minimum detection speed of the proposed algorithm can be 14.9% of the motor phase current fundamental period, which is essential for real-time control in electric vehicles.