1. Introduction
With the sharply decreasing amount of global fossil energy, increasing building energy in developing countries, especially in China [
1], and continuous ambient air pollution [
2], it is of great significance to use renewable and clean energy feasibly and efficiently for our living environment and economic growth [
3]. As the representative of solar thermal utilization, a solar house has great advantages in building energy saving. According to the forms of solar energy utilization and solar energy equipment, solar houses can be divided into an active, passive, and hybrid solar house [
4].
Active solar houses often make use of fans or pumps to deliver heat from solar energy into indoor spaces so that lower heat load and better indoor thermal environment are realized. Through heat transfer mediums such as water, active solar houses often work with other energy application systems. Yumrutas and Ünsal [
5] studied how an active solar house cooperated with a heat pump and an underground energy storage system, and the longtime performance was simulated by the proposed model. Active solar houses with photovoltaic modules are a common manner of solar energy utilization in buildings, and the photovoltaic module can provide electrical demand not only for lighting and other indoor power equipment but also for the delivery fans or pumps in an active solar house to lower building energy consumption. Measurements and theoretical analysis were made to research the performance efficiency of this kind of solar energy usage by some researchers [
6,
7,
8,
9]. Since active solar houses often need electric energy to drive fans or pumps, it is not convenient in some regions; also equipment management and maintenance is a problem sometimes. Therefore, passive solar houses are developed because they focus mainly on envelope design and thermal performance, and the building can absorb, store, or release solar energy without any heating equipment in winter. Rabani [
10] presented an innovative Trombe wall with three directions for solar energy to enable the absorber to receive solar radiation from three directions. However, the wall may decrease direct solar gain into living spaces although the wall had advantage in space heating. Some different solar houses were proposed in different regions [
11,
12,
13], and the measured results indicated that comfortable living conditions and low costs can be reached in the house. Also, the effects of some factors [
14,
15,
16] including orientation, colors, and opaque envelopes on the thermal energy efficiency of passive solar houses were investigated. To solve cooling problems in solar houses, other technologies were integrated with solar houses, such as geothermal energy, an air source heat exchanger, and a solar chimney system [
17].
For both active and passive solar houses, solar energy storage is a key problem for matching solar energy adsorption and heating demand. Therefore, some energy storage materials are applied in solar houses. Phase change materials are used in some researches [
18,
19,
20]. Though solar houses can reach much better thermal comfort with phase change materials heat storage systems, some other materials such as pebble beds are still used in some solar house because of low investment cost. Many scholars have combined heat storage in pebble beds with active solar houses in case of intermittent and acutely variable solar radiation. Singh and Deshpandey [
21] studied the thermal performance of the packed bed solar heat storage system under varying solar and ambient conditions in different months, and the solar collection and heat retrieval efficiency ranged between 36%–51% and 75%–77%, respectively. Also, a solar air heating system with a pebble bed was modeled through TRNSYS (Transient System Simulation Program) by Zhao and Li [
22], the designed system can meet 32.8% of thermal energy demand in the heating season through system and operation optimization.
For making full use of solar energy, a combination of passive and active solar application was put forward, which is the so-called hybrid solar house. However, there are still some shortcomings in the existing hybrid solar house design, such as a lack of efficient and cheap heat storage systems that work at night or in cloudy days. For exploring new design methods of a solar house and improving the efficiency of solar energy application, a heating system with energy storage by pebble bed in a solar house is proposed, and the performance analysis of the system is carried out in northwest China. In the region, the climate is a typical continental climate with cold winters (−15.7 to 3.0 °C average temperature in January in most areas), a whole arid year (about 40% relative humidity), and relatively rich solar irradiation (average annual solar irradiation of 4300 to 7000 MJ·m−2·a−1). Heating in winter is one of the key problems affecting people’s welfare.
2. Description and Mathematical Model of the Heating System
2.1. Design and Introduction of the Heating System
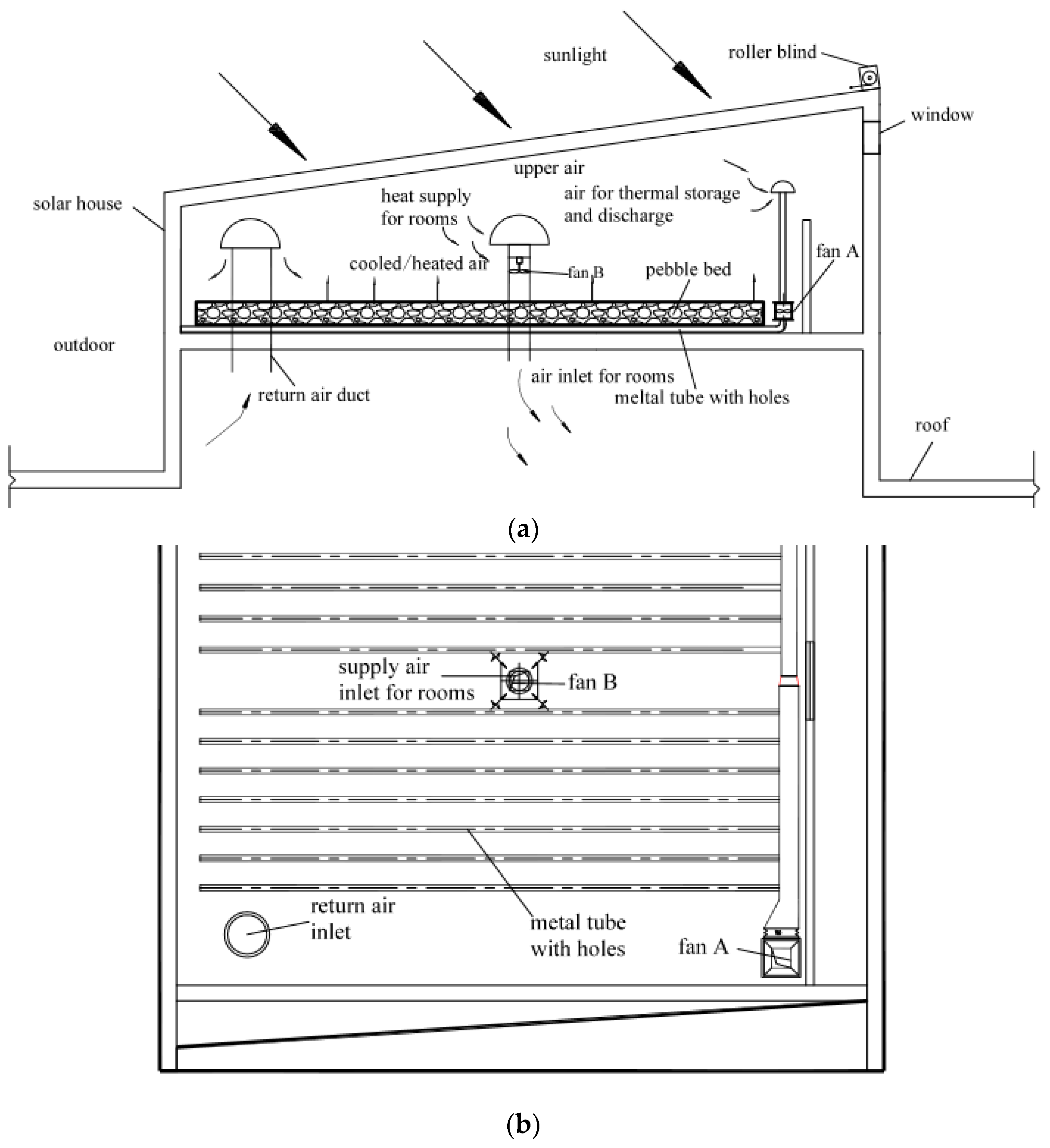
The heating system with energy storage by pebble bed in a solar attic is designed as
Figure 1, which presents a generic proposition without specific design dimensions, such as length, width and height of the pebble bed. The heating system is composed of three parts; the solar attic, the pebble bed, and the heating space. The solar attic is designed on the roof of a residence, and for absorbing more solar energy, the transparent roof of the house is built on an incline. On the roof of the solar attic, a roller blind is equipped, which can not only get the house insulated on winter nights but also prevents solar radiation on summer days. In the north wall, a window can get more fresh air into the solar attic and also provides the outlet for natural ventilation in summer or transition seasons. The pebble bed consists of the pebble and the air ducts below. The air ducts with holes are arranged in parallel on the floor of the solar attic and connected vertically in a main pipe with fan A. Above the air ducts, the pebble bed is packed by a metal mesh bag and fixed by supporting pillars. Considering the mass of the pebble bed, the structure of the residence below should be constructed by load-bearing materials. The heating space and the solar attic are connected by an air supply pipe and a return air duct, so the enclosed solar attic can get the pressure stable. It should be mentioned that in our present research the pebble bed is exposed directly in the air. Actually, this simple design may lead to heat losses during cold days of low solar radiation and at night and hard maintenance in life-time operation due to all kinds of pollutions. It may be a good idea to place a membrane-cover with selective coating on the pebble bed to solve the problem, but this needs to be studied in the future.
With the heating system, the residence heat load is reduced by passive and active solar energy utilization. For passive application, the roof envelope is improved by the pebble bed and insulated by the attached sunspace. For active use, three operational conditions are presented: (1) in the heat storage period, the upper warm air in the solar attic is extracted through tubes into the pebble bed to get heat exchange by fan A, while fan B is powered off so the energy is stored; (2) when heat supply is needed, fan B is powered on, and the warm air is transported into the room directly; (3) if the air temperature in the solar attic is low but heating is still in demand, fan A is powered on, so energy can be released into solar attic until its air temperature is high enough for heat supply. Furthermore, in case of an airflow short circuit, it is not recommended to run fan A and fan B simultaneously.
2.2. Model of the Heating System
Model-based simulation is often adopted to evaluate the energy performance of buildings [
23] or retrofitting for building energy saving [
24,
25]. For evaluating the operational performance of the heating system, the numerical model for the system is established. Considering the relatively low air temperature, energy equations that govern the heat transfer in the pebble bed are based on the following assumptions: heat transfer by radiation is ignored; heat conduction in the gas phase is negligible; the physical property parameters of gas and solid phases are constant; and inlet air is regarded as plug flow. The governing equations are shown as Equations (1) and (2):
where subscript
s and
f stand for the solid and fluid phase, respectively;
e is the void fraction;
ρ is the density (kg·m
−3);
T is the temperature (K);
t is the time (s);
x is coordinate of the height direction (m)
λs,eff is the effective thermal conductivity [
26] (W·m
−1·K
−1);
hs,f,eff is the effective convective heat transfer coefficient [
27] (W·m
−3·K
−1);
c is the specific heat capacity (J·Kg
−1·K
−1); and
G is mass flow (kg·m
−2·s
−1). All the main symbols are included in Nomenclature at end of the paper.
For simplifying the process of heat transfer through envelopes, some assumptions are also made; the change of solar azimuth is not considered in details, the air temperature of the heating space and solar attic is uniform, and heat transfer in the envelope is regarded as one-dimensional heat conduction. Transparent and non-transparent envelopes are taken into consideration. For the transparent envelopes, single glass is regarded as isothermal along its thickness direction because of the low heat capacity. Taking double gazing as an example, the mathematical model is given by:
where subscript
A,
B, and
k represent the exterior, interior glass, and other different internal envelopes of the solar attic, respectively;
d1 is the thickness of a single glass (m);
hin and
hout are the convective heat transfer coefficient between the indoor or outdoor air and the surface of glass (W·m
−2·K
−1);
Tout and
Tin are the outdoor and indoor temperature, respectively (K);
hr is the equivalent radiation heat transfer coefficient (W·m
−2·K
−1);
hsky is equivalent sky heat transfer coefficient (W·m
−2·K
−1);
Tsky is the sky background temperature (K); and
w is solar radiation per unit area adsorbed by glass (W·m
−2).
For the non-transparent envelopes, their heat capacity can’t be ignored, so the heat transfer model can be expressed as below for simplification:
and the boundary conditions are:
where
wsun,out and
wsun,in are the solar radiation absorbed by the external and internal wall (W·m
−2), respectively;
d2 is the thickness of the wall (m); and
i represents other different internal walls.
The heat balance of the solar attic and heating space is built as below:
where subscript 1 and 2 stand for the heating space and solar attic, respectively;
V is the volume (m
3);
A is the surface area (m
2);
Qsu is the heat supply from the solar attic to heating space (W);
Qloss is the heat loss by air infiltration (W); and
j represents the different interior surface of the solar attic.
Qsu and
Qloss are calculated as below:
where
qB and
qloss are the air volume caused by fan B and penetration, respectively (m
3·h
−1).
2.3. Verification of the Model
Equations (1)–(11) are too complex to obtain an analytic solution, so numerical methods are employed to solve the equations. Difference methods are adopted to discretize Equations (1)–(11) in space and time. Thus, Equations (1)–(11) are changed into a linear algebraic equation system. A MATLAB (Mathworks, 2010 release) program is developed by us to solve the linear algebraic equation system for obtaining the temperature with time in different parts of the solar attic. Through the numerical method, when the outdoor meteorological parameters, physical property parameters of the envelopes, and the initial conditions are input, the indoor base temperature will be calculated, and when the indoor design target temperature is determined, the heat load of the heating space will be output.
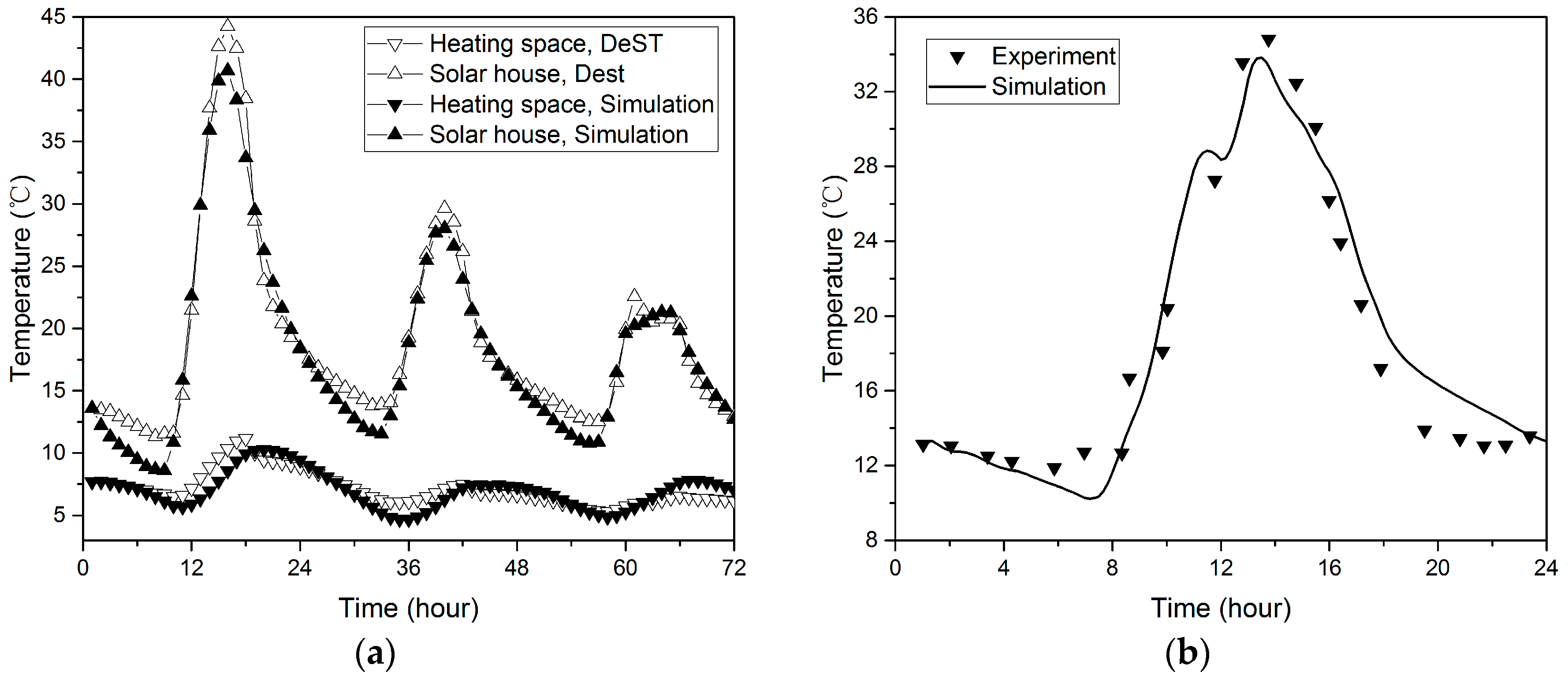
The model is validated based on the indoor base temperature by DeST (Designer’s Simulation Toolkit) [
28] and experimental data in the literature [
29], and the temperature comparison is shown in
Figure 2. The results of calculation indicate that the margin of error is within 10% and meets the requirements of engineering application, so the established model is acceptable for calculating the base temperature and heat load.
3. Results and Discussion
3.1. Envelope Design
As described in
Figure 2, for storing more energy, it is beneficial to increase the area of the transparent envelopes of the solar attic. However, it may cause more energy loss at the same time. Also, in the type of transparent envelopes in question, fewer layers of glass have an advantage in better light transmission but provide poorer insulation, so for choosing proper envelopes for each side of the solar attic, heat transfer simulation between indoor and outdoor air through the glass in Xi’an is carried out. Single glass, double-layer glass, and three-layer hollow glass are applied as the transparent envelopes, and the simulated results are listed in
Table 1.
Due to the larger heat transfer coefficient of single glass, the cold interior side of single glass can cause a larger heat transfer temperature difference, so it leads to twice that heat loss of double glass. However, better transmission performance contributes to more solar radiation gain. In general, single glass has more disadvantages in heat storage than do double and triple glass. Compared with triple glass, double glass leads to higher transmission heat gain and heat loss but has little advantage in overall heat storage for the solar attic.
Considering the lower solar radiation in the east and west wall, the heat gain by solar transmission may not make up for the heat loss by temperature difference, so a comparison of thermal performance with different types of eastward and westward glass is presented in
Table 2. The results indicate that more layers of glass are beneficial to more energy storage.
From
Table 1 and
Table 2, it can be seen that net heat gain is dominated by solar radiation in the southward glass because the heat gain is much larger than the heat loss so that more solar radiation will increase the net heat gain. Thus, when designing the envelopes for the solar attic, take the solar transmission as the first consideration in the south face and the roof, while for eastward and westward envelopes, both heat loss and gain are important for net heat gain. Thus, though transparency reinforcement may increase the heat gain from solar radiation, it will lead to a heat loss increase due to a heat transfer coefficient increase. Therefore, there should be a balance for transparency and heat insulation to obtain the largest net heat gain. In other words, solar transmission and insulation should been taken into account in balance when designing the eastward and westward envelopes, and the north wall must be insulated for less heat loss.
The aforementioned discussion provides the envelope design method for the solar attic in Xi’an. For other cities, the conclusions will depend on the meteorological conditions and the duration of the heating period. For further discussion, average solar radiation and temperature are applied to stand for different places, and average heat storage power is regarded as the evaluation index.
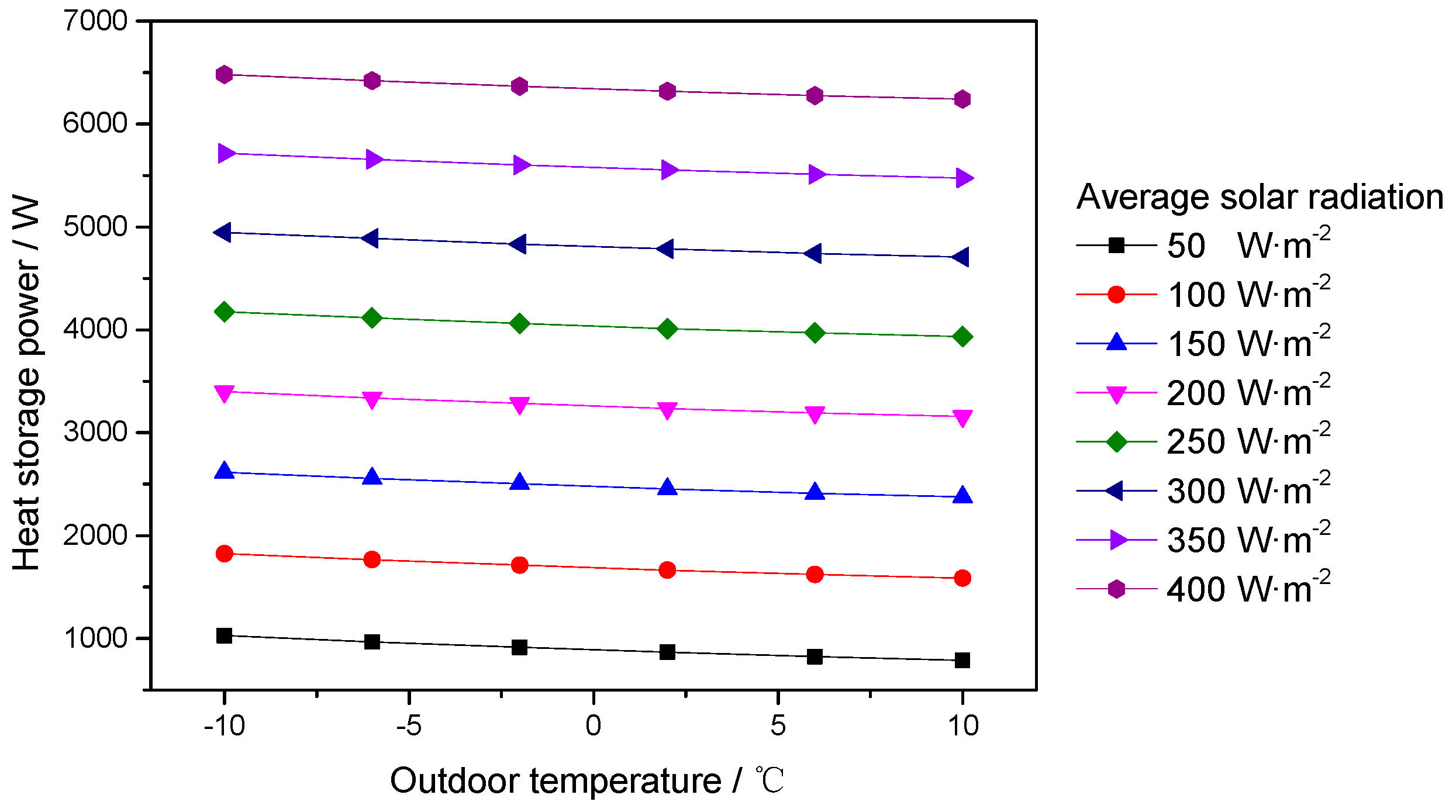
The influence of different solar radiation and exterior temperatures on heat storage power is illustrated in
Figure 3. It can be seen that the higher the solar radiation is, the higher the heat storage power is, and a 50 W/m
2 rise in solar radiation can increase the average heat storage power by 1 kW. By contrast, the outdoor temperature has less influence on heat storage. From
Figure 3, only about 300 W heat storage power is shown when the temperature changes by 20 °C, and when the solar radiation is more than 150 W/m
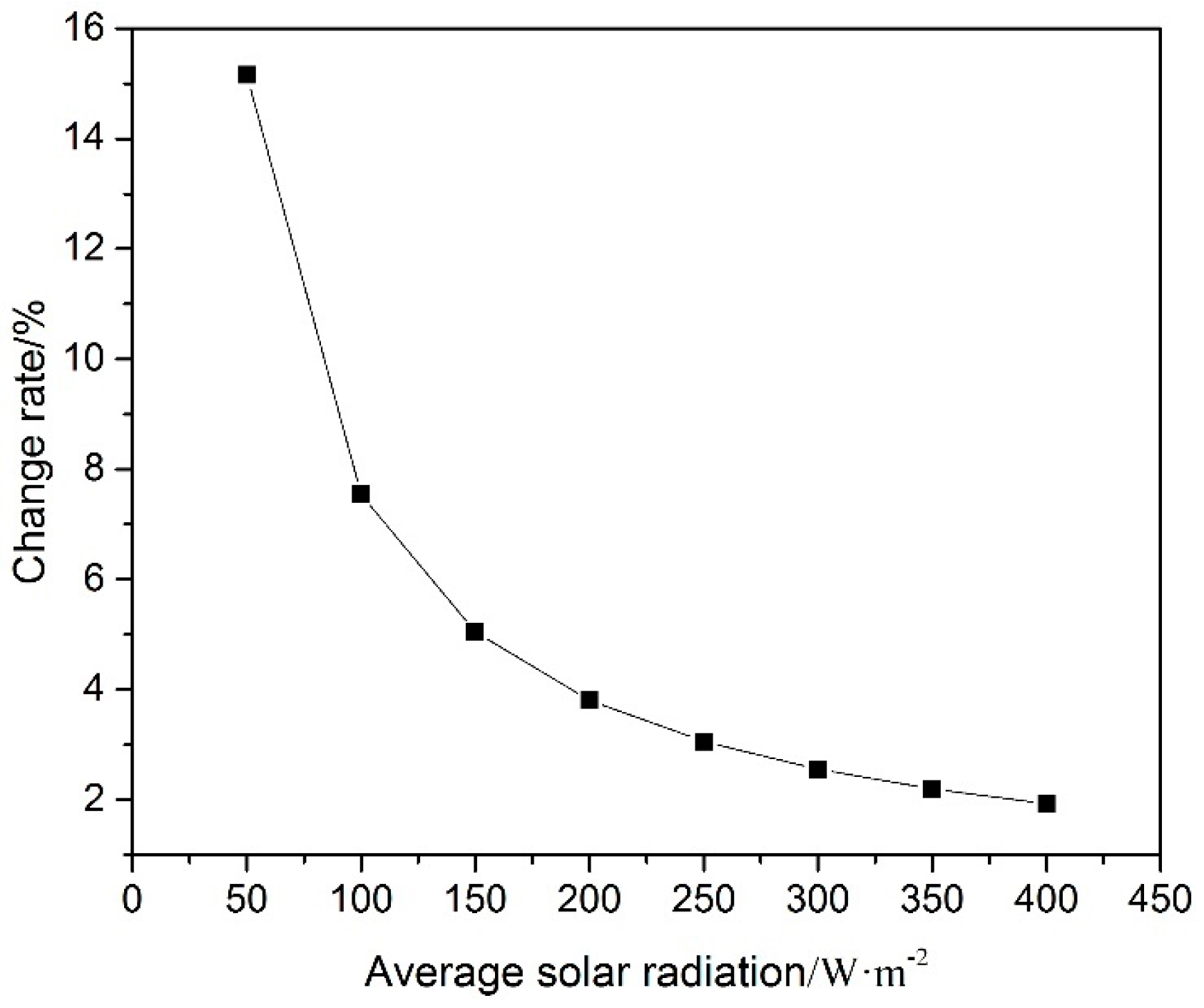
2, the percentage change of heat storage power is less than 5% by per 10 °C variation (seen in
Figure 4), so it can be concluded that heat storage performance of the solar attic is independent of outdoor temperature if the solar radiation is larger than a certain value. It should be pointed out that the conclusion is based on the average meteorological data; the detailed data may be different, but the trend should be the same when the practical transient meteorological data is adopted.
3.2. Energy Saving of the System
For predicting the operational performance of the proposed heating system described in
Figure 1, the typical northwest rural residence investigated by Chen and Liu [
29] is regarded as the research target in the above design. The meteorological data is quoted from the specialized meteorological dataset for building Chinese thermal environments [
30]. Considering the possible living habits and previous research results, 14 °C is regarded as the design target temperature for a solar residence. In order to obtain the maximum solar energy, the roof of the building is covered completely by a pebble bed with a height of 0.3 m, a length of 12 m, and a width of 4.5 m. The physical parameters of the pebble bed are listed in
Table 3. Also, the internal heat source is neglected. The system operational strategy is shown in
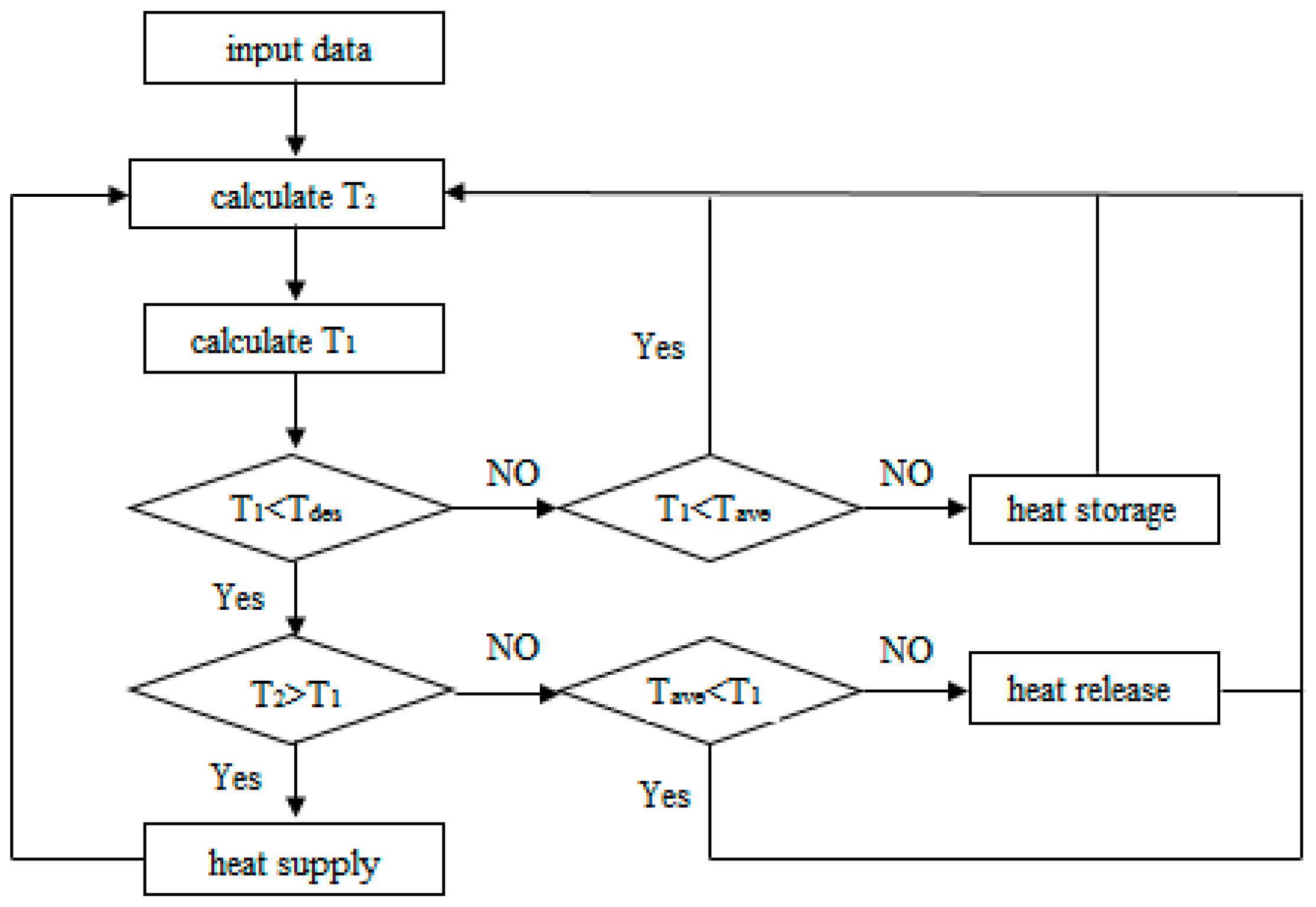
Figure 5.
When the solar energy is abundant, with Fan A off and Fan B on, the heated air in the solar attic is delivered in the room for heating. If the room is warm enough and the bed average temperature is lower than that of the solar attic, with Fan A on and Fan B off, the energy is stored in the bed. When the solar radiation is poor or it is night, if needed, the energy stored in the bed can be extracted and then delivered into the room.
For evaluating the performance of the heating system, the residence energy saving rate is defined as below:
where
ηsun is energy saving rate of the solar residence;
ηa and
ηb are the energy saving rates of the solar attic by the active and passive utilization, respectively;
wsup is the heat power per unit area supplied into the room by Fan B (W·m
−2);
wpa is the decreased heat load per unit area by passive solar application (W·m
−2); and
wload is the heat load per unit area of the typical northwest rural residence without the proposed heating system (W·m
−2).
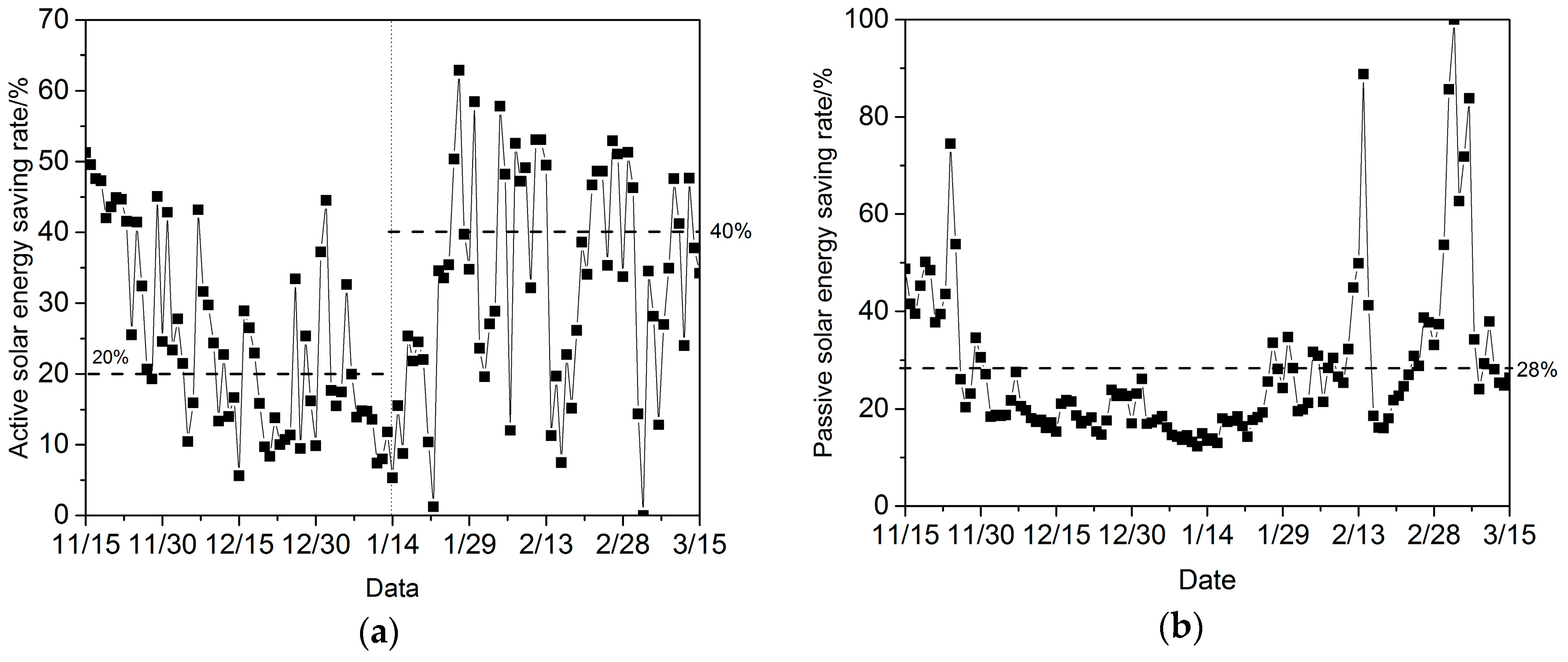
Figure 6 shows the daily active and passive solar energy saving rate during the heating season with the values for daily average
wsup,
wpa, and
wload. The energy saving rate by active utilization of the solar house varies with the outdoor temperature and the solar radiation. During December and early January, because of the low temperature and solar radiation, the average active solar energy saving rate is only 20%. With the increase of temperature and solar radiation in the late heating period, the average active energy saving rate rises to 40% gradually. On contrary, the passive energy saving rate is relatively stable, and the average passive energy rate is about 28% during the heating period. Above all, the overall energy saving rate can get to 56% with the proposed heating system, considering the solar resource in Xi’an; the operational performance is acceptable.
In the above simulation, the height of the pebble is 0.3 m. Whether there is an optimal value for the engineering design is worth studying. As
Figure 7 depicts, the active solar energy saving rate increases with the height of the bed, but it tends to become stable gradually when the height gets to 0.5 m. One possible reason is that when the height is quite small, a larger height means more energy stored and also more energy supplied into the room. However, too large a height leads to a low average temperature of the pebble bed, so the energy cannot be absorbed from the bed for room heating. Due to the attached solar attic on the roof, the increasing height of the bed makes little contribution to a decrease in heat load, and the passive solar residence energy saving rate will remain 28% on average when the height of the pebble bed changes. Considering that the building is weight bearing, 0.3–0.5 m is reasonable.
3.3. Suitability of Different Regions
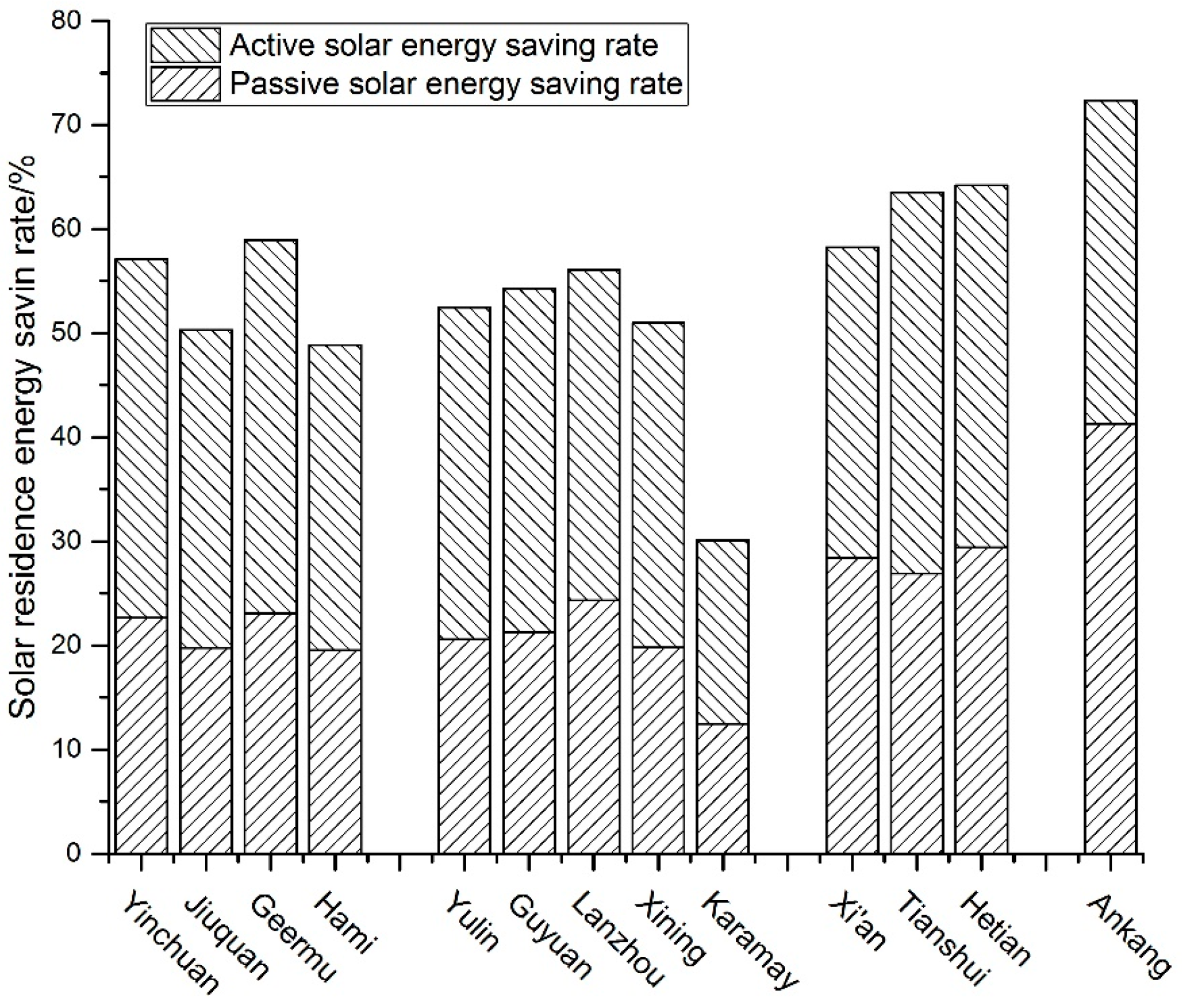
The feasibility of the proposed heating system in Xi’an is verified, and, for extending the system application to the northwest China, 13 typical cities throughout the five northwestern provinces are picked as the research target regions. The operational performance of the heating system in the above selected cities is simulated and the results are shown in
Figure 8.
According to a declining sequence by solar energy resources, the cities are divided into four groups as in the horizontal axis from left to right in
Figure 8. With the proposed heating system, the energy saving rate can reach 70% in Ankang, though the solar resources in the city are the poorest of the 13 picked cities. Further, the active and passive energy saving rates are 30% and 40%, respectively, which are not lower than those of other cities. The reason is that the outdoor temperature is higher than in other cities so the heat loss by the temperature difference between the solar attic and outdoor air is the smallest. On the contrary, in Karamay, which is rich in solar energy but has a low outdoor temperature, the heating system runs poorly with the energy saving rate of 30%. Therefore, it is not reasonable to evaluating the suitability of the proposed heating system by solar resource.
Commonly, when designing the thermal insulation of the exterior envelopes, not only both the outdoor air temperature and the solar shortwave radiation but also the natural cooling effect of the effective solar longwave radiation of the outer surface of the envelopes should be considered. For ease of calculation, a single outdoor meteorological parameter, external comprehensive temperature, is presented under the comprehensive consideration of the above three factors, as defined in Equation (15).
where
Tsa is the external comprehensive temperature (K),
α is the solar radiation absorbance of the exterior wall,
wsun is the south solar radiation per unit area (W·m
−2), and
Tlr is effective longwave radiation temperature (K).
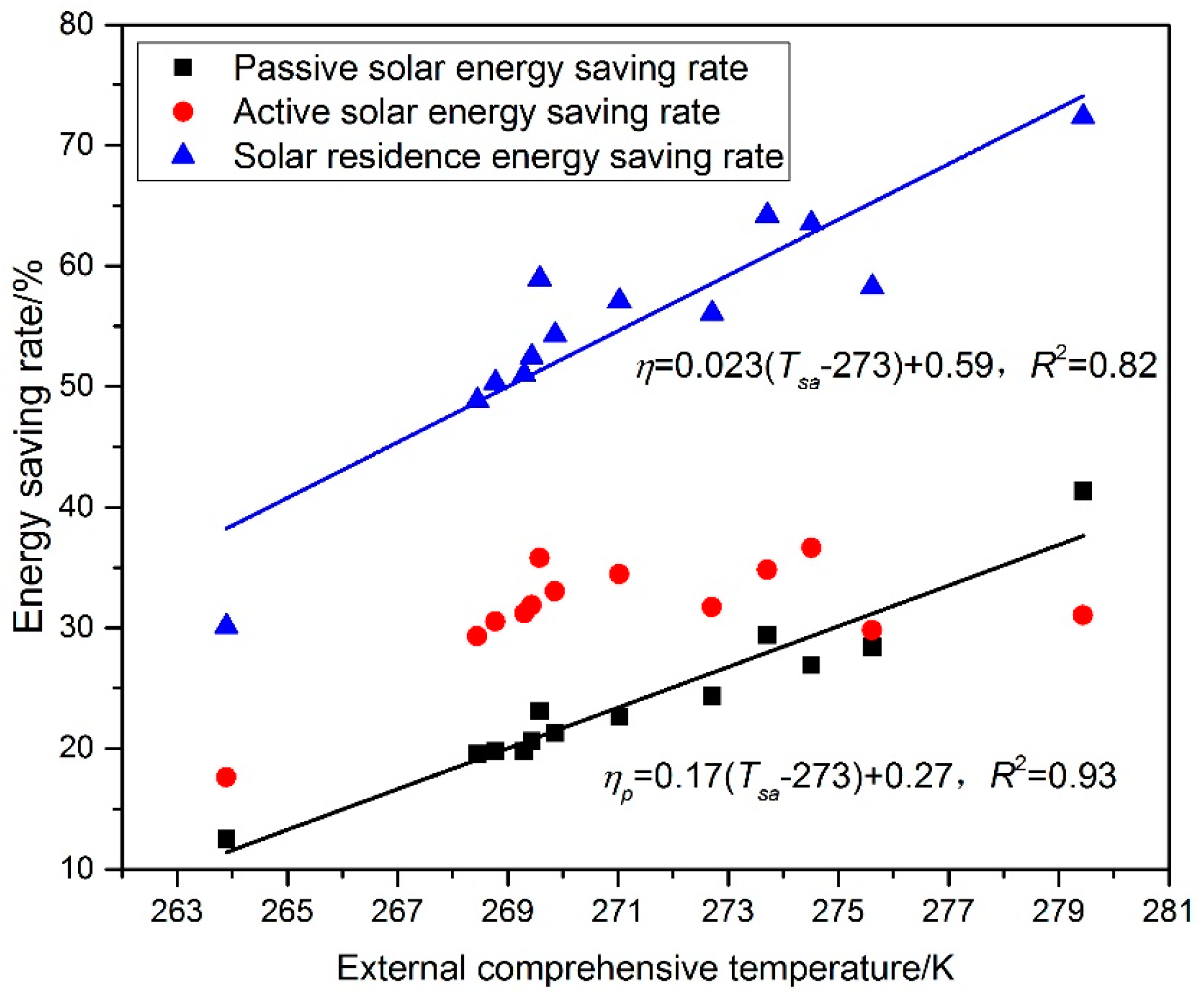
The simulated results showed that there is good linear correlation between the energy saving rate and the external comprehensive temperature, as presented in
Figure 9. From that, as the growth of the external comprehensive temperature, the passive and solar residence energy saving rates increase linearly as in Equations (16) and (17), respectively:
Equation (17) provides an alternative simple method to estimate the feasibility of the proposed system. According to Equation (17), it can be found that if an energy saving rate of 50% is expected, 269 K is a recommended value as the lower limitation of external comprehensive temperature for feasibility of the system. Certainly, due to the correlation derived from the regression of the simulated data, the actual solar residence energy saving rate for a city may deviate from the estimation by the correlation. That is the reason why the difference of the simulated energy saving rate between 264 K and 269 K looks big while the predicted difference of energy saving rate between 264 K and 269 K by the correlation is small. The detailed estimation of the solar residence energy saving rate relies on the results simulated by the model. In addition, because the number of the simulated cities are limited, the suitability of Equation (11) needs to be validated in the further research and application.
The active energy saving rate remains at 30% for the preset airflow of Fan B, so if 50% of the solar residence energy saving rate is expected, the external comprehensive temperature should be more than 269 K for the feasible application of the proposed heating system.
4. Conclusions
A heating system with energy storage by pebble bed in a passive solar attic is proposed with the combination of active and passive utilization of solar energy. To study the characteristics of the proposed heating system, a validated numerical model for optimizing the system design and predicting the heat load is presented. Through the analysis of the simulated results from the model, the following conclusions can be drawn.
- (1)
For as much energy stored as possible, the south and top envelopes of the solar attic should be more transparent, while transparency and thermal insulation should be in balance in the east and west faces, which depends on the meteorological characteristics of the site. Different from other faces, the north side must be more thermally insulated and be opaque.
- (2)
With the above optimal envelope design, the simulated results show that, when the average solar radiation is more than 150 W/m2, the heat storage capacity of the solar attic is hardly influenced by the outdoor temperature.
- (3)
Based on the proposed performance index and the energy saving rate, the simulation indicates that the heating system can reduce energy consumption by up to 56% in winter in Xi’an when the height of the bed is 0.3 m. Certainly, the height is based on a balance consideration between energy saving and the weight bearing capacity of the building and is dependent on pebble properties, the climate, the addition of insulated cover, and other factors.
- (4)
From the simulated results of heating performance in the 13 chosen cities, it turns out that it is not reasonable to judge the feasibility of the proposed system only based on a single traditional index such as solar radiation or outdoor temperature.
- (5)
External comprehensive temperature is suggested as an alternative index for feasibility assessment. Linear correlation between the energy saving rate and external comprehensive temperature as is found from the simulated results. Based on the correlation, it can be concluded that a 50% energy saving rate can be reached when the external comprehensive temperature in a region is higher than 269 K.
Of course, some factors such as energetic, social, and economic perspectives are not considered in the paper, which are also important for design scheme selection [
24]. In addition, in the future, some design developments may be taken into consideration to expand the application of the system, such as the influence of properties of the pebble on bed height (volume), the more efficient insulation of the pebble bed in case of cloudy days and nights, and measures to prevent the deterioration of air quality in the solar attic, in combination with other technologies to save building energy consumption and so on.