Abstract
Latent thermal energy storage (LTS) systems are versatile due to their high-energy storage density within a small temperature range. In shell-and-tube type storage systems fins can be used in order to achieve enhanced charging and discharging power. Typically, circular fins are evenly distributed over the length of the heat exchanger pipe. However, it is yet to be proven that this allocation is the most suitable for every kind of system and application. Consequently, within this paper, a simulation model was developed in order to examine the effect of different fin distributions on the performance of shell-and-tube type latent thermal storage units at discharge. The model was set up in MATLAB Simulink R2015b (The MathWorks, Inc., Natick, MA, USA) based on the enthalpy method and validated by a reference model designed in ANSYS Fluent 15.0 (ANSYS, Inc., Canonsburg, PA, USA). The fin density of the heat exchanger pipe was increased towards the pipe outlet. This concentration of fins was implemented linearly, exponentially or suddenly with the total number of fins remaining constant during the variation of fin allocations. Results show that there is an influence of fin allocation on storage performance. However, the average storage performance at total discharge only increased by three percent with the best allocation compared to an equidistant arrangement.
1. Introduction
Thermal energy storage is currently an important topic in energy science and research. Latent thermal energy storage (LTS) is of particular interest, because of its high-energy storage density. The phase change material (PCM) within the LTS stores a high amount of energy within a small temperature range by changing its phase state.
Originally used for spacecraft thermal control applications, the development and exploration of new PCM for different temperature ranges has led to a wide range of applications []. Latent thermal storage units can be found in heat pumps, building temperature control, off-peak electricity storage, waste heat recovery systems, the cooling of electronic devices and many other fields [,]. Furthermore, the combination of solar power and LTS, like solar heating systems and solar cooking, is currently being researched []. Malan et al. [] examined the potential use of LTS in solar thermal power plants for performance optimisation. Due to the variety of possible applications, several reviews have been carried out inter alia by Sharma et al. []; Zalba et al. []; and Farid et al. [].
Depending on the type of application, an adequate storage material has to be applied. Besides a suitable temperature range of the phase transition, the thermal energy capacity and the thermal conductivity are main criteria []. Due to the phase change enthalpy, the heat capacity of PCM is high in small temperature ranges, while the heat conductivity of PCM is generally low. Since the low heat conductivity presents a disadvantage on discharging when high heat transfer rates are required, the low thermal conductivity can limit the applications of PCM [,].
In order to extend the range of application and to achieve better storage performances, research activities have been carried out to examine the heat transfer process [,,]; storage types and configurations like a combination of different PCMs within one storage unit [,,,,,,]; and the integration of highly heat conductive materials into the storage material, examples of which are copper, aluminum, stainless steel or carbon fiber [,,,,,,]. These materials can be integrated in different forms, such as fins, honeycombs, wool or brush-form. For detailed information, the reader is referred to the reviews of Fan and Khodadadi [], as well as Jegadheeswaran and Pohekar [].
The most common way to improve the performance of shell-and-tube LTS is to integrate longitudinal or circular fins into the storage unit []. Khalifa et al. [] showed that the extracted energy per time of a LTS could be improved by 86% by adding four longitudinal fins into a shell-and-tube type LTS unit. Various articles investigate the performance enhancement by fin shape and design variation. For instance, Al-Abidi et al. [] studied the design of shell-and-tube LTS using longitudinal fins. Furthermore, the influence of circular fin quantity and diameter have been examined by Erek et al. [] with evenly distributed fins, which is the most common way of fin placement. Since the fin material is only relevant if highly conductive material is applied [], fins can be the main costing of a thermal energy storage. Therefore, an increase of the number of fins is not economically viable in many cases. Furthermore, adding additional fins increases the storage weight whereas the storage capacity is generally decreased, which is a disadvantage particularly for mobile application. Therefore, the objective of this study was to investigate whether and to what extend it is possible to improve storage performance of shell-and-tube type LTS on discharge with a constant amount of fin and storage material by adjustment of fin positioning.
For this purpose, simulation models for shell-and-tube type LTS with circular fins were developed in MATLAB [] Simulink []. The distribution of these fins was varied in 30 different ways and their storage power during discharging was examined. Most of the examined designs increased their fin density towards the end of the storage, whereas one geometry represented a homogeneous distribution of fins. For validation, a comparison of these models to an ANSYS Fluent [] model was undertaken. Since conduction is the dominant heat transfer type during discharge [,], convectional effects in the liquid PCM were neglected for reasons of model simplification.
In the following sections, the mathematical description and numerical implementation; the validation; the boundary conditions; and the results will be demonstrated and discussed.
2. Description of the Simulation Model
2.1. Storage Setup
The setup of a shell-and-tube type LTS is shown in Figure 1. Within a container (shell), several storage elements are consistently distributed. The main component of the storage elements is a tube with heat transfer fluid (HTF) on the inside and PCM on the outside. For charging and discharging, the HTF flows through the pipes. The temperature difference between the HTF and the other parts of the storage elements causes charging or discharging of the storage system. Typically, the PCM changes its phase during these processes. On charging, the PCM melts and solidifies on discharging. Since the PCM has a comparatively low heat conductivity, fins can be included into the storage unit to improve the charge and discharge power. In the following, several different types of fin allocations and their effects on the storage performance during discharge will be examined with numerical simulations, examples of which are pictured in Figure 2. The types of analyzed fin allocations can be categorized into five groups. Each allocation consisted of a storage element with 100 fins. Mostly, the fin density (fins per axial distance) increased towards the storage unit outlet in order to adapt the fin density to the temperature difference between HTF and PCM.
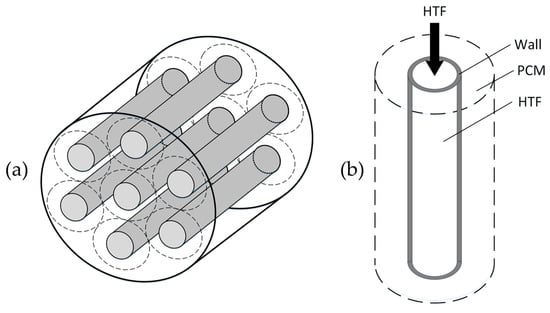
Figure 1.
(a) shell-and-tube latent thermal energy storage (LTS) and (b) single storage element. HTF: heat transfer fluid; and PCM: phase change material.
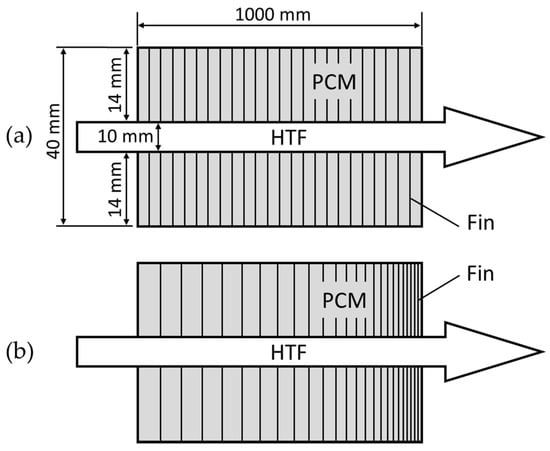
Figure 2.
Single storage element with (a) homogeneous; and (b) uneven distribution of circular fins.
The examined groups of arrangements are described as follows:
- Division of the storage into three sections of the same length, with a different fin density in each section—the density ratio is calculated according to Equation (1):
- Division of the storage into two sections of the same length, with a different fin density in each section—the density ratio is calculated according to Equation (2):
- Linear increase of distances between the fins towards the storage element inlet with a minimum distance between two fins—the distance between the fins n and n + 1 is calculated in consideration of the factor for linear increasing distances :
- Exponential increase of distances between the fins towards the storage element inlet—the factor for exponential increasing distances is calculated according to Equation (4):
- Homogeneous arrangement
Altogether, 30 different distributions of fins were investigated with a storage containing 20 storage elements of one-meter length, an outer storage element diameter of 40 mm and an inner tube diameter of 10 mm. The pipe wall thickness and the thickness of the fins was one millimeter.
The material properties of the HTF and the PCM are listed in Table 1. The phase change of the PCM RT42 takes place within a temperature range of 4 °C. The water inlet temperature was set to 22 °C. The material properties of the pipe walls and fins corresponded to the material properties of pure copper.

Table 1.
Properties of applied materials.
2.2. Numerical Model
The model was set up in MATLAB Simulink. The simulation was based on the transport equation:
From this equation, the energy conservation equation can be deduced:
To simplify the model and to achieve a shorter computational time, the impulse and mass conservation equations were neglected and a constant HTF volume flow rate was assumed. The following adaptions have been made in relation to the PCM calculation:
- Neglect of convectional effects in the liquid PCM;
- Neglect of the temperature dependency of material properties within one phase;
- Application of an enthalpy method with apparent heat capacity;
- Integration of the phase change enthalpy according to Rösler and Brüggemann [] by applying an apparent heat capacity.The governing equation for the PCM isBesides the adaptations for the PCM, the following simplifications were determined for the HTF:
- Incompressible fluid;
- One-dimensional convection (axial);
- Constant predefined velocity.
In order to further reduce the computational effort, geometrical symmetry was included in the calculation. Therefore, the shell-and-tube storage system was simplified by considering only a single storage element within the simulation, as seen in Figure 1. This storage element was rotationally symmetric, thus the storage could be simulated like a two-dimensional model as shown in Figure 3.
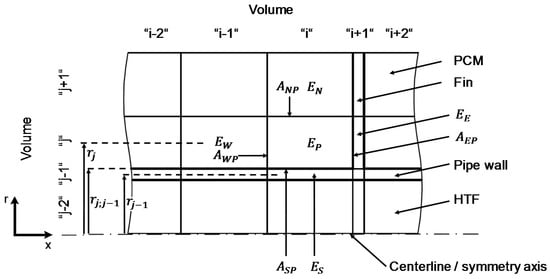
Figure 3.
Section of the discretized two-dimensional model with exemplary declaration of elements, interfaces and radii.
This model was spatially discretized using the finite volume method resulting in Equation (11), while the time discretization was executed by MATLAB Simulink.
With the element declaration indices of Figure 3, the geometrical indices of the coefficients are explained in Equation (12):
The subsequent coefficients for Equation (11) are listed in the following:
The radii, which contain a semicolon in its indices, mark the border between the associated elements, while the other radii mark the center of the elements.
In order to calculate the convection of the HTF, the coefficients of the equations calculating the tube wall and the HTF have to be adapted. The convectional heat transfer within the fluid can be considered by adjusting the coefficient of Equation (11) for the HTF volumes:
while the convectional heat transfer between the HTF and the pipe wall was calculated by modifying the coefficient of the HTF and the coefficient of the pipe wall elements:
In order to account for the boundary conditions, the coefficients of the discretization equation of the boundary elements were adapted. An adiabatic boundary condition was calculated by setting the appropriate coefficient to zero. Furthermore, losses to the surrounding were calculated by:
Although included into the model, ambient losses were neglected within the following simulations, in order to avoid as many sources of uncertainties as possible. Similar to the ambient losses, Equation (24) was applied to include the inlet temperature:
Altogether, the following starting and boundary conditions were set in relation to the coordinate system of Figure 3:
- for every element
- for
- for
- for and
- for and
- for and
- for and
- for and
- for and
- Simulation domain length of 1 m
- Simulation domain radius of 20 mm
The spatial discretization was defined within a s-function. To solve the system of semi-discretized ordinary differential equations, the ode113 (Adams) solver was chosen.
In each simulation, the storage was discharged completely within a physical time of 9000 s. The condition defining the state of total discharge was the remaining storage energy of 0.1% in relation to the starting conditions.
2.3. Validation
In order to validate the model, the storage unit with equidistant spacing was modeled in the commercial computational fluid dynamics (CFD) tool ANSYS Fluent []. Similar to the other simulation models, the storage unit was simplified by simulating only a single storage element and exploiting its geometry. Hence, the storage could be simulated using a two-dimensional model.
All material properties were set in conformity with the MATLAB Simulink model. The boundary conditions of both the ANSYS Fluent and the MATLAB Simulink model were set adiabatic to ensure heat loss independency. However, the flow speed was increased by a factor of 30 to obtain a high Reynolds number of about 2000. In this way, deviations caused by the different types of flow discretization were minimized while the flow was still laminar. The absolute output powers of both simulation environments are shown in Figure 4.
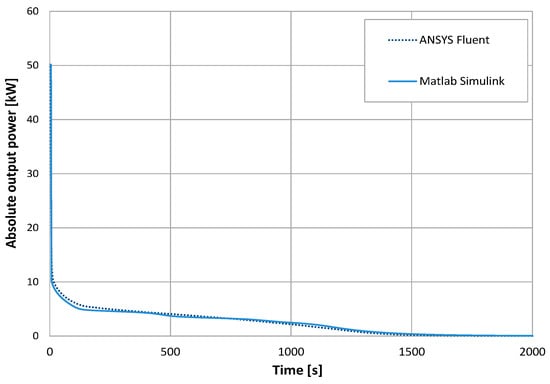
Figure 4.
Comparison of equidistant allocation in ANSYS Fluent and MATLAB Simulink.
Even though the simulations do not show total congruency, the performance of both storage models are very similar and deviations are negligible. Differences between the simulations can be seen shortly after the start of the simulation. Although the Reynolds number was increased, these differences were caused by the different flow discretization types. The HTF of the Simulink model was defined to be one-dimensional, while the ANSYS Fluent model calculates two-dimensionally. Therefore, the ANSYS model had a higher flow speed in the middle of the inner pipe and a lower flow speed close to the pipe wall. Furthermore, it considers radial convection. Consequently, the output temperature of the ANSYS Fluent model drops at an earlier point in time. Since this output temperature drop involves a lower output power, the level of discharge of the ANSYS storage after 20 s is lower than that of the Simulink model. As the times of total discharge are almost the same, the output power of the ANSYS Fluent storage unit has a higher output power within a time of 50–500 s. In spite of these small deviations, the difference of the power integrals of both simulations is less than 0.5%.
Apart from the deviations caused by different types of flow discretization, the results show a very good compliance. Since the effects of the flow discretization are consistent for all MATLAB Simulink fin allocations, the results of the arrangement analysis simulation are reliable. Furthermore, simulations with increased numbers of elements in MATLAB Simulink were performed to ensure grid independency.
3. Results and Discussion
Figure 5 shows the average absolute storage power until full discharge of all fin arrangements. It can be seen that the examined allocations differ, therefore, the storage performance was affected by fin allocation. The most efficient geometry consisted of storage elements with a distribution of fins that linearly increased the fin density using a growth rate of . This geometry achieved an average output power of about 716 W until total discharge, while the least efficient arrangement with an exponential growth rate factor of had an average output power of 655 W leading to a difference of 8.5%. The equidistant distribution of fins achieved an average absolute power of 695 W, which is about three percent less than the achieved maximum average power. Consequently, a homogeneous distribution of fins is not the best type of arrangement in any case considering total storage discharge. It has to be noted that three of the four kinds of uneven fin distribution pass a maximum value within the variation of growth rate. Therefore, it can be assumed that a further variation of the growth rate factors would not cause significant improvements in terms of storage performance compared to the achieved maximum values.
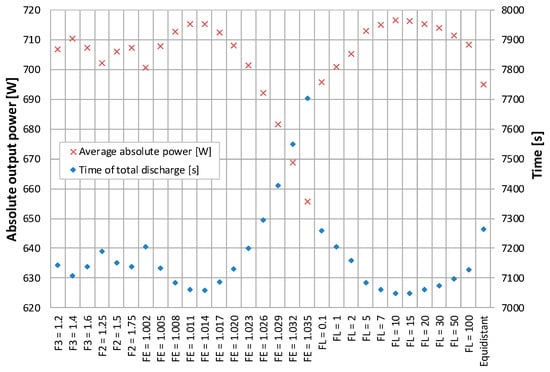
Figure 5.
Absolute average power until total storage discharge of all examined arrangements of fins.
Within all different kinds of fin arrangements, a growth rate F close to the equidistant model did not lead to the shortest discharge time. The shortest times of discharge were achieved using linear growth rates of and , followed by an exponential growth rate of . The difference between these discharge times was only 12 s (0.17%). Due to this fact, both types of distribution are of interest for further research.
Since the yet discussed values only represent the final state, it was also useful to look at the discharge progress to examine intermediate results. Figure 6 depicts the progress of absolute output power of selected arrangement types. For reasons of clarity, only the most efficient storage unit in relation to the average power until total discharge and the storage unit with equidistant arrangement of fins are represented.
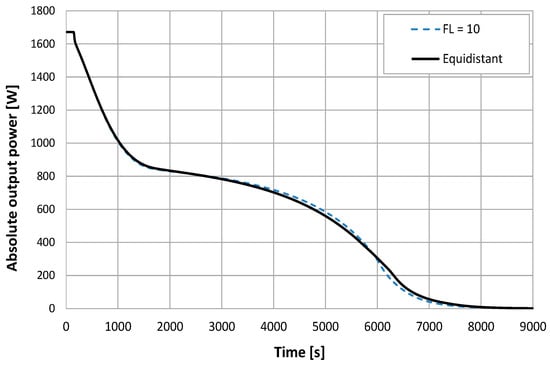
Figure 6.
Storage performances of two simulated allocations of fins.
The figure shows the typical plot for LTS with regard to the performance. From 3000 s physical time until about 5900 s, the output power of the inhomogeneous distribution was higher than the arrangement with equidistant fin distribution. At 5000 s, the relative difference in output power between the allocations was about 5.2%. In addition, most of the non-equidistant arrangements provided higher average power until a simulation time of about 5900 s. At that time, the average output power of the homogeneous distribution was about 0.8% less than the maximum average power. Although the arrangement with a linear growth rate factor of is the fastest type for total discharge, it did not provide the highest power all over the time. In the time range between 5900 s and 8000 s physical time, the storage unit using a homogeneous distribution had a higher output power.
In Figure 7, the power values for discharge times of 6300 s and 5000 s can be seen. At these times, the difference between the allocations are clearly recognizable. At 6300 s, the equidistant geometry provided about 26% more power than the allocation with the highest output power at total storage discharge. Furthermore, at 5000 s it can be seen that the higher the growth rate factor gets at that time, the more output power the storage units generate temporarily.
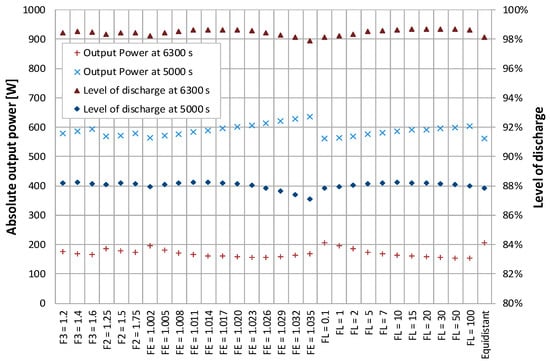
Figure 7.
Comparison of absolute output power and level of discharge at 5000 s and 6300 s for all allocations.
The differences in storage performance also caused different levels of discharge at certain times of simulation, which is also depicted in Figure 7. These differences can be explained by considering the storage temperatures. Figure 8 and Figure 9 show the temperatures of the HTF and pipe wall elements within a storage unit with the linear growth rate of on one hand, and the equidistant fin distribution on the other. The depicted physical times are 5000 s and 6300 s, respectively. The HTF temperature of the last element is directly proportional to the output power. It is recognizable that both fin arrangements have different material temperatures at the displayed points in time.
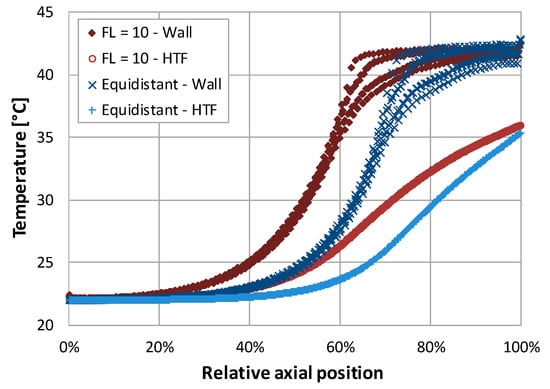
Figure 8.
Heat transfer fluid (HTF) and wall element center temperatures of two distributions at 5000 s physical time.
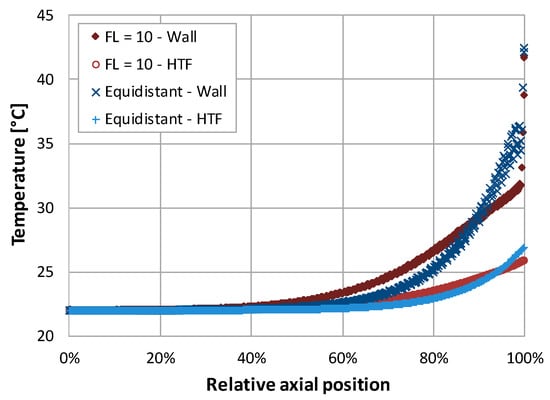
Figure 9.
Heat transfer fluid (HTF) and wall element center temperatures of two distributions at 6300 s physical time.
At 5000 s of physical time, the PCM was not yet totally solidified. Due to the high heat conductivity of the fins, the pipe wall was close to the phase change temperature in a wide range at the storage outlet. In addition, high temperature deviations occurred between adjacent pipe wall elements from 60% to 100% relative axial position. Due to different material properties of the fins and the PCM, pipe wall elements adjoining fins had a higher temperature than adjacent pipe wall elements, which border the PCM elements.
Although both storage units still contained liquid PCM, the storage unit with an allocation with linear growth rate factor of had a higher amount of PCM that was still not solidified. This led to a larger difference in temperature between the pipe wall and the HTF within a relative length of 30% to 100% when comparing the storage unit with the one containing an equidistant arrangement of fins. Consequently, the storage with non-equidistant fin allocation had a higher output power at 5000 s of physical time.
In contrast, at 6300 s of physical time, almost all of the PCM changed its phase in the non-equidistant case, while the pipe wall of the other arrangement was still close to the phase change temperature at the outlet of the storage unit. This indicates that the storage unit cooled more uniformly. Furthermore, the high pipe wall temperature in the end of the storage unit led to a higher HTF temperature at the outlet since the mass flow rate in the simulation was moderate. Consequently, the output power of the storage with equidistant fin allocation was higher at that time. The simulation results show that non-equidistant arrangements of fins can achieve a higher average output power than the homogeneous distribution of fins. These types of thermal energy storage units can be applied for all targeted levels of discharge. It should be noted that these results may vary using different storage types or mass flow rates, since higher heat transfer coefficients between the fluid and the tube might enhance the effect of fin arrangement modification. Further parameters, which might have an impact on the results, are the fin and the storage material, the number and width of the fins such as the outer storage element diameter. Decreasing the thermal conductivity of the storage material might increase the effect of adjusted fin distributions, whereas decreasing the latent heat of fusion might reduce the effect. Although the heat conductivity of copper is high, an even higher heat conductivity of the fins such as higher storage unit diameters, a lower number of fins such as thinner fins can also amplify the effect on storage performance. However, a modification of these parameters might also have an influence on the optimum growth rate factors. Due to the large variety of parameters, an optimization depending on the case of application is recommendable.
Since the charging process of the storage unit was not examined within this work and the influence on the system performance is small, further investigations have to be conducted with respect to technical application.
4. Conclusions
Within this study, LTS performance enhancement by varying circular fin positioning was examined. Therefore, different kinds of circular heat conduction fin distributions with a constant amount of fins and storage material were investigated numerically in order to improve the storage power at discharge. The latent thermal storage units were set up within MATLAB Simulink. The models examine shell-and- tube type LTS containing copper fins and tubes and the paraffin Rubitherm RT42 as a storage material. Different fin allocations were studied including the linearly and exponentially increased fin density towards the outlet of the storage units, the section by section change of the fin density, and the equidistant fin distribution.
In order to validate the results, appropriate thermal energy storage was set up in ANSYS Fluent. A comparison of the different simulation environments was conducted by examining the storage performance at discharge. Apart from small deviations caused by different flow discretization, the performances of both storage units show very good congruency.
The results of varying the fin arrangements within the LTS show that fin allocation affects storage performance. Non-equidistant distributions can cause a higher average output power at all levels of storage discharge than equidistant ones. At total storage discharge, the average output power of a homogeneous fin arrangement could be improved by three percent using a linear growth rate factor of 10. Exponentially increased fin densities towards the storage element outlet also showed promising results. A detailed investigation of the storage material and the HTF temperatures demonstrated that uneven distributions of fins could induce a more uniform discharge. Since the present work examined storage discharge exclusively and the achieved increase of storage performance was generally low, further work analyzing the effects of fin distribution on storage charge and the significance for applications is recommended.
Acknowledgments
The authors gratefully acknowledge financial support of the Bavarian State Ministry of Education, Science and the Arts within the framework TechnologieAllianzOberfranken (TAO). This publication was funded by the German Research Foundation (DFG) and the University of Bayreuth in the funding programme Open Access Publishing.
Author Contributions
All authors contributed to this work by collaboration. Sebastian Kuboth is the main author of this manuscript. Andreas König-Haagen had the initial idea, particularly contributed to the Simulink model and assisted in the conceptual design of the study as well as in the writing of the manuscript. The whole project was supervised by Dieter Brüggemann. All authors revised and approved the publication.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Nomenclature
| Latin symbols | |
| a | Temperature conductivity (m2·s−1) |
| A | Area (m2) |
| c | Specific heat capacity (J·kg−1·K−1) |
| E | Element (-) |
| F | Factor for fin concentration |
| l | Length of the storage (m) |
| L | Latent heat (J·kg−1) |
| Mass flow (kg·s−1) | |
| N | Number of fins |
| r | Radius (m)/radial coordinate (m) |
| Heat flux (J·s−1) | |
| S | Heat source term |
| t | Time (s) |
| T | Temperature (K) |
| u | Flow velocity (m·s−1) |
| Flow velocity vector | |
| V | Volume (m3) |
| x | Axial coordinate (m) |
| Greek symbols | |
| α | Heat transfer coefficient (W·m−2·K−1) |
| Difference (-) | |
| ρ | Density (kg·m−3) |
| ϕ | General variable |
| Γ | Diffusion coefficient (m2·s−1) |
| λ | Heat conductivity (W·m−1·K−1) |
| Subscripts | |
| amb | Ambience |
| app | Apparent value |
| E | Concerning the element left of the calculation element/exponential |
| edge | Concerning the edge of the calculation element, that borders the ambience |
| EP | Concerning the element east of the calculation element (CE) and the CE |
| F | Heat transfer fluid |
| h | Concerning the specific enthalpy |
| HTF | Concerning the outer radius of the HTF |
| in | Inlet |
| I | Concerning the first section |
| II | Concerning the second section |
| III | Concerning the third section |
| j | Position indicator in radial direction |
| l | Liquid phase |
| L | Linear/latent |
| m | Thermodynamic mean |
| n | Counting variable |
| N | Concerning the element above the calculation element |
| NP | Concerning the element north of the calculation element (CE) and the CE |
| P | Concerning the calculation element |
| s | Solid phase |
| S | Concerning the element below the calculation element |
| sec | Concerning one section of the storage element |
| sen | Concerning the sensible heat capacity |
| SP | Concerning the element south of the calculation element (CE) and the CE |
| su | Storage unit |
| W | Concerning the element right of the calculation element |
| wall | Pipe wall |
| WP | Concerning the element west of the calculation element (CE) and the CE |
| 0 | Concerning minimum distance |
| 1 | First element |
| 2 | Storage element divided into two parts |
| 3 | Storage element divided into three parts |
| α | Convective heat transfer |
| ϕ | Concerning the general variable |
| Superscripts | |
| i | Position indicator in axial direction |
| 0 | Concerning the last time step |
References
- Sharma, A.; Tyagi, V.V.; Chen, C.R.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Tan, F.L.; Tso, C.P. Cooling of mobile electronic devices using phase change materials. Appl. Therm. Eng. 2009, 24, 159–169. [Google Scholar] [CrossRef]
- Malan, D.J.; Dobson, R.T.; Dinter, F. Solar thermal energy storage in power generation using phase change material with heat pipes and fins to enhance heat transfer. Energy Procedia 2015, 69, 925–936. [Google Scholar] [CrossRef]
- Zalba, B.; Marín, J.M.; Cabeza, L.F.; Mehling, H. Review on thermal energy storage with phase change: Materials, heat transfer analysis and applications. Appl. Ther. Eng. 2003, 23, 251–283. [Google Scholar] [CrossRef]
- Farid, M.M.; Khudhair, A.M.; Razack, S.A.K.; Al-Hallaj, S. A review on phase change energy storage: Materials and applications. Energy Convers. Manag. 2004, 45, 1597–1615. [Google Scholar] [CrossRef]
- Sharma, S.D.; Sagara, K. Latent heat storage materials and systems: A review. Int. J. Green Energy 2005, 2, 1–56. [Google Scholar] [CrossRef]
- Seddegh, S.; Wang, X.; Henderson, A.D. Numerical investigation of heat transfer mechanism in a vertical shell and tube latent heat energy storage system. Appl. Ther. Eng. 2015, 87, 698–706. [Google Scholar] [CrossRef]
- Kozak, Y.; Rozenfeld, T.; Ziskind, G. Close-contact melting in vertical annular enclosures with a non-isothermal base: Theoretical modeling and application to thermal storage. Int. J. Heat Mass Transf. 2014, 72, 114–127. [Google Scholar] [CrossRef]
- Adine, H.A.; el Qarnia, H. Numerical analysis of the thermal behaviour of a shell-and-tube heat storage unit using phase change materials. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Nithyanandam, K.; Pitchumani, R. Analysis and optimization of a latent thermal energy storage system with embedded heat pipes. Int. J. Heat Mass Transf. 2011, 54, 4596–4610. [Google Scholar] [CrossRef]
- Trp, A.; Lenic, K.; Frankovic, B. Analysis of the influence of operating conditions and geometric parameters on heat transfer in water-paraffin shell-and-tube latent thermal energy storage unit. Appl. Therm. Eng. 2006, 26, 1830–1839. [Google Scholar] [CrossRef]
- Fang, M.; Chen, G. Effects of different multiple PCMs on the performance of a latent thermal energy storage system. Appl. Therm. Eng. 2007, 27, 994–1000. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, K.; Wang, L.; He, Y. Numerical study of the heat charging and discharging characteristics of a shell-and-tube phase change heat storage unit. Appl. Therm. Eng. 2013, 58, 542–553. [Google Scholar] [CrossRef]
- Khalifa, A.; Tan, L.; Date, A.; Akbarzadeh, A. Performance of suspended finned heat pipes in high-temperature latent heat thermal energy storage. Appl. Therm. Eng. 2015, 81, 242–252. [Google Scholar] [CrossRef]
- Regin, A.F.; Solanki, S.C.; Saini, J.S. Heat transfer characteristics of thermal energy storage system using PCM capsules: A review. Renew. Sustain. Energy Rev. 2008, 12, 2438–2458. [Google Scholar] [CrossRef]
- Rozenfeld, T.; Kozak, Y.; Hayat, R.; Ziskind, G. Close-contact melting in a horizontal cylindrical enclosure with longitudinal plate fins: Demonstration, modeling and application to thermal storage. Int. J. Heat Mass Transf. 2015, 86, 465–477. [Google Scholar] [CrossRef]
- Agyenim, F.; Eames, P.; Smyth, M. A comparison of heat transfer enhancement in a medium temperature thermal energy storage heat exchanger using fins. Sol. Energy 2009, 83, 1509–1520. [Google Scholar] [CrossRef]
- Languri, E.M.; Aigbotsua, C.O.; Alvarado, J.L. Latent thermal energy storage system using phase change material in corrugated enclosures. Appl. Therm. Eng. 2013, 50, 1008–1014. [Google Scholar] [CrossRef]
- Al-Abidi, A.A.; Mat, S.; Sopian, K.; Sulaiman, M.Y.; Mohammada, A.T. Internal and external fin heat transfer enhancement technique for latent heat thermal energy storage in triplex tube heat exchangers. Appl. Therm. Eng. 2013, 53, 147–156. [Google Scholar] [CrossRef]
- Khalifa, A.; Tan, L.; Date, A.; Akbarzadeh, A. A numerical and experimental study of solidification around axially finned heat pipes for high temperature latent heat thermal energy storage units. Appl. Therm. Eng. 2014, 70, 609–619. [Google Scholar] [CrossRef]
- Rathod, M.K.; Banerjee, J. Thermal performance enhancement of shell and tube Latent Heat Storage Unit using longitudinal fins. Appl. Therm. Eng. 2015, 75, 1084–1092. [Google Scholar] [CrossRef]
- Fukai, J.; Kanou, M.; Kodama, Y.; Miyatake, O. Thermal conductivity enhancement of energy storage mediausing carbon fibers. Energy Convers. Manag. 2000, 41, 1543–1556. [Google Scholar] [CrossRef]
- Fan, L.; Khodadadi, J.M. Thermal conductivity enhancement of phase change materials for thermal energy storage: A review. Renew. Sustain. Energy Rev. 2011, 15, 24–46. [Google Scholar] [CrossRef]
- Jegadheeswaran, S.; Pohekar, S.D. Performance enhancement in latent heat thermal storage system: A review. Renew. Sustain. Energy Rev. 2009, 13, 2225–2244. [Google Scholar] [CrossRef]
- Erek, A.; İlken, Z.; Acar, M.A. Experimental and numerical investigation of thermal energy storage with a finned tube. Int. J. Energy Res. 2005, 29, 283–301. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Mehling, H.; Hiebler, S.; Ziegler, F. Heat transfer enhancement in water when used as PCM in thermal energy storage. Appl. Therm. Eng. 2002, 22, 1141–1151. [Google Scholar] [CrossRef]
- The MathWorks, Inc. Release; The MathWorks, Inc.: Natick, MA, USA, 2015. [Google Scholar]
- The MathWorks, Inc. Simulink Release; The MathWorks, Inc.: Natick, MA, USA, 2015. [Google Scholar]
- ANSYS, Inc. Fluent Release 15.0; ANSYS, Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Rösler, F.; Brüggemann, D. Shell-and-tube type latent heat thermal energy storage: Numerical analysis and comparison with experiments. Heat Mass Transf. 2011, 47, 1027–1033. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).