Computational Study of the Noise Radiation in a Centrifugal Pump When Flow Rate Changes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Flow Field Solver
2.2. The Acoustic Submodel
2.3. Numerical Issue Concerning the Set-Up
3. Results and Discussion
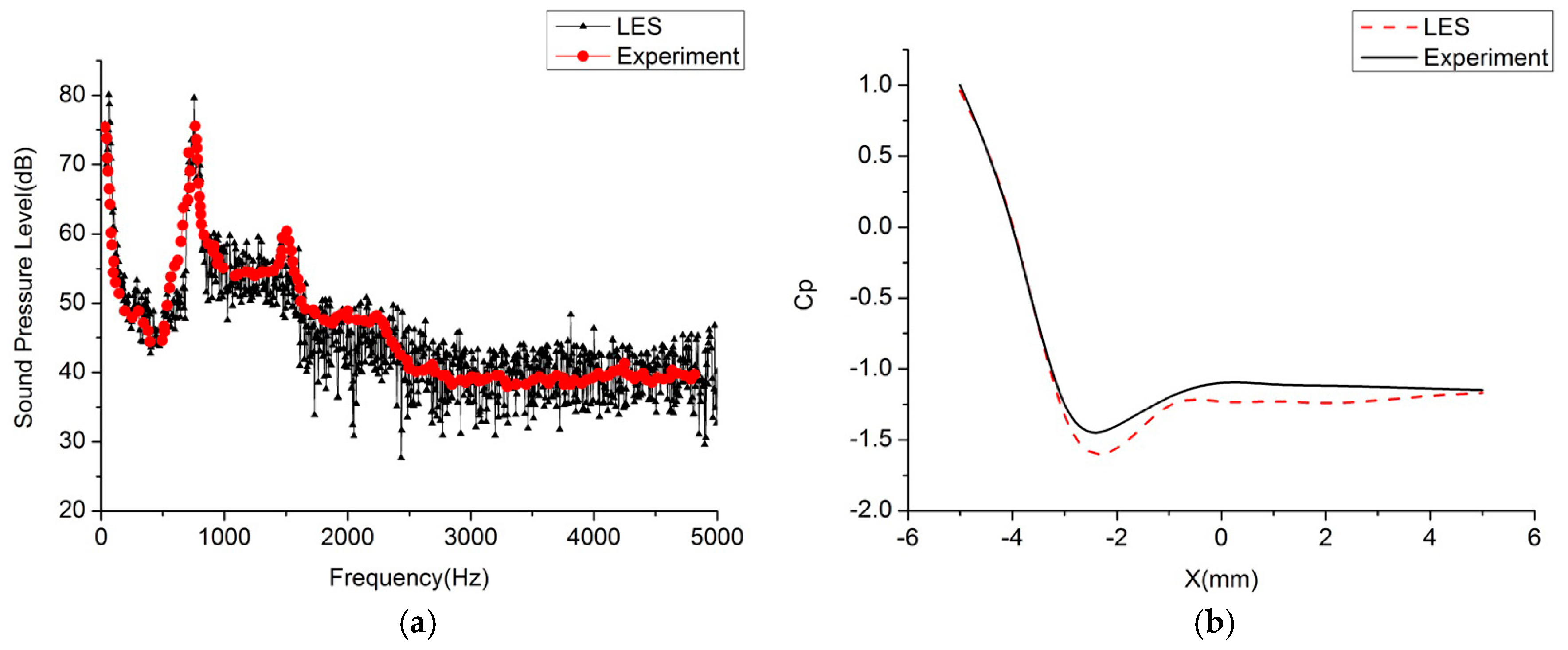
3.1. Numerical Validaton
3.2. Flow Field
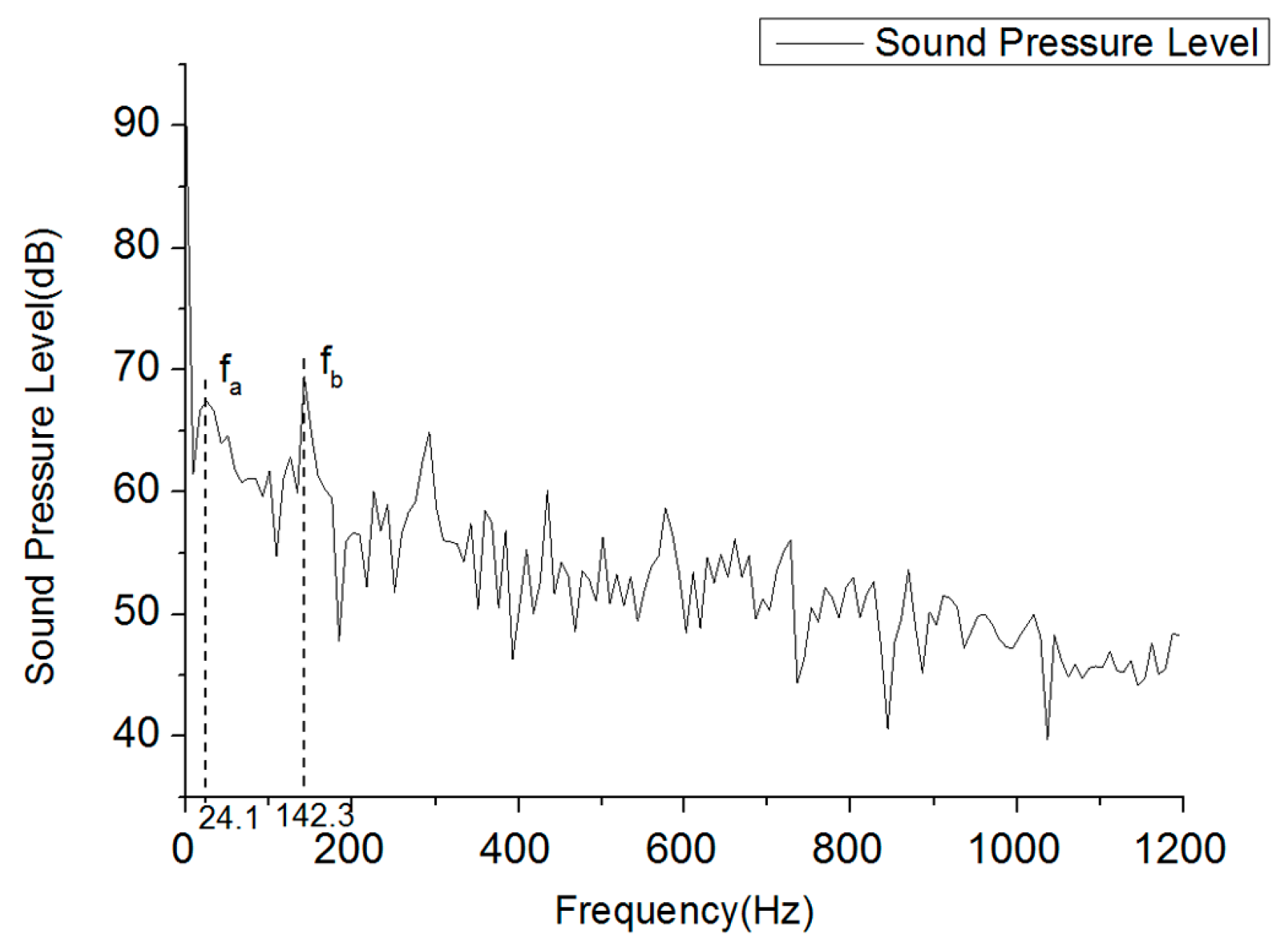
3.3. Noise Analysis
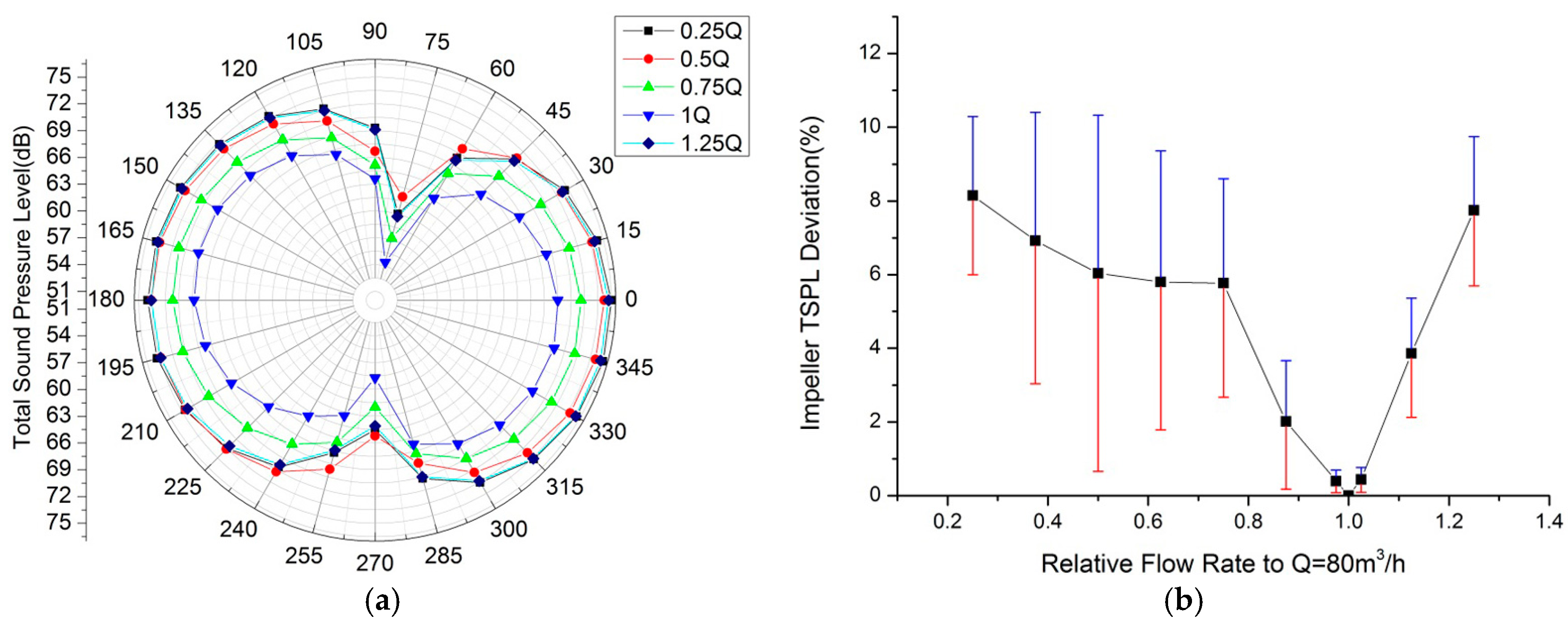
3.3.1. The Impeller Radiation Noise
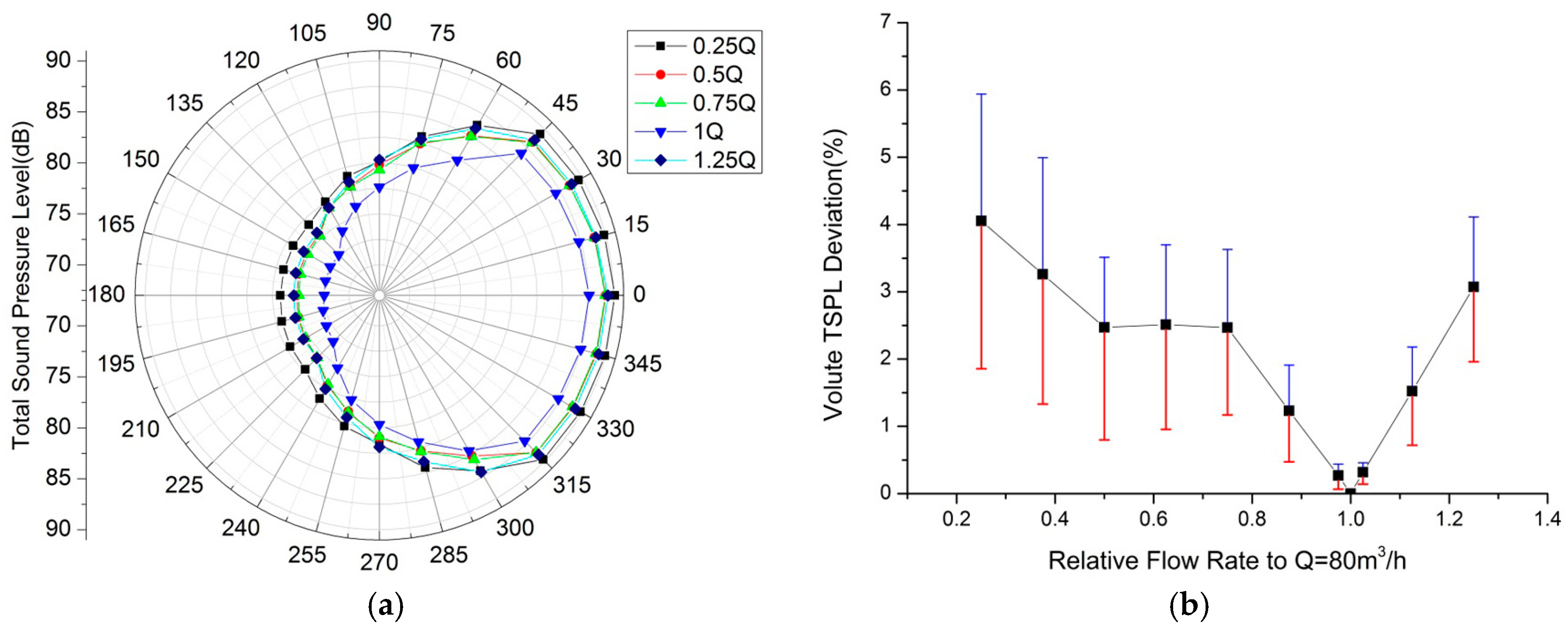
3.3.2. The Volute Radiation Noise
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Cs | Smagorinsky constant |
| Δ | Size of the grid filter |
| p’ | Far-field acoustic pressure |
| a0 | Speed of sound |
| Reference density of fluid | |
| δ(f) | Dirac delta function |
| H(f) | Heaviside function |
| Pref | Reference sound pressure |
| K | Step number in a rotational period |
| n | Rotational speed |
| P(t) | Transient static pressure |
| Time-averaged static pressure |
References
- Johann, F.G. Centrifugal Pumps; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2008. [Google Scholar]
- Brennen, C.E. A review of the dynamics of cavitating pumps. J. Fluids Eng. 2012, 135. [Google Scholar] [CrossRef]
- Wang, J.; Feng, T.; Liu, K.; Zhou, Q.J. Experimental research on the relationship between the flow-induced noise and the hyaraulic parameters in centrifugal pump. Fluid Mach. 2007, 6, 1–13. [Google Scholar]
- Choi, J.S.; Mclaughlin, D.K.; Thompson, D.E. Experiments on the unsteady flow field and noise generation in a centrifugal pump impeller. J. Sound Vib. 2003, 263, 493–514. [Google Scholar] [CrossRef]
- Parrondo, J.; Pérez, J.; Barrio, R.; González, J. A simple acoustic model to characterize the internal low frequency sound field in centrifugal pumps. Appl. Acoust. 2011, 72, 59–64. [Google Scholar] [CrossRef]
- Liu, H.L.; Dai, H.W.; Ding, J. Numerical and experimental studies of hydraulic noise induced by surface dipole sources in a centrifugal pump. J. Hydrodyn. Ser. B 2016, 28, 43–51. [Google Scholar] [CrossRef]
- Chu, S.; Dong, R.; Katz, J. Relationship between unsteady flow, pressure fluctuations, and noise in a centrifugal pump—Part A: Use of PDV data to compute the pressure field. J. Fluids Eng. 1995, 117, 24–29. [Google Scholar] [CrossRef]
- Chu, S.; Dong, R.; Katz, J. Relationship between unsteady flow, pressure fluctuations, and noise in a centrifugal pump—Part B: Effects of blade-tongue interactions. J. Fluids Eng. 1995, 117, 30–35. [Google Scholar] [CrossRef]
- Langthjem, M.A.; Olhoff, N. A numerical study of flow-induced noise in a two-dimensional centrifugal pump. Part I. Hydrodynamics. J. Fluids Struct. 2004, 19, 349–368. [Google Scholar] [CrossRef]
- Langthjem, M.A.; Olhoff, N. A numerical study of flow-induced noise in a two-dimensional centrifugal pump. Part II. Hydroacoustics. J. Fluids Struct. 2004, 19, 369–386. [Google Scholar] [CrossRef]
- Kato, C.; Yamade, Y.; Wang, H.; Guo, Y.; Miyazawa, M.; Takaishi, T.; Takano, Y. Numerical prediction of sound generated from flows with a low Mach number. Comput. Fluids 2007, 36, 53–68. [Google Scholar] [CrossRef]
- Kato, C.; Kaiho, M.; Manabe, A. An overset finite-element large-eddy simulation method with applications to turbomachinery and aeroacoustics. Trans. Am. Soc. Mech. Eng. J. Appl. Mech. 2003, 70, 32–43. [Google Scholar] [CrossRef]
- Huang, J. Comparison of noise characteristics in centrifugal pumps with different types of impellers. Acta Acust. 2010, 35, 113–118. [Google Scholar]
- Li, K.; Yu, J.; Shi, F.; Huang, A.X. Dimension splitting method for the three dimensional rotating Navier-Stokes equations. Acta Math. Appl. Sin. Engl. Ser. 2012, 28, 417–442. [Google Scholar] [CrossRef]
- Seif, M.S.; Asnaghi, A.; Jahanbakhsh, E. Implementation of PISO algorithm for simulating unsteady cavitating flows. Ocean Eng. 2010, 37, 1321–1336. [Google Scholar] [CrossRef]
- Williams, J.F.; Hawkings, D.L. Sound generated by turbulence and surfaces in arbitrary motion. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 264, 321–342. [Google Scholar] [CrossRef]
- Ghasemian, M.; Nejat, A. Aerodynamic noise prediction of a horizontal axis wind turbine using improved delayed detached eddy simulation and acoustic analogy. Energy Convers. Manag. 2015, 99, 210–220. [Google Scholar] [CrossRef]
- Tao, J.; Lu, X.; Wang, L.; Wang, L.; Li, J. Methods of Measuring and Evaluating Noise of Pumps; Chinese Quality Supervision Bureau: Beijing, China, 2013; pp. 4–6. [Google Scholar]
- Fluent Inc. Gambit 2.4 User’s Guide; Fluent Inc.: New York, NY, USA, 2007; pp. 1–17. [Google Scholar]
- Choi, H.; Moin, P. Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 2012, 24. [Google Scholar] [CrossRef]
- Tsai, C.H.; Fu, L.M.; Tai, C.H.; Huang, Y.L.; Leong, J.C. Computational aero-acoustic analysis of a passenger car with a rear spoiler. Appl. Math. Model. 2009, 33, 3661–3673. [Google Scholar] [CrossRef]
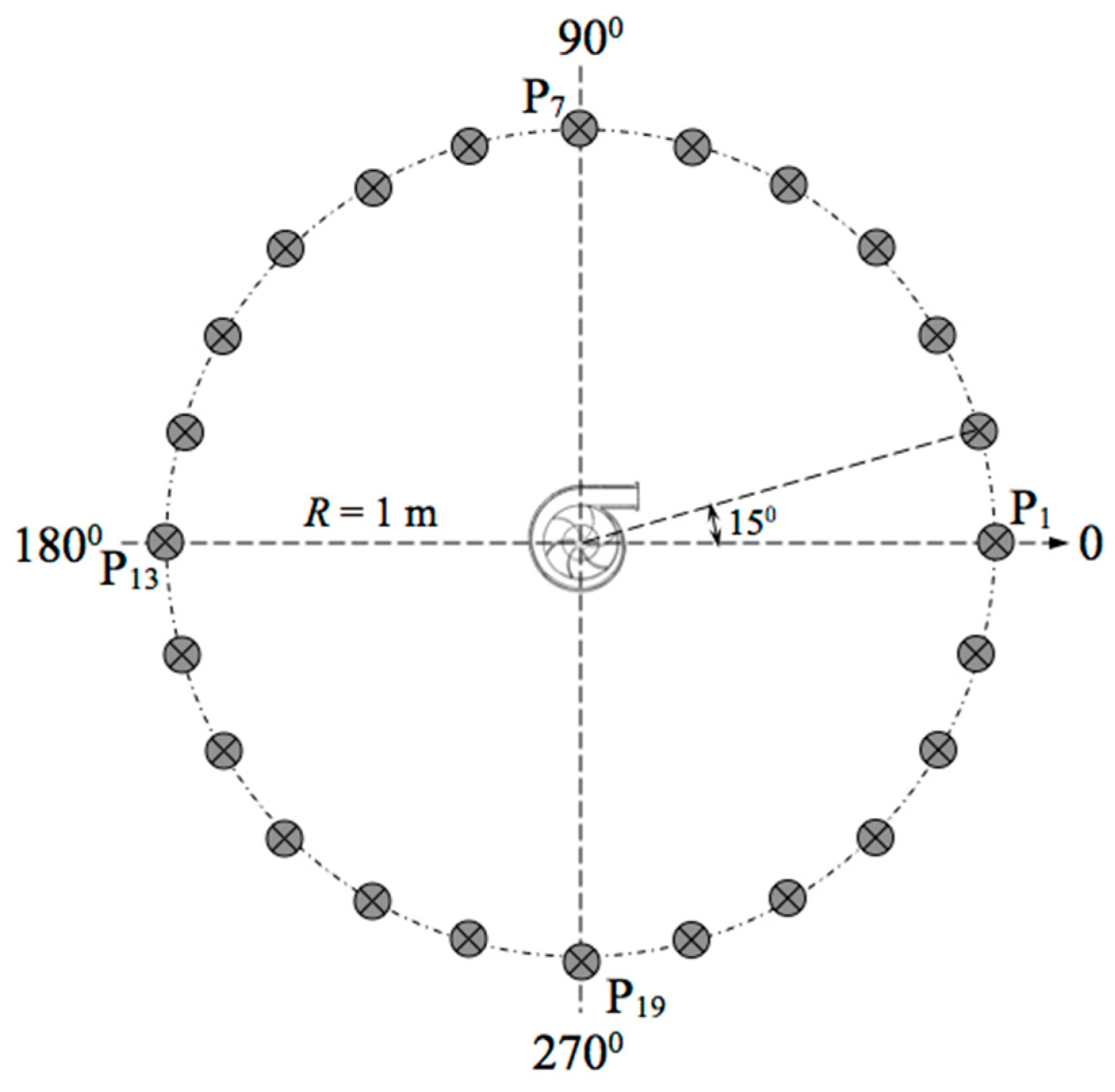
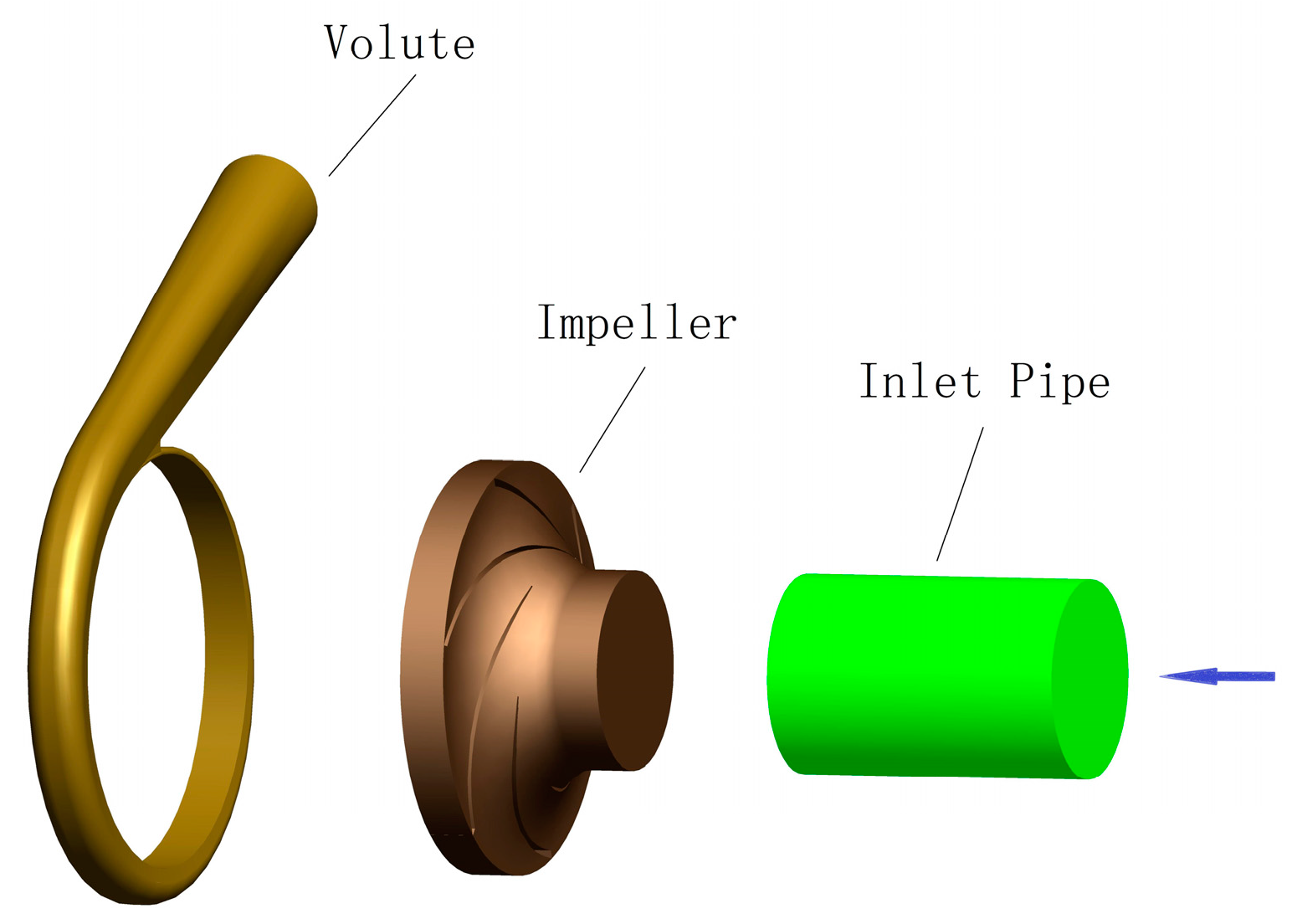

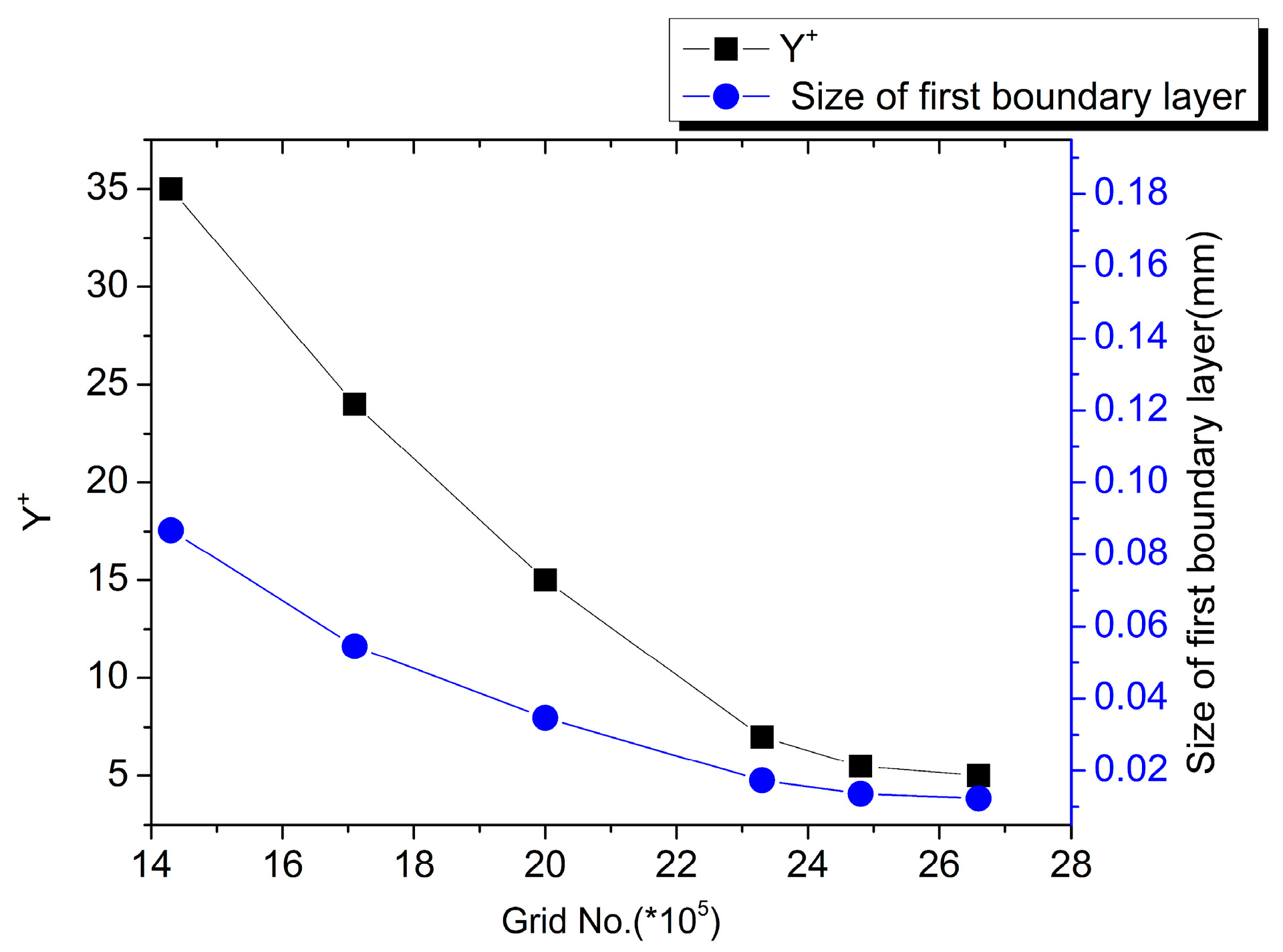
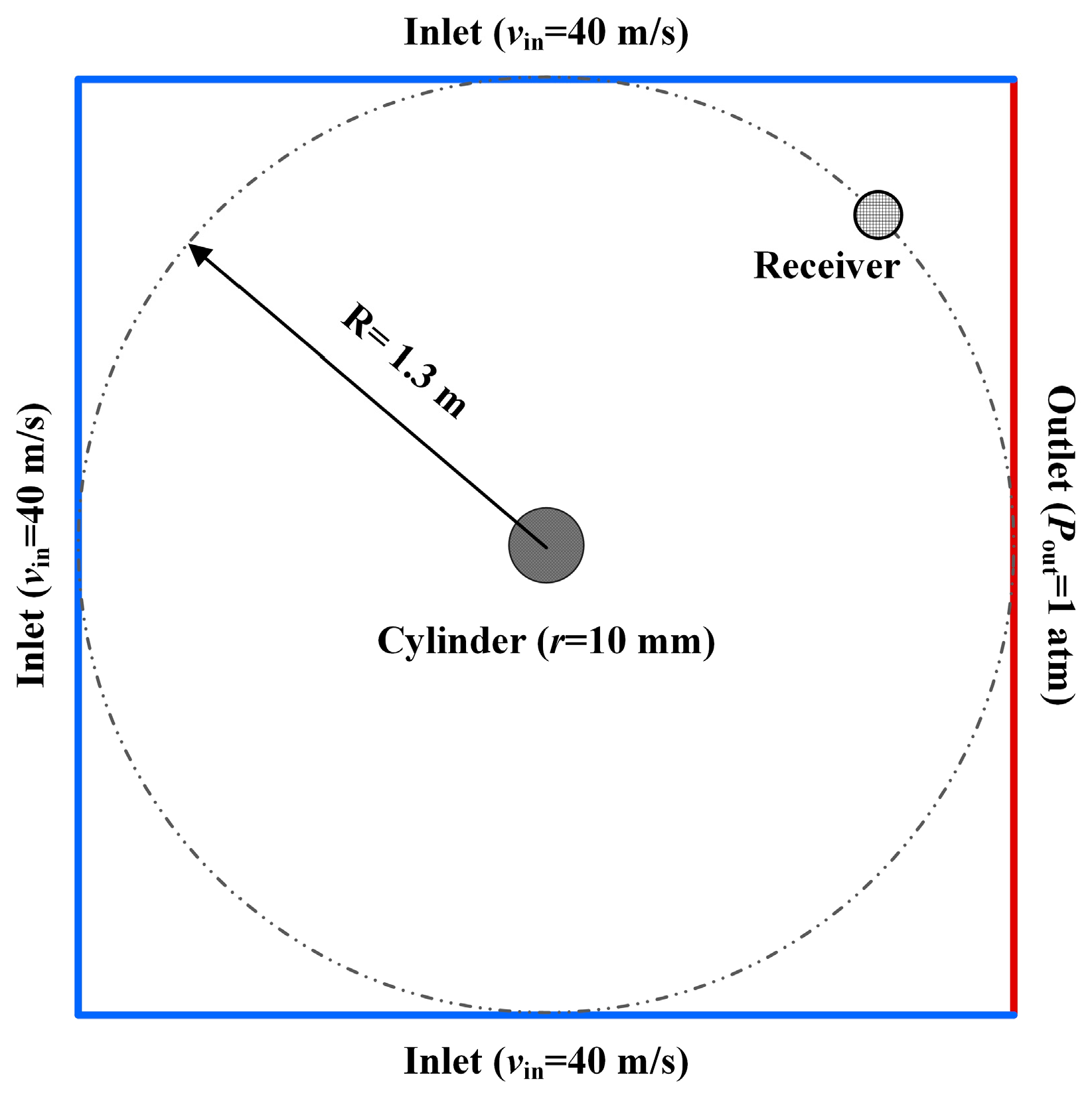

| Parameter | Value | Unit |
|---|---|---|
| Impeller outlet diameter D2 | 270 | mm |
| Impeller outlet width D | 30 | mm |
| Design flow rate Q | 80 | m3/h |
| Design head H | 28 | m |
| Design rotational speed n | 1450 | r/min |
| Blade number Z | 6 | 1 |
| Axis pass frequency fa (APF) | 24.2 | Hz |
| Blade pass frequency fb (BPF) | 145 | Hz |
| Grid System | Grid Number | Head (m) |
|---|---|---|
| Grid-A | 2,012,658 | 28.82 |
| Grid-B | 2,324,567 | 28.70 |
| Grid-C | 2,496,543 | 28.63 |
| Grid-D | 2,676,328 | 28.62 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Dong, P.; Lei, S.; Turan, A. Computational Study of the Noise Radiation in a Centrifugal Pump When Flow Rate Changes. Energies 2017, 10, 221. https://doi.org/10.3390/en10020221
Gao M, Dong P, Lei S, Turan A. Computational Study of the Noise Radiation in a Centrifugal Pump When Flow Rate Changes. Energies. 2017; 10(2):221. https://doi.org/10.3390/en10020221
Chicago/Turabian StyleGao, Ming, Peixin Dong, Shenghui Lei, and Ali Turan. 2017. "Computational Study of the Noise Radiation in a Centrifugal Pump When Flow Rate Changes" Energies 10, no. 2: 221. https://doi.org/10.3390/en10020221
APA StyleGao, M., Dong, P., Lei, S., & Turan, A. (2017). Computational Study of the Noise Radiation in a Centrifugal Pump When Flow Rate Changes. Energies, 10(2), 221. https://doi.org/10.3390/en10020221








