Abstract
Plane-of-array (PoA) irradiation data is a requirement to simulate the energetic performance of photovoltaic devices (PVs). Normally, solar data is only available as global horizontal irradiation, for a limited number of locations, and typically in hourly time resolution. One approach to handling this restricted data is to enhance it initially by interpolation to the location of interest; next, it must be translated to PoA data by separately considering the diffuse and the beam components. There are many methods of interpolation. This research selects ordinary kriging as the best performing technique by studying mathematical properties, experimentation and leave-one-out-cross validation. Likewise, a number of different translation models has been developed, most of them parameterised for specific measurement setups and locations. The work presented identifies the optimum approach for the UK on a national scale. The global horizontal irradiation will be split into its constituent parts. Divers separation models were tried. The results of each separation algorithm were checked against measured data distributed across the UK. It became apparent that while there is little difference between procedures (14 Wh/m2 mean bias error (MBE), 12 Wh/m2 root mean square error (RMSE)), the Ridley, Boland, Lauret equation (a universal split algorithm) consistently performed well. The combined interpolation/separation RMSE is 86 Wh/m2).
1. Introduction
Solar photovoltaic device (PV) provide 40% of world’s renewable electricity capacity. This is expected to increase by 825 GW by 2021 [1]. Photovoltaic installations in the UK stood at 11 GW as of the end of August 2016 [2]. The economics of these systems depend on a multitude of factors, but one major element is the supposed risk associated with their performance, i.e., deviation of real performance from the predicted performance. It has been shown that in the case of modelling accuracy, one of the main determinants is the prediction of the plane-of-array irradiance [3]. Meteorological data is usually only available as total global horizontal irradiation at specific locations and thus needs to be translated to plane-of-array (PoA) irradiance, which incurs a significant uncertainty in the overall modelling chain. PoA irradiation may be obtained from horizontal radiation in the following sequence:
- (1)
- Interpolate weather station readings of global horizontal irradiation to produce a national map of values.
- (2)
- Compute the solar declination angle, an essential input to the clearness index (kt). kt is a component of the next stage.
- (3)
- Split global horizontal irradiation into its components: beam and diffuse irradiation.
- (4)
- Convert each component from horizontal radiation to the PoA inclination and azimuth.
- (5)
- Sum the results: beam on tilted surface plus diffuse on tilted surface.
- (6)
- Allow for albedo.
Total tilt irradiance = beam on tilted surface plus diffuse on tilted surface plus ground-reflected.
This final figure is now appropriate for PV performance estimations.
Work has already taken place in Loughborough on Stages 3 and 4 [4]. Now, this paper focusses on selecting the optimum models for the interpolation of, and deriving horizontal beam and diffuse irradiation from, global horizontal irradiation. The research will be limited to models suitable for hourly datasets and therefore to those which are capable of automatically processing large numbers of results.
2. Interpolation Outline
2.1. Why Interpolate?
Solar irradiation data is normally obtained from either of two sources: ground observations or satellite-derived data. Quality ground-measured data is usually accepted as more accurate than satellite-modelled data [5]. However, satellite-modelled data is frequently quoted as being more accurate at distances greater than 34 km from a weather station, based on the work of Perez et al. [6]. Weather stations in the UK are, on average, only 40 km apart. A 34 km area around UK weather stations covers 90% of the country. The gaps are in the Welsh and Scottish mountains which are unfit for solar installations due to slope. Satellite-based data is also less suitable for the UK because it has reduced accuracy at latitudes greater than 50°, in coastal zones and in regions with constant occurrence of clouds [7]. Due to the good network of weather stations and limitations of satellite modelling in the specific circumstances, interpolation of ground measurements was utilised in this research.
2.2. Review of Interpolation Techniques
Interpolation is the process of filling gaps between sample observations to produce a grid of values [8]. There are a dozen or more methods, each with a set of up to ten criteria. Prominent examples include linear regression, nearest neighbour, inverse distance weighting, spline (a polynomial function) and kriging. Confusingly, names vary between authors and computer packages. Different techniques can produce very different results [9]. The chosen tool should be accurate, robust, flexible enough to handle large and varied datasets with input errors, computationally efficient and easy to use. No existing method can satisfy all of these conditions. For this reason, the approach here is to single out only the best known interpolation techniques. Having narrowed down the number of possibilities, several will be examined and the most suitable selected in terms of appropriateness of match to the input data. The original data is evaluated in terms of quantity, spread across the sample area and trends in direction.
Linear regression fits a straight line through the data points. It may be criticised for over-simplifying complex real-world processes. Nearest neighbour (also known as triangulation or Thiessen) obtains the value of a grid cell from the three adjacent points. It requires many data points in order to work well—a feature which meteorological data does not possess. As with the previous procedure, it lacks realism.
The inverse distance weighted (IDW) interpolation method is frequently used. It estimates values as weighted averages, allocating the greatest weights to the nearest points to produce a smooth distance decay effect. However, solar irradiance does not vary continuously. It may display sudden change because of rapid alteration in cloud cover.
Spline uses “rubber-sheeting”. A surface is constructed which passes through known points whilst minimising the overall surface curvature. Spline works well when it is acceptable for the calculated values to exceed maximum and minimum input points and when the number of sample values is comparatively small. It is not appropriate where sample points are clustered together and have extremely different readings (as can be the case with weather stations in London). In addition, spline needs a gentle data variation. As mentioned above, solar irradiance does not exhibit this characteristic.
Kriging is a complex interpolation technique. Like IDW, the closest measurements exert the greatest influence. In contrast to IDW’s simple distance-based algorithm, kriging applies weights derived from a semi-variogram. The semi-variogram is a graph which models the difference between a value at one location and the value at another location according to the distance and direction between them.
Kriging has proven useful and popular in many fields [10]. It is utilised by the most respected solar insolation databases photovoltaic geographical information system (PVGIS-3, European Commission, Joint Research Centre) and Meteonorm (Meteotest, Bern, Switzerland)—up to Version 6) and is a good choice where the sample points are poorly distributed or there are few of them. It can also mirror directional bias in the data. (According to the UK Met Office, solar radiation increases from north to south and from east to west—Kent westwards to Wiltshire and Dorset). Furthermore, kriging has the advantage that it is a geostatistical method. This means that it encompasses autocorrelation (i.e., everything is related to everything else, but near things are more related than distant things). This statistical relationship between the measured points enables estimation errors (kriging variance) to be reckoned. All the previously discussed interpolation methods are deterministic, therefore do not include autocorrelation and cannot provide error calculations. On account of its widespread use, suitability for the data and error calculations, some form of kriging will be investigated in this research.
3. Decomposition/Separation Model Appraisal
A search of the literature has revealed a large number of models which separate beam and diffuse from global horizontal irradiation. De Miguel identified 250 such models [11] since the ground-breaking work of Liu and Jordan [12]. Comprehensive appraisals may be found in [13,14]. A representative few are reviewed here. Lui and Jordan’s early model uses a piece-wise first-order fit of the clearness index to derive the diffuse fraction. Most later models augment Lui and Jordan’s, still proceeding piece-wise by binning the data into three clearness index divisions. A common feature between all of them is that they are parameterised by local or regional observational data. Some models are suitable only for monthly data, whilst others accept all lengths of timestamp, down to seconds. Having said that, smaller time steps are known to generate larger random errors.
Separation (also known as decomposition) models may be categorised according to the number of contributory variables they demand (one, two or many). The de Miguel (Climatic Synthetic Time Series for the Mediterranean Belt (CLIMED)), Erbs, Orgill, and Reindl (No. 1) models are fitted by the measured diffuse fraction only [11,15,16,17]. Reindl’s second model additionally employs solar elevation, that is, it is bivariate [18]. Maxwell’s Direct Insolation Simulation Code (DISC) model is more complex since it requires sun zenith angle, day of year, and average site atmospheric pressure [19]. Perez et al. [20] modified the DISC model by binning inputs according to sky condition. A more recent multivariate model is that of Ridley et al. [21,22]. Unlike prior research, this utilises a logistic function to include solar altitude and a persistence factor into just one equation, i.e., there is no binning.
Separation models are site-dependent [23]. In this research, the aim is to determine the most suitable separation model for weather conditions in Great Britain and to discover whether the same paradigm is applicable to the UK as a whole. Yang et al. [24] and Gueymard [25] find that sophisticated models with several inputs do not improve upon the simpler approaches, in contrast to Gueymard’s earlier conclusion, when he discovered more detailed models offer enhanced performance [14]. (More recent work from these authors has focused on 1-min models [26,27].) This lack of consensus led the current author to test models from two categories. Two univariate models (de Miguel and Erbs [11,15]) and one complex model (Ridley et al. [21,22]) were trialled.
4. Methodology
The method falls into two stages:
- Use the kriging interpolation method to construct a national map of solar irradiation;
- Separate the global horizontal irradiation into two solar components.
It allows the two parts to be performed in either order, i.e., “kriging–decomposition” or “decomposition–kriging”, for the reasons detailed below.
Separation may be performed before interpolation, so that the kriging creates countrywide maps of beam and diffuse irradiation. Alternatively, interpolation may take place first, producing UK coverage of global horizontal irradiation. One or more points may then be selected and the decomposition algorithm applied to synthesise the beam and diffuse components for those locations only. The order in which the steps are performed depends on convenience for the user and the final output required; there is little impact on the eventual accuracy. Burgess [28] found that interpolation before separation gave a smaller mean bias but had no effect on root mean square error (RMSE). Carrying out decomposition to begin with will furnish information on nationwide cloud cover. On the other hand, starting with interpolation can be more expedient. This is so when the user intends to proceed to the next stage and incorporate a transposition model to calculate PoA irradiation, which must obviously always be last, because tilt and orientation are site specific. Just one map of interpolated global horizontal data needs to be loaded and searched for the points of interest, rather than two maps of beam and diffuse values. Moreover, it can be useful to have the interpolation and separation procedures available as two separate packages so that beam and diffuse figures can be estimated directly from original Meteorological Office or University weather station readings. It can be helpful to have the option to use original, non-interpolated data when the place under investigation is very close to a pyranometer position. For instance, it is only 2.2 km from the site of a proposed new solar farm on the outskirts of Loughborough to the University where irradiation is recorded.
5. The Kriging Stage
This section of the paper details the data, software, models and parameters employed by this research for kriging hourly global horizontal irradiation nationally for the UK. The results are validated and displayed.
Initially the four inter-related steps involved in kriging are elaborated: (1) calculate the empirical variogram; (2) fit a model; (3) create the matrices; and (4) make a prediction. The distinct forms of kriging are discussed and ordinary kriging is determined upon by an evaluation of the features of the different algorithms. Its precise mathematical structure (semi-variogram) is singled out by comparing the results of five ways of deciding (matching spatial autocorrelation, data visualisation, manual fitting of semi-variograms, cross-validation and ability to represent reality). Semi-variogram parameters are automatically fitted. The number of input points is prescribed by RMSE. Both pragmatic and scientific methods of specifying output pixel size were trialled before accepting an approximation guideline dictated by time and processing limits.
Eventually the following kriging model is chosen: ordinary kriging, exponential semi-variogram, automated parameters, all input points, 2.5 km grid. This is validated by leave-one-out cross validation and kriging variance. The results are then meaningfully classified for presentation as thematic maps.
5.1. Current Progress in the UK and Europe
Very little research has been published on the subject of selection of appropriate interpolation techniques for solar insolation in British weather conditions. A literature review discovered just two references [28,29], both of which prefer kriging to IDW. Turning to Europe, research on this topic has taken place in regions with rather different climates to the UK. Alsamamra et al. [30] employed residual (related to universal) kriging in the complex mix of climatic types which exist in southern Spain; Bezzi and Vitti [31] used universal kriging in an alpine region of Italy, whilst Caglayan et al. [32] chose universal kriging in Turkey because of the robust average annual trends displayed by global solar radiation in that country. The tangential topic of spatio-temporal kriging has been covered by [33,34,35].
5.2. Data and Software
The UK Meteorological Office currently has a network of approximately 85 automatic weather stations throughout the UK which observe irradiation as well as other meteorological conditions. The data is aggregated to hourly timestamps before being made available for public use as the MIDAS (Meteorological Office Integrated Data Archive System) database hosted by the British Atmospheric Data Centre (BADC) of the Centre for Environmental Data Archival [36].
Two software packages were used in the kriging research phase. ArcGIS (ArcGIS Desktop: Release 10, Environmental Systems Research Institute (ESRI), Redlands, CA, USA) was used for exploration and visualisation of initial results. It contains a good range of interpolation models. Once the technique was worked out, the free, open-source R software (automap package, Version 3.3.2, R Foundation for Statistical Computing, Vienna, Austria) was preferred for automatic processing and because it is easy to parallelise for big data.
5.3. Kriging Operations
Kriging comprises an initial data exploration, followed by a predictive process. The empirical semi-variogram of the input data is plotted. This is the first use of data to estimate the spatial dependency of the data. Afterward, the theoretical semi-variogram is fitted to the points forming the empirical semi-variogram. This is a second use of data to predict values at unsampled locations.
In kriging, the estimations, i.e., output grid pixels Ẑ, are calculated as weighted averages (Wi) of known input point values (Zi) (Equation (1)):
W is based on autocorrelation measures (semivariance), that is, the weight of each point decreases as distance to the point increases. A number of processes are involved:
- (1)
- Construct the empirical semi-variogram (see Section 5.5).
- (2)
- Fit a model (see Section 5.6).
- (3)
- For all possible input point pairings, determine the straight-line distance between the points and swap into the chosen theoretical semi-variogram model (see later). Put differently, each point-pair distance is multiplied by the slope of the user-selected semivariance graph. The semi-variogram values obtained fill a data covariance matrix (dcm), to be inverted in preparation for subsequent use (idcm). It is necessary to replace the empirical semi-variogram with a theoretical one to comply with mathematical laws for the kriging equations to be solved.
- (4)
- For each output pixel (Ẑ) whose irradiation value is to be predicted, create a vector of distances between itself and all input points. Again, substitute distance for semi-variance obtained from the semi-variogram graph to create an output pixel semi-variance vector (opsv).
- (5)
- Generate a vector of weight factors (w) by multiplying the inverted input points semi-variogram matrix (idcm from Step 3) by the output pixel semi-variogram vector (opsv from Step 4). This is possible on the grounds that the kriging equation, Ẑ = Sum(Wi × Zi), can be expressed as opsv = w × dcm. Re-arranging the equation gives w = idcm × opsv.
- (6)
- Finally, for every output pixel, calculate the predicted irradiation value by multiplying each entry in the weight factors vector w by the original input point measurements and summing the set of products. In this case, the irradiance recorded at each weather station is multiplied by a weight and the results totalled for 85 locations. The weights have to be recalculated for each output pixel because the distances to the input points (weather stations) constantly change as the algorithm moves on to make the next prediction. The dcm matrix stays the same but opsv and therefore w constantly change.
This is the basis of simple kriging [37].
As highlighted previously, one of the benefits of using this approach is that it enables spatial configuration to be quantified. The error variance is worked out by multiplying the weight factors vector, w (result of Step 5) with the output pixel semi-variance vector, opsv (result of Step 4) and totalling the products. The standard error or standard deviation is the square root of the error variance.
5.4. Forms of Kriging
Having identified kriging as the interpolation method to be used, there is still a convoluted set of choices to be made, summarised in the decision tree in Figure 1.
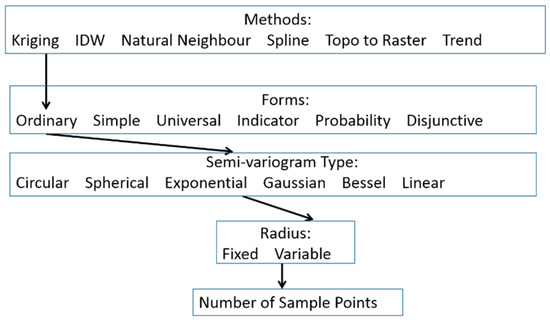
Figure 1.
Interpolation decision tree.
Simple kriging assumes a known mean which frequently poses problems. Unlike simple kriging, ordinary kriging limits the number of points used to calculate the output pixel by dictating a limiting distance and cut-off values for the amount of points. The other forms are far more complex. Universal kriging recognises local trends or drifts, creating a gradually changing lattice overlain by regional limits chosen by the user. Indicator kriging classifies the input variables, as does probability kriging. Neither is suitable for data containing trends. Disjunctive kriging has specific data distribution requirements and entails difficult to justify decisions. The trends existing in solar irradiation data are elaborate and defy straightforward explanation (see Appendix for example). This rules out universal kriging which needs elementary dominant trends. Ordinary kriging is generally applicable and is the most commonly used form of kriging. It is the default choice and should be accepted unless there is a strong mathematical rationale for doing otherwise [38].
5.5. Semi-Variogram Type
As indicated above, kriging partitions the spatial variation of natural phenomena into three: a deterministic trend or drift; a random spatially correlated element; and uncorrelated noise [39]. The characteristics of spatially correlated part may be drawn by the semi-variogram relation. The object is to select the optimal values for interpolation weights. The semi-variogram is constructed as follows:
- (1)
- Measure the distance between two locations.
- (2)
- Reckon half the difference squared between the values at the locations. On the x-axis is the distance between the locations (or simplified distance, grouped into lag bins, h), and on the y-axis is the difference of their values squared, i.e., the semivariance, y(h). Thus, for the purposes of this research, x = distance in km, whilst y = [(irradiation at location i − irradiation at location j)2] ÷ 2.
There are several theoretical semi-variogram models (e.g., spherical, exponential, gaussian). Bailey and Gatrell [40] give details of the graphs and equations. The parameters of the theoretical semi-variogram (drawn in Figure 2) must be optimised to obtain the best fit to the empirical.
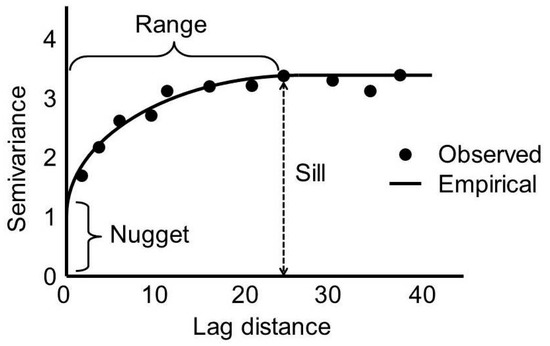
Figure 2.
A typical example of semivariogram showing different components (Creative Commons [41]).
As point-pair distances on the semi-variogram plot increase (proceeding to the right of the x-axis), spatial dependency decreases, until it reaches a value (the range) where the graph flattens and it ceases entirely. The value of semivariance on the y-axis at which this event occurs is called the sill. In theory, points at the same location should have identical values (e.g., of insolation). Therefore, the plot should pass through (0,0) on the axes. In actual fact, the intercept occurs at a low value on the y-axis, known as the nugget. This represents spatially uncorrelated random noise in the data such as measurement errors. The names of the semi-variogram parameters are gold-mining terms, reflecting the historical origins of kriging.
5.6. Choice of Theoretical Semi-Variogram and Optimisation of Parameters
Advice on how to fit a model to an empirical semi-variogram varies. Bohling [42] describes the exercise as “more of an art than a science” and is of the opinion that because empirical semi-variograms routinely contain errors and corrupt data, model selection may be influenced by subjective judgment. In an attempt to avoid bias, the author has identified five different methods of selecting a model. The results of applying these to irradiation data are detailed in Section Appendix A.2 and summarized in the next section.
The semi-variogram has about a dozen forms. Not all of these are recommended. Several authors including Herzfeld [43] state that only positive-definite models should be used. Positive definiteness means the kriging equation can be solved and kriging variance is positive [44]. This characteristic is hard to prove.
The four positive definite models are:
- (1)
- Spherical: this plot is linear close to the origin, making it suitable for the depiction of phenomena with close range variability. It demonstrates a progressive decrease of spatial autocorrelation until it reaches the sill (top of the semi-variogram curve), where autocorrelation is zero.
- (2)
- Exponential: this is also linear near the origin but the exponential model differs from the spherical in that it approaches the sill gradually. Autocorrelation only ceases at infinity.
- (3)
- Gaussian: the gaussian model traces a parabolic curve at the origin, representing smoothly varying properties. Like the exponential, it rises gradually to a straight sill at infinite distance.
- (4)
- Linear: this model resembles the side of a trapezoid. It factors in a cease in autocorrelation between point-pairs at a determinable distance.
5.6.1. Summary of Variogram Selection
Table 1 sums up the findings of the various methods of fitting a suitable semi-variogram model (see Appendix A.2 for details). It can be seen that the exponential model receives slightly more recommendations. It is reliable, produces a detailed surface and is endorsed by the well-documented cross-validation method. For this reason, large quantities of results were generated with this model.

Table 1.
Results of five methods of selection of theoretical semi-variogram.
5.6.2. Setting Parameter Values
Having specified the model, the parameters of the semi-variogram curve (nugget, range and sill) need to be given values which minimise deviation from the empirical points. According to the literature, parameter values can best be set manually, next best by cross-validation. However, the object is to avoid going through thousands of variograms assessing the fits by eye or comparing large statistical datasets. For this reason, the autofitVariogram technique from R software is employed. This calculates parameters as follows:
- Sill—the mean of the maximum and median semi-variance values;
- Range—0.1 multiplied by the value read from the diagonal of the bounding box of the map;
- Nugget—the minimum of the semi-variance.
Another necessary decision is: should the output value for each location be determined using all the input points or a specified number? Guidance in the literature ranges from a minimum of 20 points to 100 points. Experimentation revealed that using fewer points (e.g., 10) creates a surface which is, to some extent, more detailed than using all 85 weather stations. However, the more points used, the lower the RMSE. Therefore, since there was access to sufficient computer processing power, the eventual maps were calculated using all the input points.
The final decision regards the output grid cell (pixel) size. Cell size needs to be detailed enough for future analysis whilst being feasible because this is a computationally demanding algorithm. Naturally, there is a considerable effect on results, depending in which pixel the point of interest falls. As with most kriging decisions, there is no preferred method of selecting a suitable grid resolution for output maps. The results of applying several methods to the irradiation data are outlined in Table 2.

Table 2.
Results of five methods of Selection of Grid Resolution. ESRI: Environmental Systems Research Institute.
Pixel size varies from 1 km to 5 km. There is a need to balance processing time against accuracy. The 1 km map, although possible, did take some time (overnight with ArcGIS for one map) to generate. Therefore, the 2.5 km cell size was decided on as a trade-off between time and detail (10 min with ArcGIS for one map).
5.7. Synopsis of Kriging Decisions
It is comparatively easy to choose kriging options manually for one data set but circumstances dictate that a compromise solution, capable of fitting thousands of hourly datasets, is needed for automated processing. The selections detailed above are presented as suitable for this purpose. Unlike much research employing kriging which simply accepts default options (usually the spherical model), here all choices are scientifically justified to achieve optimal results.
The problem is that there is no “gold standard” solar irradiation map to enable comparison of generated surfaces. Insolation is recorded at comparatively few locations. RMSE can only be estimated for these locations but modelled values can show over 100 Wh/m2, i.e., about 10% difference between weather stations. On the other hand, kriging does have the advantage that it provides the ability to calculate error variance. This provides an indication of where on the map the interpolated values are least trustworthy.
There are more refined statistical techniques for prediction at points without data [38] but these are labour intensive, involving up to four different error calculations for each hourly dataset. After an initial trial, it was found impossible to validate output for thousands of prediction surfaces by this method. The simpler statistics described in the Appendix and viewing videos of results were preferred.
If there were plenty of well-dispersed weather stations (about 200 for the UK), the choice of kriging model and parameters would be less important but this is not the case. Consequently, kriging options must be carefully selected since they exert a noticeable influence on output. In conclusion, the chosen kriging options are ordinary kriging, exponential semi-variogram, sill and nugget from semi-variance, range from map size, all sample points, 2.5 km grid.
5.8. Success of the Kriging Choices
Interpolation methods can be validated using three techniques: data splitting, cross validation and calculation of the kriging variance [46]. Data splitting cannot be carried out for the UK irradiation data because the number of observations is relatively low and the weather stations are not evenly dispersed. Therefore, cross validation was scrutinised.
The input data was 51,164 hourly global horizontal solar irradiation datasets for 2005–2014 from MIDAS (all the daylight hours for this period). Kriging took approximately 35 h of actual computer time using an i7 32 GB computer (8300 CMT, Hewlett Packard, Palo Alto, CA, USA) parallelised on all eight cores.
Averaged over the period 2005–2014, the kriging process yields an average hourly cross-validation RMSE of 56 Wh/m2 (11%) and an average maximum cross-validation RMSE of 211 Wh/m2 (42%). This compares very favourably to PVGIS (yearly average cross-validation RMSE 146 Wh/ m2/day (4.5%)).
Kriging variance is estimated between measurement locations. It provides a spatial view on the measure of success [46]. In the case of MIDAS data, 50% of the UK has high kriging variance. Standard kriging error increases by approximately 50 Wh/m2 every 25–30 km distance band from the nearest weather station.
Having examined uncertainty, output surfaces can at last be displayed. Even this requires decisions. The rasters exhibit a wide range of unique values and must be classified for viewing. This is a seemingly trivial exercise but there are innumerable choices of symbolisation. The author has found that over-simple classification can result in as much loss of detail as a large cell size or a smoother kriging model.
The majority of the datasets contain uniformly distributed values, so an equal interval classification method is appropriate. Matlab jet colour scheme is familiar to the intended audience. The audience are accustomed to interpreting complex issues, hence a fairly large number of classes may be used. Sturge’s rule (class number = 1 + 3.3log(Number of Observations)) suggests seven classes. Experimentation showed that more than nine classes may be confusing if weather patterns are fragmented rather than trending. In the event, it was found convenient to divide the kriged hourly global horizontal irradiation data in 12 equal classes of 100 Wh/m2 each, representing a maximum hourly annual range in the UK of 0–1200 Wh/m2. In practice, only six bands at most appear in one hourly map. That is, in any one hour, global horizontal irradiation is no more than 600 Wh/m2 greater in Cornwall than in Scotland. Figure 3 illustrates a small sample of the 51,164 surfaces created by this technique. Figure 4 is the average of the 5045 hourly irradiation maps for 2013. This masks hourly variations and results in the southwest to northeast irradiation trend expected of Great Britain.
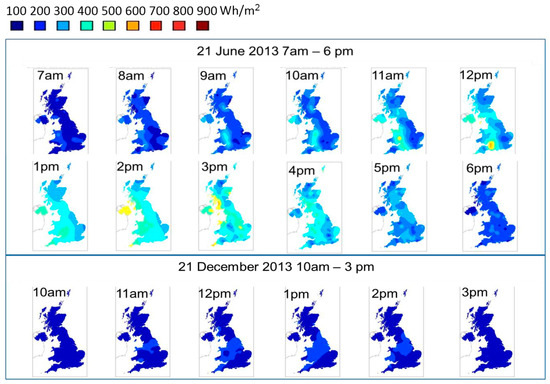
Figure 3.
Kriged hourly global horizontal irradiation (bands of 100 Wh/m2) of two sample days (21 June 2013 and 21 December 2013).
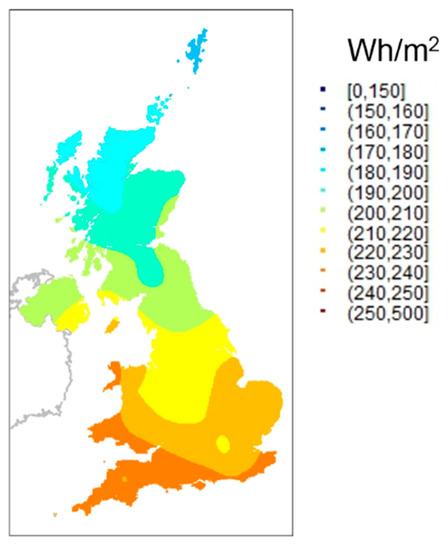
Figure 4.
Average hourly global horizontal irradiation for 2013.
6. The Separation Stage
The plan was to obtain measured values of global horizontal, beam and diffuse irradiation. A series of models was then applied to generate beam and diffuse irradiation from the measured input global horizontal. The models were as follows. First, the Strous equation [47] was employed to generate the solar declination angle which is an input to the separation model. Next, the Erbs et al. [15], De Miguel et al. [11] and Ridley et al. [21,22] separation models were tested. The diffuse values calculated by these models were compared to the measured diffuse values using the mean bias error (MBE) and RMSE statistical techniques. The separation model achieving the closest match to measured values (i.e., lowest errors) was selected.
6.1. Data
The component parts of irradiation are recorded at just a few Principal Radiation Stations using a pyranometer fitted with a ring that obscures the sun. Following automation about 10 years ago, there are just two of these stations in the UK: one at Camborne, east of St Ives Bay in Cornwall, and one at Lerwick, capital and main port of the Shetland Islands. The UK Meteorological Office operates Kipp and Zonen AP2 trackers with instruments measuring horizontal global, horizontal diffuse, planar direct, and downwelling longwave irradiation at these two sites. The data is recorded at minute intervals and archived by the Baseline Surface Radiation Network (BSRN, http://bsrn.awi.de/). In order to be compatible with the hourly MIDAS data employed for kriging in this research, hourly aggregated means from the Global Atmosphere Watch (GAW) dataset at the World Radiation Data Centre (WRDC) in St Petersburg (http://wrdc.mgo.rssi.ru/) were utilised. Hourly data for 2013 was downloaded.
This research would like to investigate nationwide applicability of decomposition models. Therefore, data from the recently commissioned Solys 2 Solar Tracker at Loughborough University was also used to test beam/diffuse split calculations. Although only available for one year (19 March 2015 to April 2016), this data is compatible with that of the UK Meteorological (Met.) Office, since the new pyranometer provides WMO-GAW-BSRN level performance. The data is recorded at one second intervals and was aggregated to hourly values to match the publicly available Camborne and Lerwick data. Hence, data has been obtained for sites in the north, centre and south of the country.
6.2. UK Weather
The UK has a temperate maritime climate. On the other hand, it is famous for its variability. In addition to this, different parts of the UK have slightly different regional climates:
- (1)
- North West—cool summer, mild winter, heavy rain;
- (2)
- North East—cool summer, cold winter, moderate rain;
- (3)
- South East—warm summer, mild winter, light rain;
- (4)
- South West—warm summer, mild winter, heavy rain.
The south coast receives the greatest number of sunshine hours and insolation despite the longer summer days in the north. This is due to southern coastal areas being more likely to be freed of cloud cover by the prevailing south west wind.
The available Met. Office data falls into two of these regional climatic zones (Camborne in the South West and Lerwick in the North East). Loughborough has less rain than either Camborne or Lerwick. Is has less sunshine hours and is colder than Camborne but is sunnier and warmer than Lerwick. Therefore, a check was carried out to discern if the same models fitted all locations.
6.3. Software Employed for Decomposition Models
There are several high-level languages, equally suitable for this research, e.g., Matlab and Python. However, the decision was taken to employ R software (package solaR), primarily because it was already in use in this project. R is used for meteorological modelling by National Aeronautics and Space Administration (NASA), National Oceanic and Atmospheric Administration (NOAA) and United States Geological Survey (USGS).
6.4. Irradiation Component Separation Models
The decision has been taken to trial two univariate (Erbs et al. [15] and De Miguel et al. [11]) and one multivariate model (Ridley et al. [21,22]), these being the intra-daily algorithms available in the chosen modelling language. (Model details in Section Appendix A.3). We refer to them from now on as EKD (Erbs, Klein, Duffie), CLIMED and BRL (Boland, Ridley, Lauret) to comply with R conventions. All three correlate between the clearness index and the diffuse fraction. The clearness index is the ratio between global horizontal irradiation measured on the earth’s surface and calculated extra-terrestrial horizontal irradiation at the top of the atmosphere. That is, it is the fraction of extra-terrestrial horizontal irradiation which penetrates earth’s atmosphere. It depends on cloud cover and may range from 0.8 under clear blue skies to practically zero when conditions are overcast. Another factor is the latitude. The UK has relatively high latitudes and therefore may be expected to have a low clearness index because of the longer distance the sun’s rays must travel through the atmosphere under large zenith angles (Table 3).

Table 3.
Zenith angles for Camborne, Loughborough and Lerwick.
6.5. Results of Irradiation Component Separation Models
Table 4 shows the MBE and RMSE between the calculated global horizontal diffuse irradiation delivered by each separation model and the WRDC/Loughborough Solys 2 measured value. Irradiation values of less than 100 Wh/m2 were filtered out to avoid the inherent inaccuracy in low radiation values. It may be seen that the BRL model delivers the lowest errors for UK locations. This is probably because it has been found to be less dependent on the zenith angle than the other models [28].

Table 4.
Mean bias error (MBE) and root mean square error (RMSE) between modelled global horizontal diffuse and World Radiation Data Centre (WRDC)/Loughborough measured value. BRL: Boland, Ridley, Lauret; CLIMED: Climatic Synthetic Time Series for the Mediterranean Belt; and EKD: Erbs, Klein, Duffie.
Plotting all of the modelled values (Figure 5) discloses the tendency of each one of the models to underestimate diffuse values, especially during non-winter months (April to October inclusive). Thus, there remain opportunities for enhancement of even the best performing algorithm. The seasonal effect is probably due to the fact that radiation values increase in the summer, therefore the discrepancy between measured and modelled values is intensified because percentage differences result in higher unit values. The BRL model delivers implausibly low values under clear sky conditions; however, in the UK, these most frequently occur in February and March because cold air cannot hold as much moisture as warm air can. In early spring, irradiation values are reduced in any case.
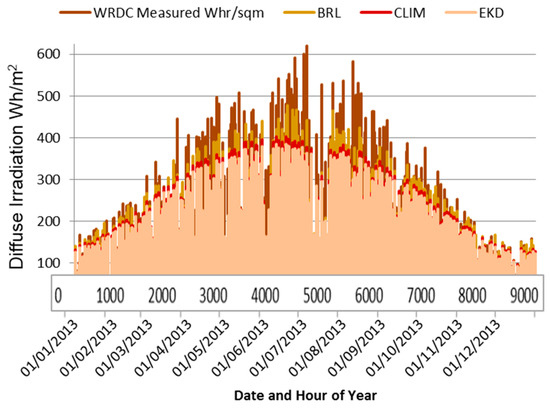
Figure 5.
Comparison between Diffuse Irradiation values from three separation models and measured values: Camborne 2013.
This graph also displays the results of the BRL model following the measured values more closely than any other calculated outcomes.
There are only small differences in performance between any of the models, that is, a maximum of 14 Wh/m2 MBE, 12 Wh/m2 RMSE. These errors may possibly be within the range of pyranometer uncertainty. Despite the minor variations in calculated results, it is still necessary to select the separation technique logically, in order to deliver the required data for PV performance modelling. BRL has been identified as the procedure which most accurately reproduces measured values. This finding is to some extent predictable because it is a universal algorithm, whilst the EKD equation was fitted to US data and the CLIMED to Mediterranean information. Given the regional climate of Lerwick, it is reasonable that the CLIMED equation would not be suitable. It is useful to note from the researcher’s point of view, that the same model is effective for all UK sites tested.
7. Combination of Stages
The following interpolation/separation model combination generates the most accurate results for UK-wide data input and therefore is recommended for PV performance modelling in the UK: ordinary kriging with exponential semi-variogram/BRL separation. Hourly and average annual national maps are produced for five years (2009–2014) for the UK using these algorithms.
Examples of the results of combining the interpolation and separation procedures are given in Figure 6 and Figure 7. Figure 6 presents diffuse irradiation calculated from the kriging/BRL sequence for one location (Loughborough), whilst Figure 7 shows calculated national diffuse irradiation for the UK.
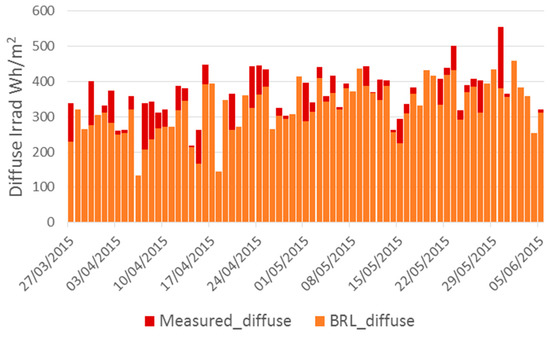
Figure 6.
Diffuse irradiation at Loughborough: Solys 2 measured value compared to calculated value. Calculation by interpolation of hourly global horizontal irradiation from Met Office weather stations (Meteorological Office Integrated Data Archive System (MIDAS) data) followed by application of the BRL model to separate out the diffuse value. (10 weeks, from the end of March 2015 to mid-June 2015 illustrated).
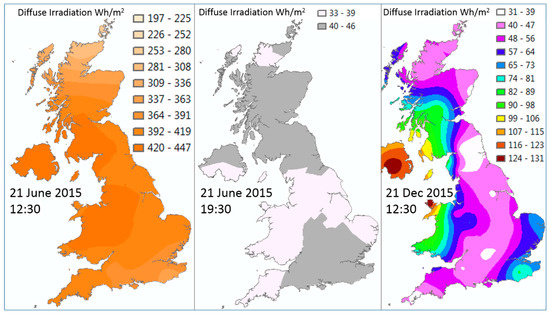
Figure 7.
Diffuse irradiation UK-wide: produced by application of the BRL model to separate the diffuse value from global horizontal irradiation provided by Meteorological (Met.) Office weather stations (MIDAS data).
Figure 6 again indicates the underestimation of the BRL model. Figure 7 gives three examples of national maps of calculated diffuse irradiation values. The June midday map displays high values. The June evening and December midday maps are instances of when sun elevation and therefore irradiation are low. The December map has higher values than the June evening because diffuse irradiation comprises a higher fraction of the total irradiation in the winter. This is particularly so in a high latitude, cloudy location such as the UK.
RMSE values for both the single location and national application were determined. The kriging RMSE for Loughborough was 80 Wh/m2, generated from a dataset of April–December 2015 inclusive. This being a period when both Solys 2 and Met. Office data are available. The overall combined RMSE for Loughborough (from data produced by kriging and the BRL model in sequence and compared to Solys 2 measured diffuse values) was 42 Wh/m2.
The national RMSE of the kriging and separation stages together may be estimated by combining the individual errors as follows (Equation (2)):
Using the kriging interpolation algorithm, national average (56 Wh/m2) and average of Lerwick, Camborne and Loughborough sites’ RMSE for the BRL separation model (64 Wh/m2 calculated from values in Table 4); the expected composite UK national RMSE on an hourly time step is 86 Wh/m2. The separation stage is responsible for more than half (54%) of the overall error. These results compare well to related work. Burgess [28] obtained a composite RMSE of 46% following comparison of sequential application of IDW interpolation, EKD separation and Perez transposition [48] models to measured data for one site in Cornwall.
Considering the succession of the kriging and BRL models used in this research, the underestimation of the decomposition model tends to balance out the overestimation of the interpolation, giving a lower combined error.
8. Conclusions
This research has presented a method for accurate derivation of horizontal diffuse solar irradiation from publicly available data. The procedures selected are applicable for both single locations and UK-wide. Prior to this work, publicly accessible diffuse irradiation data was only obtainable in the form of measured data for just two sites in the UK. The complete irradiation interpolation and beam/diffuse separation sequence described here is fully validated with one year’s measured data.
There are many possible models and model parameters for both the interpolation and separation stages. This work describes how to make a scientific selection. Ordinary kriging was decided upon because it is compatible with the characteristics of solar radiation in the UK. The exponential semi-variogram was chosen for kriging as it results in the lowest cross-validation RMSE. Kriging offers flexibility in terms of input and output data and can generate prediction error maps. The disadvantage is that it also demands a lot of decision-making. There is a large quantity of advice on offer as to how to make those decisions. Some of this guidance is scientific, some pragmatic. It is not clear what is the most appropriate for particular circumstances. This research experiments with a wide range of methods to make the most suitable choices. This is in contrast to the majority of work involving interpolation which often relies on default options supplied by the software or program. The error inherent in the statistical processes cannot easily be removed but selection of less than optimal choices can be avoided.
Turning to the separation stage, the BRL model again provided the lowest RMSE. Kriging decisions require a meticulous approach since values at a given UK location may vary by over 100 Wh/m2 depending on kriging model used. The same cannot be said of the separation models since there is little to choose between them in terms of error values. Nonetheless, this research logically determines the model which is employed. This results in a newer alternative being chosen, rather than relying on a usual long-standing choice.
9. Future Work
Although the choice of model is more important for the interpolation stage than for the separation, it is the separation process which contributes most to the overall error of the two-stage methodology. Even so, both stages present possibilities for improvement.
The BRL model could be enhanced, for instance by an atmospheric aerosol loading factor, or by other means. The UK is subject to sea spray aerosols. Additionally, summer anticyclones may result in increased water holding capacity in the atmosphere and elevated mass concentrations of secondary pollutants.
This paper established that standard kriging errors increase with distance from the closest weather station. Therefore, spatial distribution of solar radiation interpolated from ground-based sensor values could be improved by integration with satellite measurements.
Whilst both stages may be further developed, this research demonstrates the systematic selection and application of the most accurate models currently available to produce countrywide diffuse horizontal irradiation for the UK.
Supplementary Materials
Supplementary materials can be found at www.mdpi.com/1996-1073/10/2/181/s1.
Acknowledgments
This work has been conducted as part of the research project “PV2025—Potential Costs and Benefits of Photovoltaic for UK Infrastructure and Society” project which is funded by the RCUK’s Energy Programme (Contract No.: EP/K02227X/1).
Author Contributions
Diane Palmer, Thomas Betts and Ralph Gottschalg conceived and designed the experiments; Diane Palmer analyzed the data; Ian Cole contributed data and analysis tools; Diane Palmer wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Example of Complex UK Solar Irradiation Trend
Figure A1a illustrates how the expected trend of irradiation increasing towards the west of the UK (decreasing Easting) shown in June (graph top left of figure) may reverse, as demonstrated in the January graph (graph top right of figure). The trend plots for the same months (Figure A1b) show trends of irradiation increasing to the south in January as normal (green line in plot lower right of figure) but with lower values in the south in June (green line in plot lower left of figure).
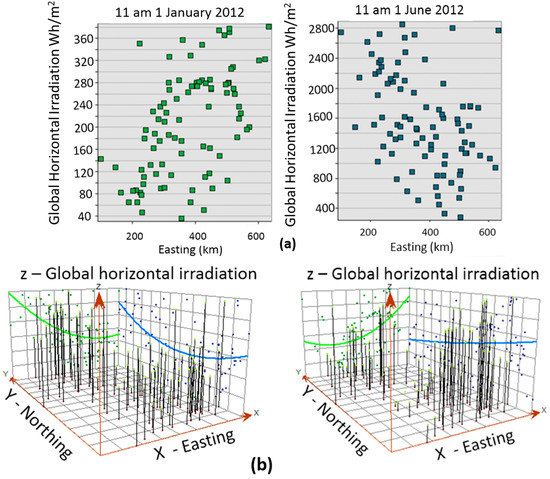
Figure A1.
(a) Graphs and (b) trend plots of global horizontal irradiation (Wh/m2) plotted against Easting of Weather Station (graph) and Easting/Northing (trend).
Appendix A.2. Selection of Theoretical Semi-Variogram Model
Appendix A.2.1. Model Selection Based on Spatial Autocorrelation
Solar irradiance in the UK is renowned for exhibiting rapid local changes as clouds repeatedly obscure and reveal the sun. This suggests that a model with an element of linear behaviour would most nearly mirror reality.
Spatial autocorrelation of solar irradiation has never been investigated for the entire UK. Here, it is explored by constructing the semi-variogram cloud for twelve sample MIDAS datasets. Hourly global horizontal solar irradiation recorded at 11:00 a.m. on the first of every month of 2012. The semi-variogram cloud is a chart of empirical data in raw form (not binned), i.e., half the squared irradiation difference on the y-axis and distance in km on the x-axis. In principle, as the gap between point-pairs increases (further right on the x-axis), the difference between values should increase (bigger value on y-axis). In practice, some point-pairs do manifest these characteristics, as seen in Figure A2 where weather stations at opposite ends of the UK have very different irradiation values. However, this diagram also shows sites close together on the south coast and in the Scottish mountains with large divergences. In other months, this situation also arises in South Wales, Cornwall and Yorkshire. Mountainous areas are noted for their variability. Causes in other areas could be coastal cloud and Yorkshire’s fogs.
Spatial autocorrelation is ceasing at any distance between 25 km and 1000 km. A model capable of reflecting local variation is required. It is reasonable to suppose that a cut-off may be set at the length of the UK (approximately 1300 km, Scilly to Shetland). The linear variogram is not a prudent choice because the sill is reached at a precise point. The slope of the model is needed and slope cannot be determined at a point. Evidence so far supports the adoption of the spherical model.
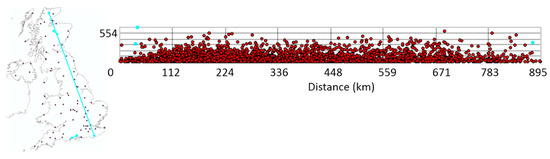
Figure A2.
Semi-variogram cloud of global irradiation for 11:00 a.m. on 1 November 2012. Sites with very different irradiation values (end-to-end of UK mainland, Scottish mountains and south coast) linked by lines on the map and highlighted on the semi-variogram.
Appendix A.2.2. Data Visualisation and Variance
Prediction output surfaces were generated from the spherical, exponential and gaussian variogram models for the twelve datasets from 2012 (36 rasters created). An example of the results (for 11:00 a.m. on 1 January 2012) are shown in Figure A3.
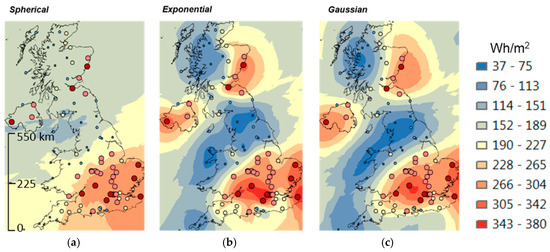
Figure A3.
Output surfaces of hourly global irradiation for 11:00 a.m. on 1 January 2012 produced by three kriging semi-variograms: (a) spherical; (b) exponential; and (c) gaussian.
The resultant grids reveal that the individual models have a large impact on the outcome. The maps manufactured by the exponential and gaussian models are more detailed and show a greater range of irradiation than the smoother spherical raster, indicating these are to be preferred, in contrast to the findings based on spatial autocorrelation.
The spherical algorithm produced a prediction surface for the January example with a range of 212 Wh/m2 between the highest and lowest value. The exponential algorithm created a wider range (343 Wh/m2), with the gaussian falling between the two (300 Wh/m2). The difference between the exponential and spherical surfaces is obvious in Figure A4. The neutral colour represents the lower differences (0–60 Wh/m2). Note these roughly correspond to where the weather stations dots are more clustered. Clustering is displayed by constructing 25 km distance bands around the weather stations. Where these join together, weather stations are closer. Differences are greatest (red in Figure A4, 125–190 Wh/m2) where weather stations are further apart (single, circular distance bands) and in coastal regions.
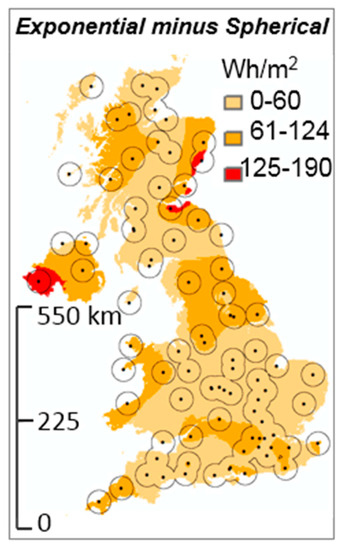
Figure A4.
Difference between the exponential and spherical models of hourly global irradiation for 11:00 a.m. on 1 January 2012.
A more sophisticated way of analysing the effect of the spatial configuration of data points is to study a map of the standard kriging error. This does not quantify uncertainty; rather it is a reflection of the position of the weather stations and does not directly depend on the measurements they take. It scales distance to the nearest weather station by how much irradiation changes between stations. Kriging standard error decreases as measurement points are approached. It is affected by the version of kriging used. The ideal would be a nationwide map of low standard errors. As Figure A5 reveals, this is not so in Great Britain. More than half of the country is subject to substantial kriging variance.
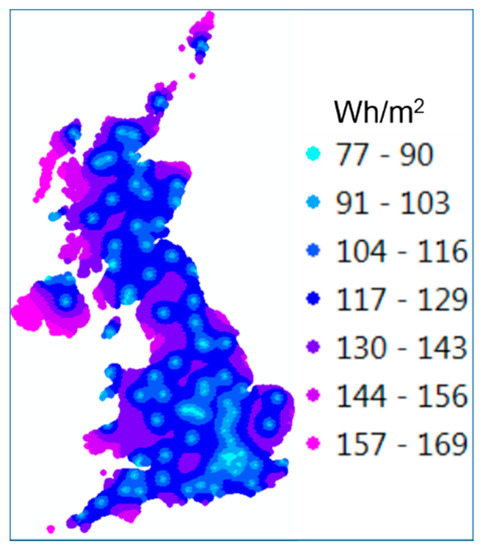
Figure A5.
Kriging standard error (Wh/m2) 11:00 a.m. on 1 June 2012.
Appendix A.2.3. Manual Fitting of Semivariogram Graphs
The semivariogram graph was constructed in its spherical, exponential and gaussian forms for the above-mentioned twelve datasets (i.e., 36 graphs) and scored as to how well each graph fitted the data points. The gaussian model gave the best performance in the majority of cases, with the spherical and exponential forms scoring joint second.
Appendix A.2.4. Cross-Validation
Leave-one-out-cross-validation (LOOCV) was executed on the twelve sample data sets for the three semi-variogram models (spherical, exponential and gaussian). Namely, comparison of the root mean square standardized errors (RMSSE) was carried out as follows (Equation (A1)):
- Remove a known point from data set;
- Use remaining points to estimate the value at the point removed;
- Compare the estimated to known value;
- Repeat for all points and calculate root mean squares.
The method that produces the least difference is selected (RMSSE close to 1).
Looking at the RMSSE for the twelve datasets, the spherical model produces the least difference the most number of times. However, the mean difference between models is only 0.07 and for the September, October and November datasets, RMSSE is identical. In this instance, root mean square standardized error is somewhat inconclusive, so the simplier RMSE was tried (Equation (A2)).
The smaller this error, the better the accuracy achieved. RMSE was calculated for the spherical and exponential models (not gaussian—see next section). The input data was 5022 hourly global horizontal solar irradiation datasets for 2013 from MIDAS. This constitutes all the daylight hours for that year. Exponential gave the lowest RMSE 67% of times (minimum 0, maximum 214, average 57 Wh/m2) and the spherical 33% of times (minimum 0, maximum 237, average 58 Wh/m2). Whilst the average difference between the exponential and spherical RMSE was 0.96 Wh/m2, the maximum was 21 Wh/m2. Larger differences are recorded randomly throughout the year; there is no period when one algorithm performs better than the other. For the most part the exponential model delivers the lowest RMSE. Hence, this analysis recommends the exponential semi-variogram.
Appendix A.2.5. Ability of Model to Represent Reality/Not Fail When Automated
The spherical, exponential and gaussian algorithms were tested with the 5022 hourly global horizontal solar irradiation datasets for 2013. The gaussian model delivered some highly implausible values, albeit for six datasets only. This was discovered by animating the rasters to allow fast visual inspection. For instance, for the dataset relating to 1400 h 21 June 2013, a value of −9000 Wh/m2 was interpolated in the London area. The probable cause was the fact that one London weather station recorded an irradiation value of 46 Wh/m2 whilst the adjacent one is over 400 Wh/m2. In scientific terms, there are outliers in the data that cause high semi-variance at a short distance. These can most likely be explained by rapidly passing clouds.
The algorithms also resulted in the occasional failure due to plotting negative values. One factor which contributes towards this is the distribution of UK weather stations. These are clustered in some areas and widely spaced in others. The exponential model was slightly less likely to fail than the spherical. It resulted in 13 failures in 5022 datasets, as compared to 16 failures by the spherical.
These discoveries lead the author to reject the gaussian model from further consideration. When generating results for thousands of hours of data, unless time-consuming manual checking is undertaken, this risks negative results contaminating the output. The exponential variogram is singled out as it is slightly more reliable.
Appendix A.3. Separation Stage Details
Features of Irradiation Component Separation Models
The EKD and CLIMED models are similar (Table A1). Both employ piecewise linear approaches. They apportion data into three sets depending on the clearness index. For intermediate cloud cover conditions, i.e., varying degrees of broken cloud, a linear trend is used to describe the data. The diffuse fraction decreases and the clearness index increases as the sky clears. For low clearness index conditions (overcast, typical of the UK), a separate linear expression with a much shallower slope is utilised. For cloudless skies, a constant is applied.

Table A1.
Models for deriving the diffuse fraction of horizontal solar irradiation, kd.
| Separation Model | Clearness Index | kd | kt |
|---|---|---|---|
| EKD/Erbs (1982) Model | Low clearness index, completely overcast, almost all irradiation diffuse | kd = 1 − 0.09kt | kd ≤ 0.22 |
| Intermediate | kd = 0.9511 − 0.1604kt + 4.388kt2 − 16.638kt3 + 12.336kt4 | kt > 0.22 or kt < 0.8 | |
| High clearness index, bright, sunny, nearly all irradiation direct | kd = 0.165 | kt ≥ 0.8 | |
| CLIMED/De Miguel (2001) Model | Low clearness index, completely overcast, almost all irradiation diffuse | kd = 0.995 − 0.08kt | kt ≤ 0.21 |
| Intermediate | kd = 0.724 − 2.738kt + 8.32kt2 − 4.967kt3 | kt > 0.21 or kt < 0.76 | |
| High clearness index, bright, sunny, nearly all irradiation direct | kd = 0.180 | kt ≥ 0.76 |
The EKD model was developed with data from five weather stations in the USA, representing a range of climate zones. The CLIMED technique focussed on sites in southern and central Greece, Portugal, France and Spain (North Mediterranean Belt climatic zone). As can be seen in Table 4, the two models differ only in their cut-off values and one is third order polynomial, whilst the other is fourth.
The BRL team adopted a different method. A logistic function gives a smoother data-fitting curve, described by the following single equation (Equation (A3)):
where AST is apparent solar time; α is solar altitude; Kt is daily clearness index; and is persistence factor.
Multiple parameters are inserted into the one equation: hourly and daily clearness indices, solar altitude, apparent solar time and a measure of persistence based on averaging the clearness index over two hours. This model originated in Australia but the authors suggest it has universal applicability. The single equation for all clearness indices overcomes the problem of where to place “cut-offs”, which are location-specific. It is known that the BRL model does not perform well in clear sky conditions when it persistently delivers unrealistically low values for the diffuse fraction. However, uniform blue skies seldom occur in the UK.
References
- Medium-Term Renewable Energy Market Report 2016; International Energy Agency (IEA): Paris, France, 2016.
- National Statistics—Solar Photovoltaics Deployment 29 September 2016; Department for Business, Energy & Industrial Strategy (DBEIS): London, UK, 2016.
- Friesen, G.; Dittmann, S.; Williams, S.; Gottschalg, R.; Beyer, H.G.; de Montgareuil, A.G.; van der Borg, N.J.C.M.; Burgers, A.R.; Kenny, R.P.; Huld, T.; et al. Intercomparison of different energy prediction methods within the European project “performance”—Results on the 2nd round robin. In Proceedings of the 24th European Photovoltaic Solar Energy Conference, Hamburg, Germany, 21–25 September 2009; pp. 3189–3197.
- Zhu, J.; Betts, T.; Gottschalg, R. Accuracy assessment of models estimating total irradiance on inclined planes in Loughborough. In Proceedings of the 4th Photovoltaic Science Applications and Technology, Bath, UK, 2–4 April 2008; Hutchins, M., Pearsall, N., Eds.; Bath University: Bath, UK, 2008; pp. 207–210. [Google Scholar]
- Stackhouse, P.W.; Westberg, D.J.; Hoell, J.M.; Chandler, W.S.; Zhang, T. Surface Meteorology and Solar Energy (SSE) Release 6.0 Methodology Version 3.1.2; National Aeronautics and Space Administration (NASA) Langley Research Center: Hampton, VA, USA, 2015.
- Perez, R.; Seals, R.; Zelenka, A. Comparing satellite remote sensing and ground network measurements for the production of site/time specific irradiance data. Sol. Energy 1997, 60, 89–96. [Google Scholar] [CrossRef]
- Suri, M.; Cebecauer, T. Satellite-based solar resource data: Model validation statistics versus user’s uncertainty. In Proceedings of the American Solar Energy Society (ASES) SOLAR 2014 Conference, San Francisco, CA, USA, 7–9 July 2014.
- Longley, P.A.; Goodchild, M.F.; Maguire, D.J.; Rhind, D. Geographic Information Systems and Science; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Mitas, L.; Mitasova, H. Spatial Interpolation. In Geographic Information Systems Principles Technical Management Application, 2nd ed.; Longley, P.A., Goodchild, M.F., Maguire, D.J., Rhind, D.W., Eds.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Hofstra, N.; Haylock, M.; New, M.; Jones, P.; Frei, C. Comparison of six methods for the interpolation of daily, European climate data. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- De Miguel, A.; Bilbao, J.; Aguiar, R.J.; Kambezidis, H.; Negro, E. Diffuse solar irradiation model evaluation in the north Mediterranean belt area. Sol. Energy 2001, 70, 143–153. [Google Scholar] [CrossRef]
- Liu, B.Y.H.; Jordan, R.C. The interrelationship and characteristic distribution of direct, diffuse and total solar radiation. Sol. Energy 1960, 4, 1–19. [Google Scholar] [CrossRef]
- Gueymard, C.A.; Ruiz-Arias, J.A. Performance of separation models to predict direct irradiance at high frequency: Validation over arid areas. In Proceedings of the EuroSun 2014: International Conference on Solar Energy and Buildings, Aix-les-Bains, France, 16–19 September 2014.
- Gueymard, C.A.; Myers, D. Validation and ranking methodologies for solar radiation models. In Modeling Solar Radiation at the Earth’s Surface; Badescu, V., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 479–509. [Google Scholar]
- Erbs, D.G.; Klein, S.A.; Duffie, J.A. Estimation of the diffuse radiation fraction for hourly, daily and monthly-average global radiation. Sol. Energy 1982, 28, 293–302. [Google Scholar] [CrossRef]
- Orgill, J.F.; Hollands, K.J.T. Correlation equation for hourly diffuse radiation on a horizontal surface. Sol. Energy 1977, 19, 357–359. [Google Scholar] [CrossRef]
- Reindl, D.T.; Beckman, W.A.; Duffie, J.A. Diffuse fraction correlations. Sol. Energy 1990, 45, 1–7. [Google Scholar] [CrossRef]
- Reindl, D.T.; Beckman, W.A.; Duffie, J.A. Evaluation of hourly tilted surface radiation models. Sol. Energy 1990, 45, 9–17. [Google Scholar] [CrossRef]
- Maxwell, E.L. Quasi-Physical Model for Converting Hourly Global Horizontal to Direct Normal Insolation; Solar Energy Research Institute: Golden, CO, USA, 1987. [Google Scholar]
- Perez, R.; Ineichen, P. Dynamic global-to-direct irradiance conversion models. ASHRAE Trans. 1992, 98, 354–369. [Google Scholar]
- Ridley, B.; Boland, J.; Lauret, P. Modelling of diffuse solar fraction with multiple predictors. Renew. Energy 2010, 35, 478–483. [Google Scholar] [CrossRef]
- Boland, J.; Huang, J.; Ridley, B. Decomposing solar radiation into its direct and diffuse components. Renew. Sustain. Energy Rev. 2013, 28, 749–756. [Google Scholar] [CrossRef]
- Gueymard, C.A. Parameterized transmittance model for direct beam and circumsolar spectral irradiance. Sol. Energy 2001, 71, 325–346. [Google Scholar] [CrossRef]
- Yang, D.; Dong, Z.; Nobre, A.; Khoo, Y.S.; Jirutitijaroen, P.; Walsh, W.M. Evaluation of transposition and decomposition models for converting global solar irradiance from tilted surface to horizontal in tropical regions. Sol. Energy 2013, 97, 369–387. [Google Scholar] [CrossRef]
- Gueymard, C.A. Direct and indirect uncertainties in the prediction of tilted irradiance for solar engineering applications. Sol. Energy 2009, 83, 432–444. [Google Scholar] [CrossRef]
- Yang, D. Solar radiation on inclined surfaces: Corrections and benchmarks. Sol. Energy 2016, 136, 288–302. [Google Scholar] [CrossRef]
- Gueymard, C.; Ruiz-Arias, J.A. Extensive worldwide validation and climate sensitivity analysis of direct irradiance predictions from 1-min global irradiance. Sol. Energy 2016, 128, 1–30. [Google Scholar] [CrossRef]
- Burgess, P.A. Analysis of Historical Solar Irradiance Data And Development of A Virtual Pyranometer Method For Real-Time PV Monitoring. Ph.D. Thesis, University of Reading, Reading, UK, April 2014. [Google Scholar]
- Cairns, G.; Burnett, D. Development of a High Resolution Solar Model for the UK. Available online: http://www.grahamcairnsmengproject.weebly.com/interpolation-techniques.html (accessed on 8 May 2015).
- Alsamamra, H.; Ruiz-Arias, J.A.; Pozo-Vazquez, D.; Tovar-Pescador, J. A comparative study of ordinary and residual kriging techniques for mapping global solar radiation over southern Spain. Agric. For. Meteorol. 2009, 149, 1343–1357. [Google Scholar] [CrossRef]
- Bezzi, M.; Vitti, A. A comparison of some kriging interpolation methods for the production of solar radiation maps. In Proceedings of the 6th Italian GRASS Users Meeting, Roma, Italy, 14–15 April 2005; pp. 1–17.
- Caglayan, N.; Ertekin, C.; Evrendilek, F. Spatial viability analysis of grid-connected photovoltaic power systems for Turkey. Int. J. Electr. Power Energy Syst. 2014, 56, 270–278. [Google Scholar] [CrossRef]
- Aryaputera, A.W.; Yang, D.; Zhao, L.; Walsh, W.M. Very short-term irradiance forecasting at unobserved locations using spatio-temporal kriging. Sol. Energy 2015, 122, 1266–1278. [Google Scholar] [CrossRef]
- Yang, D.; Dong, Z.; Reindl, T.; Jirutitijaroen, P.; Walsh, W.M. Solar irradiance forecasting using spatio-temporal empirical kriging and vector autoregressive models with parameter shrinkage. Sol. Energy 2014, 103, 550–562. [Google Scholar] [CrossRef]
- Yang, D.; Gu, C.; Dong, Z.; Jirutitijaroen, P.; Chen, N.; Walsh, W.M. Solar irradiance forecasting using spatial-temporal covariance structures and time-forward kriging. Renew. Energy 2013, 60, 235–245. [Google Scholar] [CrossRef]
- UK Met Office. MIDAS: UK Hourly Weather Observation Data. NCAS British Atmospheric Data Centre 2006. Available online: http://catalogue.ceda.ac.uk/uuid/b4c028814a666a651f52f2b37a97c7c7 (accessed on 17 August 2016).
- Kriging Algorithm. Available online: http://www.spatial-analyst.net/ILWIS/htm/ilwisapp/kriging_algorithm.htm (accessed on 31 October 2016).
- ArcGIS 10 Help 2010; Environmental Systems Research Institute (ESRI): Redlands, CA, USA, 2011.
- Hurley, F. IEHIAS—The Integrated Environmental Health Impact Assessment System 2011. Available online: http://www.integrated-assessment.eu/eu/index.html (accessed on 31 October 2016).
- Bailey, T.C.; Gatrell, A.C. Interactive Spatial Data Analysis; Longman Scientific & Technical: Harlow, UK, 1995. [Google Scholar]
- Biswas, A.; Si, B.C. Model averaging for semivariogram model parameters. In Advances in Agrophysical Research; Grundas, S., Stepniewski, A., Eds.; InTech: Rijeka, Croatia, 2013. [Google Scholar]
- Bohling, G.C. Introduction to Geostatistics and Variogram Analysis. Available online: http://people.ku.edu/~gbohling/cpe940/ (accessed on 31 October 2016).
- Herzfeld, U.C. Atlas of Antarctica: Topographic Maps from Geostatistical Analysis of Satellite Radar Altimeter Data; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Pyrcz, M.J.; Deutsch, C.V. Geostatistical Reservoir Modelling; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Hengl, T. Finding the right pixel size. Comput. Geosci. 2006, 32, 1283–1298. [Google Scholar] [CrossRef]
- Sluiter, R. Interpolation Methods for Climate Data: Literature Review; Royal Netherlands Meteorological Institute (KNMI): De Bilt, The Netherlands, 2009; pp. 1–28. [Google Scholar]
- Position of the Sun 2011. Available online: http://www.aa.quae.nl/en/reken/zonpositie.html#mjx-eqn-eqm (accessed on 31 October 2016).
- Perez, R.; Ineichen, P.; Seals, R.; Michalsky, J.R.S. Modeling daylight availability and irradiance components from direct and global irradiance. Sol. Energy 1990, 44, 271–289. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).