Adjusting the Parameters of Metal Oxide Gapless Surge Arresters’ Equivalent Circuits Using the Harmony Search Method
Abstract
:1. Introduction
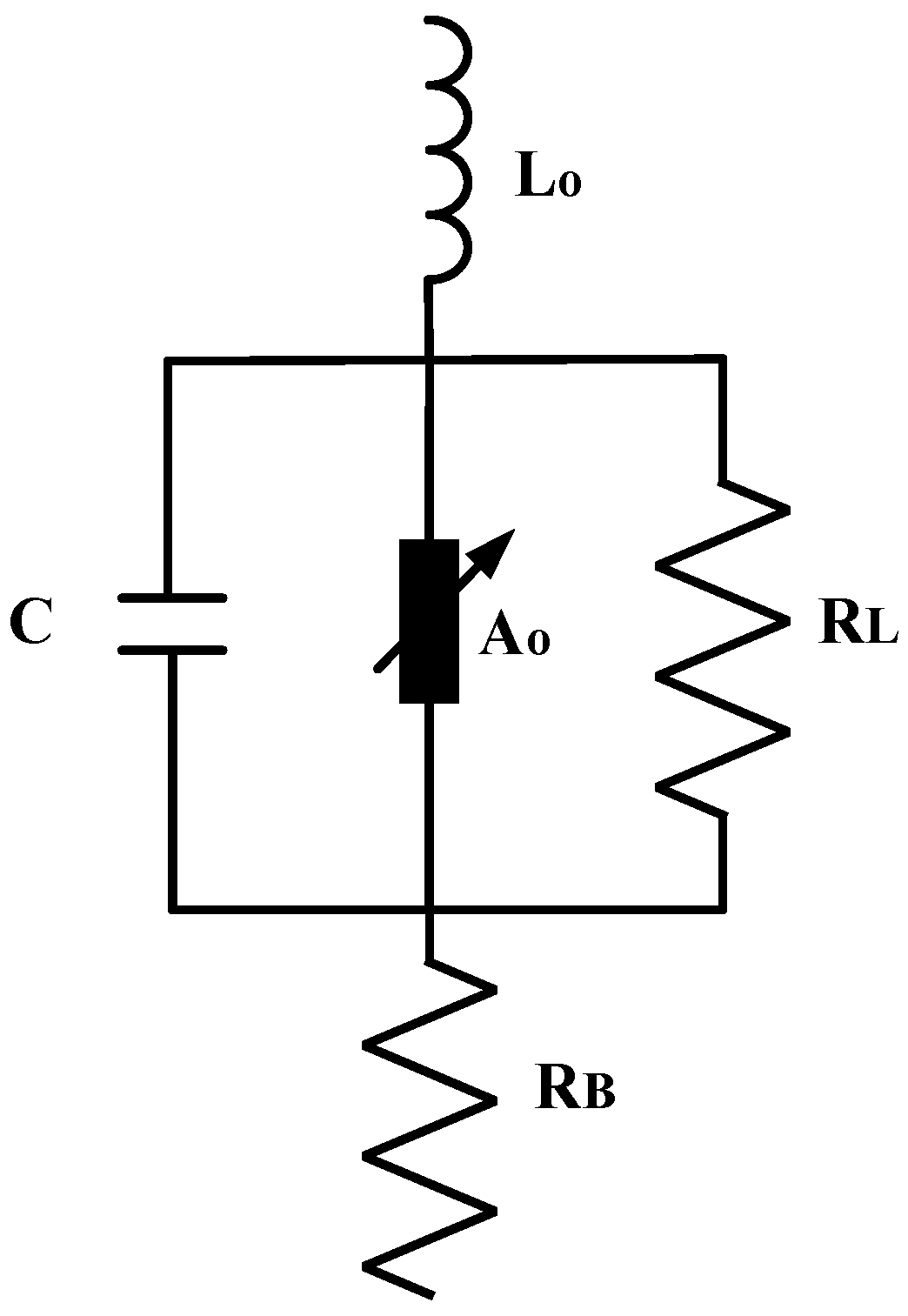
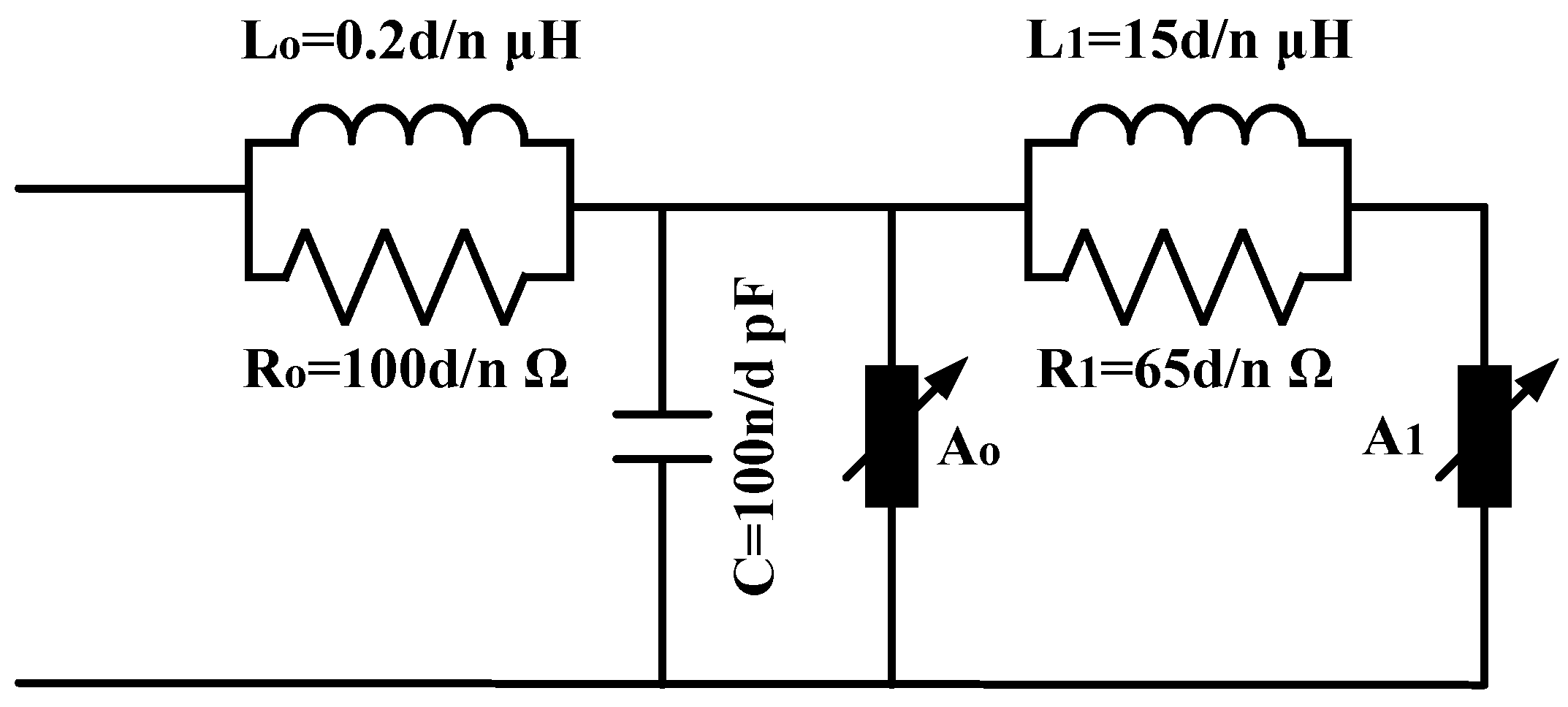
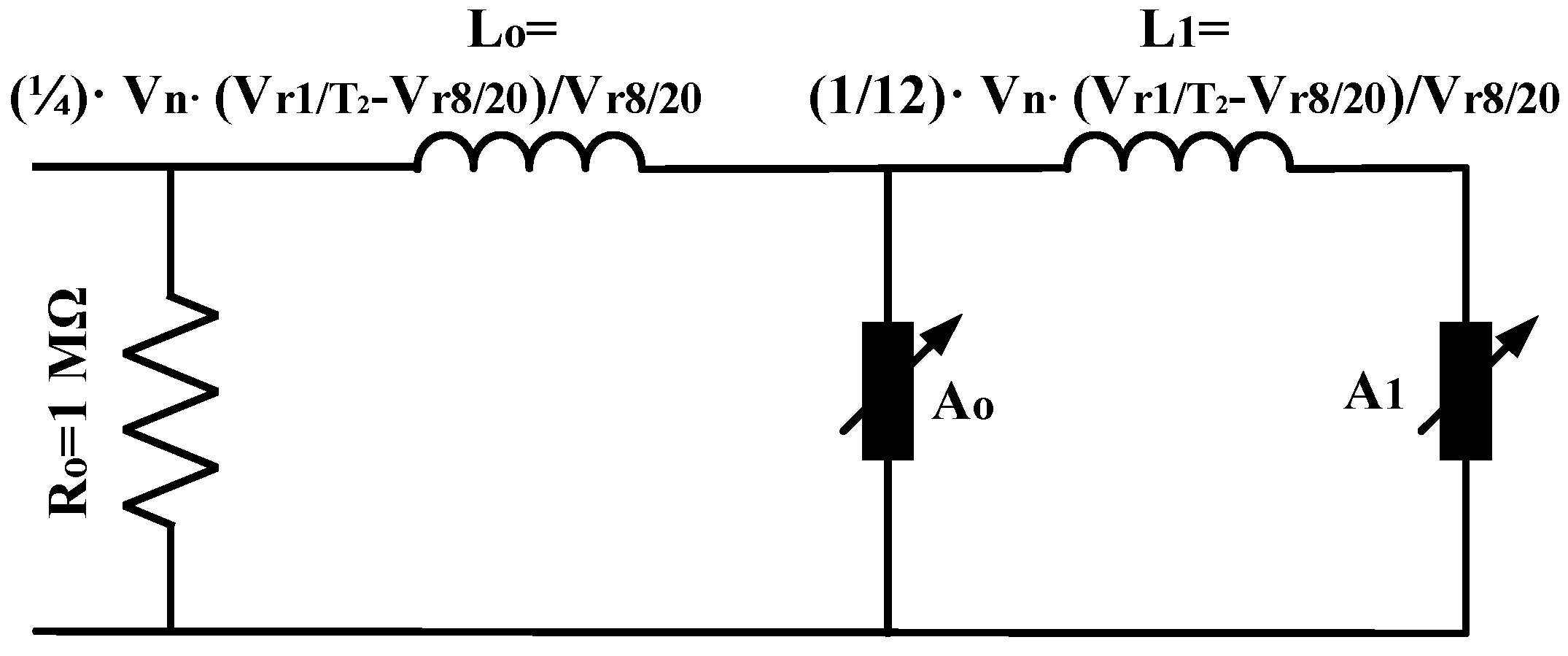
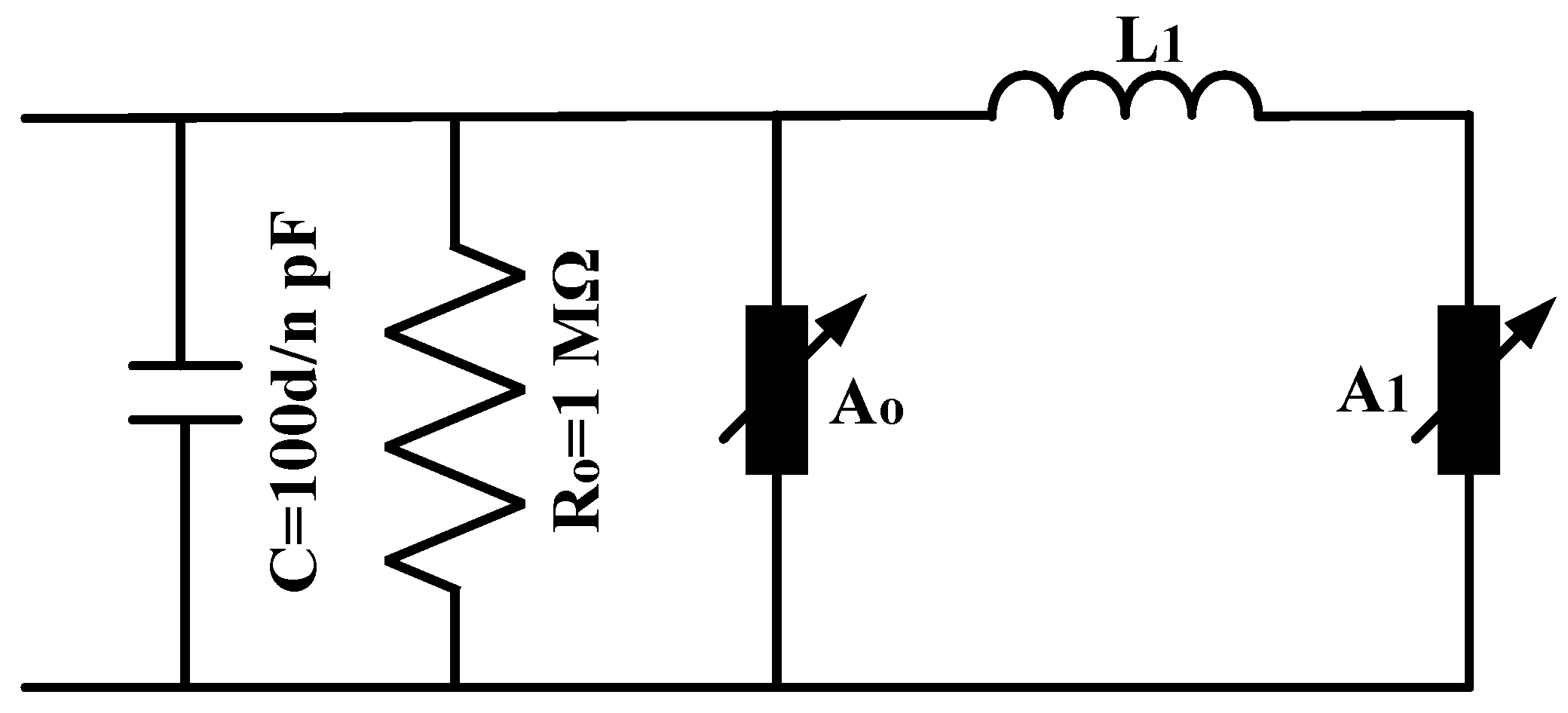
2. Equivalent Circuit Models of Metal Oxide Gapless Arresters
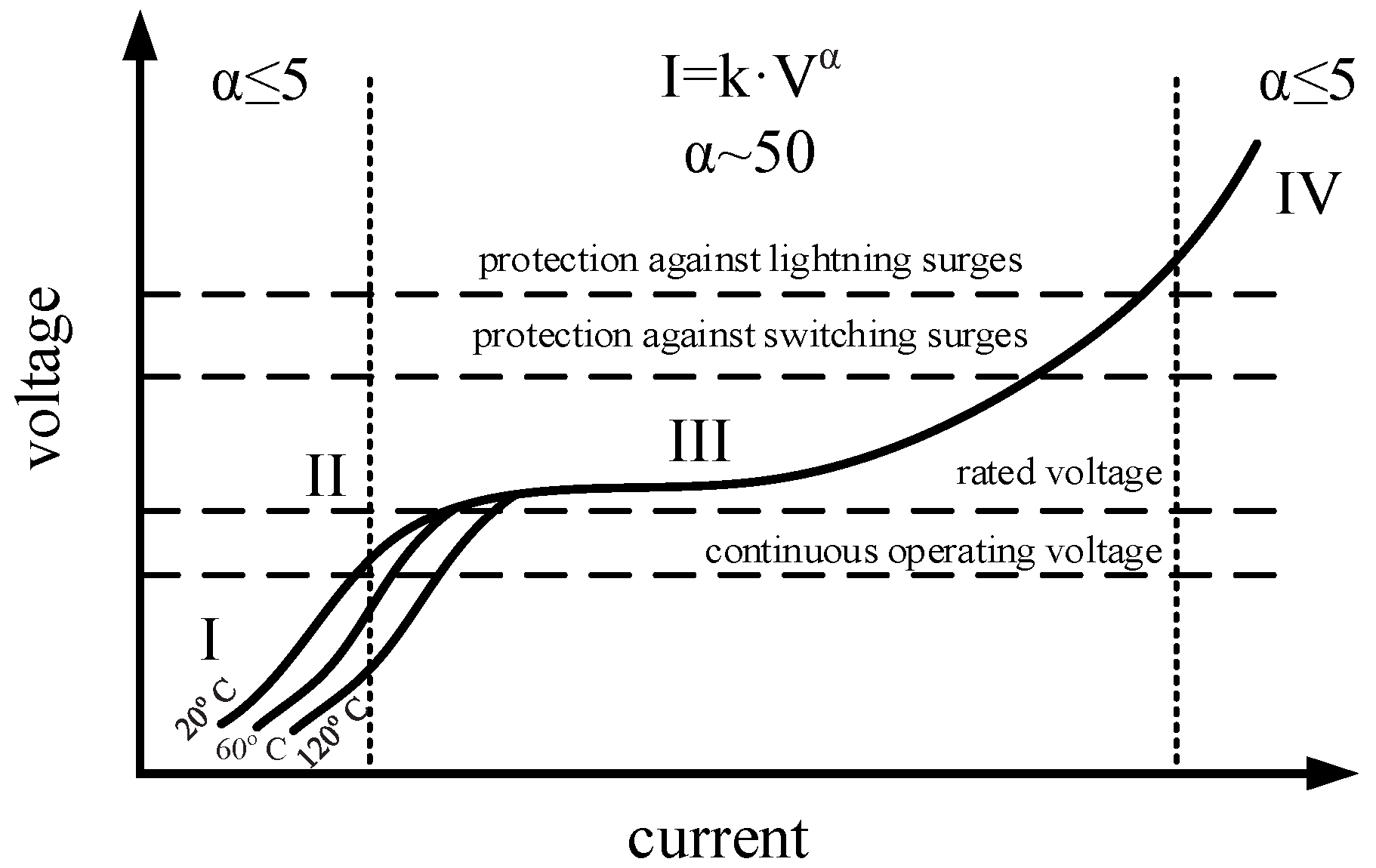
- I is the discharge current that passes through the arrester,
- k is a measure of its current-carrying capacity depending on geometrical configuration and characteristics of the arrester (cross-sectional area, length),
- V is the residual voltage at the terminals of the arrester, and
- α is a measure of non-linearity between V and I, depending on the composition of the oxides.
3. Definition and Analysis of the Optimization Problem
- Vres is the magnitude of the residual voltage of the arrester,
- s is an indicator for the results obtained by simulation procedures,
- m is an indicator for the data provided by the manufacturer,
- I is the injected impulse current (peak value, time),
- i is an indicator that corresponds to the curve of the injected impulse current (i = 1: 8/20 μs, i = 2: 1/20 μs, i = 3: 30/60 μs, i = 4: long duration impulse),
- E is the absorbed energy by the arrester in Joules, given as following:
- u(t) is the waveform of the residual voltage of the arrester,
- i(t) is the waveform of the discharge current that passes through the arrester, and
- is the duration of the injected impulse current.
4. Harmony Search Method
- x is the set of each decision variable xi,
- n is the number of decision variables,
- Xi is the set of the possible range of values for each decision variable, considering lower and upper bounds for each decision variable.
- are randomly generated solutions,
- HMS is the harmony memory size,
- i = 1, 2, …, n, and
- j = 1, 2, …, HMS
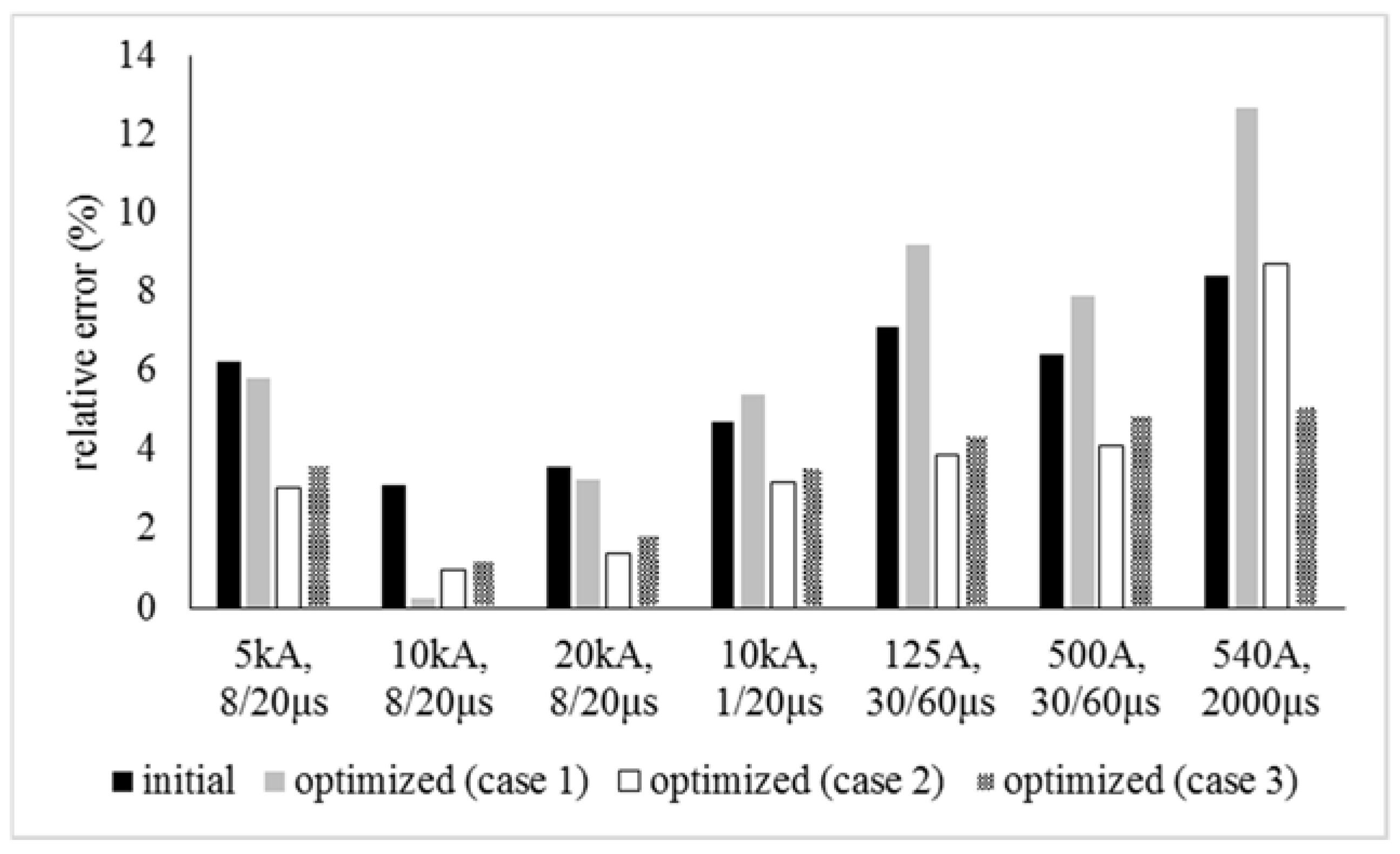
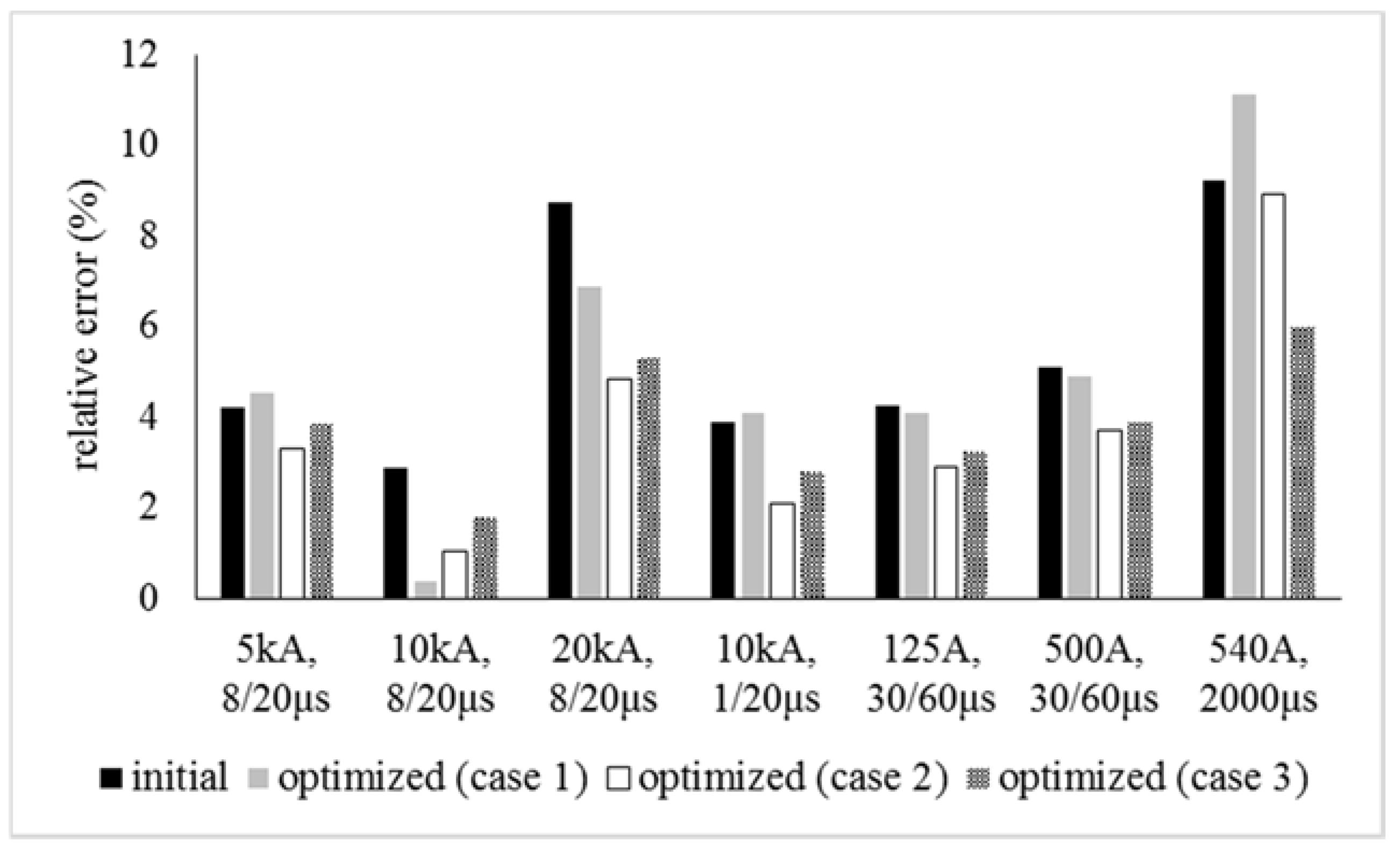
5. Results and Discussion
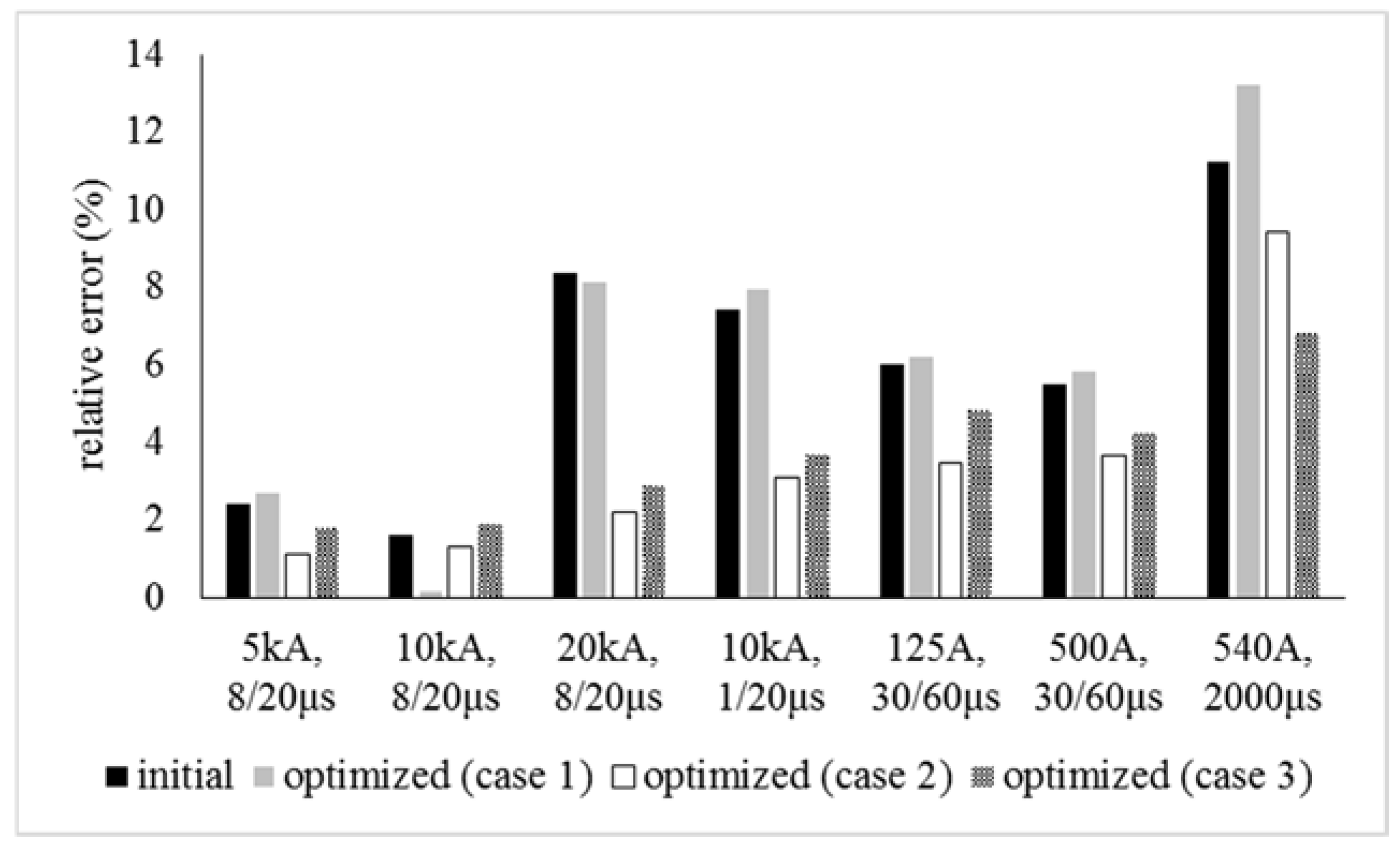
- Case 1: implementation of the algorithm considering the response for a 10 kA, 8/20 μs current.
- Case 2: implementation of the algorithm considering the response for all the current waveforms of Table 1.
- Case 3: implementation of the algorithm considering the response for all the current curves and the energy for long duration impulse of Table 1.
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Agrawal, K.C. Electrical Power Engineering: Reference and Applications Handbook; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Laughton, M.A.; Warne, J. Electrical Engineer’s Reference Book, 16th ed.; Newnes: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Christodoulou, C.A.; Vita, V.; Maris, T.I. Lightning protection of distribution substations by using metal oxide gapless surge arresters connected in parallel. Int. J. Power Energy Res. 2017, 1, 1–7. [Google Scholar] [CrossRef]
- Tarchini, J.A.; Gimenez, W. Line surge arrester selection to improve lightning performance of transmission lines. In Proceedings of the IEEE PowerTech Conference, Bologna, Italy, 23–26 June 2003. [Google Scholar]
- Christodoulou, C.A.; Ekonomou, L.; Fotis, G.P.; Gonos, I.F.; Stathopulos, I.A. Assessment of surge arrester failure rate and application studies in Hellenic high voltage transmission lines. Electr. Power Syst. Res. 2010, 80, 176–183. [Google Scholar] [CrossRef]
- IEEE. IEEE Std 1243-1997: IEEE Guide for Improving the Lightning Performance of Transmission Lines; IEEE: New York, NY, USA, 1997. [Google Scholar]
- IEC. IEC 60099-4: Surge Arresters-Part 4: Metal-Oxide Surge Arresters without Gaps for a.c. Systems, 2nd ed.; IEC: Geneva, Switzerland, 2004–2005.
- IEEE Working Group 3.4.11. Modeling of metal oxide surge arresters. IEEE Trans. Power Deliv. 1992, 7, 302–309.
- Pinceti, P.; Giannettoni, M. A simplified model for zinc oxide surge arresters. IEEE Trans. Power Deliv. 1999, 14, 393–398. [Google Scholar] [CrossRef]
- Ceaki, O.; Seritan, G.; Vatu, R.; Mancasi, M. Analysis of power quality improvement in smart grids. In Proceedings of the 10th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 23–25 March 2017; pp. 797–801. [Google Scholar] [CrossRef]
- Nieto, A.; Vita, V.; Maris, T.I. Power quality improvement in power grids with the integration of energy storage systems. Int. J. Eng. Res. Technol. 2016, 5, 438–443. [Google Scholar]
- Ceaki, O.; Vatu, R.; Mancasi, M.; Porumb, R.; Seritan, G. Analysis of electromagnetic disturbances for grid-connected PV. In Proceedings of the 5th International Conference on Modern Electric Power Systems (MEPS2015), Poland, Wroclaw, 6–9 July 2015. [Google Scholar] [CrossRef]
- Fernandez, F.; Diaz, R. Metal oxide surge arrester model for fast transient simulations. In Proceedings of the International Conference on Power System Transients IPAT’01, Rio De Janeiro, Brazil, 24–26 June 2001. [Google Scholar]
- Bayadi, A.; Harid, N.; Zehar, K.; Belkhiat, S. Simulation of metal oxide surge arrester dynamic behavior under fast transients. In Proceedings of the International Conference on Power Systems Transients 2003, New Orleans, LA, USA, 28 September–2 October 2003. [Google Scholar]
- Christodoulou, C.A.; Ekonomou, L.; Fotis, G.P.; Karampelas, P.; Stathopulos, I.A. Parameters’ optimisation for surge arrester circuit models. IET Sci. Meas. Technol. 2010, 4, 86–92. [Google Scholar] [CrossRef]
- Christodoulou, C.A.; Vita, V.; Ekonomou, L.; Chatzarakis, G.E.; Stathopulos, I.A. Application of Powell’s optimization method to surge arrester circuit models’ parameters. Energy J. 2010, 35, 3375–3380. [Google Scholar] [CrossRef]
- Christodoulou, C.A.; Gonos, I.F.; Stathopulos, I.A. Estimation of the parameters of metal oxide gapless surge arrester equivalent circuit models using genetic algorithm. Electr. Power Syst. Res. 2011, 81, 1881–1886. [Google Scholar] [CrossRef]
- Bayadi, A. Parameter identification of ZnO surge arrester models based on genetic algorithms. Electr. Power Syst. Res. 2008, 78, 1204–1209. [Google Scholar] [CrossRef]
- Nafar, M.; Gharehpetian, G.B.; Niknam, T. Improvement of estimation of surge arrester parameters by using modified particle swarm optimization. Energy 2011, 36, 4848–4854. [Google Scholar] [CrossRef]
- Lira, G.R.S.; Fernandes, D.; Costa, E.G. Parameter identification technique for a dynamic metal-oxide surge arrester model. In Proceedings of the International Conference on Power Systems Transients (IPST2009), Kyoto, Japan, 2–6 June 2009. [Google Scholar]
- Li, H.J.; Birlasekaran, S.; Choi, S.S. A parameter identification technique for metal-oxide surge arrester models. IEEE Trans. Power Deliv. 2002, 17, 736–741. [Google Scholar] [CrossRef]
- ABB: High Voltage Surge Arresters, 5th ed.; ABB: Baden, Switzerland, 2004–2010.
- Suljanovic, N.; Mujcic, A.; Murko, V. Practical issues of metal-oxide varistor modeling for numerical simulations. In Proceedings of the 28th International Conference on Lightning Protection, Kazanawa, Japan, 18–22 September 2006; pp. 1149–1154. [Google Scholar]
- Hinrichsen, V. Metal-Oxide Surge Arresters in High Voltage Power Systems, 3rd ed.; Siemens: Munich, Germany, 2011. [Google Scholar]
- Christodoulou, C.A.; Ekonomou, L.; Mitropoulou, A.D.; Vita, V.; Stathopulos, I.A. Surge arresters’ circuit models review and their application to a Hellenic 150 kV transmission line. Simul. Model. Pract. Theory 2010, 18, 836–849. [Google Scholar] [CrossRef]
- Wang, X.; Gao, X.Z.; Zenger, K. An Introduction to Harmony Search Optimization Method; Springer Briefs in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Omran, M.G.H.; Mahdavi, M. Global-best harmony search. Appl. Math. Comput. 2008, 198, 643–656. [Google Scholar] [CrossRef]
- Lee, K.S.; Geem, Z.W. A new meta-heuristic algorithm for continuous engineering optimization: Harmony search theory and practice. Comput. Methods Appl. Mech. Eng. 2005, 194, 3902–3933. [Google Scholar] [CrossRef]
- Engelbrecht, A.P. Fundamentals of Computational Swarm Intelligence; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Lin, C.J.; Wang, J.G.; Chen, S.M. 2D/3D face recognition using neural network based on hybrid Taguchi-particle swarm optimization. Int. J. Innov. Comput. Inf. Control 2011, 7, 537–553. [Google Scholar]
- Cai, X.; Cui, Z.; Zeng, J.; Tan, Y. Particle swarm optimization with self-adjusting cognitive selection strategy. Int. J. Innov. Comput. Inf. Control 2008, 4, 943–952. [Google Scholar]
- Lee, K.S.; Geem, Z.W. A new structural optimization method based on the harmony search algorithm. Comput. Struct. 2004, 82, 781–798. [Google Scholar] [CrossRef]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
| Rated Voltage (Ur) | 30 kV | ||
| Maximum Continuous Operating Voltage (Uc) | 24 kV | ||
| Nominal Discharge Current | 10 kA | ||
| Line Discharge Class according to IEC 60099-4 | 2 | ||
| Long Duration Current Impulse (2000 μs) | 540 A | ||
| Energy for Long Duration Impulse | 5.8 kJ/kV Uc | ||
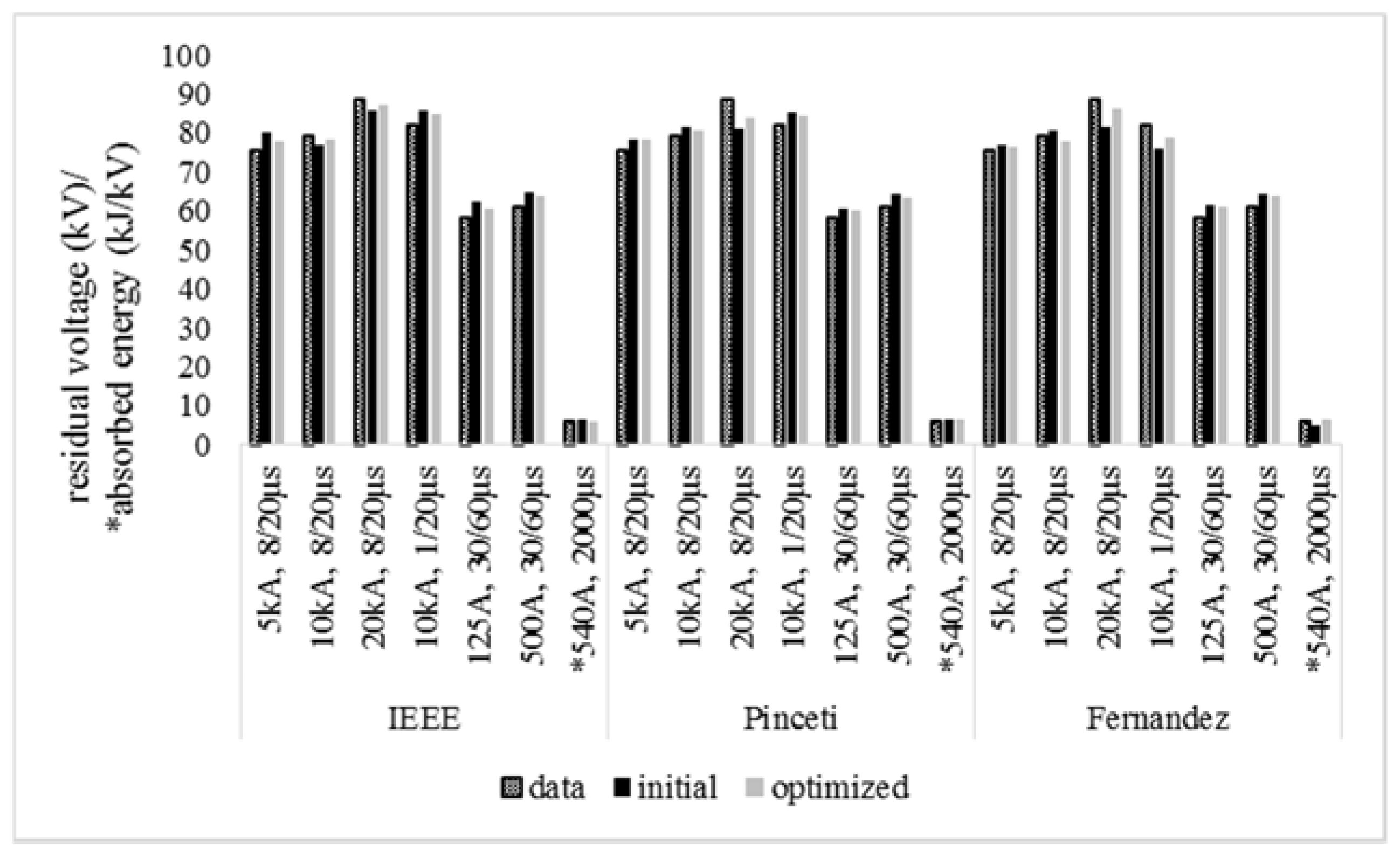
| Residual Voltage | 8/20 μs | 5 kA | 75.29 kV |
| 10 kA | 79.27 kV | ||
| 20 kA | 88.78 kV | ||
| 1/20 μs | 10 kA | 82.01 kV | |
| 30/60 μs | 125 A | 58.14 kV | |
| 500 A | 61.02 kV | ||
| Sheds | 11 | ||
| Height | 302 mm | ||
| Creepage | 762 mm | ||
| IEEE Model [8] | Pinceti–Giannettoni Model [9] | Fernandez–Diaz Model [13] | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | Optimized | Initial | Optimized | Initial | Optimized | |||||||
| Case | Case | Case | ||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | ||||
| R0 (Ω) | 30.20 | 17.82 | 94.81 | 54.19 | 1 × 106 | 1 | 0.952 × 106 | 1.102 × 106 | 1 × 106 | 0.998 × 106 | 1.051 × 106 | 1.088 × 106 |
| R1 (Ω) | 19.63 | 24.48 | 27.88 | 37.54 | - | - | - | - | - | - | - | - |
| L0 (μΗ) | 0.0604 | 0.108 | 0.141 | 0.421 | 0.259 | 0.192 | 0.314 | 0.419 | - | - | - | - |
| L1 (μΗ) | 4.530 | 2.470 | 1.982 | 2.217 | 0.086 | 0.057 | 0.028 | 0.041 | 0.630 | 0.587 | 0.681 | 0.701 |
| C (pF) | 331.1 | 784.2 | 860.9 | 1008.1 | - | - | - | - | 334.4 | 481.2 | 287.7 | 398.4 |
| 5 kA 8/20 μs | 10 kA 8/20 μs | 20 kA 8/20 μs | 10 kA 1/20 μs | 125 A 30/60 μs | 500 A 30/60 μs | 540 A 2000 μs | |||
|---|---|---|---|---|---|---|---|---|---|
| IEEE Model [8] | initial | 6.22 | 3.1 | 3.58 | 4.77 | 7.19 | 6.41 | 8.4 | |
| Optimized (Case 1) | Harmony | 5.84 | 0.25 | 3.27 | 5.41 | 9.24 | 7.90 | 12.7 | |
| Simplex | 6.81 | 0.66 | 4.2 | 5.20 | 9.51 | 8.38 | 11.4 | ||
| Powell | 6.94 | 0.72 | 4.47 | 5.61 | 10.1 | 8.84 | 13.1 | ||
| GA | 5.95 | 0.37 | 3.41 | 5.27 | 9.83 | 6.98 | 11.9 | ||
| Optimized (Case 2) | Harmony | 3.04 | 0.97 | 1.4 | 3.2 | 3.9 | 4.12 | 8.70 | |
| Simplex | trapped in local minima | ||||||||
| Powell | trapped in local minima | ||||||||
| GA | 3.24 | 1.19 | 1.38 | 3.46 | 4.21 | 4.40 | 9.45 | ||
| Optimized (Case 3) | Harmony | 3.65 | 1.21 | 1.85 | 3.58 | 4.42 | 4.87 | 5.10 | |
| Simplex | trapped in local minima | ||||||||
| Powell | trapped in local minima | ||||||||
| GA | 4.03 | 1.58 | 2.24 | 3.92 | 5.10 | 5.51 | 5.95 | ||
| Pinceti–Giannettoni Model [9] | initial | 4.21 | 2.87 | 8.74 | 3.87 | 4.24 | 5.08 | 9.2 | |
| Optimized (Case 1) | Harmony | 4.52 | 0.35 | 6.89 | 4.10 | 4.21 | 4.89 | 11.1 | |
| Simplex | 4.91 | 0.50 | 7.08 | 4.74 | 5.58 | 6.24 | 12.9 | ||
| Powell | 4.64 | 0.41 | 6.72 | 4.67 | 5.14 | 5.78 | 12.2 | ||
| GA | 4.81 | 0.62 | 6.71 | 4.73 | 4.95 | 5.32 | 12.6 | ||
| Optimized (Case 2) | Harmony | 3.31 | 1.04 | 4.84 | 2.1 | 2.91 | 3.70 | 8.91 | |
| Simplex | trapped in local minima | ||||||||
| Powell | trapped in local minima | ||||||||
| GA | 3.68 | 1.41 | 4.58 | 2.43 | 3.08 | 4.12 | 9.21 | ||
| Optimized (Case 3) | Harmony | 3.84 | 1.77 | 5.30 | 2.78 | 3.25 | 3.87 | 6.04 | |
| Simplex | trapped in local minima | ||||||||
| Powell | trapped in local minima | ||||||||
| GA | 4.09 | 2.16 | 5.12 | 3.22 | 4.10 | 4.15 | 6.59 | ||
| Fernandez–Diaz model [13] | initial | 2.41 | 1.59 | 8.35 | 7.41 | 5.97 | 5.45 | 11.23 | |
| Optimized (Case 1) | Harmony | 2.71 | 0.15 | 8.1 | 7.88 | 6.20 | 5.81 | 13.2 | |
| Simplex | 3.55 | 0.41 | 8.29 | 8.31 | 6.54 | 6.77 | 15.1 | ||
| Powell | 3.29 | 0.37 | 8.15 | 8.04 | 6.31 | 6.28 | 12.2 | ||
| GA | 2.94 | 0.30 | 7.82 | 7.94 | 6.48 | 5.59 | 11.7 | ||
| Optimized (case 2) | Harmony | 1.1 | 1.31 | 2.21 | 3.08 | 3.45 | 3.64 | 9.4 | |
| Simplex | trapped in local minima | ||||||||
| Powell | trapped in local minima | ||||||||
| GA | 1.54 | 1.92 | 2.73 | 3.50 | 3.68 | 4.01 | 10.7 | ||
| Optimized (case 3) | Harmony | 1.77 | 1.91 | 2.89 | 3.71 | 4.81 | 4.19 | 6.81 | |
| Simplex | trapped in local minima | ||||||||
| Powell | trapped in local minima | ||||||||
| GA | 1.95 | 2.24 | 3.11 | 4.02 | 4.61 | 4.42 | 6.40 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christodoulou, C.A.; Vita, V.; Perantzakis, G.; Ekonomou, L.; Milushev, G. Adjusting the Parameters of Metal Oxide Gapless Surge Arresters’ Equivalent Circuits Using the Harmony Search Method. Energies 2017, 10, 2168. https://doi.org/10.3390/en10122168
Christodoulou CA, Vita V, Perantzakis G, Ekonomou L, Milushev G. Adjusting the Parameters of Metal Oxide Gapless Surge Arresters’ Equivalent Circuits Using the Harmony Search Method. Energies. 2017; 10(12):2168. https://doi.org/10.3390/en10122168
Chicago/Turabian StyleChristodoulou, Christos A., Vasiliki Vita, Georgios Perantzakis, Lambros Ekonomou, and George Milushev. 2017. "Adjusting the Parameters of Metal Oxide Gapless Surge Arresters’ Equivalent Circuits Using the Harmony Search Method" Energies 10, no. 12: 2168. https://doi.org/10.3390/en10122168
APA StyleChristodoulou, C. A., Vita, V., Perantzakis, G., Ekonomou, L., & Milushev, G. (2017). Adjusting the Parameters of Metal Oxide Gapless Surge Arresters’ Equivalent Circuits Using the Harmony Search Method. Energies, 10(12), 2168. https://doi.org/10.3390/en10122168