1. Introduction
The energy sharing across a neighbourhood is important as it fosters sustainability through the efficient utilization of local energy resources and reducing reliance on the utility grid. Utilizing renewable energy resources for energy sharing, the carbon footprint can be reduced and the energy supply in the critical infrastructures can be maintained during blackouts.
Many houses in Australia, as well as around the world have been installing solar photovoltaic (PV) systems over the past few years, which are mainly motivated by generous gross and net state and/or federal government feed-in tariff schemes along with other financial incentives. Recently, consistently declining prices of battery energy storage systems (BESSs) have attracted some house owners to install BESSs in order to better manage and control the solar PV system for domestic usages. However, the recent termination or reduction of the feed-in tariff necessitates the investigation of alternative measures for the surplus energy utilization. Subject to jurisdictional review, one possible alternative way of feeding energy back to the grid is to set up a local energy sharing framework (LESF) within a neighbourhood [
1,
2,
3]. In this energy sharing framework, different end-users with an excess or shortage of energy can actively participate to manage their electricity and, hence, reduce the pressure on the ageing grid [
4]. The energy management system (EMS) needs to be designed for the efficient utilization of PV and BESS resources and sharing energy among the neighbourhood.
There are different energy management strategies for hybrid renewable energy systems [
5,
6]. The EMS of a small house with solar PV system is proposed in [
7] along with the parametric optimization of the building. In [
8], the EMS of a hybrid system with the solar PV unit, fuel cell, BESS and superconductor is proposed to effectively manage the energy with the utilization and procurement. An optimal control-based EMS is presented in [
9] for automotive power systems with battery and supercapacitor storage devices to increase the overall operational efficiency. A cooperative home EMS for a house with the solar PV unit and BESS is proposed in [
10] to make a balance between the generation and load while forecasting the solar irradiation. The EMSs as presented in [
7,
8,
9,
10] are only used to manage energy either for a single house with renewable energy sources (RESs) with energy storage systems (ESSs) or for RESs with local loads and the main power grid. For this reason, the structures of these EMSs in [
7,
8,
9,
10] are quite simple. However, the EMS will be more complicated if several houses with different features are connected together in order to share energy among themselves.
The energy management of microgrids is discussed in [
11,
12] where RESs are considered as distributed energy resources. In [
11,
12], the main objective of the EMS is to reduce the energy consumption without any prediction of demand and generation. An EMS, considering load and generation prediction, is proposed in [
13] with the aim of utilizing the BESS in an optimal way for better grid support. In [
14,
15], the EMS for the microgrid is designed to reduce the utilization cost of the BESSs under the uncertainties in RESs through optimal generation scheduling. A similar approach for the EMS is presented in [
16] for the least expensive pricing options in the local energy market and maximization of the energy utilization from the RESs. The EMSs in [
11,
12,
13,
14,
15,
16] are useful for managing power under different operating scenarios of microgrids. However, the RESs in these microgrids are lumped at some specific points, which is not the case in residential microgrids, as each house comprises RESs (especially solar PV systems) and BESSs. Thus, the EMS need to be designed in a different way that carries information from each house.
The multi-agent frameworks are useful for carrying information from different entities or subsystems within a system, as well as sharing information among these entities [
17,
18,
19]. A decentralized multi-agent framework is proposed in [
20] for the energy management and autonomous control of microgrids. Similar EMSs based on multi-agent frameworks are proposed in [
21]. A cognitive decision agent architecture is used in [
22] to effectively manage the energy in microgrids. In [
22], the neighbourhood energy sharing is considered without considering any strategy for prioritizing the houses, charging or discharging the BESSs, etc. However, the effective energy management capability of an EMS depends on the intelligence of the agents. The multi-agent frameworks as discussed in [
17,
18,
19,
20,
21,
22] did not consider the detailed power generation and consumption features of different entities in a microgrid, and some of these approaches have also neglected the battery charging or discharging features.
The hierarchical approaches are useful for sharing energy information among different entities in a microgrid. A hierarchical EMS is proposed in [
23] where two layers are considered for static and dynamic frequency. Another hierarchical approach is used in [
24] where the upper level of the EMS is used to manage the microgrids along with associated components, and the lower level is used for the optimization of operational costs. A multi-level EMS for multi-source electric vehicles is proposed in [
25] based on an integrated rule-based meta-heuristic approach. In [
26], a hierarchical framework is presented as a day-ahead scheduling and double-layer intra-hour (master-client) adjustment system where these two layers are used to optimize the operational costs and tie-line power smoothing. A multi-source multi-product microgrid with a hierarchical EMS is proposed in [
27] where the hierarchical framework includes supervisory, optimization and execution control layers. A hierarchical EMS based on master and slave control strategies is presented in [
28] to maintain the power balance within the microgrid while considering the state of charge (SOC) of the battery. All these hierarchical approaches are proposed in [
23,
24,
25,
26,
27,
28]; the energy management at the household level is not considered, but rather some overall specific activities.
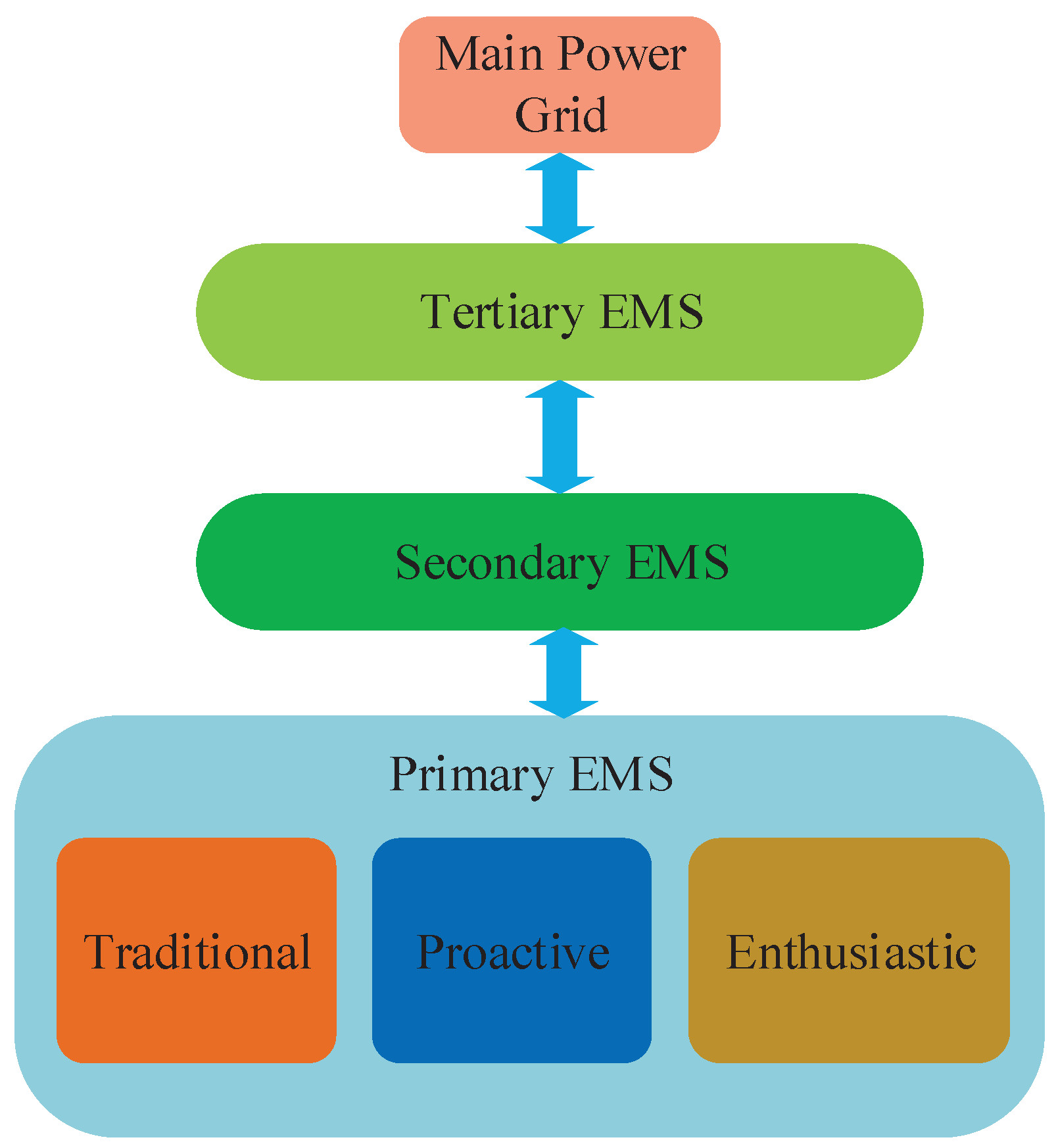
This paper aims to design a hierarchical EMS for residential microgrids where the houses are categorized into three different types based on the inclusion of solar PV units and BESSs. Energy sharing priorities are also defined in this paper by considering both grid-connected and islanded operation of microgrids. In the proposed hierarchical framework, the levels are considered to effectively manage the energy within the microgrids. At the primary level, three different primary EMSs are considered for three houses, which usually share the energy information (e.g., energy excess, shortage, generation from the solar PV units, status of the BESSs, etc.) with the secondary EMS. The secondary EMS first distributes the excess energy to the houses within the microgrid through the respective primary EMSs. The secondary EMS either purchases or sells energy from or to the main grid through the tertiary EMS if there is still energy shortage or excess within the microgrid even after sharing excess energy. The effectiveness of the proposed hierarchical framework is validated on a test residential microgrid.
2. Houses in Residential Microgrids
In a traditional power grid, there are different types of houses, which are connected to the main grid, and the total load demand of these houses is usually met by energy supplied from the main grid. However, this is not the case for a microgrid where different types of houses can be connected together along with the grid. In microgrids, the primary aim is not to purchase energy from the main grid, rather satisfying their own demands from the installed renewable energy sources, especially solar PV systems. The houses that can be connected to a microgrid through an EMS can be categorized into the following three types:
2.1. Traditional Houses
The first set of consumers who are very passive in adopting renewable energy technologies is clustered as traditional consumers, and the set of traditional houses in a residential microgrid can be represented as follows:
where
is the set of traditional houses,
represents a variable to denote households in the set of traditional houses and
is the total number of traditional houses in the microgrid. Traditional houses do not use any solar PV systems to produce energy and heavily depend on the utility to meet their energy demands. In a microgrid, this set can be considered as the poorest community member who cannot afford the cost of solar PV systems or a person who can afford the cost, but is unwilling to install solar PV systems. The owners of these houses only care about the prices of electricity, i.e., they just look for the least expensive options to purchase energy, and it really does not matter to them from where the energy is coming.
2.2. Proactive Houses
The second set of houses is proactive, who adopt only renewable energy sources, but these houses are not interested in installing BESSs. The set of proactive houses in a microgrid can be defined as follows:
where
is the set of proactive houses,
represents a variable to denote households in the set of proactive houses and
is the total number of proactive houses in the microgrid. The owners of these proactive houses are willing to share (sell or buy) energy with their neighbours. However, if the neighbours do not require energy or are not willing to purchase energy, these proactive houses sell their extra energy to the grid.
2.3. Enthusiastic Houses
The third set of houses is grouped as enthusiastic houses, which are the ideal houses in the context of the microgrid. These houses are defined through the following set:
where
is the set of enthusiastic houses,
represents a variable to denote houses in the set of enthusiastic houses and
is the total number of enthusiastic houses in the microgrid. These houses have both solar PV systems and BESSs. These houses first try to meet their own energy demands from the installed solar PV within the premises and store the excess energy in their batteries. After fulfilling their own requirements, the additional energy is shared amongst the neighbours in a similar way as proactive houses do.
Before developing the hierarchical energy management framework, it is essential to define the priorities for energy sharing among different houses, which is discussed in the following section.
3. Energy Sharing Priorities
If it is assumed that there are several houses in a microgrid including all three types of houses, and there is no energy sharing among these houses; there will be both energy shortage and wastage. The traditional houses will always be in energy shortage, and the proactive houses will waste the extra energy during the day while these houses will face energy shortage during the night. On the other hand, the enthusiastic houses may or may not waste energy during the day as these will store the extra energy in their batteries. However, these enthusiastic houses may have an energy crisis during the night.
Microgrids can operate either in islanded or grid-connected mode. The energy sharing strategy needs to be defined by considering both operating modes. From the definition of different houses, it can be said that the houses in a microgrid will have different priorities for energy sharing among themselves. In a residential microgrid, the traditional houses do not have any priority to share the energy as these houses only consume energy. On the other hand, the proactive houses fulfil their own demands first and then share the energy among the neighbours, as well as with the main power grid. Proactive houses give the highest priority to the traditional users and the lowest to the main grid. If proactive houses still have extra energy after sharing with traditional houses, the proactive houses consequently choose the proactive and enthusiastic houses. In the case of enthusiastic houses, the loads and BESSs of these houses get the top priority, and then, the energy sharing strategy is quite similar to that of proactive houses.
During the islanded mode operation of microgrids, the energy sharing priorities can be summarized as shown in
Table 1 and that for the grid-connected mode in
Table 2. From
Table 2, it can be seen that the main power grid is the last point of selling or buying energy for the residential microgrid.
However, the energy sharing will not happen automatically, and thus, it is essential to develop an EMS. The structure of an EMS is discussed in the following section.
4. Overview of an EMS
The EMS has been used in residential, commercial and industrial buildings to optimize energy usage since 1976 [
29]. The usage of the EMS includes monitoring energy usage, increasing energy savings, controlling and scheduling equipment, forecasting of demand and generation, diagnosing of faults, etc. [
29]. The technical and institutional challenges of representative EMSs are managing uncertainty associated with forecasting, developing models for different categories of appliances, operation scheduling of devices while maintaining certain comfort or tolerance levels and costs [
30]. The existing EMSs generally produce an operating schedule of appliances to achieve the desired objectives. For example, a building EMS is designed in [
31] to optimize the user comfort and energy cost subject to certain constraints. A home EMS is proposed in [
32] to schedule household appliances based on energy purchasing price from the utility in order to minimize the energy purchasing cost. A microgrid EMS is presented in [
33] to reduce pollutant emissions while minimizing the energy cost and maximizing the usage of renewable energy resources. A day-ahead scheduling approach is provided in [
34] by considering a mix of renewable energy resources, e.g., solar PV, wind turbine, energy storage, flexible demand, etc. The objectives of the EMSs in [
31,
32,
33,
34] are mainly energy scheduling, which always results in some level of discomfort, but the EMSs do not consider energy sharing among neighbours to increase energy autonomy and reduce grid dependence. The proposed EMS is different from the existing ones in that it utilizes an energy sharing approach among neighbours in a residential microgrid to manage the excess of houses with a renewable energy portfolio to meet the demand of other houses after optimizing the household energy utilization. Moreover, the proposed EMS preserves the privacy of the participants as it requires only the generation and demand profiles. For the proposed EMS, the operational cost is minimum, which will usually be distributed among all participants.
The effective energy sharing will depend on the design and intelligence of the EMS. The structure of an EMS is shown in
Figure 1 which has three different EMSs: primary, secondary and tertiary. Thus, it can be said that the EMS has a hierarchical structure with three levels of communication. Different types of houses are located at the primary level of the hierarchical EMS. Since there are three types of houses in a residential microgrid, the primary EMS can be categorized into the following three categories:
Traditional primary EMS, which is responsible for managing energy in traditional houses,
Proactive primary EMS, which manages the energy for proactive houses, and
Enthusiastic primary EMS, which takes care of managing the energy in enthusiastic houses.
The primary, secondary and tertiary EMSs are functional elements of the proposed hierarchical transactive EMS, which can be implemented in a distributed fashion or can be different parts of a centralized system with the distributed computational capability. When implemented in a distributed fashion, the algorithms for different (traditional, proactive and enthusiastic) primary EMSs can be universally integrated within the smart meters of households, which can optimize the operating schedules of available renewable resources within the household. This type of smart meter is mainly supplied by the utility, e.g., the smart meter roll-out in Victoria, Australia [
35]. The smart meters have already been integrated with the EMS of the energy-providing utility where the algorithms for the secondary and tertiary EMSs can be integrated. The utilities will benefit due to the reduction in grid dependencies through the usage of solar PV units and BESSs, which defers the commissioning of new peak power plants and transmission systems to support the peak demand. At the same time, the consumers enjoy cost savings and energy autonomy.
At the primary level, each house has its own EMS and communicates the current status to the secondary EMS. In a microgrid, the traditional, proactive and enthusiastic EMSs are considered as the primary EMSs. The secondary EMS gathers information from the primary EMSs and performs necessary actions for sharing energy according to the energy sharing priorities. The secondary EMS communicates with the tertiary EMS whose main responsibilities are to oversee the overall energy shortage or excess and make decisions for buying energy from the main grid or selling energy to the main grid. The detailed energy sharing activities of these EMSs are discussed in the following section.
5. Energy Sharing Activities of EMSs
For sharing energy among the houses in a microgrid, an EMS plays a key role. The EMS collects energy excess and shortage information from all traditional, proactive and enthusiastic houses in order to share excess energy within the neighbourhood and procure shortage energy from the grid in a manner so as to maximize the benefits of local renewable energy resources.
The EMS decides who should get the available energy from neighbours at a reduced rate rather than purchasing from the grid at a comparatively higher rate. The EMS will follow the priority as indicated in
Table 1 and
Table 2 in order to share energy among the neighbours in a microgrid. This strategy of prioritizing is aimed at reducing energy poverty within the microgrid with the assumption that traditional houses are the lowest income community members who cannot afford renewable energy resources, while proactive and enthusiastic neighbours are comparatively more solvent. Within the house groups, the priorities are given in the ascending order of energy shortage, i.e., the houses with lower energy shortage are given more priority than the house with higher energy shortage.
Energy selling priorities of the houses, on the other hand, are not prioritized according to the energy available, which gives rise to the concern about whether the available energy from a particular house is sold to neighbours or to the grid. Generally, each individual house would want to sell to neighbours at a higher rate than selling it back to the grid at a continually decreasing nominal feed-in tariff. Furthermore, there is a concern of which house should get the first priority for selling its available energy to the neighbours. These issues are addressed by not giving priorities to any particular house when it comes to the question of selling energy; rather, the EMS aggregates all available energy from the entire neighbourhood and meets the energy shortage of houses according to their priorities as discussed earlier. The rest of the energy is sold back to the grid at a lower rate. The utility of selling available energy for each house then depends on the total energy sold to neighbours and the total energy sold to the grid. By applying this rule, each house gets a fair share of earnings by selling energy to different parties at different prices. Therefore, the effectiveness of energy sharing in a microgrid relies on the intelligences of the EMS. The intelligences of different EMSs are discussed in the following sections.
6. Intelligences of Primary EMSs
This section is aimed at discussing the intelligences of primary EMSs in terms of energy sharing activities. Since there are three types of primary EMSs, the intelligences of all these EMSs will vary according to their activities. For example, the EMSs for traditional houses will act differently as compared to that of proactive and enthusiastic EMSs. The intelligences of each primary EMS are discussed in the following.
6.1. Intelligences of Primary Traditional EMSs
The primary EMSs collect energy information from their respective houses and share this information with the secondary EMS for further actions. Since the traditional houses do not generate or store any energy, the primary EMSs related to these houses will share only the energy shortage information with the secondary EMS. For example, if
is the energy demand of any traditional house
at any instant (
), the amount of energy shortage at that instant will be
where
is the amount of energy currently being supplied to the traditional house, and this information will be sent to the secondary EMS to purchase energy from neighbours or from the main grid. For traditional houses, the excess energy and energy utilized from renewable energy sources are always zero, i.e.,
and
. This information is made available to higher EMSs to perform energy sharing activities. The energy information flow within the traditional primary EMSs along with the information flow to the secondary are shown in
Figure 2.
6.2. Intelligences of Primary Proactive EMSs
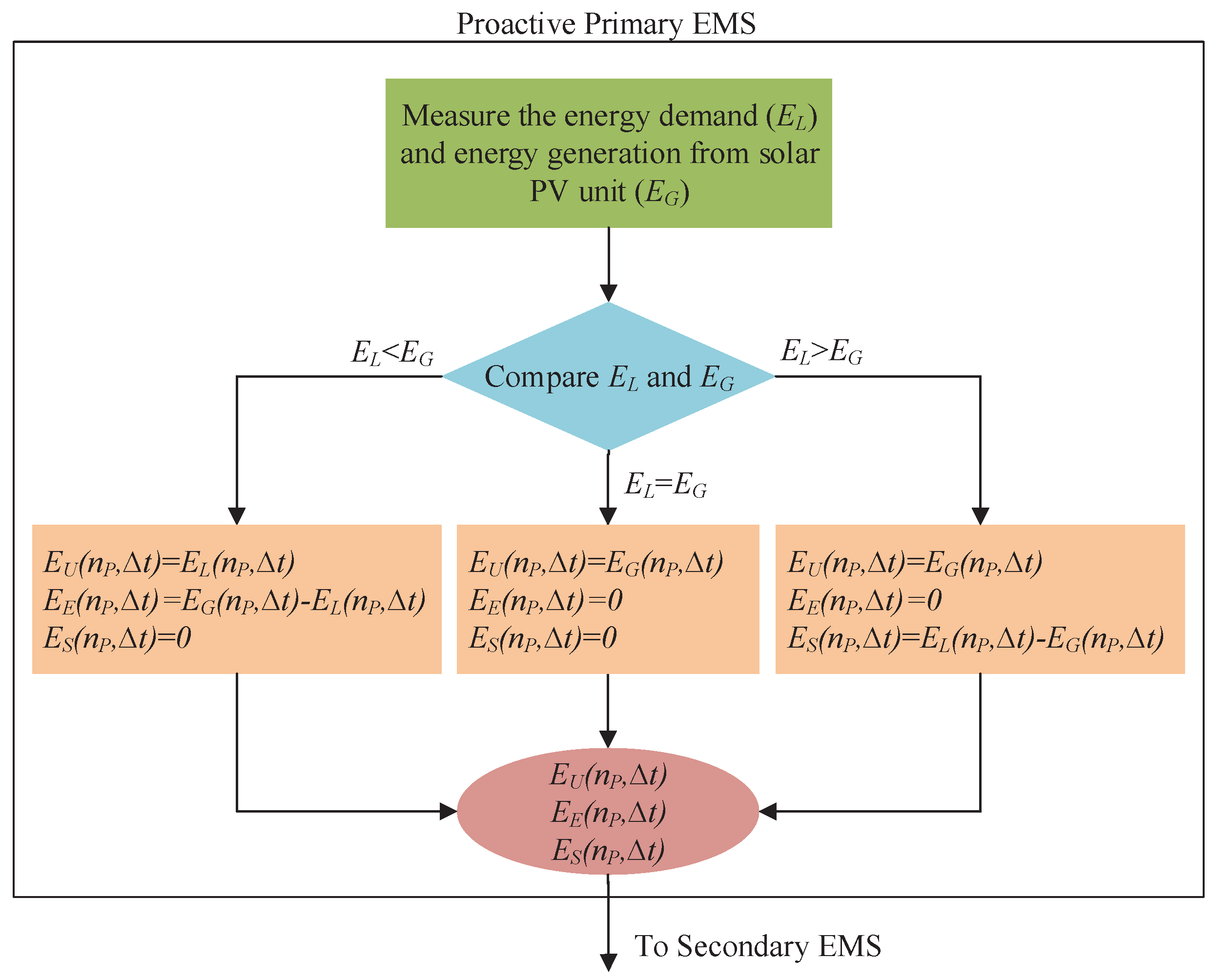
The intelligences of primary proactive EMSs are quite different from the traditional EMSs. The proactive EMSs of any arbitrary house work based on the following steps:
Step 1: Gather the energy generation information, from the solar PV unit and load energy information for a proactive house at any instant . Compare the energy consumption by loads of a proactive house with the energy generation from its own solar PV system, i.e., calculate the energy shortage as if or energy excess if .
Step 2: Calculate energy utilized from the residential solar PV unit, when or when .
Step 3: Communicate with the secondary EMS and share the energy information , and .
The overall activities of a primary proactive EMS are shown in
Figure 3.
6.3. Primary Enthusiastic EMSs
The activities of enthusiastic EMSs are quite complex as compared to those of traditional and proactive EMSs. A primary enthusiastic EMS works based on the following steps:
Gather the energy generation information, from the solar PV unit and load information for an enthusiastic house at any instant . Compare the load demand of the enthusiastic house with the energy generation from its own solar PV system. At this stage, the following three scenarios could occur:
If , the energy supplied by the solar PV unit perfectly matches the load demand. In this case, the utilized energy from the solar PV unit equals the load demand, as well as the energy generation from the PV unit, i.e., . In this case, the amount of power shortage and excess will be zero, which means and .
If , then there will be excess energy, which is the difference between these two energies, i.e., some excess energy available . This excess energy could either be stored in the BESS as the enthusiastic house has this facility or sold to the neighbours or the grid. Thus, this is not the final stage to calculate the net energy excess, for the enthusiastic house, and it is required to check the state of charge (SOC) of the battery, which is done in the next step.
There will be energy shortage if , which can be calculated as . This energy shortage must be met either by discharging the battery or by purchasing from the grid or neighbour. Therefore, the net energy shortage, also depends on the SOC of the battery.
Since the calculation of net energy utilization, shortage, excess and available energy in BESSs depends on the charging/discharging of the battery, an intermediate step (Step 2) is introduced in the following.
The charging and discharging of batteries depend on the SOC, and these will happen if the condition: is satisfied where is the state of charge of the battery and , are the minimum and maximum limits of the , respectively. In cases of energy excess or shortage from the solar PV unit, the primary enthusiastic EMS will check the current condition of the BESS to see whether the BESS could be charged or discharged and how much energy it can discharge or charge along with the amount corresponding to charging and discharging while maintaining the limits related to the .
If , the enthusiastic EMS will check whether the excess energy can be utilized to charge the BESS or not. The battery will be charged if .
If , the EMS will check that the shortage in Step 1 can be met whether by discharging the BESS or not. The battery will be discharged if .
The SOC information obtained from this step is used in the next step, and this information is still not communicated with the secondary EMS.
This is the final step for the enthusiastic EMS where the net energy excess, shortage, utilization and remaining energy in the BESS are calculated under different conditions as discussed below:
At this stage, the load demand is perfectly matched with the generation from the solar PV unit, i.e., . In this case, the net energy utilization will be similar to that as obtained in Step 1. Thus, the net energy utilization is , and the SOC of the battery will be unaffected for which the net energy available in the battery will be . Moreover, there will be no energy excess or shortage. Thus, the net energy excess and shortage are and , respectively.
If the excess energy can be utilized to charge the BESS if the condition as mentioned Step 2 is satisfied, the excess energy can be fully used to charge the battery if the sum of currently available power from the BESS () and the excess energy () is less than or equal to the maximum power capacity of the BESS, i.e., . In this situation, the net power available from the BESS will be , and the net excess power for the enthusiastic house will be zero (), which is also true for the net power shortage, i.e., . Finally, the net utilized power will be .
If the excess energy cannot fully be used to charge the BESS, i.e., , there will still be some excess energy after charging the BESS. Thus, the net excess energy that will be communicated with the secondary EMS is . In this condition, the net energy utilization is , and the net energy shortage is . Since the battery will be charged with its full capacity, the net available energy from the battery is .
If the energy shortage can be met by discharging the BESS according to the condition as discussed in Step 2, i.e., , the energy shortage for the enthusiastic house will be recovered through discharging the battery. Thus, the net energy available in the battery will be , and the net energy shortage, as well as the net energy excess will be zero, i.e., and . The net utilized energy is .
If the energy shortage cannot fully be met by discharging the BESS, i.e., , only a fraction of load demand will be met by the solar PV unit and BESS. In this condition, the battery will reach its minimum SOC and cannot further be discharged. Thus, the net available energy in the BESS will be the minimum power, which is . The net excess energy will be zero (), and there will be net energy shortage, which is . Finally, the net energy utilization for the enthusiastic house will be the energy that is only available from the BESS and PV unit, i.e., .
Thus, it can be said that all primary enthusiastic EMSs must have these intelligences to calculate the net energy excess, shortage, utilization and available energy in the batteries. Primary enthusiastic EMSs will share this net energy with the secondary EMS. The activities of a primary enthusiastic EMS is shown in
Figure 4 along with its interaction with the secondary EMS.
As discussed in this subsection, the energy sharing priorities of the primary EMS can be summarized as presented in
Table 3. The intelligences of the secondary EMS are discussed in the following subsection.
7. Intelligences of Secondary EMSs
The secondary EMS collects the energy shortage information from traditional primary EMSs, while proactive EMSs share energy utilization from the solar PV units along with the energy shortage and excess. The enthusiastic EMSs share the following information with the secondary EMS:
the net energy utilization from solar PV units and BESSs,
the net energy shortage and excess and
the net energy available in the BESS.
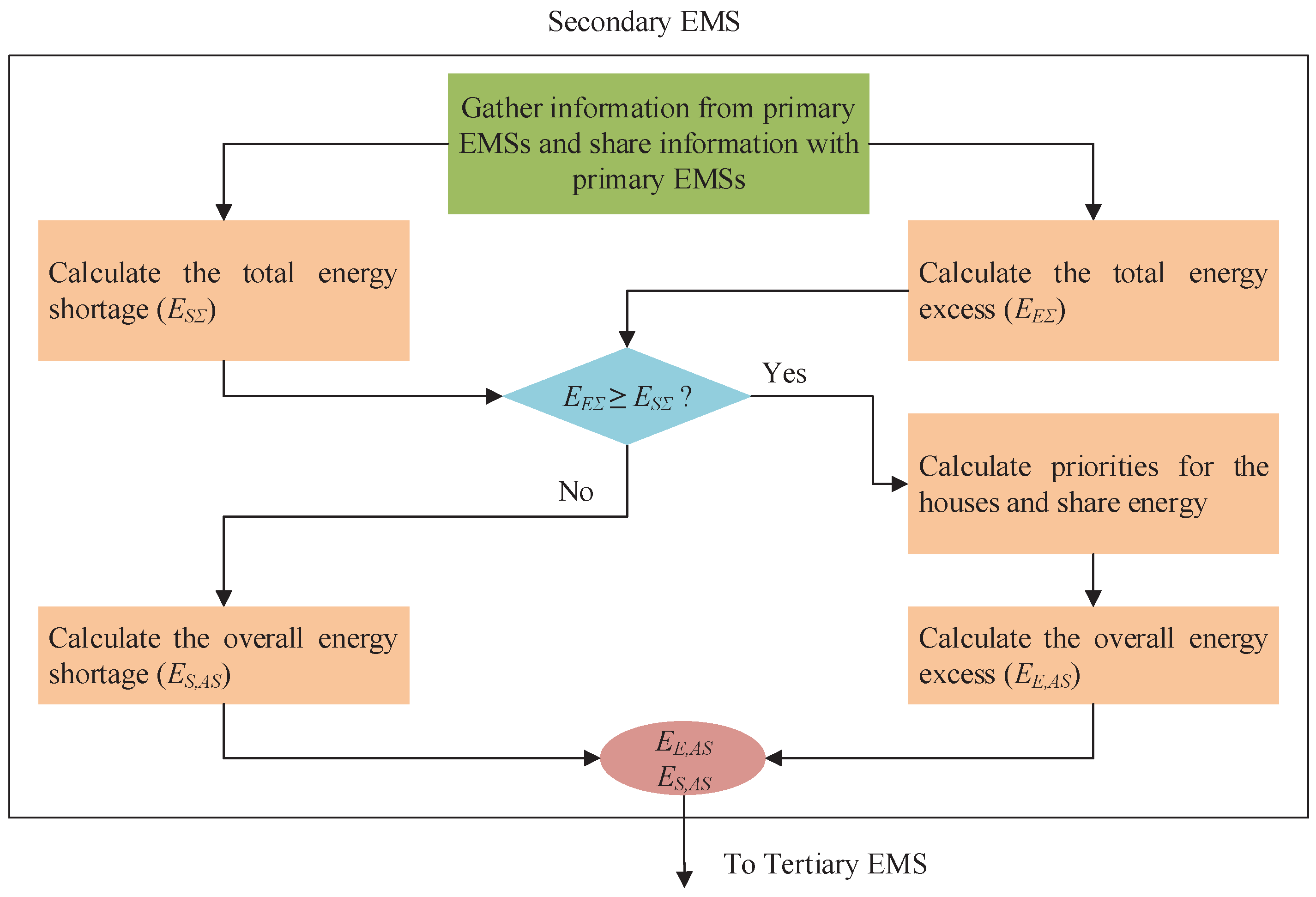
The main activities of the secondary EMS are to calculate the overall energy shortage or excess for the microgrid and taking initiatives for sharing the energy among neighbours through the primary EMSs in case of energy excess or buying energy from the main grid through the tertiary EMS in case of energy shortage. The excess energy is shared among the neighbours based on the priorities as discussed earlier in this paper. However, this section is intended to provide a detailed overview to calculate the overall energy shortage and excess of the microgrid along with further analytical defining of the energy sharing strategies. The secondary EMS also needs to make sure the energy sharing is happening in a cost-effective manner.
Based on the received information from the primary EMSs, the secondary EMS calculates the total amount of excess energy for a time interval (
) within the microgrid by using the following formula:
Here, the excess energy information is only available from the proactive and enthusiastic houses. However, the energy shortage information is available from all houses. Thus, the total energy shortage for the microgrid can be calculated in a similar manner to that of the excess, which is represented as follows:
On the other hand, while meeting the shortages of the microgrid from the excess energy available, the houses are prioritized according to
Table 4. The priorities of different houses can be represented by the following relationship:
where
,
and
are the vectors of sorted energy shortages of traditional, proactive and enthusiastic houses in ascending order; respectively. The vector of sorted shortages of traditional houses can be denoted as:
where
represents the house with minimum energy shortage within the set of traditional houses
and
is the traditional house with maximum energy shortage. Similarly, the shortage vector of proactive and enthusiastic houses can be represented as:
The secondary EMS meets the shortages of houses in ascending order of their priorities. The traditional house categories will be able to purchase energy from neighbours before any proactive and enthusiastic houses. Within the traditional houses, the house with the least energy shortage will be able to meet its demand by purchasing energy from the microgrid. In this fashion, after meeting the demand of all traditional houses, if there is still excess energy, it will be used to meet the load demand of other proactive houses and, finally, the demand for enthusiastic houses. The batteries of enthusiastic houses will get the lowest priority. After meeting the shortages of all houses, these batteries will be charged with the excess energy before it is sold to the main grid.
If the total excess energy of the microgrid is greater than or equal to the total shortage, i.e.,
, the shortages can be met by energy sharing. After sharing the remaining energy with neighbours,
can be sold to the main grid, which is the overall energy excess and can be expressed as follows:
If, however, the overall energy shortage of the microgrid is greater than the overall excess (i.e.,
), the overall shortage,
, is required to be purchased from the grid, which can be written as follows:
The secondary EMS will send overall energy excess and shortage information after sharing within the microgrid to the tertiary EMS, which will make a decision for exchanging energy with the main power grid. The energy information flow within the secondary EMS in a residential microgrid, as well as with the primary and tertiary EMSs is shown in
Figure 5.
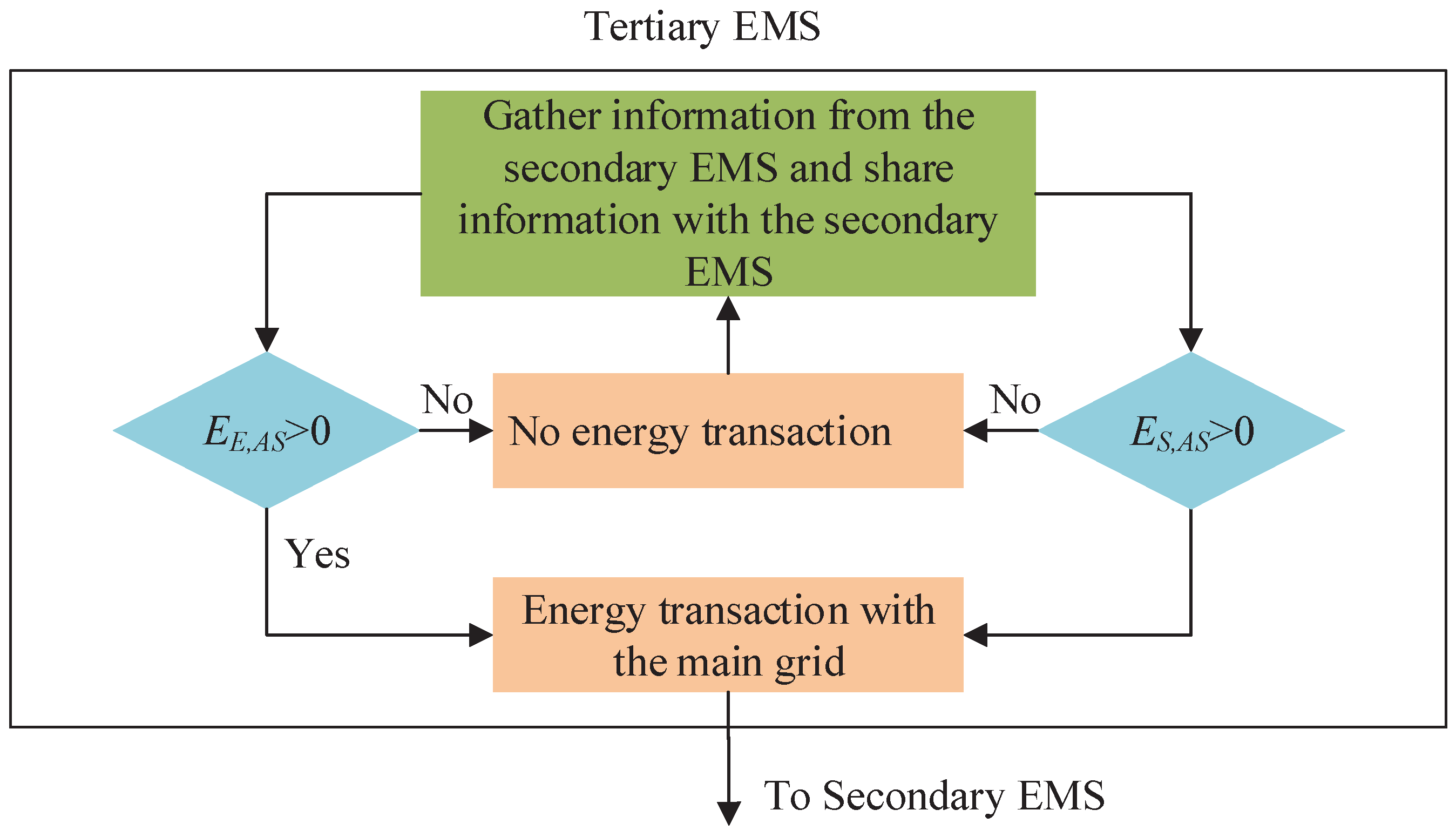
8. Intelligences of Tertiary EMS
The task of the tertiary EMS is to oversee the energy trading with the main grid. The tertiary EMS makes the decision to purchase energy from the grid if the overall shortage of energy after sharing is greater than zero, i.e.,
If the excess energy after sharing is greater than zero, the tertiary EMS sells the excess energy to the grid, which can be expressed as follows:
The energy information flow within a tertiary EMS is shown in
Figure 6 along with its information sharing with the secondary EMS.
Finally, the tertiary EMS communicates the information related to the energy transaction, and the secondary EMS considers this information to continue the power sharing action in cooperation with primary EMSs. All three EMSs constitute the hierarchical framework for energy sharing in a residential microgrids. From the collaboration and cooperation, all participants are benefited either by selling energy at a price higher than the feed-in tariff or by purchasing energy at a price lower than the utility rate. The cost and benefits are usually allocated based on the amount of energy sharing (either selling or buying). The performance of the proposed scheme in terms of power sharing is evaluated in the following section.
9. Performance Evaluation of the Proposed Hierarchical EMS
This section is devoted to analyse the power sharing capability of the proposed scheme with different operating modes. The operating modes are mainly considered based on a neighbourhood in a residential microgrid where there are different types of traditional, proactive and enthusiastic neighbours. In this paper, it is considered that the neighbourhood consists of nine households of different categories as shown in
Figure 7 where there are three traditional (
), four proactive (
) and two enthusiastic (
) houses.
The peak demands along with seasonal average daily demands for all households in the microgrid are given in
Table 5. From this table, it can be seen that the traditional households have the least demand in the microgrid, while the demands of the proactive houses are higher than those of the traditional houses. Enthusiastic houses have the highest energy demand. In general, the average daily demand of all houses is the highest in winter and is the lowest in autumn. These demand profiles are obtained from the smart grid smart city trial in Australia [
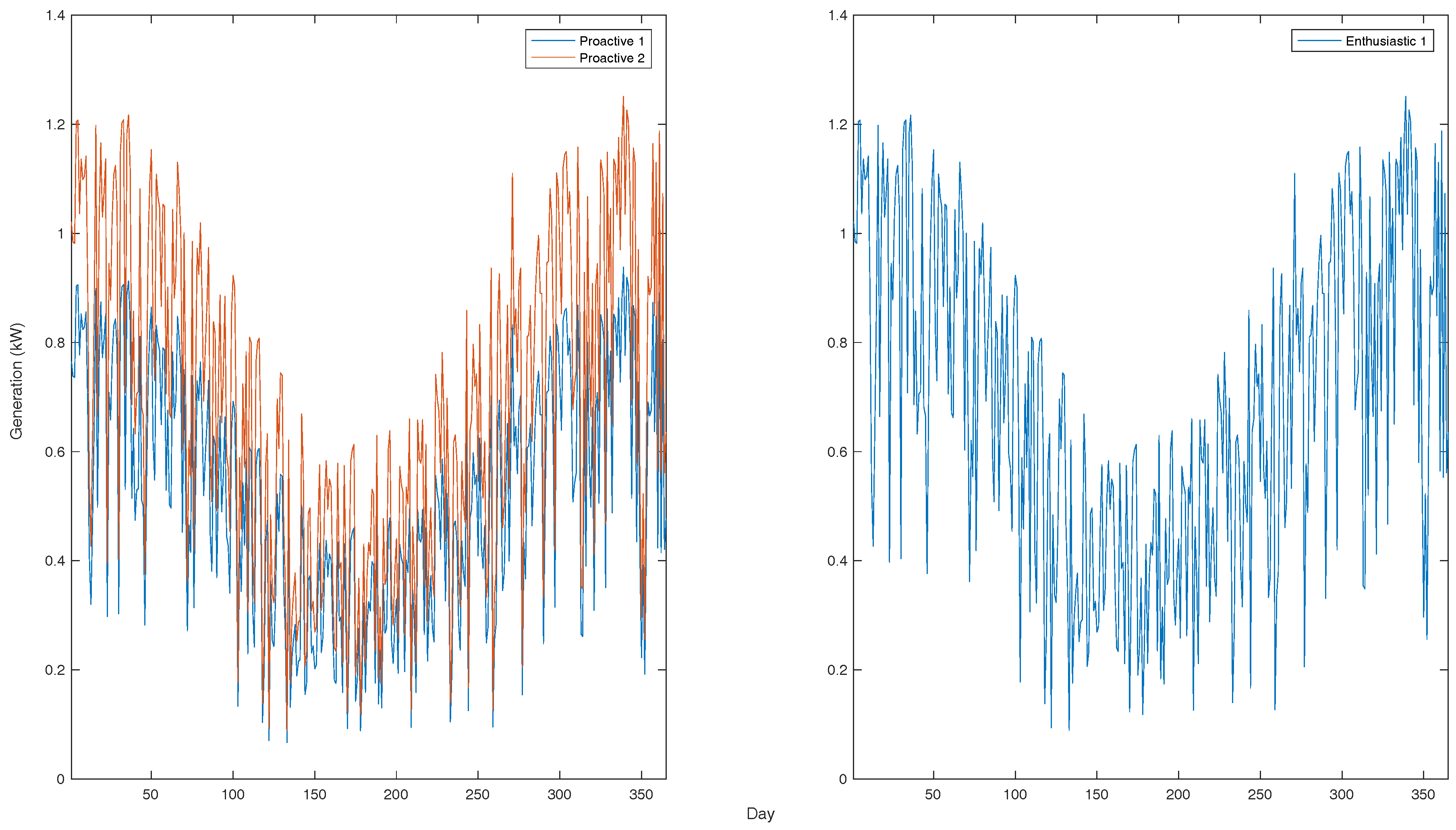
36]. The yearly demand profiles of different houses in the proposed microgrid are shown in
Figure 8. In these demand profiles, the daily profile is the average demand over 24-h periods.
The renewable energy profiles of different houses are given in
Table 6. Traditional houses do not have any solar PV units or BESSs. The sizes of installed solar PV units for Proactive Houses 1 and 3 (i.e., P1 and P3) are 3 kWp, whereas the remaining houses (i.e., P2, P4, E1and E2) have 4-kWp solar PV units. The daily average generation is maximum during the summer and spring seasons, while the generation is the minimum during the autumn season. The yearly average generation profiles for all houses are shown in
Figure 9. The daily profile is the average of generations over a day during sunny periods.
The effectiveness of the proposed EMS in terms of energy sharing along with the energy profiles of different houses in a microgrid is also discussed in this section. Based on these energy profiles, the operating hours in a typical day are categorized into several operating modes for different houses. Finally, some results are also presented by considering the overall operating scenarios of the microgrid over a year.
When there is excess energy to share or sell, the only houses within the neighbourhood that require purchasing energy are mainly traditional ones. Furthermore, in the considered microgrid, traditional houses have the least demand. Thus, only a small proportion of the excess energy is sold to neighbours, and the rest is sold to the grid. The energy purchased from neighbours for proactive and enthusiastic houses is zero because of the fact that these houses do not have any shortage when selling to the main grid. Traditional houses purchase more energy from the grid than the neighbours since most of the houses consume more power during the evening time when there is no power from the solar generation. In order to gain more insights into the operation of EMSs at different stages while sharing energy among the loads of the neighbourhood in a microgrid, as well as the main grid, it is necessary to observe the energy profiles at the various time intervals rather than just for the whole day, which has been done in the following subsections.
9.1. Operating Modes of the EMS for Traditional Houses
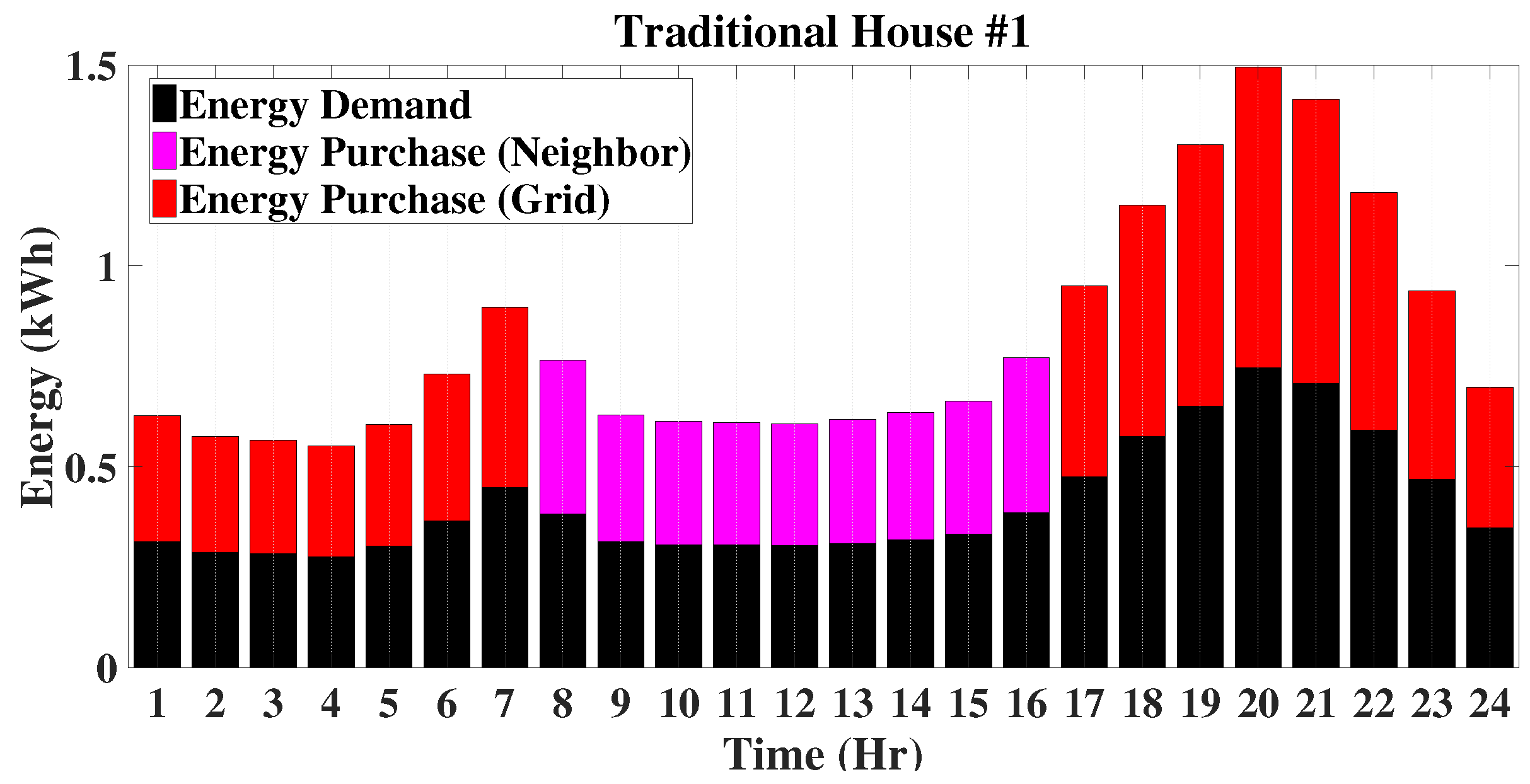
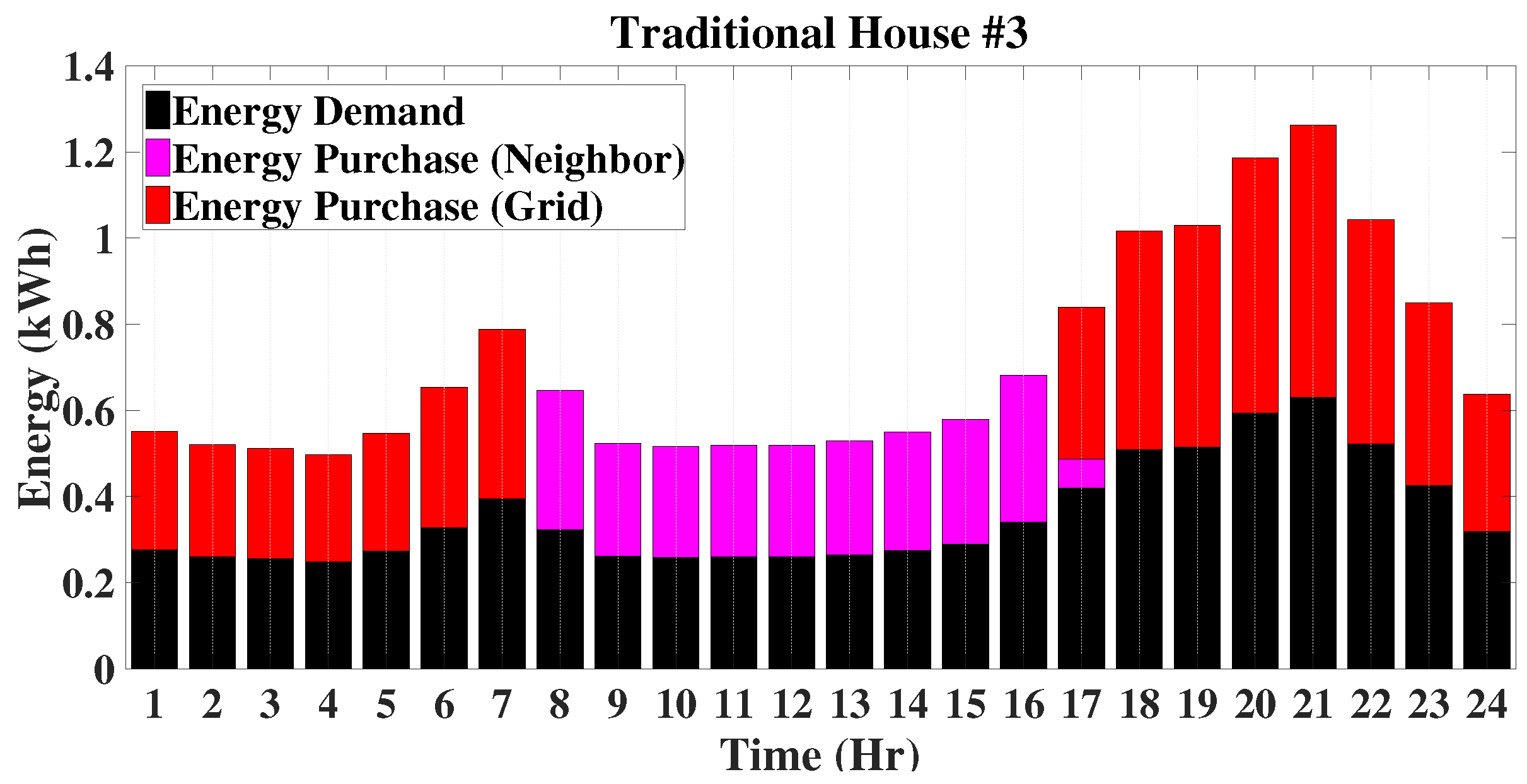
The operating modes of the EMS for traditional houses are discussed in terms of the energy trading framework in a transactive energy market. These modes are mainly discussed based on the energy profiles of different traditional houses for an entire period of twenty four hours (one day). These energy profiles for traditional houses include the energy demand, energy purchased from neighbours and energy purchased from the grid. As traditional houses are always short of energy, their demands in a power sharing energy framework are first met by purchasing energy from neighbours when there is abundant energy for sharing from proactive and enthusiastic neighbours. When the demands of traditional houses cannot be met by the local energy from the microgrid, it is purchased from the main the grid. The energy profiles of traditional houses are shown in
Figure 10,
Figure 11 and
Figure 12. Based on the energy profiles of traditional houses, the operating modes of the EMS are categorized into three distinct types as described below.
When there is no or very low solar generation from the solar PV units of proactive and enthusiastic houses in a microgrid, traditional houses cannot purchase energy from the neighbourhood. In this case, traditional houses solely depend on the utility grid to meet their energy demands. In this case, the energy balance can be written as follows:
The primary EMS of these houses will send the energy shortage information to the secondary EMS. This secondary EMS will first observe the overall energy excess, and in this situation, there will be no energy excess, rather just shortage, and this energy shortage information will be communicated with the tertiary EMS to purchase energy from the grid. From these energy profiles in
Figure 10,
Figure 11 and
Figure 12, it can be seen that Traditional House 3 (T3) operates in this mode from 18:00 h–07:00 h, which is the shortest among traditional houses as Traditional Houses 1 and 2 (i.e., T1 and T2) operate from 17:00 h–07:00 h.
In this operating mode, the excess power available from the proactive and enthusiastic neighbours is not sufficient to meet the load demands of traditional houses in a microgrid, and the remaining energy shortages of these traditional houses are met by purchasing energy from the main grid. Thus, the energy balance equation can be written as follows:
where
is the energy purchased from neighbours for a traditional house
of the set
for the time-interval
. From
Figure 10,
Figure 11 and
Figure 12, it can be seen that the traditional houses T2 and T3 operate in this mode for a very short time period, which is from 16:00 h–17:00 h. The house T2 operates during 08:00 h, while T3 operates during 17:00 h, and T1 does not operate in this mode.
When the amount solar generation from proactive and enthusiastic houses is much more than their load demands and the BESSs of enthusiastic houses are fully charged, there will be excess energy. In this mode, the load demands of traditional houses will fully be met by the excess power from the neighbourhood which usually occurs during solar peak hours on a sunny day. In this instance, the energy balance equation can be written as follows:
From
Figure 10,
Figure 11 and
Figure 12, it can be seen that T1 and T3 operate in this mode from 08:00 h to 16:00 h, while T2 starts at 09:00 h, but finishes at the same time as other houses.
9.2. Operating Modes of the EMS for Proactive Houses
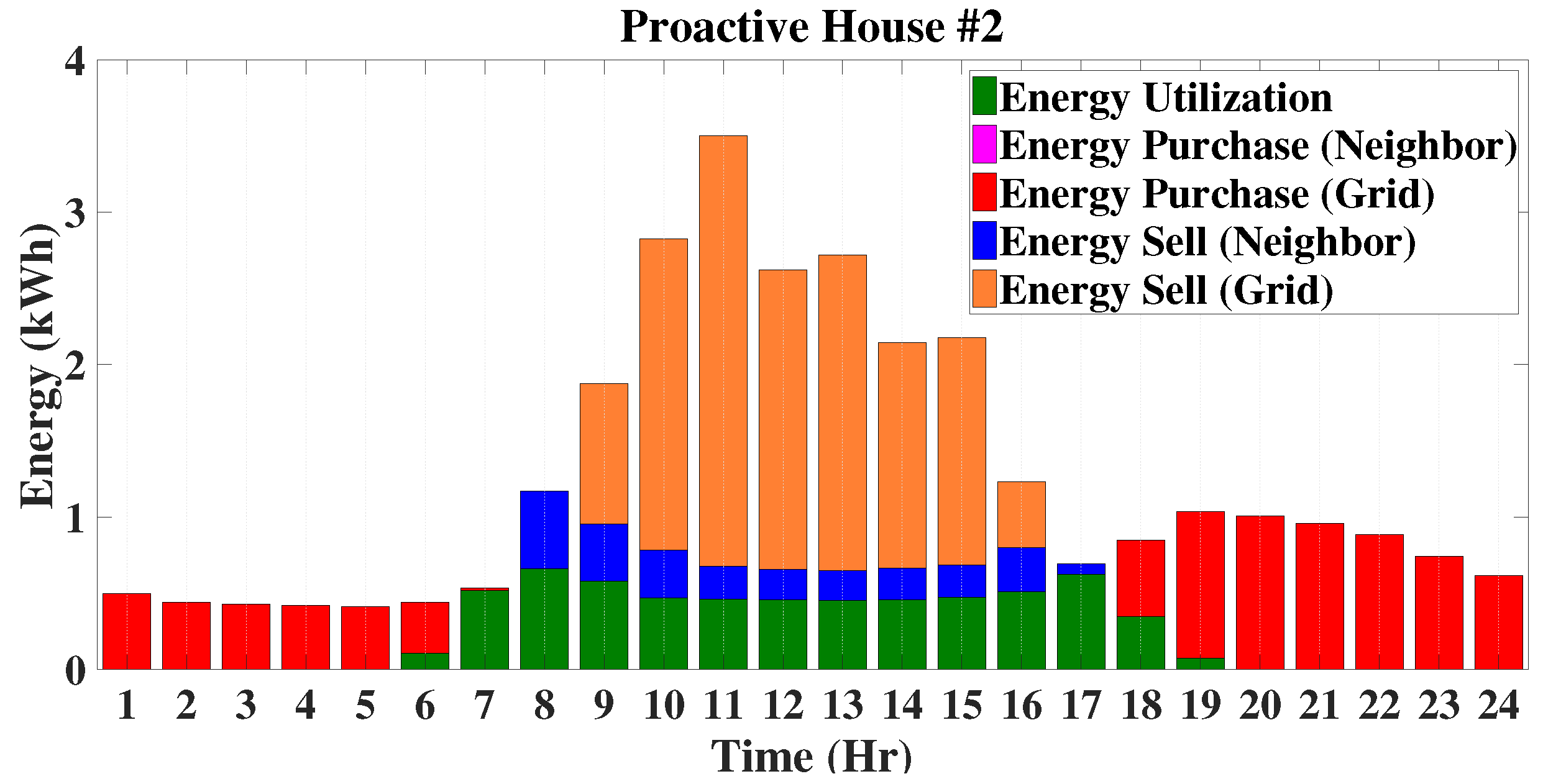
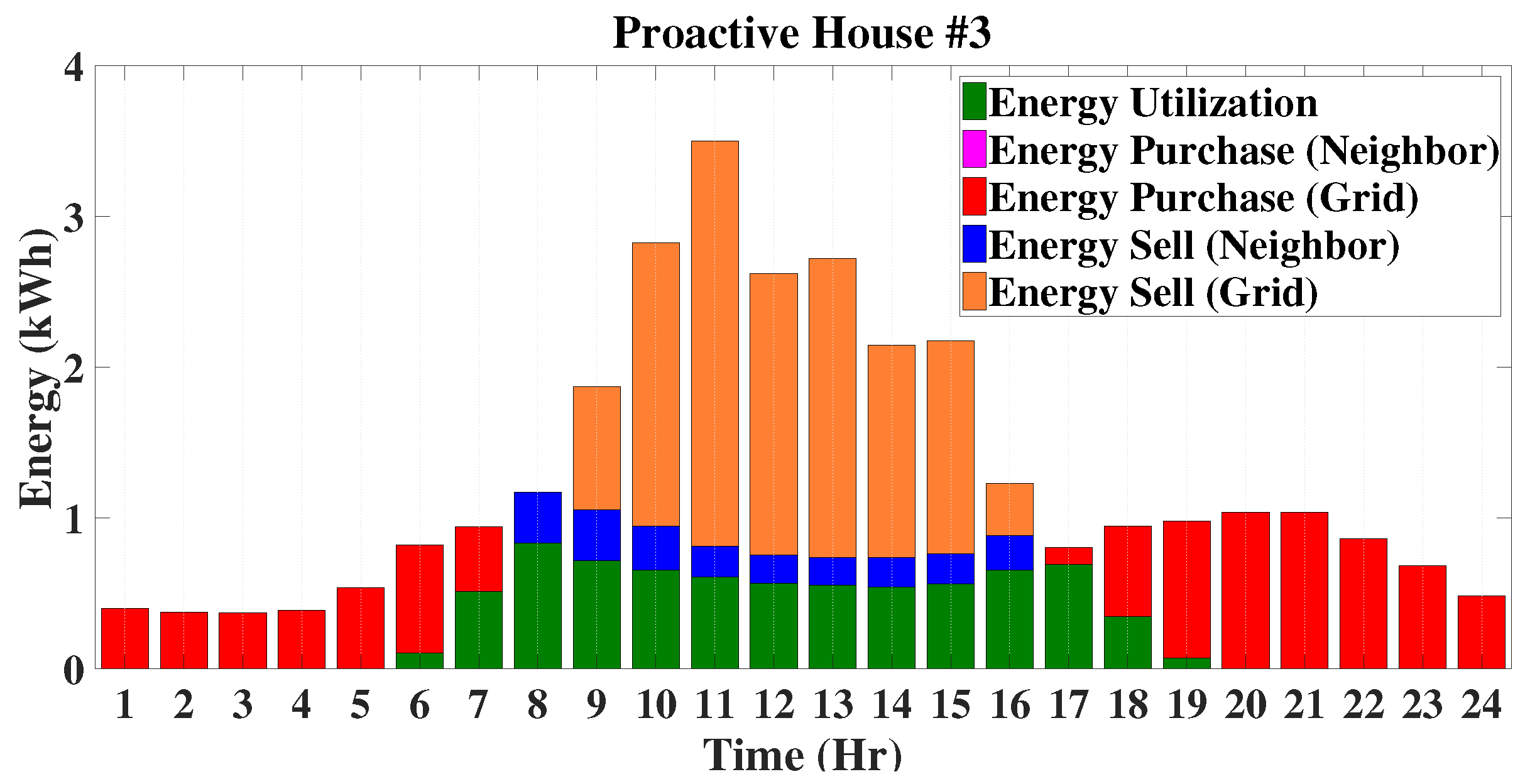
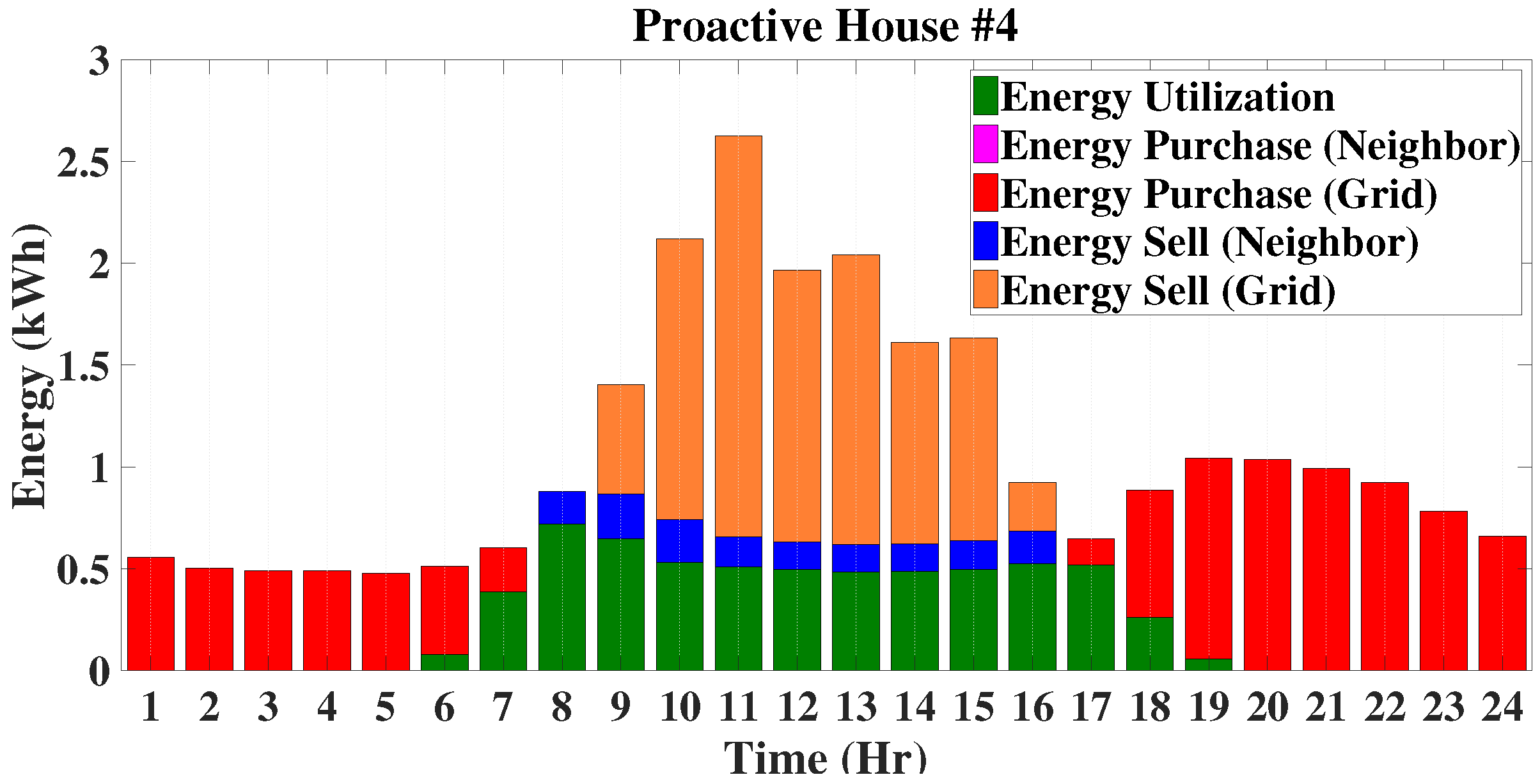
In this case, the operating modes of the EMS for proactive houses are presented in a similar manner to those of traditional houses. The energy profiles of these houses are also quite similar to those of traditional houses, i.e., the energy profiles include energy demand, energy purchased from the grid and energy purchased from neighbours. In addition to these profiles of traditional houses, the energy profiles of proactive houses will include energy sold to the grid, as well as energy utilized from the solar PV unit. These modes are mainly discussed based on the energy profiles of different proactive houses for an entire period of 24 h. It is obvious that, generally, purchasing energy from neighbours, as all are located in the same geographical area, would not benefit proactive houses. When a proactive house has a shortage of energy generation, other houses within the microgrid would have lower generation, as well. After meeting individual load demands, proactive houses sell the excess energy first to neighbours, especially traditional ones, and the rest to the grid. The energy profiles of proactive houses are shown in
Figure 13,
Figure 14,
Figure 15 and
Figure 16. Based on the energy profiles of proactive houses, the operating modes of the EMS are categorized into four distinct types as described below.
This mode is quite similar to that as discussed for the traditional houses, and in this mode, the only option to purchase energy for proactive houses is the main power grid. The energy balance equation for this operating mode can be written as follows:
When the power generated from the solar PV units of proactive houses is less than their own load demands, as well as there is no excess power to purchase from neighbours, the rest of the demand is met by purchasing energy from the grid. Thus, the load balance can be represented as follows:
From
Figure 13, it can be seen that Proactive House 1 (P1) operates in this mode between 06:00 h and 08:00 h in the morning time and in the evening from 17:00 h–19:00 h. In the morning, Proactive House 2 (P2) operates in this mode only for one hour (06:00 h), while in the evening, from 18:00 h–19:00 h, which can be seen from
Figure 14.
Figure 15 and
Figure 16 indicate that both Proactive House 3 (P3) and Proactive House 4 (P4) operate in this mode from 06:00 h–07:00 h in the morning and from 17:00 h–19:00 h in the evening.
In this mode, the power generated by the solar PV unit is more than the load demand, and the excess energy is shared with the neighbours according to the proposed power sharing priorities. For this operating mode, the energy balance equation will be as follows:
From
Figure 13, it can be seen that P1 does not operate in this mode, whereas the operating period for P2 in this mode is between 07:00 h and 08:00 h in the morning and 17:00 h in the afternoon, as shown in
Figure 14. The remaining two proactive houses (P3 and P4) sell energy to the neighbours between 07:00 h and 08:00 h in the morning, which is shown in
Figure 15 and
Figure 16, respectively.
This operating mode exists if there is still excess energy after locally meeting the load demand of traditional houses. In this situation, proactive and enthusiastic houses sell the excess energy both to the neighbours and power grid. The energy balance equation can written as follows:
9.3. Operating Modes of the EMS for Enthusiastic Houses
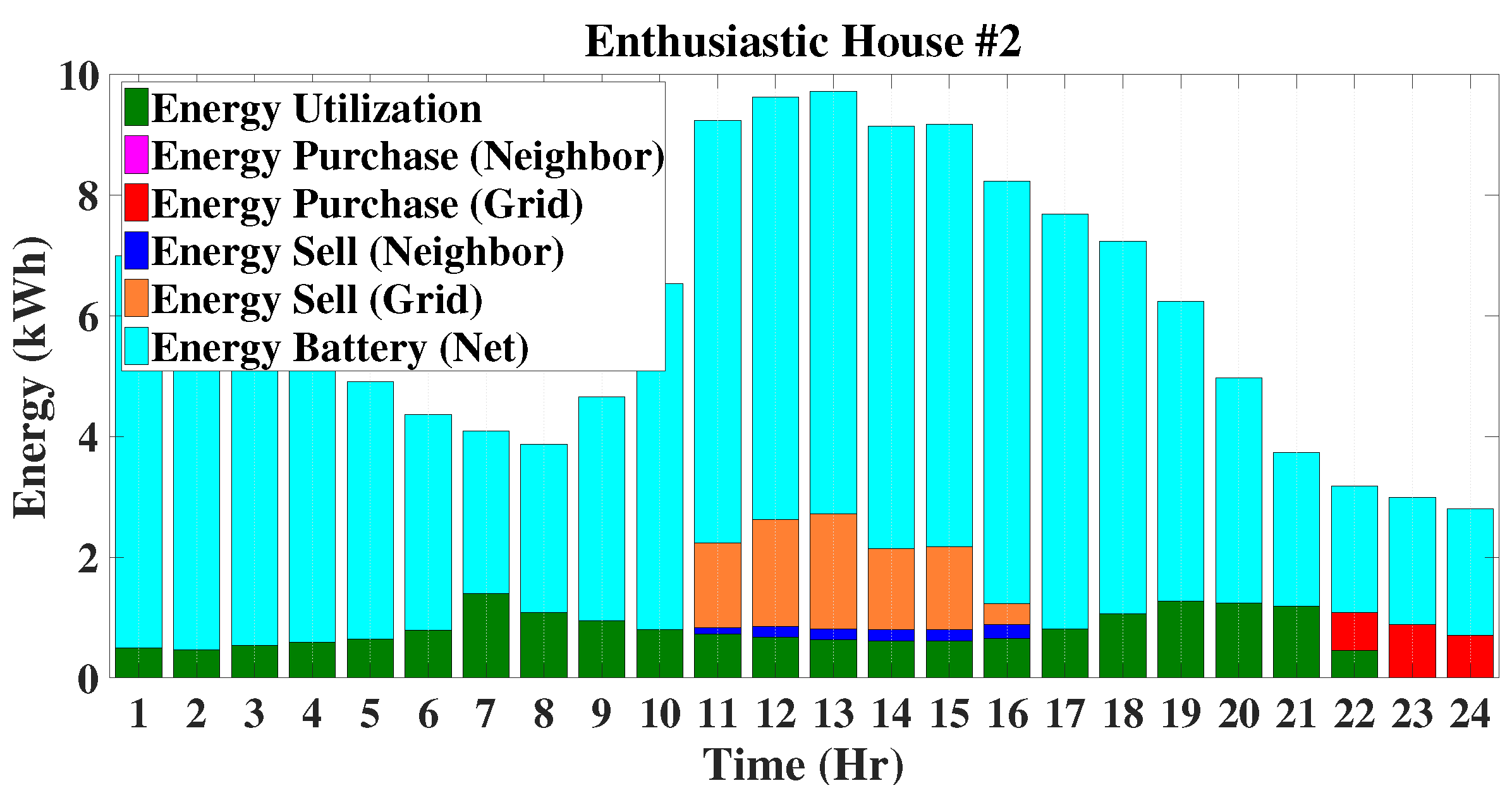
Enthusiastic houses utilize energy from solar PV units and BESSs before purchasing energy from the grid to meet the energy demand. Similarly, the excess energy from these enthusiastic houses is utilized to charge the BESS first before sharing with neighbours and/or selling back to the grid. In this operating mode, the enthusiastic houses are not buying any energy from neighbours to charge their BESSs. The energy profiles of enthusiastic houses are exactly similar to those of proactive houses, and the only addition is the incorporation of the overall energy status of BESSs. The energy profiles for enthusiastic houses are shown in
Figure 17 and
Figure 18. Based on the hourly operations of EMSs, the operating modes for enthusiastic houses can be represented by the following six situations.
When there is no solar generation and the BESS SOC is below its lower threshold, i.e.,
, the only option is to purchase energy from the grid. Thus, the energy balance equation for this operating mode of enthusiastic houses can be written as follows:
The energy profiles for enthusiastic houses are shown in
Figure 17 and
Figure 18, from where it can be seen that E1 and E2 operate in this mode from 21:00 h–24:00 h and 23:00 h–24:00 h, respectively. From
Figure 17 and
Figure 18, it can be seen that there is still energy available from the BESSs while purchasing from the main grid. This occurred as the energy available from the BESSs is the net energy obtained from other cases as discussed in the following.
In this case, the BESSs of enthusiastic houses provide the full support to meet the load demands, and the energy balance can be discussed through the following equations:
where
is the utilized energy from the BESS for the enthusiastic house
of the set
for the time-interval
. The house E1 operates in this mode between 01:00 h and 05:00 h in the morning and during 19:00 h in the evening, while E2 operates in this mode between 01:00 h and 06:00 h in the morning and between 19:00 h and 21:00 h in the evening, as shown in
Figure 17 and
Figure 18, respectively.
In this situation, the only option to supply the load demand of enthusiastic houses is to discharge the BESS and purchase energy from the grid. For such a condition, the energy balance equation can be written as follows:
This mode exists when the BESS does not have enough capacity to supply the full load demand. From
Figure 17 and
Figure 18, it can be said that this mode exists for E1 during 06:00 h and 20:00 h and that of for E2 during 22:00 h.
This mode can be considered as the situation when the solar PV units of enthusiastic houses have just started generating power, which is not enough to supply the load demand, as well as the BESSs are not in a situation to provide the full support to meet the load demand. The energy balance equation for this mode can be written as follows:
From
Figure 17, it can be seen that E1 has this mode only during 07:00 h, while E2 does not operate in this mode, which can be seen from
Figure 18.
In this operating mode, the load demands of enthusiastic houses are usually met from the output power of solar PV units and from the stored energy of BESSs. In this mode, the energy balance can be represented by the following equation:
For E1, this mode occurs from 08:00 h–10:00 h in the morning and 17:00 h–18:00 h in the evening. On the other hand, E2 operates in this mode during 07:00 h–10:00 h in the morning and 17:00 h–18:00 h in the evening. For E2, this mode lasts for a longer period as the battery capacity of E2 is larger than that of E1.
If there is sufficient energy after meeting self-load and charging battery, the rest is shared to serve loads of neighbours. If there is still excess energy after meeting the demand of neighbours, it will be sold to the grid. In this case, the energy balance equation will be as follows:
From
Figure 17 and
Figure 18, it can be seen that both E1 and E2 operate in this mode from 11:00 h–16:00 h, which are usually the solar peak hours.
Thus, it can be said that the primary EMSs facilitate appropriate energy sharing among different houses in a microgrid. However, the secondary EMS does the calculation of overall energy shortage and excess, which are discussed in the following subsection.
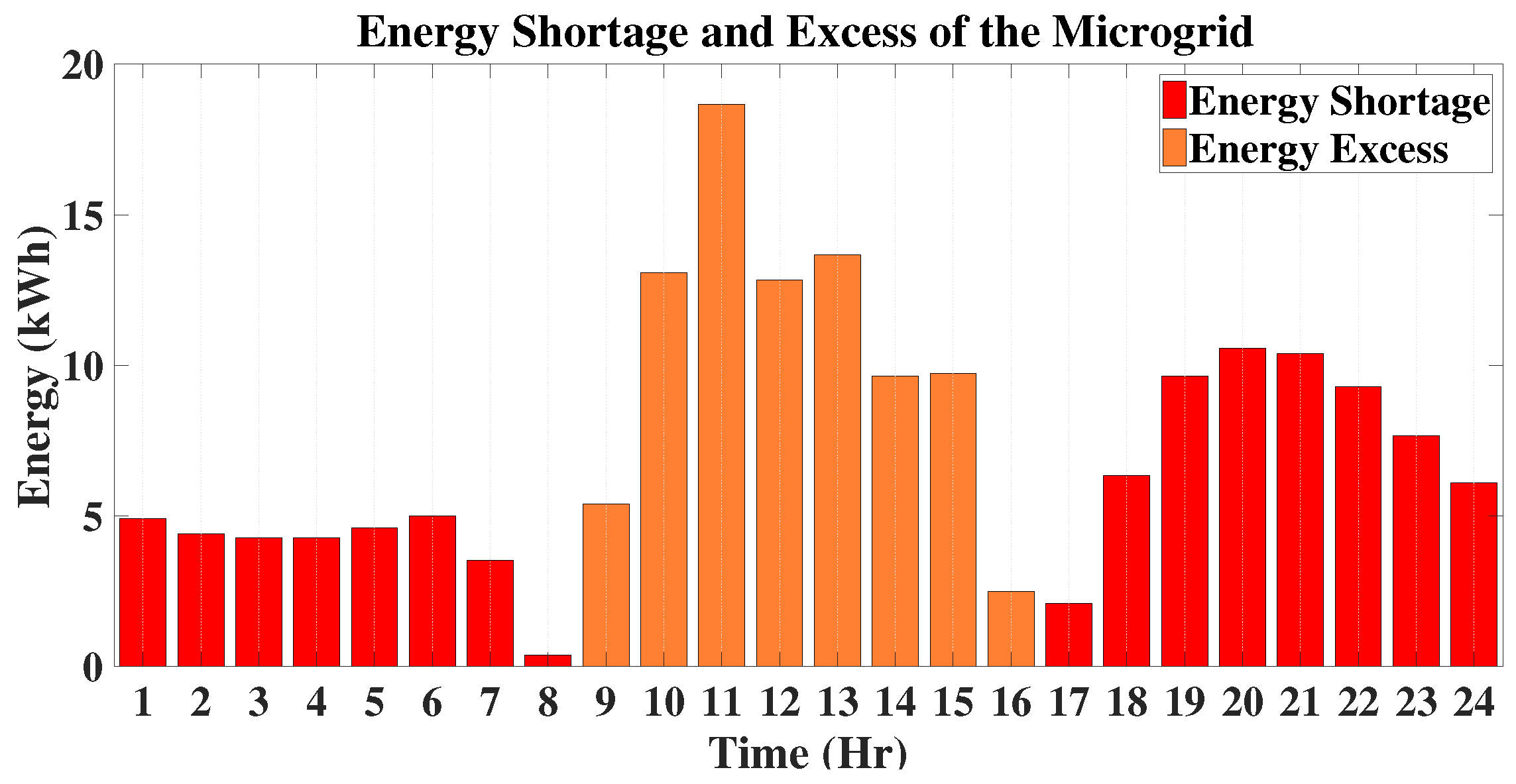
9.4. Overall Energy Shortage and Excess
There will be energy shortage if the demand of all houses is not met even after sharing the excess power from the proactive and enthusiastic houses. In this cases, the overall situation for the microgrid will be to purchase energy from the main grid. This usually happens in early morning and from evening to the late night. However, the excess energy, after meeting the local demand can be sold to the grid, which happens during the solar peak hours. The overall energy sold (excess) to the grid, as well as purchased (shortage) from the grid for the microgrid is presented in
Figure 19. From
Figure 19, it is clear that during the solar peak hours, there is no shortage of energy, and the excess energy is fed back to the grid. However, some energy needs to be purchased from the grid when the Sun is not shining. The purchased energy is the highest during evening coinciding with peak load profiles of the individual houses.
9.5. Seasonal Variations and Cost-Benefit Analysis
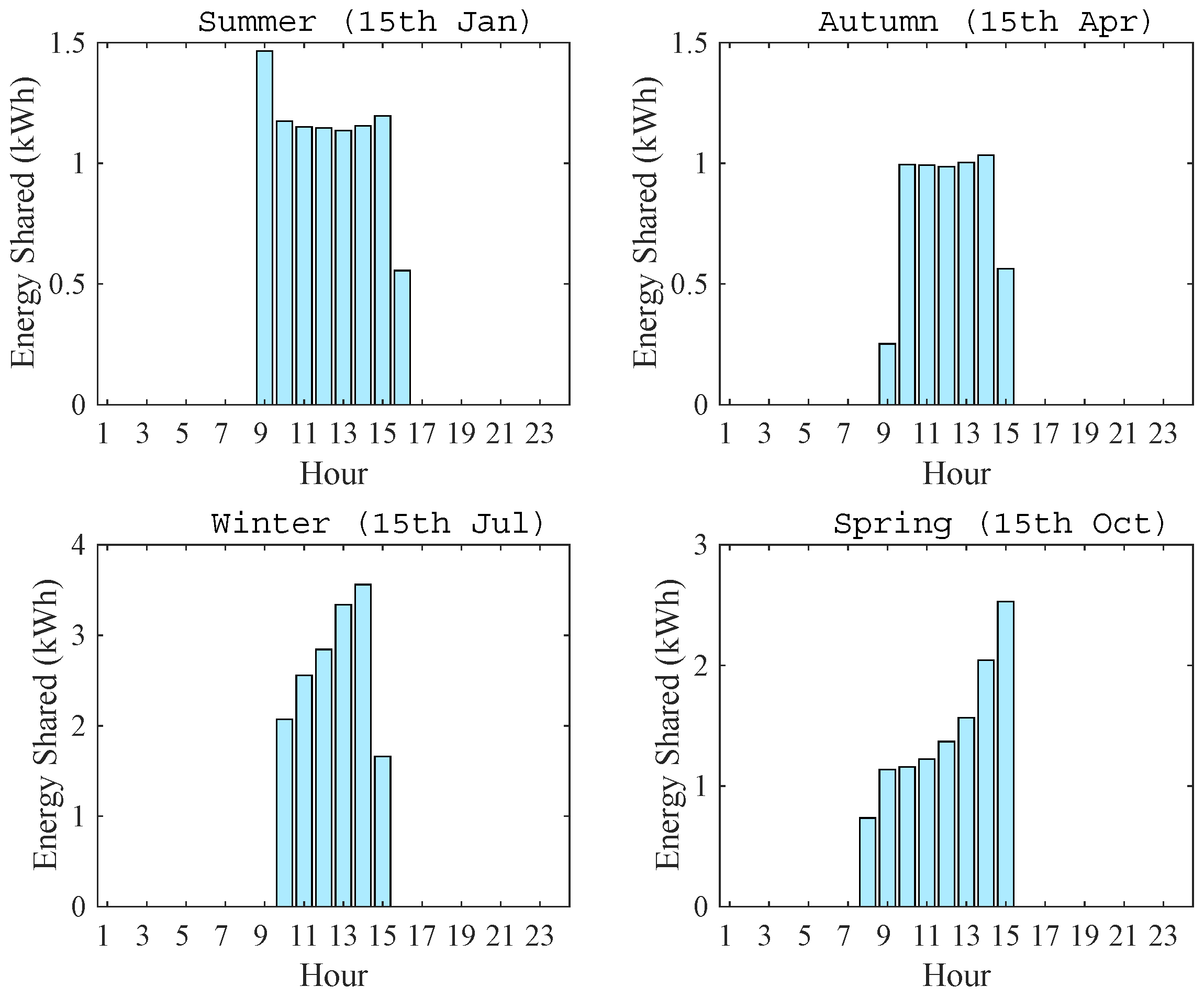
The energy sharing with the proposed hierarchical EMS in a representative day for four seasons is shown in
Figure 20. The highest energy sharing occurs on 15 July among the four cases as shown in
Figure 20. The energy sharing in the spring is comparatively lower than the winter. Although the energy generation is the lowest during winter, the high demand together with energy availability for sharing results in the highest energy sharing during this particular day. The net annual energy profile of the microgrid is shown in
Table 7 from where it can be seen that the proposed transactive energy sharing scheme would allow up to 31% grid independent operation of the microgrid.
The payback period is calculated for the investment in the microgrid under the flat tariff structure by considering the investment cost, replacement cost, expense and earning. The overall cost-benefit analysis for the proposed microgrid project is shown in
Table 8. From simple payback calculation as presented in
Table 8, it can be seen that the proposed energy sharing approach is financially beneficial. The return falls within the life time (10 years) of the BESS. The net present value (NPV) is calculated by using an interest rate of 4%, the value of which is positive. From
Table 8, it can be seen that the discounted payback period is longer than simple payback, but this falls within the life time (25 years) of solar PV units.
Finally, it can be said that the developed hierarchical EMS framework can be applied to any situation in a transactive energy market, which is very clear from the results under different operating modes. Moreover, the proposed energy sharing and cost-benefit analysis with the hierarchical EMS provide effective solutions under different operating scenarios.
10. Conclusions
A detailed energy sharing framework for managing energy in a transactive energy trading market is presented through the development of a hierarchical EMS. The primary layer of the hierarchical EMS is used to manage the energy of all houses and passing the information of overall excess and shortage energy to the secondary EMS, which is further responsible for energy sharing among the houses and communicating with the tertiary layer. The tertiary layer of the EMS oversees the energy management task and performs the energy trading activities with the grid. A microgrid with nine houses including three different house categories is considered in this paper. In this microgrid, different houses with various renewable energy profiles form an energy sharing and trading mechanism based on the developed analytical framework. The energy sharing results are presented for a typical summer day by considering different operating modes. These operating modes reflect the possibilities of all situations that could happen in a microgrid with a real-time operation. Simulation results clearly indicate the effectiveness of the proposed hierarchical EMS in terms of energy sharing under different operating modes.
The proposed mechanism considers a neighbourhood with traditional consumers, which have no renewables, and prosumers with solar PV units and BESSs, which represent the common picture of residential neighbourhoods in Australia. However, the proposed mechanism is fully distributed and scalable. As a result, different types of other distributed energy resources such as heat pumps, micro-wind and fuel cells can be integrated with the proposed architecture. Moreover, the houses can participate in the form of a community or individually. The proposed framework is a way forward for an energy independent microgrid; however, the energy management of the BESS requires multi-time step decision making considering future energy values, and future works will be devoted to this issue. Moreover, a local energy market needs to be in place in order to enable energy sharing among neighbours. In these local markets, the participants with energy excesses can be considered as sellers, while the participants with energy shortages can be considered as buyers. In the local energy markets, sellers will announce the amount of energy excess along with a price range, and buyers will bid to purchase the energy. The energy sharing and trading mechanisms in local energy markets can be formulated as a multi-player non-cooperative game, which can be autonomously operated through the intelligent EMS. Future works will also focus on developing such energy trading mechanisms.