Numerical Simulation of Hydraulic Fracture Propagation Guided by Single Radial Boreholes
Abstract
:1. Introduction
2. Establishment of a Fluid-Solid Coupling Mathematical Model and Its Finite Element Discretization
2.1. Stress Balance Equation
2.2. Continuity Equation
2.3. Boundary Conditions
2.4. Finite Element Discretization Method and Stress-Seepage Coupling Equation
3. Numerical Simulation of Propagation of Hydraulic Fracture
3.1. Introduction to the Model
3.1.1. Simulation of Initial Fracture
3.1.2. Level-Set Simulation of Fracture Propagation
3.1.3. Criteria for Initiation of Fracture
3.1.4. Damage Evolution Law
3.1.5. Energy Release Rate Criterion
3.1.6. Solution
3.2. Assumptions
- (1)
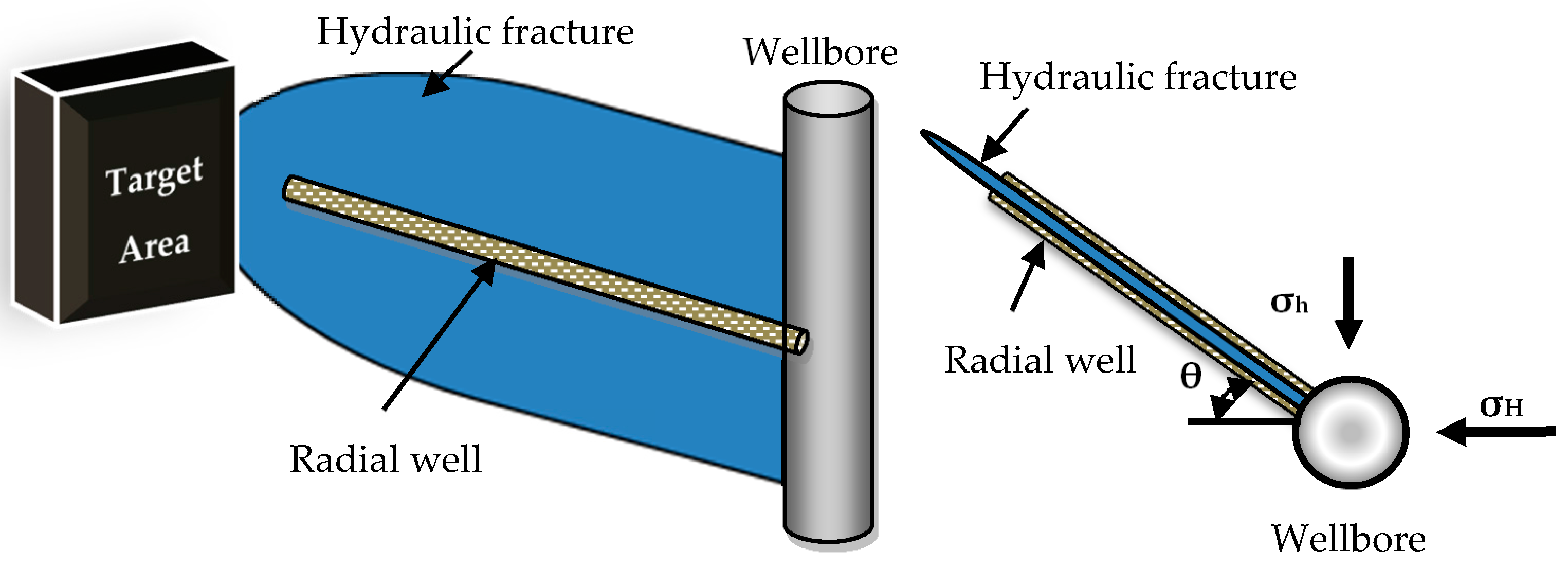
- Only a strip of hydraulic fracture is generated during fracturing, which is initiated along the azimuth of the radial borehole [34].
- (2)
- The formation rock is isotropic.
3.3. Fundamental Parameters of Model
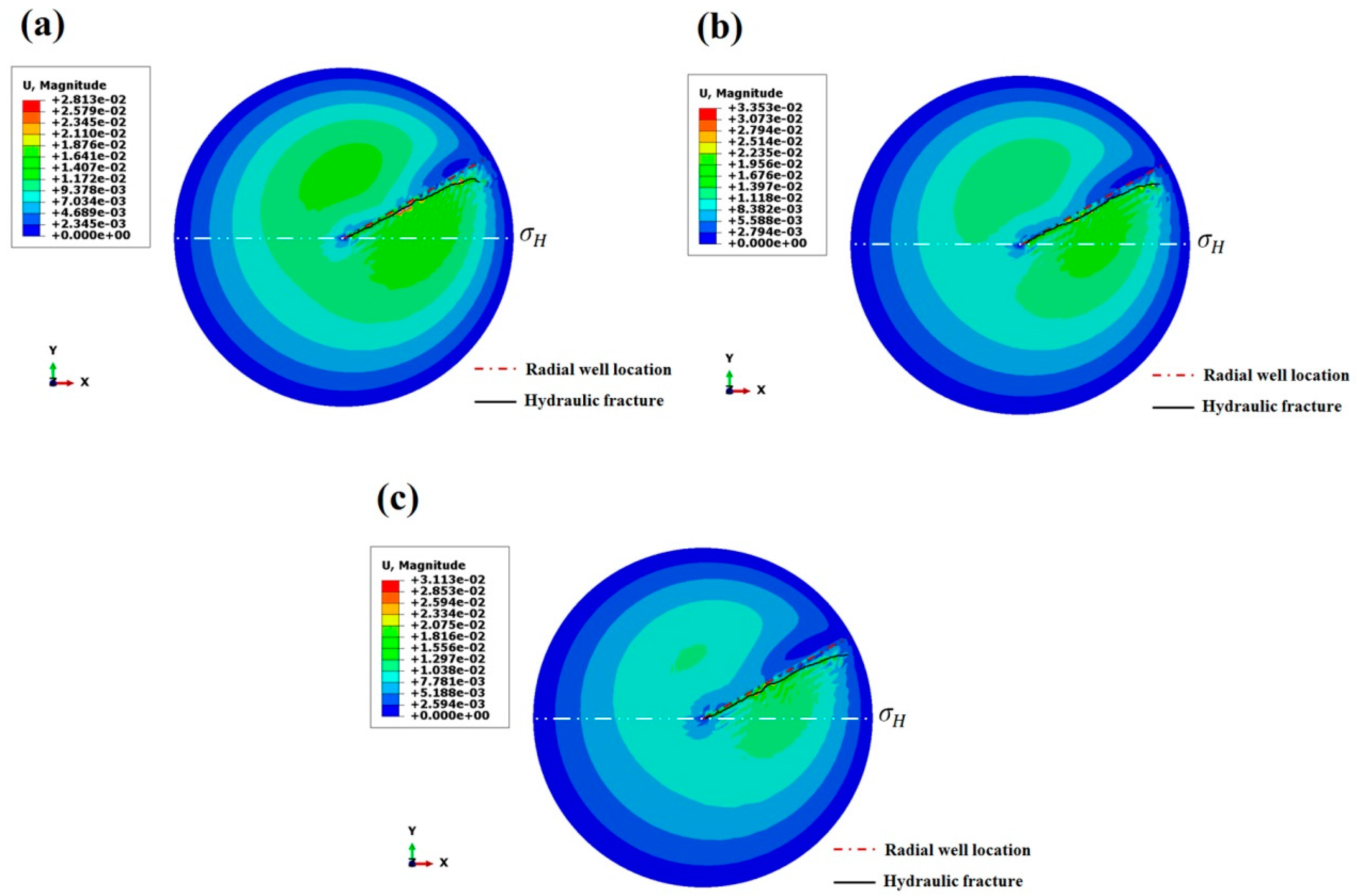
4. Analysis of Simulation Results
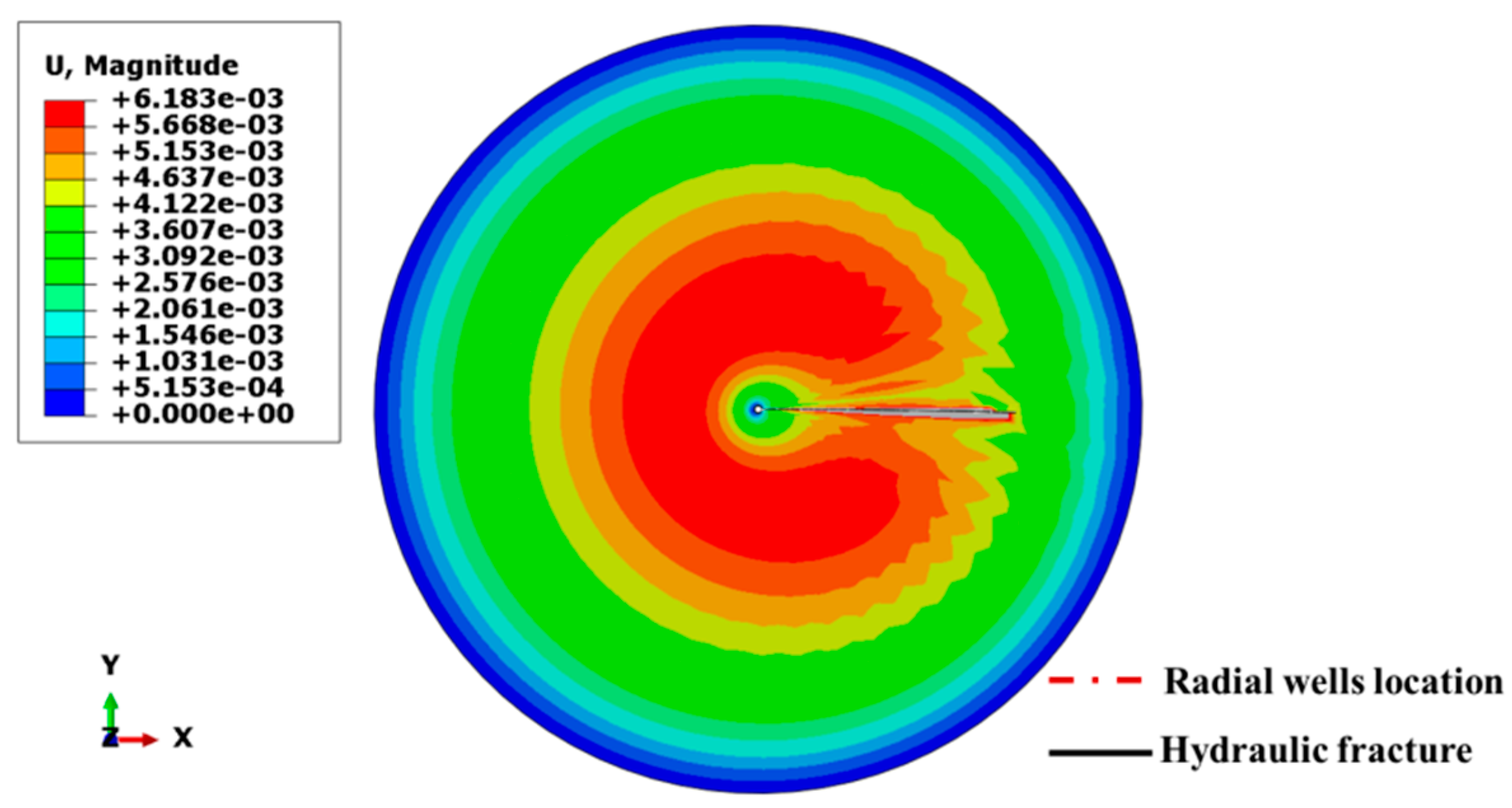
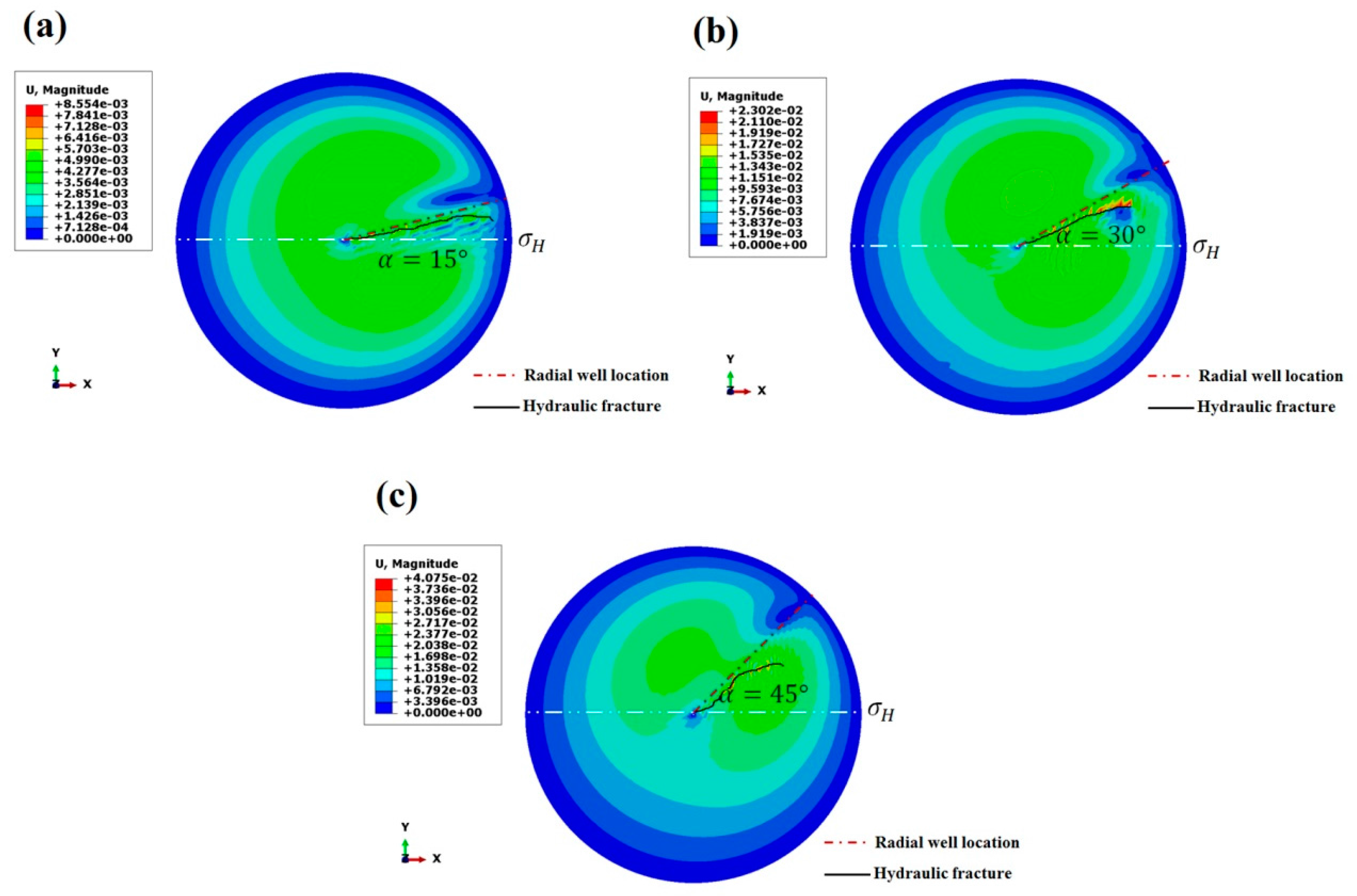
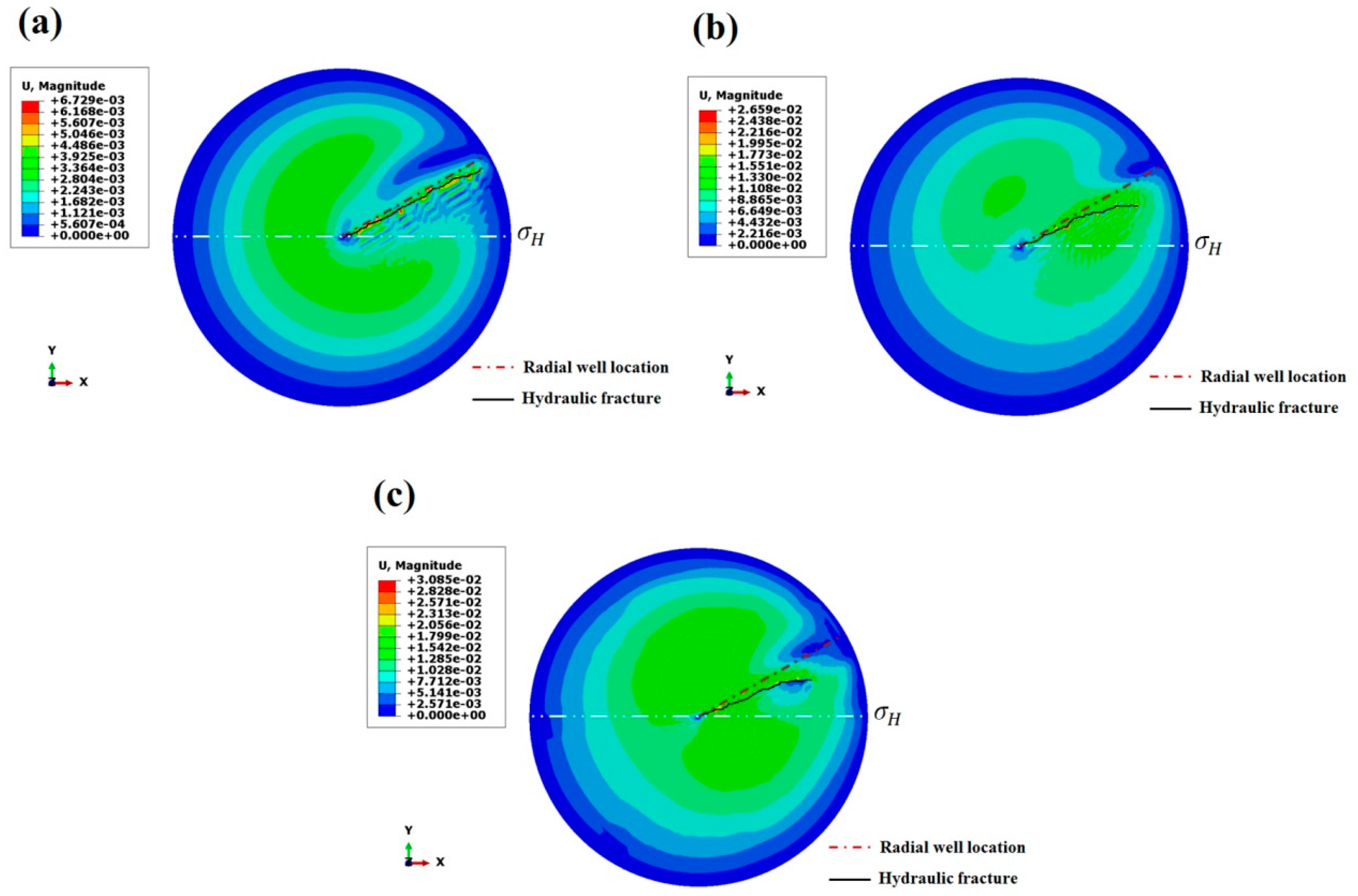
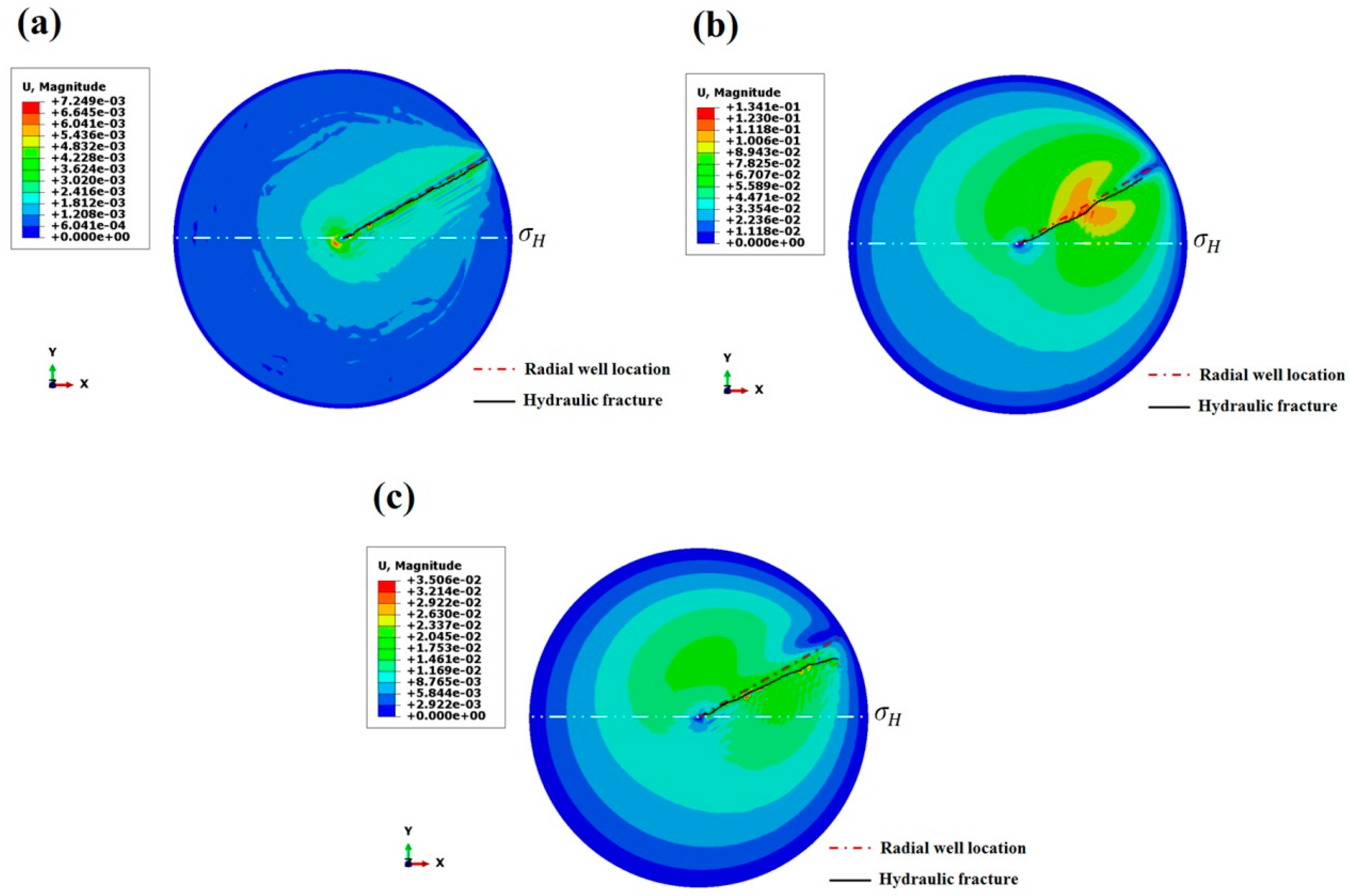
4.1. Azimuth of Radial Borehole
4.2. Horizontal In-Situ Stress Differences
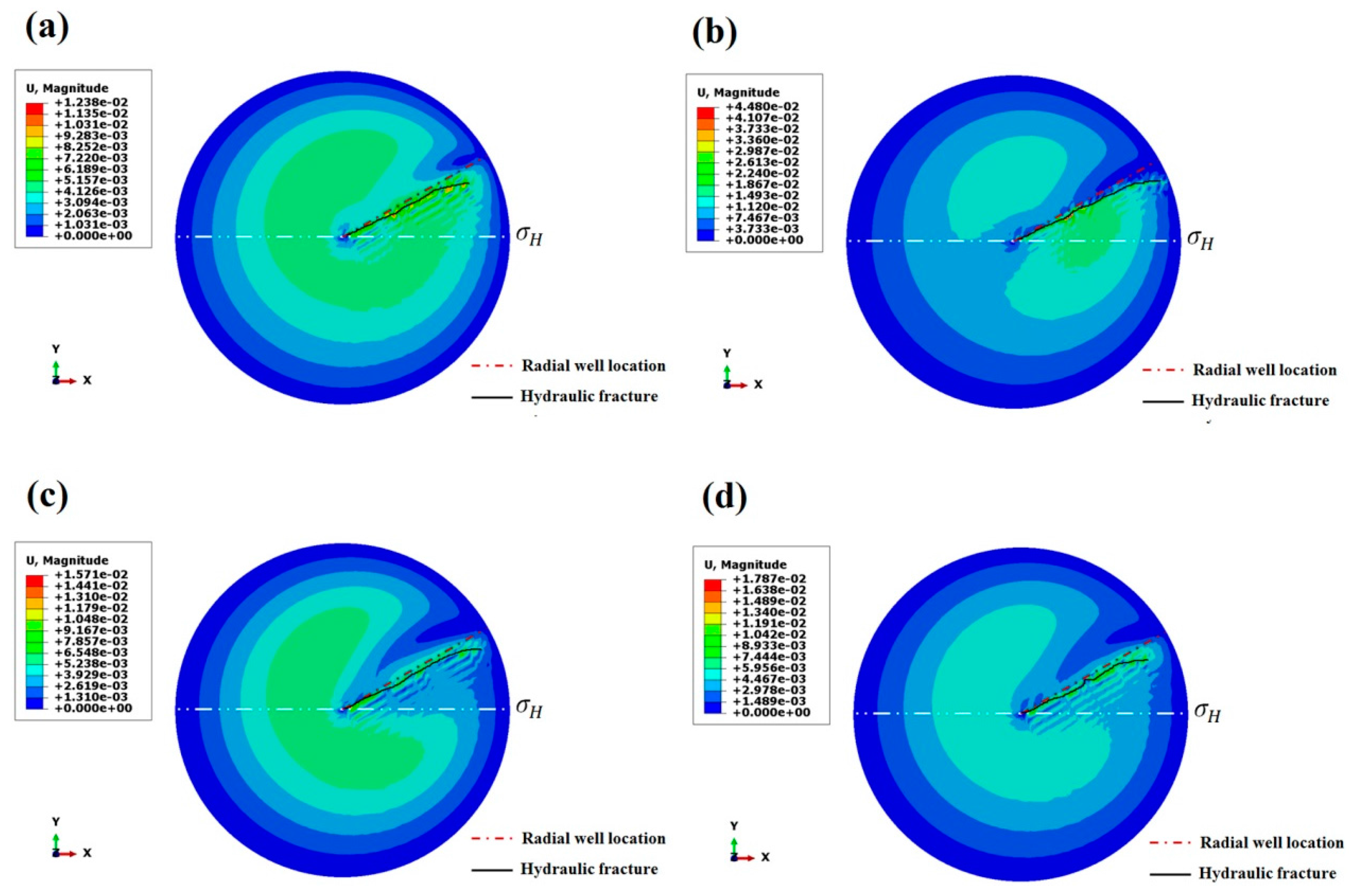
4.3. Radial Borehole Diameter
4.4. Length of Radial Borehole
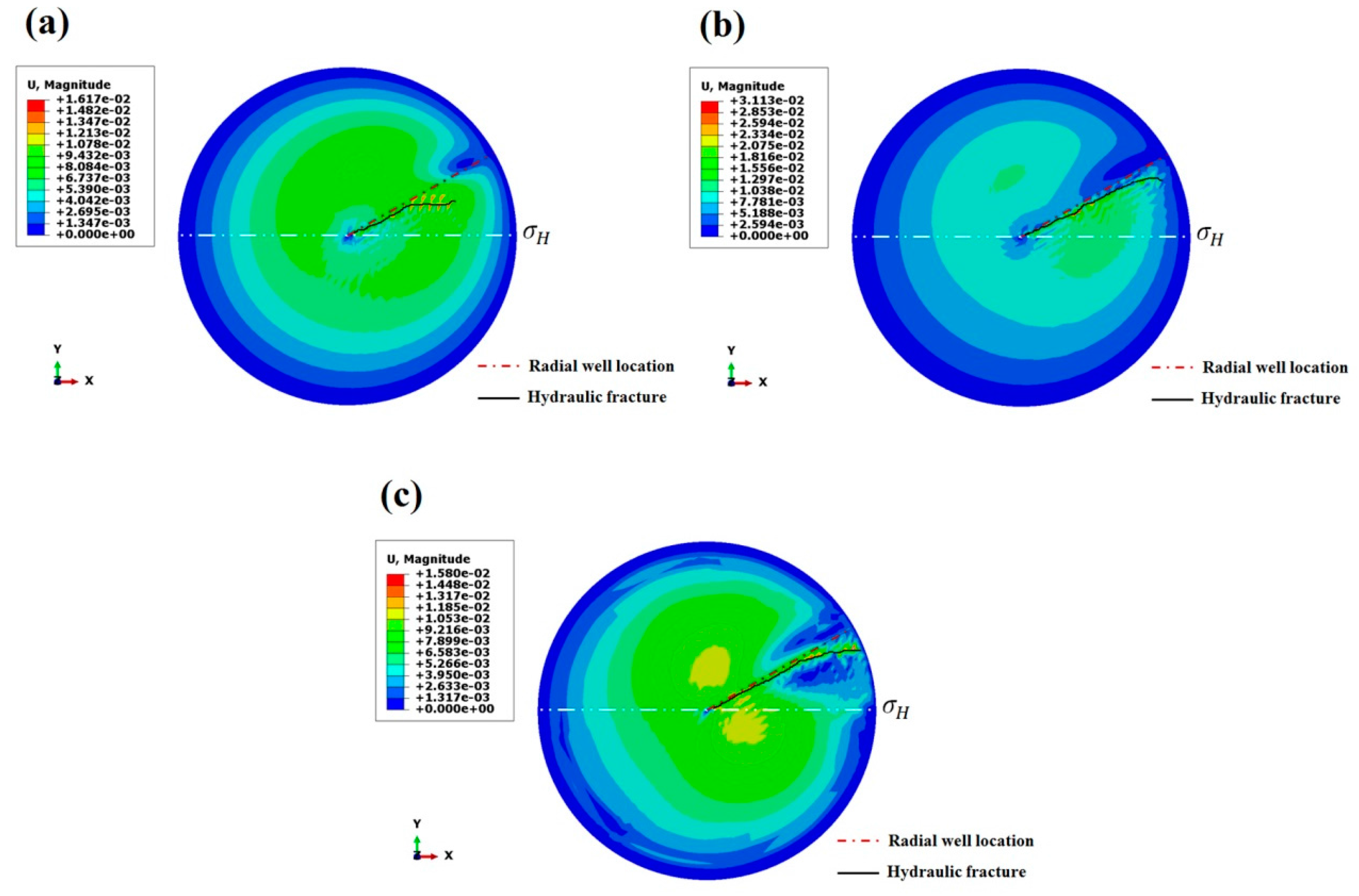
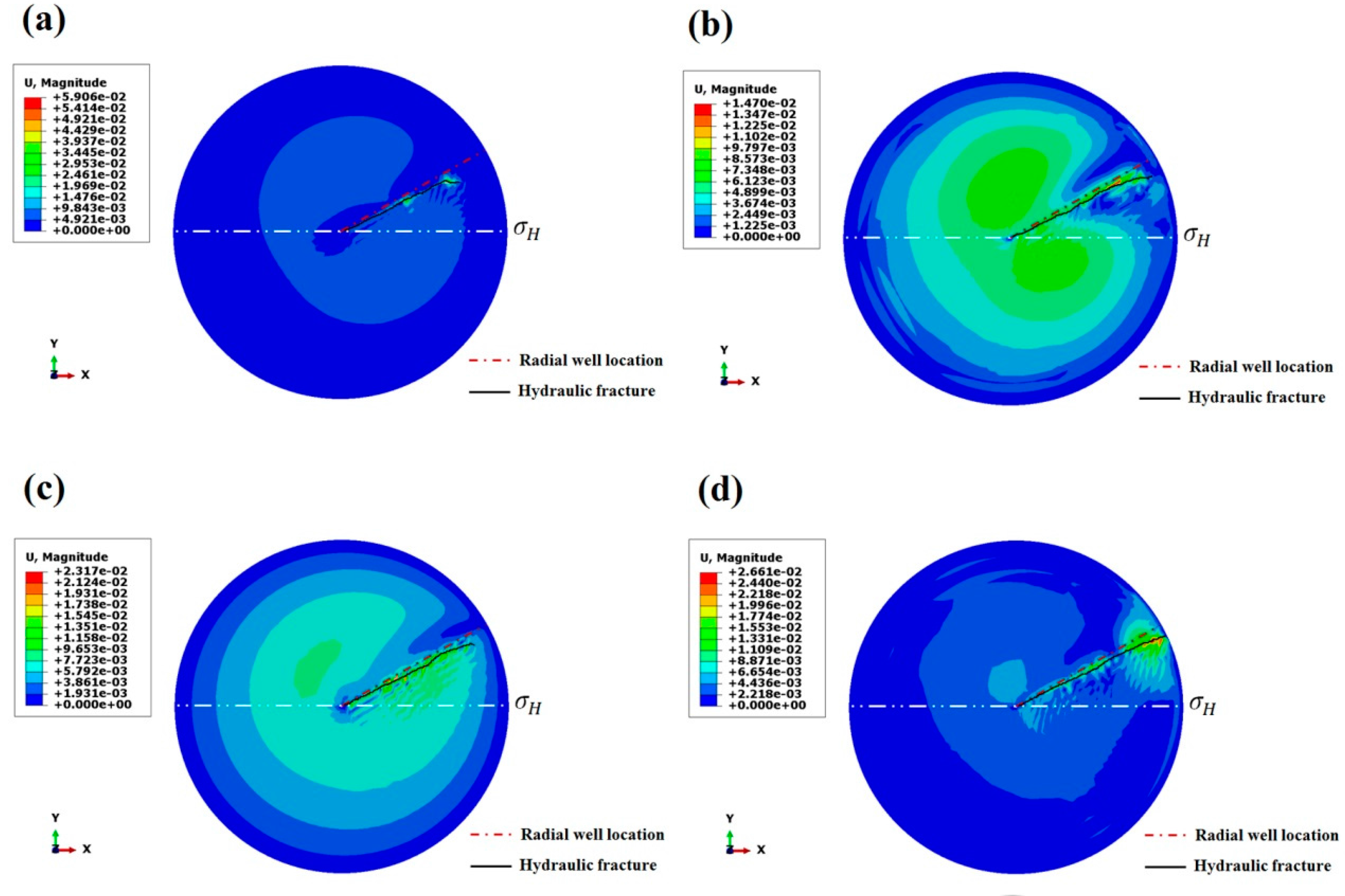
4.5. Young’s Modulus of Reservoir Rock
4.6. Poisson’s Ratio of Reservoir Rock
4.7. Reservoir Permeability
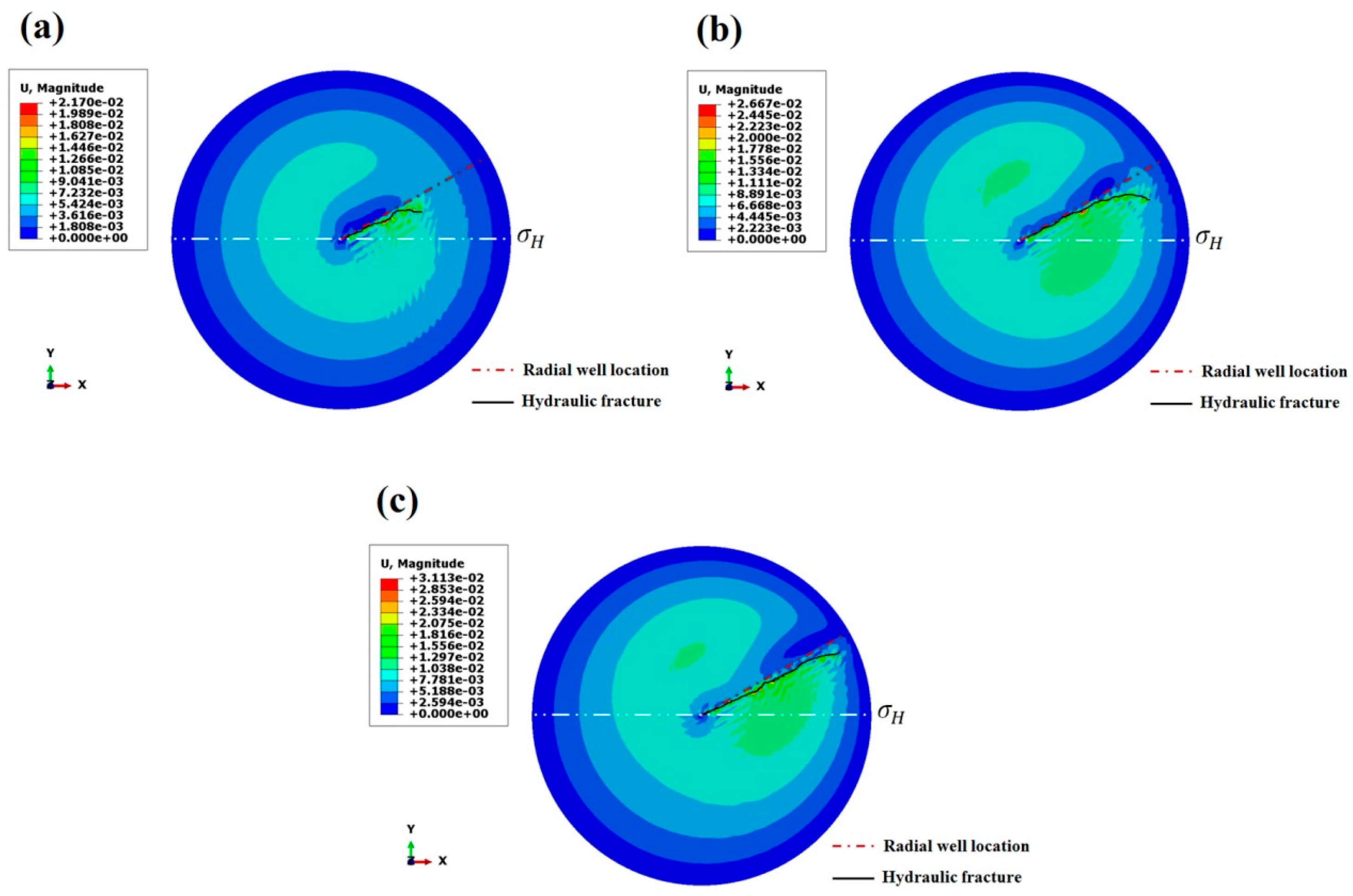
4.8. Fracturing Fluid Viscosity
4.9. Fracturing Fluid Injection Rate
4.10. Gray Correlation Analysis of Guidance Factors
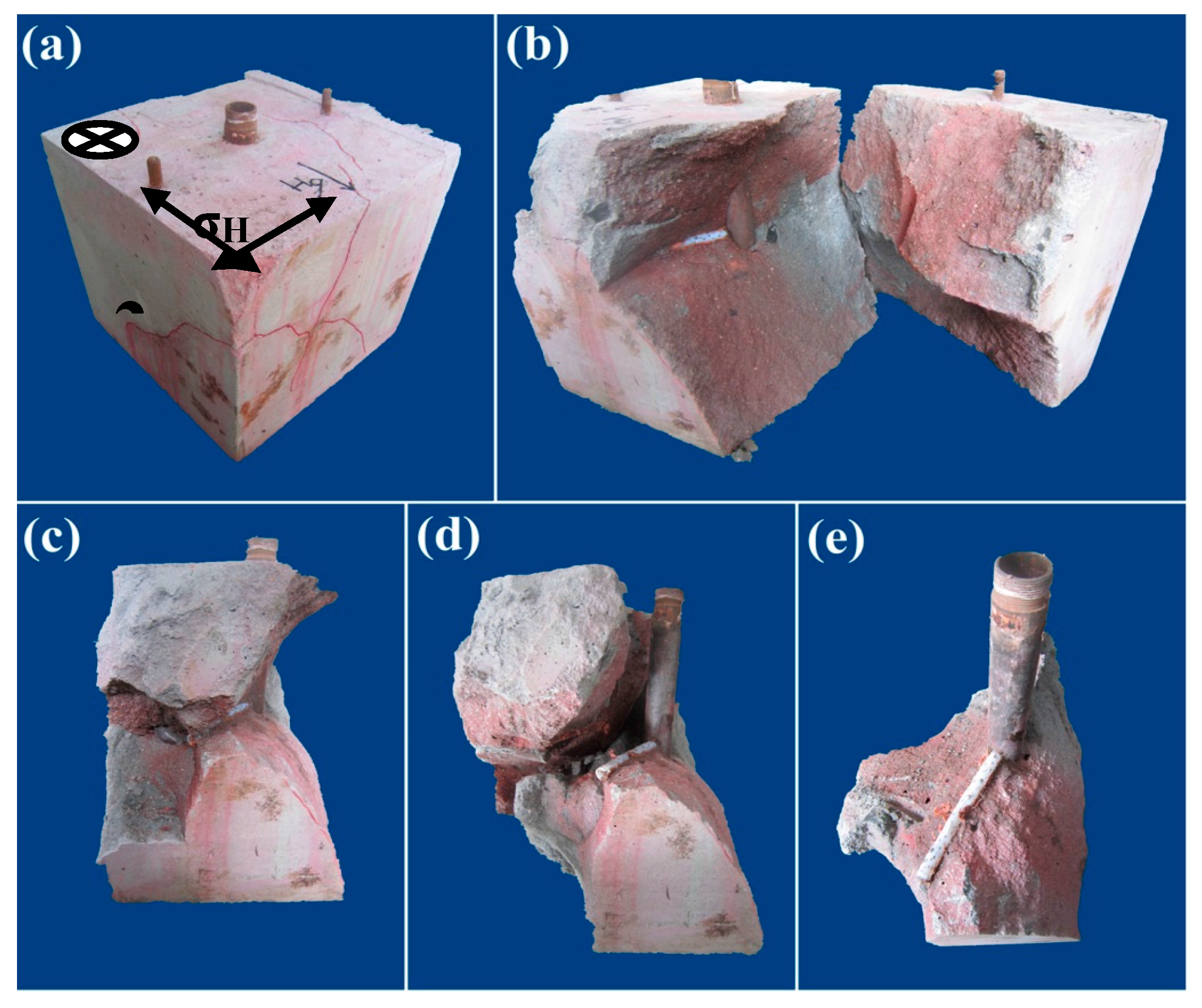
5. Experimental Verification
6. Conclusions and Suggestions for Future Work
- (1)
- The influence of in-situ stress could be overcome by scientifically arranging the single radial borehole under certain reservoir conditions, which realizes directional propagation towards target area. Thus, the problem that the hydraulic fracture only propagates along the direction parallel to horizontal maximum in-situ stress, and the available wellbores fail to develop the remaining oil and trap reservoir, and complex multi-fractures tend to generate in the immediate vicinity of wellbore, which makes it hard to realize the deep penetration of fractures, are solved to improve the effectiveness of fracturing operations and recovery efficiency in oil fields.
- (2)
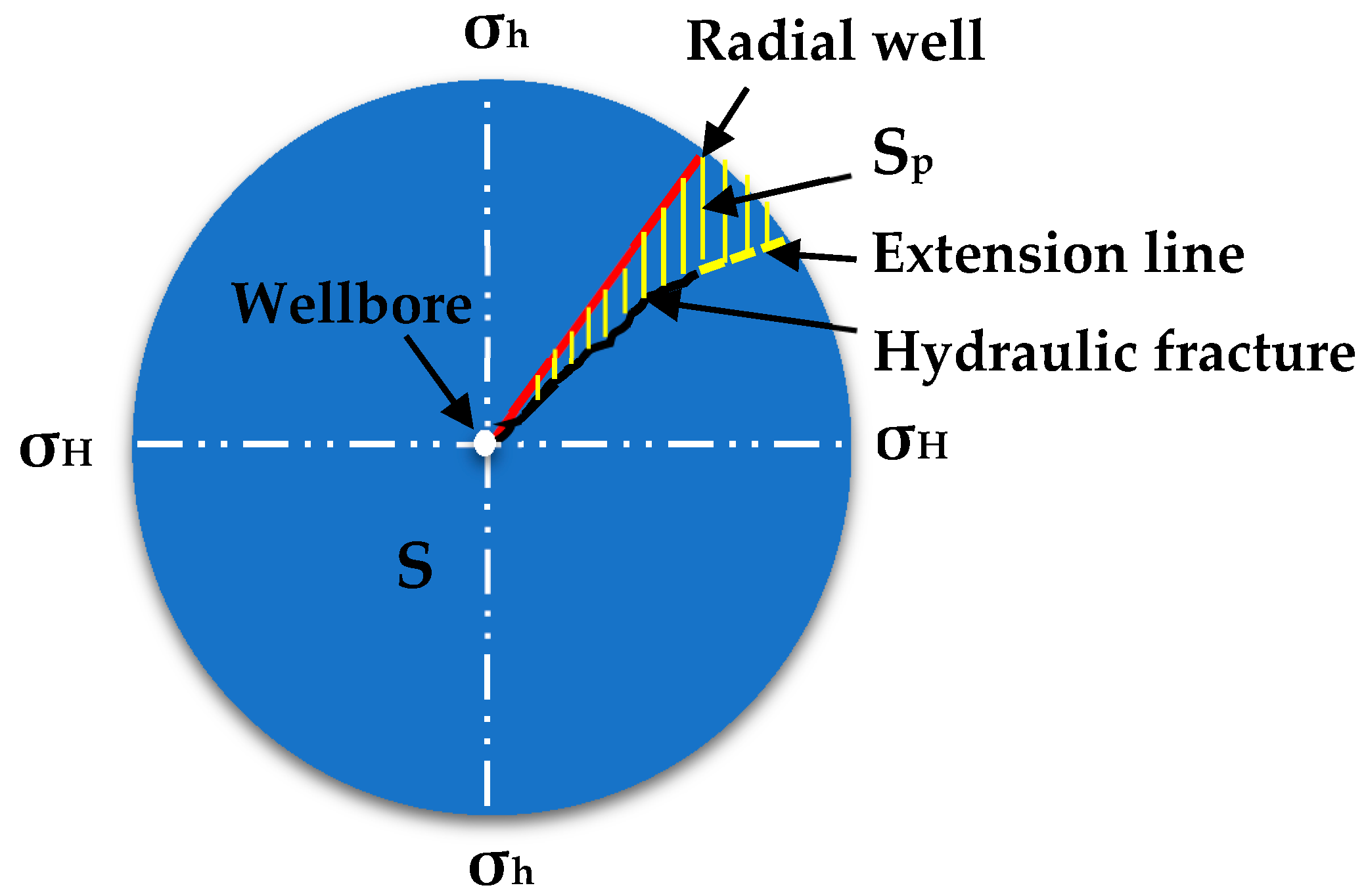
- The concept of ‘guidance factor’ is introduced for the first time to quantify the guidance of a radial borehole on hydraulic fractures. A large amount of simulation shows that the ‘guidance factor’ reflects the guidance of a radial borehole on hydraulic fractures, and larger guidance factor reflects weaker guidance strength.
- (3)
- A smaller radial borehole azimuth, horizontal in-situ stress difference and larger radial borehole diameter and length create stronger guidance strength, and vice versa. When the azimuth of the radial borehole increases from 15°to 45°, the guidance factor increases 2.6 times as much; when the horizontal in-situ stress difference increases from 2 MPa to 8 MPa, the guidance factor increases 3.6 times; when the wellbore diameter increases from 3 cm to 7 cm, the guidance factor decreases 75%; when the well length increases from 10 m to 20 m, the guidance factor decreases 69%.
- (4)
- Both reservoir physical properties and fracturing operation parameters influence the guidance of radial boreholes on hydraulic fractures. The increased Poisson’s ratio and injection rate strengthen the radial borehole guidance, and the increased Young modulus and permeability weaken the radial borehole guidance, both excessive high and low viscosity go against radial borehole guidance of hydraulic fractures, and a fracturing fluid viscosity between 50–100 mPa·s creates the best guidance on propagation of hydraulic fractures.
- (5)
- The gray correlation analysis results show that the influence level (from strong to weak) of the above factors on radial borehole guidance may be listed as follows: horizontal in-situ stress differences > azimuth > borehole diameter > length > fracturing fluid injection rate > Young modulus of rock > reservoir permeability > fracturing fluid viscosity > Poisson’s ratio. The parameters of the radial borehole, physical property parameters of the reservoir and fracturing operation parameters together influence the guidance strength of a radial borehole on hydraulic fractures.
- (6)
- The numerical model is based on real rock parameters from a practical field. It is recommended that the numerical model of different fields and areas should be established based on their rock physical mechanical parameters, and the influence of different factors on guidance be analyzed to obtain radial borehole parameters and fracturing operation parameters applicable to their conditions, which is beneficial to improving the fracturing success rate.
- (7)
- The experimental results show that the guidance of a single radial borehole on hydraulic fracture propagation is limited by the radial borehole azimuth and horizontal in-situ stress difference. A single radial borehole with larger azimuth and larger horizontal in-situ stress difference has poor guidance of the directional propagation of hydraulic fractures. The experimental results are consistent with the numerical simulation results, which shows that the numerical simulation results are reliable to some extent.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dickinson, W.; Dykstra, H.; Nees, J.M.; Dickinson, E. The ultra-short radius radial system applied to thermal recovery of heavy oil. In Proceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 30 March–1 April 1992. [Google Scholar]
- Li, Y.H.; Wang, C.J.; Shi, L.H.; Guo, W.Y. Application and development of drilling and completion of the ultra short-radius radial well by high pressure jet flow techniques. In Proceedings of the International Oil and Gas Conference and Exhibition, Beijing, China, 7–10 November 2000. [Google Scholar]
- Gong, D.G.; Qu, Z.Q.; Guo, T.K.; Tian, Y.; Tian, K.H. Variation rules of fracture initiation pressure and fracture starting point of hydraulic fracture in radial well. J. Pet. Sci. Eng. 2016, 140, 41–56. [Google Scholar] [CrossRef]
- Ursegov, S.; Bazylev, A.; Taraskin, E. First results of cyclic stimulations of vertical wells with radial horizontal bores in heavy oil carbonates (Russian). In Proceedings of the SPE Russian Oil and Gas Technical Conference and Exhibition, Moscow, Russia, 28–30 October 2008. [Google Scholar]
- Megorden, M.P.; Jiang, H.; Bentley, P.J.D. Improving hydraulic fracture geometry by directional drilling in a coal seam gas formation. In Proceedings of the SPE Unconventional Resources Conference and Exhibition-Asia Pacific, Brisbane, Australia, 11–13 November 2013. [Google Scholar]
- Guo, T.K.; Li, Y.C.; Ding, Y.; Qu, Z.Q.; Gai, N.C.; Rui, Z.H. Evaluation of acid fracturing treatments in shale formation. Energy Fuels 2017, 31, 10479–10489. [Google Scholar] [CrossRef]
- Zhang, X.; Jeffrey, R.G.; Bunger, A.P.; Thiercelin, M. Initiation and growth of a hydraulic fracture from a circular wellbore. Int. J. Rock Mech. Min. Sci. 2012, 48, 984–995. [Google Scholar] [CrossRef]
- Cherny, S.G.; Lapin, V.N.; Chirkov, D.V.; Alekseenko, O.; Medvedev, O.O. 2D modeling of hydraulic fracture initiating at a wellbore with or without microannulus. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 19–21 January 2009. [Google Scholar]
- Yuan, Y.; Abousleiman, Y.; Weng, X. Three-dimensional elastic analysis on fracture initiation from a perforated borehole. In Proceedings of the Low Permeability Reservoirs Symposium, Denver, CO, USA, 19–22 March 1995. [Google Scholar]
- Alekseenko, O.P.; Potapenko, D.I.; Cherny, S.G.; Esipov, D.; Kuranakov, D.; Lapin, V. 3-D modeling of fracture initiation from perforated non-cemented wellbore. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 6–8 February 2012. [Google Scholar]
- Zhu, H.; Deng, J.; Jin, X.; Hu, L.B.; Luo, B. Hydraulic gracture initiation and propagation from wellbore with oriented perforation. Rock Mech. Rock Eng. 2015, 48, 585–601. [Google Scholar] [CrossRef]
- Lei, X.; Zhang, S.C.; Xu, G.Q.; Zou, Y.S. Impact of perforation on hydraulic fracture initiation and extension in tight natural gas reservoirs. Energy Technol. 2015, 3, 618–624. [Google Scholar] [CrossRef]
- Fallahzadeh, S.H.; Rasouli, V.; Sarmadivaleh, M. An investigation of hydraulic fracturing initiation and near-wellbore propagation from perforated boreholes in tight formations. Rock Mech. Rock Eng. 2015, 48, 573–584. [Google Scholar] [CrossRef]
- Chen, M.; Jiang, H.; Zhang, G.Q.; Jin, Y. The experimental investigation of fracture propagation behavior and fracture geometry in hydraulic fracturing through oriented perforations. Pet. Sci. Technol. 2010, 28, 1297–1306. [Google Scholar] [CrossRef]
- Hong, J.M.; Shin, S.R.; Lim, J.S.; Jeong, W.K.; Jang, W.Y. A study on the model for effective hydraulic fracturing by using guide Hole. Tunn. Undergr. Space 2014, 24, 440–448. [Google Scholar]
- Gunde, A.C.; Bera, B.; Mitra, S.K. Investigation of water and CO2 (carbon dioxide) flooding using micro-CT (micro-computed tomography) images of Berea sandstone core using finite element simulations. Energy 2010, 35, 5209–5216. [Google Scholar] [CrossRef]
- Fries, T.P.; Belytschko, T. The extended/generalized finite element method: An overview of the method and its applications. Int. J. Numer. Methods Eng. 2010, 84, 253–304. [Google Scholar] [CrossRef]
- Dong, Y.W.; Ren, Q.W. An extended finite element method for modeling hydraulic fracturing in gravity dam. J. Hydraul. Eng. 2011, 42, 1361–1367. [Google Scholar]
- Gordeliy, E.; Peirce, A. Coupling schemes for modeling hydraulic fracture propagation using the XFEM. Comput. Methods Appl. Mech. Eng. 2012, 253, 305–322. [Google Scholar] [CrossRef]
- Wang, T.; Gao, Y.; Liu, Z.L.; Wang, Y.H.; Yang, L.F.; Zhuang, Z. Numerical simulations of hydraulic fracturing in large objects using an extended finite element method. J. Tsinghua Univ. (Sci. Technol.) 2014, 54, 1304–1309. [Google Scholar]
- He, J.M.; Zhang, Z.B.; Li, X. Numerical analysis on the formation of fracture network during the hydraulic fracturing of shale with pre-existing fractures. Energies 2017, 10, 736. [Google Scholar] [CrossRef]
- Moës, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 69, 813–833. [Google Scholar] [CrossRef]
- Rui, Z.; Lu, J.; Zhang, Z.; Guo, R.; Ling, K.; Zhang, R.; Patil, S. A quantitative oil and gas reservoir evaluation system for development. J. Nat. Gas Sci. Eng. 2017, 42, 31–39. [Google Scholar] [CrossRef]
- Meixner, J.; Schill, E.; Grimmer, J.C.; Gaucher, E.; Kohl, T.; Klingler, P. Structural control of geothermal reservoirs in extensional tectonic settings: An example from the Upper Rhine Graben. J. Struct. Geol. 2016, 82, 1–15. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Li, Z.W.; Guo, L.L.; Gao, P.; Jin, X.P. Electricity generation from enhanced geothermal systems by oilfield produced water circulating through reservoir stimulated by staged fracturing technology for horizontal wells: A case study in Xujiaweizi area in Daqing Oilfield, China. Energy 2014, 78, 788–805. [Google Scholar] [CrossRef]
- Tang, C.A.; Tham, L.G.; Lee, P.K.K.; Yang, T.H.; Li, L.C. Coupled analysis of flow, stress and damage (FSD) in rock failure. Int. J. Rock Mech. Min. Sci. 2002, 39, 477–489. [Google Scholar] [CrossRef]
- Chen, W.Z.; Wu, G.J.; Jia, S.P. The Application of Abaqus in Tunnels and Underground Engineering, 1st ed.; China Water & Power Press: Beijing, China, 2009; pp. 228–235. ISBN 978-7-5084-6995-9. [Google Scholar]
- Guo, L.L.; Chen, Z.F.; Luo, J.R.; Chen, G. A review of the extended finite element method and its applications. Chin. Q. Mech. 2011, 2, 612–625. [Google Scholar]
- Yue, Q.X.; Li, J. Aresearch on saturated soil dynamic response with Abaqus. Earthq. Eng. Eng. Vib. 2006, 26, 238–241. [Google Scholar]
- Sepehri, J.; Soliman, M.Y.; Morse, S.M. Application of extended finite element method (XFEM) to simulate hydraulic fracture propagation from oriented perforations. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 3–5 February 2015. [Google Scholar]
- Kachanov, L.M. Time of the rupture process under creep conditions. Izv. Akad. Nauk SSR 1958, 8, 26–31. [Google Scholar]
- Haddad, M.; Sepehrnoori, K. XFEM-based CZM for the simulation of 3D multiple-stage hydraulic fracturing in quasi-brittle shale formations. In Proceedings of the 49th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 28 June–1 July 2015. [Google Scholar]
- Remmers, J.J.C.; Borst, R.D.; Needleman, A. The simulation of dynamic crack propagation using the cohesive segments method. J. Mech. Phys. Solids 2008, 56, 70–92. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Chen, M.; Zhao, Y.B. Study on initiation and propagation mechanism of fractures in oriented perforation of new wells. Acta Pet. Sin. 2008, 29, 116–119. [Google Scholar]
- Kadier, A.; Abdeshahian, P.; Simayi, Y.; Ismail, M.; Hamid, A.A.; Kalil, M.S. Gray relational analysis for comparative assessment of different cathode materials in microbial electrolysis cells. Energy 2015, 90, 1556–1562. [Google Scholar] [CrossRef]
- Fallahzadeh, S.H.; Hossain, M.M.; Cornwell, A.J.; Rasouli, V. Near wellbore hydraulic fracture propagation from perforations in tight rocks: The roles of fracturing fluid viscosity and injection rate. Energies 2017, 10, 359. [Google Scholar] [CrossRef]




| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Reservoir saturation | 1 | Poisson ratio of rock | 0.25 |
| Initial pore pressure | 20 MPa | Young’s modulus of rock | 12.9 GPa |
| Initial porosity | 0.16 | Reservoir permeability | 60 × 10−3 μm2 |
| Horizontal maximum principal stress (σH) | 41 MPa | Filtration coefficient | 10−10 m s−1 |
| Horizontal minimal principal stress (σh) | 36 MPa | Injection rate of fracturing fluid | 3.2 m3 min−1 |
| Overburden stress | 45 MPa | Fracturing fluid viscosity | 50 mPa·s |
| Tensile strength of rock | 3.0 MPa | Fracturing fluid density | 9525 kg/m3 |
| Casing diameter | 139.7 mm | Reservoir model size (diameter) | 40 m |
| No. | Parameters | Correlation Coefficient |
|---|---|---|
| 1 | Radial well azimuth | 0.7680 |
| 2 | Radial well diameter | 0.7537 |
| 3 | Radial well length | 0.7485 |
| 4 | Horizontal principal stress difference | 0.7921 |
| 5 | Young’s modulus of rock | 0.7465 |
| 6 | Poisson ratio of rock | 0.5312 |
| 7 | Reservoir permeability | 0.7367 |
| 8 | Fracturing fluid viscosity | 0.7354 |
| 9 | Injection rate of fracturing fluid | 0.7476 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, T.; Qu, Z.; Gong, F.; Wang, X. Numerical Simulation of Hydraulic Fracture Propagation Guided by Single Radial Boreholes. Energies 2017, 10, 1680. https://doi.org/10.3390/en10101680
Guo T, Qu Z, Gong F, Wang X. Numerical Simulation of Hydraulic Fracture Propagation Guided by Single Radial Boreholes. Energies. 2017; 10(10):1680. https://doi.org/10.3390/en10101680
Chicago/Turabian StyleGuo, Tiankui, Zhanqing Qu, Facheng Gong, and Xiaozhi Wang. 2017. "Numerical Simulation of Hydraulic Fracture Propagation Guided by Single Radial Boreholes" Energies 10, no. 10: 1680. https://doi.org/10.3390/en10101680
APA StyleGuo, T., Qu, Z., Gong, F., & Wang, X. (2017). Numerical Simulation of Hydraulic Fracture Propagation Guided by Single Radial Boreholes. Energies, 10(10), 1680. https://doi.org/10.3390/en10101680






