Modeling of HVDC System to Improve Estimation of Transient DC Current and Voltages for AC Line-to-Ground Fault—An Actual Case Study in Korea
Abstract
:1. Introduction
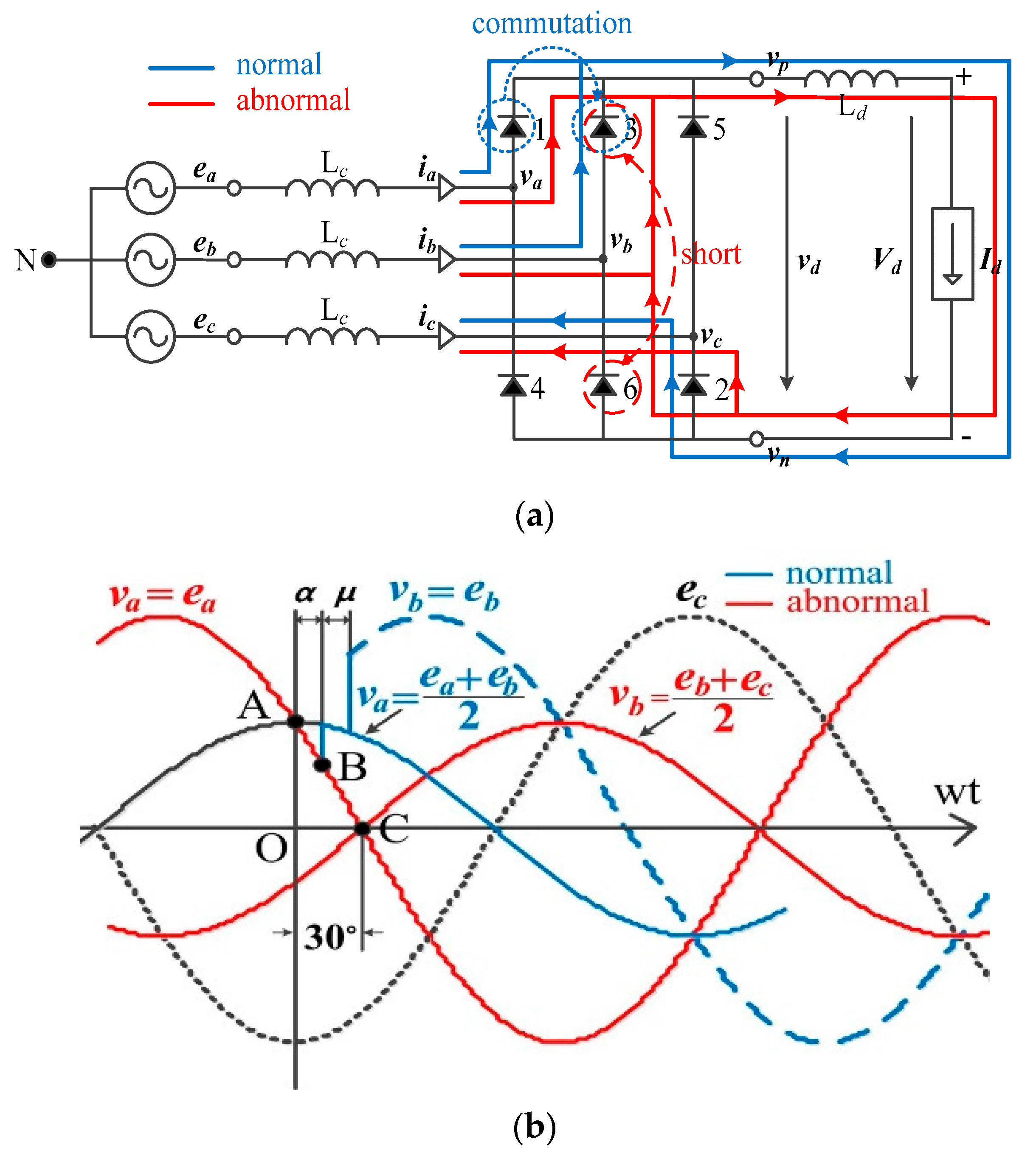
- The converting equations for abnormal operation, which particularly arise because of commutation failure under the conditions of fault occurrence in the AC transmission network, are developed and integrated into PSS/E to estimate the variations in the DC voltages and currents of the HVDC system.
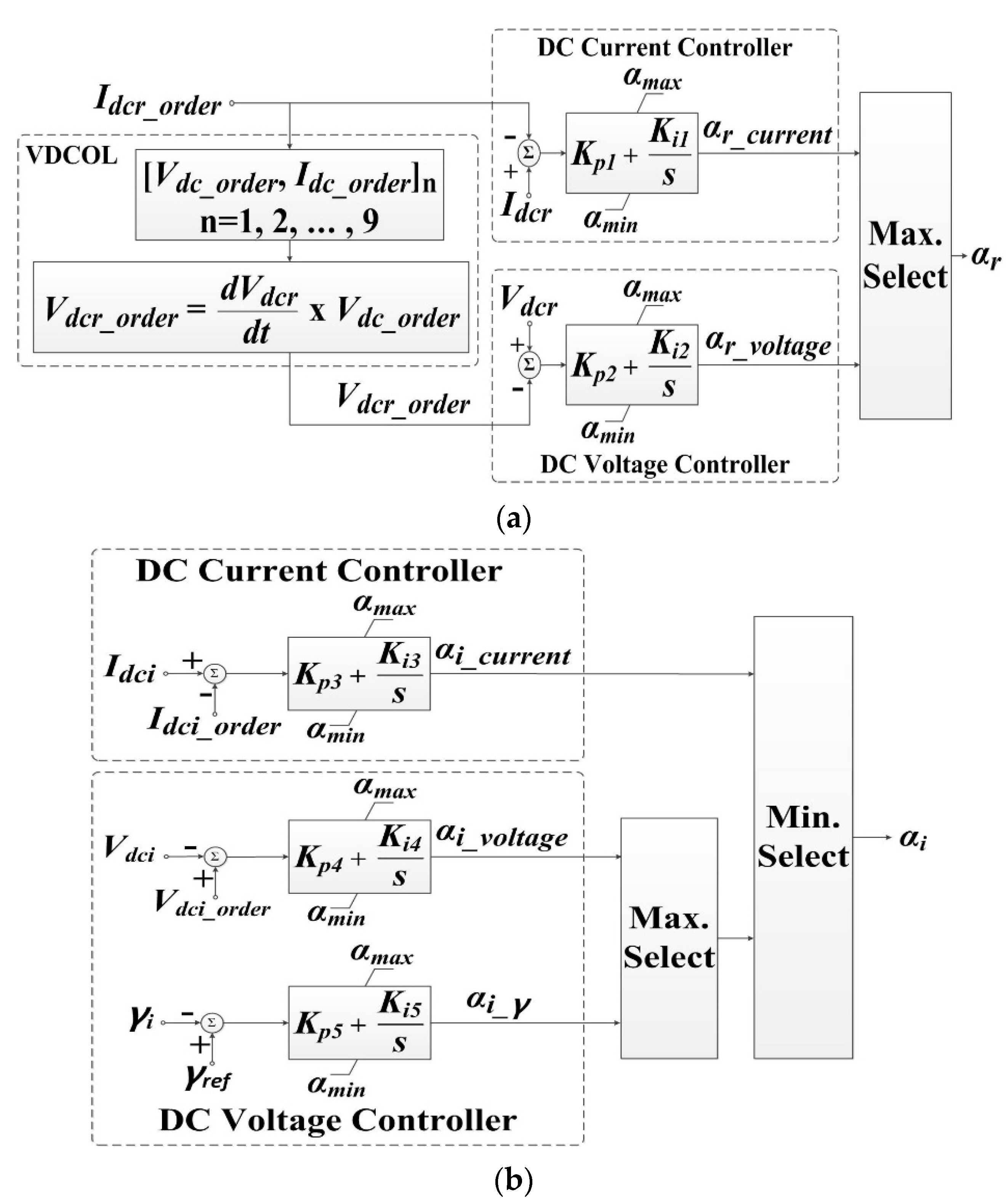
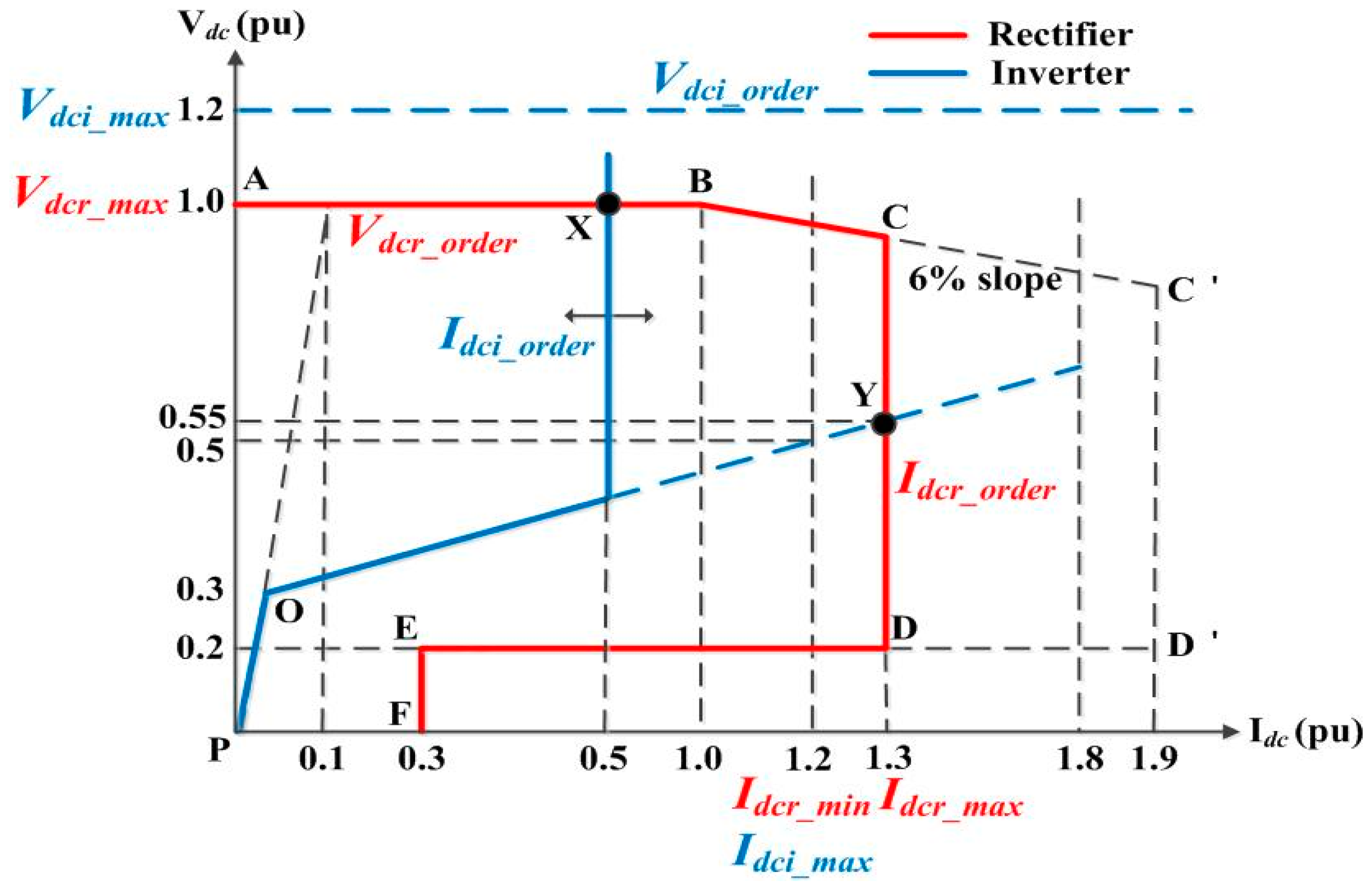
- The HVDC system converters are equipped with feedback controllers. These enable us to easily determine the firing angles and obtain sufficiently accurate characteristic V-I curves, particularly with respect to the VDCOL function. Furthermore, the DC line is modeled using multiple π-sections for accurate estimation of the DC voltages and currents of the HVDC system.
- The proposed modeling method provides accurate estimates of the DC voltages and currents arising from AC line-to-ground faults. To the best of our knowledge, this paper is the first demonstration of an HVDC system model developed specifically with a quasi steady state (QSS)-type simulator using actual operating data from a real HVDC system for a single line-to-ground fault. The proposed model is also verified through comparisons with simulation results obtained from the comprehensive HVDC system model, developed using PSCAD, for the three-phase line-to-ground fault.
- The proposed method leads to a significant reduction in computational time. This will allow grid operators to perform efficient case studies of LCC-based HVDC systems under a variety of conditions. Furthermore, the proposed method can be implemented in coordination with commercial software, and independently of the built-in subsystems or algorithms for other dynamic power devices. It is easy to adapt the model to reflect the operating characteristics of specific HVDC systems without affecting the built-in functions. Hence, this model has a wide range of potential applications.
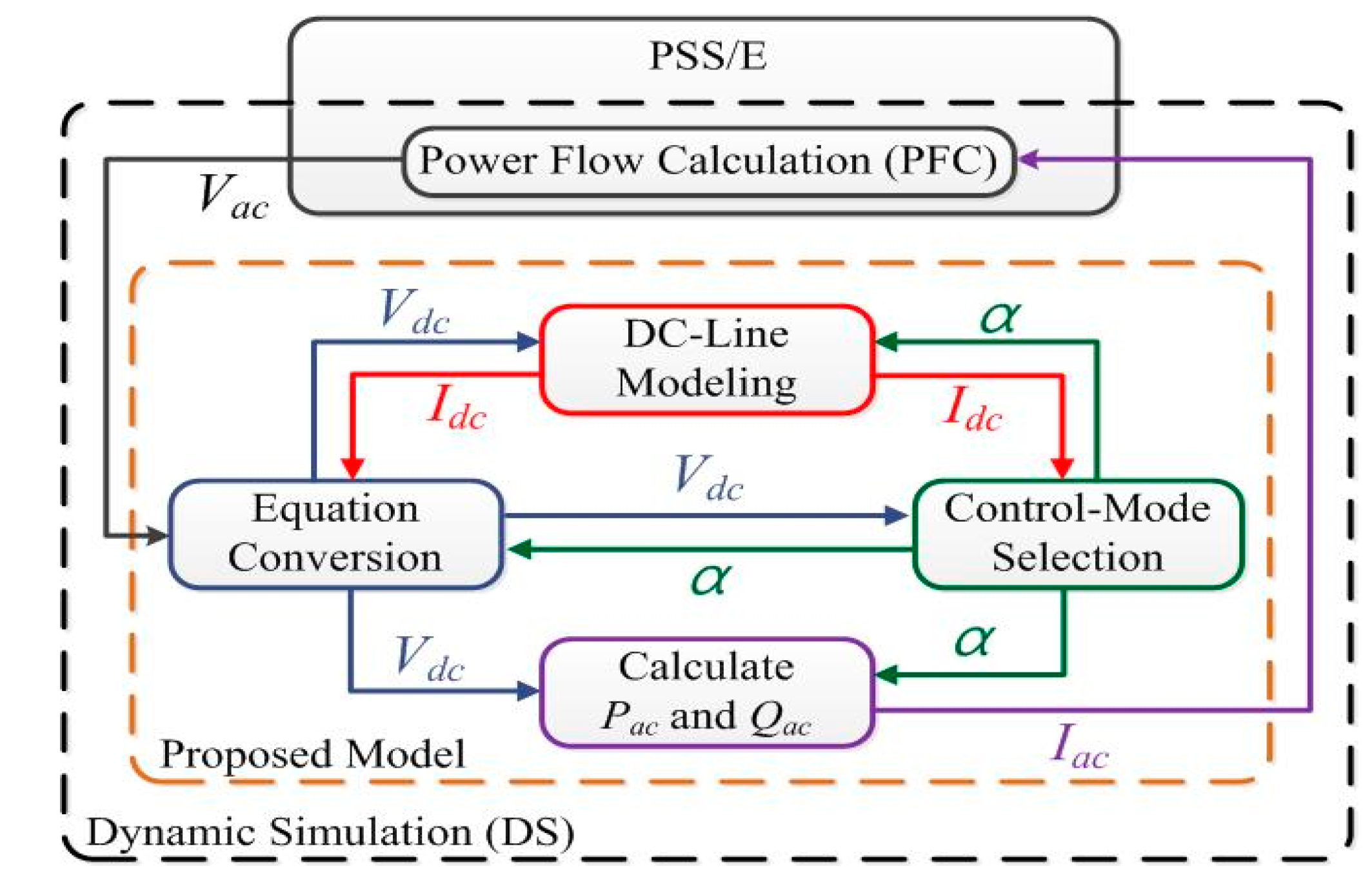
2. Modeling the HVDC System in the PSS/E Simulation Environment
3. Proposed Modeling Method for Improved Transient-State Analysis of HVDC Systems
3.1. Equation Conversion
3.2. Control-Mode Selection
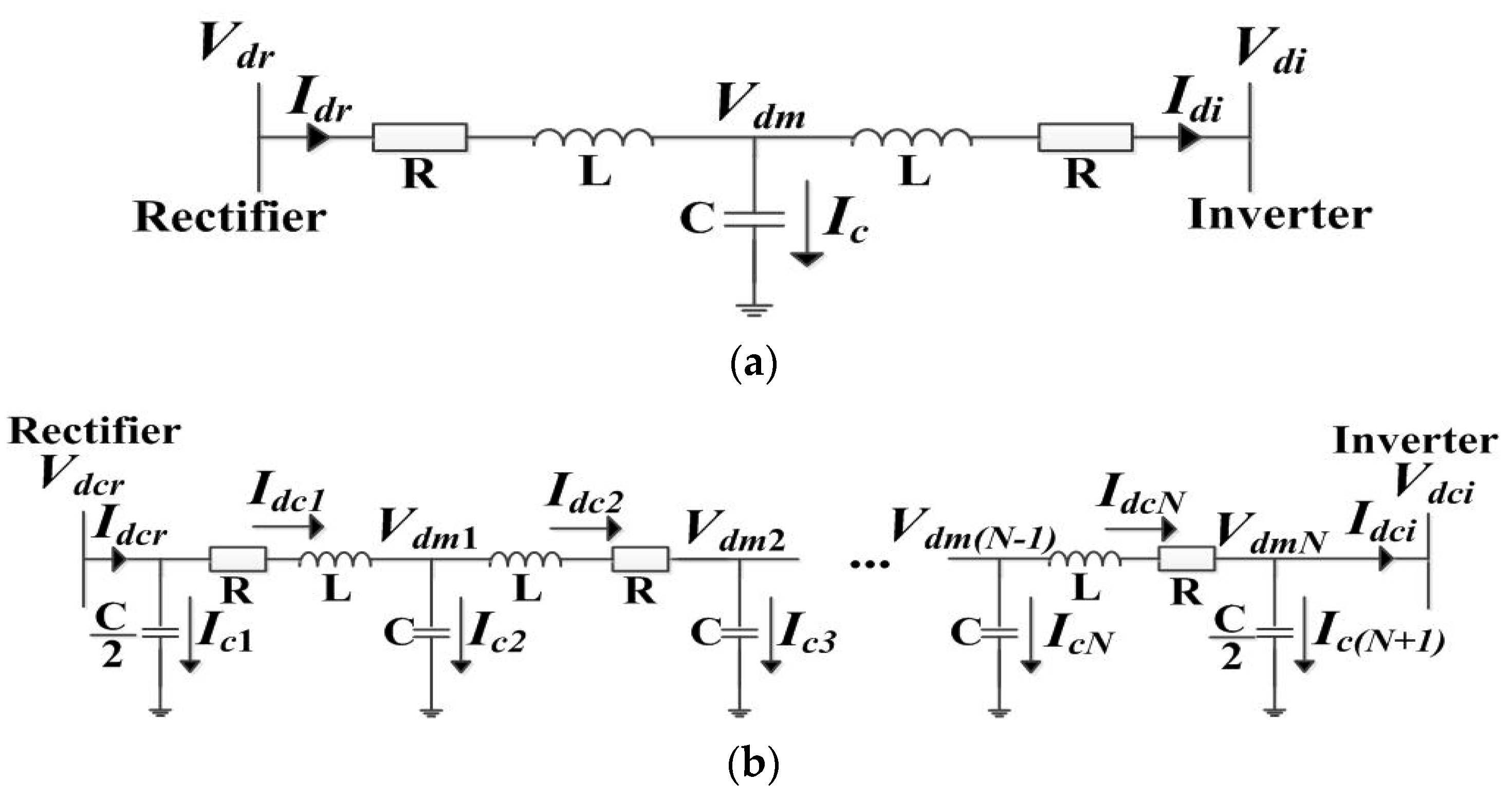
3.3. DC-Line Modeling
4. Simulation Case Studies and Results
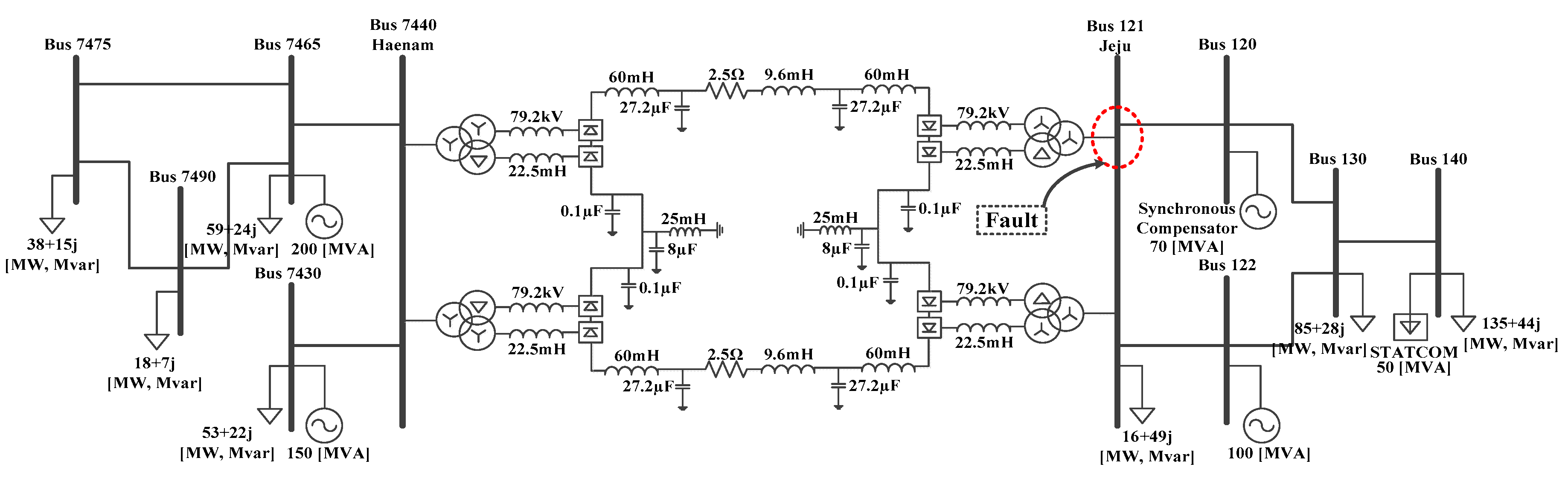
4.1. Test System and Simulation Conditions
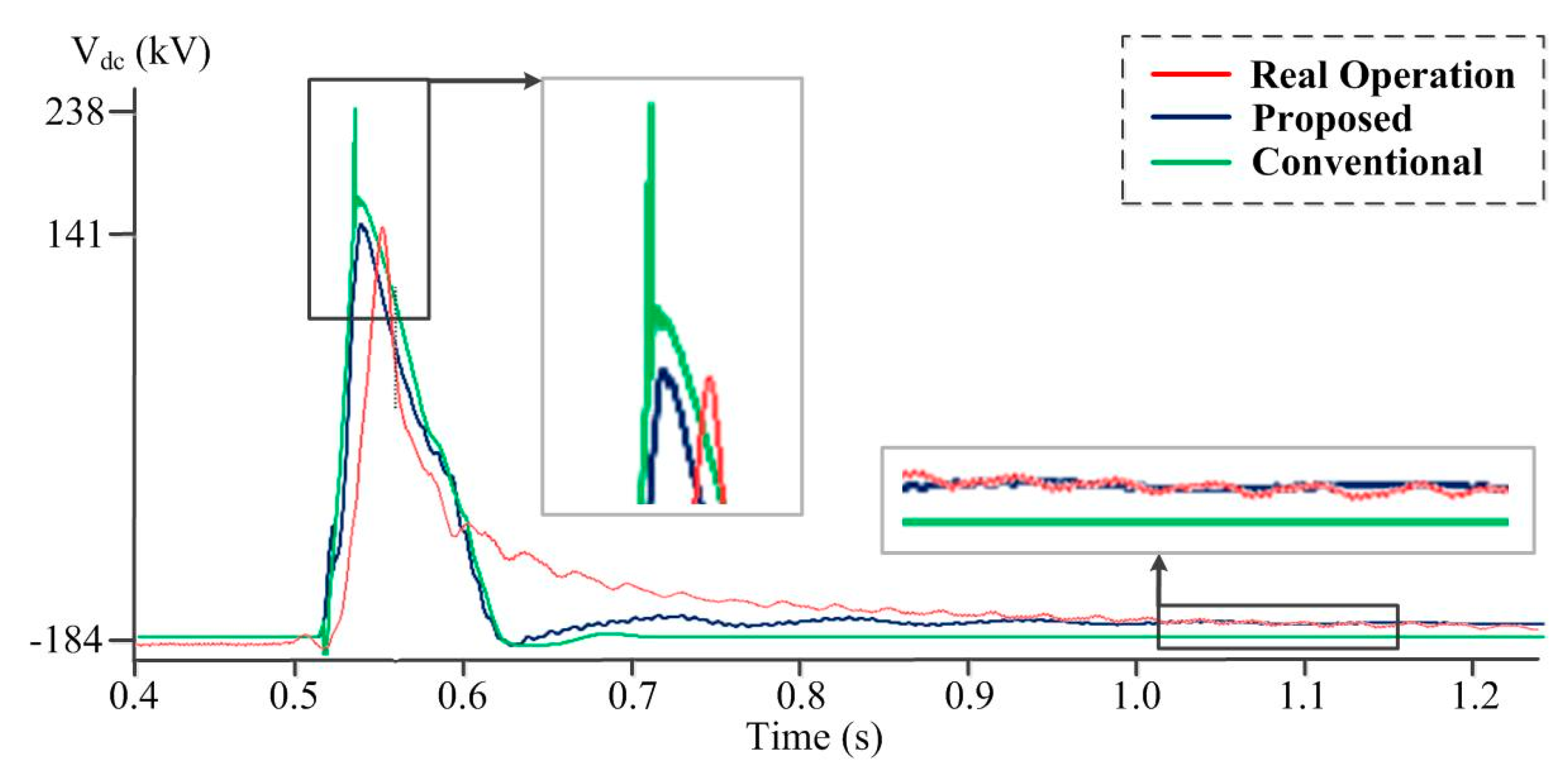
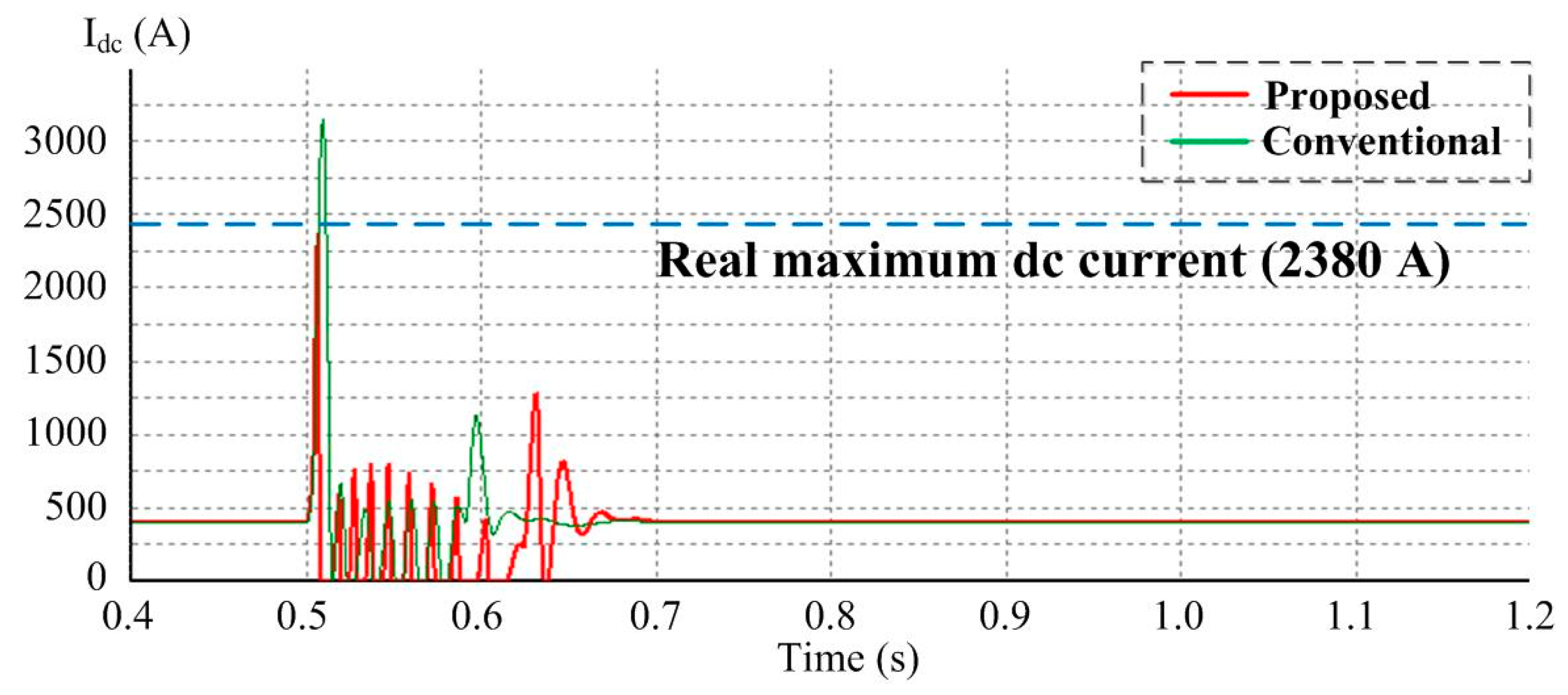
4.2. Case Study A: Comparision with Real HVDC System
4.3. Case Study B: Comparision with the PSCAD Model
5. Conclusions
- The converting equations for abnormal operation, which particularly arises because of commutation failure under the conditions of fault occurrence in the AC transmission network, are developed and integrated into PSS/E to estimate the variations in the DC voltages and currents of the HVDC system accurately. Furthermore, the DC line is modeled using multiple π-sections for accurate estimation of the DC voltages and currents of the HVDC system considering the trade-off between the modeling accuracy and computational complexity. The simulation results show that the proposed modeling method, which includes the converting equations for abnormal operation and the π-section model of DC line, estimate the more accurate DC voltage and current variation than the conventional methods for single-phase and three-phase line-to-ground faults in PSS/E environment.
- To the best of our knowledge, this paper is the first in which an HVDC system model developed particularly in the PSS/E simulator is demonstrated using the actual operating data of a real HVDC system (i.e., the KEPCO benchmark model) for a single line-to-ground fault. The proposed model is also verified via comparisons with simulation results obtained from the comprehensive HVDC system model, developed using PSCAD, for the three-phase line-to-ground fault.
- The proposed method leads to a significant reduction in computational time, which allows grid operators to perform efficient case studies on LCC-based HVDC systems under a variety of conditions. In addition, the proposed method can be implemented in conjunction with commercial software and independently from the built-in subsystems or algorithms used to model other dynamic power devices. It is also easy to modify the models to reflect the operating characteristics of specific HVDC systems without affecting the built-in functions Therefore, the proposed modeling method enables grid operators in other countries to effectively perform similar case studies considering various size, types, and modeling complexities of LCC-based HVDC systems with some minor modifications.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Vdc, Idc | DC-line voltage (kV) and current (A) |
| Pac, Qac | converter active and reactive power outputs (pu) |
| Vdcr, Vdci | DC voltages at the rectifier and inverter (kV) |
| Idcr, Idci | DC currents at the rectifier and inverter (A) |
| R, L, C | resistance (Ω), inductance (mH), and capacitance (μC) of the DC-line |
| Prated | rated DC power (MW) of the HVDC system |
| Vrated | rated DC voltage (kV) of the HVDC system |
| Nc | number of bridges connected in series for the converter |
| Xcc, Rcc | reactance and resistance of the DC-side winding of the converter transformer (Ω) |
| Eacc | open-circuit secondary AC voltage of the converter transformer (kV) |
| Vdm | DC voltage at the middle of the DC-line (kV) |
| ν | instantaneous AC voltage at the valve (V) |
| e | instantaneous AC line-to-neutral voltage (V) |
| Ic | AC current at the capacitor of the DC-line (A) |
| Vac | primary AC voltage of the converter transformer (pu) |
| Iac | AC current injected at the AC bus (pu) |
| αr, αi | firing angles α at the rectifier and inverter (°) |
| γ | extinction angle (°) |
| μ | overlap angle (°) |
| δ | extinction delay angle (°) |
| ϕ | converter AC power angle (°) |
| Kp, Ki | PI controller gains for the control-mode selection module |
References
- HVDC Project Listing. Available online: http://www.ece.uidaho.edu/hvdcfacts/Projects/HVDCProjectsListing2013-planned.pdf (accessed on 2 October 2017).
- Bahrman, M.P.; Johnson, B. The ABCs of HVDC transmission technologies. IEEE Power Energy Mag. 2007, 5, 32–44. [Google Scholar] [CrossRef]
- Jang, G.; Oh, S.; Han, B.M.; Kim, C.K. Novel reactive-power-compensation scheme for the Jeju-Haenam HVDC system. IEE Proc. Gen. Transmiss. Distrib. 2005, 152, 514–520. [Google Scholar] [CrossRef]
- Wang, L.; Thi, M.S. Stability enhancement of a PMSG-based offshore wind farm fed to a multi-machine system through an LCC-HVDC link. IEEE Trans. Power Syst. 2013, 28, 3327–3334. [Google Scholar] [CrossRef]
- Bidadfar, A.; Nee, H.P.; Zhang, L.; Harnefors, L.; Namayantavana, S.; Abedi, M.; Karrari, M.; Gharehpetian, G.B. Power system stability analysis using feedback control system modeling including HVDC transmission links. IEEE Trans. Power Syst. 2016, 31, 116–124. [Google Scholar] [CrossRef]
- Karawita, C.; Annakkage, U.D. Multi-infeed HVDC interaction studies using small-signal stability assessment. IEEE Trans. Power Deliv. 2009, 24, 910–918. [Google Scholar] [CrossRef]
- Torres-Olguin, R.E.; Molinas, M.; Undeland, T. Offshore wind farm grid integration by VSC technology with LCC-based HVDC transmission. IEEE Trans. Sustain. Energy 2012, 3, 899–907. [Google Scholar] [CrossRef]
- Liu, C.; Bose, A.; Tian, P. Modeling and analysis of HVDC converter by three-phase dynamic phasor. IEEE Trans. Power Deliv. 2014, 29, 3–12. [Google Scholar] [CrossRef]
- Son, H.I.; Kim, H.M. An algorithm for effective mitigation of commutation failure in high-voltage direct-current systems. IEEE Trans. Power Deliv. 2016, 31, 1437–1446. [Google Scholar] [CrossRef]
- Chou, C.J.; Wu, Y.K.; Han, G.Y.; Leaa, C.Y. Comparative evaluation of the HVDC and HVAC links intergrated in a large offshore wind farm—An actual case study in Taiwan. IEEE Trans. Ind. Appl. 2012, 48, 1639–1648. [Google Scholar] [CrossRef]
- Xiao-ming, M.; Yao, Z.; Lin, G.; Xiao-chen, W. Coordinated control of interarea oscillation in the China Southern Power Grid. IEEE Trans. Power Syst. 2006, 21, 845–852. [Google Scholar] [CrossRef]
- Rahimi, E.; Gole, A.M.; Davies, J.B.; Fernando, I.T.; Kent, K.L. Commutation failure in single- and multi-infeed HVDC systems. In Proceedings of the IEE International Conference AC and DC Power Transmission, London, UK, 28–31 March 2006; pp. 182–186. [Google Scholar]
- Thio, C.V.; Davies, J.B.; Kent, K.L. Commutation failures in HVDC transmission systems. IEEE Trans. Power Deliv. 1996, 11, 946–953. [Google Scholar] [CrossRef]
- Lidong, Z.; Dofnas, L. A novel method to mitigate commutation failures in HVDC systems. In Proceedings of the IEEE International Conference on Power System Technology, Kunming, China, 13–17 October 2002; pp. 51–56. [Google Scholar]
- Wei, Z.; Yuan, Y.; Lei, X.; Wang, H.; Sun, G.; Sun, Y. Direct-current predictive control strategy for inhibiting commutation failure in HVDC converter. IEEE Trans. Power Syst. 2014, 29, 2409–2417. [Google Scholar] [CrossRef]
- Meisingset, M.; Gole, A.M. A comparison of conventional and capacitor commutated converters based on steady-state and dynamic considerations. In Proceedings of the 7th IEE International Conference AC and DC Power Transmission, London, UK, 28–30 November 2001; pp. 49–54. [Google Scholar]
- Guo, C.; Li, C.; Zhao, C.; Ni, X.; Zha, K.; Xu, W. An evolutional line-commutated converter integrated with thyristor-based full-bridge module to mitigate the commutation failure. IEEE Trans. Power Electron. 2017, 32, 967–976. [Google Scholar] [CrossRef]
- Ghanbari, T.; Farjah, E. A multiagent-based fault-current limiting scheme for the microgrids. IEEE Trans. Power Deliv. 2014, 29, 525–533. [Google Scholar] [CrossRef]
- Radmanesh, H.; Fathi, S.H.; Gharehpetian, J.B.; Heidary, A. A novel solid-state fault current-limiting circuit breaker for medium-voltage network applications. IEEE Trans. Power Deliv. 2016, 31, 236–244. [Google Scholar] [CrossRef]
- Jovcic, D. Thyristor-based HVDC with forced commutation. IEEE Trans. Power Deliv. 2007, 22, 557–564. [Google Scholar] [CrossRef]
- Atighechi, H.; Chiniforoosh, S.; Jatskevich, J.; Davoudi, A.; Martinez, J.A.; Faruque, M.O.; Sood, V.; Saeedifard, M.; Cano, J.M.; Mahseredjian, J.; et al. Dynamic average value modeling of CIGRE HVDC benchmark system. IEEE Trans. Power Deliv. 2014, 29, 2046–2054. [Google Scholar] [CrossRef]
- Faruque, M.O.; Zhang, Y.; Dinavahi, V. Detailed modeling of CIGRE HVDC benchmark system using PSCAD/EMTDC and PSB/SIMULINK. IEEE Trans. Power Deliv. 2006, 21, 378–387. [Google Scholar] [CrossRef]
- Rao, A.T.; Ramana, P.; Rao, P.K. Modeling of CIGRE HVDC benchmark system in MATLAB/SIMULINK. Int. J. Educ. Appl. Res. 2014, 4, 1–4. [Google Scholar]
- Siemens Energy Inc. PSS/E 32.0 Model Library, 1st ed.; Siemens Energy Inc.: Schenectady, NY, USA, 2009. [Google Scholar]
- Guo, C.; Liu, Y.; Zhao, C.; Wei, X.; Xu, W. Power component fault detection methods and improved current order limiter control for commutation failure mitigation in HVDC. IEEE Trans. Power Deliv. 2015, 30, 1585–1593. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Z. A flexible power control method of VSC-HVDC link for the enhancement of effective short-circuit ratio in a hybrid multi-infeed HVDC system. IEEE Trans. Power Syst. 2013, 28, 200–209. [Google Scholar] [CrossRef]
- Siemens Energy Inc. PSS/E 32.0 GUI Users Guide, 1st ed.; Siemens Energy Inc.: Schenectady, NY, USA, 2009; pp. 1–2. [Google Scholar]
- Kwon, D.H.; Moon, H.J.; Kim, R.G.; Kim, C.G.; Moon, S.I. Modeling of CIGRE benchmark HVDC system using PSS/E compared with PSCAD. In Proceedings of the International Youth Conference on Energy, Pisa, Italy, 27–30 May 2015; pp. 1–8. [Google Scholar]
- Muthusamy, A. Selection of Dynamic Performance Control Parameters for Classic HVDC in PSSE. Master’s Thesis, Chalmers University, Göteborg, Sweden, 2010. [Google Scholar]
- Yoon, D.H.; Song, H.; Jang, G.; Joo, S. K. Smart operation of HVDC systems for large penetration of wind energy resources. IEEE Trans. Smart Grid 2013, 4, 359–366. [Google Scholar] [CrossRef]
- Pinares, G.; Bongiorno, M. Modeling and analysis of VSC-based HVDC systems for DC network stability studies. IEEE Trans. Power Deliv. 2016, 31, 848–856. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Z.; Rehranz, C.; Luo, L.; Rüberg, S.; Liu, F. Study on steady- and transient-state characteristics of a new HVDC transmission system based on an inductive filtering method. IEEE Trans. Power Electron. 2011, 26, 1976–1986. [Google Scholar] [CrossRef]
- Daryabak, M.; Filizadeh, S.; Jatskevich, J.; Davoudi, A.; Saeedifard, M.; Sood, V.K.; Martinez, J.A.; Aliprantis, D.; Cano, J.; Mehrizi-Sani, A. Modeling of LCC-HVDC systems using dynamic phasors. IEEE Trans. Power Deliv. 2014, 29, 1989–1998. [Google Scholar] [CrossRef]
- Yoon, M.; Park, J.; Jang, G. A study of HVDC installation in Korean capital region power system. In Proceedings of the IEEE PES General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–5. [Google Scholar]
- Koh, B.E.; Jung, G.J.; Moon, I.H.; Kim, S.K. Introduction of Haenam-Jeju HVDC system. In Proceedings of the IEEE International Symposium on Industrial Electronics, Pusan, Korea, 12–16 June 2001; pp. 1006–1010. [Google Scholar]
- Keller, J.; Kroposki, B. Understanding Fault Characteristics of Inverter-Based Distributed Energy Resources; National Renewable Energy Laboratory: Golden, CO, USA, 2010. [Google Scholar]
- Kunder, K. Power System Stability and Control, 1st ed.; McGraw-Hill: New York, USA, 1971; pp. 528–533. [Google Scholar]
- Kim, C.K.; Jang, G.; Kim, J.B.; Shim, U.B. Transient performance of Cheju-Haenam HVDC system. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Vancouver, BC, Canada, 15–19 July 2001 ; pp. 343–348. [Google Scholar]
- Xue, Y.; Zhang, X. P.; Yang, C. Elimination of commutation failures of LCC HVDC system with controllable capacitors. IEEE Trans. Power Syst. 2016, 31, 3289–3299. [Google Scholar]
| Parameters | Jeju–Haenam HVDC | CIGRE HVDC |
|---|---|---|
| AC base voltage | Rectifier: 154 kV | Rectifier: 345 kV |
| Inverter: 154 kV | Inverter: 230 kV | |
| Nominal DC voltage | 184 kV | 500 kV |
| Nominal DC current | 0.815 kA | 2 kA |
| Source impedance (Rec) | R = 0.00675 Ω | R = 3.737 Ω |
| L = 0.04653 H | L = 0 H | |
| Source impedance (inv) | R = 0.00675 Ω | R = 0.7406 Ω |
| L = 0.04653 H | L = 0.0365 H | |
| System frequency | 60 Hz | 50 Hz |
| Converter control | Rectifier: voltage | Rectifier: current |
| Inverter: current | Inverter: voltage |
| Parameter | Value | Parameter | Value | |
|---|---|---|---|---|
| Input parameters for PSS/E | Prated (MW) | 75 | Vrated (kV) | 184 |
| Nc | 2 | R | 0.744 | |
| Xcc | 7.99 | L | 133.33 | |
| Rcc | 0 | C | 27 | |
| Parameters for proposed model | Vdcr_max (pu) | 1 | Vdci_max (pu) | 1.2 |
| Idcr_min (pu) | 1.2 | Idcr_max (pu) | 1.3 | |
| Idci_max (pu) | 1.2 | αmax (°) | 165 | |
| αmin (°) | 5 | γref (°) | 18 | |
| Kp1 | 0.01 | Ki1 | 0.001 | |
| Kp2 | 1.3 | Ki2 | 2.5 | |
| Kp3 | 1.42 | Ki3 | 5.5 | |
| Kp4 | 0.01 | Ki4 | 0.01 | |
| Kp5 | 0.1 | Ki5 | 0.01 |
| DC Voltages | PSCAD | Proposed PSS/E | Conventional PSS/E | |||
|---|---|---|---|---|---|---|
| Value | Error (%) | Value | Error (%) | Value | Error (%) | |
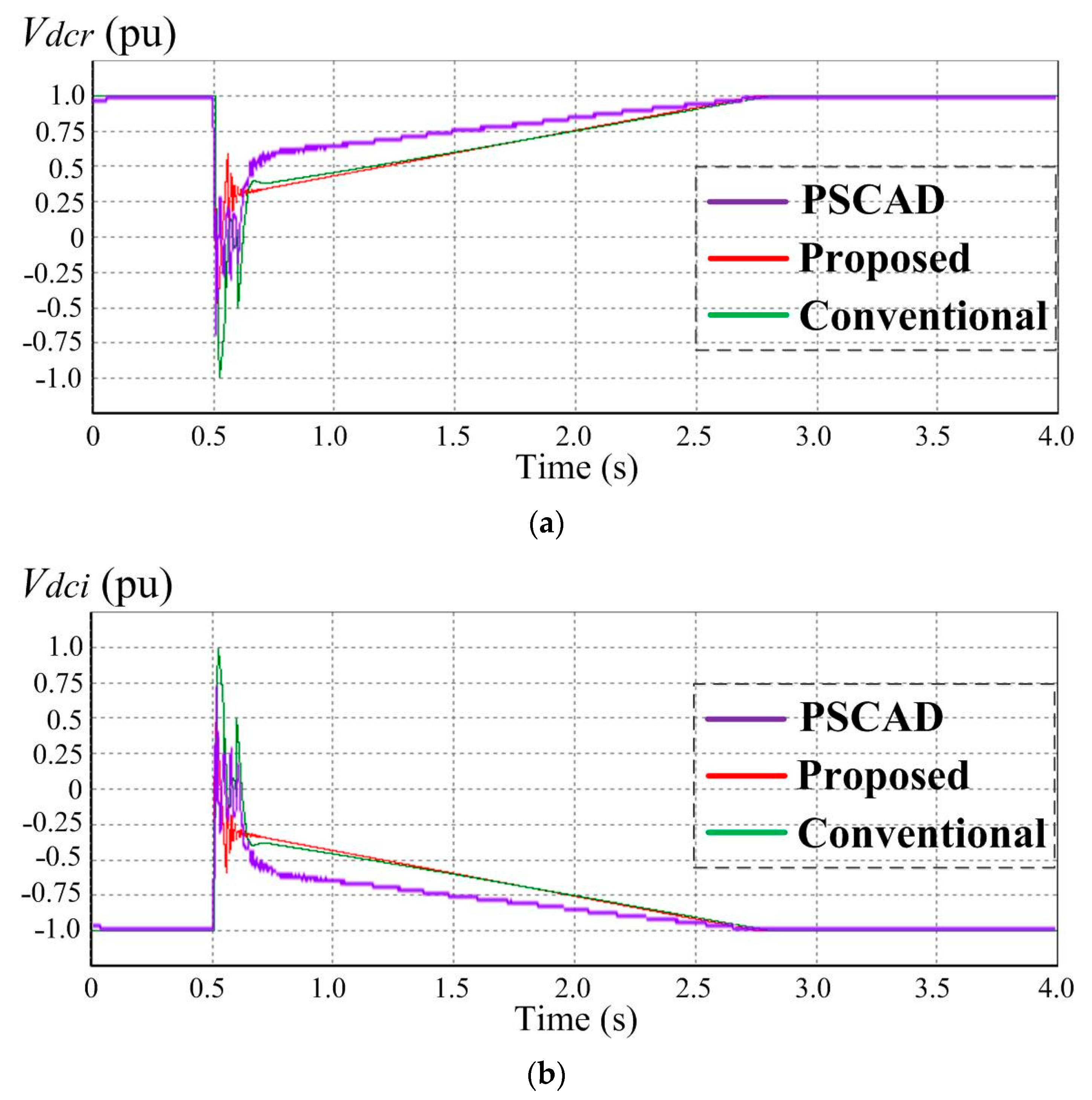
| min. Vdcr (kV) | −126.4 | - | −121.1 | 4.2 | −180.5 | 42.8 |
| max. Vdci (kV) | 129.9 | - | 127.5 | 1.9 | 186.4 | 43.5 |
| Key Quantities | Real Data | Proposed PSS/E Model, Error (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 3 π-Sections | 2 π-Sections | 1 π-Section | T-Line | ||||||
| Value | Error | Value | Error | Value | Error | Value | Error | ||
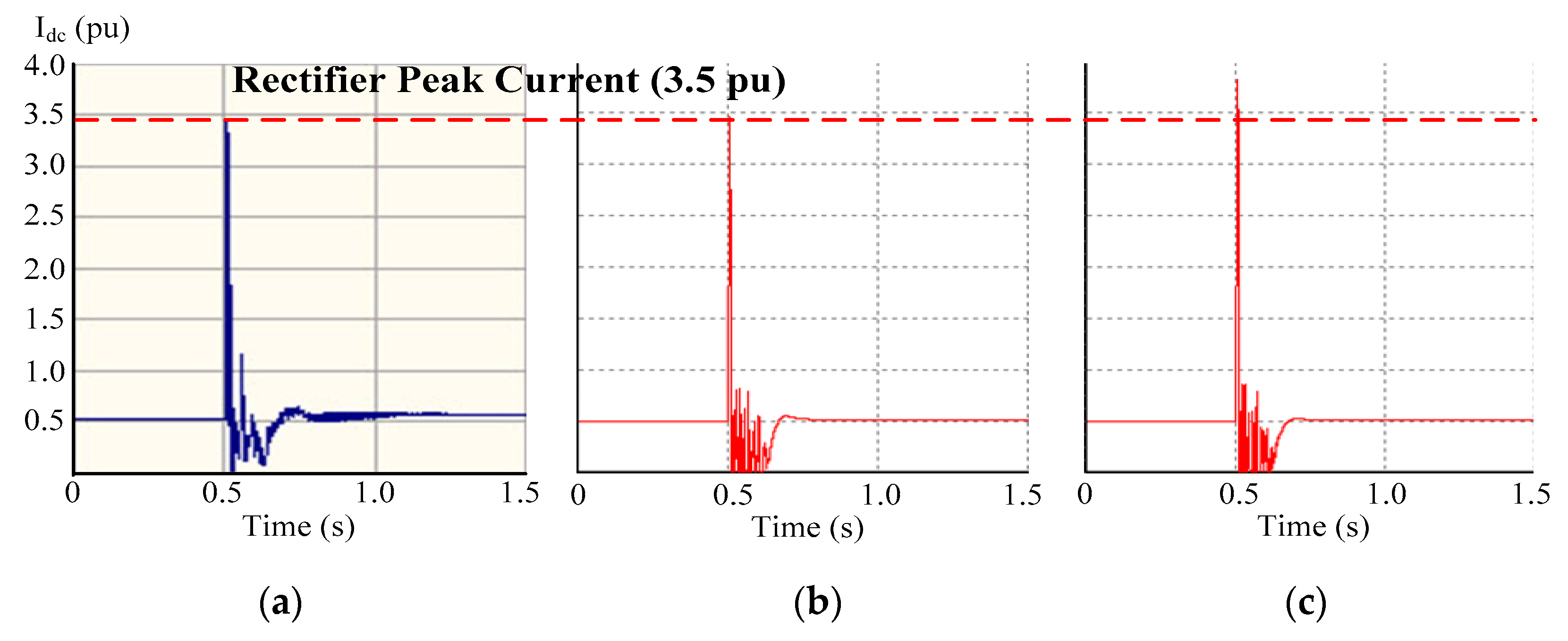
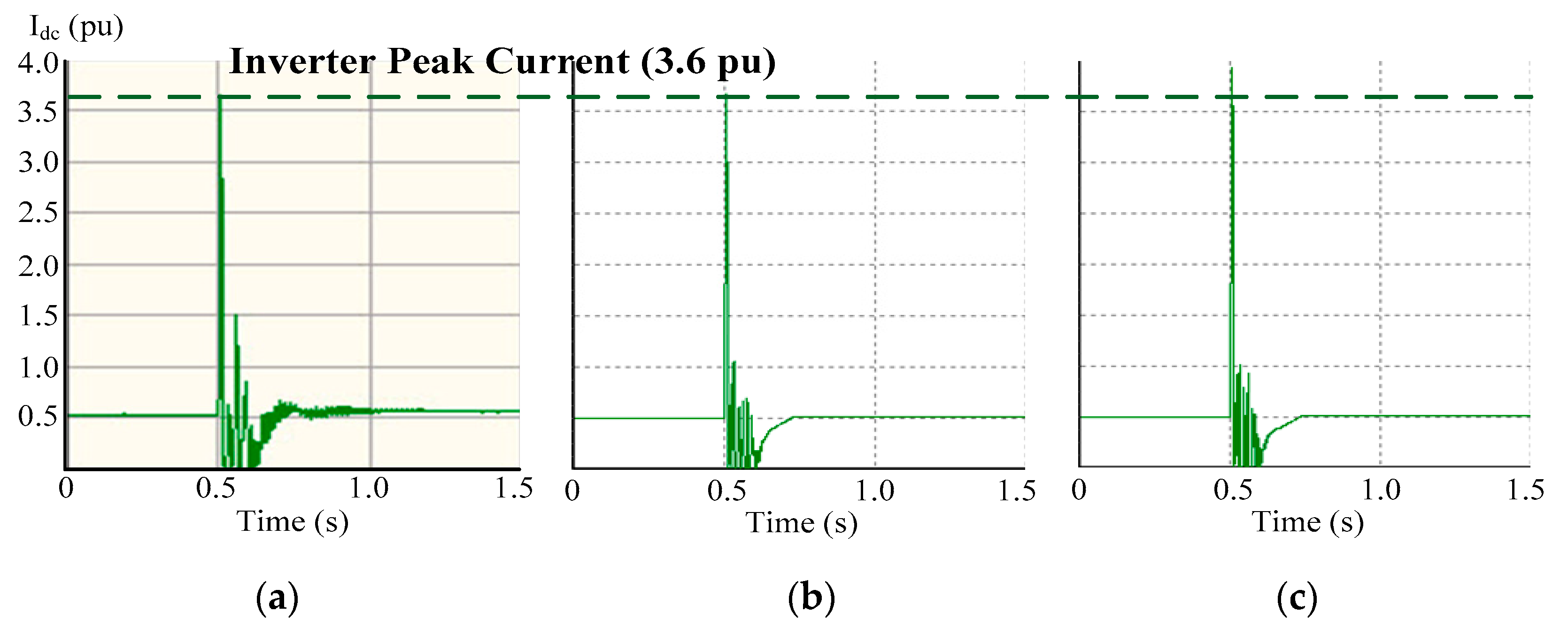
| max. Vdci (kA) | 141 | 145 | 2.8 | 161 | 14.1 | 198 | 40.4 | 238 | 68.8 |
| max. Idci (A) | 2380 | 2375 | 0.2 | 2643 | 11.1 | 2881 | 21.4 | 3120 | 31.1 |
| Models | Proposed (PSS/E) | Conventional (PSS/E) | PSCAD |
|---|---|---|---|
| Time (s) | 25 | 24 | 1276 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, D.; Kim, Y.; Moon, S.; Kim, C. Modeling of HVDC System to Improve Estimation of Transient DC Current and Voltages for AC Line-to-Ground Fault—An Actual Case Study in Korea. Energies 2017, 10, 1543. https://doi.org/10.3390/en10101543
Kwon D, Kim Y, Moon S, Kim C. Modeling of HVDC System to Improve Estimation of Transient DC Current and Voltages for AC Line-to-Ground Fault—An Actual Case Study in Korea. Energies. 2017; 10(10):1543. https://doi.org/10.3390/en10101543
Chicago/Turabian StyleKwon, Dohoon, Youngjin Kim, Seungil Moon, and Chanki Kim. 2017. "Modeling of HVDC System to Improve Estimation of Transient DC Current and Voltages for AC Line-to-Ground Fault—An Actual Case Study in Korea" Energies 10, no. 10: 1543. https://doi.org/10.3390/en10101543
APA StyleKwon, D., Kim, Y., Moon, S., & Kim, C. (2017). Modeling of HVDC System to Improve Estimation of Transient DC Current and Voltages for AC Line-to-Ground Fault—An Actual Case Study in Korea. Energies, 10(10), 1543. https://doi.org/10.3390/en10101543




