An Improved Forecasting Method for Photovoltaic Power Based on Adaptive BP Neural Network with a Scrolling Time Window
Abstract
:1. Introduction
2. Nonlinear and Time-Varying Characteristics of PV Output Power
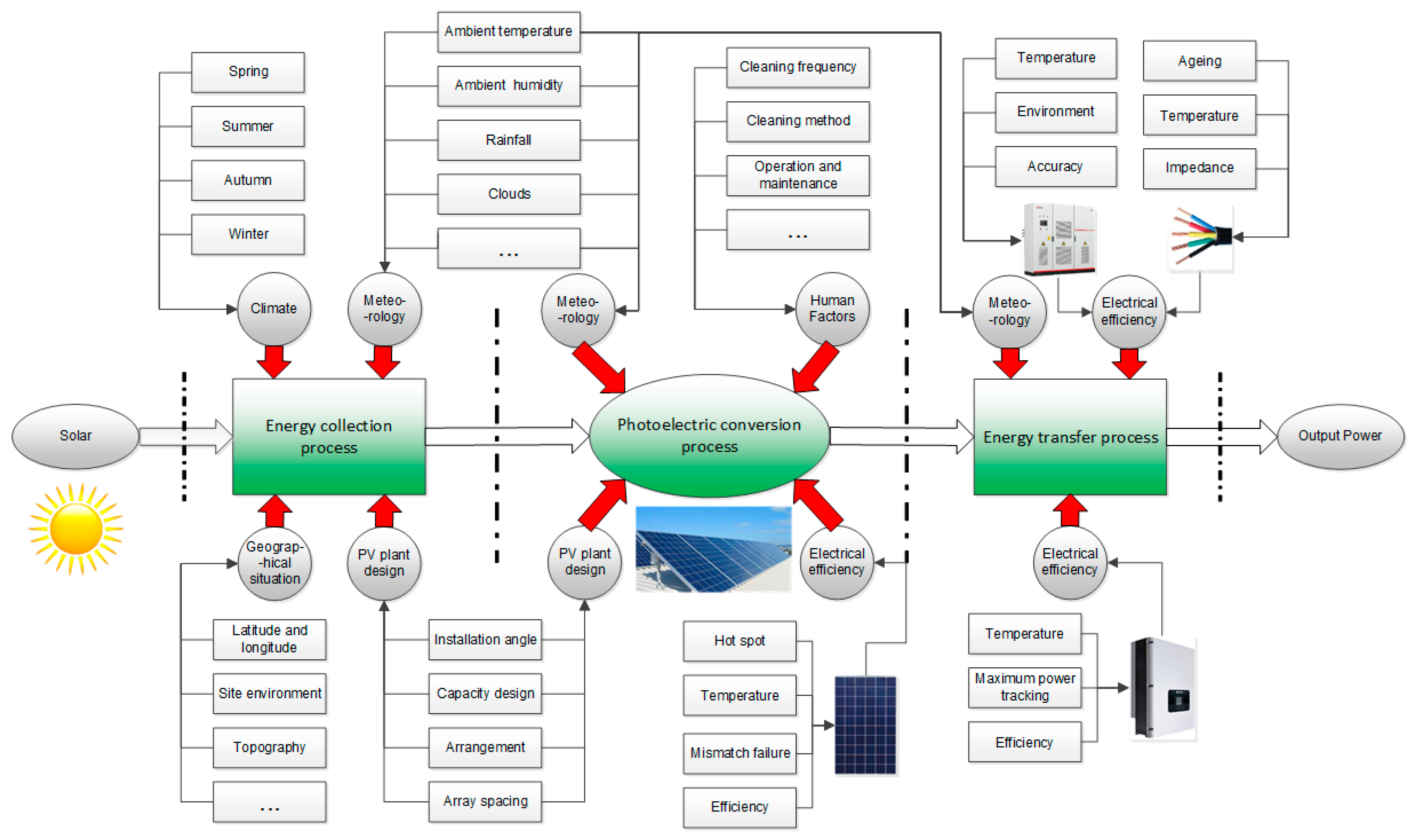
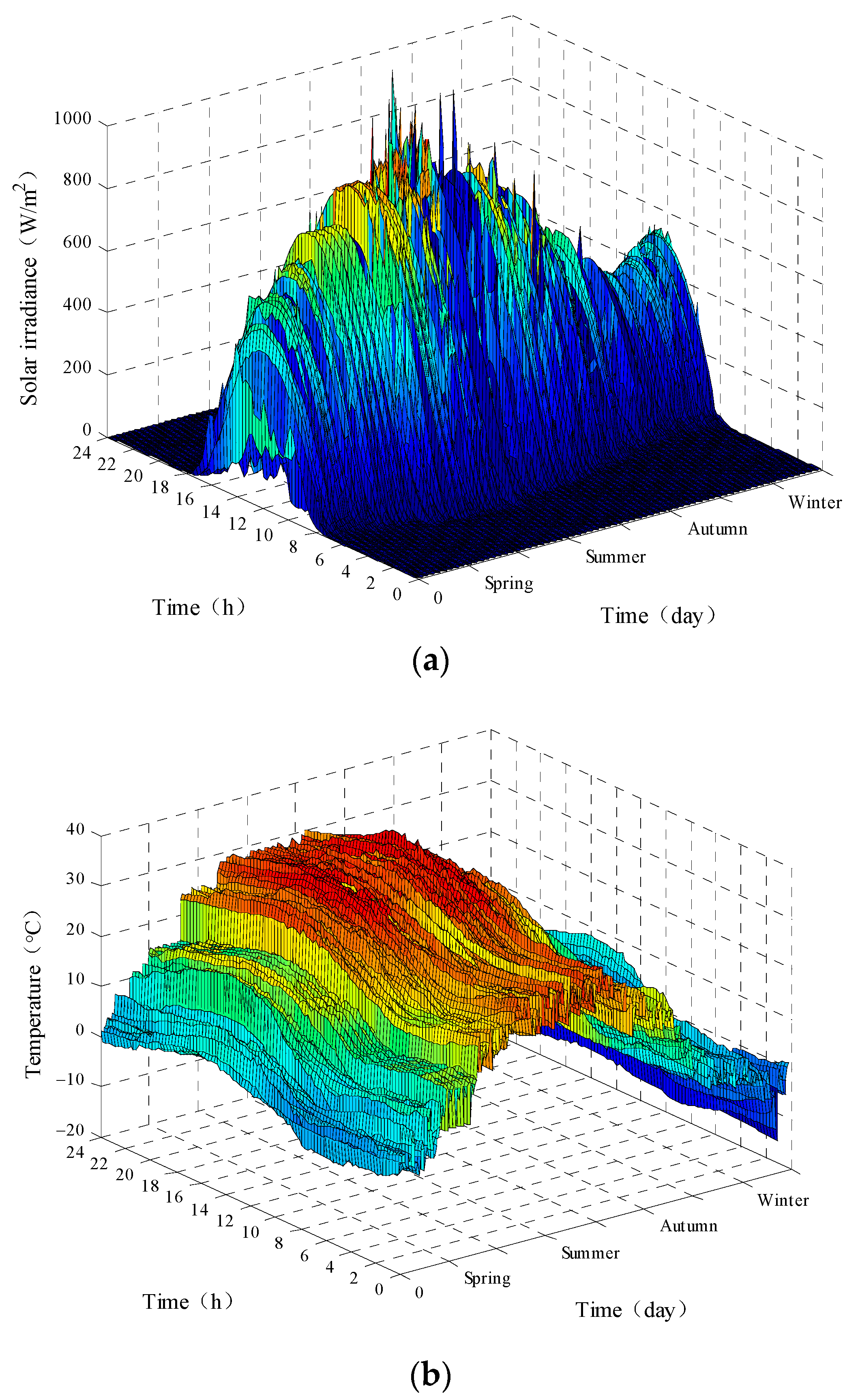
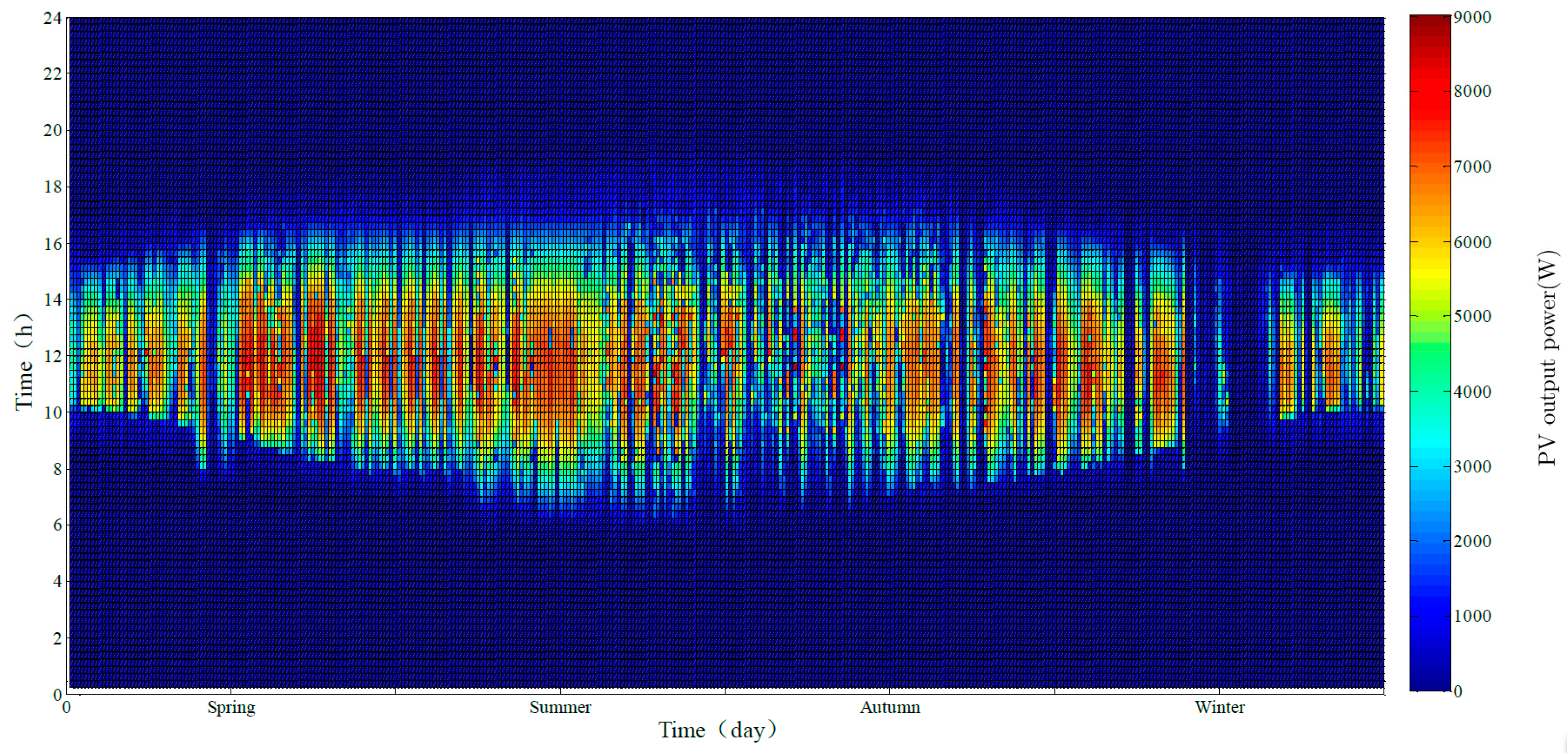
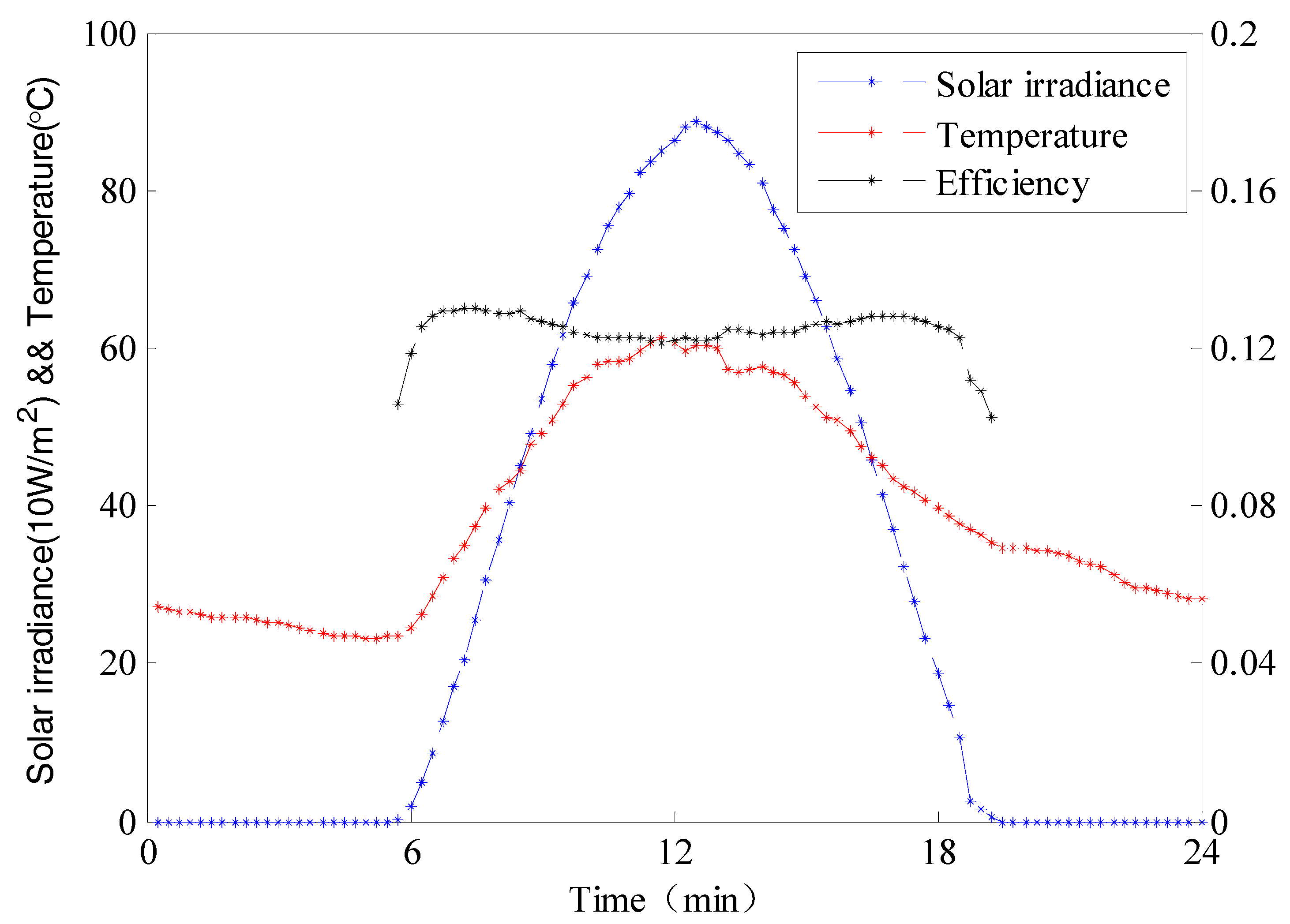
2.1. Influence of External Factors
2.2. Influence of Internal Factors
2.3. Brief Summary
3. The Proposal of Improved Method
3.1. BP Neural Network Principle
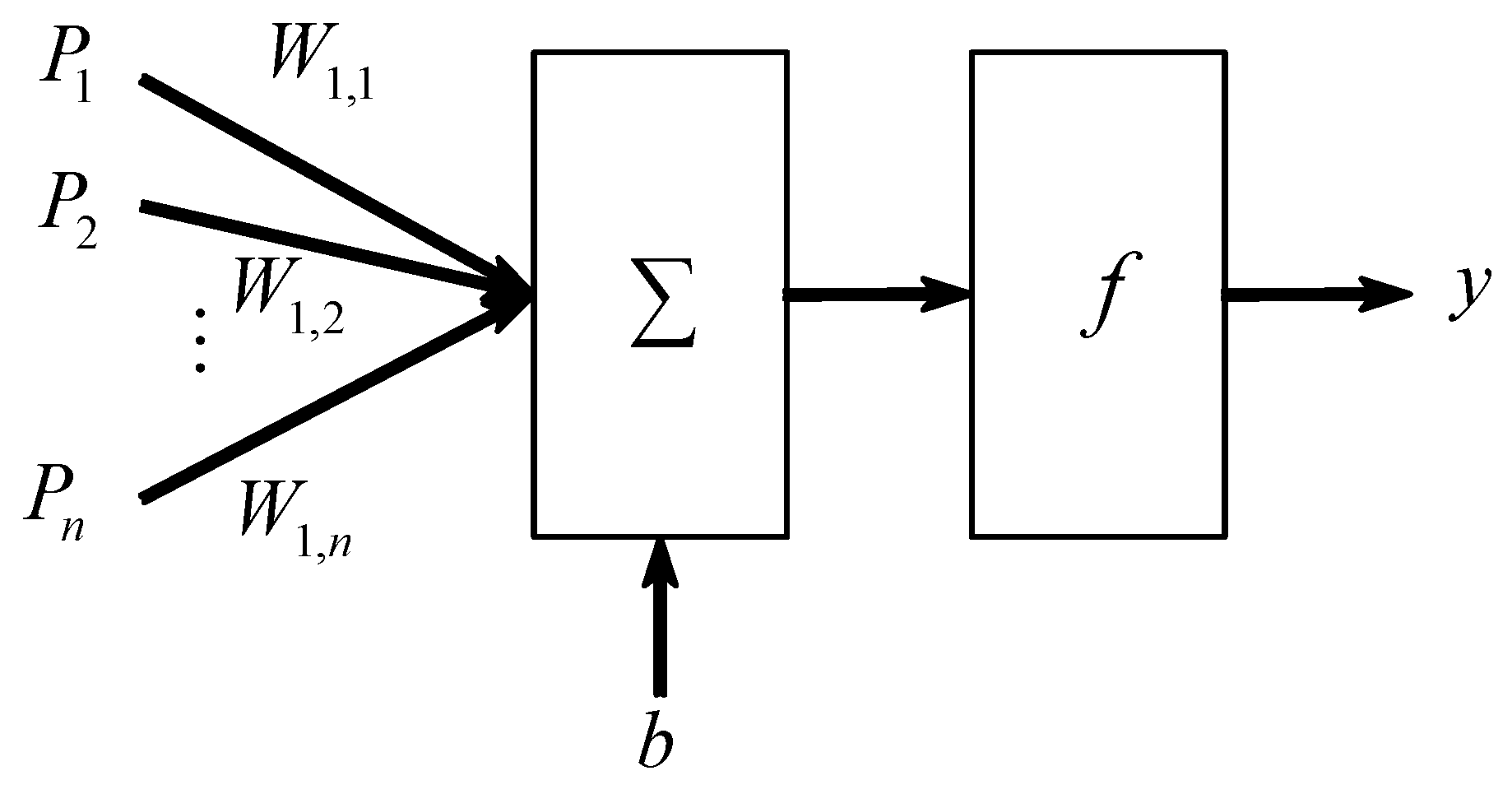
- The gradient descent and learning rate of a traditional neural network are slow, typically requiring thousands of training steps. Therefore, it may have a long-time error flat region.
- Since the training process is long, it can only weakly dynamically track nonlinear time-varying objects.
- Each training process is a brand new process for BP neural network, and its stability often suffers from the effect of initial weight value selection.
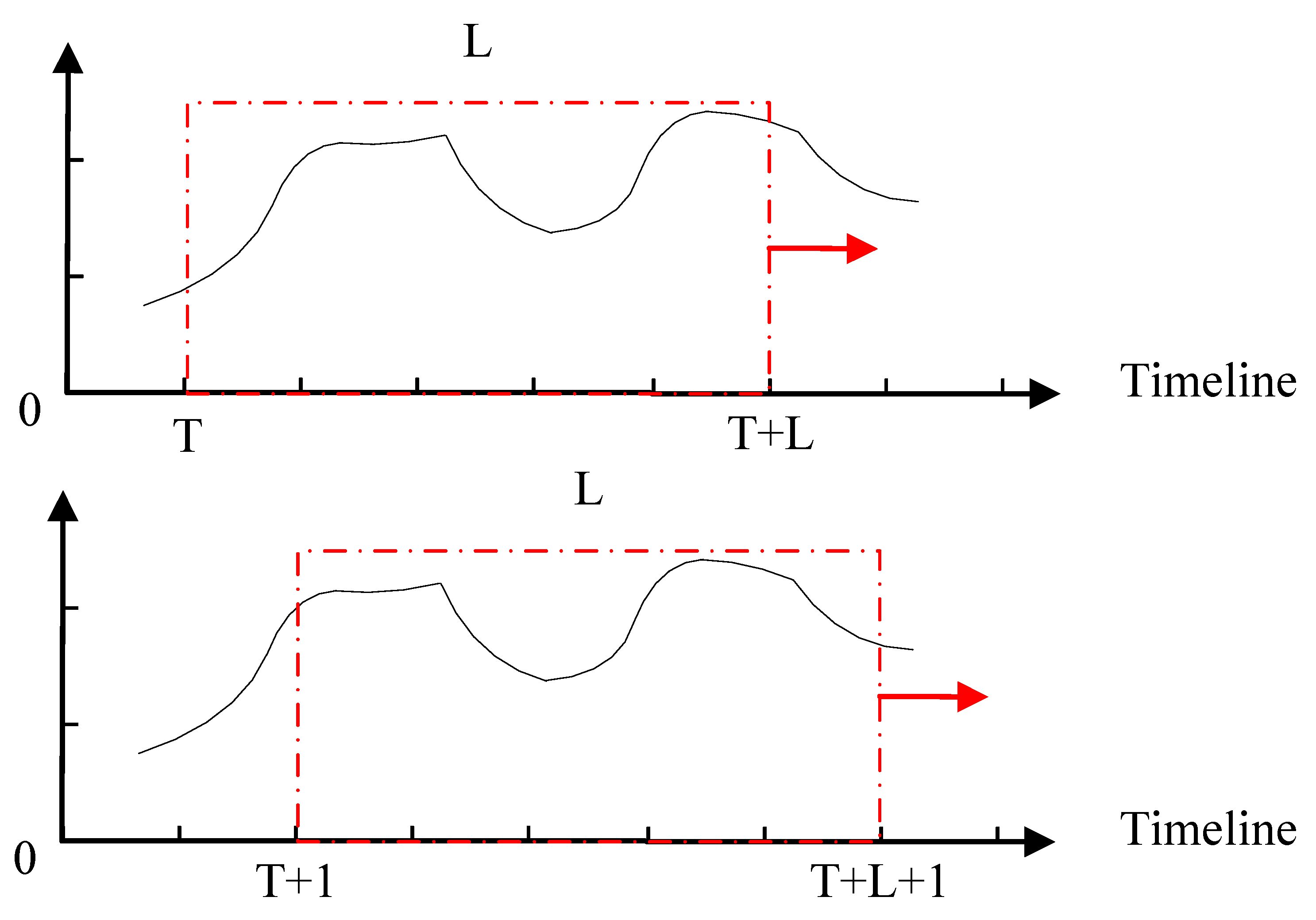
3.2. Scrolling Time Window Technology
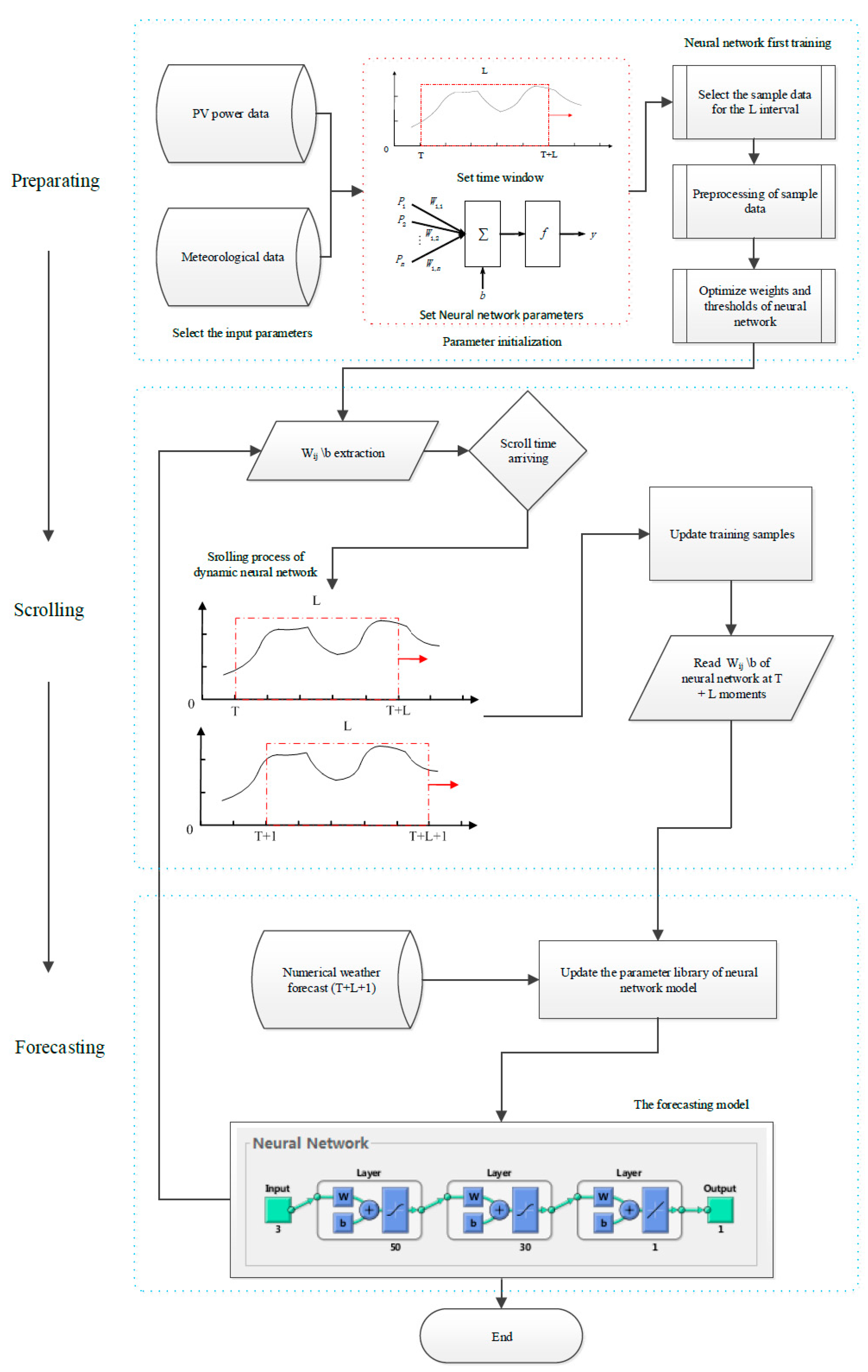
3.3. The New Proposed Method
4. The Application and Result
4.1. Design of Experimental Method
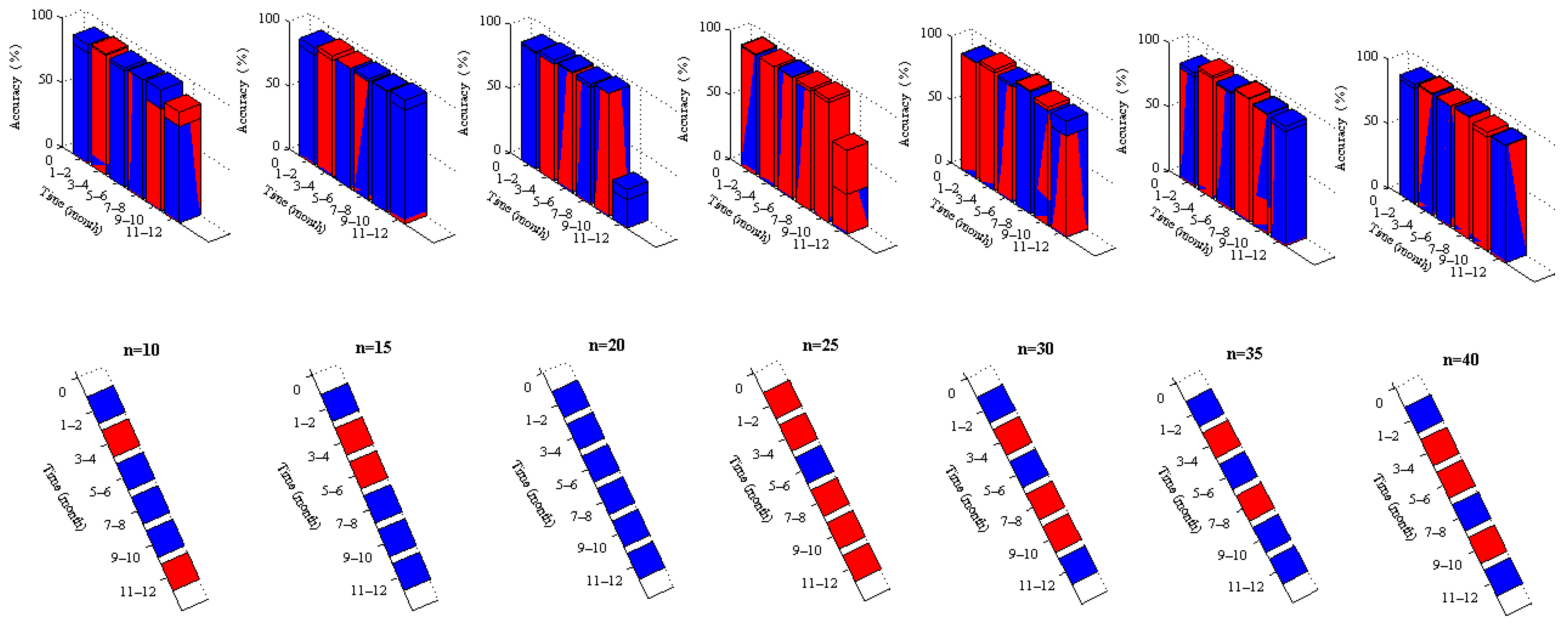
4.2. Determination of Length of Time Window
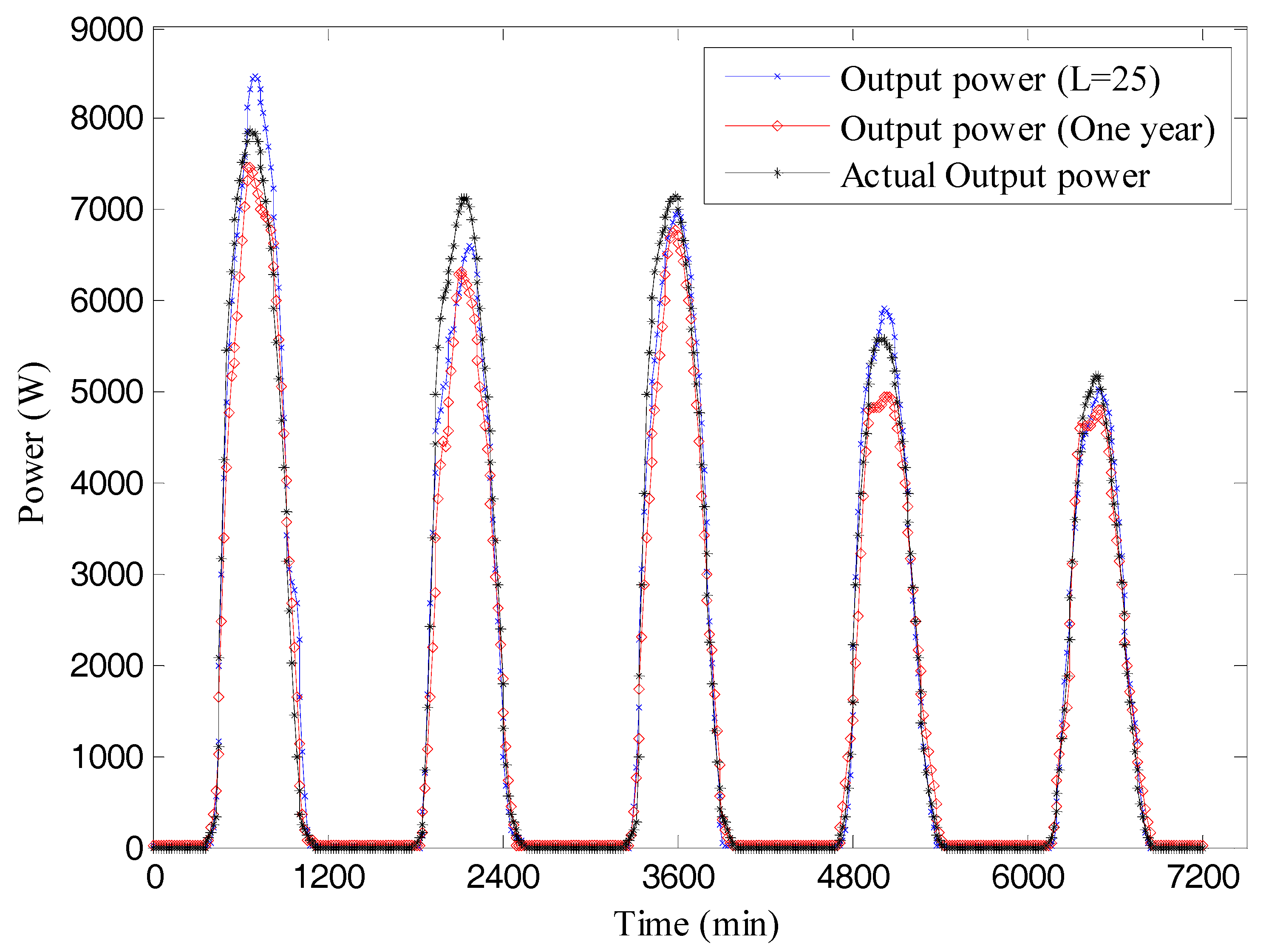
4.3. Performance Analysis of Algorithm
- As the length of time window extends, the quantity of sample data increases, and the training time of the model also increases gradually.
- Compared with the training time (about 20 min) of the annual forecasting model, the training time of scrolling time window model is short, and the rate of convergence is fast.
- Since the short-term forecasting of PV power requires that the time for single calculation is shorter than 5 min, the training time of a 25-day scrolling time window model is shorter than 2 min, which can meet the corresponding requirements, perform calculation quickly, and exhibit good performance.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Cap | average operating capacity |
| E | the output error |
| G | solar irradiance (W/m2) |
| GT | solar irradiance on module plane (W/m2) |
| K | the number of iterations |
| L | the length of the modeling data |
| MAE | mean absolute error |
| MaxError | maximum error |
| P | electrical power (W) |
| RMSE | root mean square error |
| STD | standard deviation |
| Ttem | temperature (°C) |
| Ttem,c | cell/module operating temperature (°C) |
| V | the input variable |
| W | the weight |
| Z | the input and output time-varying data sample set |
| Subscripts | - |
| c | cell (module) |
| Mi | the measured value at time i. |
| mean | the average value |
| n | sample size |
| Pi | the predicted value at time i. |
| r | the rated state |
| ref | reference value, at reference conditions |
| s | the start state |
| T | on module’s tilted plane |
References
- Raza, M.Q.; Nadarajah, M.; Ekanayake, C. On recent advances in PV output power forecast. Sol. Energy 2016, 136, 125–144. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M.; Lughi, V. Short-term forecasting of power production in a large-scale photovoltaic plant. Sol. Energy 2014, 105, 401–413. [Google Scholar] [CrossRef]
- Eltigani, D.; Masri, S. Challenges of integrating renewable energy sources to smart grids: A review. Renew. Sustain. Energy Rev. 2015, 52, 770–780. [Google Scholar] [CrossRef]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the North Am. Power Symp. (NAPS), Arlington, TX, USA, 26–28 September 2010; pp. 1–8. [Google Scholar]
- Graditi, G.; Ferlito, S.; Adinolfi, G. Comparison of photovoltaic plant power production prediction methods using a large measured dataset. Renew. Energy 2016, 90, 513–519. [Google Scholar] [CrossRef]
- Piliougine, M.; Elizondo, D.; Mora-Lo’pez, L.; Sidrach-de-Cardona, M. Modelling photovoltaic modules with neural networks using angle of incidence and clearness index. Prog. Photovolt. Res. 2015, 23, 513–523. [Google Scholar] [CrossRef]
- Huang, L.; Shu, J.; Jiang, G.; Zhang, J. Photovoltaic generation forecast based on multidimensional time-series and local support vector regression in microgrids. Autom. Electr. Power Syst. 2014, 38, 19–24. [Google Scholar]
- Ding, M.; Xu, N. A Method to Forecast Short-Term Output Power of Photovoltaic Generation System Based on Markov Chain. Power Syst. Technol. 2011, 35, 152–157. [Google Scholar]
- Almonacid, F.; Pérez-Higueras, P.J.; Fernández, E.F.; Hontoria, L. A methodology based on dynamic artificial neural network for short-term forecasting of the power output of a PV generator. Energy Convers. Manag. 2014, 85, 389–398. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osoriob, N.; Escobar, R.; Urraca, R.; Martinez-de-Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Zhu, H.; Li, X.; Sun, Q.; Nie, L.; Yao, J.; Zhao, G. A power prediction method for photovoltaic power plant based on wavelet decomposition and artificial neural networks. Energies 2015, 9, 11. [Google Scholar] [CrossRef]
- Ye, L.; Chen, Z.; Zhao, Y. Photovoltaic power forecasting model based on genetic algorithm and fuzzy radial basis function neural network. Autom. Electr. Power Syst. 2015, 39, 16–22. [Google Scholar]
- Wang, X.; Zhou, X.; Xing, J.; Yang, J. A prediction method of PV output power based on the combination of improved grey back propagation neural network. Power Syst. Prot. Control 2016, 44, 81–87. [Google Scholar]
- Zhang, G. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Vaz, A.G.R.; Elsinga, B.; van Sark, W.; Brito, M.C. An artificial neural network to assess the impact of neighbouring photovoltaic systems in power forecasting in Utrecht, The Netherlands. Renew. Energy 2016, 85, 631–641. [Google Scholar] [CrossRef]
- Ferlito, S.; Adinolfi, G.; Graditi, G. Comparative analysis of data-driven methods online and offline trained to the forecasting of grid-connected photovoltaic plant production. Appl. Energy 2017, 205, 116–129. [Google Scholar] [CrossRef]
- Li, C.; Liu, X.; Cao, Y.; Zhang, P.; Shi, H.; Ren, L.; Kuang, Y. A time-scale adaptive dispatch method for renewable energy power supply systems on islands. IEEE Trans. Smart Grid 2016, 7, 1069–1078. [Google Scholar] [CrossRef]
- Eleonora, R.S.; Roberto, G.; Gaetano, Z.; Gallea, R.; Quang, N.N. A self-adapting approach for forecast-less scheduling of electrical energy storage systems in a liberalized energy market. Energies 2013, 6, 5738–5759. [Google Scholar]
- Dash, P.K.; Liew, A.C.; Ramakrishna, G. Power-demand forecasting using a neural network with an adaptive learning algorithm. IEE Proc. Gener. Transm. Distrib. 1995, 142, 560–568. [Google Scholar] [CrossRef]
- Liu, K.; Subbarayan, S.; Shoults, R.R.; Manry, M.T.; Kwan, C.; Lewis, F.I.; Naccarino, J. Comparison of very short-term load forecasting techniques. IEE Trans. Power Syst. 1996, 11, 877–882. [Google Scholar] [CrossRef]
- Xu, Y.; Milanović, J.V. Day-Ahead prediction and shaping of dynamic response of demand at bulk supply points. IEEE Trans. Power Syst. 2016, 31, 3100–3108. [Google Scholar] [CrossRef]
- Rosato, A.; Rosa, A.; Rodolfo, A.; Araneo, R.; Panella, M. Prediction in photovoltaic power by neural networks. Energies 2017, 10, 1003. [Google Scholar] [CrossRef]
- Dolara, A.; Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. A physical hybrid artificial neural network for short term forecasting of PV plant power output. Energies 2015, 8, 1138–1153. [Google Scholar] [CrossRef] [Green Version]
- Al-Messabi, N.; Goh, C.; El-Amin, I.; Li, Y. Heuristically enhanced dynamic neural networks for structurally improving photovoltaic power forecasting. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014. [Google Scholar]
- Ceci, M.; Corizzo, R.; Fumarola, F.; Malerba, D.; Rashkovska, A. Predictive modeling of PV energy production: How to set up the learning task for a better prediction. IEEE Trans. Ind. Inform. 2017, 13, 956–966. [Google Scholar] [CrossRef]
- Saberian, A.; Hizam, H.; Radzi, M.A.M.; Kadir, M.Z.A.A.; Mirzaei, M. Modelling and prediction of photovoltaic power output using artificial neural networks. Int. J. Photoenergy 2014, 2014. [Google Scholar] [CrossRef]
- Izgi, E.; Öztopal, A.; Yerli, B.; Kaymak, M.K.; Şahin, A.D. Short-mid-term solar power prediction by using artificial neural networks. Sol. Energy 2012, 86, 725–733. [Google Scholar] [CrossRef]
- Jordan, D.C.; Kurtz, S.R. Photovoltaic degradation rates—An analytical review. Prog. Photovolt. Res. Appl. 2013, 21, 12–29. [Google Scholar] [CrossRef]
- Zheng, H.; Hu, B.; Shen, H.; Ge, W. Analysis of performance and degradation of silicon PV modules after long term operation. Acta Energ. Sol. Sin. 2012, 33, 614–617. [Google Scholar]
- Skoplaki, E.; Palyvos, J.A. On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Sol. Energy 2009, 83, 614–624. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Li, B.; Fan, H. The window-sliding forecast on the time series of the parameter-varying chao tic system using neural networks. J. Wuhan Univ. Technol. 2010, 34, 456–459. [Google Scholar]
- Phua, S.K. Data Base Preparation in Power Systems Management: Measurement Selection, Short-Term Load Prediction and Load Modeling; Monash University: Melbourne, Victoria, Australia, 1977. [Google Scholar]

| Sample Data | L = 10 | L = 15 | L = 20 | L = 25 | L = 30 | L = 35 | L = 40 | |
|---|---|---|---|---|---|---|---|---|
| Group 1 | Training | 1–10 January | 1–15 January | 1–20 January | 1–25 January | 1–30 January | 1–4 January | 1 January–14 February |
| Test | 11–13 January | 16–18 January | 21–23 January | 26–28 January | 31 January–2 February | 5–7 February | 15–17 February | |
| Group 2 | Training | 1–10 March | 1–15 March | 1–20 March | 1–25 March | 1–30 March | 1 March–4 April | 1 March–14 April |
| Testing | 11–13 March | 16–18 March | 21–23 March | 26–28 March | 31 March–2 April | 5–7 April | 15–17 April | |
| Group 3 | Training | 1–10 May | 1–15 May | 1–20 May | 1–25 May | 1–30 May | 1 May–4 June | 1 May–14 June |
| Testing | 11–13 May | 16–18 May | 21–23 May | 26–28 May | 31 May–2 June | 5–7 June | 15–17 June | |
| Group 4 | Training | 1–10 July | 1–15 July | 1–20 July | 1–25 July | 1–30 July | 1 July–4 August | 1 July–14 August |
| Testing | 11–13 July | 16–18 July | 21–23 July | 26–28 July | 31 July–2 August | 5–7 August | 15–17 August | |
| Group 5 | Training | 1–10 September | 1–15 September | 1–20 September | 1–25 September | 1–30 September | 1 September–5 October | 1 September–15 October |
| Testing | 11–13 September | 16–18 September | 21–23 September | 26–28 September | 1–3 October | 6–8 October | 16–18 October | |
| Group 6 | Training | 1–10 November | 1–15 November | 1–20 November | 1–25 November | 1–30 November | 1 November–5 December | 1 November–15 December |
| Testing | 11–13 November | 16–18 November | 21–23 November | 26–28 November | 1–3 December | 6–8 December | 16–18 December | |
| Grouping | Accuracy (%) | ||||||
|---|---|---|---|---|---|---|---|
| L = 10 | L = 15 | L = 20 | L = 25 | L = 30 | L = 35 | L = 40 | |
| Group 1 | 85.19 | 86.6 | 90.21 | 94.16 | 91.46 | 85.4 | 89.74 |
| One year | 91.74 | 92.28 | 91.45 | 93.21 | 91.88 | 88.65 | 92.7 |
| Group 2 | 93.84 | 94.91 | 90.79 | 93.79 | 95.53 | 95.45 | 95.09 |
| One year | 92.65 | 91.41 | 94.1 | 93.73 | 92.91 | 93.43 | 94.21 |
| Group 3 | 89.83 | 94.51 | 93.11 | 94.41 | 91.05 | 91.06 | 94.55 |
| One year | 92.14 | 94.35 | 94.07 | 94.94 | 93.03 | 92.46 | 94.21 |
| Group 4 | 92.09 | 93.31 | 91.22 | 95.35 | 97.53 | 96.69 | 95.18 |
| One year | 92.35 | 95.3 | 93.96 | 93.04 | 96.48 | 96.13 | 95.52 |
| Group 5 | 79.01 | 94.9 | 95.76 | 96.24 | 93.68 | 93.32 | 92.44 |
| One year | 93.62 | 95.42 | 95.85 | 93.48 | 90.91 | 93.96 | 88.7 |
| Group 6 | 85.87 | 89.33 | 22.19 | 65.4 | 79.96 | 89.17 | 91.27 |
| One year | 74.66 | 97.2 | 30.17 | 31.05 | 91.71 | 93.12 | 91.87 |
| Grouping | Training Time (s) | ||||||
|---|---|---|---|---|---|---|---|
| L = 10 | L = 15 | L = 20 | L = 25 | L = 30 | L = 35 | L = 40 | |
| Group 1 | 58.76 | 71.56 | 79.22 | 90.78 | 113.10 | 126.15 | 150.69 |
| Group 2 | 54.34 | 72.82 | 82.72 | 101.05 | 126.23 | 135.25 | 158.69 |
| Group 3 | 61.78 | 64.03 | 89.30 | 94.44 | 118.27 | 139.39 | 151.50 |
| Group 4 | 58.75 | 67.49 | 77.17 | 91.80 | 110.00 | 123.69 | 138.30 |
| Group 5 | 60.95 | 74.78 | 91.40 | 109.30 | 172.88 | 154.26 | 162.03 |
| Group 6 | 56.27 | 71.04 | 78.95 | 91.79 | 287.36 | 137.73 | 139.91 |
| Average | 58.48 | 70.29 | 83.13 | 96.53 | 154.64 | 136.08 | 150.19 |
| One year | Average = 1175.00 | ||||||
| Training Data | Testing Data | MaxError (W) | STDError (W) | RMSE (%) | MAE (%) |
|---|---|---|---|---|---|
| 1–25 January | 26–28 January | 1749.05 | 349.56 | 5.84 | 2.86 |
| One year | 26–28 January | 2016.98 | 399.26 | 6.79 | 3.50 |
| 1–25 March | 26–28 March | 2278.84 | 420.11 | 6.21 | 3.30 |
| One year | 26–28 March | 2123.48 | 410.97 | 6.27 | 3.58 |
| 1–25 May | 26–28 May | 1367.68 | 261.36 | 5.59 | 3.48 |
| One year | 26–28 May | 908.60 | 233.44 | 5.06 | 3.22 |
| 1–25 July | 26–28 July | 947.60 | 181.09 | 4.65 | 2.71 |
| One year | 26–28 July | 1217.28 | 275.83 | 6.96 | 3.91 |
| 1–25 September | 26–28 September | 1114.98 | 221.62 | 3.76 | 2.00 |
| One year | 26–28 September | 1679.96 | 383.25 | 6.52 | 3.50 |
| 1–25 November | 26–28 November | 3398.66 | 555.22 | 34.60 | 15.26 |
| One year | 26–28 November | 4557.20 | 1101.77 | 68.95 | 30.94 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Lian, W.; Lu, L.; Dai, S.; Hu, Y. An Improved Forecasting Method for Photovoltaic Power Based on Adaptive BP Neural Network with a Scrolling Time Window. Energies 2017, 10, 1542. https://doi.org/10.3390/en10101542
Zhu H, Lian W, Lu L, Dai S, Hu Y. An Improved Forecasting Method for Photovoltaic Power Based on Adaptive BP Neural Network with a Scrolling Time Window. Energies. 2017; 10(10):1542. https://doi.org/10.3390/en10101542
Chicago/Turabian StyleZhu, Honglu, Weiwei Lian, Lingxing Lu, Songyuan Dai, and Yang Hu. 2017. "An Improved Forecasting Method for Photovoltaic Power Based on Adaptive BP Neural Network with a Scrolling Time Window" Energies 10, no. 10: 1542. https://doi.org/10.3390/en10101542
APA StyleZhu, H., Lian, W., Lu, L., Dai, S., & Hu, Y. (2017). An Improved Forecasting Method for Photovoltaic Power Based on Adaptive BP Neural Network with a Scrolling Time Window. Energies, 10(10), 1542. https://doi.org/10.3390/en10101542





