Dummy Eye Measurements of Microsaccades: Testing the Influence of System Noise and Head Movements on Microsaccade Detection in a Popular Video-Based Eye Tracker

Abstract

Whereas early studies of microsaccades have predominantly relied on custom-built eye trackers and manual tagging of microsaccades, more recent work tends to use video-based eye tracking and automated algorithms for microsaccade detection. While data from these newer studies suggest that microsaccades can be reliably detected with video-based systems, this has not been systematically evaluated. I here present a method and data examining microsaccade detection in an often used video-based system (the Eyelink II system) and a commonly used detection algorithm (Engbert & Kliegl, 2003; Engbert & Mergenthaler, 2006). Recordings from human participants and those obtained using a pair of dummy eyes, mounted on a pair of glasses either worn by a human participant (i.e., with head motion) or a dummy head (no head motion) were compared. Three experiments were conducted. The first experiment suggests that when microsaccade measurements make use of the pupil detection mode, microsaccade detections in the absence of eye movements are sparse in the absence of head movements, but frequent with head movements (despite the use of a chin rest). A second experiment demonstrates that by using measurements that rely on a combination of corneal reflection and pupil detection, false microsaccade detections can be largely avoided as long as a binocular criterion is used. A third experiment examines whether past results may have been affected by possible incorrect detections due to small head movements. It shows that despite the many detections due to head movements, the typical modulation of microsaccade rate after stimulus onset is found only when recording from the participants’ eyes.

Introduction

Microsaccades are small eye movements made during attempted visual fixation with properties similar to those of larger saccadic eye movements aimed to bring one’s gaze toward different regions of the visual field (for reviews, see Collewijn & Kowler, 2008; Martinez- Conde, Macknik, Troncoso, & Hubel, 2009; Rolfs, 2009). For example, microsaccades and larger amplitude saccades have both been found to follow the main sequence, displaying a linear relationship between the amplitude of the saccade and the peak velocity (Zuber, Stark, & Cook, 1965). Further shared aspects are their binocular nature, the distribution of inter-saccadic intervals, the involvement of voluntary control, and their relation with spatial attention (for overviews, see Engbert, 2006; Rolfs, Kliegl, & Engbert, 2008).

Because microsaccades are very small eye movements, the issue arises how to most reliably measure these movements. In contrast to past studies of microsaccades, which often employed custom-built eye trackers (for an overview, see Collewijn & Kowler, 2008), more recent studies have mostly relied on videobased eye trackers. These eye trackers use an infrared camera to record images from the eyes, which are then analyzed for eye movements. Typically, two properties in the images are used (Morimoto & Mimica, 2005): the estimated position of the pupil and a reflection from the cornea (‘corneal reflection’ or the first Purkinje image). Studies of microsaccades, however, often rely on the estimate pupil position alone (all studies in

Table 1. Slope, intercept, and proportion of variance explained (R²) of the best fitting regression lines of the logarithm of the saccade amplitude and the logarithm of the peak velocity across the different conditions.

Condition	Slope	Intercept	R2
Dummy eye + dummy head, without correction	0.89	4.81	0.88
Dummy eye + dummy head, with correction	0.86	4.62	0.48
Dummy eye + human head, without correction	0.51	3.50	0.66
Dummy eye + human head, with correction	0.57	3.77	0.58
Human eye + human head, without correction	0.68	4.31	0.83
Human eye + human head, with correction	0.69	4.33	0.83

of Martinez-Conde et al., 2009, that use the Eyelink II system at 500Hz), possibly because pupil-only detection allows for a higher sampling rate in the eye tracker used in these studies. The disadvantage, however, of using pupil detection only is that recordings are relatively noisy and sensitive to the movement of the participant’s head relative to the cameras (for example, due to movement of the head-band of the system). These are reflected in two possible sources of noise. The first is caused by the uncertainty about which pixels in the image belong to the pupil, dictated by factors such as the detection threshold, the quality of the image, light-sources in the room, and properties of the eyes of the research participant. The second source involves small head movements which lead to the movement of the recorded image, which may be confused with eye movements.

A recent comparison between a popular older system (a scleral search coil) and a video-based system (the Eyelink 1000) has suggested that for microsaccade detection the two types of system may be comparable (Kimmel, Mammo, & Newsome, 2012). This comparison, however, was conducted in primates, allowing for more stringent head stabilization than typically possible in human observers. In humans, video-based systems are often preferred, as they are less invasive than scleral coil systems. Video-based systems allow for testing of a larger range of participants (e.g., naive participants rather than the authors or associated lab members) and longer measurement intervals, allowing for more complex research designs and more repeated measurements per condition. Furthermore, video-based systems are commercially available, often requiring little maintenance and easy to use. Studies using video-based systems often apply head stabilization by means of a chin rest, and the question therefor arises to which extent small head movements in these chin rests, added to system noise, influences the detection of microsaccades. I here present a method and data aimed to answer this question. The methods adds to a surrogate data technique used in earlier studies (Engbert & Mergenthaler, 2006; Mergenthaler & Engbert, 2010; Rolfs et al., 2008; Otero-Millan, Castro, Macknik, & Martinez-Conde, 2014) in which detection is compared for actual data and surrogate data, for example, to determine the optimal settings of the algorithm for detection. Surrogate data is obtained by shuffling the original data in such a way that important properties of the signal are maintained. While this method allows for evaluating detection methods, it does not specifically address the influences of different sources of noise.

The method presented here is based on a recently introduced technique to examine the role of the system’s noise levels on the detection of microsaccades (Hermens & Walker, 2010). In this method, we used two small black discs, serving as artificial pupils, attached to a glass dummy head on which the eye tracker rested. Before each recording, the eye tracker was calibrated on a research participant, after which the headband was transferred to the dummy head and recordings were made from the dummy eyes. Whereas this method provides information about the noise levels of the recordings of the eye tracker, it does not estimate the influence of head movements of the research participant. In the present work, I therefore modified this setup by mounting the artificial pupils onto a pair of glasses (Figure 1a) that can either be worn by the dummy head (to estimate the amount of noise in the recordings in the absence of head motion) or by a human participant (to estimate the influence of head movements on the detection of microsaccades). A second change to the original setup involves the mounting of two metal clips, generating a signal that can be interpreted by the system as a corneal reflection (details provided in Experiment 2). For practical reasons (availability of the eye tracker and computer code for data analysis), I decided to focus on eye tracking with the Eyelink II system (SR Research) and analysis with the algorithm proposed by Engbert and colleagues (Engbert & Kliegl, 2003; Engbert & Mergenthaler, 2006). Incidentally, this combination of methods appears to be the most commonly used technique to study microsaccades in recent research. For example, in the overview by Martinez-Conde and collegues (2009) 25 of the 37 studies listed their Table 1 use this particular setup.

Three experiments were conducted, all applying a cueing paradigm (Engbert & Kliegl, 2003; Hermens & Walker, 2010; Laubrock, Engbert, & Kliegl, 2005; Rolfs et al., 2008). The first experiment focused on the influence of system noise and head movements on the overall properties of microsaccades. Participants were asked to wear the pair of glasses with artificial pupils as normal glasses, thereby blocking their view of the screen. In this first experiment, in which only the pupil center was used to estimate gaze direction (in agreement with the typical setup of many past microsaccade studies), high microsaccade rates were obtained in the head movement condition, despite the use of the eye tracker’s motion correction setting. Experiment 2 investigated whether this high detection rate can be reduced by using the combined corneal reflection and pupil center setting of the system. Finally, Experiment 3 investigated the extent to which the incorrect detections due to head movements may have influenced an important finding in the literature, sometimes referred to as the ’microsaccade signature’, reflecting the initial decrease and subsequent increase of the microsaccade rate after the onset of a stimulus.

Experiment 1: Microsaccade properties

In Experiment 1, the influence of noise in the recordings from the Eyelink II system on the detection of eye movements is investigated by comparing dummy eyes mounted on a dummy head, dummy eyes mounted on a human head and human eyes.

Method

Participants. Test runs with the dummy eye setup with the author as the participant showed that the rate of false microsaccade detections depended on the calibration of the system. To best mimic the setup of a typical microsaccade study, data were therefore collected across several participants (each with their own calibration). Eleven students from the university of Leuven and author FH took part in the experiment. The students all provided written consent for participation in the study, which was approved by the local ethics committee. They received 8.50 Euro for their participation.

Apparatus. Eye movements were recorded using an Eyelink II setup (SR research), consisting of two PCs and a head-mounted eye tracking device. One of the PCs recorded eye movements at a sampling rate of 500Hz in the pupil-only mode, while the other PC was used to present the stimuli to the participants. These stimuli were presented on a 21 inch Iiyama computer monitor at a 75Hz refresh rate placed at a distance of 57cm from the participant. Dummy eye recordings were obtained using a custom-built pair of glasses, constructed from a pair of reading glasses, white stickon paper and black insulation tape for the pupils, as shown in Figure 1a. Before deciding on the size of dummy eye pupil to use, various size pupils were tested, suggesting that the results were only weakly influenced by the size of the dummy pupils. Because larger pupils could be more easily cut into a circular shape, a slightly larger diameter (1.5cm) was used. This somewhat large size compared to human pupils was, in part, compensated for by the larger distance from the dummy eyes where the cameras had to be placed due to the space taken by the glasses. The dummy pupils were placed in the center of a white background (oval shape) measuring 5.5cm by 3.2cm. Head movements of the participants were restricted with a chin rest that could be adjusted to the participant’s height.

Stimuli. As in earlier studies (e.g., Engbert & Kliegl, 2003; Hermens & Walker, 2010), a cueing paradigm was adopted. Participants maintained fixation on a centrally presented fixation symbol (1 by 1 degree in visual angle; see Figure 1b), which turned into an arrow, after which a peripherally presented target (star shape, 0.7 by 0.7 degrees in visual angle) was presented inside one of four laterally positioned place-holders (circles), presented at a distance of 9 degrees from visual fixation. The stimuli were presented in all of the recording conditions, including those in which recordings were made from the dummy eyes.

Design and procedure. Participants performed six blocks of 60 trials. Half of the blocks used the head motion correction of the Eyelink II system, whereas in the other half of the blocks this option was switched off. This motion correction option makes use of a sensor on the head-band worn by the participant and four markers on the corners of the screen, which provides information about the location of the head-band with respect of the screen. Orthogonally to this manipulation, the type of input to the eye tracking system was varied. Before each block, participants performed the nine-point calibration procedure of the Eyelink II system, in which they fixated a series of sequentially presented dots on the computer screen, until calibration was considered ‘good’ by the system (no obvious problems) and the recorded eye positions were aligned with a three by three grid corresponding to the locations of the fixation targets. After calibration, there were three possibilities. Either the head-band of the eye tracker was moved to the dummy-head (Figure 1a) and the block was completed while the system recorded from the dummy eyes. Alternatively, after calibration, participants put on the dummy eye glasses, after which the block continued while the system recorded from the dummy eyes. In these blocks, participants were instructed to sit with their chin in the chin rest, close their eyes, and to try and sit as still as possible. In a third condition calibration was followed by the standard cueing task while the system recorded from the participants’ eyes. Also in this task, participants were asked to sit in the chin rest and to avoid moving their head. The cueing task is illustrated in Figure 1b (see also, Hermens & Walker, 2010). Participants were asked to fixate a central fixation target that changed into an arrow after 1000 to 1500ms. Participants remained fixated until the appearance of a peripheral target that they were asked to fixate as quickly as possible after it appeared. Peripheral targets appeared equally often left or right of fixation (never above or below fixation). They were paired with a valid arrow cue (pointing in the same direction as the target) on 80% of the trials and with an invalid cue (pointing in the opposite direction) on the remaining 20% of the trials. Note that while a cueing paradigm was used, it is not believed that this paradigm is critical for the present results. Instead, it provides a means to collect fixation data across intervals of a typical duration in microsaccade research.

The order of the six blocks was randomized across participants, leading to a similar distribution of the conditions across participants without the need for keeping a record of the order of presentation. Recording of eye movements during each trial continued until the detection of a large eye movement, based on a combined 80 deg/sec velocity and 3,000 deg/sec² criterion (similar to Hermens & Walker, 2010). In all blocks, drift correction was performed before each tenth trial, which involved participants fixating a centrally presented fixation target, confirmed by a key-press by the experimenter (similar to Hermens & Walker, 2010). This correction shifts all recorded eye positions according to the recorded position of gaze. While influencing the accurate localization of each recorded gaze position, it is not expected to influence detections of shifts of gaze, as required for microsaccade detection. In between blocks, participants were allowed a short break.

Data analysis. The recorded eye gaze positions during the fixation intervals (presentation of the fixation target and presentation of the cue; interval durations between 2500ms and 3500ms) were analyzed for microsaccades using the algorithm by Engbert and colleagues (Engbert & Kliegl, 2003; Engbert & Mergenthaler, 2006). In the algorithm, the two-dimensional velocity of each eye is compared to a threshold based on the observed variance in the recorded eye position on that trial (adopted to have blinks excluded to prevent undefined thresholds). Sections of the eye trace with a velocity exceeding a 6 median-based SD threshold, temporally overlapping in both eyes for at least 1 sample, and lasting for at least 6ms (3 data samples) were classified as microsaccades. For statistical comparisons across more than two levels univariate repeated measures ANOVAs were used and a Greenhouse-Geisser correction when appropriate. For t-tests, Hedges’s g is reported as a measure of effect size, computed using the effect size toolbox for Matlab (Hentschke & Stüttgen, 2011).

Results

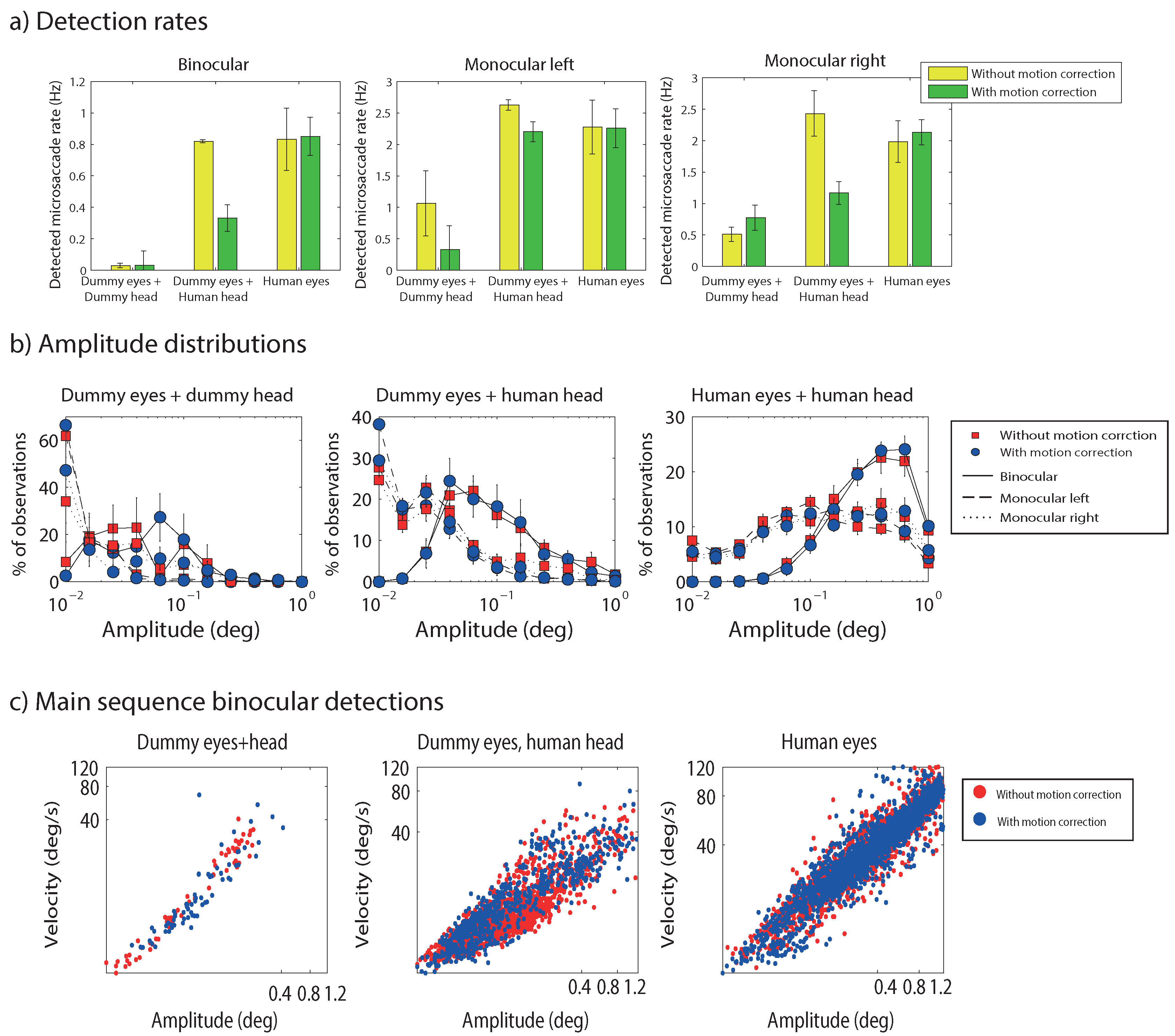
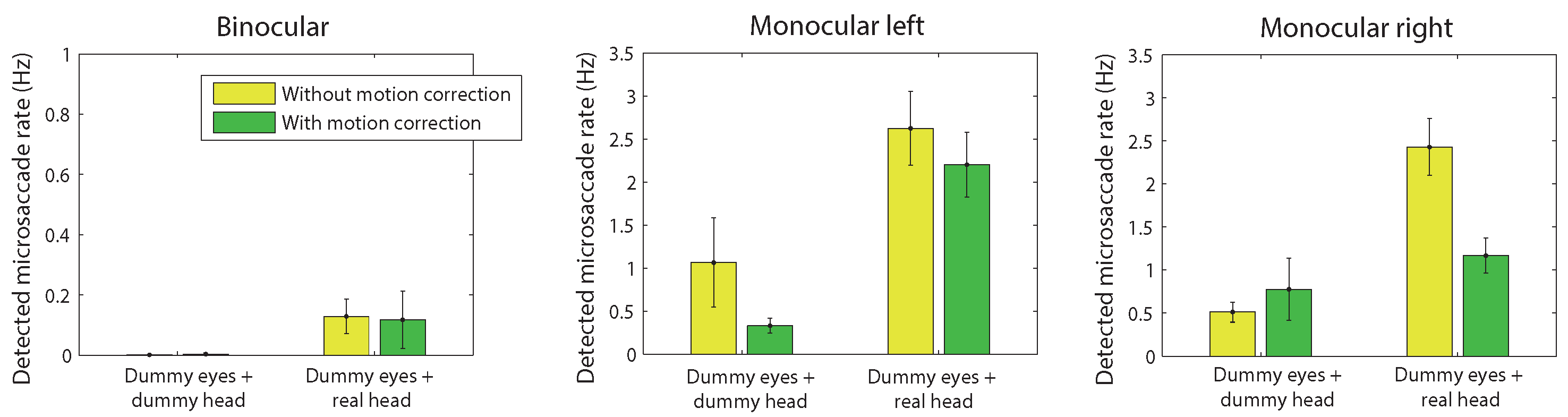
Figure 2a plots microsaccade rates (in Hz) across the different conditions until target onset. In agreement with Hermens and Walker (2010), low detection rates were found when the dummy eyes were mounted onto the dummy head. In contrast, high detection rates were observed when the dummy eyes were mounted on a human head, suggesting that head movements led to incorrect microsaccade detections. Rates for head-mounted dummy eyes were almost as high as when eye movements were recorded from human eyes. Note that these results do not automatically mean that all microsaccades in the human eyes condition were due to head movements. The reason is that the threshold for detection depends on the overall variability in the signal, which may be lower for head movement related signals than for eye movement signals. The high false detection rates are important, because the head-mounted dummy eyes reflect trials without microsccades. Such trials are not uncommon considering that microsaccade rates vary across participants between around 0.2 Hz to 2.5 Hz (Engbert & Kliegl, 2003) and typical trials last around 2 to 3 seconds. The data therefore suggest that thresholds set on a trial by trial basis should be avoided, and instead thresholds are better estimated on the basis of the entire distribution of thresholds for each participant. I will return to this issue later. To access the statistical significance of the differences between conditions, a repeated measures ANOVA was conducted, taking into account the different experimental factors. This analysis, however, showed several significant interactions, which makes the main effects difficult to interpret. Subsequent analyses were therefore performed in the form of pairwise comparisons. These comparisons suggested that the effect of the motion correction approached significance (given Bonferroni corrections) for the dummy eyes mounted on the human head for binocular and monocularly right eye movements (t(11) = 2.57, p = 0.026, Hedges’s g = 0.88; and t(11) = 3.21, p = 0.008, Hedges’s g = 1.28). The effect of recording mode (dummy eye+dummy head, dummy eye+human head, human eye+human head) was significant for most comparisons (except in some of the monocular conditions). Significant differences were also found for the contrasts between binocular and monocular recordings (dummy eyes + dummy head, uncorrected: F(1,11) = 8.31, p = 0.015, partial η² = 0.43; dummy eyes + dummy head, corrected: F(1,11) = 8.63, p = 0.013, partial η² = 0.44; dummy eyes + dummy head, uncorrected: F(1,11) = 119.2, p < 0.001, partial η² = 0.92; dummy eyes + dummy head, corrected: F(1,11) = 76.8, p < 0.001, partial η² = 0.86; human eyes, uncorrected: F(1,11) = 131.5, p < 0.001, partial η² = 0.92; human eyes, corrected: F(1,11) = 80.0, p < 0.001, partial η² = 0.88). This indicates that incorrect detections are significantly higher when recording from only one eye, and that binocular recording and detection is effective in reducing the number of false detections.

Figure 2b shows the distribution of the amplitudes of detected microsaccades across the different conditions. Most of these distributions peak at low amplitudes, except for binocular microsaccades from the dummy eyes on a human head and binocular detections from human eyes. Part of the differences between the amplitudes of dummy eyes and human eyes may be due to the procedure used to detect microsaccades in the dummy eyes. Because the dummy eyes were stationary, the calibration procedure had to be performed on human eyes. After moving the head-band with the cameras from the participant to the dummy head or by changing the orientation of the cameras to focus on the dummy eyes on the glasses, the cameras often had to be moved slightly away from the head due to the extra space taken by the glasses onto which the dummy eyes were mounted. Because of this larger distance, the amplitude of the dummy eye movements may be underestimated. The microsaccade detection algorithm adjusts its thresholds to the data, so detection rates are less likely to be less influenced by the slightly larger distance of the cameras to the eyes. While the magnitude of amplitudes of dummy eye microsaccades may be less informative, the shape of the distribution suggests a difference between dummy eye movements and human eye movements.

A method sometimes suggested to examine whether detected microsaccades are actual saccades, is to examine the relationship between saccade amplitude and peak velocity, known as the main sequence (Zuber et al., 1965), typically plotted on a log-log scale. Figure 2c examines this relationship across the different conditions. Details about the best fitting regression lines for these (log transformed) data are provided in Table 1. The data plots suggest that signals classified by the algorithm as (micro)saccades are likely to result in a linear pattern linking saccade amplitude and peak velocity, regardless of their source. One difference that may be noticed are the intermediate values for the slopes for the human eyes, so in order to use the main sequence to determine whether detected signals are actual saccades, it may be necessary not just to examine the linear relationship, but also to compare the slope with earlier observations or to the slope for large amplitude saccades in the same participant.

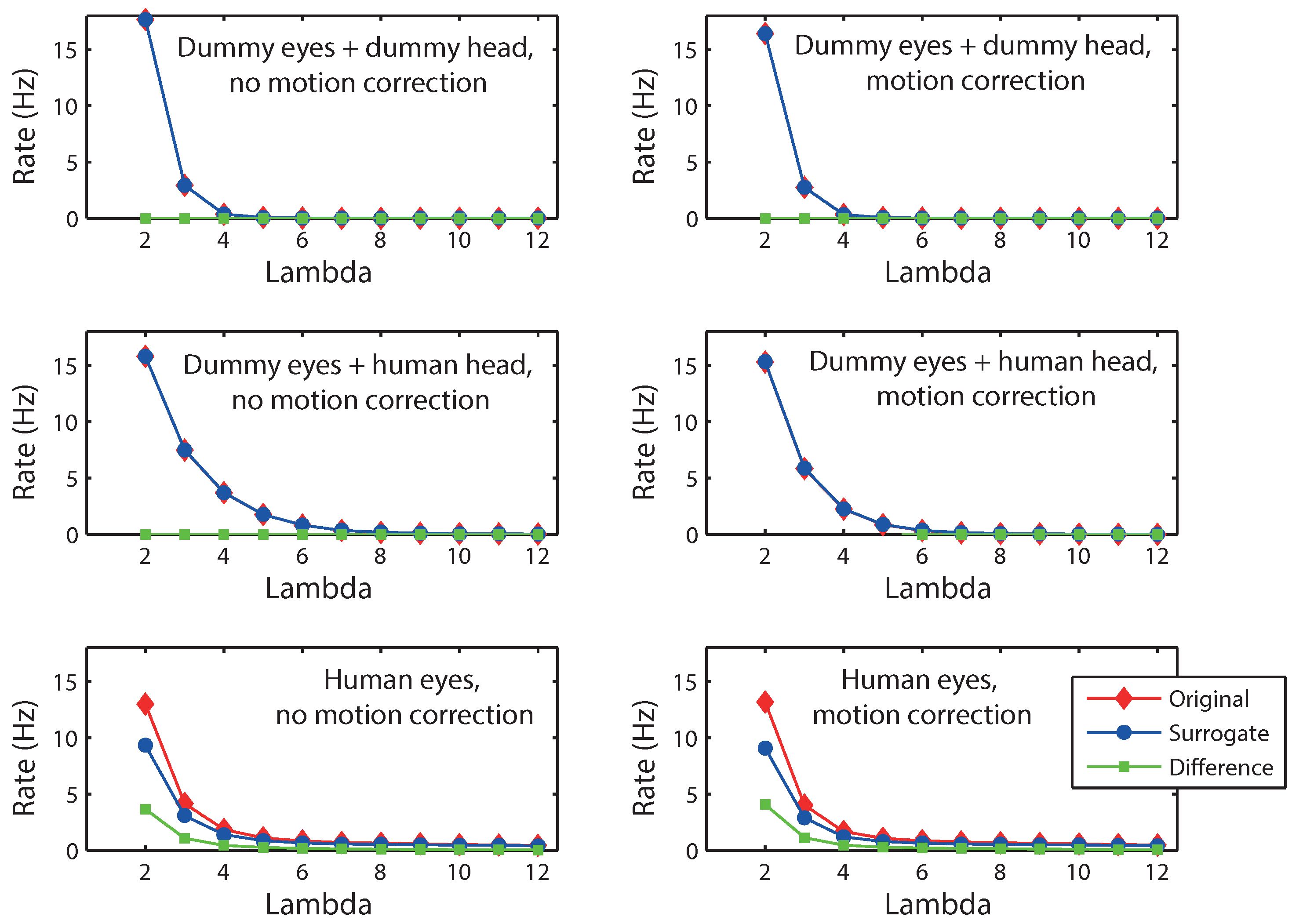
As a further method to detect microsaccades against noise, constrained shuffling of the data to generate surrogate data has been proposed (Engbert & Mergenthaler, 2006; Mergenthaler & Engbert, 2010). In particular, the method shuffles the velocity samples such that the distribution of velocity values is maintained and the autocorrelation function of the surrogate data approximates that of the original data (Engbert & Mergenthaler, 2006). Figure 3 shows the results when this procedure is applied to the present dummy eye and human data. For the human eyes, surrogate detection rates are lower than for the original data, suggesting that meaningful signals are being picked up from the data that are no longer present when the order of the data is disturbed. For dummy eyes (either on a dummy head or on a human head), no such reduction in the rate for surrogate data is found, suggesting that signals that are detected are not specific to the order of the samples, probably because they reflect random variations rather than an actual signal. Interestingly, whereas the analysis by Engbert and Mergenthaler (2006) revealed a maximum difference between the original and surrogate detection rates (at λ = 5), the difference between rates for the present data monotonically decreases with λ. It is unclear at this point what causes this difference in the results. The results, however, do suggest that surrogate data can be used (on a distribution level) to distinguish between eye movement signals and noise.

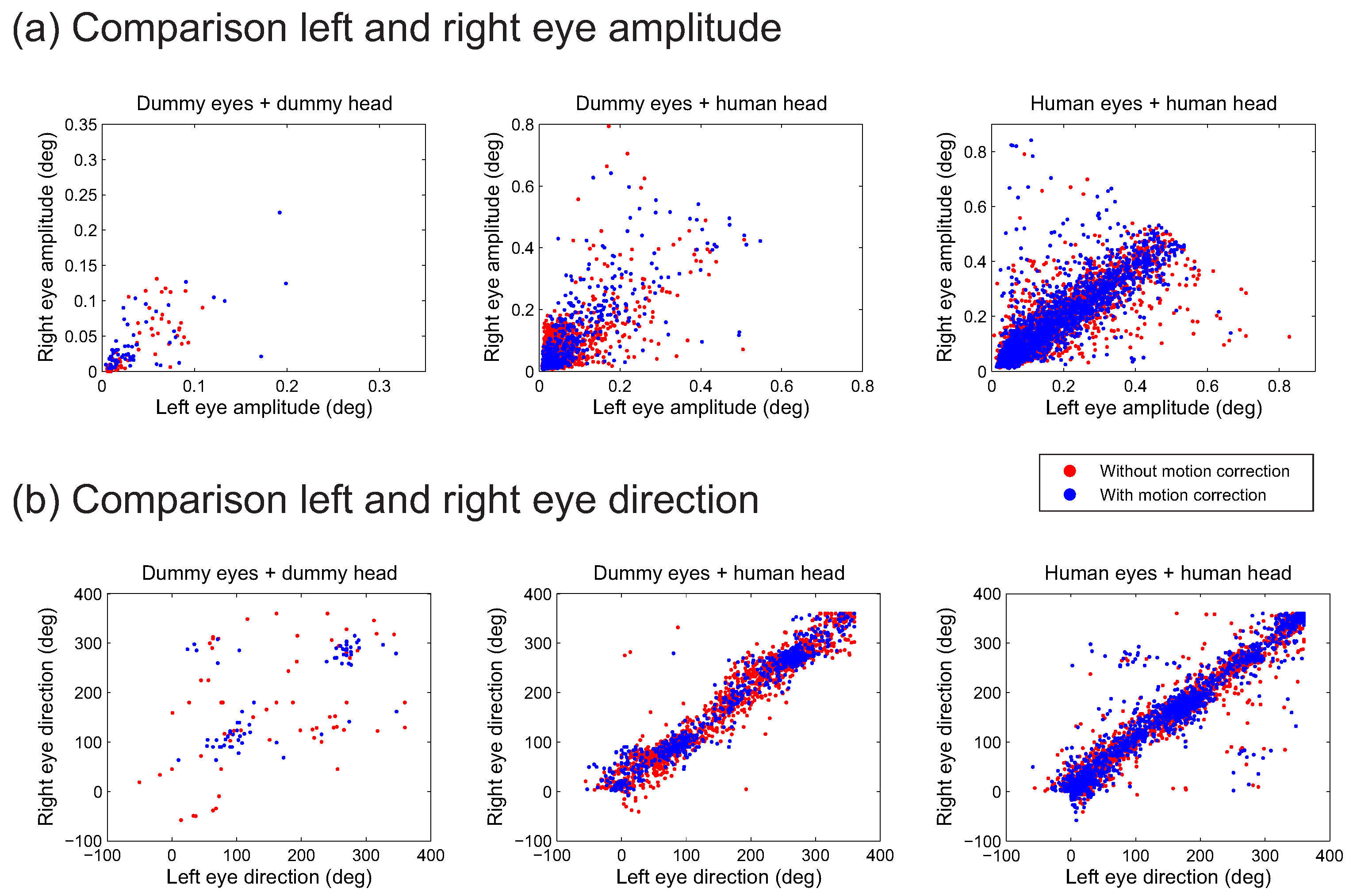
An often made assumption is that microsaccades occur simultaneously in both eyes. This assumption is used in the final step of the algorithm by Engbert and colleagues (Engbert & Kliegl, 2003; Engbert & Mergenthaler, 2006), requiring at least one sample overlap between the eye movements in the two eyes. To improve detection other overlaps may be considered, such as similarities in amplitude and or saccade direction. To examine this overlap for microsaccades across the different conditions, Figure 4 provides scatterplots of the amplitude (in degrees of visual angle) and direction (expressed as an angle between 0 and 360 degrees) of the two eyes, while

Table 2. Correlations of saccade amplitude and saccade direction between the two eyes for binocularly detected microsaccades.

Condition	Correlation of amplitude	Correlation of direction
Dummy eye + dummy head, without correction	0.82	0.40
Dummy eye + dummy head, with correction	0.69	0.66
Dummy eye + human head, without correction	0.68	0.97
Dummy eye + human head, with correction	0.78	0.97
Human eye + human head, without correction	0.77	0.96
Human eye + human head, with correction	0.76	0.95

provides the correlation of the measures between the two eyes. For many of the conditions, the correlations between the two eyes are high (r ≥ 0.68), meaning that not only do the movements occur in the two eyes at the same time, they also have similar amplitudes and directions. The correlation is somewhat lower for detections in the dummy eyes on the dummy head, but otherwise, the plots suggest that comparisons of movements between the two eyes will not aid the distinction between actual and falsely detected microsaccades. A likely reason is that in all instances, the signals leading to the detected microsaccades have a common source, which can either be the brain signaling to both eyes that an eye movement has to be made, or the movement of the pupils with respect to the cameras due to head movement.

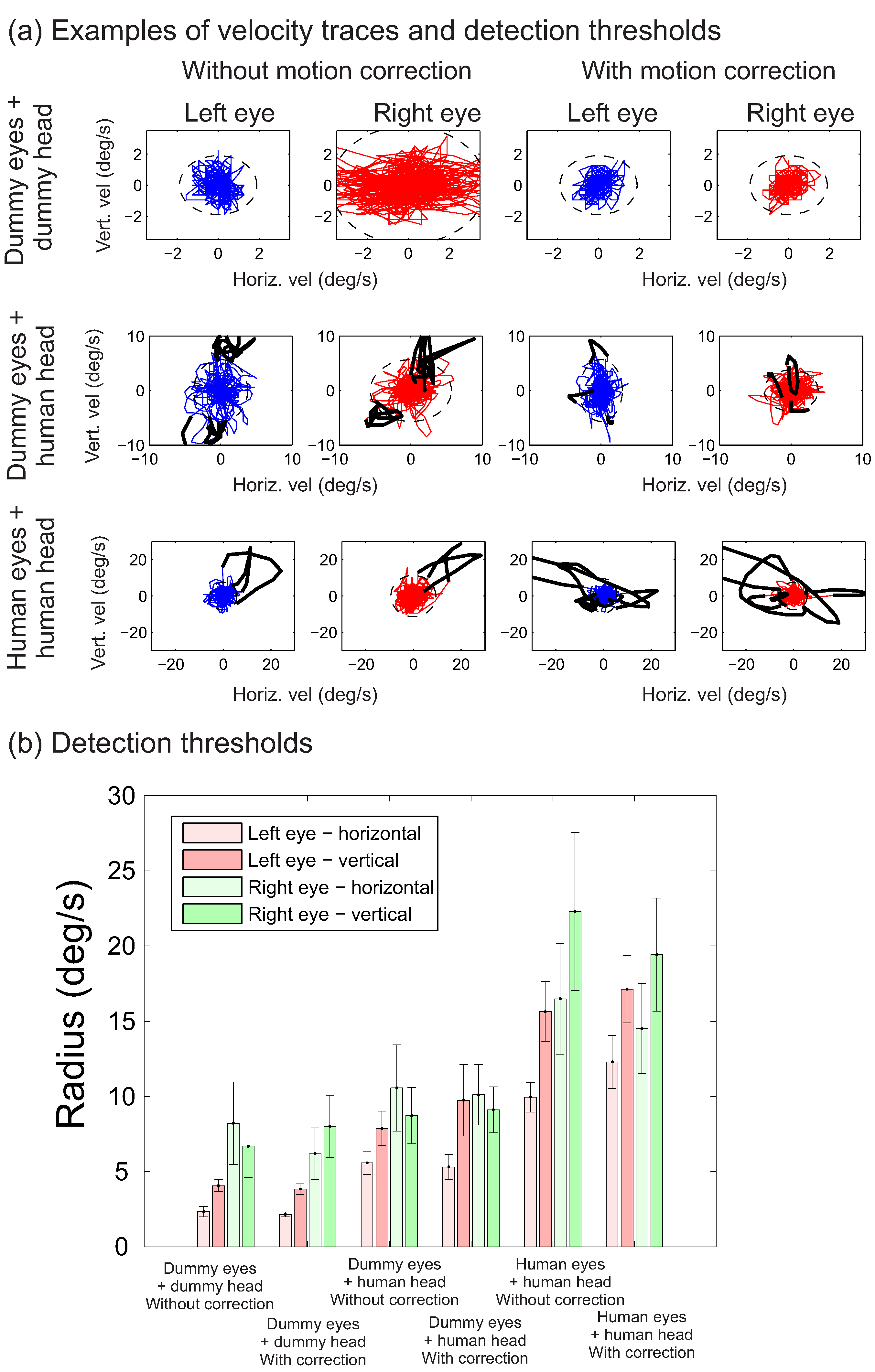
As mentioned earlier, the high rate of detections for the dummy eyes mounted on a human head is likely to relate to lower detection thresholds in these conditions, compared to the human eyes conditions. This point is illustrated in Figure 5a, showing velocity traces for six trials across the different conditions, together with the threshold (dashed ellipses; note that the axes are scaled to best fit the velocities). These example traces from one of the participants suggest that thresholds are lower for dummy eyes than for human eyes. To examine this possible difference in thresholds further, Figure 5b plots the average threshold across participants for each of the conditions. To determine whether these thresholds differ across conditions, the thresholds for the two eyes and the two directions (horizontal versus vertical) were pooled into one mean for each condition and a repeated measures ANOVA was used to test the effects of the source of the recordings (dummy eyes + dummy head, dummy eyes + human head, human eyes) and whether motion correction was used. A significant main effect of the source of the recordings was found (F(1.38, 15.13) = 21.11, p<0.001, partial η² = 0.66), without a main effect of the motion correction (F(1,11) = 0.042, p = 0.96, partial η²<0.01) and without an interaction between the two factors (F(2,22) = 0.23, p = 0.79, partial η² = 0.021). Posthoc tests, involving pairwise comparisons between the different recording sources using a two by two repeated measures ANOVA, testing the effects of recording source and motion correction, showed significant differences in the thresholds across each of the conditions without an effect of motion correction and no interaction (dummy eyes + dummy head versus dummy eyes + human head: F(1,11) = 10.36, p = 0.008, partial η² = 0.49; dummy eyes + human head versus human eyes: F(1,11) = 16.23, p = 0.002, partial η² = 0.60; dummy eyes + dummy head versus human eyes: F(1,11) = 27.78, p<0.001, partial η² = 0.72).

In the analyses so far, thresholds for microsaccade detection were set on a trial by trial basis taking into account the level of noise in the data for that trial. The data with the dummy eyes on the human head indiccates that in the absence of microsccades, this method may result in thresholds that are too low to avoid incorrect detections of microsaccades due to head movements. An alternative method of setting thresholds would be to take into account thresholds across all trials, and to extract an estimate of the overall threshold for detection for that person. To evaluate this method, thresholds were set to the median of the human eyes conditions for each participant and then applied to the dummy eye conditions, resulting in the detection rates shown in Figure 6. Binocular detections for the dummy eyes on a dummy head condition were already low previously, and vanished completely when median thresholds were used. Binocular detections for dummy eyes on the human head (simulating head motion) are lower when the median threshold method is used, but incorrect detections still occur at a rate of about 0.1 to 0.2 Hz. Monocular detections are high for median thresholds and are best avoided.

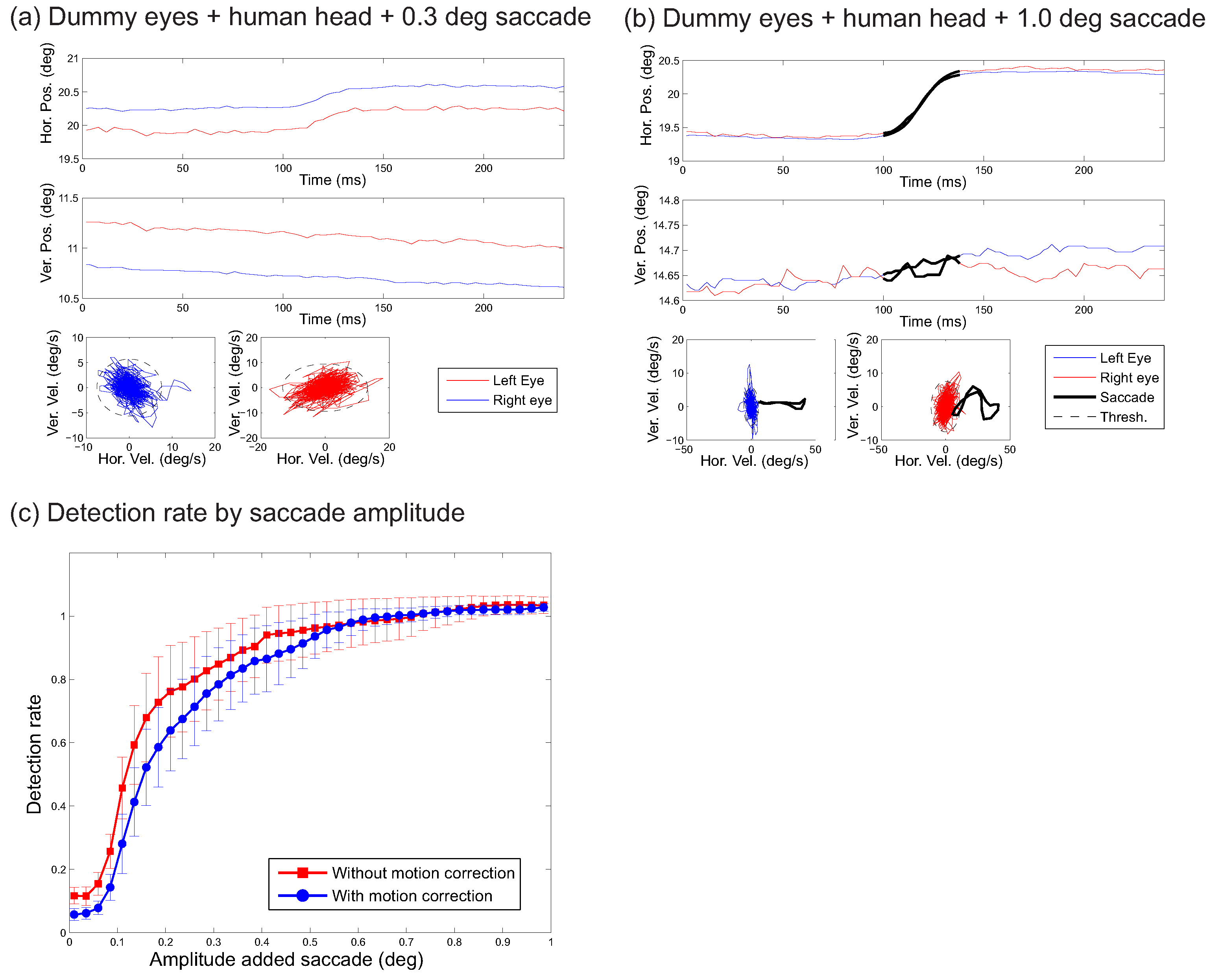
The recordings of the dummy eyes can also be used to examine what amplitudes of saccades can be reliably detected in the presence of system noise and head movements. Figure 7a and Figure 7b show how this may be done. The two plots show the recorded eye position over time (top) together with the horizontal and vertical velocity (bottom). Figure 7a shows a signal to which a 0.3 degrees amplitude saccade was added in the form of a sigmoid function (A sigmoid function was used to create a uniform shape for the added saccade. Visual inspection suggested that the sigmoid functions provided an excellent fit of the profile of the saccades) whose parameters (except for the amplitude) were fitted on response saccades of the corresponding participant (across all trials in the human eyes conditions). Figure 7b shows a similar plot, but now for an added 1.0 degree saccade. The ellipses around the velocity trace indicate the detection threshold, and the black sections of the trace in the 1.0 degree saccade plot (Figure 7b) indicate that the 1.0 degree saccade is detected, but the 0.3 saccade is not. To examine how the head movements influence the detection of saccades of various amplitudes, sigmoid functions saccades were added to each trial of the dummy eyes + head movement condition for each participant, and the number of detected microsaccades within an interval around the inserted saccades was counted. Figure 7c shows this number of detected microsaccades as a function of the amplitude of the inserted microsaccade, showing an increasing function approaching a level slightly above 1 (detection of signals additional to the inserted saccade). Interestingly, the use of the head motion correction leads to slightly lower detection rates (t(39) = 5.54, p<0.001, Hedges’s g = 0.16; across the 40 samples shown in Figure 7c).

The large number of microsaccade detections in the absence of eye movements due to head movements is worrisome, as is the lack of distinctive features between head movement and eye movement detections among the features considered so far, such as the direction of the microsaccades in the two eyes. Using a median threshold across all trials helped to reduce the number of false detections. Another possible method of reduing the number of incorrect detections may be to rely on both the corneal reflection signal and the pupil center estimate (as used, for example, by Kimmel et al., 2012). Experiment 2 will examine whether microsaccade detections in the absence of eye movements can be avoided by including the corneal reflection signal.

Experiment 2: Corneal reflection

Experiment 1 showed large numbers of microsaccade detections in conditions in which, in fact, no eye movements were present (recordings from dummy eyes, mounted on a human head). The experiment relied on the pupil only mode of the Eyelink II system, as have many past studies (all studies applying an Eyelink system at 500Hz in Table 1 of Martinez- Conde et al., 2009). A possible reason is that a stable corneal reflection signal is sometimes difficult to obtain for all gaze directions in the calibration procedure, and that the pupil only mode allows for a higher sampling rate (500Hz rather than 250Hz) in the system. With newer systems, which often use the corneal reflection setting by default and allow for high sampling rates even when using the corneal reflection (e.g., 1000Hz in the Eyelink 1000 system), there should be fewer reasons to rely on pupil only measurements. In Experiment 2, it is investigated whether the addition of the corneal reflection aids to reduce signals that may lead to incorrect microsaccade detections. The experiment is carried out in an Eyelink II system, meaning that if an improvement is found, the addition of the corneal reflection signal trumps the reduction of the sampling frequency.

Methods

To obtain a corneal reflection in the images, two metal clips were attached to the glasses, as shown in Figure 8a. After trying several size clips, one configuration was found to yield a stable corneal reflection in the system, as shown in the image in Figure 8b. In this image, the large cross-hair superimposed on one of the blue sections indicates the estimated center of the pupil. The smaller yellow section with a superimposed cross-hair indicates the detected corneal reflection. Three conditions were tested, all applying the motion correction setting of the system. In the first condition, the dummy eyes were placed on a dummy head (measuring the system noise). In the second condition, the dummy eyes were mounted on a participant’s head (measuring the combined influence of system noise and head movements, despite the use of a chin rest). In the third and final condition, recordings were made from the participant’s eyes. One participant (the author) served as the source of the calibrations and the actual eye movements. Six blocks of each 60 trials were conducted for each of the three conditions (resulting in a total of 360 trials per condition). Calibration was repeated before each block to mimic the influence of recalibrating the system. In the dummy eyes on the participants’ head and the actual eyes conditions, the participant performed the cueing task from Experiment 1 (but now with the glasses on the tip of the nose in the dummy eye condition). As in Experiment 1, an Eyelink II system was used for the recordings. Because of the use of the corneal reflection mode, the sampling rate was reduced to 250Hz (from 500Hz for Experiment 1). For the two conditions with the participant’s head, a chin rest was used to reduce head movements, placed at a distance of 57cm from a 19inch flat screen used for stimulus presentation. As in Experiment 1, microsaccade detections were based on a 6 median-based SD threshold, a minimum 6ms duration, and a one-sample minimum overlap for binocular microsaccades. For statistical comparisons, the repeated calibrations were treated as the participants in the analysis.

Results

Figure 8c shows the rate of microsaccade detection across the different conditions (using the same algorithm as in Experiment 1, based on the work by Engbert & Kliegl, 2003; Engbert & Mergenthaler, 2006) for the interval until presentation of the target, and trial by trial estimation of the detection thresholds. The left three bars in this plot show detections on the basis of signals from both (dummy) eyes, for which a temporal overlap between the two eyes was required for detection. Detection rates in the two dummy eyes conditions were significantly lower than for the participant’s eyes (dummy head: t(5) = 6.21, p = 0.0016, Hedges’ g = 3.32; participant’s head: t(5) = 6.27, p = 0.0015, Hedges’ g = 3.01). Detection rates between the two dummy eyes conditions did not differ significantly (t(5) = 2.20, p = 0.079, Hedges’ g = 1.30). The results also show that the microsaccade detecion rate in human eyes was around 1Hz, in agreement with earlier observations (e.g., Engbert & Kliegl, 2003). In the two dummy eye conditions, this rate was substantially reduced. Interestingly, the effect of the corneal reflection on incorrect detections was restricted to binocular detection. When detection was based on measurements from one eye only (‘monocular left’ or ‘monocular right’ in Figure 8c), large numbers of microsaccades were detected across all three conditions.

Experiment 3: Microsaccade signature

Experiment 1 showed that large numbers of microsaccades are detected in the presence of head movements but in the absence of eye movements. Experiments 1 and 2 also showed that the incorrect detection rates can be brought down by estimating the detection thresholds across many trials and when the corneal reflection signal is used. Past studies, however, have often relied on the pupil only mode of the Eyelink II system, and the question arises to which extent incorrect detections due to head movements may have influenced the results. Experiment 3 is aimed to examine this issue and focuses in particular on the modulation of microsaccade rate by stimulus onsets (the ‘microsaccade signature’). Head movements may influence the microsaccade signature, because studies have demonstrated effects of covert shifts of attention on other motor (sub)systems, such as the neck muscles (Corneil, Munoz, Chapman, Admans, & Cushing, 2007) and the arm (Cohen & Rosenbaum, 2007). In contrast to Experiment 1 but similar to Experiment 2, the dummy eyes were placed on the tip of the nose, to allow for stimulus events to influence the dummy eye measurements.

Method

Participants. Thirteen new participants and the author took part in Experiment 3. Data of two participants had to be excluded from the data set because of a failure to record the eye position in the right eye in some of the blocks, leaving data of twelve participants for the data analysis. Participants other than the author were students from the University of Leuven, taking part in return for course credit.

Apparatus, stimuli, design, procedure and data analysis

An identical setup was used as in Experiment 1, with a few small modifications. Instead of six blocks, participants conducted four blocks of each sixty trials. In two blocks, participants placed the glasses on the tip of their nose, allowing for the tracking of the dummy eyes while participants performed the cueing task normally. In these blocks, the tracker recorded from the dummy eyes. In the remaining two blocks, participants did not wear the glasses and eye movements were recorded from their eyes. Motion correction was varied across participants, so that the two repeated blocks from each participant together provided data of 120 trials to allow for a better estimate of the microsaccade signature. To ensure that participants were performing the task in all blocks (although not believed to be critical for the present purpose of the study), the experimenter, on selected trials, briefly inspected the gaze behavior of participants to determine whether they were making an eye movement in the correct direction after the onset of the target. As in Experiments 1 and 2, microsaccade detections were based on a 6 median-based SD threshold, a minimum of 6ms duration, and a one-sample minimum overlap for binocular microsaccades. For the plot of microsaccade frequency as a function of the time before or after cue onset, a moving average was used, computing the frequency within a 100ms window in steps of 1ms across the -1000ms (before cue onset) and 1500ms (after cue onset) interval.

Results

Figure 9a plots the overall detection rates in Experiment 3 until presentation of the target. A mixed factor ANOVA, testing the effects of the source of the recordings (dummy eyes or human eyes, within-subjects), the eyes analyzed (binocular, monocular left, or monocular right, within-subjects) and motion correction (on versus off, between-subjects) revealed a significant interaction between the source and the eyes analyzed (F(2,20) = 3.35, p = 0.006, partial η² = 0.40). Posthoc analyses were therefore performed examining the effects of the source of the recording and motion correction for each of the eyes analyzed. For binocular saccades, a significant difference between detection rates from head movements and eye movements was found (F(1,10) = 28.24, p<0.001, partial η² = 0.74), without an effect of the motion correction (F(1,10) = 0.60, p = 0.46, partial η² = 0.056) and no interaction between the two factors (F(1,10) = 0.57, p = 0.47, partial η² = 0.054). For monocular left (p-values all above 0.16) and right microsaccades (p-values all above 0.17) none of the effects were significant. While binocular rates due to head movements appear to be lower than in Experiment 1, t-tests comparing the rates across the two experiments do not reveal significant differences (t(16) = 0.65, p = 0.52, Hedges’s g = 0.31 without motion correction, t(16) = 0.24, p = 0.82, Hedges’s g = 0.11 with motion correction), suggesting that visual input did not modulate the detection rate. Detections from human eyes were higher in Experiment 3 than in Experiment 1, without motion correction correction (t(16) = 2.81, p=0.013, Hedges’s g = 1.34), but not with motion correction (t(16) = 1.67, p = 0.12, Hedges’s g = 0.79).

Figure 9b shows the microsaccade rate across the stimulus interval for the different conditions. A clear modulation of the microsaccade rate around the onset of the cue was found for the human eye measurements, but not for the dummy eyes on a human head, meaning that the stimulus dependent modulation of microsaccade rates (the ‘microsaccade signature’) is a property of eye movements, not of head movements. The difference between the eye movement and head movement conditions is confirmed by comparing the estimated minimum and maximum rates across the interval. For both the motion corrected (t(5) = 2.62, p = 0.047; Hedges’s g = 1.67) and uncorrected (t(5) = 3.029, p = 0.0.29; Hedges’s g = 1.30) groups, a significant difference was found in the size of the rate modulation between the recordings from the dummy eyes on the human head and the human eyes.

Discussion

In three experiments, the influence of system noise and participants’ head movements on the detection of microsaccades was examined for arguably the most popular eye tracking system in recent microsaccade research (the Eyelink II system, used in 25 of the 37 studies in Table 1 of Martinez-Conde et al., 2009). Noise in this system has two likely sources: Fluctuations of pixels in the image that are assigned to the pupil area (falling below or above detection threshold, due to small variations in illumination), and shifts of the entire image due to movement of the cameras or the head band (due to small head movements made by participants despite the use of a chin rest). To measure the influence of these noise sources, dummy eyes were created from circular patches of insulation tape on a white background mounted on a pair of glasses, worn either by a dummy head or a human participant. Recordings from these dummy eyes and from human eyes were analyzed for microsaccades using one of the most popular algorithms, namely that by Engbert and colleagues (Engbert & Kliegl, 2003; Engbert & Mergenthaler, 2006). Relatively few microsaccades were detected for the dummy eyes on a dummy head, suggesting that the system’s internal noise (due to fluctuations in the pixels assigned to the pupil area) had little influence on the detection of microsaccades. In contrast, when relying on the pupil only mode, frequent microsaccade detections were observed for the dummy eyes mounted on a human head. Further analysis demonstrated that detections for the dummy eyes were often of low amplitude and had similar amplitudes and directions in both eyes. They also displayed an approximately linear relationship between saccade amplitude and peak velocity, known as the main sequence, normally found for microsaccades and saccades (Zuber et al., 1965). The incorrect detection rate could be reduced by estimating thresholds across all trials (Experiment 1; assuming that participants do make microsaccades in a significant proportion of trials) and by using the corneal reflection signal (Experiment 2). Detection, however, should be based on binocular recordings, and is therefore restricted to video-based systems that can record from both eyes simultaneously (although good detection in monkeys was reported for monocular recordings; Kimmel et al., 2012). Experiment 3 showed that past results, and in particular the modulation of the microsaccade rate after stimulus onsets, were not systematically affected by the large number of incorrect recordings due to head movements. In three experiments, the influence of system noise and participants’ head movements on the detection of microsaccades was examined for arguably the most popular eye tracking system in recent microsaccade research (the Eyelink II system, used in 25 of the 37 studies in Table 1 of Martinez-Conde et al., 2009). Noise in this system has two likely sources: Fluctuations of pixels in the image that are assigned to the pupil area (falling below or above detection threshold, due to small variations in illumination), and shifts of the entire image due to movement of the cameras or the head band (due to small head movements made by participants despite the use of a chin rest). To measure the influence of these noise sources, dummy eyes were created from circular patches of insulation tape on a white background mounted on a pair of glasses, worn either by a dummy head or a human participant. Recordings from these dummy eyes and from human eyes were analyzed for microsaccades using one of the most popular algorithms, namely that by Engbert and colleagues (Engbert & Kliegl, 2003; Engbert & Mergenthaler, 2006). Relatively few microsaccades were detected for the dummy eyes on a dummy head, suggesting that the system’s internal noise (due to fluctuations in the pixels assigned to the pupil area) had little influence on the detection of microsaccades. In contrast, when relying on the pupil only mode, frequent microsaccade detections were observed for the dummy eyes mounted on a human head. Further analysis demonstrated that detections for the dummy eyes were often of low amplitude and had similar amplitudes and directions in both eyes. They also displayed an approximately linear relationship between saccade amplitude and peak velocity, known as the main sequence, normally found for microsaccades and saccades (Zuber et al., 1965). The incorrect detection rate could be reduced by estimating thresholds across all trials (Experiment 1; assuming that participants do make microsaccades in a significant proportion of trials) and by using the corneal reflection signal (Experiment 2). Detection, however, should be based on binocular recordings, and is therefore restricted to video-based systems that can record from both eyes simultaneously (although good detection in monkeys was reported for monocular recordings; Kimmel et al., 2012). Experiment 3 showed that past results, and in particular the modulation of the microsaccade rate after stimulus onsets, were not systematically affected by the large number of incorrect recordings due to head movements.

In the present work, only one algorithm was considered (Engbert & Kliegl, 2003; Engbert & Mergenthaler, 2006), which raises the question whether other algorithms would fare better in deciding that no microsaccades were present when recording in pupil only mode. This would allow for the re-analysis of past data. One possible method was already introduced in which thresholds are estimated across trials, but then pooled into an estimate for each participant, thereby reducing incorrect detections in trials without microsaccades. Alternatively, thresholds could be set on the basis of earlier findings or on the basis of theoretical considerations. Studies that appear to have used such fixed threshold methods are those by Martinez-Conde and colleagues (2000, 2002), using a combined velocity and change of direction of movement criterion, Hafed and Clark (2002), using a velocity criterion based on the horizontal component of the position trace and using the main sequence, by Zanker, Doyle and Walker (2003), using an acceleration criterion on the smoothed signal, and by Møller and colleagues (2002; 2006), using a combined velocity and acceleration criterion, and a requirement for the signal to show an overshoot. A comparison between such a fixed threshold algorithm and the adaptive threshold algorithm by Engbert and colleagues (Engbert & Kliegl, 2003; Engbert & Mergenthaler, 2006) suggests similar performance across the two algorithms when applied to human data. Alternatively, detection could rely on visual detection by expert human observers (Steinman, 1965; Steinman, Cunitz, Timberlake, & Herman, 1967; Otero-Millan et al., 2014). This method, however, is labor intensive, particularly if multiple raters are used to avoid subjective biases in detection. A new automatic method was recently introduced that relies on a clustering algorithm and principal component decomposition to establish the number of clusters, but this method relies on the presence of microsaccades, and should therefore rely on sufficiently long sampling intervals to ensure that microsaccades occur (Otero-Millan et al., 2014).

The present work focused on head stabilization by means of a chin rest, which appears to be the preferred method in human participants. Future research should demonstrate whether alternative methods of head stabilization, such as a bite-bar, would reduce the influence of head movements on microsaccade detections. Another domain for future research involves the reliance on a human participant for calibration of the dummy eyes. While the fixed dummy eyes ensured that no motion was present, shifting the eye tracker from the human head to the dummy head, or adjusting the cameras to focus on the dummy eyes after calibration may have influenced the measurements. The cameras were often placed further away from the dummy eyes than the human eyes used for calibration, and therefore the amplitude of the measured eye gaze shifts are likely to be affected. It is unclear to which extent this influence is linear in nature, given the non-linear proprietary algorithm used by the studied system (Eyelink II, SR Research). Using dummy eyes that can rotate and perform the calibration procedure would improve the situation. The possible difference in the size of the pupil of the human eyes and the dummy eyes will be difficult to compensate for, given the fluctuations in the pupil diameter in human observers with changes in ambient luminance levels. Similar factors may also explain why, for the present data, there were often differences between the two eyes in monocular detection rates. The cameras may have been at slightly different angles with respect to the dummy eyes, light sources in the room may have influenced the two dummy eyes differently (and more strongly than human eyes), and differences in the focus of the two cameras may be amplified in dummy eyes compared to human eyes. Overall, the data strongly suggest that accurate detection should rely on binocular recordings and a temporal overlap of detection in both eyes.

With respect to the data collected to date, the present results are reassuring. While a broad range of studies have used a combination of the Eyelink II system, pupil only detection, and the algorithm by Engbert and colleagues (Engbert & Kliegl, 2003; Engbert & Mergenthaler, 2006), the present Experiment 3 demonstrates that the modulation of microsaccade frequency after stimulus onset can only be found when recording from human eyes. However, it will need to be demonstrated that this result extends to other recent findings, such as those involving the direction of microsaccades in relation to covert attention (Engbert & Kliegl, 2003; Horowitz, Fine, Fencsik, Yurgenson, & Wolfe, 2007; Horowitz, Fencsik, Fine, Yurgenson, & Wolfe, 2007; Laubrock, Engbert, Rolfs, & Kliegl, 2007; Laubrock, Kliegl, Rolfs, & Engbert, 2010; Pastukhov & Braun, 2010; Rolfs, Engbert, & Kliegl, 2004; Tse, Sheinberg, & Logothetis, 2002, 2004).

Conclusion

The present work presents and evaluates a dummy eye method to examine the influence of system noise and head movements on the detection of microsaccades. Application of this method for possibly the most often used method (the Eyelink II system in combination with the algorithm by Engbert and colleagues, 2003, 2006) in recent microsaccade work, suggests that although detections due to head movements were frequent, they did not influence the often reported modulation of microsaccade frequency following stimulus onset. Moreover, detections were strongly suppressed when the corneal reflection was used or when thresholds were estimated on the basis of many trials, as long as binocular detection was used. Future work should examine the use of other detection algorithms, other methods of head stabilization and rely more on combined pupil detection and corneal reflection measurements.

This study was supported by funding from the Research Foundation-Flanders (FWO-Vlaanderen). The author wishes to thank Johan Wagemans, Cees van Leeuwen and Chie Nakatani for the use of equipment that enabled this work. Part of this work was carried out at the Laboratory of Experimental Psychology, University of Leuven, Belgium. Frouke Hermens is now at the School of Psychology, University of Lincoln, UK. E-mail: frouke.hermens@gmail.com