Conditional Co-Occurrence Probability Acts like Frequency in Predicting Fixation Durations
Abstract
:Introduction
Motivation for choosing CCP
Method
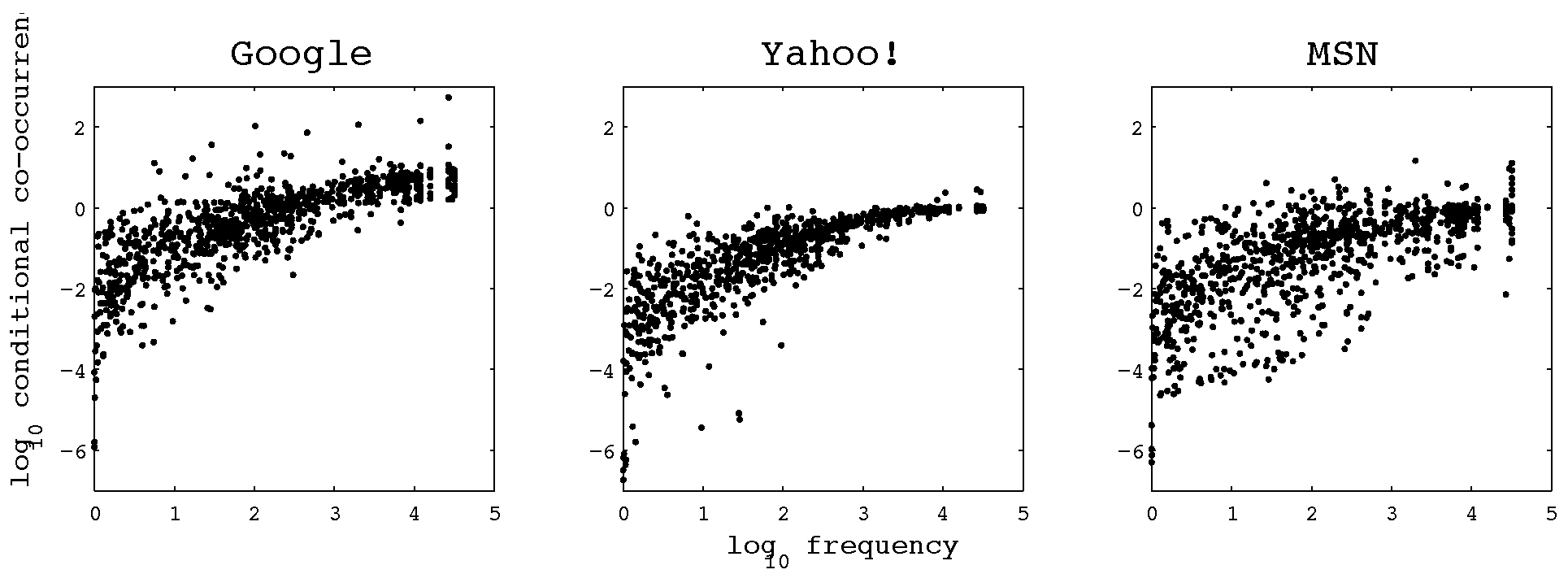
Definition of CCP


Comparison of conditional co-occurrence with other lexical features
Regression analysis
- Fixation duration is transformed into log fixation duration;
- Saccade amplitude is measured in letters;
- Fixation position in letters is divided by word length to give a relative fixation position;
- Length is transformed into reciprocal word length;
- Frequency is transformed into log frequency, and then nested within lexical status to produce two variables, which we will call content word frequency and function word frequency;
- Predictability is transformed into logit predictability;
- Lexical status is a binary variable that is zero for content words and one for function words;
- Skipping status, which is only defined for words n – 1 and n + 1, is a binary variable that is zero for fixated words and one for skipped words.
- Pairwise interactions with word length;
- Pairwise interactions with word frequency, nested within lexical status;
- Pairwise interactions with predictability;
- Interactions with the lexical status of words n, n – 1, and n + 1, and the skipping status of words n – 1 and n + 1.
Results
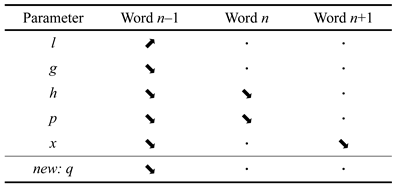
Single fixation durations
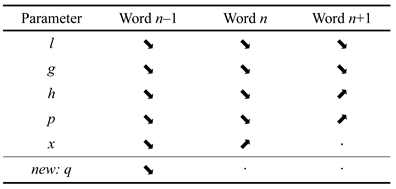
Gaze durations
Discussion

Acknowledgments
References
- Bates, D. 2007. lme4: Linear mixed-effects models using S4 classes [Computer software manual]. (R package version 0.99875-9). [Google Scholar]
- Boston, M. F., J. Hale, R. Kliegl, U. Patil, and S. Vasishth. 2008. Parsing costs as predictors of reading difficulty: An evaluation using the Potsdam Sentence Corpus. Journal of Eye Movement Research. [Google Scholar] [CrossRef]
- Frisson, S., K. Rayner, and M. J. Pickering. 2005. Effects of contextual predictability and transitional probability on eye movements during reading. Journal of Experimental Psychology: Learning, Memory, and Cognition 31, 5: 862–877. [Google Scholar] [CrossRef] [PubMed]
- Keller, F., and M. Lapata. 2003. Using the web to obtain frequencies for unseen bigrams. Computational Linguistics 29, 3: 459–484. [Google Scholar] [CrossRef]
- Kennedy, A., and W. S. Murray. 1987. Spatial coordinates and reading: Comments on Monk (1985). The Quarterly Journal of Experimental Psychology Section A 39, 4: 649–656. [Google Scholar] [CrossRef]
- Kliegl, R. 2007. Toward a perceptual-span theory of distributed processing in reading: A reply to Rayner, Pollatsek, Drieghe, Slattery, and Reichle (2007). Journal of Experimental Psychology: General 136, 3: 530–537. [Google Scholar] [CrossRef]
- Kliegl, R., E. Grabner, M. Rolfs, and R. Engbert. 2004. Length, frequency, and predictability effects of words on eye movements in reading. European Journal of Cognitive Psychology 16, 1/2: 262–284. [Google Scholar] [CrossRef]
- Kliegl, R., A. Nuthmann, and R. Engbert. 2006. Tracking the mind during reading: The influence of past, present, and future words on fixation durations. Journal of Experimental Psychology: General 135, 1: 12–35. [Google Scholar] [CrossRef] [PubMed]
- Landauer, T. K., and S. T. Dumais. 1997. A solution to Plato's problem: The Latent Semantic Analysis theory of the acquisition, induction, and representation of knowledge. Psychological Review 104, 211–240. [Google Scholar] [CrossRef]
- McDonald, S. A., and R. C. Shillcock. 2003. Eye movements reveal the on-line computation of lexical probabilities during reading. Psychological Science 14, 648–652. [Google Scholar] [CrossRef] [PubMed]
- Pynte, J., and A. Kennedy. 2006. An influence over eye movements in reading exerted from beyond the level of the word: Evidence from reading English and French. Vision Research 46, 3786–3801. [Google Scholar] [CrossRef] [PubMed]
- Pynte, J., B. New, and A. Kennedy. in press. A multiple regression analysis of syntactic and semantic influences in reading normal text. Journal of Eye Movement Research. [Google Scholar]
- R Development Core Team. 2008. R: A language and environment for statistical computing [Computer software manual]. Vienna, Austria: http://www.R-project.org/ISBN 3-90005107-0.
- Rayner, K., J. Ashby, A. Pollatsek, and E. D. Reichle. 2004. The effects of frequency and predictability on eye fixations in reading: Implications for the E-Z reader model. Journal of Experimental Psychology: Human Perception and Performance 30: 720–732. [Google Scholar] [CrossRef] [PubMed]
- Taylor, W. L. 1953. Cloze procedure: A new tool for measuring readability. Journalism Quarterly 30: 415–433. [Google Scholar] [CrossRef]
- Turney, P. D. 2001. Edited by L. D. Raedt and P. A. Flach. Mining the web for synonyms: PMI-IR versus LSA on TOEFL. In Machine learning: ECML 2001, 12th European Conference on Machine Learning, Freiburg, Germany, September 5-7, 2001 Proceedings. Springer: Vol. 2167, pp. 491–502. [Google Scholar]
- White, S. J. 2008. Eye movement control during reading: Effects of word frequency and orthographic familiarity. Journal of Experimental Psychology: Human Perception and Performance 34, 1: 205–223. [Google Scholar] [CrossRef] [PubMed]
- White, S. J., and S. P. Liversedge. 2006. Linguistic and nonlinguistic influences on the eyes' landing positions during reading. The Quarterly Journal of Experimental Psychology 59, 4: 760–782. [Google Scholar] [CrossRef] [PubMed]

 |
 |
 |
 |
 |
Copyright © 2008. This article is licensed under a Creative Commons Attribution 4.0 International License.
Share and Cite
Ong, J.K.Y.; Kliegl, R. Conditional Co-Occurrence Probability Acts like Frequency in Predicting Fixation Durations. J. Eye Mov. Res. 2008, 2, 1-7. https://doi.org/10.16910/jemr.2.1.3
Ong JKY, Kliegl R. Conditional Co-Occurrence Probability Acts like Frequency in Predicting Fixation Durations. Journal of Eye Movement Research. 2008; 2(1):1-7. https://doi.org/10.16910/jemr.2.1.3
Chicago/Turabian StyleOng, James K. Y., and Reinhold Kliegl. 2008. "Conditional Co-Occurrence Probability Acts like Frequency in Predicting Fixation Durations" Journal of Eye Movement Research 2, no. 1: 1-7. https://doi.org/10.16910/jemr.2.1.3
APA StyleOng, J. K. Y., & Kliegl, R. (2008). Conditional Co-Occurrence Probability Acts like Frequency in Predicting Fixation Durations. Journal of Eye Movement Research, 2(1), 1-7. https://doi.org/10.16910/jemr.2.1.3



