Filtering Eye-Tracking Data From an EyeLink 1000: Comparing Heuristic, Savitzky-Golay, IIR and FIR Digital Filters
Abstract
:Introduction
Methods
Subjects
Eye movement data collection
Signal processing of fixation data
Digital filter design
“A general observation from the best filter list is the increasing prevalence of BW filters at higher sampling rates, ending in a total absence of other filter types at 1 kHz. This can be explained by considering the smoothness of the signal. At higher sampling rates more noise is present in the data. Such high-frequency noise can be more efficiently suppressed by the steeper roll-off of the BW filters compared to the two FIR filters, resulting in a smoother signal…”.
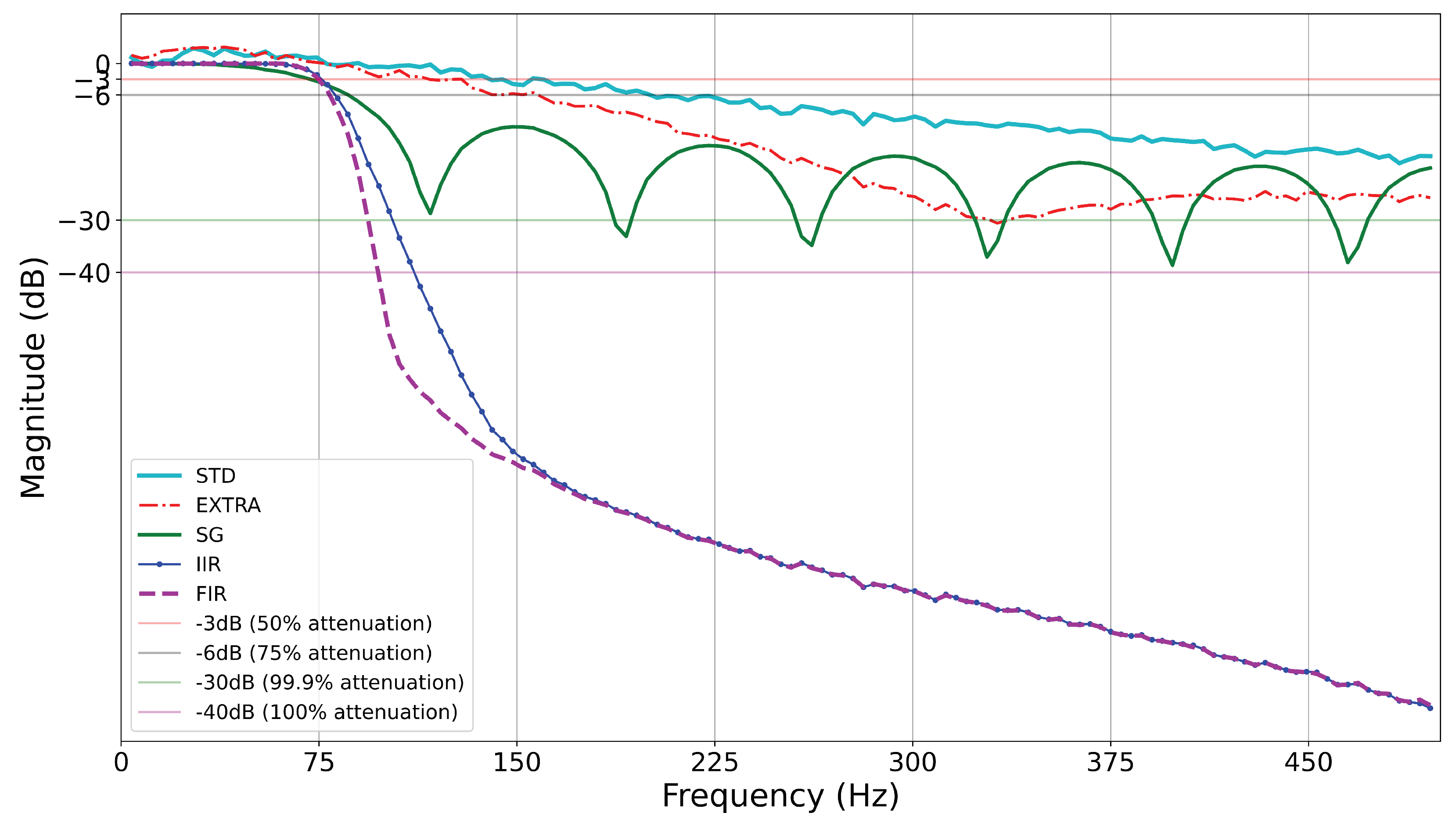
Estimation of filter frequency response
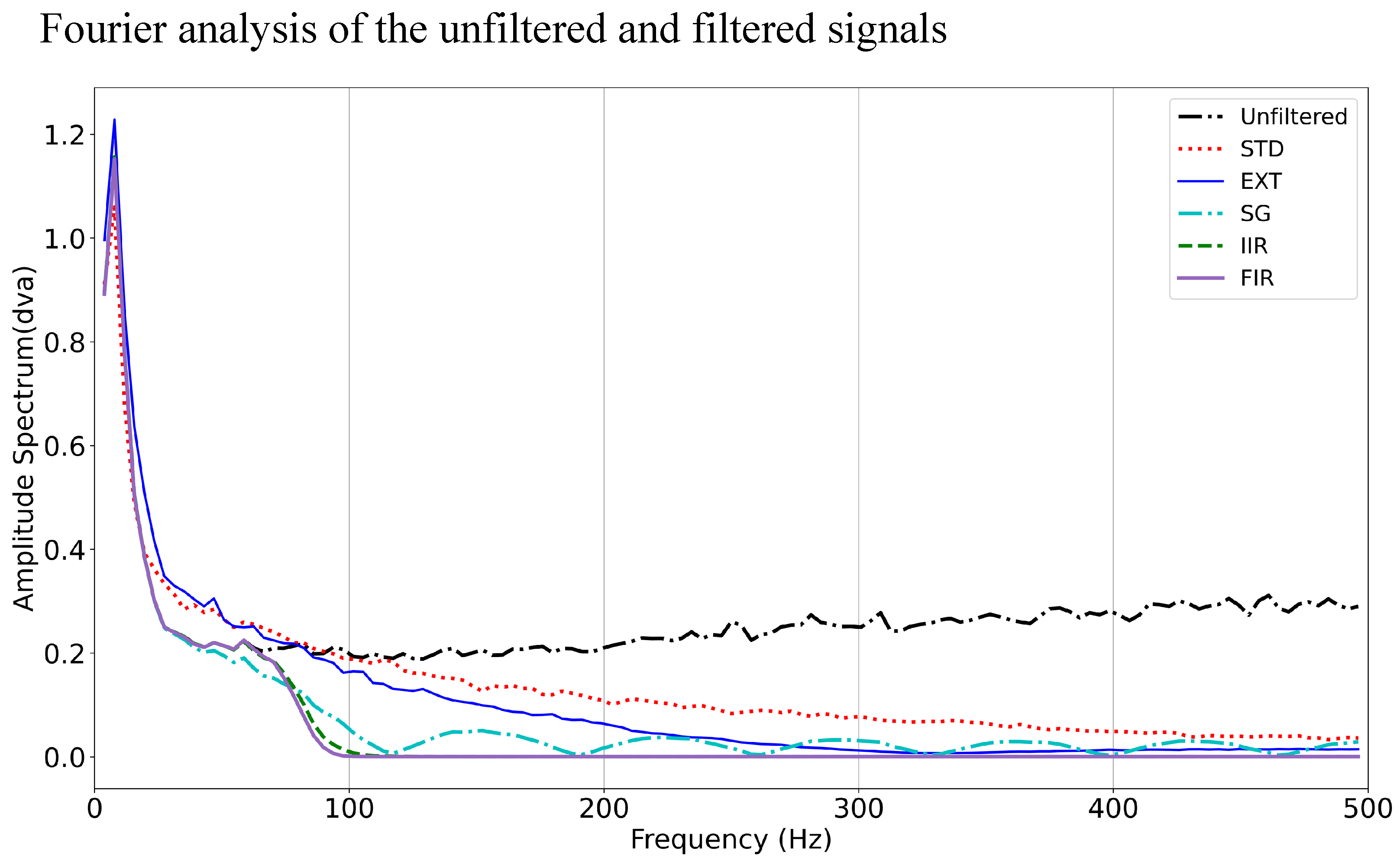
Fourier analysis of fixation before and after filtering
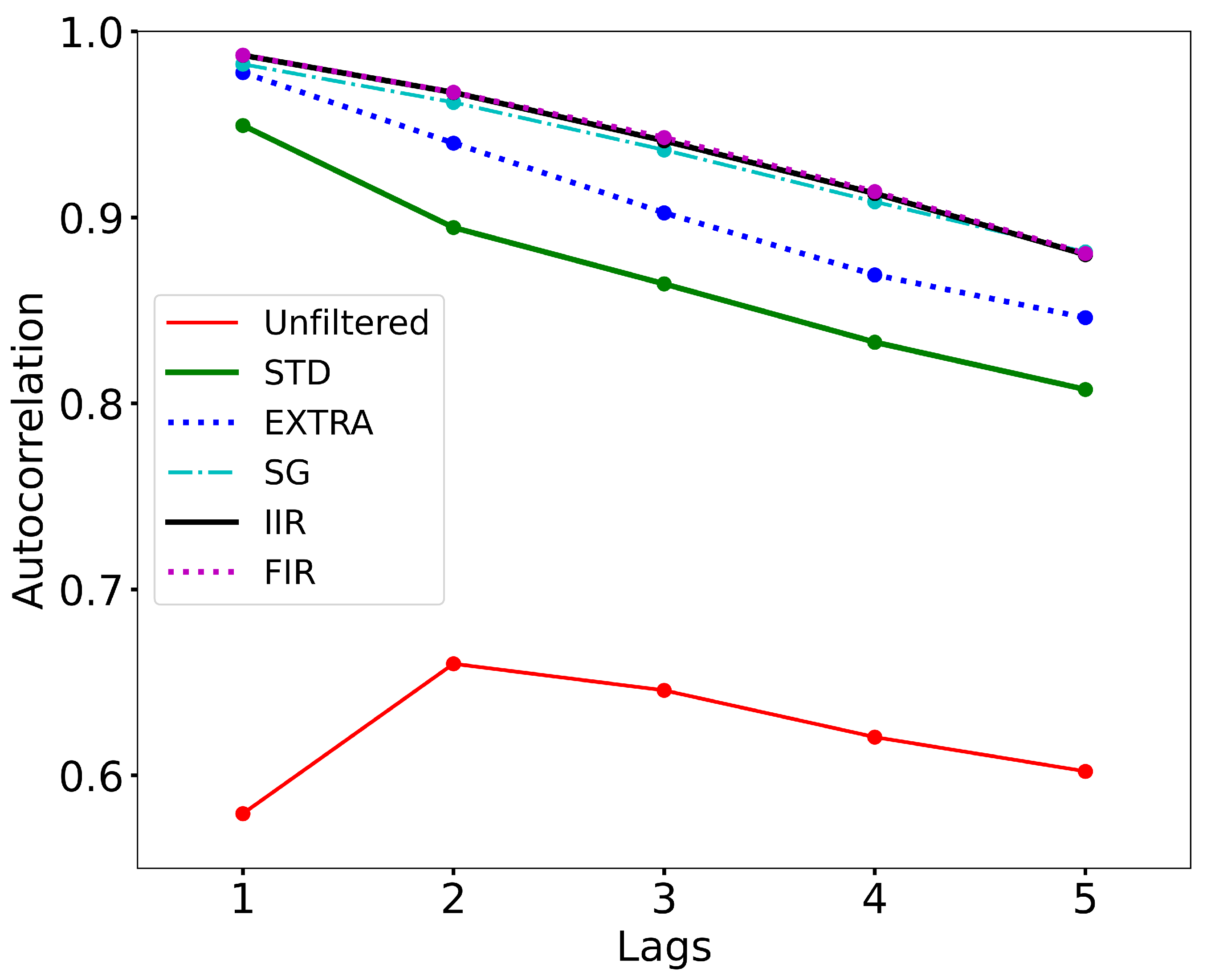
Study of the effects of filtering on temporal auto-correlation
Study of the effects of filtering on positional signal and velocity
Results
Analysis of filter frequency response
Fourier analysis of the unfiltered and filtered signals
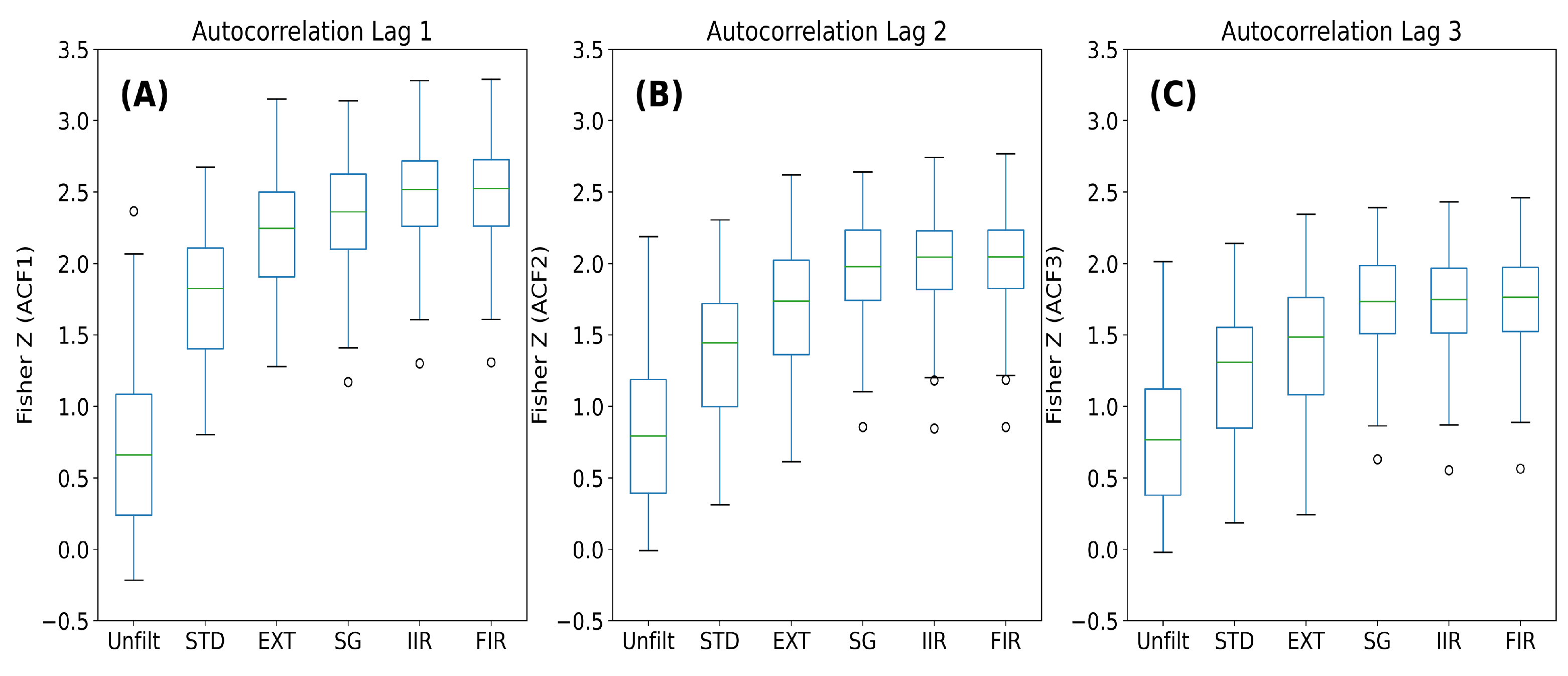
Effect of filtering on temporal auto-correlation
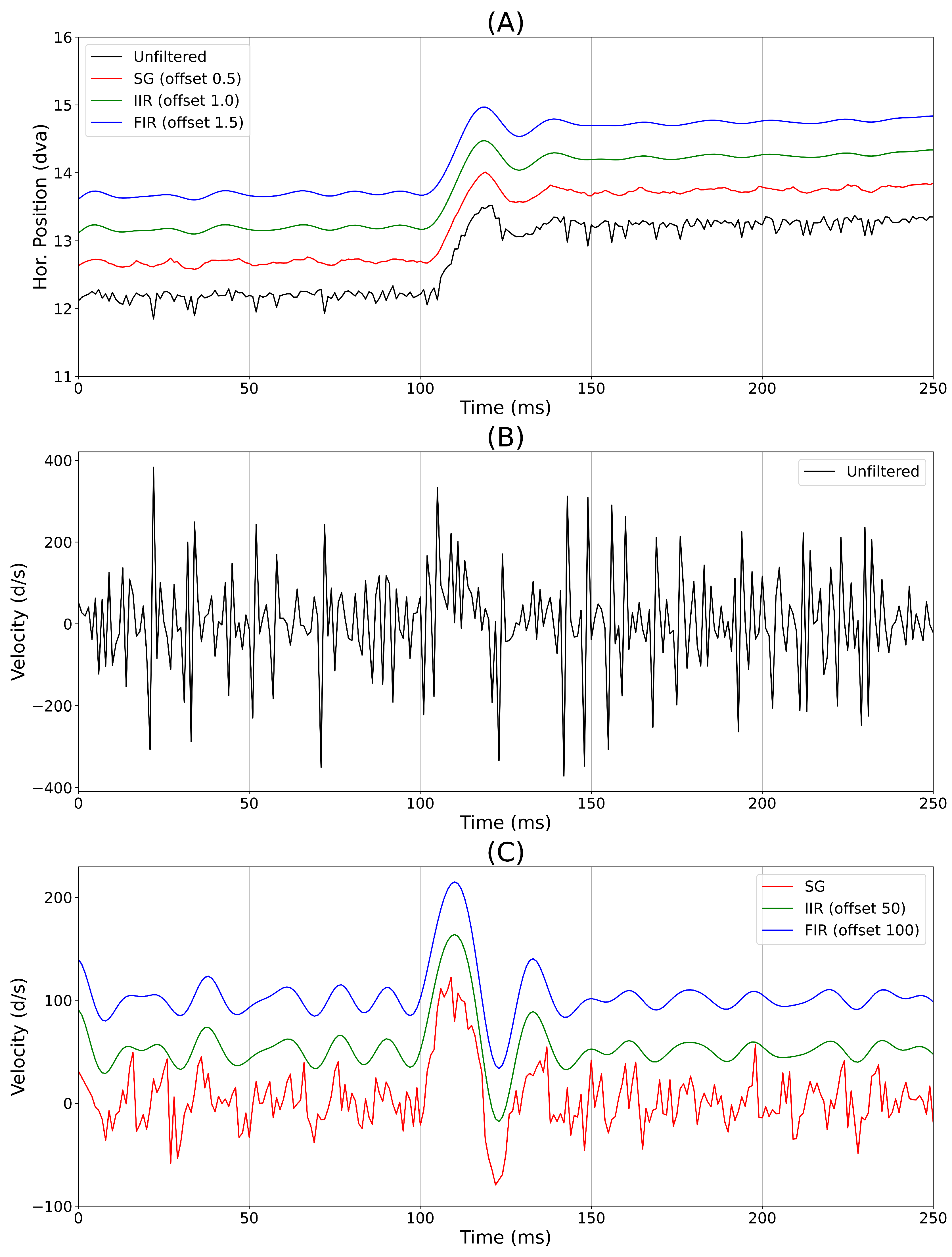
Illustration of the Effects of Filtering on Positional Signal and Velocity
Discussion
Conclusion
Data Availability Statement
Ethics and Conflict of Interest
Acknowledgements
Appendix A
EyeLink from SR research
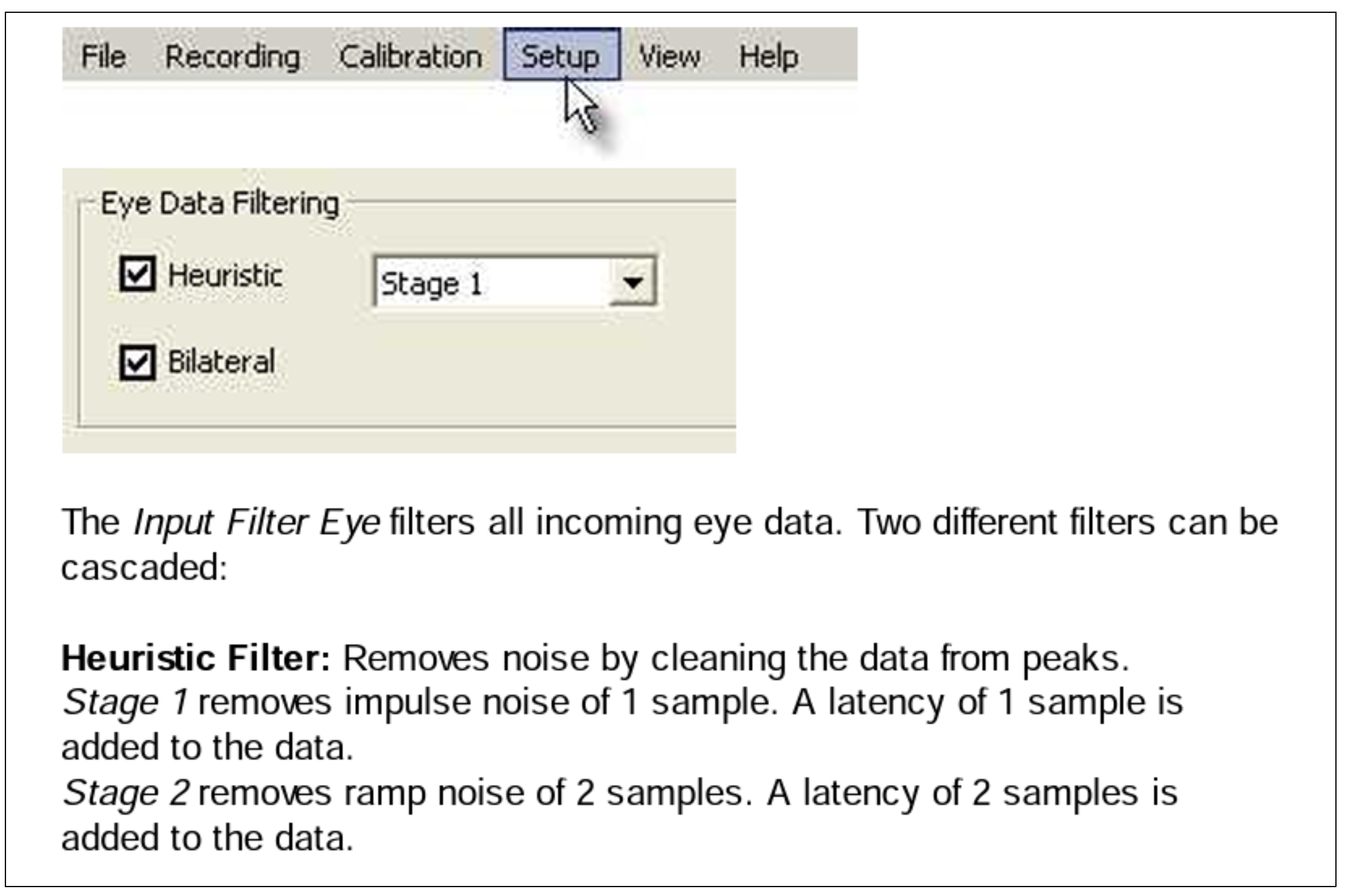
- Run the EyeLink Software on the Host PC.
- Click on Set Options on the Camera Setup page.
- File Sample filter option is now visible.
- Turn it OFF for collecting data Unfiltered, STD for standard filtering and EXTRA for extra filtering.


- Click on Setup.
- Eye Data Filtering option is now visible. See the following screenshot for assistance.
References
- Bahill, A. T., A. Brockenbrough, and B. T. Troost. 1981. Variability and development of a normative data base for saccadic eye movements. Invest Ophthalmol Vis Sci 21, 1 Pt 1: 116–125. [Google Scholar] [PubMed]
- Bahill, A. T., J. S. Kallman, and J. E. Lieberman. 1982. Frequency limitations of the two-point central difference differentiation algorithm. Biological cybernetics 45, 1: 1–4. [Google Scholar] [CrossRef] [PubMed]
- Bellanger, M. 2000. Digital processing of signals: Theory and practice. John Wiley & Sons. [Google Scholar]
- Butterworth, S. 1930. On the theory of filter amplifiers. Wireless Engineer 7, 6: 536–541. [Google Scholar]
- Chatterjee, A., and U. K. Roy. 2018. PPG based heart rate algorithm improvement with Butterworth IIR Filter and Savitzky-Golay FIR Filter. 2018 2nd International Conference on Electronics, Materials Engineering & Nano-Technology (IEMENTech). [Google Scholar]
- Chauhan, M., P. Thorwe, M. J. Mukherjee, and Y. S. Rao. 2018. Sensor Data Analysis Using Moving Average Filter and 256-Point FFT for Wireless Sensor Networks. 2018 9th International Conference on Computing, Communication and Networking Technologies (ICCCNT). [Google Scholar]
- Cooley, J. W., and J. W. Tukey. 1965. An algorithm for the machine calculation of complex Fourier series. Mathematics of computation 19, 90: 297–301. [Google Scholar] [CrossRef]
- Das, V. E., C. W. Thomas, A. Z. Zivotofsky, and R. J. Leigh. 1996. Measuring eye movements during locomotion: Filtering techniques for obtaining velocity signals from a video-based eye monitor. Journal of Vestibular Research 6, 6: 455–461. [Google Scholar] [CrossRef] [PubMed]
- Friedman, L., T. Hanson, H. S. Stern, and O. V. Komogortsev. 2023. Checking the Statistical Assumptions Underlying the Application of the Standard Deviation and RMS Error to Eye-Movement Time Series: A Comparison between Human and Artificial Eyes. arXiv preprint arXiv:2303.06004. [Google Scholar] [CrossRef]
- Griffith, H., D. Lohr, E. Abdulin, and O. Komogortsev. 2021. GazeBase, a large-scale, multi-stimulus, longitudinal eye movement dataset. Scientific Data 8, 1: 184. [Google Scholar] [CrossRef] [PubMed]
- Kalman, R. E. 1960. A new approach to linear filtering and prediction problems. [Google Scholar] [CrossRef]
- Kennedy, H. L. 2020. Improving the frequency response of Savitzky-Golay filters via colored-noise models. Digital Signal Processing 102: 102743. [Google Scholar] [CrossRef]
- Mack, D. J., S. Belfanti, and U. Schwarz. 2017. The effect of sampling rate and lowpass filters on saccades-A modeling approach. Behav Res Methods 49, 6: 2146–2162. [Google Scholar] [CrossRef] [PubMed]
- Miles, W. R. 1930. Ocular dominance in human adults. The journal of general psychology 3, 3: 412–430. [Google Scholar] [CrossRef]
- Raju, M. H., L. Friedman, T. M. Bouman, and O. V. Komogortsev. 2023. Determining Which Sine Wave Frequencies Correspond to Signal and Which Correspond to Noise in Eye-Tracking Time-Series. arXiv preprint arXiv:2302.00029. [Google Scholar] [CrossRef] [PubMed]
- Raju, M. H., D. J. Lohr, and O. Komogortsev. 2022. Iris Print Attack Detection using Eye Movement Signals. 2022 Symposium on Eye Tracking Research and Applications. [Google Scholar]
- Rigas, I., and O. V. Komogortsev. 2015. Eye movement-driven defense against iris print-attacks. Pattern Recognition Letters 68: 316–326. [Google Scholar] [CrossRef]
- Roy, A. G., P. M. Biron, and M. F. Lapointe. 1997. Implications of low-pass filtering on power spectra and autocorrelation functions of turbulent velocity signals. Mathematical Geology 29: 653–668. [Google Scholar] [CrossRef]
- Savitzky, A., and M. J. Golay. 1964. Smoothing and differentiation of data by simplified least squares procedures. Analytical chemistry 36, 8: 1627–1639. [Google Scholar] [CrossRef]
- Shannon, C. E. 1949. Communication in the presence of noise. Proceedings of the IRE 37, 1: 10–21. [Google Scholar] [CrossRef]
- Stampe, D. M. 1993. Heuristic filtering and reliable calibration methods for video-based pupil-tracking systems. Behavior Research Methods, Instruments, & Computers 25: 137–142. [Google Scholar] [CrossRef]
- Virtanen, P., R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, and J. Bright. 2020. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nature methods 17, 3: 261–272. [Google Scholar] [CrossRef] [PubMed]
| Filter name | Filter characteristics | Final -3db point |
|---|---|---|
| Savitzky-Golay (SG) | Window length=23, polynomial order =5 | 75 Hz (74.9) |
| Infinite impulse response (IIR) | Butterworth type, Order=7, Cut-off (-3dB) =81 Hz, Zero-phase | 75 Hz (75.4) |
| Finite impulse response (FIR) | Number of coefficients, taps = 80, Cut-off (-3dB) = 84 Hz, Zero-phase | 75 Hz (75.0) |
| 1st filter | 2nd filter | ACF 1 | ACF 2 | ACF 3 | |||
|---|---|---|---|---|---|---|---|
| χ2= 711.5† | χ2= 604.2† | χ2= 492.1† | |||||
| Difference | P-value | Difference | P-value | Difference | P-value | ||
| Unfiltered | STD | -1.495 | p<0.001 | -1.361 | p<0.001 | -1.505 | p<0.001 |
| Unfiltered | EXTRA | -3.056 | p<0.001 | -2.62 | p<0.001 | -2.505 | p<0.001 |
| Unfiltered | SG | -2.44 | p<0.001 | -2.551 | p<0.001 | -2.722 | p<0.001 |
| Unfiltered | FIR | -3.875 | p<0.001 | -3.491 | p<0.001 | -3.116 | p<0.001 |
| Unfiltered | IIR | -3.94 | p<0.001 | -3.727 | p<0.001 | -3.403 | p<0.001 |
| STD | EXTRA | -1.56 | p<0.001 | -1.259 | p<0.001 | -1.000 | p<0.001 |
| STD | SG | -0.944 | p<0.001 | -1.119 | p<0.001 | -1.218 | p<0.001 |
| STD | FIR | -2.38 | p<0.001 | -2.13 | p<0.001 | -1.611 | p<0.001 |
| STD | IIR | -2.44 | p<0.001 | -2.366 | p<0.001 | -1.898 | p<0.001 |
| EXTRA | SG | 0.616 | 0.0082 | ||||
| EXTRA | FIR | -0.819 | p<0.001 | -0.87 | p<0.001 | -0.611 | 0.0090 |
| EXTRA | IIR | -0.884 | p<0.001 | -1.107 | p<0.001 | -0.898 | p<0.001 |
| SG | FIR | -1.435 | p<0.001 | -0.94 | p<0.001 | ||
| SG | IIR | -1.5 | p<0.001 | -1.176 | p<0.001 | -0.681 | 0.0022 |
| FIR | IIR | ||||||
| Unfiltered | SG Filter | IIR Filter | FIR Filter | |
|---|---|---|---|---|
| Velocity SD | 120.19 | 29.01 | 23.46 | 23.31 |
| Velocity RMS | 209.53 | 24.46 | 5.67 | 5.55 |
Copyright © 2023. This article is licensed under a Creative Commons Attribution 4.0 International License.
Share and Cite
Raju, M.H.; Friedman, L.; Bouman, T.M.; Komogortsev, O.V. Filtering Eye-Tracking Data From an EyeLink 1000: Comparing Heuristic, Savitzky-Golay, IIR and FIR Digital Filters. J. Eye Mov. Res. 2021, 14, 1-16. https://doi.org/10.16910/jemr.14.3.6
Raju MH, Friedman L, Bouman TM, Komogortsev OV. Filtering Eye-Tracking Data From an EyeLink 1000: Comparing Heuristic, Savitzky-Golay, IIR and FIR Digital Filters. Journal of Eye Movement Research. 2021; 14(3):1-16. https://doi.org/10.16910/jemr.14.3.6
Chicago/Turabian StyleRaju, Mehedi H., Lee Friedman, Troy M. Bouman, and Oleg V. Komogortsev. 2021. "Filtering Eye-Tracking Data From an EyeLink 1000: Comparing Heuristic, Savitzky-Golay, IIR and FIR Digital Filters" Journal of Eye Movement Research 14, no. 3: 1-16. https://doi.org/10.16910/jemr.14.3.6
APA StyleRaju, M. H., Friedman, L., Bouman, T. M., & Komogortsev, O. V. (2021). Filtering Eye-Tracking Data From an EyeLink 1000: Comparing Heuristic, Savitzky-Golay, IIR and FIR Digital Filters. Journal of Eye Movement Research, 14(3), 1-16. https://doi.org/10.16910/jemr.14.3.6



