Representative Scanpath Identification for Group Viewing Pattern Analysis
Abstract
:Introduction
Related Work
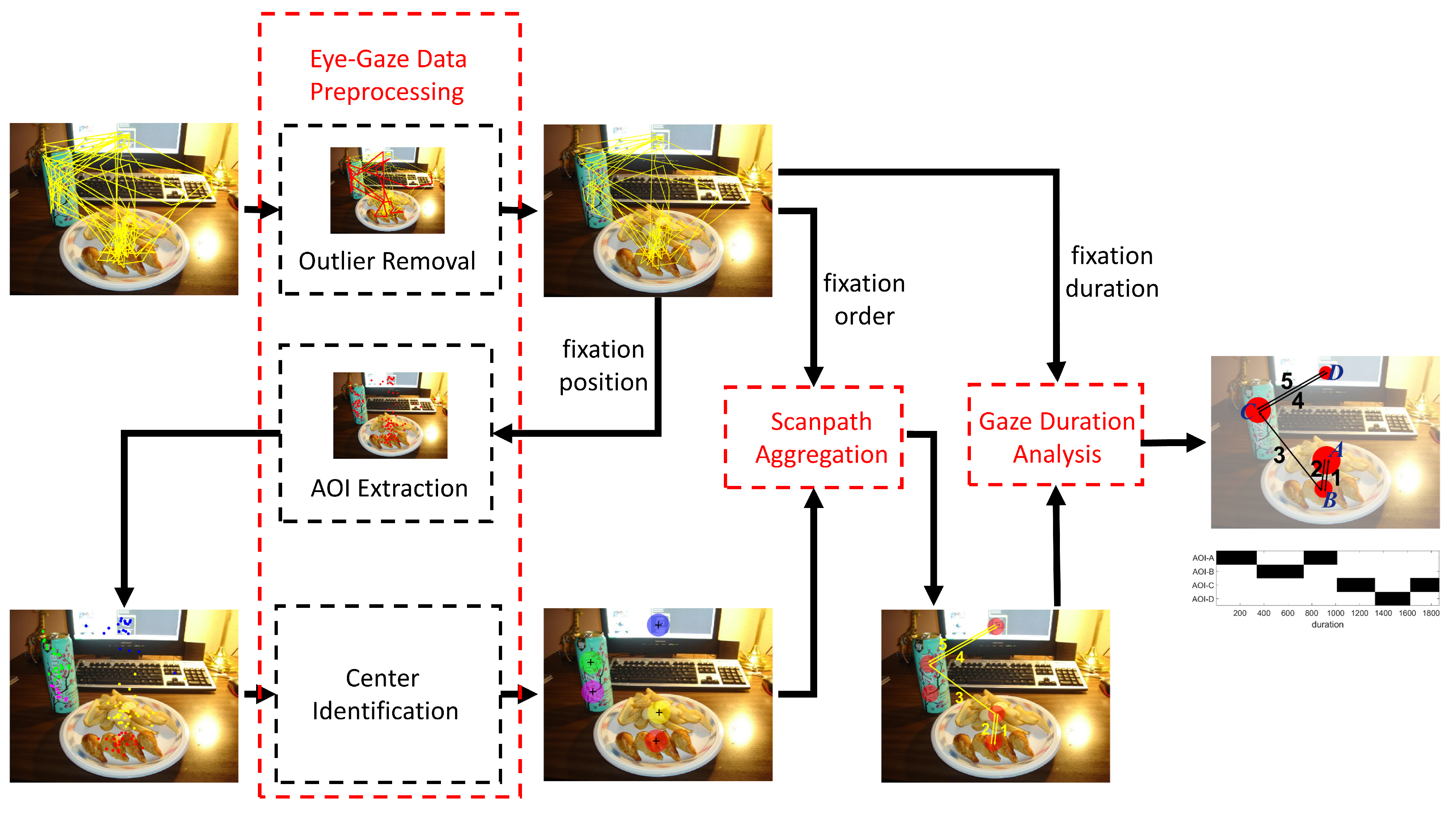
Methodology
Eye-gaze Data Preprocessing
| Algorithm 1 Outlier Scanpath Removal |
 |
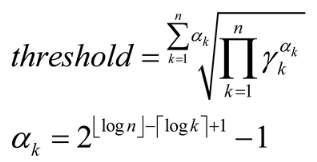


Scanpath Aggregation
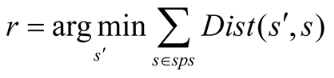
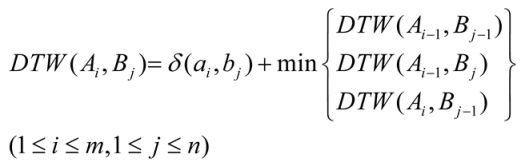
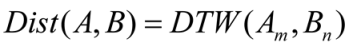
- The representative scanpath must be composed of abstract scanpath components such as AOIs;
- Any two contiguous components in the representative scanpath must be contiguous in at least one individual scanpath;
- The occurrence count of each component in the representative scanpath does not exceed the maximum occurrence count of the component in all the individual scanpaths.
- DTW computation. When computing DTW between two sequences, we can obtain the accumulation matrix and find the path of cost accumulation, which indicates the optimal alignment between sequences. The process of DTW computation is repeated between every actual scanpath and the reference scanpath.
- Scanpath update. In the update step, each component of the reference scanpath is updated by the “constrained barycenter” of fixations that are aligned to it during the computation process. The “constrained barycenter” means an AOI belonging to the candidate set and having the minimum average distance with all the aligned fixations.
| Algorithm 2 Candidate-constrained DTW Barycenter Algorithm (CDBA) |
 |
Gaze Duration Analysis
Eye Tracking Study
Eye Tracking Data
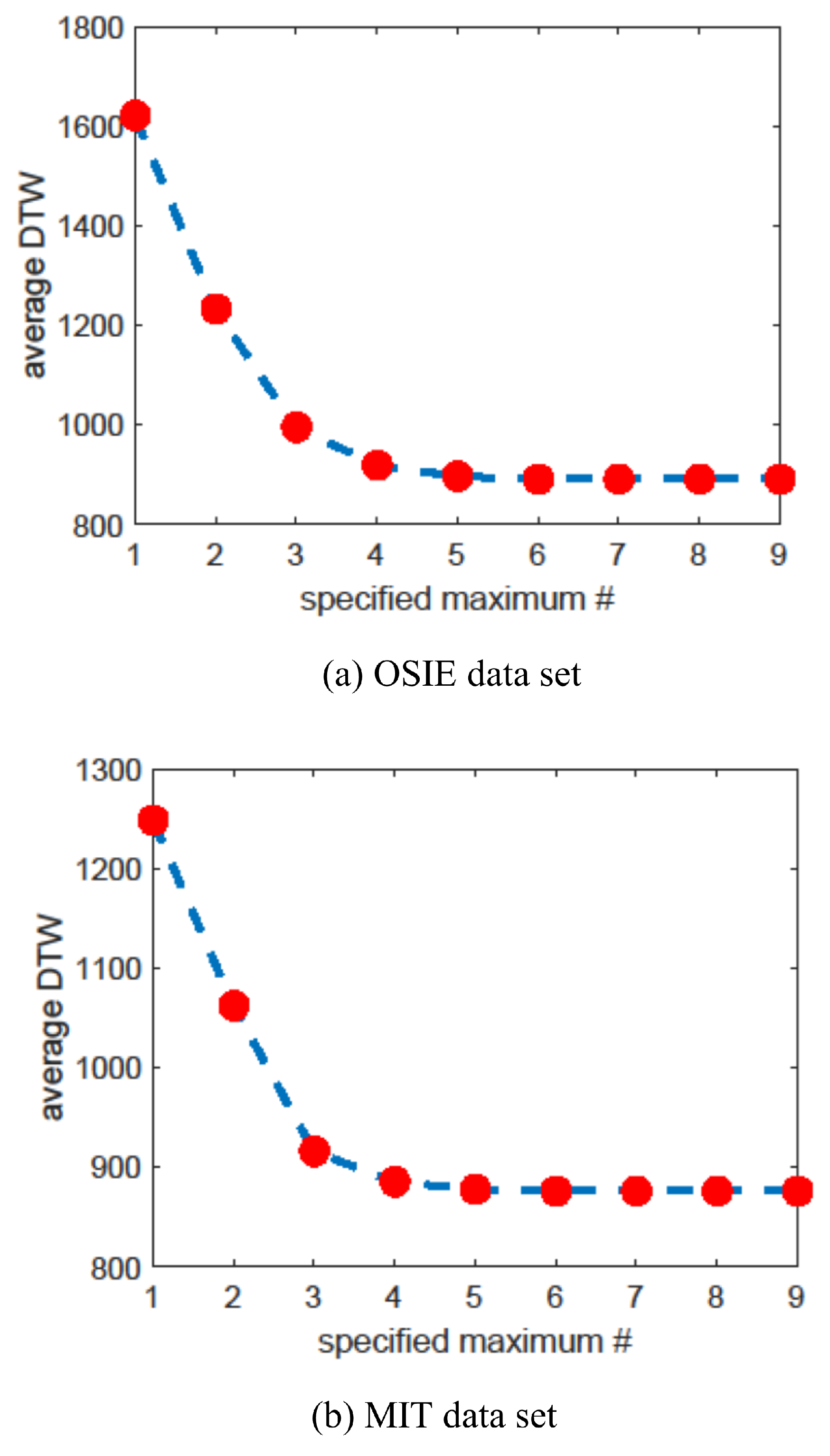
- OSIE Data Set contains 700 images. Each image is freely viewed by 15 subjects for 3 seconds. All the images are of the size 800 × 600 pixels.
- MIT1003 Data Set includes 1003 scenes freely viewed by 15 subjects for 3 seconds. The longest dimension of each image is 1024 pixels.
Procedure
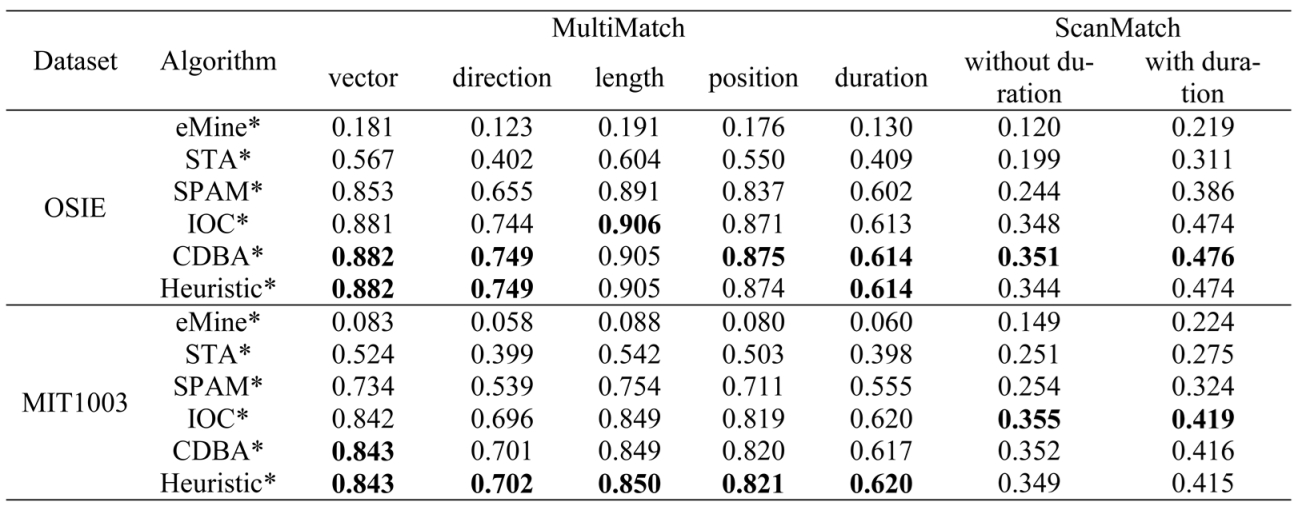
- Scanpath length: scanpath length reflects the frequency of attention shift, so we compare the length distribution to check whether representative scanpaths can reflect this property;
- Scanpath shape: scanpath shape, partly influenced by scanpath length, is related to both spatial distribution and temporal order, which is measured by DTW in our experiment;
- Overall scanpath similarity: overall scanpath similarity comprehensively considers scanpath shape and gaze duration. ScanMatch and MultiMatch can provide such comparison.
Results
Summary
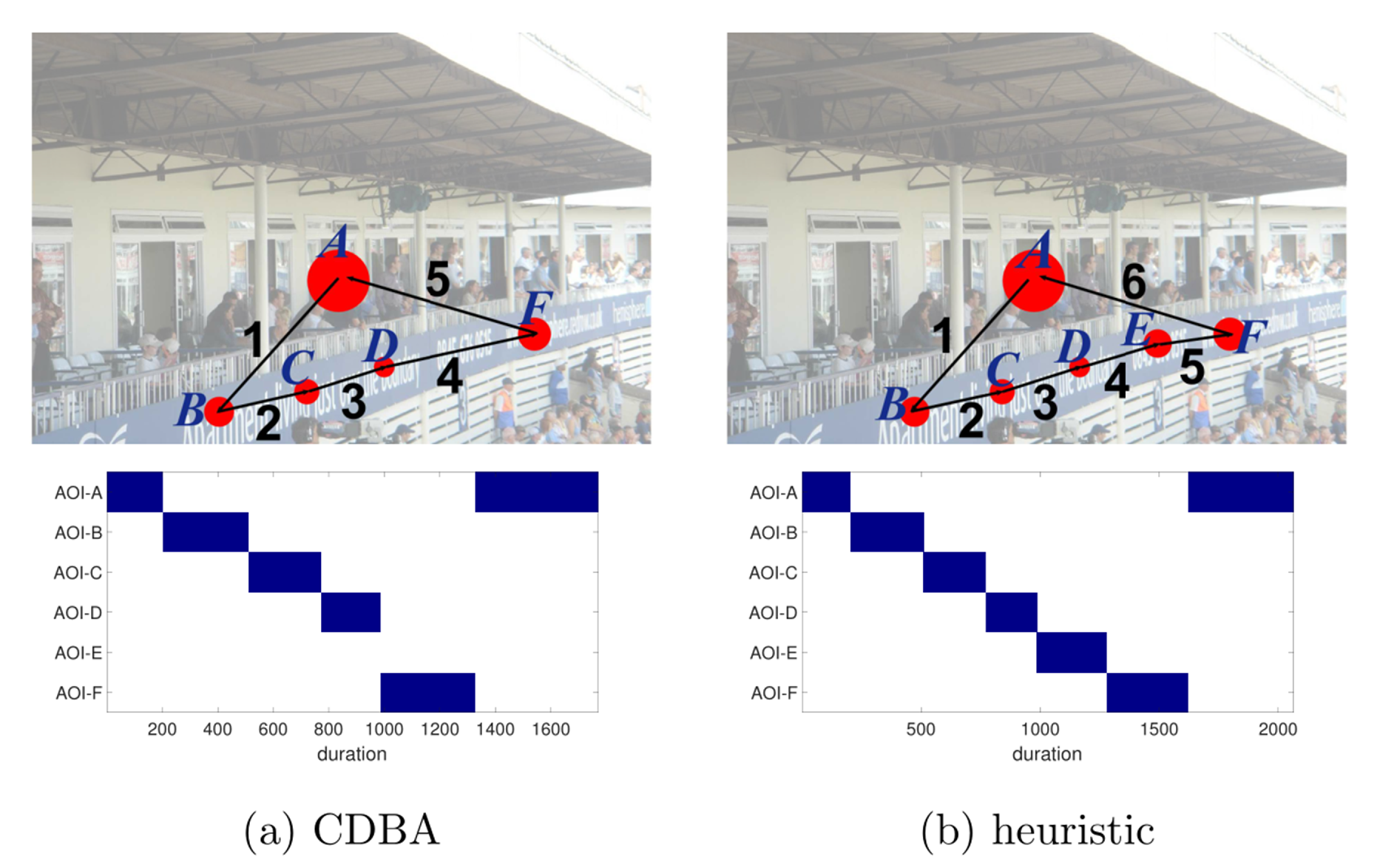
Interpretation of Representative Scanpaths
Discussion
Conclusions
Ethics and Conflict of Interest
Acknowledgements
References
- Berndt, D. J., and J. Clifford. 1994. Using dynamic time warping to find patterns in time series. In ACM SIGKDD Conference on Knowledge Discovery and Data Mining Workshop. [Google Scholar]
- Burmester, M., and M. Mast. 2010. Repeated Web Page Visits and the Scanpath Theory: A Recurrent Pattern Detection Approach. Journal of Eye Movement Research 3, 4: 5, 1–20. [Google Scholar] [CrossRef]
- Chen, X., and Z. Chen. 2017. Exploring visual attention using random walks based eye tracking protocols. Journal of Visual Communication & Image Representation 45: 147–155. [Google Scholar] [CrossRef]
- Cristino, F., S. Mathot, J. Theeuwes, and I. D. Gilchrist. 2010. Scanmatch: A novel method for comparing fixation sequences. Behavior Research Methods 42, 3: 692–700. [Google Scholar] [CrossRef] [PubMed]
- Dolezalova, J., and S. Popelka. 2016. ScanGraph: A Novel Scanpath Comparison Method Using Visualization of Graph Cliques. Journal of Eye Movement Research 9, 4: 5, 1–13. [Google Scholar] [CrossRef]
- Engelke, U., H. Liu, J. Wang, P. Le Callet, I. Heynderickx, H. J. Zepernick, and A. Maeder. 2013. Comparative study of fixation density maps. IEEE Transactions on Image Processing 22, 3: 1121–1133. [Google Scholar] [CrossRef]
- Eraslan, S., Y. Yesilada, and S. Harper. 2014. Identifying patterns in eyetracking scanpaths in terms of visual elements of web pages. In International Conference on Web Engineering. Springer. [Google Scholar]
- Eraslan, S., Y. Yesilada, and S. Harper. 2016a. Eye Tracking Scanpath Analysis Techniques on Web Pages: A Survey, Evaluation and Comparison. Journal of Eye Movement Research 9, 1: 2, 1–19. [Google Scholar] [CrossRef]
- Eraslan, S., Y. Yesilada, and S. Harper. 2016b. Scanpath Trend Analysis on Web Pages: Clustering Eye Tracking Scanpaths. ACM Transactions on the Web 10, 4: 20:1–20:35. [Google Scholar] [CrossRef]
- Eraslan, S., Y. Yesilada, and S. Harper. 2016c. Trends in eye tracking scanpaths: Segmentation effect? In Proceedings of the 27th ACM Conference on Hypertext and Social Media. [Google Scholar] [CrossRef]
- Eraslan, S., Y. Yesilada, and S. Harper. 2017a. Less Users More Confidence: How AOIs don’t Affect Scanpath Trend Analysis. Journal of Eye Movement Research 10, 4: 6, 1–18. [Google Scholar] [CrossRef]
- Eraslan, S., Y. Yesilada, and S. Harper. 2017b. Engineering Web-based Interactive Systems: Trend Analysis in Eye Tracking Scanpaths with a Tolerance. In Proceedings of the 9th ACM SIGCHI Symposium on Engineering Interactive Computing Systems, EICS. [Google Scholar] [CrossRef]
- Goldberg, J. H., and J. I. Helfman. 2010. Scanpath clustering and aggregation. In Proceedings of the 2010 Symposium on Eye Tracking Research & Applications. [Google Scholar] [CrossRef]
- Hejmady, P., and N. H. Narayanan. 2012. Visual attention patterns during program debugging with an ide. In Proceedings of the 2012 Symposium on Eye Tracking Research & Applications. [Google Scholar] [CrossRef]
- Hembrooke, H., M. Feusner, and G. Gay. 2006. Averaging scan patterns and what they can tell us. In Proceedings of the 2006 Symposium on Eye Tracking Research & Applications. [Google Scholar] [CrossRef]
- Jarodzka, H., K. Holmqvist, and M. Nyström. 2010. A vector-based, multidimensional scanpath similarity measure. In Proceedings of the 2010 Symposium on Eye-Tracking Research & Applications, ETRA ’10. ACM: pp. 211–218. [Google Scholar] [CrossRef]
- Jiang, M., X. Boix, G. Roig, J. Xu, L. Van Gool, and Q. Zhao. 2016. Learning to predict sequences of human visual fixations. IEEE Transactions on Neural Networks and Learning Systems 27, 6: 1241–1252. [Google Scholar] [CrossRef]
- Judd, T., K. Ehinger, F. Durand, and A. Torralba. 2009. Learning to predict where humans look. In Proceedings of 2009 IEEE 12th International Conference on Computer Vision. [Google Scholar] [CrossRef]
- Just, M., and P. Carpenter. 1980. A theory of reading: from eye fixations to comprehension. Psychological Review 87, 4: 329–354. [Google Scholar] [CrossRef]
- Kanizsa, G. 1979. Organization in vision: Essays on Gestalt perception. Praeger Publishers. [Google Scholar]
- Le Meur, O., and Z. Liu. 2015. Saccadic model of eye movements for free-viewing condition. Vision Research 116: 152–164. [Google Scholar] [CrossRef]
- Levenshtein, V. I. 1965. Binary codes capable of correcting deletions, insertions, and reversals. Soviet Physics Dokl. 10: 707–710. [Google Scholar]
- Li, A., Y. Zhang, and Z. Chen. 2017. Scanpath mining of eye movement trajectories for visual attention analysis. In 2017 IEEE International Conference on Multimedia and Expo (ICME). pp. 535–540. [Google Scholar] [CrossRef]
- Magnusson, M. S. 2000. Discovering hidden time patterns in behavior: T-patterns and their detection. Behavior Research Methods, Instruments, & Computers 32, 1: 93–110. [Google Scholar] [CrossRef]
- McClung, S. N., and Z. Kang. 2016. Characterization of visual scanning patterns in air traffic control. Computational Intelligence and Neuroscience 2016: 1–17. [Google Scholar] [CrossRef]
- Mishra, A., D. Kanojia, and P. Bhattacharyya. 2016. Predicting readers sarcasm understandability by modeling gaze behavior. In AAAI Conference on Artificial Intelligence. [Google Scholar]
- Mishra, A., D. Kanojia, S. Nagar, K. Dey, and P. Bhattacharyya. 2017. Scanpath complexity: Modeling reading effort using gaze information. In AAAI Conference on Artificial Intelligence. [Google Scholar]
- Needleman, S. B., and C. D. Wunsch. 1970. A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology 48, 3: 443–453. [Google Scholar] [CrossRef]
- Noton, D., and L. Stark. 1971. Scanpaths in eye movements during pattern perception. Science 171, 3968: 308–311. [Google Scholar] [CrossRef]
- Petitjean, F., A. Ketterlin, and P. Gancarski. 2011. A global averaging method for dynamic time warping with applications to clustering. Pattern Recognition 44, 3: 678–693. [Google Scholar] [CrossRef]
- Ramanishka, V., A. Das, J. Zhang, and K. Saenko. 2017. Top-down visual saliency guided by captions. In IEEE International Conference on Computer Vision and Pattern Recognition. [Google Scholar] [CrossRef]
- Razin, Y., and K. Feigh. 2017. Learning to predict intent from gaze during robotic hand-eye coordination. In AAAI Conference on Artificial Intelligence. [Google Scholar]
- Rodriguez, A., and A. Laio. 2014. Clustering by fast search and find of density peaks. Science 344, 6191: 1492–1496. [Google Scholar] [CrossRef]
- Sakoe, H., and S. Chiba. 1978. Dynamic programming algorithm optimization for spoken word recognition. IEEE Transactions on Acoustics, Speech, and Signal Processing 26, 1: 43–49. [Google Scholar] [CrossRef]
- West, J. M., A. R. Haake, E. P. Rozanski, and K. S. Karn. 2006. eyepatterns: software for identifying patterns and similarities across fixation sequences. In Proceedings of the 2006 Symposium on Eye Tracking Research & Applications. [Google Scholar] [CrossRef]
- Xu, J., M. Jiang, S. Wang, M. S. Kankanhalli, and Q. Zhao. 2014. Predicting human gaze beyond pixels. Journal of Vision 14, 1: 1–20. [Google Scholar] [CrossRef]
- Yarbus, A. L. 1967. Eye Movements and Vision. Plenum Press. [Google Scholar]
- Zhou, L., Y. Zhang, Z. Wang, L. Rao, W. Wang, S. Li, X. Li, and Z. Liang. 2016. A Scanpath Analysis of the Risky Decision-Making Process. Journal of Behavioral Decision Making 29: 169–182. [Google Scholar] [CrossRef]

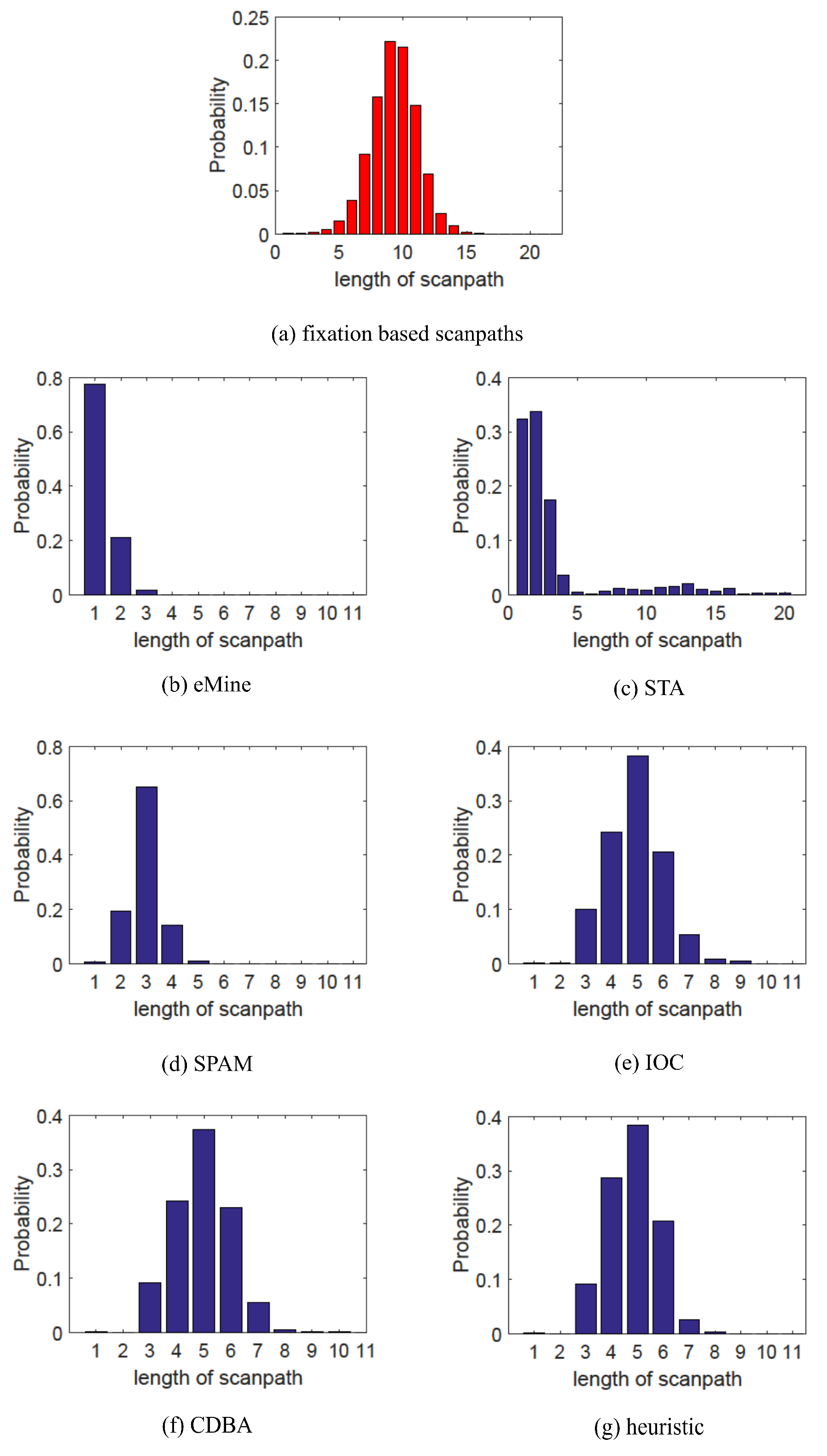
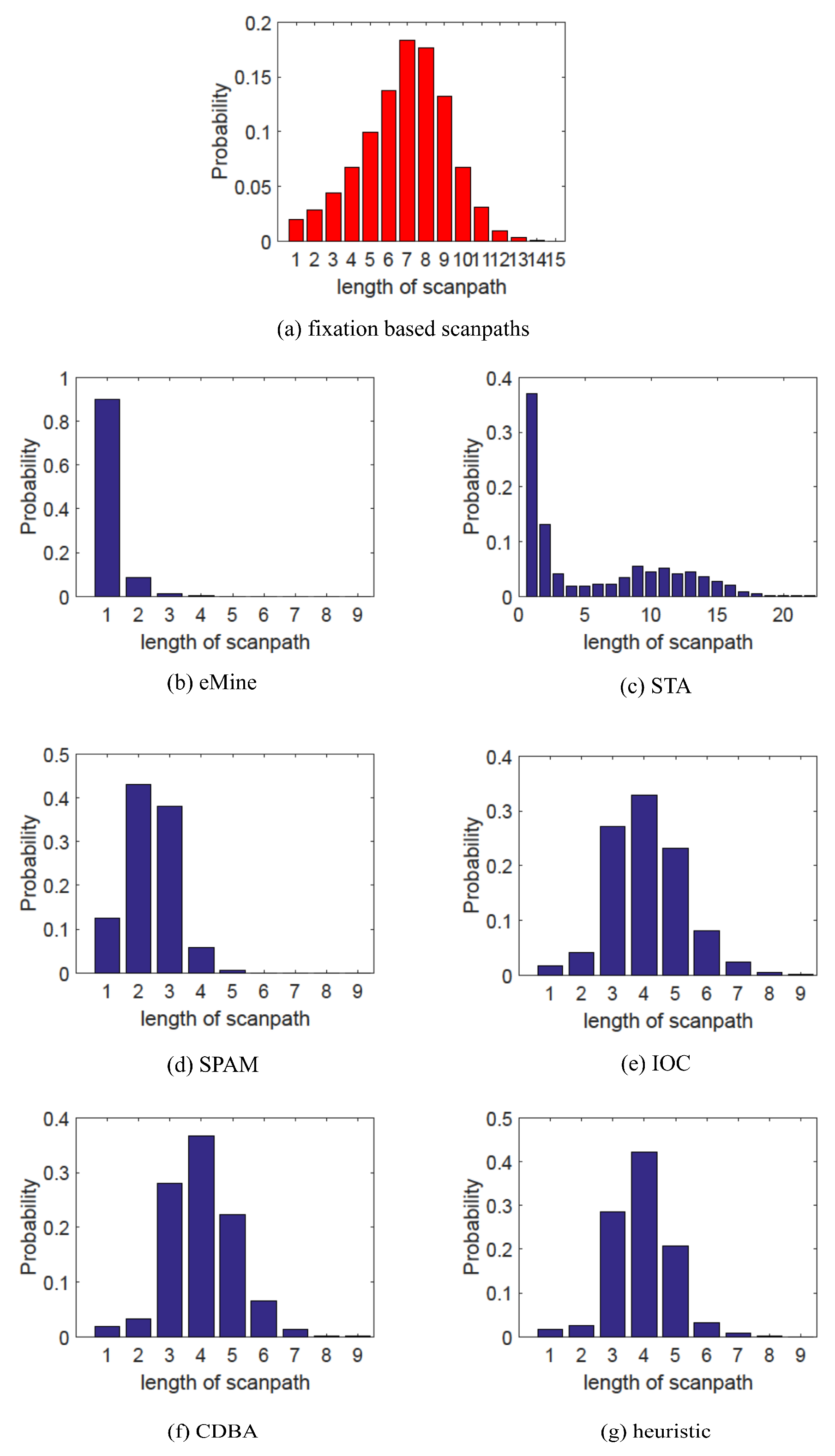


| Dataset | eMine | STA | SPAM | IOC | CDBA | heuristic |
| OSIE | 1644 | 1418 | 1050 | 921 | 899 | 891 |
| MIT1003 | 1319 | 1467 | 1007 | 910 | 882 | 876 |
| Dataset | Algrotihm | Test | N | df | T or Z value | Effect Size |
| CDBA-eMine | Wilcoxon | 531 | NA | -19.9092*** | -1.3536 | |
| CDBA-STA | Wilcoxon | 700 | NA | -22.8043*** | -1.1528 | |
| CDBA-SPAM | Wilcoxon | 700 | NA | -21.7021*** | -0.5653 | |
| CDBA-IOC | Wilcoxon | 700 | NA | -14.4308*** | -0.1025 | |
| OSIE | Heuristic-eMine | Wilcoxon | 531 | NA | -19.3612*** | -1.3612 |
| Heuristic-SPAM | Wilcoxon | 700 | NA | -21.8317*** | -0.5999 | |
| Heuristic-STA | Wilcoxon | 700 | NA | -22.8062*** | -1.1689 | |
| Heuristic-IOC | Wilcoxon | 700 | NA | -18.2585*** | -0.1443 | |
| Heuristic-CDBA | Wilcoxon | 700 | NA | -13.6244*** | -0.0420 | |
| CDBA-eMine | Wilcoxon | 484 | NA | -18.6447*** | -0.9658 | |
| CDBA-STA | Wilcoxon | 1003 | NA | -27.0153*** | -1.0299 | |
| CDBA-SPAM | Wilcoxon | 1003 | NA | -25.1192*** | -0.4019 | |
| CDBA-IOC | Wilcoxon | 1003 | NA | -19.7691*** | -0.1033 | |
| MIT1003 | Heuristic-eMine | Wilcoxon | 484 | NA | -18.6447*** | -0.9761 |
| Heuristic-STA | Wilcoxon | 1003 | NA | -27.1454*** | -1.0398 | |
| Heuristic-SPAM | Wilcoxon | 1003 | NA | -25.3895*** | -0.4236 | |
| Heuristic-IOC | Wilcoxon | 1003 | NA | -22.3411*** | -0.1273 | |
| Heuristic-CDBA | Wilcoxon | 1003 | NA | -15.3338*** | -0.0243 |
 |
| Dataset | Algrotihm | Test | N | df | T or Z value | Effect Size |
| CDBA-eMine | Paired t-test | 531 | 530 | 54.1696*** | 1.6125 | |
| CDBA-STA | Wilcoxon | 700 | NA | 22.6372*** | 1.2585 | |
| CDBA-SPAM | Wilcoxon | 700 | NA | 20.9515*** | 0.8052 | |
| CDBA-IOC | Wilcoxon | 700 | NA | 1.7021 | 0.0279 | |
| OSIE | Heuristic-eMine | Wilcoxon | 531 | NA | 19.8712*** | 1.6068 |
| Heuristic-STA | Wilcoxon | 700 | NA | 22.5733*** | 1.2461 | |
| Heuristic-SPAM | Wilcoxon | 700 | NA | 20.9413*** | 0.7875 | |
| Heuristic-IOC | Wilcoxon | 700 | NA | 0.1103 | 0.0057 | |
| Heuristic-CDBA | Wilcoxon | 700 | NA | -1.8394 | -0.2222 | |
| CDBA-eMine | Wilcoxon | 484 | NA | 18.6006*** | 1.3676 | |
| CDBA-STA | Wilcoxon | 1003 | NA | 26.6705*** | 1.0802 | |
| CDBA-SPAM | Wilcoxon | 1003 | NA | 24.0124*** | 0.7038 | |
| CDBA-IOC | Wilcoxon | 1003 | NA | -2.0228* | -0.0253 | |
| MIT1003 | Heuristic-eMine | Wilcoxon | 484 | NA | 18.6003*** | 1.3736 |
| Heuristic-STA | Wilcoxon | 1003 | NA | 26.5807*** | 1.0766 | |
| Heuristic-SPAM | Wilcoxon | 1003 | NA | 23.9828*** | 0.6980 | |
| Heuristic-IOC | Wilcoxon | 1003 | NA | -2.4115* | -0.0353 | |
| Heuristic-CDBA | Wilcoxon | 1003 | NA | -1.1309 | -0.0099 |
Copyright © 2018. This article is licensed under a Creative Commons Attribution 4.0 International License.
Share and Cite
Li, A.; Chen, Z. Representative Scanpath Identification for Group Viewing Pattern Analysis. J. Eye Mov. Res. 2018, 11, 1-17. https://doi.org/10.16910/jemr.11.6.5
Li A, Chen Z. Representative Scanpath Identification for Group Viewing Pattern Analysis. Journal of Eye Movement Research. 2018; 11(6):1-17. https://doi.org/10.16910/jemr.11.6.5
Chicago/Turabian StyleLi, Aoqi, and Zhenzhong Chen. 2018. "Representative Scanpath Identification for Group Viewing Pattern Analysis" Journal of Eye Movement Research 11, no. 6: 1-17. https://doi.org/10.16910/jemr.11.6.5
APA StyleLi, A., & Chen, Z. (2018). Representative Scanpath Identification for Group Viewing Pattern Analysis. Journal of Eye Movement Research, 11(6), 1-17. https://doi.org/10.16910/jemr.11.6.5



