1. Introduction
Commodity and energy markets have been the engine of economic development and have allowed many countries to increase their success. In this way, economic, commercial, and socio-cultural interdependence between various nations has been fostered. In fact, oil and gas are key determinants of energy security, energy geopolitics, and the international political economy. These dynamics have undergone changes when socioeconomic and climate events and geopolitical tensions have had their effects on the markets, especially energy markets, producing sudden variations in direction. Geopolitical risk can be defined as the probability that events of a political, social, or military nature occurring in one state could potentially jeopardize the stability of a country, region, or even the global economy. Thus, geopolitical risk is a global risk that goes beyond geographical borders and specific economic sectors and that implies the failure of global governance. For these reasons it is inevitable that this risk will have a considerable impact on international financial markets (
Choi, 2024), with a corresponding effect on energy commodity price volatility. This is corroborated by the plethora of studies that have addressed this issue. The correlation between geopolitical risk and the variability of energy commodity prices was fully confirmed following the outbreak of the Russia–Ukraine conflict in 2022; this global energy crisis has disrupted the financial and energy markets (
Manelli et al., 2024).
In recent years, the academic literature on geopolitical risk and its implications for commodity markets has been expanded by a substantial number of contributions examining various aspects of this topic (
Micallef et al., 2023;
Ozdemir et al., 2025). One area of research that has emerged is the examination of the relationship between geopolitical risk and energy commodity prices (
Liang et al., 2020;
Tiwari et al., 2021).
Gong and Xu (
2022) posit that geopolitical risk is the primary factor contributing to instability in the energy market. They assert that geopolitical risk significantly affects the dynamics of energy product supply and demand, leading to heightened volatility in energy prices. Additionally, the authors highlight that at the macroeconomic level, countries with emerging economies have exerted a pronounced influence on energy commodity demand and price volatility. In their research work,
Abdel-Latif and El-Gamal (
2020) relate three variables: financial liquidity, oil prices and geopolitical risk. The authors confirm the existence of a self-sustaining cycle. Specifically, a negative oil price shock leads to an increase in geopolitical risk and a decrease in global financial liquidity. Conversely, a positive shock to geopolitical risk leads to an increase in oil prices.
Abid et al. (
2023) conclude that there is a relationship between geopolitical risk and the prices of five commodities (energy, precious metals, agriculture, industrial metals, and livestock products) when analyzing the data from 2013 to 2023. All commodities demonstrate responsiveness to geopolitical risk shocks, with energy products exhibiting greater sensitivity than the others. Additionally,
Mo et al. (
2024) highlight the heightened susceptibility of the energy sector to geopolitical risk, in comparison to non-energy sectors. In a research work,
Bompard et al. (
2017) developed a survey methodology for evaluating a country’s energy security, encompassing both external supply and the reliability of its internal infrastructure. The application of the analytical model to the Italian context, a country with a low level of energy self-sufficiency, revealed the high sensitivity of the crude oil market to shocks caused by geopolitical risks. This finding underscores the strategic importance of energy diversification for risk reduction. Further studies have addressed the topic either by considering traditional energy markets or by focusing on a single country. In fact, in their analysis of the relationships between geopolitical risk, the traditional energy sector (coal, oil, and gas), and the carbon market,
Jiang et al. (
2024) suggest that geopolitical risk exerts a more significant influence on other markets in the medium to long-term, whereas in the short-term, this impact is more variable. Additionally, a distinctive feature of the carbon market emerges, whereby it appears to exert a greater influence on geopolitical risk than vice versa. A study on the combined impact of Chinese economic policy uncertainty and Chinese geopolitical risk on the global commodities market was conducted by
Hu et al. (
2023). The analysis revealed that from 2006 to 2023, Chinese commodity prices were influenced by shocks in economic policy and geopolitical risk. Notably, the latter also had a significantly positive impact on commodity prices during the global financial crisis. Furthermore, about the Chinese economic context, the study by
Meng and Li (
2024) adopts a contrasting approach, examining the impact of natural resource volatility on geopolitical risk. The authors conclude that geopolitical risk is asymmetrically influenced by natural resource volatility and propose that policymakers should prioritize the adoption of renewable energy sources, invest in the extraction of natural resources and reduce oil imports to mitigate geopolitical risk. Finally, an intriguing contribution to the discourse was suggested by
Jiao et al. (
2023) who concentrated on the indirect mechanisms through which geopolitical risk exerts an influence on oil prices. The transmission modes of geopolitical risk are divided into two categories: micro media (demand, supply, and speculative behavior) and macro media (global economy). The analysis yielded the following results: oil prices are influenced by geopolitical risk through supply and demand dynamics, with the effect being amplified in periods of high geopolitical tensions due to the speculative behavior assumed by investors.
A second area of research concerns the role played by geopolitical risk in the functioning mechanisms of financial markets (
Bouras et al., 2019). From this perspective, it becomes evident that the existence of highly integrated and globalized financial markets gives rise to a considerable risk contagion phenomenon, which serves to exacerbate the instability of international economic and financial systems (
Forbes & Warnock, 2021). Indeed, a substantial body of empirical evidence demonstrates that geopolitical risk exerts a pronounced influence on financial markets, affecting both financial liquidity and investor behavior (
Su et al., 2019).
Zheng et al. (
2023) examine the interrelationship between geopolitical risk and diverse segments of the financial market, encompassing both short-term and long-term perspectives. These include the stock market, bond market, foreign exchange market, and crude oil market. The findings suggest that the oil market is more closely associated with geopolitical risk than other markets. In the same field,
Alqahtani and Klein (
2021) examine the impact of oil prices and geopolitical risks on equities in the Gulf Cooperation Council (GCC) countries. The results of the analysis demonstrate that local geopolitical risk exerts a significant negative influence on the stock markets of the surveyed countries. Furthermore, equity markets exhibit sensitivity to fluctuations in oil prices, except for Qatar, where global geopolitical risk has a detrimental impact.
In the wake of the recent upheavals in Europe (the Russian invasion of Ukraine) and the Middle East (the war between Israel and Palestine, with subsequent spillovers into Lebanon and Syria), and the concomitant rise in global tensions, the literature on geopolitical risk has witnessed a surge in contributions seeking to ascertain the extent and direction of the impact of geopolitical risk induced by wars on energy markets (
Kostaridou et al., 2024). In a similar vein,
Khan et al. (
2024) investigate the impact of geopolitical risk on the performance of global commodities, contextualizing their analysis within the broader temporal framework of the ongoing conflicts, namely the Russia–Ukraine war and the Israeli–Palestinian conflict. The study demonstrates a low interconnection between geopolitical risk and commodity prices in the pre-crisis periods. Additionally, it indicates a heterogeneous reaction of commodities to geopolitical shocks, which are perceived as very positive. This highlights the necessity for diversified investment strategies. Conversely, during crisis periods, there are significant opportunities for investors to diversify their portfolios, as commodities demonstrate considerable resilience to shocks, both positive and negative, that arise from geopolitical tensions. A similar analysis of geopolitical risk during conflicts was conducted by
Wang et al. (
2022), who focused specifically on the impact on systematic commodity risk during the conflict between Russia and Ukraine. The data confirm a notable increase in spillover indices during the conflict and an increase in the volatility of commodity markets. It is also possible to include in this line of research contributions that have analyzed the implications of geopolitical risk in situations that are not overt conflicts, but which are characterized by tension between different states. In particular, the subject of geopolitical risk and the political relations between two states, specifically China and the United States, was addressed by
Mignon and Saadaoui (
2024). The authors examined two indicators, the Political Relationship Index (PRI) and the Geopolitical Risk Index (GPR), with the objective of understanding the relationship between these two factors. The analysis demonstrates that an improvement in political relations between states and an increase in geopolitical risk are both associated with higher oil prices. The authors conclude that political tensions are related to consumer expectations, while geopolitical risk is related to energy market expectations.
Although, the current literature offers a various perspective on energy market analysis, there is still room for improvement. Firstly, many studies consider only the US energy market, focusing primarily on the relationship between energy, commodity, and financial markets separately. In a context dominated by uncertainty generated by numerous geopolitical events of various kinds, in which energy prices have exhibited anomalies and violent fluctuations, the objective of this paper is to provide new evidence of the interaction between various uncertainty indices and the dynamic connection between energy markets of different countries and EUA index within a unified framework. To this end, it uses a time-varying vector autoregression model (TVP-VAR) to explore the dynamic spillover effect of returns between these markets and clearly obtain the strength and direction of information transfer between the energy markets of various countries and the EUA index. Furthermore, the time–frequency dependence between uncertainty indices and the dynamic connectedness of different energy market returns is studied using wavelet coherence analysis, with the aim of examining how various uncertainty indices interact with connectedness in energy markets across different time scales. Here, we hypothesize the following:
H1: The oil markets are the main transmitters of information to other markets.
H2: The geopolitical risk index (GPR) and the VIX index influence the energy markets’ connectedness.
H3: Geopolitical and significant events can change the previous situation and increase the dependences between energy markets and uncertainty indices.
Our research stems from the growing importance of global geopolitical risks and their effects on economic and financial markets. It is well known how geopolitical tensions predict global oil price volatility, and the effects that they cause on energy markets (
Leone et al., 2025). Considering the importance of energy markets our study attempts, for the first time, to analyze how are the various uncertainty indices interrelated with the dynamic connectedness among different oil and gas markets? How does mutual interdependence manifest itself? Therefore, this article will try to answer these questions.
The reminder of this paper is organized as follows.
Section 2 presents the methodology;
Section 3 outlines the data used and shows our empirical findings; and
Section 4 offers this study’s conclusions and implications.
3. Results
This study aims to analyze the dynamic connection of returns between energy markets. It is based on a dataset consisting of returns related to oil and natural gas futures prices, to which the S&P Carbon Credit EUA index (Eua) is added and used as a benchmark of the performance of carbon emission markets. Indeed, although it is designed to measure the performance of the European Union’s carbon emission trading system, this EU ETS is the world’s first large experiment for carbon pricing (
Ellerman & Buchner, 2007).The indices related to this last market have become increasingly important following the adoption of measures aimed at limiting CO
2 emissions and, hence, the use of fossil energy sources. Consequently, we collect the daily futures prices quotes of the main oil and natural gas market indices such as WTI, Brent, MCX Crude oil index (MCX Oil), Henry Hub natural gas (NG), ICE Dutch TTF natural gas (TTF), and MCX natural gas index (MCX Gas). As can be seen, the analyzed indices refer to different geopolitical areas. In particular the three main energy markets are considered: the US, European, and Indian. In fact, these are among the main countries that consume energy raw materials and therefore represent a significant sample of the relevant market. To these, two indices that measure uncertainty are added, such as the geopolitical risk index (GPR) constructed by
Caldara and Iacoviello (
2022) and the volatility index (VIX). The GPR allows the quantification of the economic effects caused by the manifestation of geopolitical risks, while the VIX measures the sentiment of American stock market and therefore is usually used as a measure of volatility expectations. The data cover the period from 3 November 2014, to 31 October 2024. It is a fairly long period of time during which numerous events of different type and magnitude occurred. To analyze the connection between energy markets and S&P Eua index, we utilize the first differentiated series of logarithms:
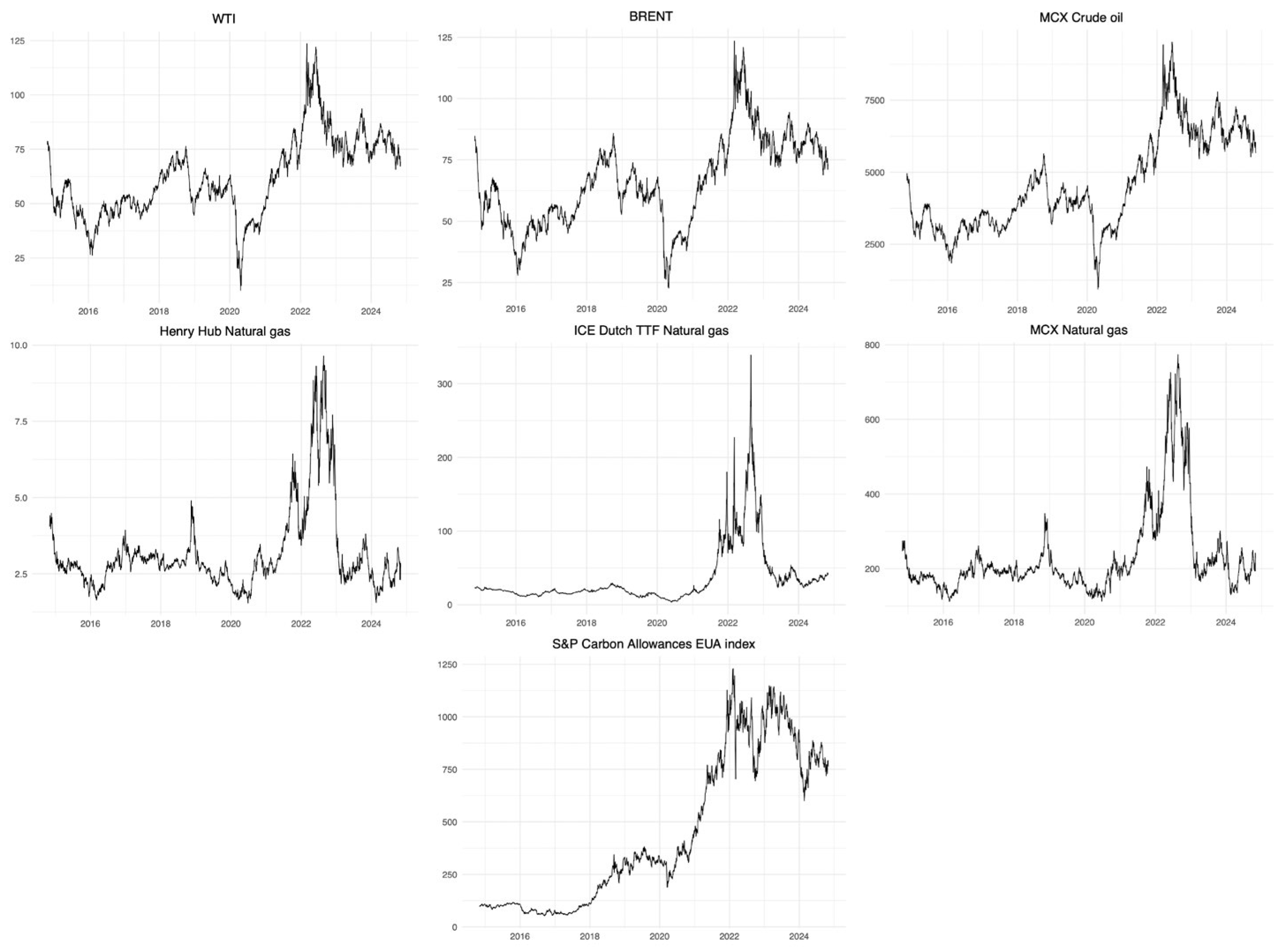
Figure 1 illustrates the trend of the historical series. Notably, it is observed how the oil and gas markets follow similar trends. Regarding the former, after the peak detected during the pandemic, a strong subsequent co-movement is noted, and in particular during the war between Russia and Ukraine. Regard the gas market, plot show a certain synergy between the NG and MCX Gas. Instead TTF shows heterogeneous movements that diverge significantly until the 2022 energy crisis, when they anticipate and exacerbate the price peaks that occur during the year. A separate discussion deserves the S&P Carbon Credit EUA index which shows continuous growth starting from 2018 and exacerbated before the energy crisis of 2022.
In turn, as can be seen in
Table 1 which presents the statistical description of the returns, all means and medians have values around 0. Furthermore, the standard deviation is higher for gas markets than for the others, with the TTF showing the highest value. All oil markets and EUA index show a negative skewness, they are left-skewed distributions. Instead, all gas markets are right-skewed distributions. Moreover, all series are significantly leptokurtic; the kurtosis are greater than 3. The Jarque–Bera test significantly rejects the hypothesis of normality as all variables exhibit a clear leptokurtosis and fat tails. The results of the unit-root test, ADF test, and Phillips–Perron stationarity test confirm that all returns are stationary at the 1% significance level. In conclusion, as shown in
Table 2, the unconditional correlations between oil markets are highest (with values above 0.7), while the correlation between gas markets and between gas, oil, and Eua markets is moderately high (with values around 0.2).
We start our discussion by analyzing the total dynamic connectedness (TCI) and net return (NET) between energy commodity markets and the Eua index.
Table 3 shows that the main shock transmitter is the WTI followed by Brent, MCX Oil, and NG, while the net shock recipients are the Eua index followed by TTF and MCX Gas. This is confirmed by the pairwise net directional transmission dominance value which for these last three markets shows negative values equal to −7.57, −6.12, and −0.81, respectively. Furthermore, the TCI explains that on average the co-movement of energy markets, and therefore the risk equality of the entire network, is 56.68%, which in turn means that on average 48.58% (= 56.68% · 67) of the variance of the forecast error of a market return can be explained by the influence of the returns of all other markets. The results suggest that the Eua index is the largest recipient of the system, i.e., it is dominated by other energy markets, as is logical given the type of linkage that it has with traditional energy markets. This indicates that price changes in the Eua index have a limited role and lower propensity to transmit shocks to the other markets in the system. Instead, oil markets emerge as the main sources of shocks, (
Chen et al., 2024). Then, dynamic total connectedness captures the temporal variation of the TCI for the entire period of study.
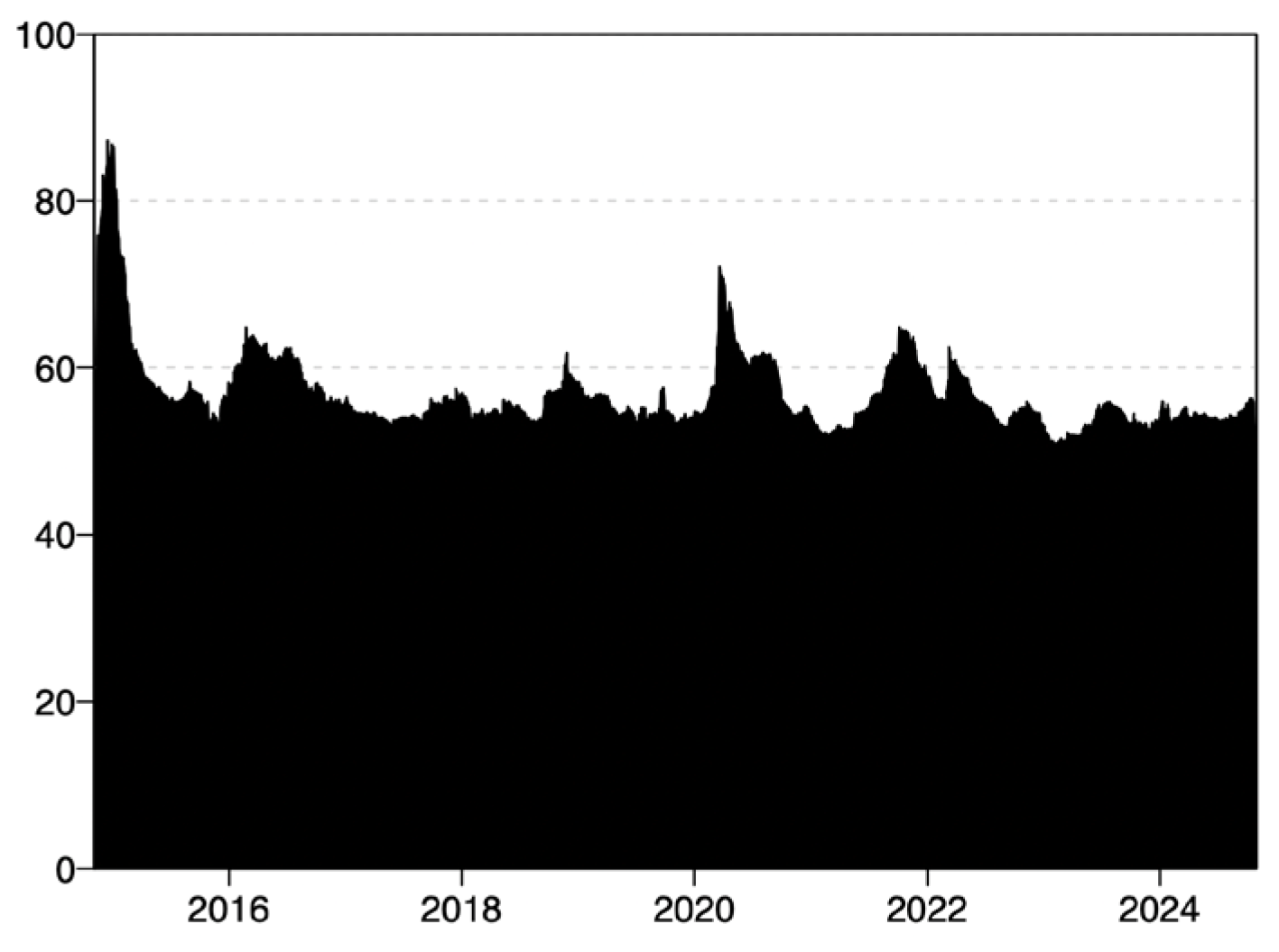
At this point, we focus our attention on the analysis of the total dynamic connectedness (TCI), which provides the interconnectedness of the network over time.
Figure 2 shows how the total dynamic return connectedness is variable over time, but always above 40%, indicating, thus, a solid interconnectedness between energy markets and Eua index. Significantly, the total dynamic return connectedness reaches values greater than 60% in 2014—at the beginning of the analysis period—in 2020, and in 2022. This adapts with periods of tension in the commodity markets, pandemic and Russia–Ukraine war. These very strong connections denote how in times of significant crisis and uncertainty the interconnectedness between energy markets is significantly consolidated. This may be because in the presence of unlooked-for and uncertain events investors are more cautions in diversifying their portfolios and less willing to take risk, this causes a greater interconnectedness between markets (
Adekoya et al., 2021).
Figure 3 represents the dynamic connectedness of the net directional returns among energy markets. A positive value indicates that the information spillover is positive and, thus the related market behaves as a net transmitter. On the other hand, a negative value signals a negative information spillover which indicates that the market is a net receiver. The oil markets, markedly WTI and Brent, are the main transmitters of information to other markets. This can be explained by the fact that crude oil is the one of world’s most important commodities, and its price impacts the overall economy. Furthermore, trading on the oil market involves numerous participants with different motivations. In particular, investors use energy markets, mainly Wti and Brent, the most liquid, as alternatives to stock and bond investments to diversify their portfolios and hedge against inflation risks. While the gas markets, to a greater extent TTF, and Eua index receive information from other markets for the entire period analyzed. The MCX Oil market, the NG and MCX Gas alternate positive net spillover values with negative, indicating, in this way, how the role played by these markets is not always that of transmitter or receiver. Analyzing in more detail the Indian oil markets, MCX Oil, this one with a prevalence of positive values tends to follow the footsteps of the US and European ones, functioning mainly as a transmitter.
In summary, in terms of yield connectedness, the WTI and Brent crude oil markets act as a net transmitter of spillover, with very high percentage in late 2014 and after 2020. Instead, TTF gas market and Eua credit index function as a net receiver. Furthermore, the WTI market has the toughest dominant role in the connectedness among oil markets, indicating that US crude oil market has the utmost influence on the other markets. While TTF gas market emerges as the most significant information receiver, suggesting its limited influence on other markets. Additionally, as partly already highlighted, unexpected and significant events, such as pandemic, can amplify the performance connectedness among energy commodity markets.
Following the analysis of the dynamic connectedness of the return among energy markets, we analyze the way in which the uncertainty indices, the geopolitical risk index (GPR) and the VIX index, influence the dynamic connectedness systems. In this regard, the analysis of the wavelet coherence is used in order to verify the presence of dependence among the dynamic total connectedness and the already mentioned uncertainty indices. The dependence is measured in terms of time and frequency.
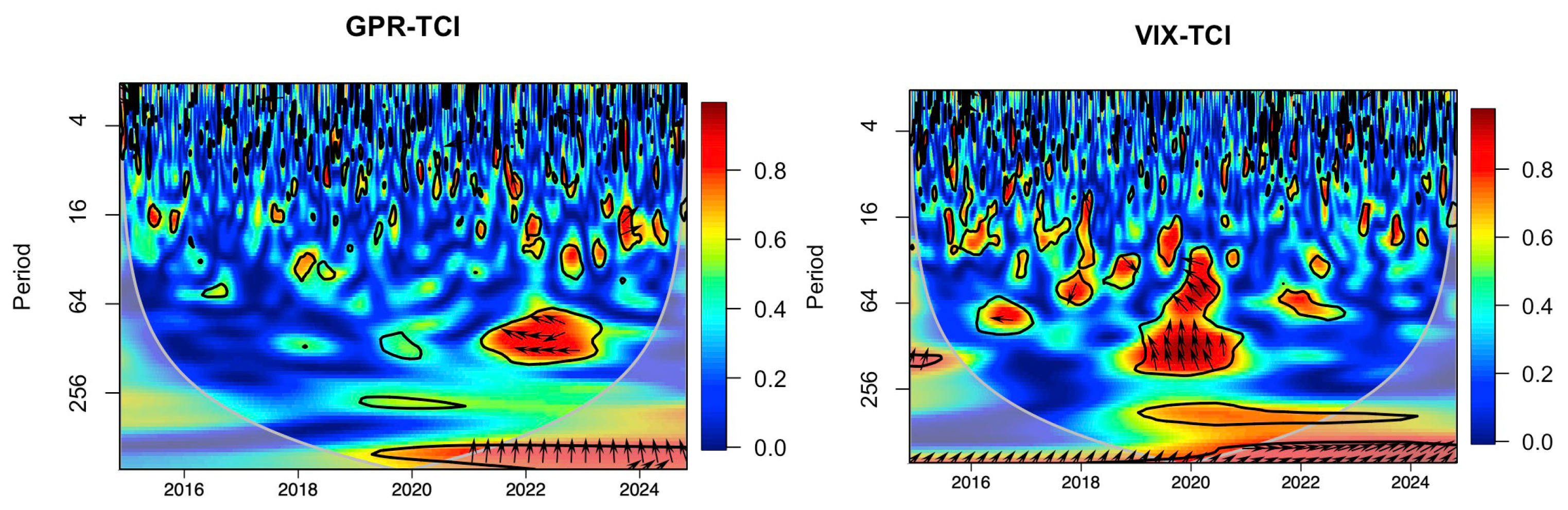
Figure 4 exhibit the results of the wavelet coherence among GPR and VIX and the dynamic total connectedness. The horizontal axis indicates the time scale, and the vertical axis the different frequency bands. A strong co-movement among the dynamic total connectedness and the uncertainty indices is represented by the red regions.
First of all, it emerges how there is a lower dependence among dynamic total connectedness and GPR. In fact, the relationship between GPR-TCI shows the presence of few red regions from 2022 onwards, and these are concentrated in the medium-long-term, with a frequency of 64 and over 256 days. Of greater interest appears the relationship VIX-TCI, in which the red region with strong coherence is larger, but always concentrated mainly in the medium—16 to 256 days—and in the long-term—over 256 days.
A further consideration concerns the fact that significant events that radically change the previous situation, such as pandemic and Russia–Ukraine war, determine an increase in intensity of the dependence between TCI and uncertainty indices. In fact, the dependence among TCI and VIX is greater in the medium-term during pandemic and in the long-term during Russia–Ukraine conflict. Instead, there is a long-term dependence among TCI and GPR only after 2022. These results may be due to the fact that during the two periods uncertainty and geopolitical risk increased. In fact, during pandemic with the lockdown of economic activities, energy prices recorded a drastic decrease. Instead, during the war the tension recorded on these markets, with particular emphasis on the gas markets, produced sudden increases in its prices. Furthermore, the two events, albeit with different modalities, affected global supply chains and particularly in energy markets (
Li et al., 2023), with interruptions in supply or the presence of higher costs.
In summary, the GPR-TCI relationship shows how in the medium-term the two variables are negatively correlated. A different scenario emerges from the analysis of the relationship between dynamic total connectedness and VIX, which shows a positive dependence in the medium and long-term with the VIX which anticipates the dynamic total connectedness. This indicates that the return spillovers within the energy markets tend to increase when the VIX increases in the medium-long-term.
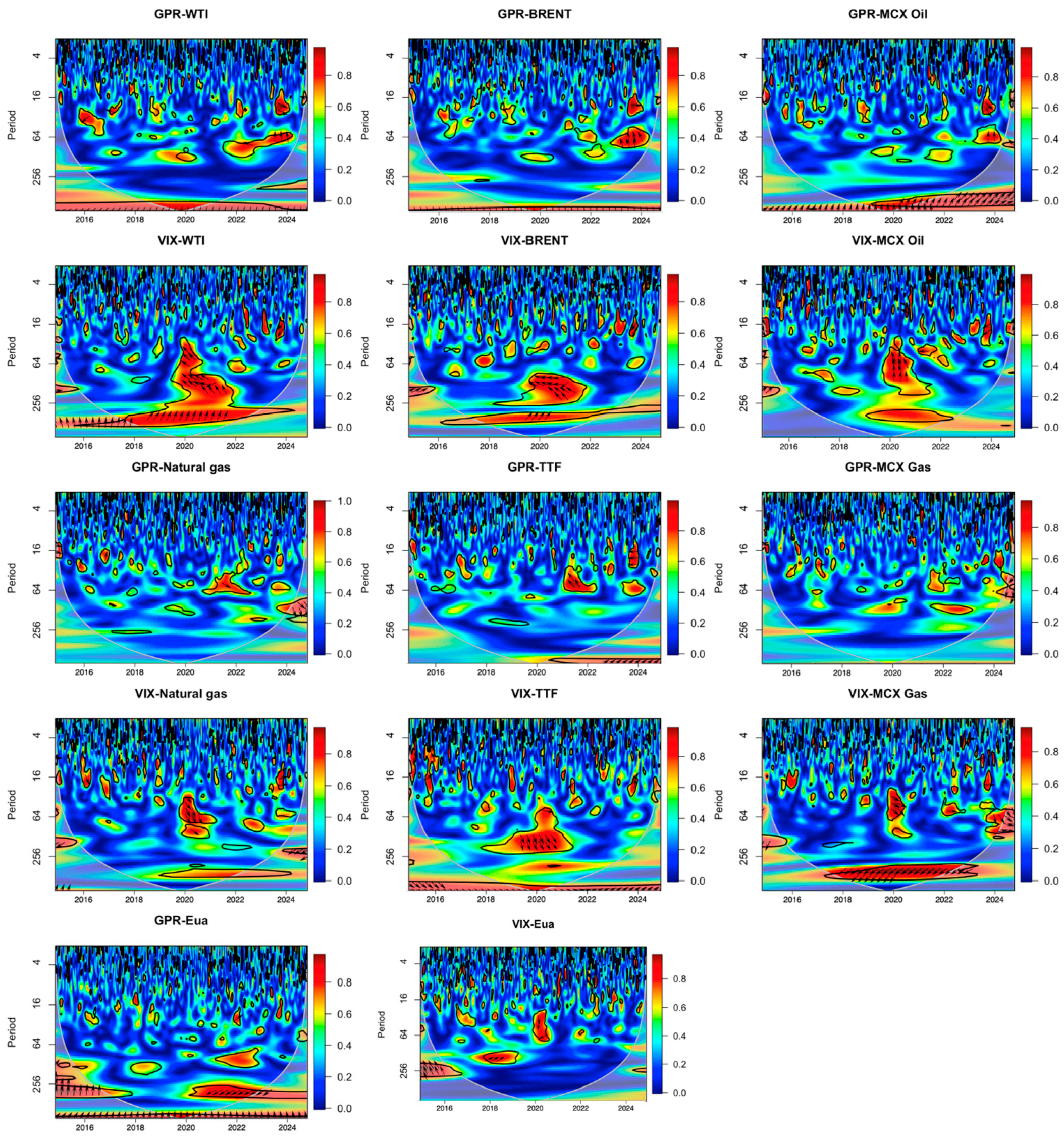
So far, the analysis carried out indicates the way in which the uncertainty indices interact with the dynamic total return connectedness of the energy markets. At this point, to have a more in-depth understanding of the individual markets, we analyze the dependence among the uncertainty indices and the dynamic connectedness of the net total return that each market has with them.
Figure 5 indicates the changing characteristics of this relationship. A first distinction concerns the dissimilar behaviors of the GPR and VIX indices. In fact, if we consider the three oil markets analyzed, it emerges that the positive relationship between these and the GPR is limited to the long-term and to a few areas of the medium-term but after 2022. In the opposite order, the relationship between the three oil markets and the VIX index is greater than the GPR. In the VIX-WTI graph, large red areas can be seen throughout the long-term with extensive spills over in the medium-term in the aftermath of the pandemic. Furthermore, if in the long-term the VIX be ahead the WTI, in the medium-term the arrows pointing to the left indicate a negative correlation. Similar conclusions, although the red areas are smaller, can be drawn for the VIX-Brent relationship. Also, in this case we note red areas in the long-term and a large negative correlation in the medium-term between pandemic and the war years. Analyzing the VIX-MCX Oil relationship we note a presence of small red areas in the short-term and a marked correlation in the medium-long-term but only during pandemic with the VIX ahead of the MCX Oil. Moving on to the analysis of the GPR and the gas markets, we note how for all three markets lone occasionally red areas appear in the short-term. Moreover, these are concentrated after 2020. If we analyze the relationship with the VIX the conclusions change. In the VIX-NG we note a relationship in the medium-term during the pandemic and a negative correlation at the beginning of the period and at the end. More marked relationships with occasional red areas in the short-term are found in the VIX-TTF graphs. In this, a large red area emerges in the medium-term between 2019 and 2021 with the TTF ahead of the VIX. In the long-term, it is noted that until 2018 the TTF is ahead of the VIX, it goes back during the pandemic, and then moves forward again during the war. Looking at the connectedness VIX-MCX Gas we note an intense connection for almost the entire long-term that also spills over into the medium-term during pandemic with the MCX Gas ahead the VIX. Furthermore, there is a large red area in the medium-term between 2023 and 2024. Finally in the analysis of GPR-Eua we note the presence of connections in the long-term with the GPR ahead. In the medium-term up to 2017 it sees the GPR ahead, and the EUA ahead after 2020. The VIX-Eua graph indicates more occasional red areas. The connectedness it is not consistent in the various time scales since the arrows point in different directions in the diagram, with the presence of positive correlations alternating with negative ones.
From the considerations carried out it can be concluded that the strong coherence among uncertainty indices and return connectedness for each markets occurs mostly in turbulent periods, such as pandemic and Russia–Ukraine war. These findings are consistent with
Tran and Vo (
2023), who documented that following increases in the VIX index, investors, having pessimistic expectations and overreacting, tend to increase selling. This leads to lower returns and increased market volatility. Unlike the VIX, GPR involve conflict and more complex relationships modifying various aspects of global economic interactions and producing long-term consequences such as disruption in supplies.
4. Conclusions
In this study, we examined the energy markets of different types of crude oil and natural gas. To have a better understanding of the energy market, in addition to those traditional markets we added the carbon market. This market is important not only for the growing attention paid to the environmental policies aimed at reducing carbon emissions but above all for the close relationship and integration between CO
2 emissions and the use of traditional energy sources such as crude oil and natural gas. The aim of this study was to examine over and above the integration and the potential contagion risk of energy markets. The variable investigated are: WTI, Brent, MCX crude oil, Henry Hub Natural Gas, Ice Dutch TTF gas, MCX gas and S&P Carbon Allowances EUA index. Finally, we seek to determine whether net connectedness among energy markets is driven by political uncertainty and risk. It has been widely demonstrated that external uncertainty influences the fluctuations of financial and commodity markets (
Bahloul et al., 2018;
Gozgor et al., 2016). On the other hand,
Papathanasiou and Koutsokostas (
2024) observe how, following the pandemic, a strong cohesion has occurred between the VIX and the total dynamic connectedness of various financial and commodity markets. This has caused a significant attraction of capital flows on the VIX, which has been influenced by other markets, including crude oil. In this study, we provide new evidence of how the geopolitical risk (GPR) and uncertainty index (VIX) interact with dynamic connectedness between energy commodity markets. To this end, by applying the dynamic connectedness approach based on a TVP-VAR model in the spirit of
Antonakakis et al. (
2020) we compute the dynamic return connectedness among energy markets. After that, we employ the wavelet coherence methodology to investigate and measure the existence and dependent relationships between uncertainty indices (GPR and VIX) and the dynamic connectedness within energy markets. Compared to previous studies, our results provide new and valuable insights.
First, the time domain analysis indicates a strong interaction within energy markets with a total spillover index exceeding 50% throughout the period and reaching significantly high levels of around 60–80% on some occasions.
Second, the main crude oil markets, (WTI and Brent), are net transmitters of spillover while the TTF gas and Eua markets function as net receivers. The other markets, MCX Oil, NG and MCX Gas, alternate periods in which they are net receivers and periods in which they are net transmitters of spillover. The WTI oil market has the most powerful dominant role in connectedness among energy markets, signaling its strong effect on the other markets, while the Eua index stands out as the most significant receiver of information, suggesting its limited influence. Furthermore, the results suggest that dynamic connectedness is highly dependent on exogenous shocks and is very sensitive to global events, like pandemic and Russia–Ukraine war. Then, we analyzed the intensity of co-movement among the examined variables and different uncertainty indices (GPR and VIX) to identify actual interaction. In this context, the most influential uncertainty index on connectedness is VIX that shows a positive dependence on dynamic total connectedness in the medium and in the long-term, while GPR mainly has a negative relationship in the long-term.
Third, the connectedness among VIX and each market is mainly seen in the mid-long-term with notable spillovers into the mid-term in the aftermath of the pandemic. While, for the GPR the connectedness is more limited and concerns only the long-term. The only exception is S&P Carbon Allowances Eua index where it is more marked and concerns also the mid-term. Furthermore, over time, the uncertainty indices have changed roles and differing from one market to another. In fact, it can be noted how, within the same market, the correlation among connectedness and uncertainty index is both positive and negative at different time scales (the arrows point in different directions). Isolated events could help explain these changes over time. In particular, amplified uncertainty about the potential effects of pandemic and the Russia–Ukraine war on economic activity potentially helps explain the prevalence of long-term connectedness.
Finally, the results of our analysis support policy makers and investors. Given that the energy market connectedness shows differentiated interactions across both the different uncertainty indices (GPR and VIX) and different time scales, it is useful for policy makers to be able to distinguish the sources from which shocks originate and the different time horizons. The transmission of spillovers between different oil and gas markets and EUA index poses risk to energy stability. Furthermore, their interconnections respond differently to international events that generate political uncertainty and have the potential to disrupt markets, accentuating or limiting the push toward clean energy. This requires energy market regulators and climate policymakers to adopt specific responses to various type and origin of uncertainty, balancing fiscal, monetary and trade policies. This is so that responses strategies stabilize the market and avoid increasing risks between different markets. Furthermore, since information spillovers interact across different markets, investors should incorporate the transmission mechanism and the dependency relationship between uncertainty and energy market connectedness. This is to understand how geopolitical risk impacts prices in order to be able to forecast prices based on changes in geopolitical risk and adapt their asset allocation and hedging strategies accordingly in light of specific geopolitical events.