A Quantum Leap in Asset Pricing: Explaining Anomalous Returns
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Cross-Sectional Regression Tests
3.2. Asset Pricing Models
3.2.1. Prominent Asset Pricing Models
- CAPM based on the market factor computed using the University of Chicago’s Center for Research in Security Prices (CRSP) value-weighted index minus the Treasury bill rate (M);
- Fama and French (1992, 1993)’s three-factor model (FF3) that augments the market factor with a size factor (small minus large firms’ stock returns, or SMB) and a value factor (high book-to-market equity minus low book-to-market equity firms’ stock returns, or HML);
- Fama and French (2015)’s five-factor model (FF5) that augments the three-factor model with a profit factor (robust operating profitability minus weak operating profitability returns, RMW) and capital investment factor (conservative investment minus aggressive investment returns, or CMA);
- Fama and French (2018)’s six-factor model (FF6) that augments the five-factor model with a momentum factor;
3.2.2. Overview of ZCAPM
4. Empirical Evidence
4.1. Cross-Sectional Regression Results
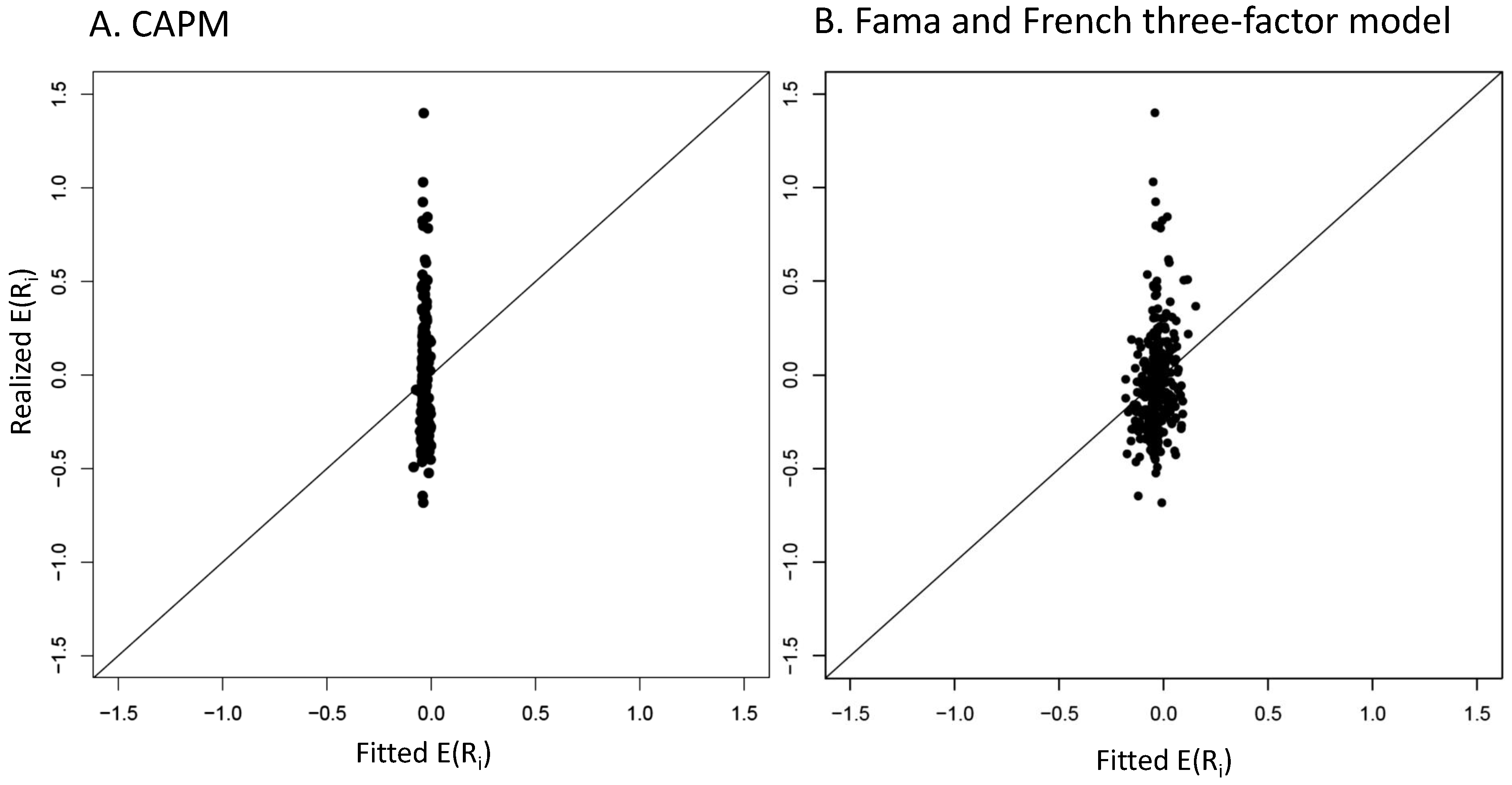
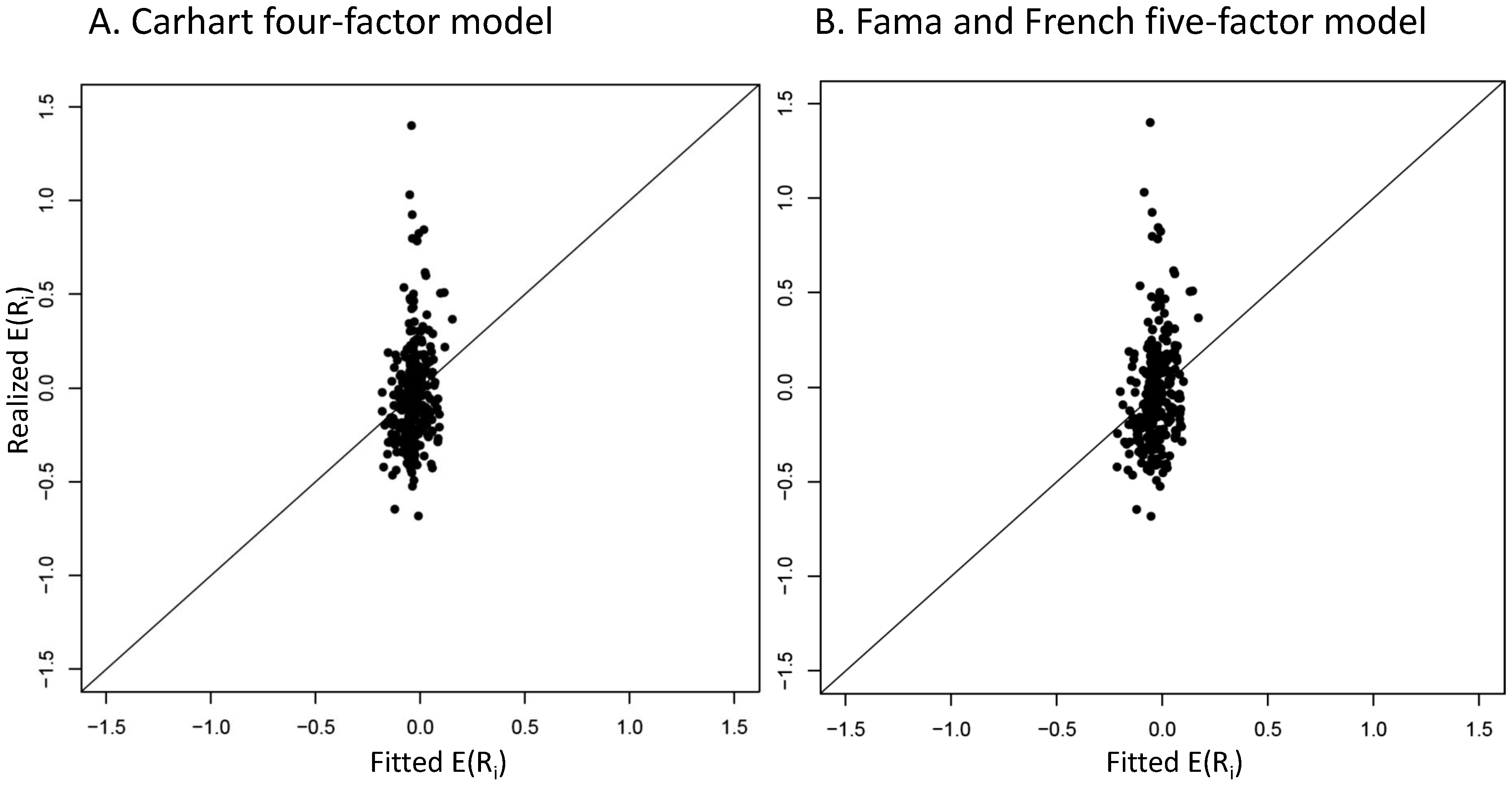
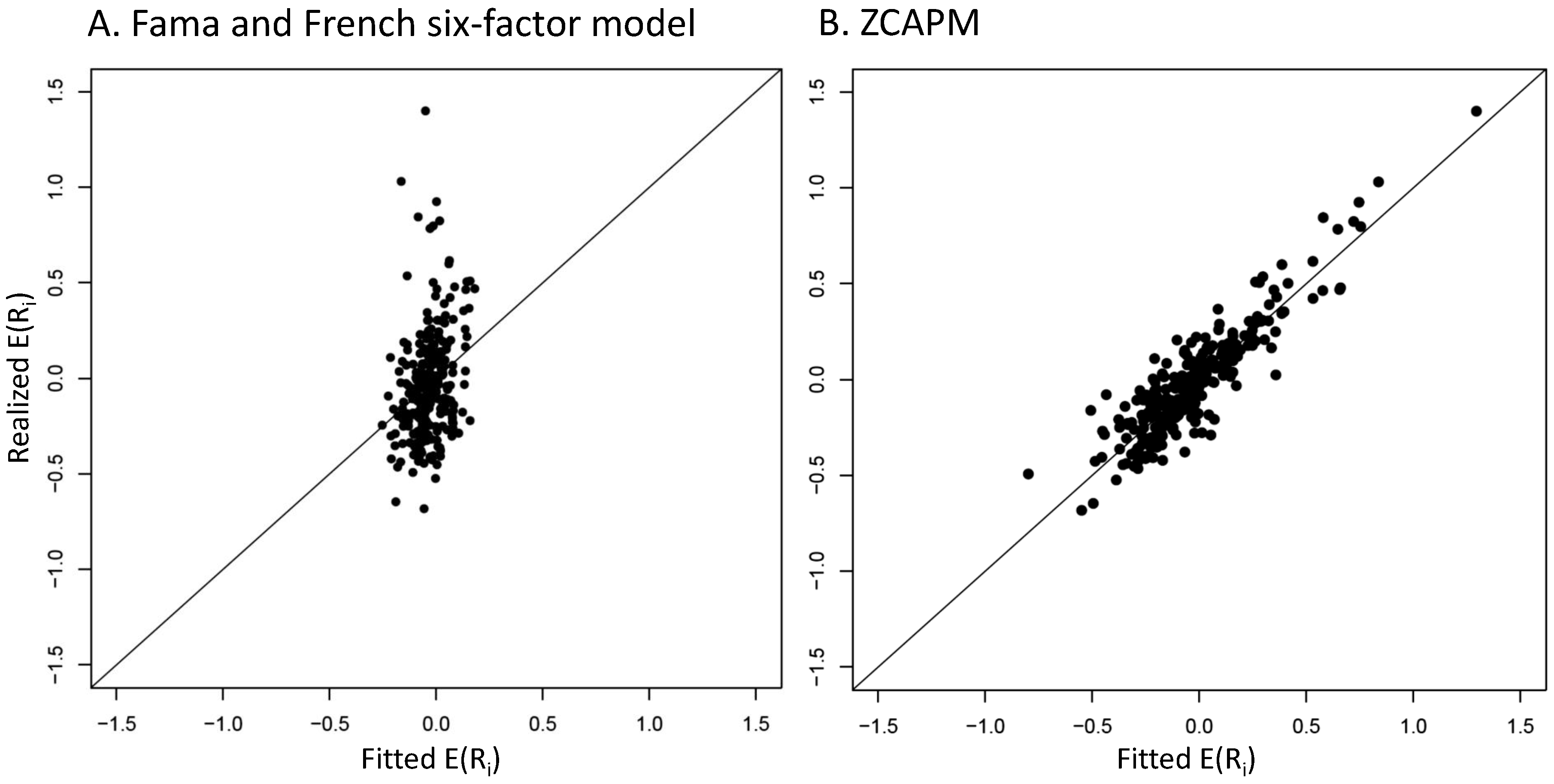
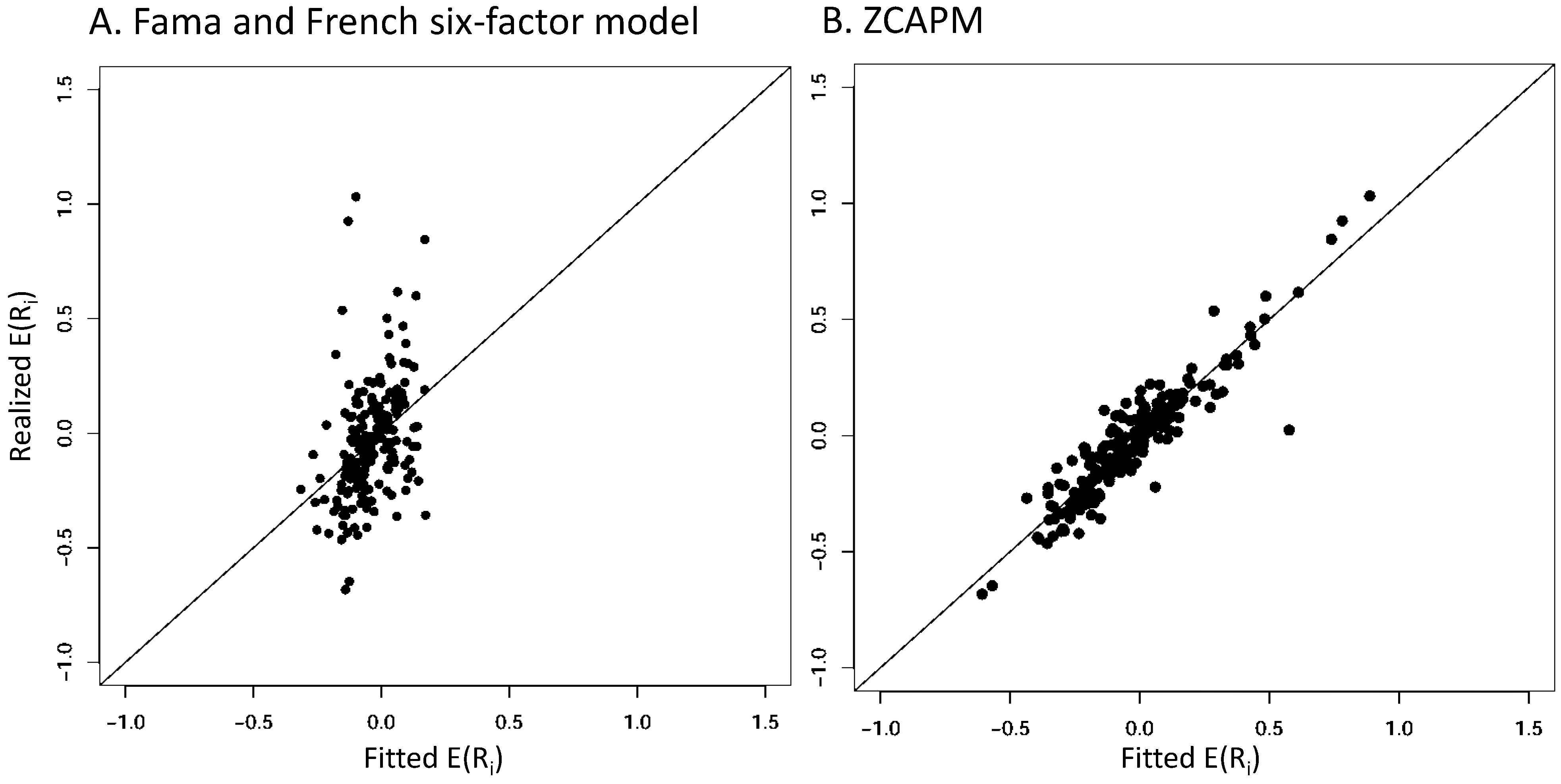
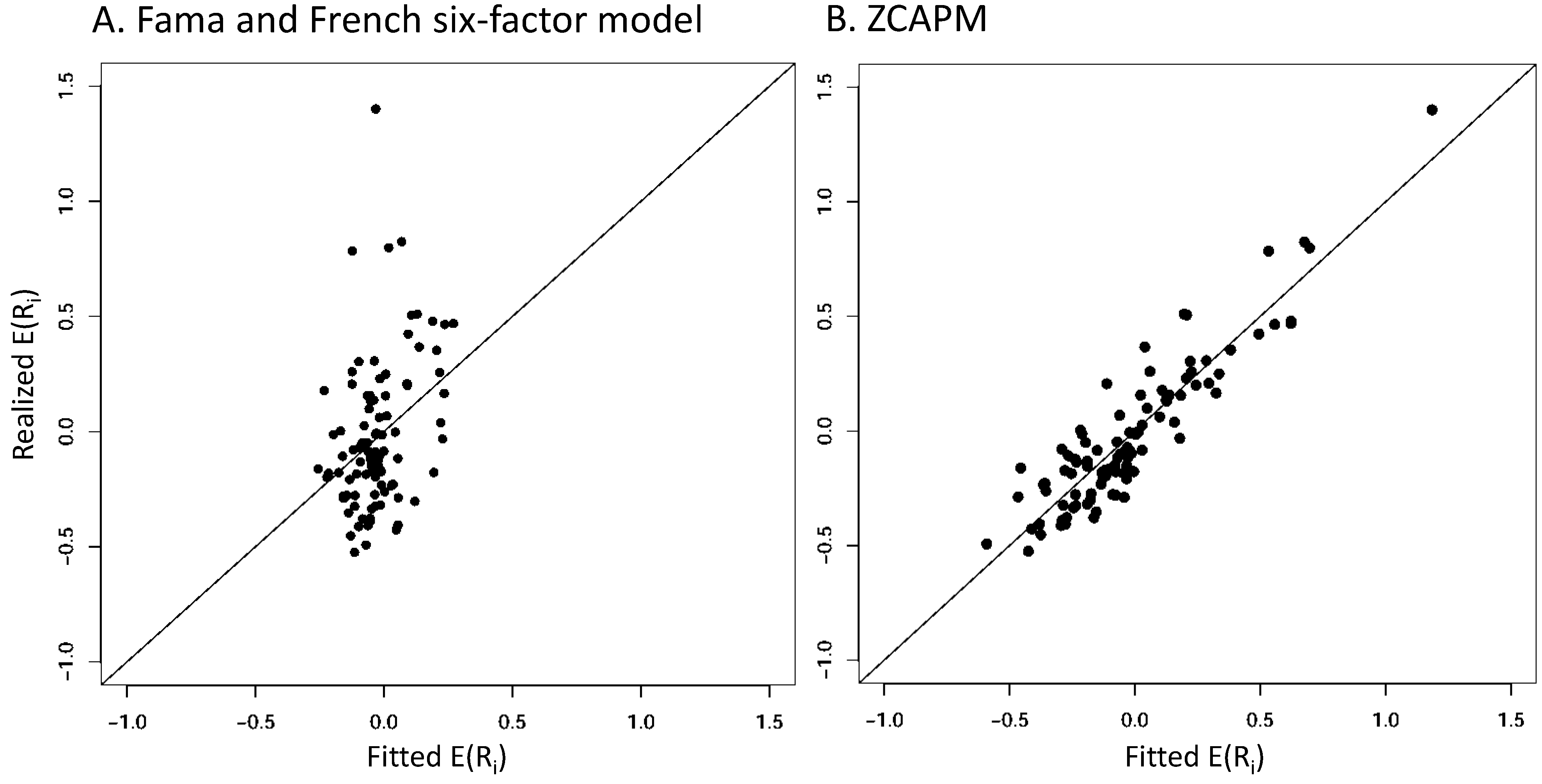
4.2. Graphical Mispricing Error Results
4.3. Robustness Tests
4.4. What Explains ZCAPM Outperformance?
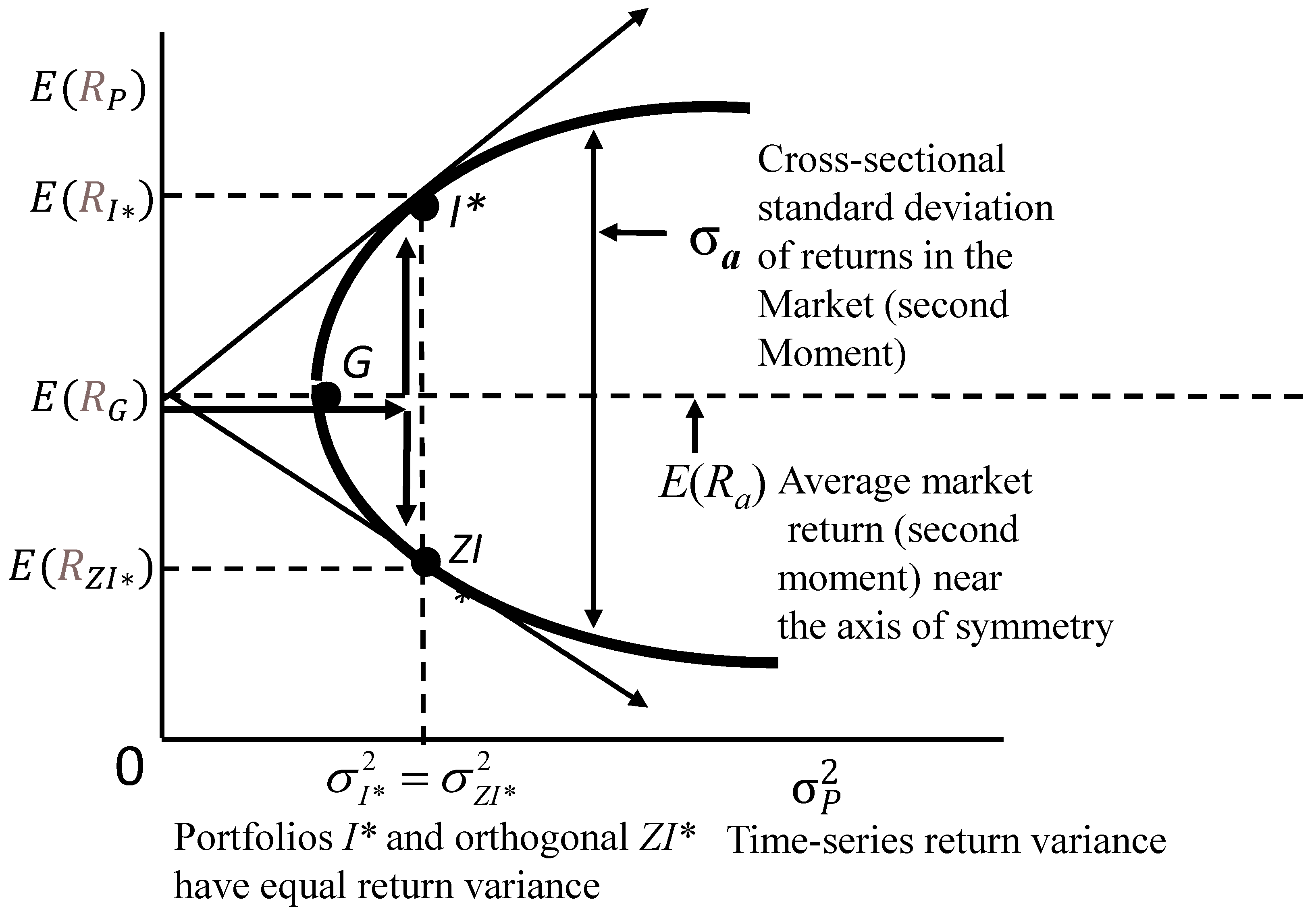
KLH conjectured that market return dispersion corresponds to Black’s second factor. Figure 1 illustrates his second factor as the difference between the returns of an efficient portfolio and inefficient, zero-beta portfolio (with equal return variance), or market return dispersion. It is not necessary to know the expected returns in these two portfolios as their difference corresponds to total market return dispersion. An important policy implication of the ZCAPM relevant to investors is that zeta risk related to market return dispersion is a salient second risk measure (in addition to beta risk associated with the market factor) when evaluating the return performance of stock portfolios.“When Fama and French say that the line relating expected return and beta is flat, they are just saying that the expected excess return on the second factor is large. If we believe it’s as large as they say, we won’t fool around with their third and fourth factors, for which they give no theory.18 We’ll go for the gold in the second factor!”(p. 170)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| N | Abbreviation | Description | Characteristic |
|---|---|---|---|
| 1 | AbnormalAccruals ret | Abnormal accruals | Firm |
| 2 | Accruals ret | Accruals | Firm |
| 3 | AdExp ret | Advertisement expense | Firm |
| 4 | AM ret | Total assets to market | Firm |
| 5 | AnnouncementReturn ret | Earnings announcement return | Market |
| 6 | AssetGrowth ret | Asset growth | Firm |
| 7 | Beta ret | CAPM beta | Market |
| 8 | BetaFP ret | Frazzini-Pedersen beta | Market |
| 9 | BetaTailRisk ret | Tail risk beta | Market |
| 10 | BidAskSpread ret | Bid-ask spread | Market |
| 11 | BM ret | Book to market using most recent ME | Firm |
| 12 | BMdec ret | Book to market using December ME | Firm |
| 13 | BookLeverage ret | Book leverage (annual) | Firm |
| 14 | BPEBM ret | Leverage component of BM | Firm |
| 15 | BrandInvest ret | Brand capital investment | Firm |
| 16 | Cash ret | Cash to assets | Firm |
| 17 | CashProd ret | Cash productivity | Firm |
| 18 | CBOperProf ret | Cash-based operating profitability | Firm |
| 19 | CF ret | Cash flow to market | Firm |
| 20 | Cfp ret | Operating cash flows to price | Firm |
| 21 | ChAssetTurnover ret | Change in asset turnover | Firm |
| 22 | ChEQ ret | Growth in book equity | Firm |
| 23 | ChInv ret | Inventory growth | Firm |
| 24 | ChInvIA ret | Change in capital investment (industry adjusted) | Firm |
| 25 | ChNNCOA ret | Change in net noncurrent operating assets | Firm |
| 26 | ChNWC ret | Change in net working capital | Firm |
| 27 | ChTax ret | Change in taxes | Firm |
| 28 | CompEquIss ret | Composite equity issuance | Firm |
| 29 | CompositeDebtIssuance ret | Composite debt issuance | Firm |
| 30 | Coskewness ret | Coskewness | Market |
| 31 | DelCOA ret | Change in current operating assets | Firm |
| 32 | DelCOL ret | Change in current operating liabilities | Firm |
| 33 | DelEqu ret | Change in equity to assets | Firm |
| 34 | DelFINL ret | Change in financial liabilities | Firm |
| 35 | DelLTI ret | Change in long-term investment | Firm |
| 36 | DelNetFin ret | Change in net financial assets | Firm |
| 37 | DNoa ret | Change in net operating assets | Firm |
| 38 | DolVol ret | Past trading volume | Market |
| 39 | EarningsConsistency ret | Earnings consistency | Market |
| 40 | EarningsSurprise ret | Earnings surprise | Market |
| 41 | EarnSupBig ret | Earnings surprise of big firms | Market |
| 42 | EBM ret | Enterprise component of BM | Firm |
| 43 | EntMult ret | Enterprise multiple | Firm |
| 44 | EP ret | Earnings-to-Price ratio | Firm |
| 45 | EquityDuration ret | Equity duration | Firm |
| 46 | FirmAge ret | Firm age based on CRSP | Firm |
| 47 | Frontier ret | Efficient frontier index | Market |
| 48 | GP ret | Gross profits/total assets | Firm |
| 49 | GrAdExp ret | Growth in advertising expenses | Firm |
| 50 | Grcapx ret | Change in capex (two years) | Firm |
| 51 | Grcapx3y ret | Change in capex (three years) | Firm |
| 52 | GrLTNOA ret | Growth in long term operating assets | Firm |
| 53 | GrSaleToGrInv ret | Sales growth over inventory growth | Firm |
| 54 | GrSaleToGrOverhead ret | Sales growth over overhead growth | Firm |
| 55 | Herf ret | Industry concentration (sales) | Firm |
| 56 | HerfAsset ret | Industry concentration (assets) | Firm |
| 57 | HerfBE ret | Industry concentration (equity) | Firm |
| 58 | High52 ret | 52 week high | Market |
| 59 | Hire ret | Employment growth | Firm |
| 60 | IdioRisk ret | Idiosyncratic risk | Market |
| 61 | IdioVol3F ret | Idiosyncratic risk (3 factor) | Market |
| 62 | IdioVolAHT ret | Idiosyncratic risk (AHT) | Market |
| 63 | Illiquidity ret | Amihud’s illiquidity | Market |
| 64 | IndMom ret | Industry momentum | Market |
| 65 | IndRetBig ret | Industry return of big firms | Market |
| 66 | IntanBM ret | Intangible return using BM | Market |
| 67 | IntanCFP ret | Intangible return using CFtoP | Market |
| 68 | IntanEP ret | Intangible return using EP | Market |
| 69 | IntanSP ret | Intangible return using Sale2P | Market |
| 70 | IntMom ret | Intermediate momentum | Market |
| 71 | Investment ret | Investment to revenue | Firm |
| 72 | InvestPPEInv ret | Change in PPE and inventory/assets | Firm |
| 73 | InvGrowth ret | Inventory growth | Firm |
| 74 | Leverage ret | Market leverage | Firm |
| 75 | LRreversal ret | Long-run reversal | Market |
| 76 | MaxRet ret | Maximum return over month | Market |
| 77 | MeanRankRevGrowth ret | Revenue growth rank | Firm |
| 78 | Mom6m ret | Momentum (6 month) | Market |
| 79 | Mom12m ret | Momentum (12 month) | Market |
| 80 | Mom12mOffSeason ret | Momentum without the seasonal part | Market |
| 81 | MomOffSeason ret | Off season long-term reversal | Market |
| 82 | MomOffSeason06YrPlus ret | Off season reversal years 6 to 10 | Market |
| 83 | MomOffSeason11YrPlus ret | Off season reversal years 11 to 15 | Market |
| 84 | MomOffSeason16YrPlus ret | Off season reversal years 16 to 20 | Market |
| 85 | MomSeason ret | Return seasonality years 2 to 5 | Market |
| 86 | MomSeason06YrPlus ret | Return seasonality years 6 to 10 | Market |
| 87 | MomSeason11YrPlus ret | Return seasonality years 11 to 15 | Market |
| 88 | MomSeason16YrPlus ret | Return seasonality years 16 to 20 | Market |
| 89 | MomSeasonShort ret | Return seasonality last year | Market |
| 90 | MRreversal ret | Medium-run reversal | Market |
| 91 | NetDebtFinance ret | Net debt financing | Firm |
| 92 | NetDebtPrice ret | Net debt to price | Firm |
| 93 | NetEquityFinance ret | Net equity financing | Firm |
| 94 | NetPayoutYield ret | Net payout yield | Firm |
| 95 | NOA ret | Net operating asset | Firm |
| 96 | NumEarnIncrease ret | Earnings streak length | Firm |
| 97 | OperProf ret | Operating profits/book equity | Firm |
| 98 | OperProfRD ret | Operating profitability R&D adjusted | Firm |
| 99 | OPLeverage ret | Operating leverage | Firm |
| 100 | OrderBacklog ret | Order backlog | Firm |
| 101 | OrderBacklogChg ret | Change in order backlog | Market |
| 102 | OrgCap ret | Organizational capital | Firm |
| 103 | PayoutYield ret | Payout yield | Firm |
| 104 | PctAcc ret | Percent operating accruals | Firm |
| 105 | Price ret | Price | Firm |
| 106 | PS ret | Piotroski F-score | Firm |
| 107 | RD ret | R&D over market cap | Firm |
| 108 | RDAbility ret | R&D ability | Firm |
| 109 | Realestate ret | Real estate holdings | Firm |
| 110 | ResidualMomentum ret | Momentum based on FF3 model residuals | Market |
| 111 | ReturnSkew ret | Return skewness | Market |
| 112 | ReturnSkew3F ret | Idiosyncratic skewness (3 factor model) | Market |
| 113 | RevenueSurprise ret | Revenue surprise | Firm |
| 114 | Roaq ret | Return on assets (qtrly) | Market |
| 115 | RoE ret | Net income/book equity | Firm |
| 116 | ShareIss1Y ret | Share issuance (1 year) | Firm |
| 117 | ShareIss5Y ret | Share issuance (5 year) | Firm |
| 118 | Size ret | Size | Firm |
| 119 | SP ret | Sales-to-price | Firm |
| 120 | Std turn ret | Share turnover volatility | Firm |
| 121 | STreversal ret | Short term reversal | Firm |
| 122 | Tang ret | Tangibility | Firm |
| 123 | Tax ret | Taxable income to income | Firm |
| 124 | TotalAccruals ret | Total accruals | Firm |
| 125 | TrendFactor ret | Trend in the general stock market | Firm |
| 126 | VarCF ret | Cash-flow to price variance | Firm |
| 127 | VolMkt ret | Volume to market equity | Market |
| 128 | VolSD ret | Volume variance | Market |
| 129 | VolumeTrend ret | Volume trend | Market |
| 130 | XFIN ret | Net external financing | Firm |
| 131 | Zerotrade ret | Days with zero trades | Market |
| 132 | ZerotradeAlt1 ret | Days with zero trades | Market |
| 133 | ZerotradeAlt12 ret | Days with zero trades | Market |
Appendix B
| N | Anomaly Abbreviation | Description | Characteristic |
|---|---|---|---|
| 1 | capex abn | Abnormal corporate investment | Firm |
| 2 | z score | Altman Z-score | Market |
| 3 | ami 126d | Amihud measure | Market |
| 4 | at gr1 | Asset growth | Firm |
| 5 | tangibility | Asset tangibility | Firm |
| 6 | sale bev | Assets turnover | Firm |
| 7 | at me | Assets-to-market | Firm |
| 8 | at be | Book leverage | Firm |
| 9 | bev mev | Book-to-market enterprise value | Firm |
| 10 | be me | Book-to-market equity | Firm |
| 11 | capx gr1 | CAPEX growth (1 year) | Firm |
| 12 | capx gr2 | CAPEX growth (2 years) | Firm |
| 13 | capx gr3 | CAPEX growth (3 years) | Firm |
| 14 | at turnover | Capital turnover | Firm |
| 15 | ocfq saleq std | Cash flow volatility | Firm |
| 16 | cop at | Cash-based operating profits-to-book assets | Firm |
| 17 | cop atl1 | Cash-based operating profits-to-lagged book assets | Firm |
| 18 | cash at | Cash-to-assets | Firm |
| 19 | dgp dsale | Change gross margin minus change sales | Firm |
| 20 | be gr1a | Change in common equity | Firm |
| 21 | coa gr1a | Change in current operating assets | Firm |
| 22 | col gr1a | Change in current operating liabilities | Firm |
| 23 | cowc gr1a | Change in current operating working capital | Firm |
| 24 | fnl gr1a | Change in financial liabilities | Firm |
| 25 | lti gr1a | Change in long-term investments | Firm |
| 26 | lnoa gr1a | Change in long-term net operating assets | Firm |
| 27 | nfna gr1a | Change in net financial assets | Firm |
| 28 | nncoa gr1a | Change in net noncurrent operating assets | Firm |
| 29 | noa gr1a | Change in net operating assets | Firm |
| 30 | ncoa gr1a | Change in noncurrent operating assets | Firm |
| 31 | ncol gr1a | Change in noncurrent operating liabilities | Firm |
| 32 | ocf at chg1 | Change in operating cash flow to assets | Firm |
| 33 | niq at chg1 | Change in quarterly return on assets | Firm |
| 34 | niq be chg1 | Change in quarterly return on equity | Firm |
| 35 | sti gr1a | Change in short-term investments | Firm |
| 36 | ppeinv gr1a | Change PPE and Inventory | Firm |
| 37 | dsale dinv | Change sales minus change Inventory | Firm |
| 38 | dsale drec | Change sales minus change receivables | Firm |
| 39 | dsale dsga | Change sales minus change SG&A | Firm |
| 40 | dolvol var 126d | Coefficient of variation for dollar trading volume | Market |
| 41 | turnover var 126d | Coefficient of variation for share turnover | Market |
| 42 | coskew 21d | Coskewness | Market |
| 43 | prc highprc 252d | Current price to high price over last year | Firm |
| 44 | debt me | Debt-to-market | Firm |
| 45 | beta dimson 21d | Dimson beta | Market |
| 46 | div12m me | Dividend yield | Firm |
| 47 | dolvol 126d | Dollar trading volume | Market |
| 48 | betadown 252d | Downside beta | Market |
| 49 | ni ar1 | Earnings persistence | Firm |
| 50 | earnings variability | Earnings variability | Firm |
| 51 | ni ivol | Earnings volatility | Firm |
| 52 | ni me | Earnings-to-price | Firm |
| 53 | ebitda mev | Ebitda-to-market enterprise value | Firm |
| 54 | eq dur | Equity duration | Firm |
| 55 | eqnpo 12m | Equity net payout | Firm |
| 56 | age | Firm age | Firm |
| 57 | betabab 1260d | Frazzini-Pedersen market beta | Market |
| 58 | fcf me | Free cash flow-to-price | Firm |
| 59 | gp at | Gross profits-to-assets | Firm |
| 60 | gp atl1 | Gross profits-to-lagged assets | Firm |
| 61 | debt gr3 | Growth in book debt (3 years) | Firm |
| 62 | rmax5 21d | Highest 5 days of return | Market |
| 63 | rmax5 rvol 21d | Highest 5 days of return scaled by volatility | Market |
| 64 | emp gr1 | Hiring rate | Market |
| 65 | iskew capm 21d | Idiosyncratic skewness from the CAPM | Market |
| 66 | iskew ff3 21d | Idiosyncratic skewness from the Fama-French 3-factor model | Market |
| 67 | iskew hxz4 21d | Idiosyncratic skewness from the q-factor model | Market |
| 68 | ivol capm 21d | Idiosyncratic volatility from the CAPM (21 days) | Market |
| 69 | ivol capm 252d | Idiosyncratic volatility from the CAPM (252 days) | Market |
| 70 | ivol ff3 21d | Idiosyncratic volatility from the Fama-French 3-factor model | Market |
| 71 | ivol hxz4 21d | Idiosyncratic volatility from the q-factor model | Market |
| 72 | ival me | Intrinsic value-to-market | Firm |
| 73 | inv gr1a | Inventory change | Firm |
| 74 | inv gr1 | Inventory growth | Firm |
| 75 | kz index | Kaplan-Zingales index | Firm |
| 76 | sale emp gr1 | Labor force efficiency | Firm |
| 77 | aliq at | Liquidity of book assets | Firm |
| 78 | aliq mat | Liquidity of market assets | Firm |
| 79 | ret 60 12 | Long-term reversal | Market |
| 80 | beta 60m | Market beta | Market |
| 81 | corr 1260d | Market correlation | Market |
| 82 | market equity | Market equity | Firm |
| 83 | rmax1 21d | Maximum daily return | Market |
| 84 | mispricing mgmt | Mispricing factor: Management | Market |
| 85 | mispricing perf | Mispricing factor: Performance | Market |
| 86 | dbnetis at | Net debt issuance | Firm |
| 87 | netdebt me | Net debt-to-price | Firm |
| 88 | eqnetis at | Net equity issuance | Firm |
| 89 | noa at | Net operating assets | Firm |
| 90 | eqnpo me | Net payout yield | Firm |
| 91 | chcsho 12m | Net stock issues | Firm |
| 92 | netis at | Net total issuance | Firm |
| 93 | ni inc8q | Number of consecutive quarters with earnings increases | Firm |
| 94 | zero trades 21d | Number of zero trades with turnover as tiebreaker (1 month) | Market |
| 95 | zero trades 252d | Number of zero trades with turnover as tiebreaker (12 months) | Market |
| 96 | zero trades 126d | Number of zero trades with turnover as tiebreaker (6 months) | Market |
| 97 | o score | Ohlson O-score | Firm |
| 98 | oaccruals at | Operating accruals | Firm |
| 99 | ocf at | Operating cash flow to assets | Firm |
| 100 | ocf me | Operating cash flow-to-market | Firm |
| 101 | opex at | Operating leverage | Firm |
| 102 | op at | Operating profits-to-book assets | Firm |
| 103 | ope be | Operating profits-to-book equity | Firm |
| 104 | op atl1 | Operating profits-to-lagged book assets | Firm |
| 105 | ope bel1 | Operating profits-to-lagged book equity | Firm |
| 106 | eqpo me | Payout yield | Firm |
| 107 | oaccruals ni | Percent operating accruals | Firm |
| 108 | taccruals ni | Percent total accruals | Firm |
| 109 | f score | Pitroski F-score | Firm |
| 110 | ret 12 1 | Price momentum t-12 to t-1 | Market |
| 111 | ret 12 7 | Price momentum t-12 to t-7 | Market |
| 112 | ret 3 1 | Price momentum t-3 to t-1 | Market |
| 113 | ret 6 1 | Price momentum t-6 to t-1 | Market |
| 114 | ret 9 1 | Price momentum t-9 to t-1 | Market |
| 115 | prc | Price per share | Firm |
| 116 | ebit sale | Profit margin | Firm |
| 117 | qmj | Quality minus Junk: Composite | Firm |
| 118 | qmj growth | Quality minus Junk: Growth | Firm |
| 119 | qmj prof | Quality minus Junk: Profitability | Firm |
| 120 | qmj safety | Quality minus Junk: Safety | Firm |
| 121 | niq at | Change in quarterly return on assets | Firm |
| 122 | niq be | Quarterly return on equity | Firm |
| 123 | rd5 at | R&D capital-to-book assets | Firm |
| 124 | rd me | R&D-to-market | Firm |
| 125 | rd sale | R&D-to-sales | Firm |
| 126 | resff3 12 1 | Residual momentum t-12 to t-1 | Market |
| 127 | resff3 6 1 | Residual momentum t-6 to t-1 | Market |
| 128 | ni be | Return on equity | Market |
| 129 | ebit bev | Return on net operating assets | Market |
| 130 | rvol 21d | Return volatility | Market |
| 131 | saleq gr1 | Sales growth (1 quarter) | Firm |
| 132 | sale gr1 | Sales growth (1 year) | Firm |
| 133 | sale gr3 | Sales growth (3 years) | Firm |
| 134 | sale me | Sales-to-market | Firm |
| 135 | turnover 126d | Share turnover | Firm |
| 136 | ret 1 0 | Short-term reversal | Firm |
| 137 | niq su | Standardized earnings surprise | Firm |
| 138 | saleq su | Standardized Revenue surprise | Firm |
| 139 | tax gr1a | Tax expense surprise | Firm |
| 140 | pi nix | Taxable income-to-book income | Firm |
| 141 | bidaskhl 21d | The high-low bid-ask spread | Firm |
| 142 | taccruals at | Total accruals | Firm |
| 143 | rskew 21d | Total skewness | Market |
| 144 | seas 1 1an | Year 1-lagged return, annual | Market |
| 145 | seas 1 1na | Year 1-lagged return, nonannual | Market |
| 146 | seas 2 5an | Years 2–5 lagged returns, annual | Market |
| 147 | seas 2 5na | Years 2–5 lagged returns, nonannual | Market |
| 148 | seas 6 10an | Years 6–10 lagged returns, annual | Market |
| 149 | seas 6 10na | Years 6–10 lagged returns, nonannual | Market |
| 150 | seas 11 15an | Years 11–15 lagged returns, annual | Market |
| 151 | seas 11 15na | Years 11–15 lagged returns, nonannual | Market |
| 152 | seas 16 20an | Years 16–20 lagged returns, annual | Market |
| 153 | seas 16 20na | Years 16–20 lagged returns, nonannual | Market |
| 1 | See, for example, Fama and French (1998), Green et al. (2013, 2017), Chordia et al. (2014), Novy-Marx and Velikov (2016), Linnainmaa and Roberts (2018), Jacobs and Muller (2020), A. Y. Chen and Zimmermann (2022), and others. |
| 2 | |
| 3 | In their five- and six-factor models, Fama and French included somewhat similar profit and investment factors to augment their three-factor model. |
| 4 | A total of 161 out of 319 anomalies were classified as clear predictors by the authors. |
| 5 | See Kahneman and Tversky (1979), Shiller (1981), DeBondt and Thaler (1987), Daniel et al. (1997), Barberis et al. (1998), Thaler (1999), and others. |
| 6 | This dataset was assembled from a number of previous anomaly studies. For further details, see A. Y. Chen and Velikov (2023). |
| 7 | In unreported results, we tested the Hou, Xue, and Zhang as well as Stambaugh and Yuan four-factor models. Our results were unchanged for the most part with poor performance from these models (similar to those of the Carhart four-factor model) but strong explanatory power for the ZCAPM. The results are available from the authors upon request. |
| 8 | |
| 9 | |
| 10 | Previous studies have incorporated time-series market volatility (e.g., VIX index) in asset pricing models, including Ang et al. (2006), Bekaert et al. (2023), Detzel et al. (2023), and citations therein. |
| 11 | For example, see work by Loungani et al. (1990), Christie and Huang (1994), Bekaert and Harvey (1997), Connolly and Stivers (2003), Gomes et al. (2003), Stivers (2003), Bansal and Yaron (2004), Zhang (2005), Pastor and Veronesi (2009), Angelidis et al. (2015), among others. Garcia et al. (2014) have conjectured that cross-sectional return dispersion in the stock market is related to aggregate idiosyncratic risk. Also, Cooper et al. (2024) have shown that macroeconomic shocks associated with market return dispersion are related to the asset growth factor in the Hou, Xue, and Zhang and Fama and French five-factor models. |
| 12 | They more precisely specified instead of simply in these equations, where is a complex function of other terms. |
| 13 | See Kolari et al. (2021, p. 71) for the mathematical derivation. Like Black (1972), the ZCAPM is extended to the existence of a riskless asset. Investors can purchase the riskless asset but cannot short (borrow) this asset. Investors are allowed to take short positions in risky assets (e.g., the zero-beta portfolio). We can derive Black’s zero-beta CAPM with a riskless asset via the following steps. From Equation (7), we can write Assuming a riskless asset, proportion of investor funds is allocated to risky assets I and and proportion (1 − ) to the riskless asset: After rearranging terms, the zero-beta CAPM becomes |
| 14 | Precedent exists in the asset pricing literature for the introduction of hidden or latent variables. For example, principal component analysis (PCA) and factor analysis use statistical methods to identify hidden factors in asset pricing models. See N.-F. Chen (1993), Lettau and Pelger (2020), and many others. |
| 15 | See Dempster et al. (1977), Jones and McLachlan (1990), McLachlan and Peel (2000), McLachlan and Krishnan (2008), and others. Some finance studies have applied EM regression, including Asquith et al. (1998), McLachlan and Krishnan (2008), Harvey and Liu (2016), Y. Chen et al. (2017), among others. See Bo and Batzoglou (2008) for a primer on the EM algorithm with application to computational biology. Also, Wikipedia provides discussion of the EM algorithm and literature citations. |
| 16 | More specifically, the E-step provides a conditional expectation of the log-likelihood function using current estimates of parameter values, and the M-step iteratively maximizes the log-likelihood (MLE) in the E-step. The EM algorithm converges to a stationary point of the likelihood equation. |
| 17 | Taking into account this time-varying factor return behavior, Ang et al. (2017) proposed a method to allow for dynamic factor loadings with some success in U.S. mutual fund portfolios. It is possible that multifactor models based on long/short factors could benefit from time-variable factors and their loadings. However, this research is beyond the scope of the present study. |
| 18 | Black was referring here to the small-firm factor and price-to-book factor, respectively. |
References
- Ang, A., Hodrick, R. J., Xing, Y., & Zhang, X. (2006). The cross-section of volatility and expected returns. Journal of Finance, 61, 259–299. [Google Scholar] [CrossRef]
- Ang, A., Madhaven, A., & Sobczyk, A. (2017). Estimating time-varying factor exposures. Financial Analysts Journal, 73, 41–54. [Google Scholar] [CrossRef]
- Angelidis, T., Sakkas, A., & Tessaromatis, N. (2015). Stock market dispersion, the business cycle and expected factor returns. Journal of Banking and Finance, 59, 256–279. [Google Scholar] [CrossRef]
- Asquith, D., Jones, J., & Kieschnick, R. (1998). Evidence on price stabilization and underpricing in early IPO returns. Journal of Finance, 53, 1759–1773. [Google Scholar] [CrossRef]
- Back, K., Kapadia, N., & Ostdiek, B. (2013). Slopes as factors: Characteristic pure plays. Working paper. Rice University. [Google Scholar]
- Back, K., Kapadia, N., & Ostdiek, B. (2015). Testing factor models on characteristic and covariance pure plays. Working paper. Rice University. [Google Scholar]
- Bansal, R., & Yaron, A. (2004). Risks for the long run: A potential resolution of asset pricing puzzles. Journal of Finance, 59, 1481–1509. [Google Scholar] [CrossRef]
- Barberis, N., Shleifer, A., & Vishny, R. (1998). A model of investor sentiment. Journal of Financial Economics, 49, 307–343. [Google Scholar] [CrossRef]
- Bartram, S. M., & Grinblatt, M. (2018). Agnostic fundamental analysis works. Journal of Financial Economics, 128, 125–147. [Google Scholar] [CrossRef]
- Bekaert, G., Engstrom, E., & Ermolov, A. (2023). The variance risk premium in equilibrium models. Review of Finance, 27, 1977–2014. [Google Scholar] [CrossRef]
- Bekaert, G., & Harvey, C. (1997). Emerging equity market volatility. Journal of Financial Economics, 43, 29–77. [Google Scholar] [CrossRef]
- Black, F. (1972). Capital market equilibrium with restricted borrowing. Journal of Business, 45, 444–454. [Google Scholar] [CrossRef]
- Black, F. (1995). Estimating expected return. Financial Analysts Journal, 49, 36–38. [Google Scholar] [CrossRef]
- Bo, C. B., & Batzoglou, S. (2008). What is the expectation maximization algorithm? Nature Biotechnology, 26, 897–899. [Google Scholar]
- Bowles, B., Reed, A. V., Ringgenberg, M. C., & Thornock, J. R. (2023). Anomaly time. Journal of Finance, 79, 3543–3579. [Google Scholar] [CrossRef]
- Carhart, M. M. (1997). On persistence in mutual fund performance. Journal of Finance, 52, 57–82. [Google Scholar] [CrossRef]
- Chen, A. Y., & Velikov, M. (2023). Zeroing in on the expected returns of anomalies. Journal of Financial and Quantitative Analysis, 58, 968–1004. [Google Scholar] [CrossRef]
- Chen, A. Y., & Zimmermann, T. (2020). Publication bias and the cross-section of stock returns. Review of Asset Pricing Studies, 10, 249–289. [Google Scholar] [CrossRef]
- Chen, A. Y., & Zimmermann, T. (2022). Open source cross-sectional asset pricing. Critical Finance Review, 11, 207–264. [Google Scholar] [CrossRef]
- Chen, N.-F. (1983). Empirical tests of the theory of arbitrage pricing. Journal of Finance, 38, 1393–1414. [Google Scholar] [CrossRef]
- Chen, Y., Cliff, M., & Zhao, H. (2017). Hedge funds: The good, the bad, and the lucky. Journal of Financial and Quantitative Analysis, 52, 1081–1109. [Google Scholar] [CrossRef]
- Chordia, T., Goyal, A., & Saretto, A. (2020). Anomalies and false rejections. Review of Financial Studies, 33, 2134–2179. [Google Scholar] [CrossRef]
- Chordia, T., Subrahmanyam, A., & Tong, Q. (2014). Have capital market anomalies attenuated in the recent era of high liquidity and trading activity? Journal of Accounting and Economics, 58, 41–58. [Google Scholar] [CrossRef]
- Christie, W., & Huang, R. (1994). The changing functional relation between stock returns and dividend yields. Journal of Empirical Finance, 1, 161–191. [Google Scholar] [CrossRef]
- Cochrane, J. H. (1996). A cross-sectional test of an investment-based asset pricing model. Journal of Political Economy, 104, 572–621. [Google Scholar] [CrossRef]
- Cochrane, J. H. (2011). Presidential address: Discount rates. Journal of Finance, 56, 1047–1108. [Google Scholar] [CrossRef]
- Connolly, R., & Stivers, C. (2003). Momentum and reversals in equity index returns during periods of abnormal turnover and return dispersion. Journal of Finance, 58, 1521–1556. [Google Scholar] [CrossRef]
- Cooper, M., Gulen, H., & Ion, M. (2024). The use of asset growth in empirical asset pricing models. Journal of Financial Economics, 151, 103746. [Google Scholar] [CrossRef]
- Copeland, T. E., & Weston, J. F. (1980). Financial theory and corporate policy. Addison-Wesley Publishing Company. [Google Scholar]
- Daniel, K., Hirshleifer, D., & Subrahmanyam, A. (1997). A theory of overconfidence, self-attribution, and security market under- and over-reactions [Unpublished working paper]. University of Michigan. [Google Scholar]
- DeBondt, W. F. M., & Thaler, R. H. (1987). Further evidence on investor overreaction and stock market seasonality. Journal of Finance, 42, 557–581. [Google Scholar] [CrossRef]
- Demirer, R., & Jategaonkar, S. P. (2013). The conditional relation between dispersion and return. Review of Financial Economics, 22, 125–134. [Google Scholar] [CrossRef]
- Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society, 39, 1–38. [Google Scholar] [CrossRef]
- Detzel, A., Duarte, J., Kamara, A., & Siegel, S. (2023). The cross-section of volatility and expected returns: Then and now. Critical Finance Review, 12, 9–56. [Google Scholar] [CrossRef]
- Engelberg, J., McLean, R. D., & Pontiff, J. (2018). Anomalies and news. Journal of Finance, 73, 1972–2001. [Google Scholar]
- Fama, E. F. (1970). Efficient capital markets: A review of theory and empirical work. Journal of Finance, 25, 383–417. [Google Scholar] [CrossRef]
- Fama, E. F. (2013). Two pillars of asset pricing. American Economic Review, 104, 1467–1485. [Google Scholar] [CrossRef]
- Fama, E. F., & French, K. R. (1992). The cross-section of expected stock returns. Journal of Finance, 47, 427–465. [Google Scholar]
- Fama, E. F., & French, K. R. (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics, 33, 3–56. [Google Scholar] [CrossRef]
- Fama, E. F., & French, K. R. (1996). The CAPM is wanted, dead or alive. Journal of Finance, 51, 1947–1958. [Google Scholar] [CrossRef]
- Fama, E. F., & French, K. R. (1998). Market efficiency, long-term returns, and behavioral finance. Journal of Financial Economics, 49, 283–306. [Google Scholar] [CrossRef]
- Fama, E. F., & French, K. R. (2008). Dissecting anomalies. Journal of Finance, 63, 1653–1678. [Google Scholar] [CrossRef]
- Fama, E. F., & French, K. R. (2015). A five-factor asset pricing model. Journal of Financial Economics, 116, 1–22. [Google Scholar] [CrossRef]
- Fama, E. F., & French, K. R. (2018). Choosing factors. Journal of Financial Economics, 128, 234–252. [Google Scholar] [CrossRef]
- Fama, E. F., & MacBeth, J. D. (1973). Risk, return, and equilibrium: Empirical tests. Journal of Political Economy, 81, 607–636. [Google Scholar] [CrossRef]
- Ferson, W. E. (2019). Empirical asset pricing: Models and methods. The MIT Press. [Google Scholar]
- Garcia, R., Mantilla-Garcia, D., & Martellini, L. (2014). A model-free measure of aggregate idiosyncractic volatility and the prediction of market returns. Journal of Financial and Quantitative Analysis, 49, 1133–1165. [Google Scholar] [CrossRef]
- Gibbons, M. R., Ross, S. A., & Shanken, J. (1989). A test of the efficiency of a given portfolio. Econometrica, 57, 1121–1152. [Google Scholar] [CrossRef]
- Gomes, J., Kogan, L., & Zhang, L. (2003). Equilibrium cross section of returns. Journal of Political Economy, 111, 693–732. [Google Scholar] [CrossRef]
- Green, J., Hand, J. R., & Zhang, F. (2017). The characteristics that provide independent information about average US monthly stock returns. Review of Financial Studies, 30, 4389–4436. [Google Scholar] [CrossRef]
- Green, J., Hand, J. R., & Zhang, X. F. (2013). The supraview of return predictive signals. Review of Accounting Studies, 18, 692–730. [Google Scholar] [CrossRef]
- Harvey, C. R., & Liu, Y. (2016). Rethinking performance evaluation. Working paper no. 22134. National Bureau of Economic Research, Inc. [Google Scholar]
- Harvey, C. R., Liu, Y., & Zhu, H. (2016). … and the cross-section of expected returns. Review of Financial Studies, 29, 5–68. [Google Scholar] [CrossRef]
- Hou, K., Xue, C., & Zhang, L. (2015). Digesting anomalies: An investment approach. Review of Financial Studies, 28, 650–705. [Google Scholar] [CrossRef]
- Hou, K., Xue, C., & Zhang, L. (2020). Replicating anomalies. Review of Financial Studies, 33, 2019–2133. [Google Scholar] [CrossRef]
- Jacobs, H., & Müller, S. (2020). Anomalies cross the globe: Once public, no longer existent? Journal of Financial Economics, 135, 213–230. [Google Scholar] [CrossRef]
- Jagannathan, R., & Wang, Z. (1996). The conditional CAPM and the cross-section of asset returns. Journal of Finance, 51, 3–53. [Google Scholar]
- Jensen, T. I., Kelly, B., & Pedersen, L. H. (2023). Is there a replication crisis in finance? Journal of Finance, 78, 2465–2518. [Google Scholar] [CrossRef]
- Jiang, X. (2010). Return dispersion and expected returns. Financial Markets and Portfolio Management, 24, 107–135. [Google Scholar] [CrossRef]
- Jones, P. N., & McLachlan, G. J. (1990). Algorithm AS 254: Maximum likelihood estimation from grouped and truncated data with finite normal mixture models. Applied Statistics, 39, 273–282. [Google Scholar] [CrossRef]
- Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47, 263–291. [Google Scholar] [CrossRef]
- Kolari, J. W., Huang, J. Z., Butt, H. A., & Liao, H. (2022). International tests of the ZCAPM asset pricing model. Journal of International Financial Markets, Institutions &Money, 79, 101607. [Google Scholar]
- Kolari, J. W., Huang, J. Z., Liu, W., & Liao, H. (2022). Further tests of the ZCAPM asset pricing model. Journal of Risk and Financial Management, 15, 137. [Google Scholar] [CrossRef]
- Kolari, J. W., Huang, J. Z., Liu, W., & Liao, H. (2023a, March 8–11). A cross-sectional asset pricing test of model validity. Annual Meetings of the Southwestern Finance Association, Las Vegas, NV, USA. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4203990 (accessed on 1 April 2025).
- Kolari, J. W., Huang, J. Z., Liu, W., & Liao, H. (2023b, July 2–6). The alpha force: Testing missing asset pricing factors. Annual Meetings of the Western Economic Association International, San Diego, CA, USA. [Google Scholar]
- Kolari, J. W., Huang, J. Z., Liu, W., & Liao, H. (2025a, February 12–14). A quantum leap in asset pricing: Explaining anomalyous returns. Annual Meetings of the Southwestern Finance Association, San Antonio, TX, USA. [Google Scholar]
- Kolari, J. W., Huang, J. Z., Liu, W., & Liao, H. (2025b). Asset pricing models and market efficiency: Using machine Learning to explain stock market anomalies. Palgrave Macmillan. [Google Scholar]
- Kolari, J. W., Liu, W., & Huang, J. Z. (2021). A new model of capital asset prices: Theory and evidence. Palgrave Macmillan. [Google Scholar]
- Kolari, J. W., Liu, W., & Pynnonen, S. (2024). Professional investment portfolio management: Boosting performance with machine-made portfolios and stock market evidence. Palgrave Macmillan. [Google Scholar]
- Lettau, M., & Ludvigson, S. (2001). Consumption, aggregate wealth, and expected stock returns. Journal of Finance, 56, 815–849. [Google Scholar] [CrossRef]
- Lettau, M., & Pelger, M. (2020). Factors that fit the time series and cross-section of stock returns. Review of Financial Studies, 33, 2274–2325. [Google Scholar] [CrossRef]
- Linnainmaa, J., & Roberts, M. (2018). The history of the cross-section of stock returns. Review of Financial Studies, 31, 2606–2649. [Google Scholar] [CrossRef]
- Lintner, J. (1965). The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Review of Economics and Statistics, 47, 13–37. [Google Scholar] [CrossRef]
- Liu, W. (2013). A new asset pricing model based on the zero-beta CAPM: Theory and evidence [Doctoral dissertation, Texas A&M University]. [Google Scholar]
- Liu, W., Kolari, J. W., & Huang, J. Z. (2012, October 17–20). A new asset pricing model based on the zero-beta CAPM. 2012 Annual Meetings of the Financial Management Association, Atlanta, GA, USA. [Google Scholar]
- Liu, W., Kolari, J. W., & Huang, J. Z. (2019). Creating superior investment portfolios. Working paper. Texas A&M University. [Google Scholar]
- Liu, W., Kolari, J. W., & Huang, J. Z. (2020, November 18–21). Return dispersion and the cross-section of stock returns. Annual Meetings of the Southern Finance Association, Palm Springs, CA, USA. [Google Scholar]
- Loungani, P., Rush, M., & Tave, W. (1990). Stock market dispersion and unemployment. Journal of Monetary Economics, 25, 367–388. [Google Scholar] [CrossRef]
- Lu, X., Stambaugh, R. F., & Yuan, Y. (2018). Anomalies abroad: Beyond data mining. Working paper. Shanghai Jiao Tong University. [Google Scholar]
- Markowitz, H. M. (1952). Portfolio selection. Journal of Finance, 7, 77–91. [Google Scholar]
- Markowitz, H. M. (1959). Portfolio selection: Efficient diversification of investments. John Wiley & Sons. [Google Scholar]
- McLachlan, G. J., & Krishnan, T. (2008). The EM algorithm and extensions (2nd ed.). John Wiley & Sons. [Google Scholar]
- McLachlan, G. J., & Peel, D. (2000). Finite mixture models. Wiley Interscience. [Google Scholar]
- McLean, R. D., & Pontiff, J. (2016). Does academic publication destroy predictability? Journal of Finance, 71, 5–32. [Google Scholar] [CrossRef]
- Mossin, J. (1966). Equilibrium in a capital asset market. Econometrica, 34, 768–783. [Google Scholar] [CrossRef]
- Novy-Marx, R., & Velikov, M. (2016). A taxonomy of anomalies and their trading costs. Review of Financial Studies, 29, 104–147. [Google Scholar] [CrossRef]
- Pastor, L., & Veronesi, P. (2009). Technological revolutions and stock prices. American Economic Review, 99, 1451–1483. [Google Scholar] [CrossRef]
- Schwert, G. W. (2003). Anomalies and market efficiency. In G. M. Constantinides, M. Harris, & R. Stulz (Eds.), Handbook of the economics of finance (pp. 939–974). North-Holland. [Google Scholar]
- Sharpe, W. F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance, 19, 425–442. [Google Scholar]
- Shiller, R. J. (1981). Do stock prices move too much to be justified by subsequent changes in dividends. American Economic Review, 71, 421–436. [Google Scholar]
- Stambaugh, R. F., & Yuan, Y. (2017). Mispricing factors. Review of Financial Studies, 30, 1270–1315. [Google Scholar] [CrossRef]
- Stivers, C. (2003). Firm-level return dispersion and the future volatility of aggregate stock market returns. Journal of Financial Markets, 6, 389–411. [Google Scholar] [CrossRef]
- Thaler, R. H. (1999). The end of behavioral finance. Financial Analysts Journal, 55, 12–17. [Google Scholar] [CrossRef]
- Treynor, J. L. (1961). Market value, time, and risk [Unpublished manuscript].
- Treynor, J. L. (1962). Toward a theory of market value of risky assets [Unpublished manuscript].
- Zhang, L. (2005). The value premium. Journal of Finance, 60, 67–103. [Google Scholar] [CrossRef]
| Statistic | |||||||
|---|---|---|---|---|---|---|---|
| Mean | 0.01 | 0.005 | 0.01 | 0.03 | 0.01 | 0.01 | 1.86 |
| Standard deviation | 1.07 | 0.57 | 0.59 | 0.79 | 0.41 | 0.37 | 0.66 |
| Maximum | 11.35 | 6.17 | 6.74 | 7.12 | 4.52 | 2.53 | 10.77 |
| Minimum | −17.47 | −11.19 | −5.00 | −14.37 | −3.01 | −5.87 | 0.68 |
| P25 | −0.46 | −0.30 | −0.24 | −0.25 | −0.17 | −0.18 | 1.47 |
| P50 | 0.04 | 0.02 | 0.01 | 0.06 | 0.01 | 0.01 | 1.73 |
| P75 | 0.53 | 0.32 | 0.26 | 0.36 | 0.19 | 0.19 | 2.04 |
| Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| CAPM | 0.44 | −0.00 | 0.01 | ||||||
| (17.77 ***) | (−0.01) | ||||||||
| FF3 | 0.42 | 0.07 | −0.09 | 0.27 | 0.11 | ||||
| (19.37 ***) | (0.39) | (−0.37) | (1.82 *) | ||||||
| C4 | 0.40 | −0.04 | −0.13 | 0.26 | 0.31 | 0.17 | |||
| (18.52 ***) | (−0.23) | (−0.61) | (1.84 *) | (1.29) | |||||
| FF5 | 0.40 | 0.12 | 0.04 | 0.12 | 0.18 | 0.32 | 0.15 | ||
| (20.33 ***) | (0.70) | (0.17) | (0.77) | (1.25) | (2.76 ***) | ||||
| FF6 | 0.38 | −0.04 | 0.03 | 0.18 | 0.40 | 0.19 | 0.26 | 0.19 | |
| (19.00 ***) | (−0.26) | (0.16) | (1.19) | (1.64) | (1.54) | (2.31 **) | |||
| ZCAPM | 0.28 | 0.30 | 0.72 | 0.84 | |||||
| (9.96) | (1.43) | (6.69 ***) |
| Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| CAPM | −0.07 | −0.14 | 0.08 | ||||||
| (−3.39 ***) | (−0.51) | ||||||||
| FF3 | −0.09 | −0.13 | 0.06 | 0.11 | 0.10 | ||||
| (−4.48 ***) | (−0.64) | (0.29) | (0.81) | ||||||
| C4 | −0.10 | −0.36 | 0.05 | 0.13 | 0.08 | 0.11 | |||
| (−5.57 ***) | (−1.73 *) | (0.23) | (0.92) | (0.35) | |||||
| FF5 | −0.12 | −0.17 | 0.10 | 0.07 | 0.09 | 0.22 | 0.13 | ||
| (−6.38 ***) | (−0.84) | (0.54) | (0.50) | (0.72) | (2.14 **) | ||||
| FF6 | −0.13 | −0.36 | 0.09 | 0.12 | 0.11 | 0.13 | 0.20 | 0.14 | |
| (−7.55 ***) | (−1.76 *) | (0.49) | (0.85) | (0.50) | (1.07) | (1.94 *) | |||
| ZCAPM | −0.01 | 0.12 | 0.67 | 0.86 | |||||
| (−0.43) | (0.47) | (7.01 ***) |
| Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| CAPM | 0.00 | 0.34 | 0.02 | ||||||
| (−0.10) | (1.48) | ||||||||
| FF3 | −0.02 | 0.32 | −0.20 | 0.16 | 0.06 | ||||
| (−0.62) | (1.87 *) | (−1.14) | (1.05) | ||||||
| C4 | −0.06 | 0.16 | −0.20 | 0.11 | 0.31 | 0.12 | |||
| (−2.48 ***) | (0.96) | (−1.22) | (0.82) | (1.52) | |||||
| FF5 | −0.05 | 0.38 | −0.06 | 0.09 | 0.31 | 0.16 | 0.07 | ||
| (−1.94 *) | (2.23 **) | (−0.35) | (0.55) | (1.91 *) | (1.27) | ||||
| FF6 | −0.08 | 0.18 | −0.06 | 0.10 | 0.36 | 0.32 | 0.05 | 0.12 | |
| (−3.58 ***) | (1.08) | (−0.40) | (0.73) | (1.72 *) | (2.29 **) | (0.46) | |||
| ZCAPM | 0.07 | 0.56 | 0.69 | 0.83 | |||||
| (2.35 ***) | (2.67 ***) | (6.46 ***) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolari, J.W.; Huang, J.; Liu, W.; Liao, H. A Quantum Leap in Asset Pricing: Explaining Anomalous Returns. J. Risk Financial Manag. 2025, 18, 362. https://doi.org/10.3390/jrfm18070362
Kolari JW, Huang J, Liu W, Liao H. A Quantum Leap in Asset Pricing: Explaining Anomalous Returns. Journal of Risk and Financial Management. 2025; 18(7):362. https://doi.org/10.3390/jrfm18070362
Chicago/Turabian StyleKolari, James W., Jianhua Huang, Wei Liu, and Huiling Liao. 2025. "A Quantum Leap in Asset Pricing: Explaining Anomalous Returns" Journal of Risk and Financial Management 18, no. 7: 362. https://doi.org/10.3390/jrfm18070362
APA StyleKolari, J. W., Huang, J., Liu, W., & Liao, H. (2025). A Quantum Leap in Asset Pricing: Explaining Anomalous Returns. Journal of Risk and Financial Management, 18(7), 362. https://doi.org/10.3390/jrfm18070362







