Mathematical Foundations for Balancing the Payment System in the Trade Credit Market
Abstract
:1. Introduction
1.1. Interbank vs. Trade Credit Clearing
- interbank network: 2770
- interbank networks: 1960
- trade credit network: 64
- trade credit networks: 51
1.2. Historical Context and Brief Literature Review
1.3. Basic Concepts
- Circular —is a situation where individual payments can only be settled in a specific order. This situation is resolvable by reordering the payment queue.
- Gridlock—is a situation in which several payments cannot be settled individually but can be settled simultaneously. This situation is resolvable with multilateral off-set.
- Deadlock—is a situation where the individual payments can be made only by adding liquidity to at least one of the system participants.
1.4. Overview of Paper
2. Materials and Methods
2.1. Notation and Definitions
- An obligation network is a directed graph where the nodes6 represent firms and the edges represent the obligations. Parallel edges are allowed to represent multiple obligations between two firms:
- A nominal liability matrix is a matrix representing total obligations or liabilities between firms. We will define special vectors to describe properties of the nominal liability matrix.
- A payment system is constructed by adding special-function nodes to the obligation network. These special nodes represent sources of funds and a store of value. They can have connections to all nodes in the obligation network, and the set of all connections for each special node is expressed as a vector.
2.1.1. Obligation Network
2.1.2. Nominal Liability Matrix
2.1.3. Balanced Net Position Vector
2.2. Obligation-Clearing with a Liquidity Source
2.3. Simple Examples
2.3.1. Obligation Chain
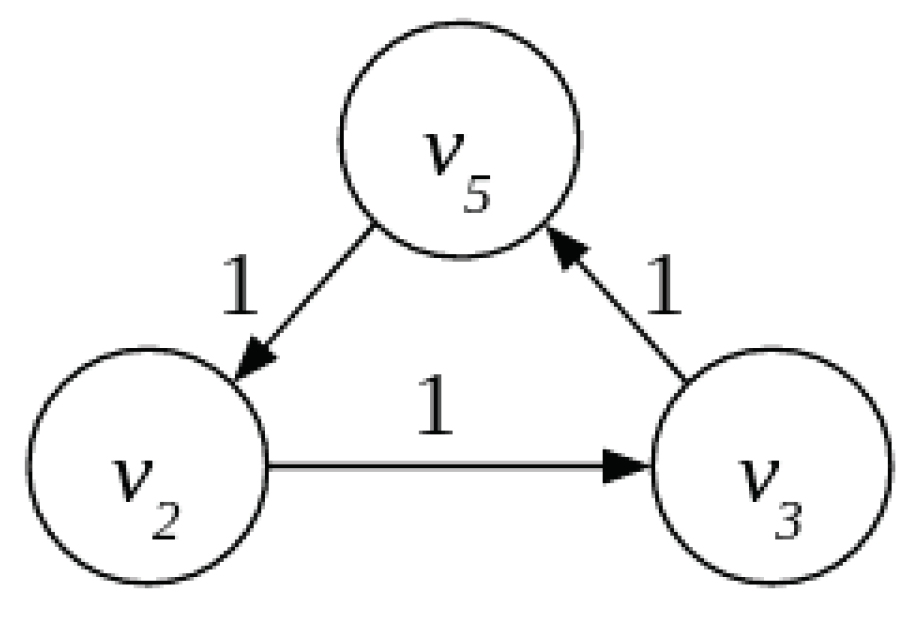
2.3.2. Obligation Cycle
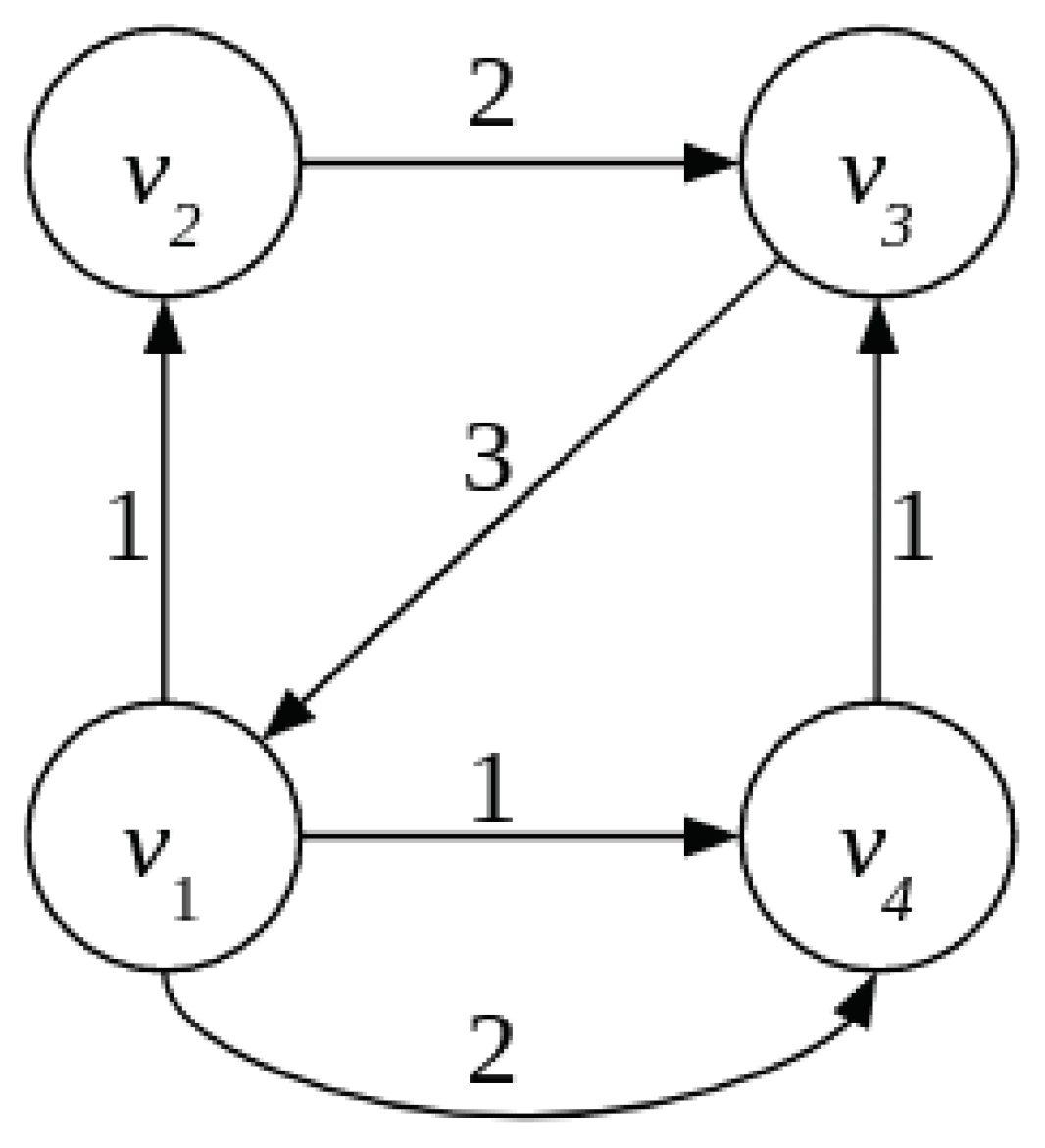
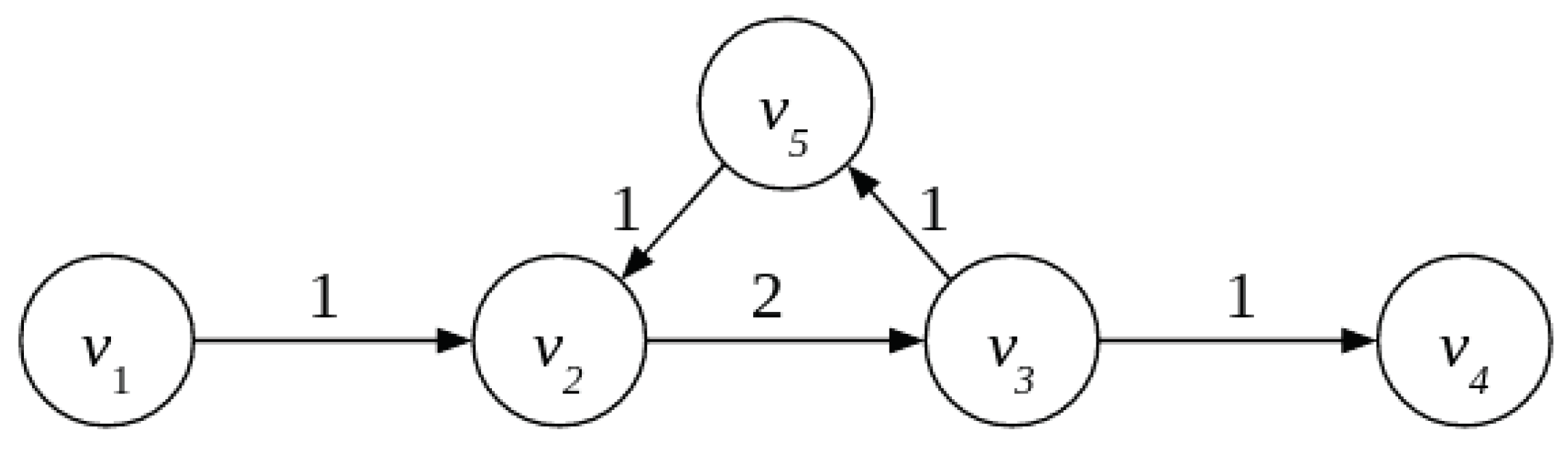
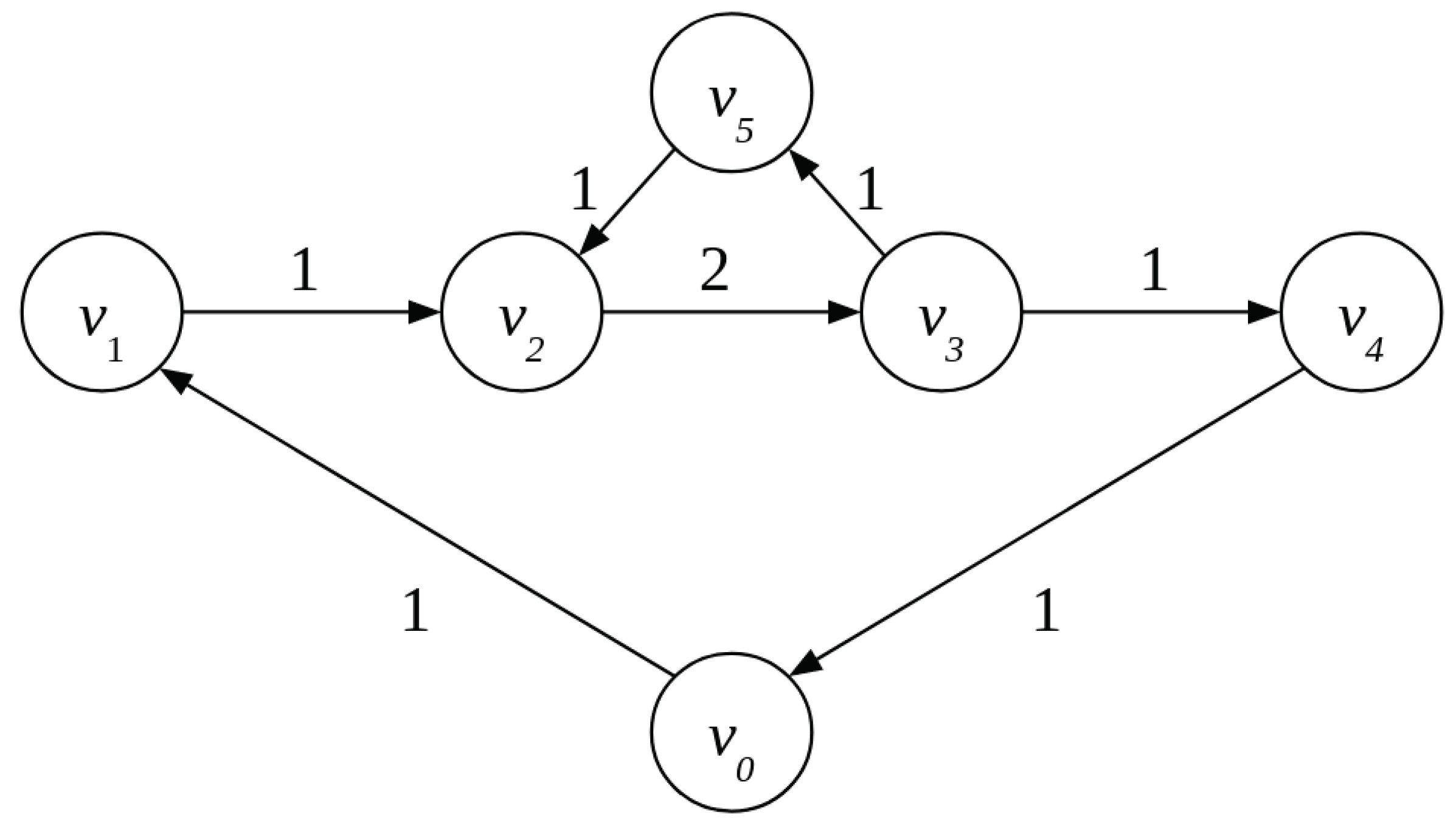
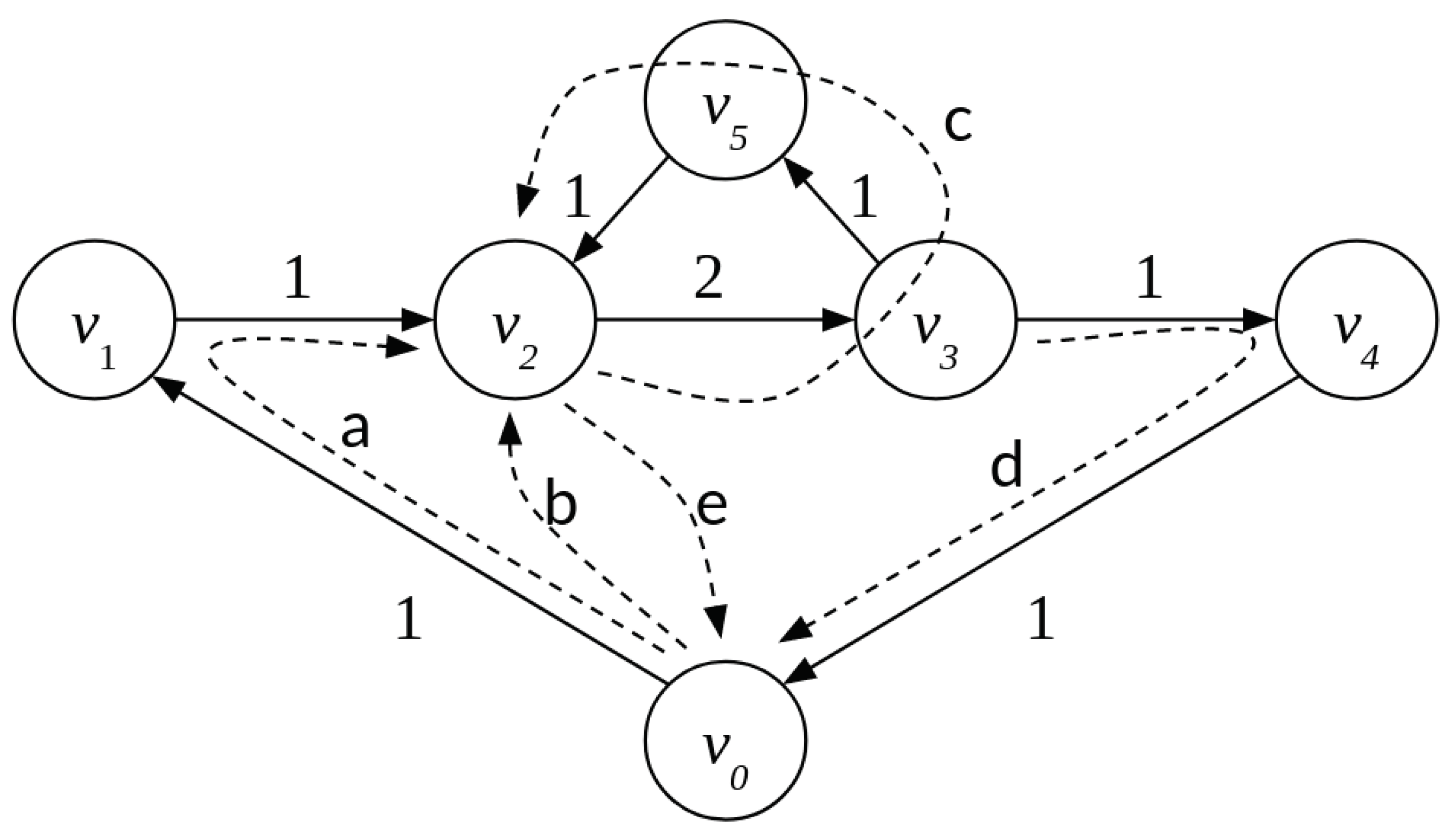
2.3.3. Small Obligation Network with a Chain and a Cycle
3. Results
3.1. General Formulation
3.1.1. A Cycle as a Balanced Payment Subsystem
3.1.2. Finding the Maximum-Weight Set of Cycles
3.1.3. The Minimum-Cost Flow Problem
- Define the object function as a Grandsum function , which is the sum of all the elements of a given square matrix. Looking for the minimum of the function is equivalent to looking for the minimum-weight sub-network .
- Make sure that the payment system is balanced. The constraint above ensures this since is balanced by construction. In fact, since and M uses the same cashflow vector , ensuring that M has the same net position vector is enough to guarantee that will be balanced too.
- Make sure we are not introducing edges between nodes in sub-network that do not exist in the obligation network . Therefore, all matrix elements must have a value between 0 and .
3.2. Using Balanced Payment Subsystems in the Trade Credit Market
- Collect obligations to form an obligation network .
- Form a nominal liability matrix L and a payment system without external financing.
- Find a maximum-weight balanced payment subsystem T.
- Discharge the obligations in the balanced payment subsystem by sending set-off notices to all pertinent firms.
- Subtract the balanced payment subsystem T, such that .
- Leave the remaining obligations in the nominal obligation matrix M to be discharged using the normal bank payment system.
4. Discussion: Practical Trade Credit Formulation
4.1. Formal Model for Single Liquidity Source
- : cashflows from firms’ bank accounts (only positive balances used)
- : overdraft cashflows up to firms’ credit lines
- : cashflows to repay firms’ overdrafts (different set of firms from ’s)
- : cashflows into firms’ bank accounts (different set of firms from ’s),
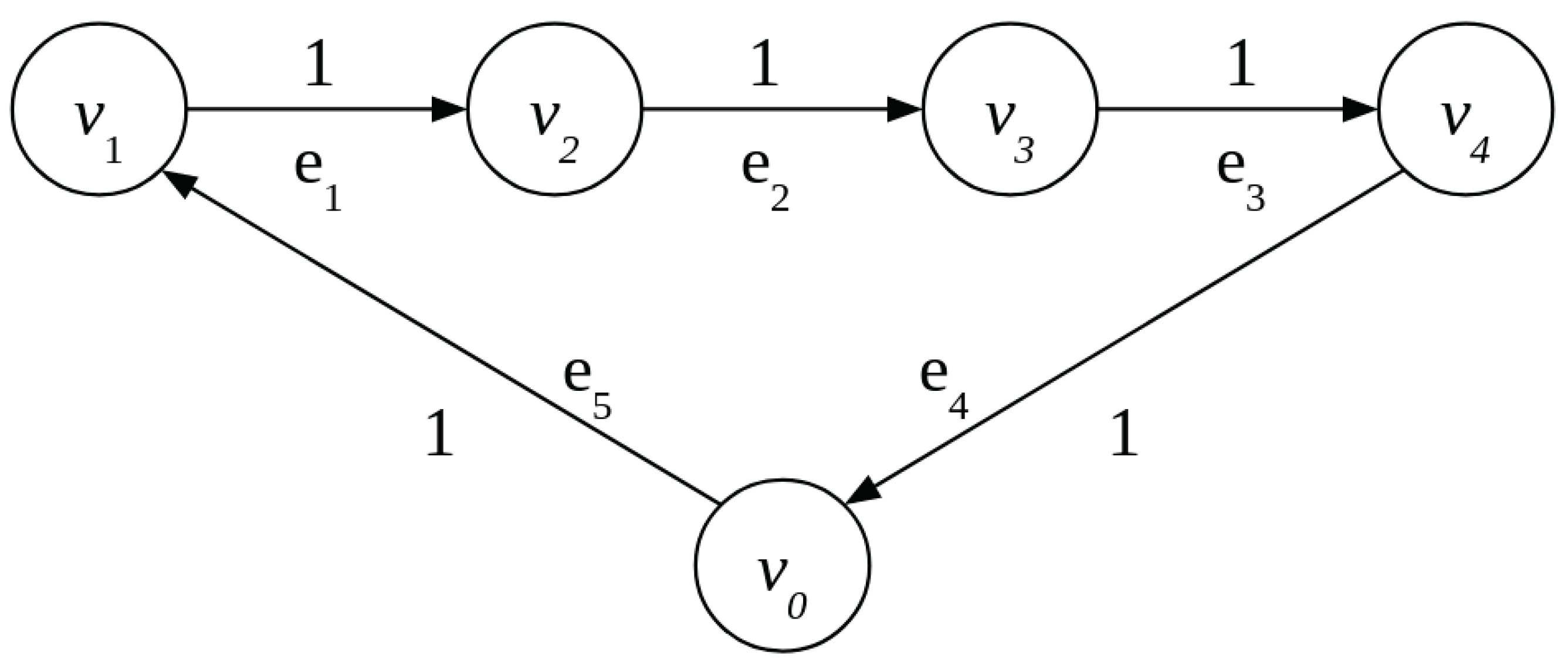
- After all the obligations have been uploaded into the repository (which could be a blockchain), an obligation network exists, but the net positions are not yet known. The network is the first output, and the input to Step 2.
- Based on the network, the net positions are calculated, i.e., the components of vector . This is the output of Step 2 and the input to Step 3.
- The cyclic structure is determined. This is the output of Step 3 and the input to Step 4.
- The cyclic structure is removed from the obligation network, i.e., multilateral set-off is performed. This results in a new, acyclic obligation network with obligation amounts that, usually, are the same as before for a subset of firms, smaller for another subset, and zero for a third subset, which is the complement of the first two.
- The TCT multilateral set-off process is completed when set-off notices are sent to all the firms instructing them about what is left to pay.
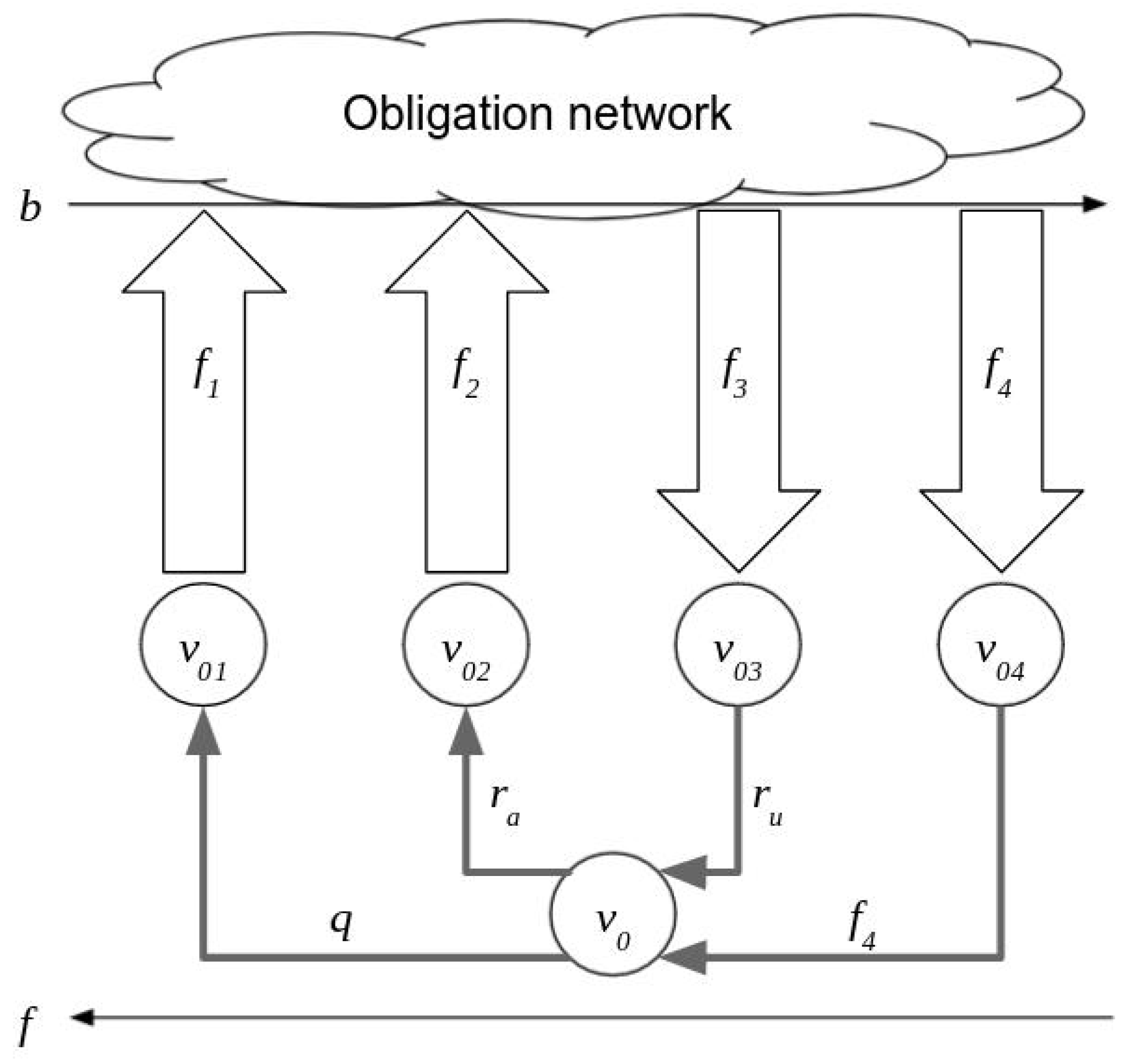
4.2. Generalization to Multiple Sources
4.3. Optimizing the Use of Available Liquidity
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
| 1 | Central Bank Digital Currency. |
| 2 | Efficiency could be loosely defined as the ratio of debt cleared to the total initial debt. Due to network effects (probably factorial) that are not yet well-understood and that will be explored in future work, the injection of liquidity increases this value even after the liquidity used is subtracted from the debt cleared. |
| 3 | https://ec.europa.eu/cefdigital/wiki/display/CEFDIGITAL/eInvoicing+in+Italy (accessed on 18 September 2021). |
| 4 | In Slovenia, it is an institution equivalent to the UK’s Companies House. |
| 5 | Such a path usually involves multiple, and different, firms or ‘hops’ in each direction. |
| 6 | Usually referred to as vertices in graph theory. |
| 7 | We note that this is opposite to the ‘balance’ function in Simić and Milanović (1992), which is defined using the standard fluid mechanics convention of ‘net flow = outflow − inflow’. In the present analysis, it is more convenient to follow financial intuition to define the net position as ‘inflow − outflow’. The only difference between Simić and Milanović (1992), and our analysis as far as this function is concerned, therefore, is merely a sign. |
| 8 | We should clarify that we are using the term ‘cashflow’ in a more general sense than its normal application in business, i.e., as the revenue per unit time of a given company. In this paper, cashflow means literally the movement or “flow” of currency over one or more hops of the network, i.e., between two or more companies. Such flow can also be a closed loop or cycle, and one of the nodes can also be a bank or other account-holding institution. The units are still , but the time period is not important and can be trivially assumed to be 1, |
| 9 | There are many possible maximum-weight sets of cycles but only one maximum weight. Interestingly, depending on which maximum-weight set of cycles one finds, q could be different. Empirical tests on larger datasets show that the number of cycles can change within a range of about 1%. |
| 10 | In the context of a multigraph, there can be multiple edges between any two nodes. One might therefore expect different cycles to be associated with different edges between the same two nodes. While this is possible, it is not necessarily the case. The same edge can be the intersection of multiple cycles such that, if it happens to be the smallest weight of multiple cycles, subtracting one cycle will break all the others. |
| 11 | The ‘object function’ in optimization theory. |
References
- Abraham, David J., Avrim Blum, and Tuomas Sandholm. 2007. Clearing algorithms for barter exchange markets: Enabling nationwide kidney exchanges. Paper present at the 8th ACM Conference on Electronic Commerce, San Diego, CA, USA, June 11–15; pp. 295–304. [Google Scholar]
- Allen, Franklin, Meijun Qian, and Jing Xie. 2018. Understanding informal financing. Journal of Financial Intermediation 39: 19–33. [Google Scholar] [CrossRef]
- Bardoscia, Marco, Paolo Barucca, Stefano Battiston, Fabio Caccioli, Giulio Cimini, Diego Garlaschelli, Fabio Saracco, Tiziano Squartini, and Guido Caldarelli. 2021. The physics of financial networks. Nature Reviews Physics 3: 490–507. [Google Scholar] [CrossRef]
- Bech, Morten, and Kimmo Soramäki. 2001. Gridlock Resolution in Interbank Payment Systems. Research Discussion Papers 9/2001, Bank of Finland. Available online: https://EconPapers.repec.org/RePEc:bof:bofrdp:2001_009 (accessed on 23 June 2021).
- Börner, Lars, and John William Hatfield. 2017. The Design of Debt-Clearing Markets: Clearinghouse Mechanisms in Preindustrial Europe. Journal of Political Economy 125: 1991–2037. [Google Scholar] [CrossRef] [Green Version]
- Cui, Huanqing, Jian Niu, Chuanai Zhou, and Minglei Shu. 2017. A Multi-Threading Algorithm to Detect and Remove Cycles in Vertex- and Arc-Weighted Digraph. Algorithms 10: 115. [Google Scholar] [CrossRef] [Green Version]
- Eisenberg, Larry, and Thomas H. Noe. 2001. Systemic Risk in Financial Systems. Management Science 47: 236–49. Available online: http://www.jstor.org/stable/2661572 (accessed on 23 June 2021). [CrossRef]
- EUBOF. 2021. Central Bank Digital Currencies and a Euro for the Future. Technical Report, EU Blockchain Observatory and Forum. Available online: https://www.eublockchainforum.eu/sites/default/files/reports/CBDC%20Report%20Final.pdf (accessed on 5 July 2021).
- Fleischman, Tomaž, Paolo Dini, and Giuseppe Littera. 2020. Liquidity-Saving through Obligation-Clearing and Mutual Credit: An Effective Monetary Innovation for SMEs in Times of Crisis. Journal of Risk and Financial Management 13: 295. Available online: https://www.mdpi.com/1911-8074/13/12/295 (accessed on 23 June 2021). [CrossRef]
- Foote, Elizabeth. 2014. Information asymmetries and spillover risk in settlement systems. Journal of Banking & Finance 42: 179–90. Available online: http://www.sciencedirect.com/science/article/pii/S0378426614000120 (accessed on 23 June 2021).
- Gaffeo, Edoardo, Lucio Gobbi, and Massimo Molinari. 2019. The economics of netting in financial networks. Journal of Economic Interaction and Coordination 14: 595–622. [Google Scholar] [CrossRef]
- Galbiati, Marco, and Kimmo Soramäki. 2010. Liquidity-Saving Mechanisms and Bank Behaviour. Bank of England Working Paper 400. Available online: http://dx.doi.org/10.2139/ssrn.1650632 (accessed on 23 June 2021).
- Garratt, Rodney, and Peter Zimmerman. 2020. Centralized netting in financial networks. Journal of Banking & Finance 112: 105270. [Google Scholar]
- Gavrila, Lucian-Ionut, and Alexandru Popa. 2021. A novel algorithm for clearing financial obligations between companies—An application within the romanian ministry of economy. Algorithmic Finance 9: 49–60. [Google Scholar] [CrossRef]
- Gazda, Vladimír, Denis Horváth, and Marcel Resovsky. 2015. An application of graph theory in the process of mutual debt compensation. Acta Polytechnica Hungarica 12: 7–24. [Google Scholar]
- Glasserman, Paul, and Peyton Young. 2016. Contagion in Financial Networks. Journal of Economic Literature 54: 779–831. [Google Scholar] [CrossRef] [Green Version]
- Gobbi, Lucio. 2018. Clearing Mechanism in Real and Financial Markets. Ph.D. thesis, University of Trento, Trento, Italy. Available online: http://eprints-phd.biblio.unitn.it/3097/1/tesi_Lucio_Gobbi.pdf (accessed on 14 August 2021).
- Hüser, Anne-Caroline. 2015. Too Interconnected to Fail: A Survey of the Interbank Networks Literature. SAFE Working Paper. Available online: https://www.econstor.eu/bitstream/10419/203293/1/safe-wp-091_3.pdf (accessed on 14 August 2021).
- Kahn, Arthur B. 1962. Topological Sorting of Large Networks. Communications of the ACM 5: 558–62. [Google Scholar] [CrossRef]
- Kavitha, Telikepalli, Christian Liebchen, Kurt Mehlhorn, Dimitrios Michail, Romeo Rizzi, Torsten Ueckerdt, and Katharina Zweig. 2009. Cycle Bases in Graphs—Characterization, Algorithms, Complexity, and Applications. Computer Science Review 3: 199–243. [Google Scholar] [CrossRef] [Green Version]
- Király, Zoltán, and Péter Kovács. 2012. Efficient implementations of minimum-cost flow algorithms. Acta Universitatis Sapientiae, Informatica 4: 67–118. Available online: https://arxiv.org/pdf/1207.6381.pdf (accessed on 23 June 2021).
- Leinonen, Harry. 2005. Liquidity, Risks and Speed in Payment and Settlement Systems: A Simulation Approach. Helsinki: Bank of Finland. [Google Scholar]
- Orlin, James. 1996. A Polynomial-Time Primal Network Simplex Algorithm for Minimum-Cost Flows. Mathematical Programming 78: 109–29. Available online: https://dspace.mit.edu/bitstream/handle/1721.1/2584/SWP-3834-33338649.pdf (accessed on 23 June 2021). [CrossRef]
- Pirrong, Craig. 2011. The Economics of Central Clearing: Theory and Practice. International Swaps and Derivatives Association (ISDA) Discussion Paper Series, Number One. Available online: https://www.isda.org/a/yiEDE/isdadiscussion-ccp-pirrong.pdf (accessed on 9 September 2021).
- Schara, Tomaž, and Rudi Bric. 2018. Deleveraging of Indebtedness in an Economy through Non-Monetary Intervention. Available online: https://www.researchgate.net/publication/322235409_Deleveraging_of_Indebtedness_in_an_Economy_through_Non-Monetary_Intervention (accessed on 23 June 2021).
- Simić, Slobodan, and Vladan Milanović. 1992. Some Remarks on the Problem of Multilateral Compensation. Publikacije Elektrotehničkog fakulteta. Serija Matematika, 27–33. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.100.8429&rep=rep1&type=pdf (accessed on 23 June 2021).
- Tompkins, Michael, and Ariel Olivares. 2016. Clearing and Settlement Systems from Around the World: A Qualitative Analysis. Bank of Canada Staff Discussion Paper, No. 2016-14. Available online: https://www.bankofcanada.ca/2016/06/staff-discussion-paper-2016-14/ (accessed on 18 September 2021).
- Vuillemey, Guillaume. 2020. The Value of Central Clearing. The Journal of Finance 75: 2021–53. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fleischman, T.; Dini, P. Mathematical Foundations for Balancing the Payment System in the Trade Credit Market. J. Risk Financial Manag. 2021, 14, 452. https://doi.org/10.3390/jrfm14090452
Fleischman T, Dini P. Mathematical Foundations for Balancing the Payment System in the Trade Credit Market. Journal of Risk and Financial Management. 2021; 14(9):452. https://doi.org/10.3390/jrfm14090452
Chicago/Turabian StyleFleischman, Tomaž, and Paolo Dini. 2021. "Mathematical Foundations for Balancing the Payment System in the Trade Credit Market" Journal of Risk and Financial Management 14, no. 9: 452. https://doi.org/10.3390/jrfm14090452
APA StyleFleischman, T., & Dini, P. (2021). Mathematical Foundations for Balancing the Payment System in the Trade Credit Market. Journal of Risk and Financial Management, 14(9), 452. https://doi.org/10.3390/jrfm14090452







