Second-Order Least Squares Method for Dynamic Panel Data Models with Application

Abstract

Management of financial risks and sound decision making rely on the accurate information and predictive models. Drawing useful information efficiently from big data with complex structures and building accurate models are therefore crucial tasks. Most commonly used methods for statistical inference in dynamic panel data models are based on the differencing transformation of data. However, differencing data may cause substantial loss of information, and therefore the subsequent analysis may fail to capture important features in the original level data. This point is demonstrated by a real data example where we use a semiparametrically efficient estimation method on the level data to reach a more favorable model. In particular, we study a second-order least squares approach which is based on the first two conditional moments of the response variable given the explanatory variables. This estimator is root-N consistent and its asymptotic variance reaches a lower bound semiparametric efficiency. Monte Carlo simulations show that this estimator performs favorably in finite sample situations compared to the first-differenced GMM and the random effects pseudo ML estimators. We also propose a new diagnostic test to check the working moments assumption based on the proposed estimator. A real data application is presented to further demonstrate the usage of this method.

1. Introduction

Modern technology and data collection techniques have produced huge amount of data in business, economics, and many other fields. On the one hand, these data provide rich information to support decision making; however, on the other hand, the big sizes and complex structures of the data make the statistical analysis very challenging. How to draw useful information from data efficiently and how to identify accurate predictive models are important issues for the management of financial risks and decision making in general. A common data type is the repeated measurements data that are collected on a large number of units over certain period of time. In business and economics, the data are typically collected at regular time points (calendar time) and are usually called panel data. Statistical methodologies for the analysis of longitudinal data have been extensively studied in statistics as well as econometrics; however, the research follows two different directions.

In statistical literature, the main stream research focuses on the likelihood or generalized estimating equations (GEE) approaches in linear and nonlinear mixed effects models (e.g., Fitzmaurice et al. 2009). In contrast, in econometric literature, the emphasis is on the likelihood and generalized method of moments (GMM) approaches in dynamic panel data models (e.g., Arellano 2003; Baltagi 2008; Hsiao 2003 2011). In particular, The GMM approach is usually based on some suitable linear transformation such as the first differencing to eliminate the unobserved subject effects (Arellano and Bover 1995; Arellano and Bond 1991; Blundell and Bond 1998). However, differencing operation may cause substantial loss of information in the data and therefore lead to the loss of estimation efficiency and inaccurate model identification. We will show through a real data example that more favorable model can be reached by applying a semiparametrically efficient estimation method to the original level data. Moreover, the model specification can be checked by our proposed diagnostic test.

In this paper, we propose a moments-based approach that is theoretically less restrictive than the likelihood-based methods and is fairly efficient and computationally tractable. This approach requires only the specification of the first two conditional moments of the unobserved subject effect given the process initial value and covariates, and does not require any other initial conditions or distributional assumptions. The data generating process can be either stationary or nonstationary, and does not need to be transformed. The so-called second-order least squares (SLS) estimator is consistent and asymptotically normally distributed when the cross section size N is large and the time series length T is fixed. In addition, this estimator reaches a semiparametric efficiency lower bound. We also propose a diagnostic test based on the SLS estimator to check the conditional moments assumption. Our extensive simulation studies show that the proposed estimator and its variants perform very well in finite sample situations and better than the GMM and likelihood based estimators in most cases.

The SLS method was first proposed by Wang (2003, 2004) to estimate the nonlinear measurement error models. It was extended to the nonlinear longitudinal data models with homoscedastic errors by Wang (2007) and to the censored linear models by Abarin and Wang (2009). Wang and Leblanc (2008) showed that under a nonlinear (homoscedastic) cross-sectional data model, the SLSE is asymptotically more efficient than the OLSE (pseudo MLE) when the error term has nonzero third moment, and both estimators are equally efficient otherwise. Kim and Ma (2012) proved that the SLSE attains the optimal semiparametric efficiency bound in general. More recently, the SLS method has also been used in optimal design problems by several researchers, e.g., Gao and Zhou (2014), Bose and Mukerjee (2015), Gao and Zhou (2017), Yin and Zhou (2017).

This paper is organized as follows. In Section 2 and Section 3 we introduce the model and the semiparametric method for estimation and testing. In Section 4 we derive the asymptotically most efficient version of the proposed estimators. In Section 5 we carry out Monte Carlo simulations to study finite sample properties of the proposed estimators and compare them with other commonly used methods. In Section 6 we apply our method to a real data set to demonstrate its practical merits. Finally, conclusions and discussion are in Section 7 and regularity conditions and mathematical proofs are in the Appendix A, Appendix B, Appendix C, Appendix D, Appendix E and Appendix F.

2. Model and SLS Estimation

Let $({\mathit{y}}_i^{\prime },{\mathit{x}}_i^{\prime },{\eta }_i),i=1,2,\dots ,N$ be independent and identically distributed random vectors where ${\mathit{y}}_i^{\prime }=(y_{i0},y_{i1},\cdots ,y_{iT})$ and ${\mathit{x}}_i^{\prime }=({\mathit{x}}_{i1}^{\prime },{\mathit{x}}_{i2}^{\prime },\dots ,{\mathit{x}}_{iT}^{\prime })$ are respectively the measurements of the response variable and p covariates taken for the ith subject over T time periods. Suppose

$$y_{it}={\alpha }_0{y}_{i(t-1)}+{\mathit{\beta }}_0^{\prime }{\mathit{x}}_{it}+{\eta }_i+{\epsilon }_{it},t=1,2,\dots ,T,$$

(1)

where ${\eta }_i$ is the unobserved subject effect and error term ${\epsilon }_{it}$ satisfies $E({\epsilon }_{it}|{\eta }_i,y_{i0},{\mathit{x}}_i)=0$, $E({\epsilon }_{it}{\epsilon }_{is}|{\eta }_i,y_{i0},{\mathit{x}}_i)={\sigma }_0^2$ if $s=t$, and zero otherwise. In addition, we assume that the conditional moments $E({\eta }_i^j|y_{i0},{\mathit{x}}_i)=f_j(y_{i0},{\mathit{x}}_i,{\mathit{\theta }}_0)$, $j=1,2$ are known up to an ℓ-dimensional unknown parameter vector ${\mathit{\theta }}_0$. This assumption is more general than the unrestricted initial conditions used by Blundell and Bond (1998) and Alvarez and Arellano (2003) to derive the conditional GLS (CGLS) and the random effects ML (RML) estimators, respectively. Note that our semiparametric assumption on ${\eta }_i$ is not as restrictive as it appears because the functional forms of $f_j(y_{i0},{\mathit{x}}_i,{\mathit{\theta }}_0)$, $j=1,2$ can be specified naturally based on some diagnostic tools as illustrated in Section 6. Moreover, any suggested specification can be tested using the test developed in Section 3. Also note that although we explicitly deal with an $AR(1)$ model for the sake of simplicity of notation, our approach can be extended to more general $AR(p)$ models as discussed later.

We propose to estimate unknown parameters in model (1) based on the first two conditional moments of the response $y_{it}$ given its initial value $y_{i0}$ and covariates ${\mathit{x}}_i$. Specifically, let ${\gamma }_0={({\alpha }_0,{\sigma }_0^2,{\mathit{\beta }}_0^{\prime },{\mathit{\theta }}_0^{\prime })}^{\prime }$ and $\Gamma \subset I{R}^{p+\ell +2}$ be the corresponding parameter space. By backward substitution in Equation (1), we obtain the reduced form equation

$$y_{it}={\alpha }_0^t{y}_{i0}+a_t({\alpha }_0){\eta }_i+{\mathit{\beta }}_0^{\prime }{\tilde{\mathit{x}}}_{it}({\alpha }_0)+{\tilde{\epsilon }}_{it}({\alpha }_0),t=1,2,...,T,$$

(2)

where $a_t(\alpha )={\sum }_{r=0}^{t-1}{\alpha }^r$, ${\tilde{\mathit{x}}}_{it}(\alpha )={\sum }_{r=0}^{t-1}{\alpha }^r{\mathit{x}}_{i(t-r)}$ and ${\tilde{\epsilon }}_{it}({\alpha }_0)={\sum }_{r=0}^{t-1}{\alpha }_0^r{\epsilon }_{i(t-r)}$. Under this model, the first two conditional moments of $y_{it}$ are given by

$$\begin{array}{ccc}\hfill {\mu }_{it}({\gamma }_0)& =& E(y_{it}|y_{i0},{\mathit{x}}_i)={\alpha }_0^t{y}_{i0}+{\mathit{\beta }}_0^{\prime }{\tilde{\mathit{x}}}_{it}({\alpha }_0)+a_t({\alpha }_0)f_1(y_{i0},{\mathit{x}}_i,{\mathit{\theta }}_0),\hfill \\ \hfill {\nu }_{its}({\gamma }_0)& =& E(y_{it}{y}_{is}|y_{i0},{\mathit{x}}_i)={\alpha }_0^{t+s}{y}_{i0}^2+a_t({\alpha }_0)a_s({\alpha }_0)f_2(y_{i0},{\mathit{x}}_i,{\mathit{\theta }}_0)\hfill \\ & & +{\mathit{\beta }}_0^{\prime }{\tilde{\mathit{x}}}_{it}({\alpha }_0){\tilde{\mathit{x}}}_{is}^{\prime }({\alpha }_0){\mathit{\beta }}_0+{\sigma }_0^2{c}_{ts}({\alpha }_0)+d_{ts}({\alpha }_0)y_{i0}{f}_1(y_{i0},{\mathit{x}}_i,{\mathit{\theta }}_0)\hfill \end{array}$$

(3)

$$\begin{array}{ccc}& & +y_{i0}{\mathit{\beta }}_0^{\prime }{\mathit{w}}_{its}({\alpha }_0)+f_1(y_{i0},{\mathit{x}}_i,{\mathit{\theta }}_0){\mathit{\beta }}_0^{\prime }{\mathit{k}}_{its}({\alpha }_0),\hfill \end{array}$$

(4)

where $c_{ts}(\alpha )={\alpha }^{t-s}{\sum }_{r=0}^{s-1}{\alpha }^{2r}$, $d_{ts}(\alpha )={\alpha }^t{a}_s(\alpha )+{\alpha }^s{a}_t(\alpha )$, ${\mathit{w}}_{its}(\alpha )={\alpha }^t{\tilde{\mathit{x}}}_{is}(\alpha )+{\alpha }^s{\tilde{\mathit{x}}}_{it}(\alpha )$ and ${\mathit{k}}_{its}(\alpha )=a_t(\alpha ){\tilde{\mathit{x}}}_{is}(\alpha )+a_s(\alpha ){\tilde{\mathit{x}}}_{it}(\alpha )$, $t\ge s$. Further, let

$${\mathit{h}}_i(\gamma )={\left(y_{it}-{\mu }_{it}(\gamma ),1\le t\le T,y_{it}{y}_{is}-{\nu }_{its}(\gamma ),1\le s\le t\le T\right)}^{\prime },\gamma \in \Gamma .$$

Then the second-order least squares (SLS) estimator for $\gamma$ is defined by

$${\widehat{\gamma }}_N=\underset{\gamma \in \Gamma }{\mathrm{argmin}}\frac{1}{N}\sum _{i=1}^N{q}_i(\gamma ),$$

(5)

where $q_i(\gamma )={\mathit{h}}_i^{\prime }(\gamma ){\mathit{W}}_i{\mathit{h}}_i(\gamma )$ and ${\mathit{W}}_i$ is a nonnegative definite matrix whose elements are real measurable functions of $(y_{i0},{\mathit{x}}_i)$. It follows from the standard M-estimation theory that the SLS estimator ${\widehat{\gamma }}_N$ has the following asymptotic properties under the regularity conditions given in Appendices Appendix A.

Theorem 1.

(1) Under Assumptions A1–A3, ${\widehat{\gamma }}_N\stackrel{a.s.}{⟶}{\gamma }_0$ as $N\to \infty$ and T is fixed.

(2) Under Assumptions A1–A6, $\sqrt{N}({\widehat{\gamma }}_N-{\gamma }_0)\stackrel{d}{\to }N(\mathbf{0},{\mathit{A}}^{-1}\mathit{B}{\mathit{A}}^{-1})$ as $N\to \infty$ and T is fixed, where

$$\mathit{A}=E\left\{\frac{\partial {\mathit{h}}_1^{\prime }({\gamma }_0)}{\partial \gamma }{\mathit{W}}_1\frac{\partial {\mathit{h}}_1({\gamma }_0)}{\partial {\gamma }^{\prime }}\right\},$$

(6)

$$\mathit{B}=E\left\{\frac{\partial {\mathit{h}}_1^{\prime }({\gamma }_0)}{\partial \gamma }{\mathit{W}}_1{\mathit{h}}_1({\gamma }_0){\mathit{h}}_1^{\prime }({\gamma }_0){\mathit{W}}_1\frac{\partial {\mathit{h}}_1({\gamma }_0)}{\partial {\gamma }^{\prime }}\right\}.$$

(7)

3. A Diagnostic Test

The estimation approach in the previous section is based on the correct specification of the first two conditional moments of the response variables. In this section we propose a test for these moments, called SW for convenience. It is designed to test hypotheses

$$H_0:E\left\{{\mathit{h}}_i({\gamma }_0)|y_{i0},{\mathit{x}}_i\right\}=\mathbf{0}vs.H_a:E\left\{{\mathit{h}}_i({\gamma }_0)|y_{i0},{\mathit{x}}_i\right\}\ne \mathbf{0}.$$

Specifically, let $\mathit{h}(\gamma )=\frac{1}{N}{\sum }_{i=1}^N{\mathit{h}}_i(\gamma )$. Then the test statistic is defined as

$$\mathrm{SW}=N{\mathit{h}}^{\prime }({\widehat{\gamma }}_N){\widehat{\mathit{G}}}_N^{-1}\mathit{h}({\widehat{\gamma }}_N),$$

(8)

where ${\widehat{\gamma }}_N$ is defined by Equation (5) and ${\widehat{\mathit{G}}}_N$ is given by

$${\widehat{\mathit{G}}}_N=\frac{1}{N}\sum _{i=1}^N{\overline{\mathit{P}}}_i({\widehat{\gamma }}_N){\mathit{h}}_i({\widehat{\gamma }}_N){\mathit{h}}_i^{\prime }({\widehat{\gamma }}_N){\overline{\mathit{P}}}_i^{\prime }({\widehat{\gamma }}_N)$$

with

$${\overline{\mathit{P}}}_i({\widehat{\gamma }}_N)=\mathit{I}-{\overline{\mathit{D}}}_N({\widehat{\gamma }}_N){\mathit{A}}_N^{-1}\frac{\partial {\mathit{h}}_i^{\prime }({\widehat{\gamma }}_N)}{\partial \gamma }{\mathit{W}}_i,$$

$${\mathit{A}}_N=\frac{1}{N}\sum _{i=1}^N\frac{\partial {\mathit{h}}_i^{\prime }({\widehat{\gamma }}_N)}{\partial \gamma }{\mathit{W}}_i\frac{\partial {\mathit{h}}_i({\widehat{\gamma }}_N)}{\partial {\gamma }^{\prime }},$$

and

$${\overline{\mathit{D}}}_N({\widehat{\gamma }}_N)=\frac{1}{N}\sum _{i=1}^N\frac{\partial {\mathit{h}}_i({\widehat{\gamma }}_N)}{\partial {\gamma }^{\prime }}.$$

The asymptotic distribution of the test statistic SW is given below.

Theorem 2.

Assume that $E\left\{{\mathit{P}}_i({\gamma }_0){\mathit{h}}_i({\gamma }_0){\mathit{h}}_i^{\prime }({\gamma }_0){\mathit{P}}_i^{\prime }({\gamma }_0)\right\}$ has full rank $K=T(T+3)/2$. Then under Assumptions A1–A6 and $H_0$, $SW\stackrel{d}{\to }{\chi }_K^2$ as $N\to \infty$ and T is fixed.

4. Optimal SLS Estimator

From Equations (6) and (7) we see that the asymptotic covariance matrix of ${\widehat{\gamma }}_N$ depends on the weights ${\mathit{W}}_i$. It is therefore desirable to chose the optimal weight so that the asymptotic variance is minimized in the following sense.

Theorem 3.

Suppose ${\mathit{U}}_1=E\left\{{\mathit{h}}_1({\gamma }_0){\mathit{h}}_1^{\prime }({\gamma }_0)|y_{10},{\mathit{x}}_1\right\}$ is nonsingular with probability one, and Assumptions A2–A6 are satisfied with ${\mathit{W}}_1={\mathit{U}}_1^{-1}$. Then the SLS estimator ${\widehat{\gamma }}_N^o$ obtained by taking ${\mathit{W}}_i={\mathit{U}}_i^{-1},i=1,2,...,N$ has asymptotic covariance matrix

$${\mathit{A}}_0^{-1}=E^{-1}\left\{\frac{\partial {\mathit{h}}_i^{\prime }({\gamma }_0)}{\partial \gamma }{\mathit{U}}_i^{-1}\frac{\partial {\mathit{h}}_i({\gamma }_0)}{\partial {\gamma }^{\prime }}\right\}.$$

(9)

Furthermore, for any SLS estimator ${\widehat{\gamma }}_N$, its asymptotic covariance matrix is such that ${\mathit{A}}^{-1}\mathit{B}{\mathit{A}}^{-1}-{\mathit{A}}_0^{-1}$ is non-negative definite.

However, since the optimal weight ${\mathit{U}}_i^{-1}$ depends on ${\gamma }_0$ and conditional moments $E({\epsilon }_{it}^j|y_{i0},{\mathit{x}}_i)$ and $E({\eta }_i^j|y_{i0},{\mathit{x}}_i),j=3,4$, the optimal SLS estimator ${\widehat{\gamma }}_N^o$ is not feasible. The corresponding feasible SLS estimator can be calculated by plugging in consistent estimators of these unknown quantities in ${\mathit{U}}_i^{-1}$. This feasible optimal SLS (FOSLS) estimator is consistent under condition (A1) in Appendix A. Moreover, the FOSLS has the same asymptotic covariance matrix as the (infeasible) optimal SLS estimator (Newey and McFadden 1994, Th. 6.1).

We also suggest another version of the FOSLS, called FOSLS1, which may be more robust to any possible stochastic dependence between ${\epsilon }_{it}$ and ${\eta }_i$, and does not require initial estimates for the third and fourth conditional moments of ${\epsilon }_{it}$ and ${\eta }_i$. It is obtained by using the weight

$${\widehat{\mathit{W}}}_i={\mathit{C}}^{\prime }\left(y_{i0},{\mathit{x}}_i,{\widehat{\mathit{\theta }}}_N^0,{\widehat{\alpha }}_N^0\right){\left(\frac{1}{N}\sum _{i=1}^N{\mathit{h}}_i^{*}({\widehat{\gamma }}_N^0){\mathit{h}}_i^{{*}^{\prime }}({\widehat{\gamma }}_N^0)\right)}^{-}\mathit{C}\left(y_{i0},{\mathit{x}}_i,{\widehat{\mathit{\theta }}}_N^0,{\widehat{\alpha }}_N^0\right),$$

(10)

where ${\widehat{\gamma }}_N^0$ is a preliminary consistent estimator of ${\gamma }_0$, and $C\left(y_{i0},{\mathit{x}}_i,\mathit{\theta },\alpha \right)$ is a transformation matrix that maps ${\mathit{h}}_i(\gamma )$ into

$${\mathit{h}}_i^{*}(\gamma )={\left(u_{it}^{*},1\le t\le T,u_{it}^{*}{u}_{is}^{*}-{\nu }_{its}^{*}({\sigma }^2,\mathit{\theta }),1\le s\le t\le T\right)}^{\prime },$$

(11)

where $u_{it}^{*}\stackrel{}{=}{y}_{it}-\alpha y_{it-1}-{\mathit{\beta }}^{\prime }{\mathit{x}}_{it}-f_1(y_{i0},{\mathit{x}}_i,\mathit{\theta })$ and ${\nu }_{its}^{*}({\sigma }_{}^2,\mathit{\theta })=f_2(y_{i0},{\mathit{x}}_i,\mathit{\theta })-f_1^2(y_{i0},{\mathit{x}}_i,\mathit{\theta })+{\sigma }_{}^2{\mathbf{1}}_{\{s=t\}}$. It can be shown that the FOSLS1 has the same asymptotic covariance matrix as the optimal SLS estimator, if ${\epsilon }_{it}$ and ${\eta }_i$ have constant second to fourth conditional central moments given the process initial value and covariate. It is worthwhile to note that the matrix C and vectors ${\mathit{h}}_i^{*}(\gamma )$ do not involve the moments in (3) and (4) which are calculated based on the reduced form (2). Therefore it is straightforward to generalize them in $AR(p)$ models.

Some researchers have studied the semiparametric efficient estimators for various dynamic panel data models. Chamberlain (1992) derived the optimal instrumental variables for the first-difference equation of model (1) under the sequential conditional moment restrictions and showed that the GMM estimator based on these optimal instrumental variables attains the semiparametric efficiency lower bound. Hahn (1997) showed that the GMM estimator based on an increasing set of instruments as the sample size grows would achieve the semiparametric efficiency bound of Chamberlain (1992). More recently, Park et al. (2007) used the geometric approach of Bickel et al. (1993) to construct a semiparametric efficient estimator under the stationary model with normal error distribution.

A natural question is whether the optimal SLS estimator efficiently uses the information in conditional moments (3) and (4). By Lemma 2 of Chamberlain (1987) the minimum bound of the asymptotic variance under $E\left\{{\mathit{h}}_i({\gamma }_0)|y_{i0},{\mathit{x}}_i\right\}=\mathbf{0}$ is given by ${\mathit{A}}_0^{-1}$ in (9). Therefore by Theorem 3 the optimal SLS estimator attains Chamberlain’s bound of variance and is a semiparametric optimal estimator in this sense.

We conclude this section by comparing the asymptotic variance of the optimal SLS estimator with that of the RML estimator which is identical to the MLE conditional on the initial observation when the errors are normally distributed. Theoretically, the optimal SLSE is at least as efficient as the RMLE by (A14)–(A16) in Appendix F. Unfortunately it is difficult to evaluate the efficiency gain of the optimal SLSE analytically, hence we compare the asymptotic variances of the two estimators numerically. We considered a large number of scenarios with various data generating processes (stationary or nonstationary) and distributions for the error and unobserved random effects.

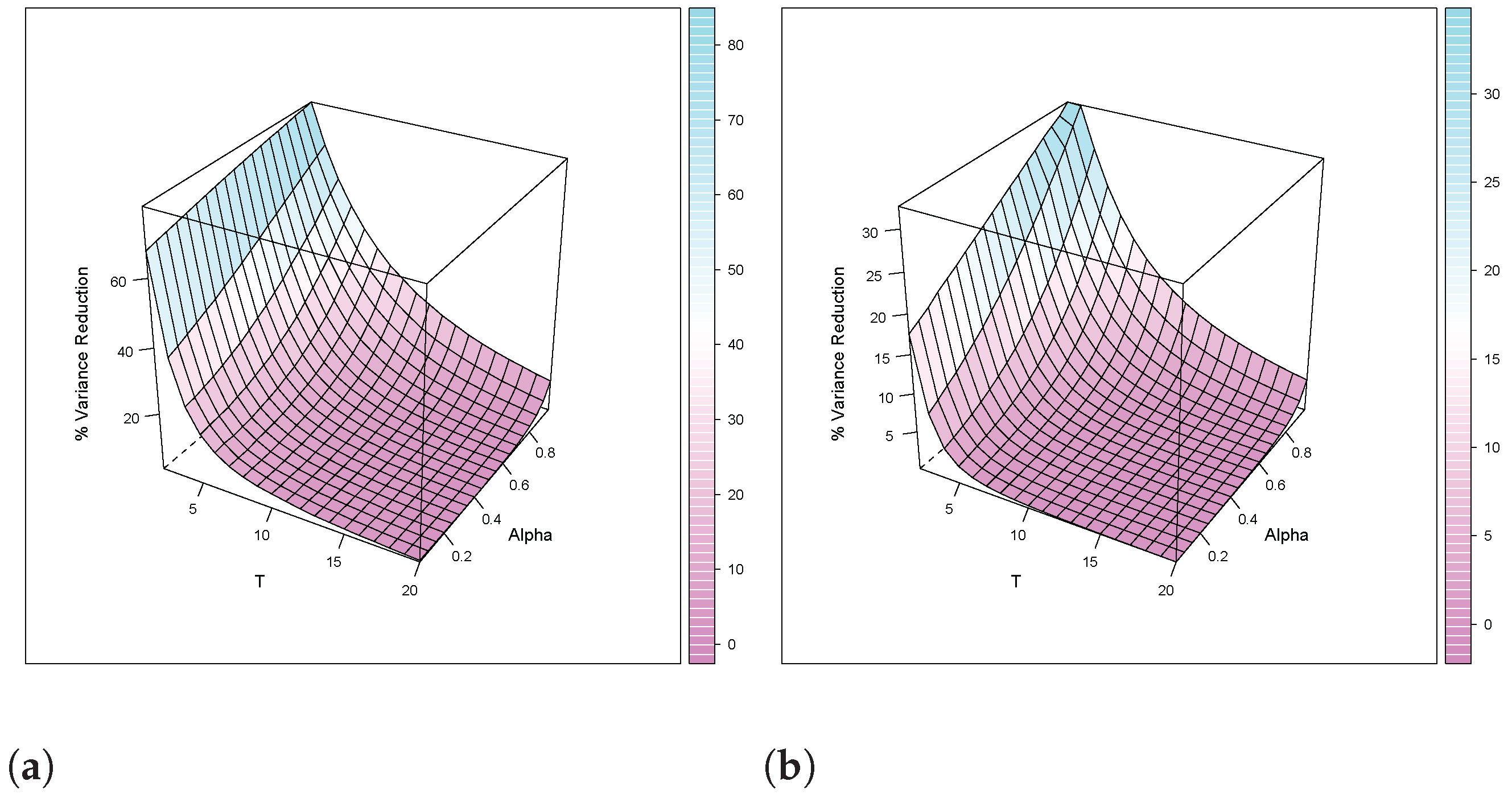
The percentage gain of efficiency in estimating ${\alpha }_0$ as a function of T and ${\alpha }_0$ is shown in Figure 1, where z-axis represents the percentage reduction in the variance of RMLE(${\alpha }_0$) by using the optimal SLSE(${\alpha }_0$). Our simulation results show convincingly that the asymptotic variance of the optimal SLSE(${\alpha }_0$) is strictly less than that of the RMLE(${\alpha }_0$) except for the case ${\mu }_{3(\epsilon )}=0$ and ${\mu }_{4(\epsilon )}=3{\sigma }_0^4$ (which is true under normal distribution), in which case both estimators have the same asymptotic variances.

5. Monte Carlo Simulation Studies

In this section we carry out extensive Monte Carlo simulations to examine the finite sample properties of FOSLS and FOSLS1 estimators, and compare them with some other popular estimators in the literature, including the linear first differenced GMM (Arellano and Bond 1991), the marginal pseudo maximum likelihood (MPML) (Arellano 2003) and the random effects pseudo maximum likelihood (RML) (Alvarez and Arellano 2003) estimators. For the sake of comparison we adopt the commonly used model setup in these literature, i.e., the model (1) with no covariates ${\mathit{x}}_{it}$ but the following specification

$$\begin{array}{ccc}\hfill E({\eta }_i|y_{i0})& =& {\theta }_{01}+{\theta }_{02}{y}_{i0},V({\eta }_i|y_{i0})=exp({\theta }_{03}),\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill E({\epsilon }_{it}^j|y_{i0})& =& {\mu }_{j(\epsilon )},E\left({({\eta }_i-{\theta }_{01}-{\theta }_{02}{y}_{i0})}^j|y_{i0}\right)={\mu }_{j(\eta )},j=3,4.\hfill \end{array}$$

(13)

This model specification is also used by Blundell and Bond (1998) to derive conditional-type estimators such as the CGLS, see also Okui (2009).

5.1. Finite Sample Properties and Comparisons

Specifically, the data are generated according to $y_{i0}\sim \mathrm{i}.\mathrm{i}.\mathrm{d}.\mathrm{N}\left(0,2/(1-{\alpha }_0^2)(1-{\alpha }_0)\right)$, ${\eta }_i|y_{i0}\sim {\theta }_{01}+{\theta }_{02}{y}_{i0}+exp({\theta }_{03})F_1$ and ${\epsilon }_{it}|{\eta }_i,y_{i0}\sim {\sigma }_0^2{F}_2$ with ${\theta }_{01}=0$, ${\theta }_{02}=c\left(1-{\alpha }_0^2\right)/2$ and ${\theta }_{03}=log\left((1-{\alpha }_0)/2\right)$, where $c,F_1,F_2$ are chosen as follows to be close to the setups in the literature.

• Normal stationary process:$c=1$ and $F_1,F_2\sim \mathrm{N}(0,1)$. Under this setup the MPML estimator is the true MLE computed using all data including the initial observations.
• Nonnormal stationary process:$c=1$ and $F_1,F_2\sim ({\chi }_{(1)}^2-1)/\sqrt{2}$.
• Normal nonstationary process:$c=20$ and $F_1,F_2\sim \mathrm{N}(0,1)$. Under this setup the y process is nonstationary in first two moments and the MPML estimator is inconsistent.
• Nonnormal nonstationary process:$c=20$ and

  (a) $F_1\sim \mathrm{N}(0,1)$, $F_2\sim ({\chi }_{(1)}^2-1)/\sqrt{2}$;	(b) $F_1\sim \mathrm{N}(0,1)$, $F_2\sim \sqrt{3/5}{t}_{(5)}$;
  (c) $F_2\sim \mathrm{N}(0,1)$, $F_1\sim ({\chi }_{(1)}^2-1)/\sqrt{2}$;	(d) $F_2\sim \mathrm{N}(0,1)$, $F_1\sim \sqrt{3/5}{t}_{(5)}$.

In all scenarios the parameter values are ${\alpha }_0=0.2,0.5,0.8$ and the sample sizes are $N=30,300$ and $T=5,10,15$. In each simulation 1000 Monte Carlo replications are done and the median estimates and median absolute deviation (MAD) are calculated to assess the performance of the estimators. To compute the FOSLS estimators, we use the RML to obtain preliminary consistent estimates of ${\gamma }_0,{\mu }_{j(\epsilon )}$ and ${\mu }_{j(\eta )},j=3,4$, and then plug them in the optimal weight ${\mathit{U}}_i^{-1}$. As mentioned earlier this does not affect the asymptotic properties of the second-step estimators.

To save space we only present the numerical results for the nonnormal-nonstationary (a) scenario in

Table 1. The MAD of FOSLS and relative MAD (bold font) of all other estimators, and their Median (regular font) for nonnormal-nonstationary scenario.

	${\mathit{\alpha }}_0=0.2$					${\mathit{\alpha }}_0=0.5$					${\mathit{\alpha }}_0=0.8$
	FOSLS	FOSLS1	RML	GMM	MPML	FOSLS	FOSLS1	RML	GMM	MPML	FOSLS	FOSLS1	RML	GMM	MPML
N	$T=5$
30	0.006	1.07	1.29	1.29	120.57	0.003	1.07	1.44	1.44	124.24	0.002	1.18	1.56	1.54	89.56
	0.200	0.20	0.20	0.20	0.90	0.500	0.50	0.50	0.50	0.94	0.800	0.80	0.80	0.80	0.96
300	0.002	0.93	1.44	1.44	394.89	0.001	0.95	1.48	1.47	413.21	0.001	0.89	1.44	1.44	255.54
	0.200	0.20	0.20	0.20	0.91	0.500	0.50	0.50	0.50	0.94	0.800	0.80	0.80	0.80	0.96
	$T=10$
30	0.005	1.26	1.38	1.34	146.48	0.003	1.32	1.55	1.52	191.90	0.001	1.16	1.46	1.45	173.13
	0.200	0.20	0.20	0.20	0.95	0.500	0.50	0.50	0.50	0.97	0.800	0.80	0.80	0.80	0.99
300	0.001	0.95	1.44	1.47	468.00	0.001	0.95	1.47	1.46	554.61	0.000	1.01	1.53	1.53	590.03
	0.200	0.20	0.20	0.20	0.95	0.500	0.50	0.50	0.50	0.97	0.800	0.80	0.80	0.80	0.99
	$T=15$
30	0.005	2.00	1.37	1.40	156.16	0.003	2.38	1.43	1.42	193.59	0.001	2.18	1.53	1.54	239.64
	0.200	0.20	0.20	0.20	0.97	0.500	0.50	0.50	0.50	0.98	0.800	0.80	0.80	0.80	0.99
300	0.001	1.06	1.50	1.52	497.46	0.001	1.10	1.56	1.57	641.36	0.000	1.18	1.59	1.60	748.73
	0.200	0.20	0.20	0.20	0.97	0.500	0.50	0.50	0.50	0.98	0.800	0.80	0.80	0.80	0.99

, where we use the MAD of the FOSLS estimator as reference and report the relative MADs for all other estimators. For the other scenarios we provide a summary and discussion of the results below.

In the normal-stationary scenario, the MAD of the FOSLS is decreasing in T and nondecreasing in ${\alpha }_0$. That the FOSLS and RML have equal asymptotic variance under the normal error components (see (A16)) appears clearly for ${\alpha }_0=0.2,0.5$, while larger values of N are required to see this fact for larger ${\alpha }_0$. As expected the MPML has the smallest MAD in almost all cases because it is the most efficient estimator under normality. However, the gap between the MPML and FOSLS is getting smaller as ${\alpha }_0$ decreases or T increases. The first-difference GMM is generally inferior and the problem of weak instruments appears clearly for large ${\alpha }_0$, which is consistent with Blundell and Bond (1998). The FOSLS1 is not reliable for small N because the numerical calculation of its weight matrix is unstable when $N<T(T+3)/2$. Moreover, the relative MADs of the FOSLS1 for $N=300$ show that the estimator has a slower convergence rate than the FOSLS, which was expected. The downward bias in FOSLS vanishes quickly as T increases.

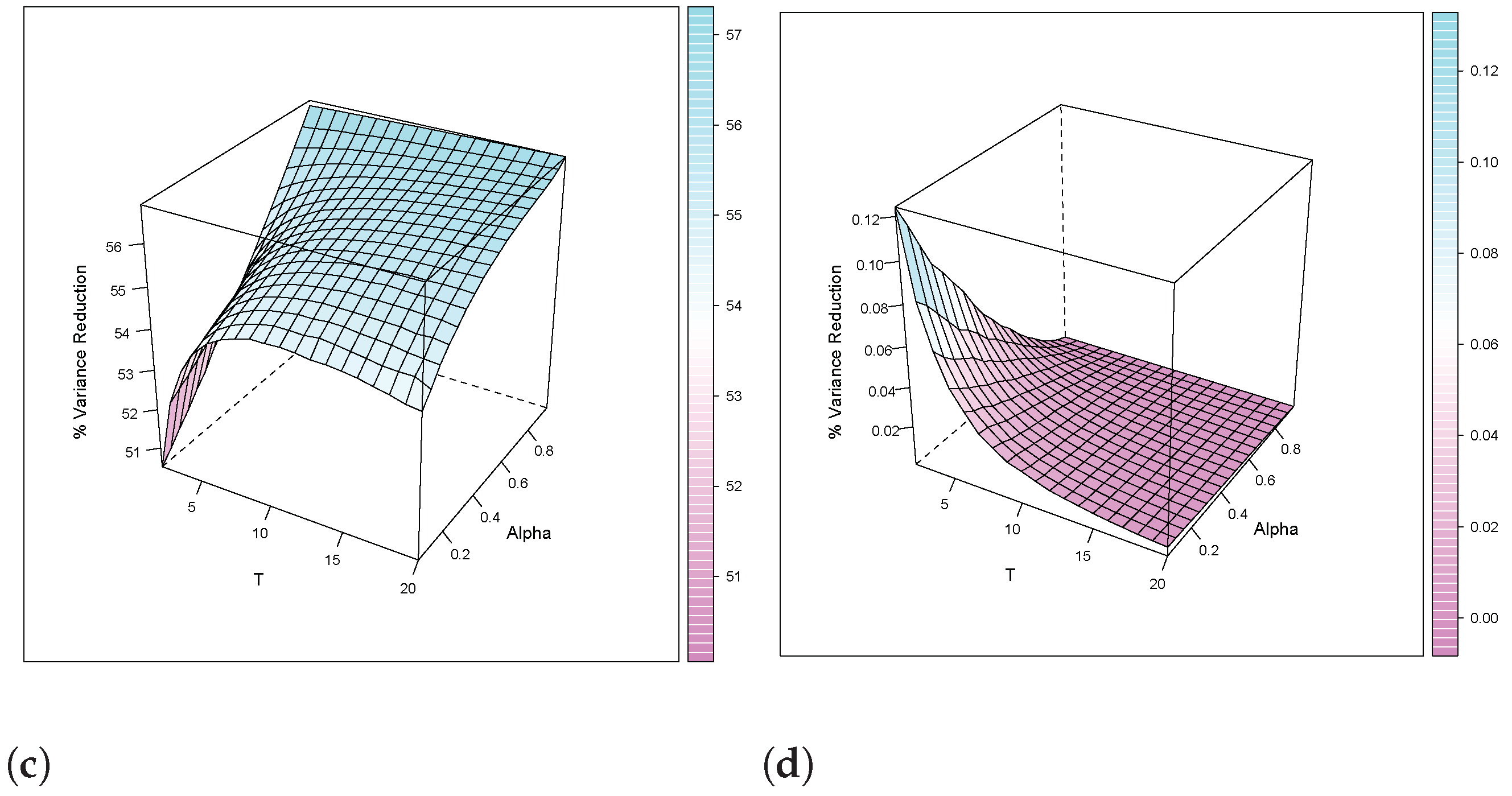
In the nonnormal-stationary scenario, the results shows wide outperformance of the FOSLS, specially for small T. The relative MADs of RML reveal that the true levels of variance reduction gained by FOSLS (see Figure 1a) require N to be larger than 300. The FOSLS competes well with the MPML for small N. Although the FOSLS1 is not reliable for small $N/T$ ratio, it performs well for $N=300$. The FOSLS has smaller bias for small N than other estimators.

In the normal-nonstationary scenario, the FOSLS, RML, and GMM compete very well for small and large N. The close performance of the FOSLS and RML is due to the normality of ${\epsilon }_{it}$. The improvement in the GMM performance is due to the nonstationarity of $y_{it}$ process. The results show clearly how the MPML breaks down everywhere under this scenario, demonstrating the consequence of misspecifying a nonstationary process. Again, the FOSLS1 requires large $N/T$ ratio to get stable so it is not recommended in this scenario.

Finally, the results of nonnormal-nonstationary scenario presented in Table 1 show the effect of the skewness of the ${\epsilon }_{it}$ distribution on the performance of the FOSLS. The RML and GMM are less efficient than the FOSLS by at least 30% for $N=30$, and by as high as 59% for $N=300$. The relative MADs of the RML for large N are consistent with Figure 1c. Although the true levels of variance reduction gained by FOSLS require N to be larger than 300, the gain of efficiency for small N is much larger than the corresponding gain in the nonnormal-stationary scenario. The numerical results of the three remaining cases (b,c,d) in this scenario clearly show the outperformance of the FOSLS(${\alpha }_0$) when ${\epsilon }_{it}$ has nonnormal distribution.

We conclude this subsection by examining to what extent the asymptotic variance formula for the OSLS in (9) can be used to approximate its finite sample counterpart. To this end we use the asymptotic formula to calculate the standard deviation of the OSLS estimator for ${\alpha }_0$ and compare with the sample RMSE calculated through Monte Carlo simulations for various values of N, T, and ${\alpha }_0$.

Table 2. The RMSE of FOSLS calculated by simulation and asymptotic formula (9) for nonnormal-nonstationary scenario.

	${\mathit{\alpha }}_0=0.2$		${\mathit{\alpha }}_0=0.5$		${\mathit{\alpha }}_0=0.8$
	Simulation	Asy Formula	Simulation	Asy Formula	Simulation	Asy Formula
N	$T=5$
30	0.00866	0.00815	0.00526	0.00501	0.00268	0.00288
300	0.00265	0.00258	0.00159	0.00158	0.00094	0.00091
	$T=15$
30	0.00729	0.00703	0.00369	0.00364	0.00119	0.00122
300	0.00229	0.00222	0.00112	0.00115	0.00038	0.00039

shows that both results are fairly close and therefore the asymptotic formula can be safely used in further inference about ${\alpha }_0$ such as confidence intervals or testing hypothesis.

5.2. Robustness of FOSLS against Unit-Root

It is well known in the literature that linear first-difference GMM is generally inferior when the autoregressive parameter ${\alpha }_0$ is close to one due to the problem of weak instruments, see e.g., Blundell and Bond (1998). On the other hand, our simulation results in the previous subsection show that the performance of FOSLS is not affected by large values of ${\alpha }_0$. Furthermore, it becomes closer to the MPML and sometimes is even better due to the efficiency gain in the case of nonnormal errors. Hence it is interesting to investigate the performance of FOSLS when ${\alpha }_0$ is very close to one (unit root case) and see if it breaks down like the GMM or it is stable like the MPML.

To answer these questions we carry out a simulation using the nonnormal-stationary model defined before. The results in

Table 3. The RMSE of FOSLS and relative RMSE (bold font) of all other estimators, and their Mean (regular font) for nonnormal near unit root scenario.

	${\mathit{\alpha }}_0=0.9$				${\mathit{\alpha }}_0=0.95$				${\mathit{\alpha }}_0=0.99$
	FOSLS	RML	GMM	MPML	FOSLS	RML	GMM	MPML	FOSLS	RML	GMM	MPML
N	$T=3$
100	0.216	1.23	4.94	0.45	0.240	1.13	5.04	0.38	0.123	2.36	10.28	0.66
	0.82	0.71	0.30	0.88	0.87	0.75	0.12	0.92	0.95	0.77	0.08	0.95
300	0.151	1.21	5.85	0.43	0.130	1.52	8.32	0.44	0.060	3.59	21.85	0.81
	0.83	0.78	0.48	0.90	0.89	0.81	0.27	0.94	0.97	0.83	0.09	0.97
	$T=6$
100	0.086	1.27	5.27	0.67	0.094	1.32	6.21	0.49	0.037	3.75	17.10	1.07
	0.87	0.83	0.52	0.90	0.91	0.86	0.43	0.94	0.98	0.88	0.43	0.97
300	0.039	1.85	7.44	0.88	0.064	1.36	7.83	0.48	0.013	7.50	47.90	1.69
	0.90	0.86	0.68	0.90	0.92	0.89	0.53	0.95	0.99	0.91	0.43	0.98

show that the FOSLS is less biased and more efficient than the RML due to the skewness in the within group errors. Although the FOSLS has larger downward bias than the MPML, the difference vanishes quickly as T and ${\alpha }_0$ increase. These results demonstrate that the FOSLS is robust in the case of near unit root and is even more efficient than the MPML for $T=6$ and ${\alpha }_0=0.99$. This may be due to nonnormality.

5.3. Performance in the Presence of Covariates

In the previous simulation studies we considered models without covariates in order to make our numerical results comparable with existing methods in the literature. Now we investigate if the finite sample performance of the FOSLS changes when the model includes covariates. A well-known work in this respect is Kiviet (1995) who compared some least squares and instrumental variable (IV) type estimators (among them the linear first-difference GMM of Arellano and Bond 1991).

Following Kiviet (1995, Section 5 and Appendix B) we consider model (1) with a covariate and $y_t$ being generated from the reduced form equation (here we omit the subscript i) $y_t=\beta {\varphi }_t+{\psi }_t+\eta /(1-\alpha )$, $t=0,1,...,T$, where ${\varphi }_t\sim AR(2)$ and ${\psi }_t\sim AR(1)$ are mutually independent stationary processes and both are independent of $\eta \sim N(0,{\sigma }_{\eta }^2)$. The orthogonality and normality assumptions of Kiviet (1995) imply $E(\eta |y_0,x_1,\dots ,x_T)={\theta }_2{y}_0+{\theta }_4{x}_1$ and $V(\eta |y_0,x_1,\dots ,x_T)=exp({\theta }_3)$ as in our notation in (12).

Kiviet (1995) reported simulation results for 14 different combinations (designs) of parameter values and sample sizes. We have simulated all the 14 designs but only present the results for four designs to save space.

Table 4. Bias, standard deviation and RMSE of estimators for Kiviet (1995) model with a covariate, $N=100$.

		Bias		Std		RMSE
Design	Estimator	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\alpha }$	$\mathit{\beta }$
II	GMM	−0.029	0.002	0.388	0.130	0.396	0.131
	RML	−0.005	−0.006	0.106	0.093	0.107	0.094
	FOSLS	−0.005	−0.006	0.107	0.098	0.107	0.099
VI	GMM	−0.060	−0.026	0.304	0.065	0.313	0.066
	RML	−0.021	0.023	0.059	0.046	0.059	0.047
	FOSLS	−0.020	0.023	0.063	0.047	0.063	0.048
X	GMM	−0.074	−0.011	0.065	0.309	0.067	0.309
	RML	−0.004	0.009	0.048	0.182	0.048	0.183
	FSOLS	−0.005	0.009	0.048	0.183	0.048	0.184
XII	GMM	−0.038	−0.019	0.088	0.344	0.096	0.344
	RML	0.000	0.006	0.058	0.178	0.058	0.179
	FOSLS	−0.030	0.003	0.058	0.180	0.058	0.180

contains the bias, standard deviation and root mean squared error of the FOSLS, RML, and linear first-difference GMM (Arellano and Bond 1991) for $\alpha$ and $\beta$. As expected, the RML (which is the conditional MLE) is the best in all cases because the data are generated using the normal distribution. However, the FOSLS (which is asymptotically as efficient as the RML) is very close to the RML. These results show that in the presence of strictly exogenous variable the FOSLS is a good alternative to the most efficient RML under normality. The calculated summary statistics of GMM are different than the corresponding values of GMM1 in Kiviet (1995), probably due to two errors in his equation B6 where ${\xi }_0$ and ${\xi }_1$ should be standardized. We have also done another simulation under nonnormal-nonstationary setup and obtained similar results as in Table 1. They also clearly show the outperformance of FOSLS compared to RML due to deviation from normality.

6. Application

In this section we use a real data example to demonstrate the practical usefulness of the SLS approach in comparison with the IV approach and to assess the practical gain of efficiency over the RML estimator. In particular, we use a data set published in Wooldridge (2010) and downloadable at http://mitpress.mit.edu/sites/default/files/titles/content/wooldridge/statafiles.zip (as of 28 April 2014). The dataset airfare.dta contains data on airfares, number of passengers, distance, and the market share of the largest carrier for each of the top 1149 city-pair markets within the contiguous 48 US states for the fourth quarters of 1997 through 2000. A detailed description of the data can be found at http://academic.reed.edu/economics/parker/s10/312/Asgns/proj3.html (as of 28 April 2014).

The main factors that influence airfares are the flight distance (ldist), average number of passengers (lpassne), and market concentration (concen). All variables except concen are measured in logarithmic scale. However, while the first factor is time invariant exogenous variable, the other two factors are clearly endogenous because they are also influenced by the airfare. Since the airlines usually set the current airfare by adjusting the previous year’s fare, a linear dynamic regression model with unobserved route heterogeneity and time dummies may be appropriate to measure the effect of the determinants. Indeed, from bivariate scatterplots one can clearly see that the linear dependence between the current and previous airfares, lfare and lfare1 respectively, and moderate positive linear association between lfare and ldist. However, although theoretically concen and lfare should be positively correlated, this is not clearly seen. A possible explanation is that the relation is masked by the negative correlation between concen and ldist, given the positive correlation between lfare and ldist.

In light of these considerations, it is reasonable to start with the following model which includes time dummies $D99$, $D00$ for years 1999, 2000, respectively:

$$\begin{array}{ccc}\hfill lfar{e}_{it}& =& {\alpha }_0+{\alpha }_{1}lfar{e}_{i(t-1)}+{\beta }_{1}ldis{t}_i+{\beta }_{2}conce{n}_{it}+{\beta }_{3}conce{n}_{i(t-1)}\hfill \\ & & +{\beta }_{4}lpasse{n}_{it}+{\beta }_{5}lpasse{n}_{i(t-1)}+{\beta }_{6}D99+{\beta }_{7}D00+{\eta }_i+{\epsilon }_{it}.\hfill \end{array}$$

(14)

We first calculate the naive ordinary least squares (OLS) estimates of the proposed Equation (14) which are shown in the OLS column of

Table 5. The models fitted to airfare data with coefficient estimates in bold and standard errors in regular font. The standard errors of FOSLS and RML are computed using (9) and (A14), respectively.

	Model-I				Model-II			Model-III			Model-IV
Coef.	OLS	GMM2	RML	FOSLS	GMM2	RML	FOSLS	GMM2	RML	FOSLS	GMM2	RML	FOSLS
Const: ${\theta }_0$	0.153	—	0.256	−0.122	—	0.248	0.723	—	0.243	0.786	—	0.279	0.708
	—	—	0.032	0.032	—	0.026	0.025	—	0.010	0.010	—	0.051	0.050
lfare1: ${\alpha }_1$	0.929	0.216	0.374	0.536	0.216	0.377	0.461	0.157	0.373	0.817	0.169	0.147	0.823
	—	0.100	0.039	0.033	0.100	0.014	0.013	0.080	0.009	0.009	0.072	0.017	0.017
ldist: ${\beta }_1$	0.031	—	0.049	0.066	—	0.051	0.091	—	0.052	−0.007	—	0.062	−0.019
	—	—	0.004	0.004	—	0.003	0.003	—	0.001	0.001	—	0.006	0.006
concen: ${\beta }_2$	0.119	−0.849	0.108	0.048	−0.849	0.091	0.162	−0.217	0.080	0.070	−0.842	0.095	0.077
	—	0.449	0.018	0.018	0.449	0.011	0.011	0.167	0.003	0.003	0.389	0.020	0.019
concen1: ${\beta }_3$	−0.076	0.325	0.013	0.040	0.325	−0.015	−0.032	—	—	—	0.320	0.000	−0.106
	—	0.215	0.022	0.022	0.215	0.011	0.011	—	—	—	0.187	0.020	0.019
lpassen: ${\beta }_4$	−0.374	−0.404	−0.367	−0.556	−0.404	−0.367	−0.108	−0.450	−0.367	−0.094	−0.382	−0.333	−0.084
	—	0.081	0.006	0.006	0.081	0.004	0.004	0.057	0.002	0.002	0.060	0.007	0.007
lpassen1: ${\beta }_5$	0.374	0.103	0.175	0.427	0.103	0.176	−0.014	0.106	0.175	0.005	—	—	—
	—	0.141	0.021	0.019	0.141	0.006	0.006	0.111	0.003	0.003	—	—	—
D99: ${\beta }_6$	0.000	0.003	0.016	0.009	0.003	0.016	0.037	0.020	0.016	−0.017	0.005	0.023	−0.014
	—	0.013	0.003	0.003	0.013	0.002	0.002	0.006	0.001	0.001	0.012	0.003	0.003
D00: ${\beta }_7$	0.042	0.070	0.074	0.060	0.070	0.073	0.092	0.087	0.073	−0.003	0.078	0.090	0.073
	—	0.015	0.003	0.003	0.015	0.003	0.002	0.011	0.001	0.001	0.012	0.003	0.003
	Diagnostic Statistics
SW/Sargan		6.41		20.98	6.41		4.01	13.90		335.80	8.16		8545.16
p-value		0.268		0.013	0.268		0.911	0.031		0.000	0.226		0.000
RMSE	0.09	5.12	4.02	3.23	5.12	4.04	2.66	5.12	4.07	0.69	5.12	6.01	0.74

. Although the OLSE are not consistent due to the correlation between ${\eta }_i$ and $lfar{e}_{i(t-1)}$, the high value of $R^2=0.95$ reflects strong explanatory power of the regressors. So we refit the model using the two stage linear first differenced GMM (GMM2) of Arellano and Bond (1991) and the lags of order at least two of $(lfare,concen,lpassen)$ as instrumental variables to deal with the possible endogeneity of these variables. The estimates are calculated using STATA 13.0 and the results are shown in Table 5 under Model-I.

Wooldridge (2010, p. 373) used the GMM2 to fit a first order linear dynamic model with only concen (treated as strictly exogenous) and dummy variables and obtained the estimated autoregressive parameter 0.333 which is not far from ours. According to the reported value of Sargan test (see Table 5), the GMM sequential moments based on the reduced form of model (14) are not rejected. However, the estimated elasticity of lfare with respect to concen is negative (p-value $=0.059$). A possible explanation for this unexpected sign is the problem of weak instruments which is likely to occur in identifying ${\mathit{\beta }}_2$ given the strong positive linear correlation between concen and concen1. This is similar to the situation where the first differenced GMM estimator is used to estimate the autoregressive parameter when it is close to one (Blundell and Bond 1998). This problem causes inflation in the coefficient variance and leads to unreliable estimates. This is an example where the RE approach with the level data is preferred over the FE approach with differenced data, because the former does not depend on the instrumental variables and hence is able to give more reliable estimates.

However, since the sequential moments are correctly specified in Model-I, the GMM estimates can still be used to recover the within group errors ${\epsilon }_{it}$ and route effect ${\eta }_i$. We follow Arellano (2003, p. 118–19) to estimate the time effect for year 1998 and subsequently ${\eta }_i$. Then realizations of ${\epsilon }_{it}$ are obtained directly from Equation (14). Since bivariate scatterplots of ${\widehat{\eta }}_i$ and the initial values (1997) of the variables (lfare0, concen0, lpassen0, and ldsit0) show possible linear relationships between ${\eta }_i$ and these initial values, we fit the following auxiliary equation where all coefficients are significant at 0.01 level of significance:

$${\widehat{\eta }}_i=-5.507+0.641lfar{e}_{i0}+0.464conce{n}_{i0}-0.041ldis{t}_{i0}+0.286lpasse{n}_{i0}.$$

(15)

Further, simple diagnostics show that ${\widehat{\epsilon }}_{it}$ have constant variance across time and no significant autocorrelation, hence the assumptions on ${\eta }_i$ and ${\epsilon }_{it}$ seem reasonable for model (14). These assumptions will be implicitly tested by using our SW test latter.

Based on Equation (15) we use the ‘lme’ command in R to calculate the RML estimates of the following equation and the results are given in Table 5 under Model-I.

$$\begin{array}{ccc}\hfill lfar{e}_{it}& =& {\theta }_0+{\alpha }_{1}lfar{e}_{i(t-1)}+{\beta }_{1}ldis{t}_i+{\beta }_{2}conce{n}_{it}+{\beta }_{3}conce{n}_{i(t-1)}\hfill \\ & & +{\beta }_{4}lpasse{n}_{it}+{\beta }_{5}lpasse{n}_{i(t-1)}+{\beta }_{6}D99+{\beta }_{7}D00+{\theta }_{1}lfar{e}_{i0}\hfill \\ & & +{\theta }_{2}conce{n}_{i0}+{\theta }_{3}lpasse{n}_{i0}+{\eta }_i^{*}+{\epsilon }_{it}.\hfill \end{array}$$

(16)

A normal QQ plot of the corresponding residuals ${\widehat{\epsilon }}_{it}$ shows a flat tail symmetric distribution that can be approximated by a Student t distribution with df $=5$, indicating the possibility of efficiency gain by applying the FOSLS estimator. Hence we use the sample skewness and kurtosis of ${\widehat{\epsilon }}_{it}$ and ${\widehat{\eta }}_i^{*}$ to calculate the optimal weight matrix for the FOSLS. To save space we report only the estimated coefficients of the main factors in Table 5, where the standard errors of GMM2 are computed using the robust formula, while the standard errors of FOSLS and RML are computed using Formula (9) and (A14), respectively.

In Model-I, while the Sargan test does not reject the GMM sequential moments (p-value $=0.268$), our SW test shows fairly strong evidence against the first and second moment specification given by Equations (3) and (4) (p-value $=0.013$). This motivates us to check the reliability of SW test by examining its empirical sampling distribution under (3) and (4) as follows. First, we use the RML estimates of Model-I to generate data from (16), and draw ${\eta }_i^{*}$ and ${\epsilon }_{it}$ from Student t distribution with df $=6$ and 5 respectively to be as close as possible to the estimated residuals and random effect of Model-I. Second, we use the generated data to fit (16) using the RML followed by FOSLS and then calculate the SW statistic. We repeat these two steps 1000 times to obtain an approximation to the sampling distribution of SW statistics under $H_0$. 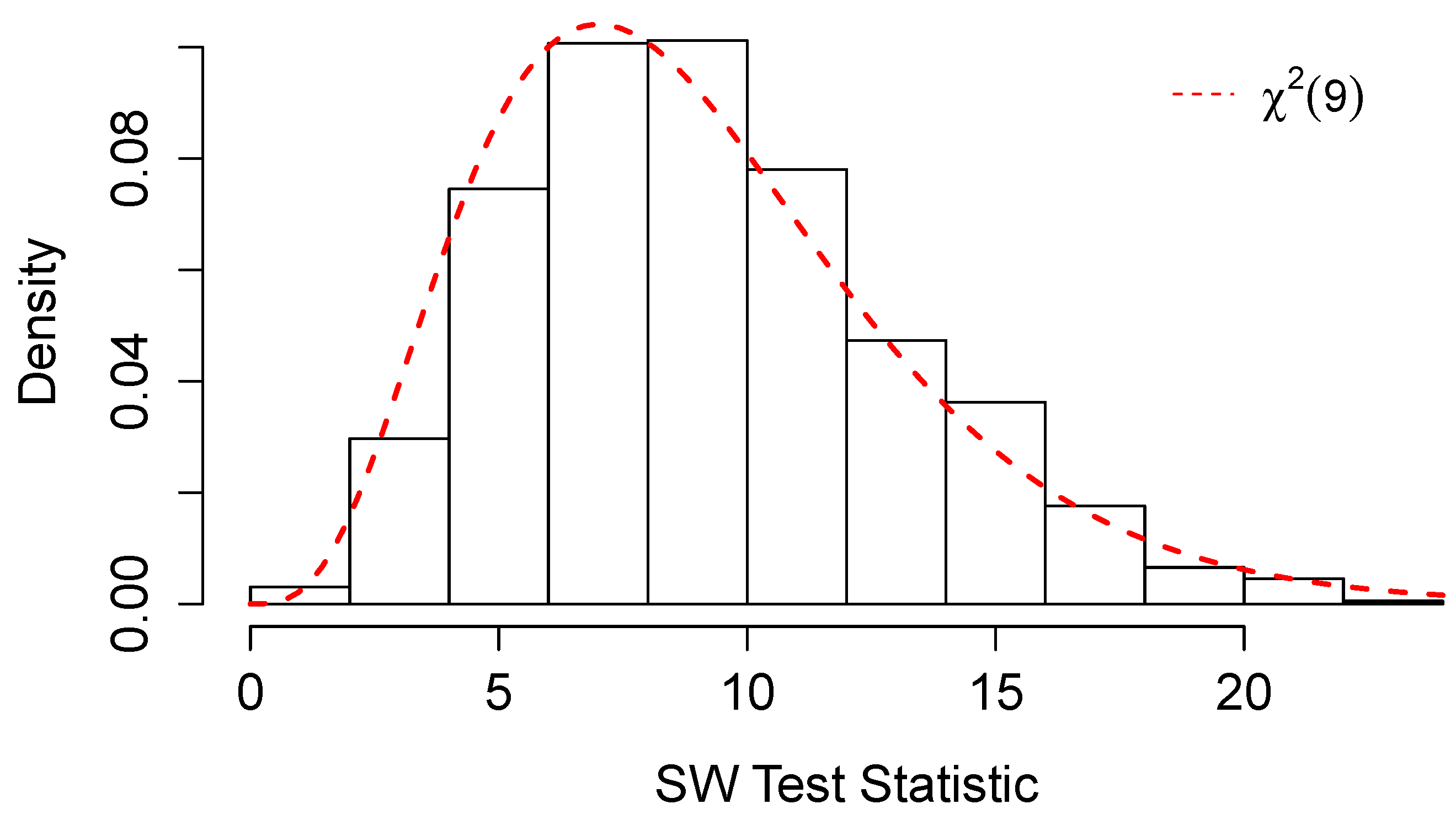Figure 2 confirms that a sample size of 1149 routes is sufficient for the empirical sampling distribution to be close to the asymptotic one ${\chi }_9^2$ under $H_0$. Consequently Model-I needs to be modified by adding or eliminating some variables to pass the SW test.

To proceed, we fit (16) again without concen0 because it is not of main interest and has weak correlation with ${\widehat{\eta }}_i$. This leads to Model-II which contains the same explanatory variables as Model-I and of course the same value of Sargan test (6.41). On the other hand, the value of SW statistic drops to 4.01 which is insignificant at any reasonable level of significance. This suggests that Model-II should be used for testing purpose provided that the signs of FOSLS estimates are consistent with the economic theory. The robust standard errors of the FOSLS are computed by Theorem 1 and are reported in

Table 6. Model-II robust standard errors of FOSLS calculated by Theorem 1.

${\mathit{\theta }}_0$	${\mathit{\alpha }}_1$	${\mathit{\beta }}_1$	${\mathit{\beta }}_2$	${\mathit{\beta }}_3$	${\mathit{\beta }}_4$	${\mathit{\beta }}_5$	${\mathit{\beta }}_6$	${\mathit{\beta }}_7$
Const.	lfare1	ldist	concen	concen1	lpassen	lpassen1	D99	D00
0.061	0.041	0.007	0.034	0.034	0.026	0.023	0.004	0.005

, according to which two variables concen1 and lpassen1 are the candidates to be dropped from the model.

Model-III is obtained by dropping concen1 only from Model-II, but this new specification is rejected by both Sargan and SW test. Consequently Model-IV is obtained by dropping lpassen1 only from Model-II. Interestingly, while SW test rejects Model-IV specification, Sargan test doesn’t reject the GMM sequential moments of this model. However, the GMM estimate of ${\beta }_2$ is negative, which contradicts the economic theory. It follows that Model-IV is not desirable and instead Model-II is preferred. It does include both concen1 and lpassen1 although they may be insignificant according to the robust standard errors. On the other hand, if the standard errors in Table 5 are used, then both concen1 and lpassen1 are significant according to FOSLS and only lpassen1 is according to RML. Since Model-III is rejected by SW test, it follows that using the information inherent in the fourth moment through FOSLS is effective in keeping the variable concen1 in Model-II.

7. Conclusions and Discussion

We studied the SLS approach as an alternative to the commonly used random effects ML (RML) or differenced-GMM estimation for linear dynamic panel data models. Our approach is based on the first two conditional moments of the outcome process and does not postulate any distributional assumptions on the error components in the model. The asymptotic and finite sample properties and practical merits of the proposed estimators are thoroughly investigated.

This research reveals the following interesting new findings. First, differencing data and using instrumental variables may cause substantial loss of information and produce misleading relations, specially when the time varying variables are generated from autoregressive process with high autocorrelation (which is common in economic data). In such a case the linear first-differenced GMM or other similar methods not only are unable to estimate the effect of the time invariant variables, but also, more harmfully, weakly identify the effect of the time variant explanatory variables. In contrast the SLS approach makes use of the information inherent in the level data and therefore can improve the estimation precision and the goodness of fit considerably.

Second, the information in the sample skewness and kurtosis of the within group residuals can be utilized by our OSLS to gain more efficiency over the RML and consequently save important explanatory variables from being wrongly eliminated. In other words, by using the extra efficiency of the OSLS one can avoid falling into misspecification traps. Third, our newly proposed diagnostic test proved to be very useful not only in validating the working conditional moments but also for model selection purpose, while usual goodness of fit criteria such as RMSE, $R^2$ or AIC may be misleading when the model is incorrectly specified.

We have explicitly dealt with an $AR(1)$ model for the simplicity of notation. However, our approach can be extended to more general $AR(p)$ models. For example, It is straightforward to calculate the FOSLS1 in Section 4 using a generalized form of the transformation matrix C and the deviation form of the moments as in (10) and (11).

This work also raises some interesting points for future research. Although our diagnostic test provides a systematic built-in tool to validate the model conditional moments assumption, in practice it would be interesting to run some sensitivity analysis to investigate the consequences of possible non-rejected deviations from this assumption. It would also be interesting to study the properties of the SW test and extend it to check the working assumption on the third and fourth moments. Last but not least, other general methods such as GMM or equivalently estimating equations applied on level data could have similar asymptotic properties as our approach. However, it is important and worthwhile to compare their finite sample properties and practical implications in real data analysis. The current work provides a complete set of tools for the inference in linear dynamic models with level data which has not been studied so far in the literature.