Efficient Variance Reduction for American Call Options Using Symmetry Arguments
Abstract
1. Introduction
2. Pricing Derivatives with Early-Exercise Features
2.1. The Valuation Problem
2.2. Least-Squares Monte Carlo
2.3. Put-Call Symmetry
3. Empirical Results
3.1. Variance Reduction for Call and Put Options
3.2. Variance Reduction and Symmetric Pricing
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Variance Reduction for American Option Prices
Appendix A.1. Variance Reduction Techniques
Appendix A.2. Implementation Issues
Appendix A.3. Selecting the Optimal Importance Density
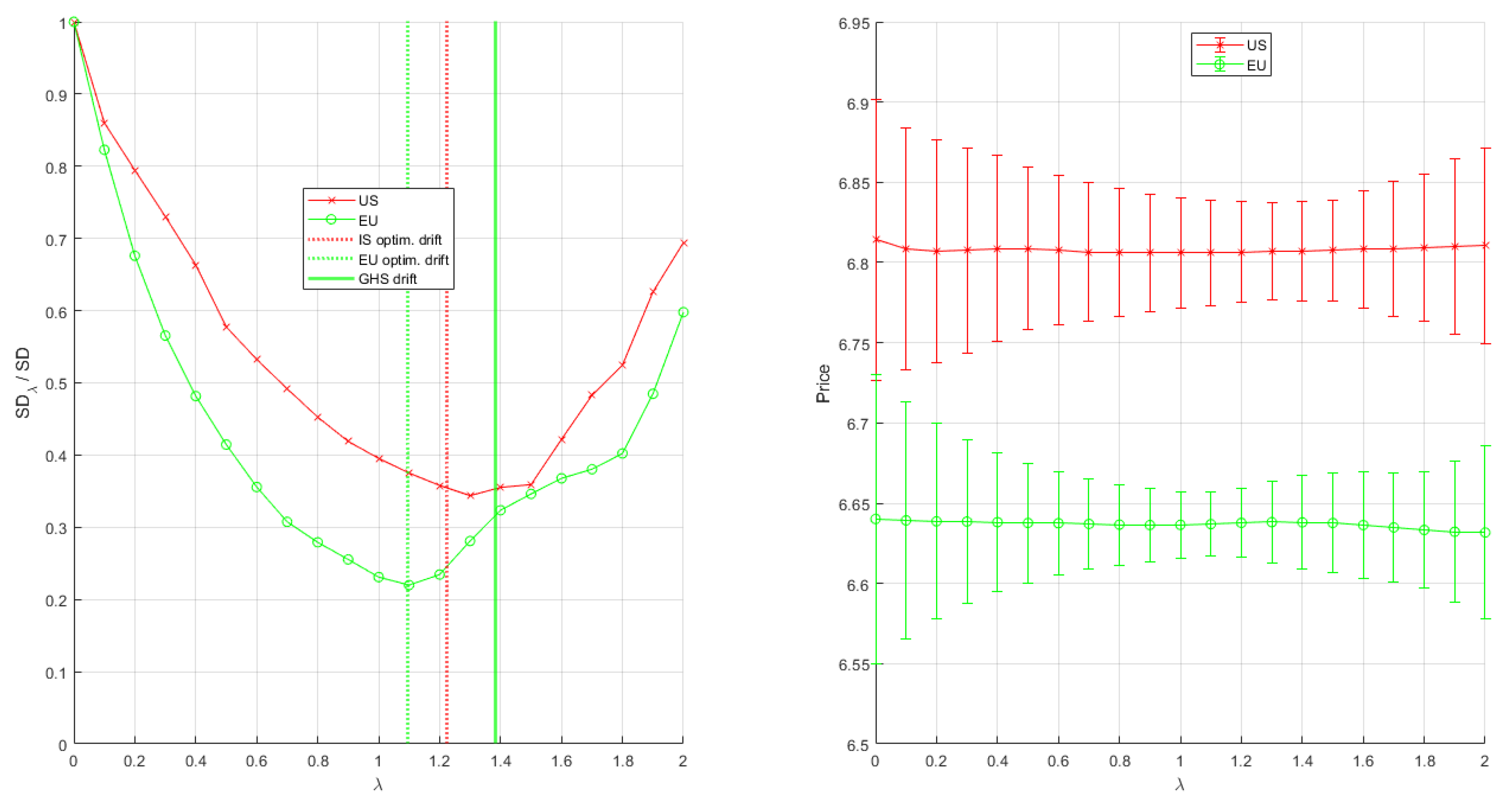
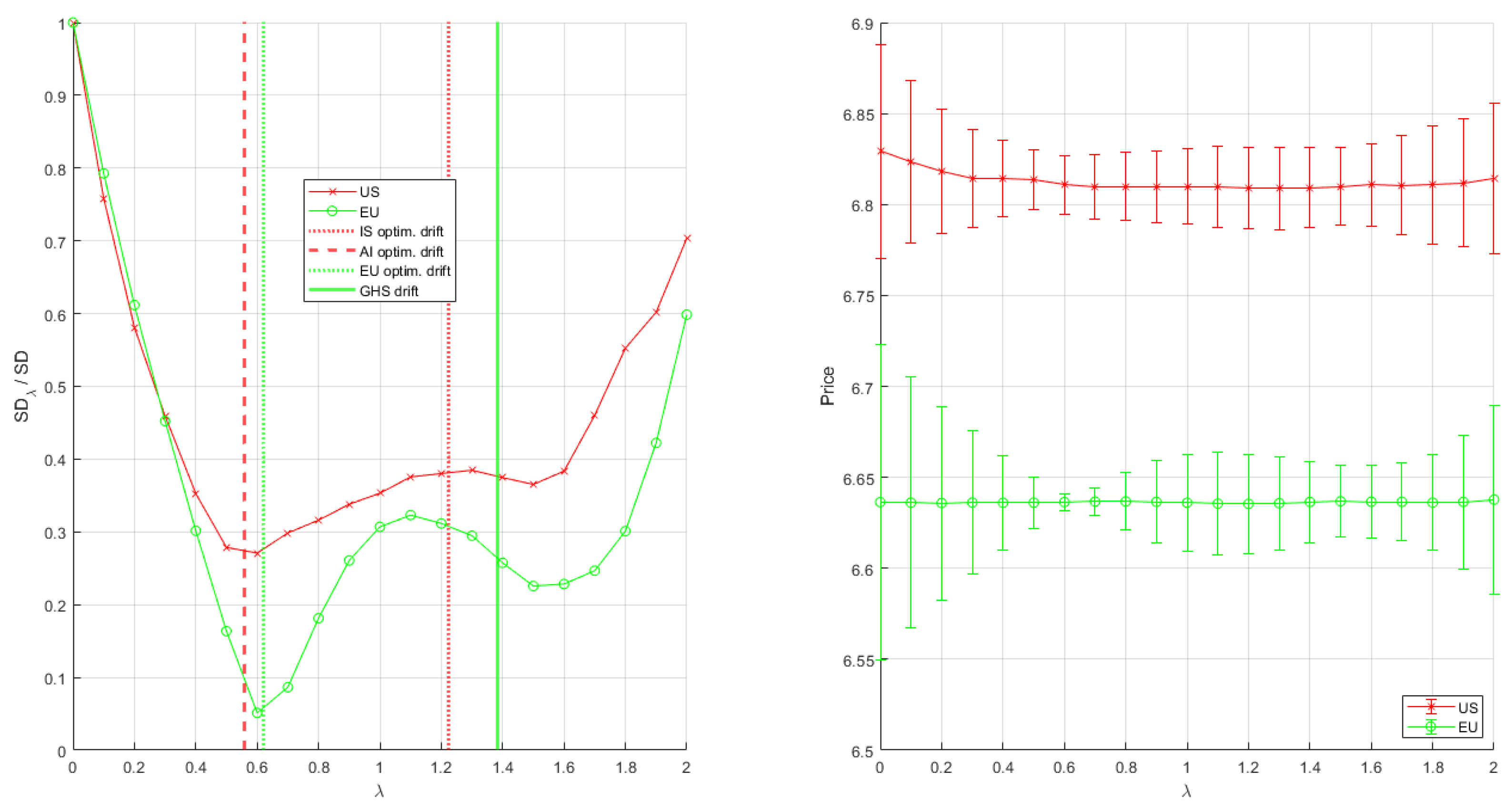
Appendix B. Additional Figures


| 1 | For additional references and examples see Chapter 8 of Glasserman (2003). |
| 2 | In our implementation we simply set such that the continuation value is the fitted value of a polynomial regression of order . This approach has been shown to be reliable with the LSM, though other orthogonal bases like Laguerre, Legendre, Hermite, or Chebyshev polynomials may be considered as well. For more details about orthogonal bases, refer to Abramowitz and Stegun (1948). |
| 3 | Appendix A discusses the variance reduction techniques and their implementation for American options. |
| 4 | The out-of-sample plots corresponding to Figure 4 that shows this are available on request. |
| 5 | When the price of a European option replicating the payoff of the American option at maturity is not readily available, one has to resort to using different European options with simpler characteristics. For instance, there is no closed-form formula for the price of an arithmetic Asian option, so the price of a geometric Asian option may be used as a control variate. Another case is if the computation of a European option prices is not feasible for a given underlying diffusion process, where the European price assuming a different process can be used. Although in both cases the European option does not replicate the American option’s payoff at maturity, their values are correlated enough to serve as adequate control variates. |
| 6 | Other interesting sampling strategies for European option pricing could potentially be extended to the LSM algorithm. Chapter 4 of Glasserman (2003) presents several cases of European-style derivatives with rare and path-dependent payoffs where the application of importance sampling and stratification techniques prove extremely efficient. For instance, in the case of a deep OTM knock-in option, the exponential change of measure of the option can be dynamically adjusted such that asset prices are first directed toward the barrier, and once the barrier has been hit, a new change of measure directs asset prices toward the money. |
References
- Abramowitz, Milton, and Irene A. Stegun. 1948. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Washington, DC: US Government Printing Office, vol. 55.
- Arouna, Bouhari. 2004. Robbins-Monro Algorithms and Variance Reduction in Finance. Journal of Computational Finance 7: 35–62. [Google Scholar] [CrossRef]
- Barraquand, Jérôme, and Didier Martineau. 1995. Numerical Valuation of High Dimensional Multivariate American Securities. Journal of Financial and Quantitative Analysis 30: 383–405. [Google Scholar] [CrossRef]
- Bolia, Nomesh, Sandeep Juneja, and Paul Glasserman. 2004. Function-Approximation-Based Importance Sampling for Pricing American Options. Paper presented at the 2004 Winter Simulation Conference, Washington, DC, USA, December 5–8, Proceedings (IEEE Cat. No.04CH37614C). vol. 1, pp. 604–11. [Google Scholar]
- Brealey, Richard A., Stewart C. Myers, Franklin Allen, and Pitabas Mohanty. 2018. Principles of Corporate Finance, 12/e. New York: McGraw-Hill Education, vol. 12. [Google Scholar]
- Broadie, Mark, and Menghui Cao. 2008. Improved Lower and Upper Bound Algorithms for Pricing American Options by Simulation. Quantitative Finance 8: 845–61. [Google Scholar] [CrossRef]
- Broadie, Mark, and Paul Glasserman. 2004. A Stochastic Mesh Method for Pricing High-Dimensional American Options. Journal of Computational Finance 7: 35–72. [Google Scholar] [CrossRef]
- Broadie, Mark, Paul Glasserman, and Gautam Jain. 1997. Enhanced Monte Carlo Estimates for American Option Prices. Journal of Derivatives 5: 25–44. [Google Scholar] [CrossRef]
- Detemple, Jérôme. 2001. American Options: Symmetry Properties. In Option Pricing, Interest Rates and Risk Management. Edited by Elyès Jouini, Jakša Cvitanić and Marek Musiela. Cambridge: Cambridge University Press. [Google Scholar]
- Duan, Jin-Chuan, and Jean-Guy Simonato. 1998. Empirical Martingale Simulation for Asset Prices. Management Science 44: 1218–33. [Google Scholar] [CrossRef]
- Glasserman, Paul. 2003. Monte Carlo Methods in Financial Engineering. New York: Springer Science & Business Media, vol. 53. [Google Scholar]
- Glasserman, Paul, Philip Heidelberger, and Perwez Shahabuddin. 1999. Asymptotically Optimal Importance Sampling and Stratification for Pricing Path-Dependent Options. Mathematical Finance 9: 117–52. [Google Scholar] [CrossRef]
- Juneja, Sandeep, and Himanshu Kalra. 2009. Variance Reduction Techniques for Pricing American Options Using Function Approximations. Journal of Computational Finance 12: 79. [Google Scholar] [CrossRef]
- Lemieux, Christiane, and Jennie La. 2005. A Study of Variance Reduction Techniques for American Option Pricing. Paper presented at the 2005 Winter Simulation Conference, Orlando, FL, USA, December 4–7; Proceedings (IEEE Cat. No.05CH37732C). p. 8. [Google Scholar]
- Longstaff, Francis A., and Eduardo S. Schwartz. 2001. Valuing American Options by Simulation: A Simple Least-Squares Approach. The Review of Financial Studies 14: 113–47. [Google Scholar] [CrossRef]
- McDonald, Robert L., and Mark D. Schroder. 1998. A Parity Result for American Options. Journal of Computational Finance 1: 5–13. [Google Scholar] [CrossRef]
- Morales, Manuel. 2006. Implementing Importance Sampling in the Least-Squares Monte Carlo Approach for American Options. Montreal: University of Montreal. [Google Scholar]
- Moreni, Nicola. 2003. Pricing American Options: A Variance Reduction Technique for the Longstaff-Schwartz Algorithm. Technical Report. 2003-256. Champs-sur-Marne: CERMICS-ENPC. [Google Scholar]
- Rasmussen, Nicki S. 2005. Control Variates for Monte Carlo Valuation of American Options. Journal of Computational Finance 9: 1. [Google Scholar] [CrossRef]
- Royden, Halsey Lawrence. 1988. Real Analysis. Englewood Cliffs: Prentice Hall. [Google Scholar]
- Stentoft, Lars. 2004. Assessing the Least Squares Monte-Carlo Approach to American Option Valuation. Review of Derivatives Research 7: 129–68. [Google Scholar] [CrossRef]
- Stentoft, Lars. 2014. Value Function Approximation or Stopping Time Approximation: A Comparison of Two Recent Numerical Methods for American Option Pricing Using Simulation and Regression. Journal of Computational Finance 18: 1. [Google Scholar] [CrossRef]
- Su, Yi, and Michael C. Fu. 2000. Importance Sampling in Derivative Securities Pricing. Paper presented at the 2000 Winter Simulation Conference, Orlando, FL, USA, December 10–13, Proceedings (Cat. No. 00CH37165). vol. 1, pp. 587–96. [Google Scholar]
- Tian, Tianhai, and Kevin Burrage. 2002. Accuracy Issues of Monte-Carlo Methods for Valuing American Options. The ANZIAM Journal 44: 739–58. [Google Scholar] [CrossRef][Green Version]
- Vázquez-Abad, Felisa J., and Daniel Dufresne. 1998. Accelerated Simulation for Pricing Asian Options. Paper presented at the 1998 Winter Simulation Conference, Washington, DC, USA, December 13–16, Proceedings (Cat. No. 98CH36274). vol. 2, pp. 1493–500. [Google Scholar]




| Call | Symmetric Put | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | K | A | C | I | AC | AI | CI | ACI | A | C | I | AC | AI | CI | ACI | |
| 1 | 36 | 0.1 | 0.5 | 8.5 | 1.1 | 9.0 | 1.3 | 7.9 | 8.9 | 0.4 | 10.0 | 0.9 | 10.5 | 1.1 | 9.5 | 10.6 |
| 1 | 36 | 0.2 | 1.2 | 7.6 | 1.4 | 7.2 | 1.6 | 7.4 | 7.4 | 1.2 | 11.2 | 1.1 | 11.6 | 1.3 | 11.1 | 12.8 |
| 1 | 36 | 0.3 | 0.9 | 6.8 | 1.6 | 6.6 | 1.9 | 6.8 | 6.7 | 1.5 | 11.4 | 1.1 | 12.8 | 1.3 | 11.4 | 14.4 |
| 1 | 36 | 0.4 | 0.6 | 6.1 | 1.8 | 5.7 | 2.2 | 6.2 | 5.8 | 1.5 | 12.5 | 1.1 | 13.4 | 1.2 | 12.6 | 15.1 |
| 1 | 38 | 0.1 | 1.3 | 8.7 | 1.3 | 8.7 | 1.6 | 8.5 | 9.1 | 1.3 | 10.5 | 1.2 | 11.1 | 1.4 | 10.3 | 12.1 |
| 1 | 38 | 0.2 | 0.8 | 8.1 | 1.5 | 7.9 | 1.8 | 8.1 | 7.9 | 1.5 | 11.1 | 1.3 | 12.3 | 1.4 | 11.1 | 13.2 |
| 1 | 38 | 0.3 | 0.6 | 7.2 | 1.7 | 7.2 | 2.1 | 7.3 | 7.3 | 1.5 | 11.9 | 1.2 | 13.2 | 1.3 | 12.0 | 14.1 |
| 1 | 38 | 0.4 | 0.5 | 6.0 | 1.8 | 5.9 | 2.2 | 6.1 | 6.0 | 1.7 | 12.2 | 1.2 | 13.6 | 1.3 | 12.4 | 14.8 |
| 1 | 40 | 0.1 | 0.5 | 9.2 | 1.6 | 9.4 | 1.9 | 9.2 | 9.4 | 0.7 | 10.8 | 1.5 | 11.8 | 1.7 | 10.8 | 11.8 |
| 1 | 40 | 0.2 | 0.4 | 8.1 | 1.7 | 8.5 | 2.1 | 8.1 | 8.6 | 0.9 | 11.8 | 1.4 | 13.0 | 1.6 | 11.9 | 13.1 |
| 1 | 40 | 0.3 | 0.4 | 7.2 | 1.8 | 7.3 | 2.3 | 7.3 | 7.3 | 1.1 | 12.2 | 1.3 | 13.4 | 1.5 | 12.4 | 13.7 |
| 1 | 40 | 0.4 | 0.3 | 6.0 | 1.9 | 5.6 | 2.3 | 6.0 | 5.6 | 1.3 | 12.7 | 1.3 | 14.0 | 1.4 | 12.9 | 14.5 |
| 1 | 42 | 0.1 | 0.1 | 8.8 | 2.0 | 8.8 | 2.3 | 8.9 | 8.8 | 0.2 | 11.8 | 2.1 | 11.3 | 2.2 | 11.9 | 11.3 |
| 1 | 42 | 0.2 | 0.2 | 7.8 | 1.8 | 7.9 | 2.3 | 7.9 | 8.0 | 0.5 | 12.5 | 1.7 | 12.6 | 1.8 | 12.5 | 12.6 |
| 1 | 42 | 0.3 | 0.2 | 7.0 | 1.9 | 6.8 | 2.4 | 7.1 | 6.8 | 0.7 | 12.8 | 1.5 | 13.2 | 1.7 | 12.9 | 13.3 |
| 1 | 42 | 0.4 | 0.2 | 5.9 | 1.9 | 5.5 | 2.4 | 6.0 | 5.5 | 0.9 | 13.3 | 1.4 | 14.0 | 1.5 | 13.6 | 14.2 |
| 1 | 44 | 0.1 | 0.1 | 10.3 | 2.9 | 10.0 | 2.8 | 10.4 | 10.2 | 0.1 | 11.4 | 2.8 | 12.2 | 2.6 | 11.6 | 12.3 |
| 1 | 44 | 0.2 | 0.1 | 8.2 | 2.2 | 7.8 | 2.4 | 8.3 | 7.9 | 0.3 | 13.0 | 1.9 | 12.3 | 2.1 | 13.0 | 12.3 |
| 1 | 44 | 0.3 | 0.1 | 6.9 | 2.0 | 6.7 | 2.5 | 7.0 | 6.7 | 0.5 | 13.8 | 1.6 | 13.4 | 1.8 | 13.8 | 13.5 |
| 1 | 44 | 0.4 | 0.2 | 5.9 | 2.0 | 5.6 | 2.5 | 6.0 | 5.7 | 0.6 | 13.7 | 1.5 | 13.9 | 1.6 | 13.9 | 14.1 |
| 2 | 36 | 0.1 | 0.7 | 9.6 | 1.8 | 9.6 | 1.8 | 9.8 | 11.3 | 0.6 | 10.0 | 1.4 | 9.8 | 1.4 | 10.2 | 11.6 |
| 2 | 36 | 0.2 | 0.9 | 8.1 | 2.0 | 7.7 | 1.9 | 8.5 | 8.7 | 1.1 | 11.3 | 1.4 | 11.2 | 1.4 | 12.5 | 16.1 |
| 2 | 36 | 0.3 | 0.5 | 6.4 | 2.2 | 6.4 | 2.2 | 6.5 | 6.8 | 1.3 | 11.9 | 1.3 | 11.6 | 1.3 | 13.5 | 16.5 |
| 2 | 36 | 0.4 | 0.4 | 4.0 | 2.1 | 4.0 | 2.1 | 4.1 | 4.1 | 1.3 | 12.6 | 1.2 | 11.8 | 1.2 | 14.3 | 16.3 |
| 2 | 38 | 0.1 | 1.1 | 9.4 | 1.9 | 8.8 | 1.8 | 9.9 | 10.6 | 1.2 | 11.4 | 1.5 | 10.6 | 1.5 | 12.4 | 14.8 |
| 2 | 38 | 0.2 | 0.6 | 7.9 | 2.1 | 8.1 | 2.1 | 8.3 | 8.7 | 1.3 | 12.9 | 1.5 | 11.5 | 1.5 | 14.1 | 14.6 |
| 2 | 38 | 0.3 | 0.4 | 6.2 | 2.2 | 6.4 | 2.3 | 6.3 | 6.6 | 1.4 | 13.3 | 1.3 | 11.8 | 1.3 | 14.5 | 15.2 |
| 2 | 38 | 0.4 | 0.3 | 3.9 | 2.1 | 4.1 | 2.2 | 4.0 | 4.2 | 1.5 | 13.7 | 1.2 | 11.9 | 1.2 | 15.0 | 15.6 |
| 2 | 40 | 0.1 | 0.5 | 9.3 | 2.1 | 9.9 | 2.2 | 9.7 | 10.4 | 0.8 | 11.9 | 1.7 | 12.7 | 1.8 | 12.3 | 13.8 |
| 2 | 40 | 0.2 | 0.4 | 7.9 | 2.3 | 8.7 | 2.4 | 8.1 | 9.0 | 1.0 | 12.9 | 1.5 | 12.8 | 1.5 | 13.5 | 14.4 |
| 2 | 40 | 0.3 | 0.3 | 5.9 | 2.3 | 6.4 | 2.5 | 6.1 | 6.6 | 1.3 | 13.4 | 1.3 | 12.4 | 1.4 | 14.3 | 14.6 |
| 2 | 40 | 0.4 | 0.3 | 4.0 | 2.2 | 4.1 | 2.3 | 4.1 | 4.2 | 1.5 | 13.9 | 1.2 | 12.8 | 1.2 | 15.1 | 15.9 |
| 2 | 42 | 0.1 | 0.3 | 10.2 | 2.4 | 10.3 | 2.8 | 10.4 | 10.4 | 0.3 | 12.4 | 1.9 | 13.2 | 2.1 | 13.0 | 13.6 |
| 2 | 42 | 0.2 | 0.3 | 7.9 | 2.4 | 8.8 | 2.8 | 8.1 | 9.1 | 0.6 | 13.4 | 1.6 | 14.0 | 1.7 | 14.3 | 15.3 |
| 2 | 42 | 0.3 | 0.3 | 6.0 | 2.5 | 6.7 | 2.8 | 6.2 | 6.8 | 1.0 | 13.4 | 1.4 | 14.2 | 1.4 | 14.2 | 15.9 |
| 2 | 42 | 0.4 | 0.3 | 4.2 | 2.3 | 4.2 | 2.5 | 4.2 | 4.3 | 1.4 | 14.0 | 1.3 | 13.4 | 1.3 | 14.8 | 15.7 |
| 2 | 44 | 0.1 | 0.1 | 9.8 | 2.6 | 9.4 | 3.2 | 10.1 | 9.6 | 0.1 | 11.9 | 2.2 | 11.8 | 2.5 | 12.4 | 12.1 |
| 2 | 44 | 0.2 | 0.2 | 8.3 | 2.6 | 8.5 | 3.0 | 8.4 | 8.6 | 0.4 | 13.5 | 1.7 | 14.6 | 1.8 | 14.5 | 15.3 |
| 2 | 44 | 0.3 | 0.2 | 6.3 | 2.6 | 6.1 | 2.9 | 6.4 | 6.2 | 0.6 | 13.7 | 1.5 | 14.3 | 1.5 | 14.8 | 15.6 |
| 2 | 44 | 0.4 | 0.2 | 4.3 | 2.4 | 4.1 | 2.6 | 4.3 | 4.2 | 1.1 | 14.0 | 1.3 | 14.6 | 1.3 | 14.9 | 16.8 |
| Average | 0.4 | 7.2 | 2.0 | 7.3 | 2.3 | 7.3 | 7.5 | 1.0 | 12.4 | 1.5 | 12.6 | 1.5 | 12.9 | 14.1 | ||
| Call | Symmetric Put | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | K | A | C | I | AC | AI | CI | ACI | A | C | I | AC | AI | CI | ACI | |
| 1 | 36 | 0.1 | 0.5 | 7.6 | 1.1 | 7.6 | 1.1 | 7.6 | 7.7 | 0.4 | 9.2 | 0.9 | 9.3 | 1.0 | 9.2 | 9.4 |
| 1 | 36 | 0.2 | 1.1 | 7.1 | 1.4 | 7.1 | 1.4 | 7.1 | 7.1 | 1.1 | 10.3 | 1.0 | 10.3 | 1.1 | 10.4 | 10.6 |
| 1 | 36 | 0.3 | 0.9 | 6.2 | 1.5 | 6.2 | 1.6 | 6.2 | 6.2 | 1.4 | 11.7 | 1.0 | 11.7 | 1.1 | 11.8 | 12.0 |
| 1 | 36 | 0.4 | 0.6 | 5.6 | 1.7 | 5.6 | 1.8 | 5.6 | 5.6 | 1.6 | 12.3 | 1.0 | 12.2 | 1.1 | 12.4 | 12.6 |
| 1 | 38 | 0.1 | 1.2 | 8.1 | 1.3 | 8.1 | 1.4 | 8.1 | 8.1 | 1.2 | 9.8 | 1.1 | 9.8 | 1.2 | 9.8 | 10.0 |
| 1 | 38 | 0.2 | 0.9 | 7.5 | 1.5 | 7.5 | 1.6 | 7.6 | 7.6 | 1.4 | 11.4 | 1.2 | 11.5 | 1.2 | 11.4 | 11.6 |
| 1 | 38 | 0.3 | 0.6 | 6.6 | 1.6 | 6.6 | 1.7 | 6.7 | 6.7 | 1.5 | 12.0 | 1.1 | 12.2 | 1.2 | 12.1 | 12.3 |
| 1 | 38 | 0.4 | 0.4 | 5.6 | 1.8 | 5.6 | 1.8 | 5.6 | 5.6 | 1.6 | 12.7 | 1.0 | 12.8 | 1.1 | 12.7 | 12.9 |
| 1 | 40 | 0.1 | 0.5 | 8.6 | 1.6 | 8.6 | 1.6 | 8.6 | 8.7 | 0.8 | 10.7 | 1.4 | 10.8 | 1.4 | 10.8 | 10.8 |
| 1 | 40 | 0.2 | 0.5 | 7.8 | 1.7 | 7.8 | 1.7 | 7.9 | 7.8 | 0.9 | 11.9 | 1.3 | 11.9 | 1.3 | 11.9 | 11.9 |
| 1 | 40 | 0.3 | 0.4 | 7.0 | 1.8 | 7.0 | 1.8 | 7.0 | 7.0 | 1.1 | 12.7 | 1.2 | 12.8 | 1.2 | 12.7 | 12.8 |
| 1 | 40 | 0.4 | 0.3 | 5.8 | 1.9 | 5.8 | 1.9 | 5.8 | 5.8 | 1.3 | 13.1 | 1.1 | 13.2 | 1.2 | 13.2 | 13.3 |
| 1 | 42 | 0.1 | 0.2 | 9.3 | 2.2 | 9.3 | 2.1 | 9.3 | 9.3 | 0.2 | 11.3 | 1.8 | 11.3 | 1.8 | 11.4 | 11.4 |
| 1 | 42 | 0.2 | 0.3 | 8.1 | 2.0 | 8.0 | 2.0 | 8.1 | 8.1 | 0.4 | 11.8 | 1.4 | 11.7 | 1.5 | 11.9 | 11.9 |
| 1 | 42 | 0.3 | 0.3 | 7.0 | 2.0 | 7.0 | 2.0 | 7.0 | 7.0 | 0.7 | 12.9 | 1.3 | 12.8 | 1.4 | 12.9 | 13.0 |
| 1 | 42 | 0.4 | 0.3 | 5.9 | 2.0 | 5.9 | 2.0 | 5.9 | 5.9 | 0.9 | 13.4 | 1.2 | 13.4 | 1.2 | 13.4 | 13.5 |
| 1 | 44 | 0.1 | 0.1 | 10.4 | 2.9 | 10.4 | 2.8 | 10.5 | 10.5 | 0.0 | 10.8 | 2.4 | 10.8 | 2.3 | 10.8 | 10.8 |
| 1 | 44 | 0.2 | 0.2 | 8.4 | 2.2 | 8.4 | 2.2 | 8.4 | 8.4 | 0.2 | 12.1 | 1.7 | 12.1 | 1.7 | 12.3 | 12.3 |
| 1 | 44 | 0.3 | 0.2 | 7.3 | 2.2 | 7.3 | 2.1 | 7.3 | 7.3 | 0.4 | 12.7 | 1.4 | 12.7 | 1.5 | 12.8 | 12.8 |
| 1 | 44 | 0.4 | 0.2 | 6.1 | 2.1 | 6.1 | 2.1 | 6.1 | 6.1 | 0.6 | 13.3 | 1.3 | 13.2 | 1.3 | 13.3 | 13.4 |
| 2 | 36 | 0.1 | 0.7 | 9.7 | 1.8 | 9.8 | 1.8 | 9.6 | 10.1 | 0.7 | 10.5 | 1.6 | 11.0 | 1.5 | 10.4 | 11.2 |
| 2 | 36 | 0.2 | 1.1 | 8.4 | 2.3 | 8.5 | 2.2 | 8.6 | 8.7 | 1.2 | 12.2 | 1.5 | 12.1 | 1.5 | 12.4 | 13.3 |
| 2 | 36 | 0.3 | 0.7 | 6.5 | 2.3 | 6.6 | 2.3 | 6.6 | 6.6 | 1.4 | 12.8 | 1.4 | 12.7 | 1.4 | 13.1 | 14.0 |
| 2 | 36 | 0.4 | 0.5 | 4.5 | 2.2 | 4.5 | 2.3 | 4.5 | 4.5 | 1.4 | 13.0 | 1.3 | 12.8 | 1.2 | 13.4 | 14.4 |
| 2 | 38 | 0.1 | 1.3 | 10.1 | 2.2 | 10.2 | 2.1 | 10.5 | 10.7 | 1.3 | 12.2 | 1.7 | 12.2 | 1.6 | 12.4 | 13.0 |
| 2 | 38 | 0.2 | 0.7 | 8.2 | 2.2 | 8.4 | 2.2 | 8.4 | 8.5 | 1.4 | 12.4 | 1.5 | 12.7 | 1.5 | 13.1 | 13.7 |
| 2 | 38 | 0.3 | 0.6 | 6.5 | 2.4 | 6.6 | 2.4 | 6.6 | 6.6 | 1.5 | 12.7 | 1.4 | 12.9 | 1.4 | 13.3 | 14.0 |
| 2 | 38 | 0.4 | 0.4 | 4.2 | 2.1 | 4.2 | 2.1 | 4.2 | 4.2 | 1.5 | 13.4 | 1.3 | 13.6 | 1.3 | 14.0 | 14.9 |
| 2 | 40 | 0.1 | 0.6 | 10.1 | 2.2 | 10.2 | 2.1 | 10.3 | 10.5 | 0.9 | 12.4 | 1.7 | 12.9 | 1.7 | 13.3 | 13.6 |
| 2 | 40 | 0.2 | 0.5 | 8.3 | 2.3 | 8.3 | 2.2 | 8.4 | 8.5 | 1.1 | 13.0 | 1.6 | 13.6 | 1.5 | 13.9 | 14.4 |
| 2 | 40 | 0.3 | 0.4 | 6.2 | 2.3 | 6.2 | 2.3 | 6.2 | 6.2 | 1.3 | 13.5 | 1.5 | 14.0 | 1.4 | 14.5 | 15.0 |
| 2 | 40 | 0.4 | 0.3 | 4.1 | 2.1 | 4.1 | 2.1 | 4.2 | 4.2 | 1.6 | 13.6 | 1.4 | 13.9 | 1.3 | 14.6 | 15.3 |
| 2 | 42 | 0.1 | 0.3 | 10.2 | 2.3 | 10.2 | 2.3 | 10.3 | 10.4 | 0.4 | 11.9 | 1.9 | 11.9 | 1.9 | 12.4 | 12.5 |
| 2 | 42 | 0.2 | 0.4 | 8.2 | 2.4 | 8.1 | 2.4 | 8.2 | 8.3 | 0.7 | 13.4 | 1.7 | 13.8 | 1.7 | 14.3 | 14.6 |
| 2 | 42 | 0.3 | 0.3 | 6.2 | 2.3 | 6.1 | 2.3 | 6.2 | 6.3 | 1.0 | 14.1 | 1.6 | 14.7 | 1.5 | 15.2 | 15.7 |
| 2 | 42 | 0.4 | 0.3 | 4.2 | 2.1 | 4.2 | 2.2 | 4.2 | 4.3 | 1.4 | 14.5 | 1.5 | 15.3 | 1.3 | 15.7 | 16.6 |
| 2 | 44 | 0.1 | 0.1 | 9.5 | 2.5 | 9.7 | 2.7 | 9.7 | 9.8 | 0.2 | 12.2 | 2.1 | 12.1 | 2.2 | 12.6 | 12.6 |
| 2 | 44 | 0.2 | 0.3 | 7.9 | 2.4 | 7.9 | 2.4 | 8.0 | 8.0 | 0.5 | 12.9 | 1.8 | 13.0 | 1.8 | 13.6 | 13.7 |
| 2 | 44 | 0.3 | 0.3 | 5.9 | 2.3 | 5.9 | 2.4 | 5.9 | 5.9 | 0.8 | 14.2 | 1.7 | 14.7 | 1.6 | 15.3 | 15.7 |
| 2 | 44 | 0.4 | 0.3 | 4.4 | 2.2 | 4.4 | 2.2 | 4.4 | 4.4 | 1.2 | 14.7 | 1.5 | 15.4 | 1.4 | 15.9 | 16.5 |
| Average | 0.5 | 7.2 | 2.0 | 7.2 | 2.0 | 7.3 | 7.3 | 1.0 | 12.4 | 1.4 | 12.5 | 1.4 | 12.8 | 13.1 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boire, F.-M.; Reesor, R.M.; Stentoft, L. Efficient Variance Reduction for American Call Options Using Symmetry Arguments. J. Risk Financial Manag. 2021, 14, 504. https://doi.org/10.3390/jrfm14110504
Boire F-M, Reesor RM, Stentoft L. Efficient Variance Reduction for American Call Options Using Symmetry Arguments. Journal of Risk and Financial Management. 2021; 14(11):504. https://doi.org/10.3390/jrfm14110504
Chicago/Turabian StyleBoire, François-Michel, R. Mark Reesor, and Lars Stentoft. 2021. "Efficient Variance Reduction for American Call Options Using Symmetry Arguments" Journal of Risk and Financial Management 14, no. 11: 504. https://doi.org/10.3390/jrfm14110504
APA StyleBoire, F.-M., Reesor, R. M., & Stentoft, L. (2021). Efficient Variance Reduction for American Call Options Using Symmetry Arguments. Journal of Risk and Financial Management, 14(11), 504. https://doi.org/10.3390/jrfm14110504







