GARCH Generated Volatility Indices of Bitcoin and CRIX
Abstract
1. Introduction
2. Literature Review
2.1. Cryptocurrency Indices
2.2. GARCH Models Applied to Cryptocurrencies
2.3. Cryptocurrency Volatility Indices
3. Theoretical Framework
Option Pricing Model
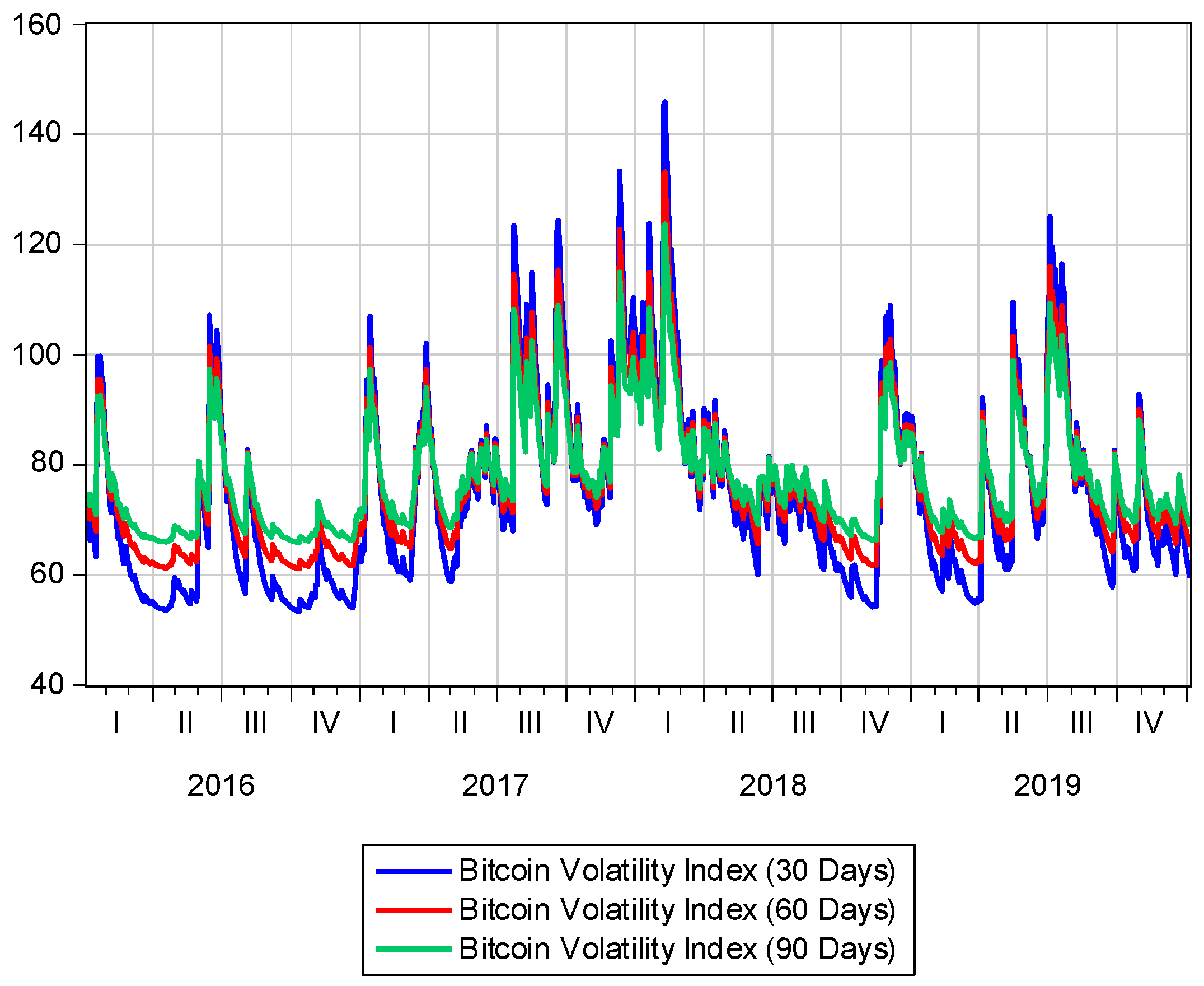
4. GARCH Volatility Index
- 1.
- is a martingale difference sequence with respect to .
- 2.
- The conditional variance process of given is a marginalisation of a stationary -adapted vector autoregressive process of dimension p:where , and the eigenvalues of Γ have a modulus smaller than one.
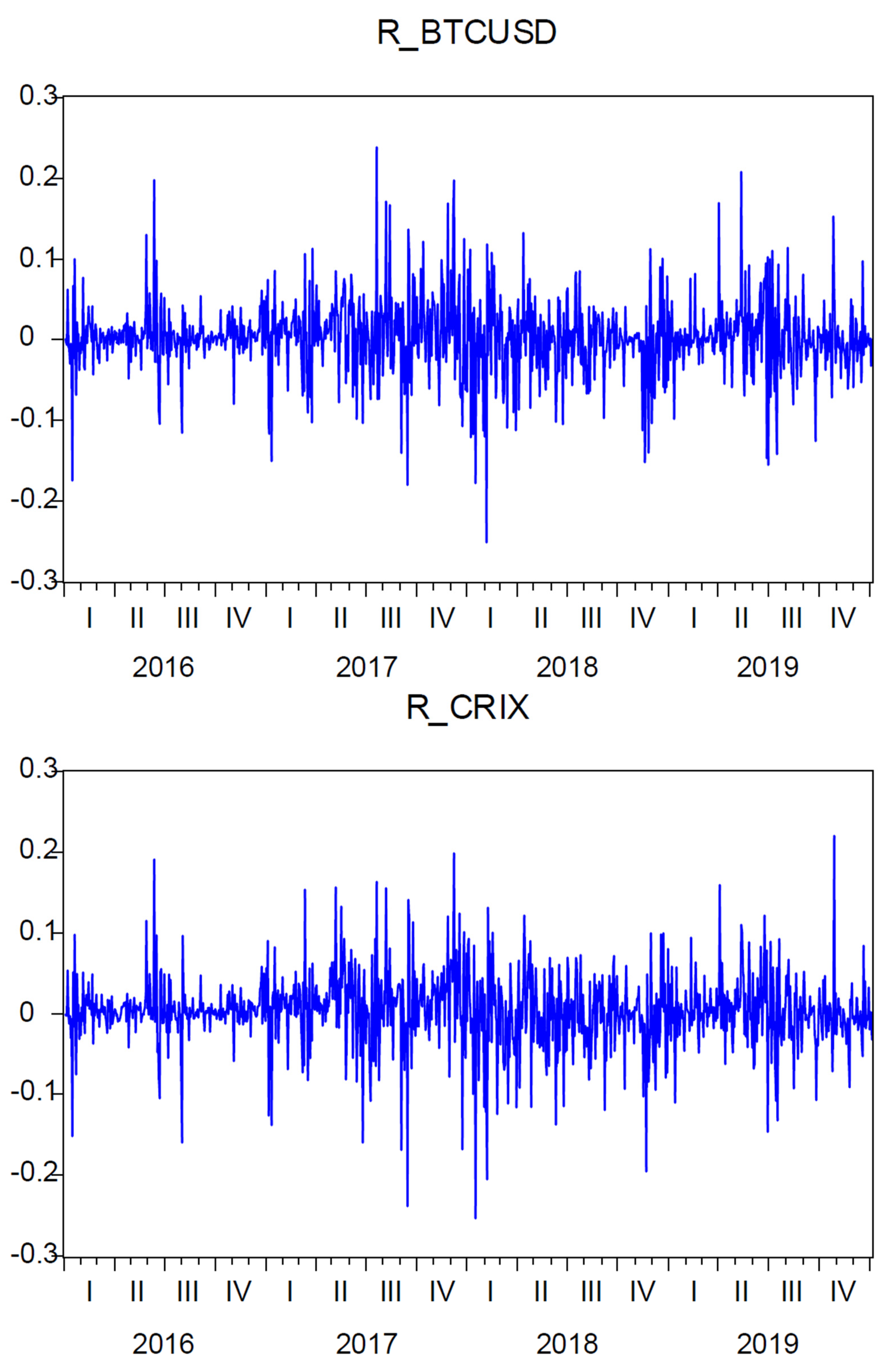
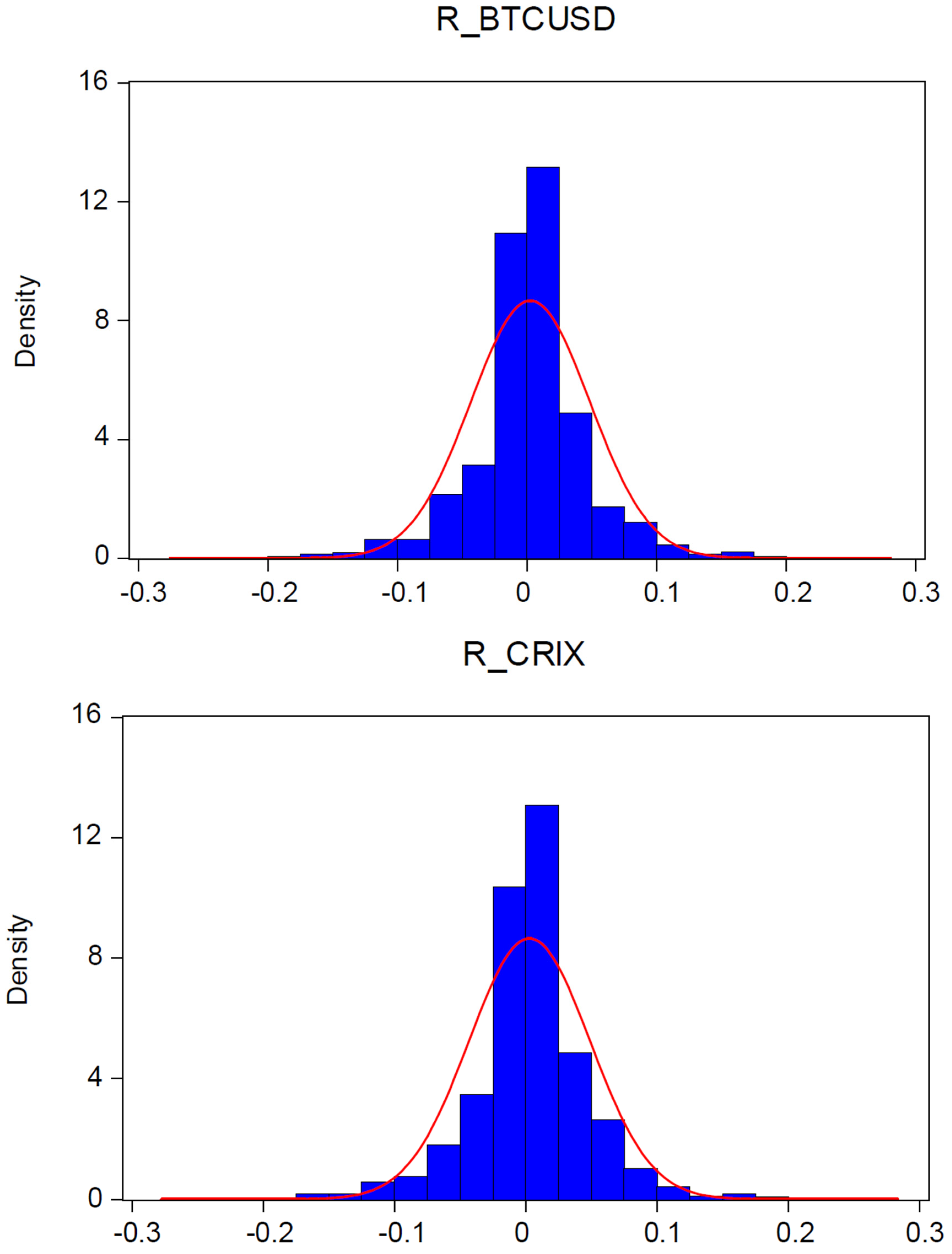
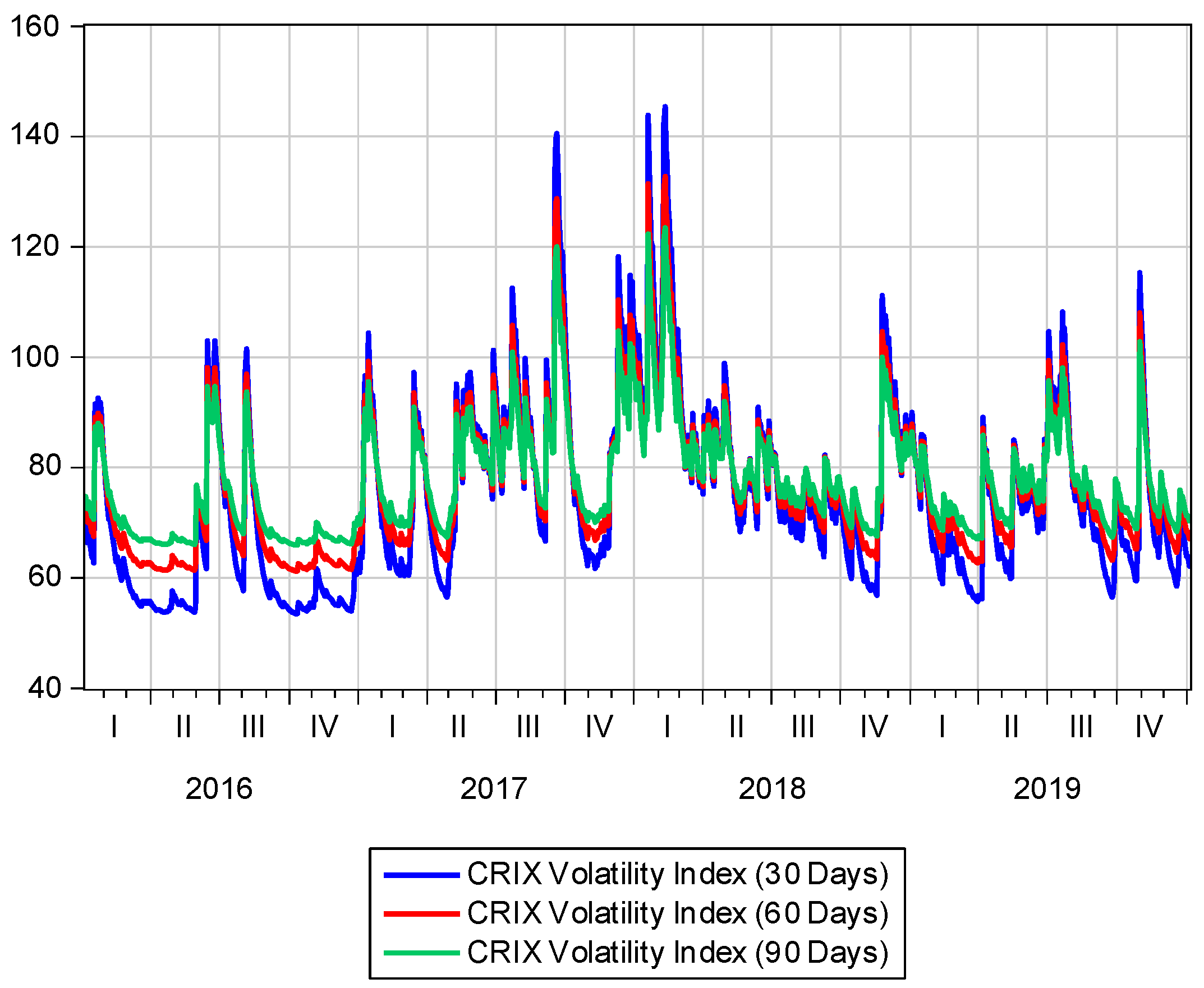
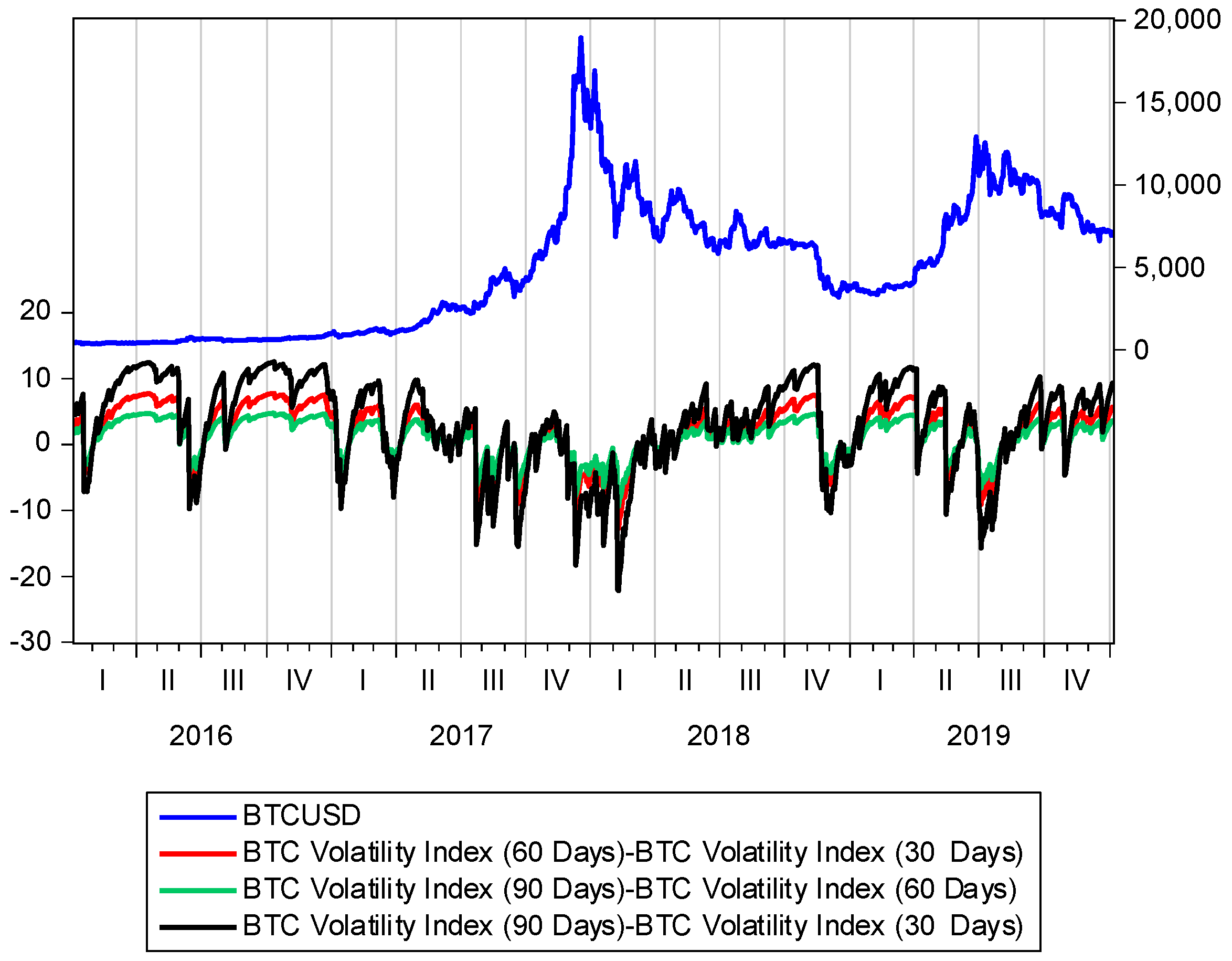
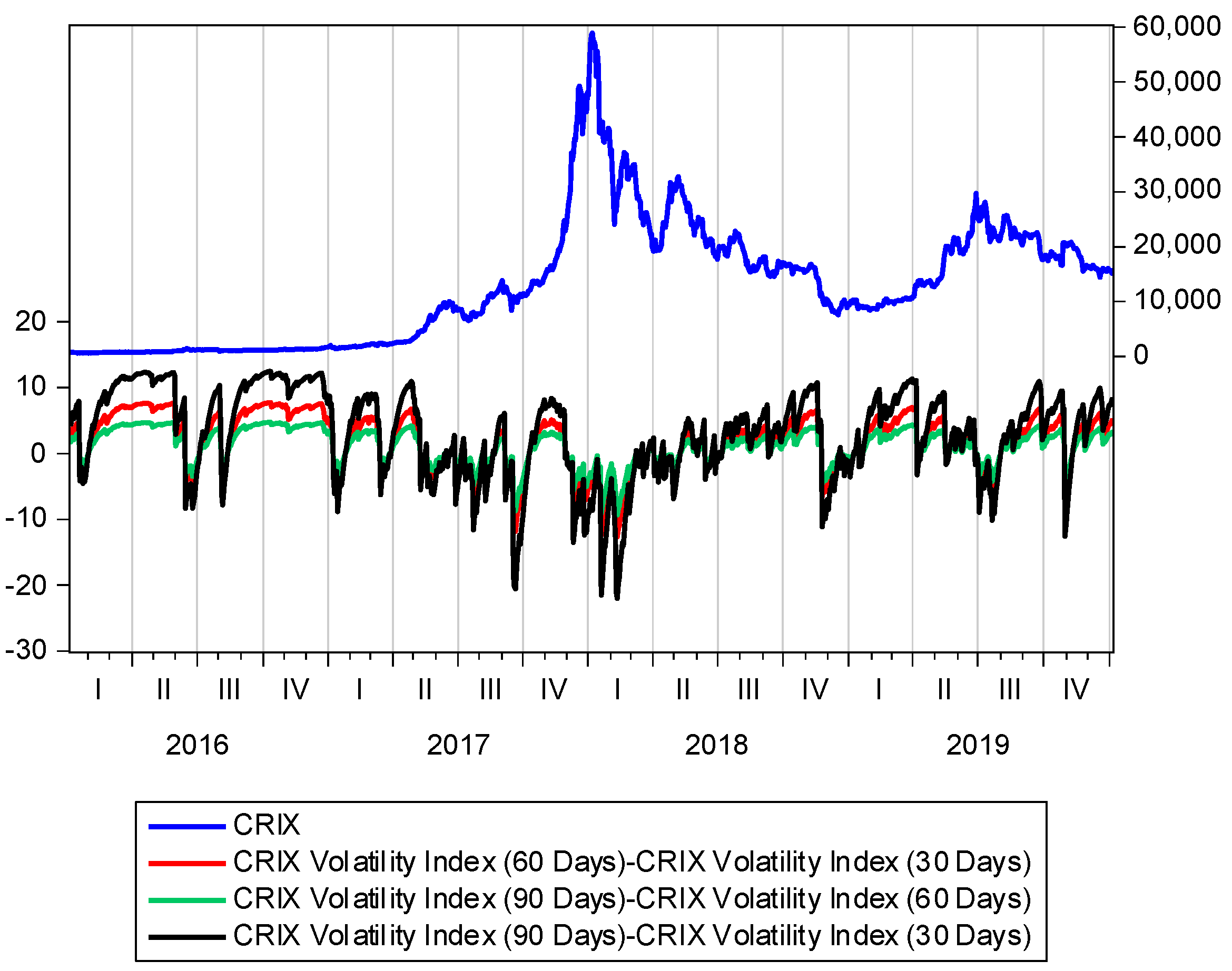
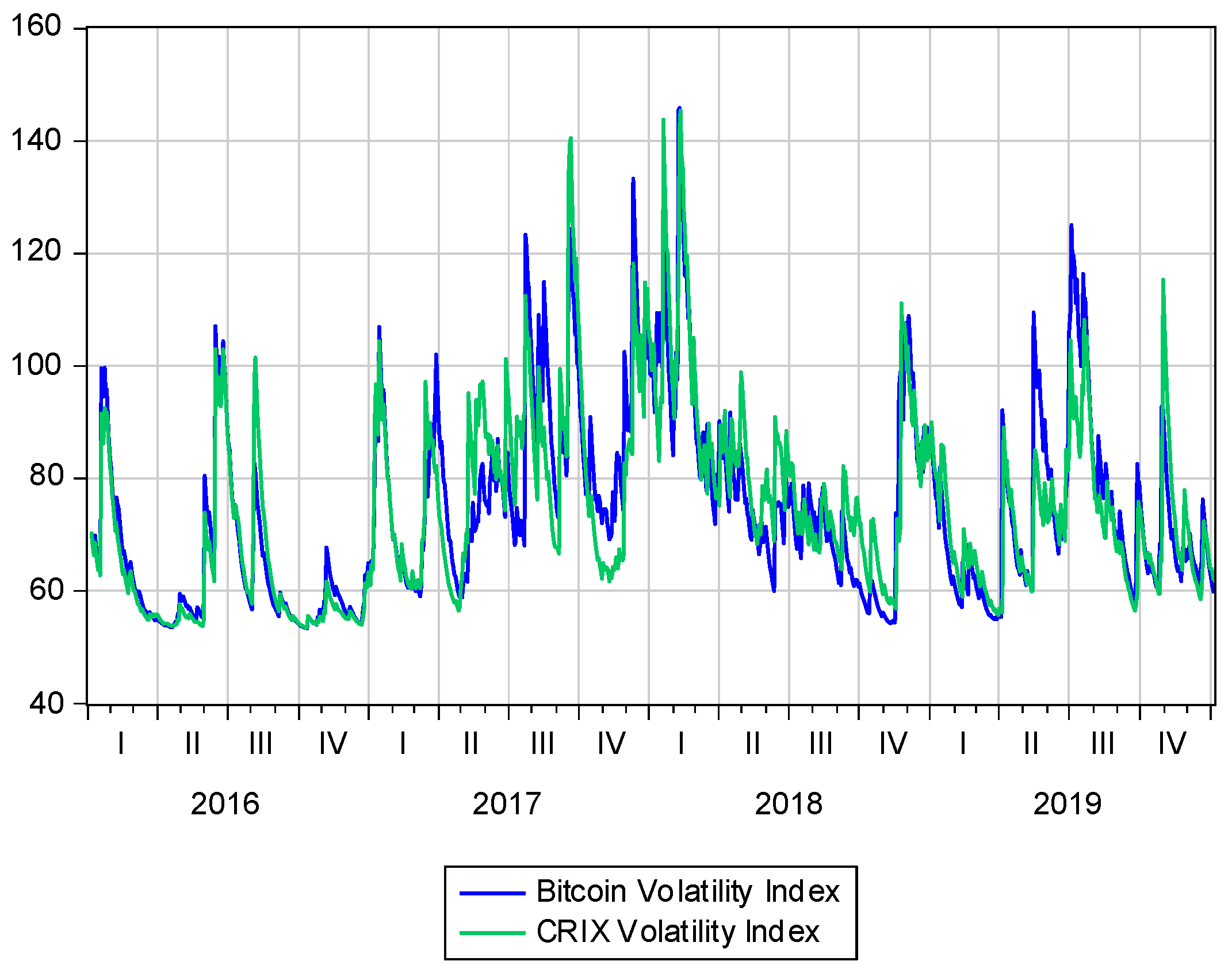
5. Data Analysis
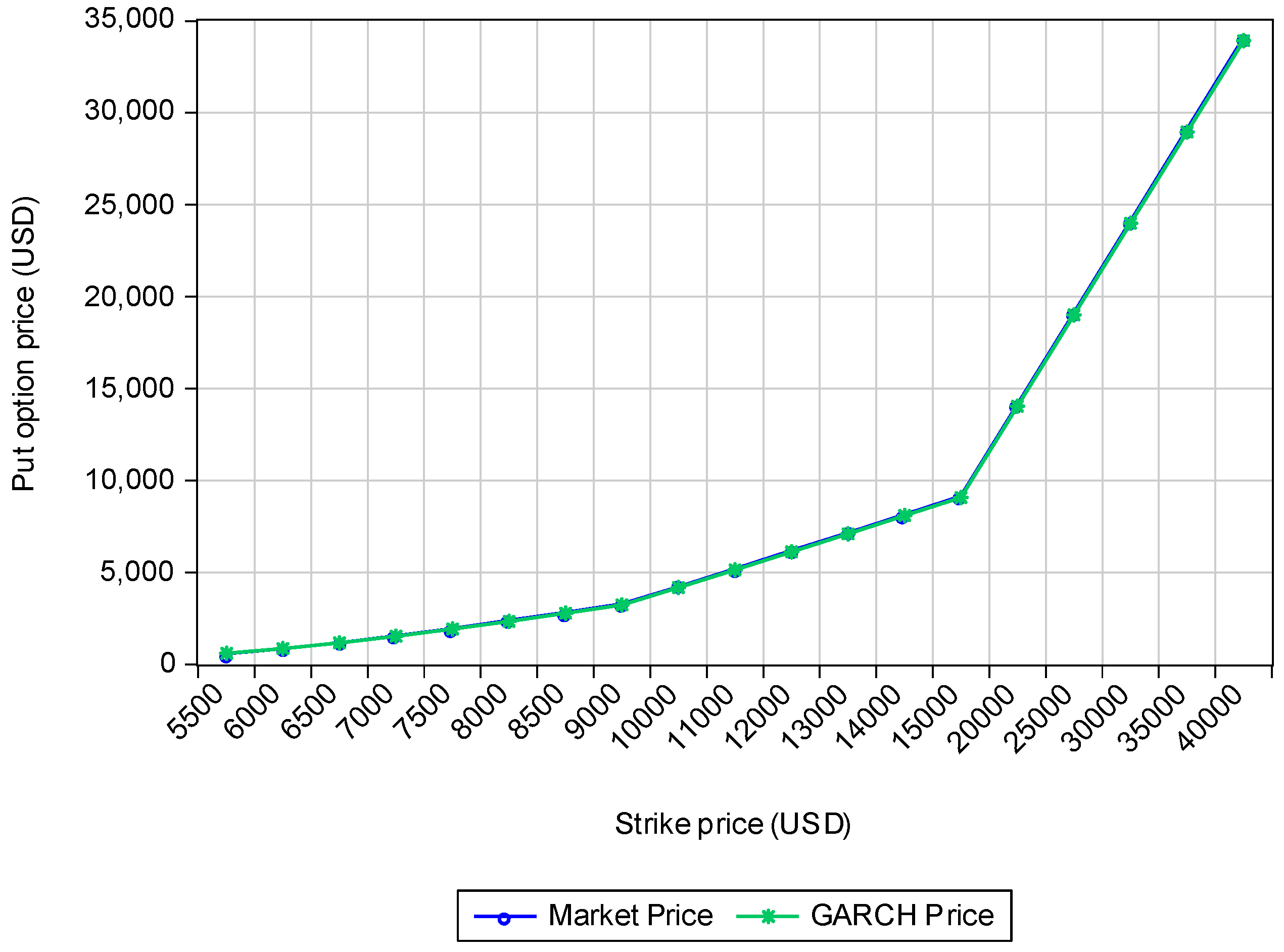
6. Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abboud, Husam. 2017. H/Rindex: The Hashing Power and Robustness Index, Computational Power-weighted Benchmark for Global Blockchain and Crypto Market. Available online: https://ssrn.com/abstract=3136635 (accessed on 1 June 2020).
- Agyarko, Kofi, Albert Buabeng, and Joseph Acquah. 2019. Modelling the Volatility of the Price of Bitcoin. American Journal of Mathematics and Statistics 9: 151–59. [Google Scholar]
- Alexander, Carol, and Arben Imeraj. 2019. The Bitcoin VIX its Variance Risk Premium. Available online: https://ssrn.com/abstract=3383734 (accessed on 26 January 2020).
- Antonopoulos, Andreas M. 2014. Mastering Bitcoin: Unlocking Digital Cryptocurrencies. Sebastopol: O’Reilly Media, Inc. [Google Scholar]
- Asteriou, Dimitrios, and Stephen G. Hall. 2015. Applied Econometrics. New York: Palgrave Macmillan. [Google Scholar]
- Baur, Dirk G., and Thomas Dimpfl. 2018. Asymmetric volatility in cryptocurrencies. Economics Letters 173: 148–51. [Google Scholar] [CrossRef]
- Böhme, Rainer, Nicolas Christin, Benjamin Edelman, and Tyler Moore. 2015. Bitcoin: Economics, technology, and governance. Journal of Economic Perspectives 29: 213–38. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bouri, Elie, Rangan Gupta, Aviral Kuma Tiwari, and David Roubaud. 2017. Does Bitcoin hedge global uncertainty? Evidence from wavelet-based quantile-in-quantile regressions. Finance Research Letters 23: 87–95. [Google Scholar] [CrossRef]
- Brooks, Chris. 2014. Introductory Econometrics for Finance. New York: Cambridge University Press. [Google Scholar]
- Chen, Shi, Cathy Yi-Hsuan Chen, Wolfgang Karl Härdle, Teik Ming Lee, and Bobby Ong. 2018. Econometric analysis of a cryptocurrency index for portfolio investment. In Handbook of Blockchain, Digital Finance, and Inclusion. London: Academic Press, vol. 1, pp. 175–206. [Google Scholar]
- Chu, Jeffrey, Stephen Chan, Saralees Nadarajah, and Joerg Osterrieder. 2017. GARCH modelling of cryptocurrencies. Journal of Risk and Financial Management 10: 17. [Google Scholar] [CrossRef]
- Conrad, Christian, Anessa Custovi, and Eric Ghysels. 2018. Long-and short-term cryptocurrency volatility components: A GARCH-MIDAS analysis. Journal of Risk and Financial Management 11: 23. [Google Scholar] [CrossRef]
- Cont, Rama. 2001. Empirical properties of asset returns: stylized facts and statistical issues. Quantitative Finance 1: 223–36. [Google Scholar] [CrossRef]
- Duan, Jin-Chuan. 1995. The GARCH option pricing model. Mathematical Finance 5: 13–32. [Google Scholar] [CrossRef]
- Dyhrberg, Anne Haubo. 2016. Bitcoin, gold and the dollar—A GARCH volatility analysis. Finance Research Letters 16: 85–92. [Google Scholar] [CrossRef]
- Elendner, Hermann, Simon Trimborn, Bobby Ong, and Teik Ming Lee. 2018. The cross-section of crypto-currencies as financial assets: Investing in crypto-currencies beyond bitcoin. In Handbook of Blockchain, Digital Finance, and Inclusion. London: Academic Press, vol. 1, pp. 145–73. [Google Scholar]
- Fernandes, Marcelo, Marcelo C. Medeiros, and Marcel Scharth. 2014. Modeling and predicting the CBOE market volatility index. Journal of Banking & Finance 40: 1–10. [Google Scholar]
- Gyamerah, Samuel Asante. 2019. Modelling the volatility of Bitcoin returns using GARCH models. Quantitative Finance and Economics 3: 739. [Google Scholar] [CrossRef]
- Hafner, Christian M. 2020. Testing for bubbles in cryptocurrencies with time-varying volatility. Journal of Financial Econometrics 18: 233–49. [Google Scholar]
- Hansen, Peter R., and Asger Lunde. 2005. A forecast comparison of volatility models: does anything beat a GARCH(1,1)? Journal of Applied Econometrics 20: 873–89. [Google Scholar] [CrossRef]
- Hao, Jinji, and Jin E. Zhang. 2013. GARCH option pricing models, the CBOE VIX, and variance risk premium. Journal of Financial Econometrics 11: 556–80. [Google Scholar] [CrossRef]
- Kathiravan, Chinnadurai, Murugesan Selvam, Balasundram Maniam, Sankaran Venkateswar, Jayapal Gayathri, and Amrutha Pavithran. 2019. Effect of Weather on Cryptocurrency Index: Evidences from Coinbase Index. International Journal of Financial Research 10: 108–118. [Google Scholar] [CrossRef]
- Kim, Alisa, Simon Trimborn, and Wolfgang Karl Härdle. 2019. VCRIX-A Volatility Index for Crypto-Currencies. Available online: https://ssrn.com/abstract=3480348 (accessed on 1 June 2020).
- Klein, Tony, Hien Pham Thu, and Thomas Walther. 2018. Bitcoin is not the New Gold—A comparison of volatility, correlation, and portfolio performance. International Review of Financial Analysis 59: 105–16. [Google Scholar] [CrossRef]
- Kolesnikova, Alisa. 2018. CRIX-Volatility Index for Crypto-currencies on the Basis of CRIX. Master’s thesis, Humboldt-Universität, Berlin, Germany. [Google Scholar]
- Leong, Kelvin, and Anna Sung. 2018. FinTech (Financial Technology): What is it and how to use technologies to create business value in fintech way? International Journal of Innovation, Management and Technology 9: 74–78. [Google Scholar] [CrossRef]
- Leong, Kelvin, Anna Sung, and Cedric Teissier. 2020. Financial Technology for Sustainable Development. In Partnerships for the Goals. Encyclopedia of the UN Sustainable Development Goals. Edited by Walter Leal Filho, Anabela Marisa Azul, Luciana Brandli, Pinar Göckin Özuyar and Tony Wall. Cham: Springer. [Google Scholar]
- Madan, Dilip B., Sofie Reyners, and Wim Schoutens. 2019. Advanced model calibration on bitcoin options. Digital Finance 1: 117–37. [Google Scholar] [CrossRef]
- McAleer, Michael, and Christian M. Hafner. 2014. A one line derivation of EGARCH. Econometrics 2: 92–97. [Google Scholar] [CrossRef]
- Meddahi, Nour, and Eric Renault. 2004. Temporal aggregation of volatility models. Journal of Econometrics 119: 355–79. [Google Scholar] [CrossRef]
- Peng, Yaohao, Pedro Henrique Melo Albuquerque, Jader Martins Camboim de Sá, Ana Julia Akaishi Padula, and Mariana Rosa Montenegro. 2018. The best of two worlds: Forecasting high frequency volatility for cryptocurrencies and traditional currencies with Support Vector Regression. Expert Systems with Applications 97: 177–92. [Google Scholar] [CrossRef]
- Trimborn, Simon, and Wolfgang Karl Härdle. 2018. CRIX an Index for cryptocurrencies. Journal of Empirical Finance 49: 107–22. [Google Scholar] [CrossRef]
- Wilmott, Paul. 2007. Paul Wilmott Introduces Quantitative Finance. Chichester: John Wiley & Sons. [Google Scholar]
| Study | Topic |
|---|---|
| Hansen and Lunde (2005) | GARCH(1,1) model |
| Duan (1995) | GARCH option pricing |
| Meddahi and Renault (2004) | SR-SARV processes |
| Hao and Zhang (2013) | GARCH implied volatility index |
| Trimborn and Härdle (2018) | The CRIX |
| Chu et al. (2017) | GARCH Modelling of cryptocurrencies |
| Hafner (2020) | GARCH Modelling of cryptocurrencies and CRIX |
| BTCUSD | CRIX | |
|---|---|---|
| Mean | 0.0027 | 0.0029 |
| Median | 0.0026 | 0.0032 |
| Maximum | 0.2384 | 0.2203 |
| Minimum | −0.2514 | −0.2533 |
| Standard Deviation | 0.046 | 0.0461 |
| Skewness | 0.0046 | −0.3903 |
| Kurtosis | 7.1336 | 7.3798 |
| Jarque–Bera | 743.2889 | 860.9537 |
| Observations | 1044 | 1044 |
| BTCUSD | |
|---|---|
| 0.1149 | |
| 0.8837 | |
| 0.1116 | |
| AIC | −6.1810 |
| Market Price | GARCH Price | Difference | % Difference |
|---|---|---|---|
| 583.665 | 589.96 | 6.295 | 1.0670% |
| 853.5 | 850.65 | −2.85 | −0.3350% |
| 1164.4 | 1163.1 | −1.3 | −0.1118% |
| 1532.495 | 1519.59 | −12.905 | −0.8492% |
| 1925.68 | 1911.84 | −13.84 | −0.7239% |
| 2373 | 2332.64 | −40.36 | −1.7302% |
| 2812.99 | 2773.88 | −39.11 | −1.4099% |
| 3273.505 | 3229.46 | −44.045 | −1.3639% |
| 4200.415 | 4170.21 | −30.205 | −0.7243% |
| 5185.985 | 5134.92 | −51.065 | −0.9945% |
| 6185.695 | 6112.5 | −73.195 | −1.1975% |
| 7150.045 | 7096.55 | −53.495 | −0.7538% |
| 8141.315 | 8084.57 | −56.745 | −0.7019% |
| 9134.05 | 9074.67 | −59.38 | −0.6543% |
| 14,115.325 | 14,038.73 | −76.595 | −0.5456% |
| 19,106.87 | 19,009.72 | −97.15 | −0.5111% |
| 24,098.41 | 23,981.97 | −116.44 | −0.4855% |
| 29,089.95 | 28,954.7 | −135.25 | −0.4671% |
| 34,082.955 | 33,927.67 | −155.285 | −0.4577% |
| BTCUSD | CRIX | |
|---|---|---|
| 0.0001 | 0.0001 | |
| 0.1035 | 0.1504 | |
| 0.8650 | 0.8203 | |
| 0.0744 | 0.0880 | |
| AIC | −6.9982 | −6.9909 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Venter, P.J.; Maré, E. GARCH Generated Volatility Indices of Bitcoin and CRIX. J. Risk Financial Manag. 2020, 13, 121. https://doi.org/10.3390/jrfm13060121
Venter PJ, Maré E. GARCH Generated Volatility Indices of Bitcoin and CRIX. Journal of Risk and Financial Management. 2020; 13(6):121. https://doi.org/10.3390/jrfm13060121
Chicago/Turabian StyleVenter, Pierre J., and Eben Maré. 2020. "GARCH Generated Volatility Indices of Bitcoin and CRIX" Journal of Risk and Financial Management 13, no. 6: 121. https://doi.org/10.3390/jrfm13060121
APA StyleVenter, P. J., & Maré, E. (2020). GARCH Generated Volatility Indices of Bitcoin and CRIX. Journal of Risk and Financial Management, 13(6), 121. https://doi.org/10.3390/jrfm13060121





