True versus Spurious Long Memory in Cryptocurrencies
Abstract
1. Introduction
2. Background Literature
3. Long Memory Explained
4. Tests of Long Memory
5. Results
5.1. Data
5.2. Findings
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Beran, Jan. 1994. Statistics for Long-Memory Processes. Boca Raton: CRC Press, vol. 61. [Google Scholar]
- Betken, Annika. 2016. Testing for Change-Points in Long-Range Dependent Time Series by Means of a Self-Normalized Wilcoxon Test. Journal of Time Series Analysis 37: 785–809. [Google Scholar] [CrossRef]
- Bouri, Elie, Rangan Gupta, Luis Gil-Alana, and David Roubaud. 2019. Modelling long memory volatility in the Bitcoin market: Evidence of persistence and structural breaks. International Journal of Finance & Economics 24: 412–26. [Google Scholar]
- Cheah, Eng-Tuck, and John Fry. 2015. Speculative bubbles in Bitcoin markets? An empirical investigation into the fundamental value of Bitcoin. Economics Letters 130: 32–36. [Google Scholar] [CrossRef]
- Davidson, James, and Dooruj Rambaccussing. 2015. A Test of the Long Memory Hypothesis Based on Self-Similarity. Journal of Time Series Econometrics 7: 115–41. [Google Scholar] [CrossRef][Green Version]
- Davidson, James, and Phillip Sibbertsen. 2009. Tests of bias in log-periodogram regression. Economics Letters 102: 83–86. [Google Scholar] [CrossRef][Green Version]
- Dehling, Herold, Aeneas Rooch, and Murad. S. Taqqu. 2013. Non-Parametric Change-Point Tests for Long-Range Dependent Data. Scandinavian Journal of Statistics 40: 153–73. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Atushi Inoue. 2001. Long memory and regime switching. Journal of Econometrics 105: 131–59. [Google Scholar] [CrossRef]
- Geweke, John, and Susan Porter-Hudak. 1983. The Estimation and Application of Long Memory Time Series Models. Journal of Time Series Analysis 4: 221–38. [Google Scholar] [CrossRef]
- Granger, Clive, and Namwon Hyung. 2004. Occasional structural breaks and long memory with an application to the S&P 500 absolute stock returns. Journal of Empirical Finance 11: 399–421. [Google Scholar] [CrossRef]
- Hurvich, Clifford, and Rohit Deo. 1999. Plug-in Selection of the Number of Frequencies in Regression Estimates of the Memory Parameter of a Long-memory Time Series. Journal of Time Series Analysis 20: 331–41. [Google Scholar] [CrossRef]
- Iacone, Fabrizio, Stephen Leybourne, and Robert Taylor. 2014. A fixed-b test for a break in level at an unknown time under fractional integration. Journal of Time Series Analysis 35: 40–54. [Google Scholar] [CrossRef]
- Katsiampa, Paraskevi. 2017. Volatility estimation for Bitcoin: A comparison of GARCH models. Economics Letters 158: 3–6. [Google Scholar] [CrossRef]
- Kaya Soylu, Pınar, Mustapha Okur, Özgur Çatıkkaş, and Ayca Altintig. 2020. Long Memory in the Volatility of Selected Cryptocurrencies: Bitcoin, Ethereum and Ripple. J. Risk Financial Management 13: 107. [Google Scholar] [CrossRef]
- Lahmiri, Salim, Stelios Bekiros, and andAntonio Salvi. 2018. Long-range memory, distributional variation and randomness of bitcoin volatility. Chaos, Solitons & Fractals 107: 43–48. [Google Scholar]
- Mensi, Walid, Khamis Hamed Al-Yahyaee, and Sang Hoon Kang. 2019. Structural breaks and double long memory of cryptocurrency prices: A comparative analysis from Bitcoin and Ethereum. Finance Research Letters 29: 222–30. [Google Scholar] [CrossRef]
- Moulines, Eric, and Phillipe Soulier. 1999. Broadband log-periodogram regression of time series with long-range dependence. Annals of Statistics 27: 1415–39. [Google Scholar] [CrossRef]
- Nadarajah, Saralees, and Jeffrey Chu. 2017. On the inefficiency of Bitcoin. Economics Letters 150: 6–9. [Google Scholar] [CrossRef]
- Ohanissian, Arek, Jeffrey Russell, and Ruey Tsay. 2008. True or spurious long memory? A new test. Journal of Business and Economic Statistics 26: 161–75. [Google Scholar] [CrossRef]
- Phillip, Andrew, Jennifer S. K. Chan, and Shelton Peiris. 2018. A new look at Cryptocurrencies. Economics Letters 163: 6–9. [Google Scholar] [CrossRef]
- Phillip, Andrew, Jennifer Chan, and Shelton Peiris. 2019. On long memory effects in the volatility measure of Cryptocurrencies. Finance Research Letters 28: 95–100. [Google Scholar] [CrossRef]
- Qu, Zhongjun. 2011. A test against spurious long memory. Journal of Business and Economic Statistics 29: 423–38. [Google Scholar] [CrossRef]
- Robinson, Peter. 1995. Gaussian Semiparametric Estimation of Long Range Dependence. The Annals of Statistics 23: 1630–61. [Google Scholar] [CrossRef]
- Shimotsu, Katsumi, and Peter Phillips. 2002. Pooled log periodogram regression. Journal of Time Series Analysis 23: 57–93. [Google Scholar] [CrossRef]
- Sibbertsen, Phillip, Christian Leschinski, and Marie Busch. 2018. A multivariate test against spurious long memory. Journal of Econometrics 203: 33–49. [Google Scholar] [CrossRef]
- Tiwari, Aviral, R. K. Jana, Debojyoti Das, and David Roubaud. 2018. Informational efficiency of Bitcoin—An extension. Economics Letters 163: 106–9. [Google Scholar] [CrossRef]
- Urquhart, Andrew. 2016. The inefficiency of Bitcoin. Economics Letters 148: 80–82. [Google Scholar] [CrossRef]
- Urquhart, Andrew. 2017. Price clustering in Bitcoin. Economics Letters 159: 145–48. [Google Scholar] [CrossRef]
- Wenger, Kai, Christian Leschinski, and Phillip Sibbertsen. 2018. A simple test on structural change in long-memory time series. Economics Letters 163: 90–94. [Google Scholar] [CrossRef]
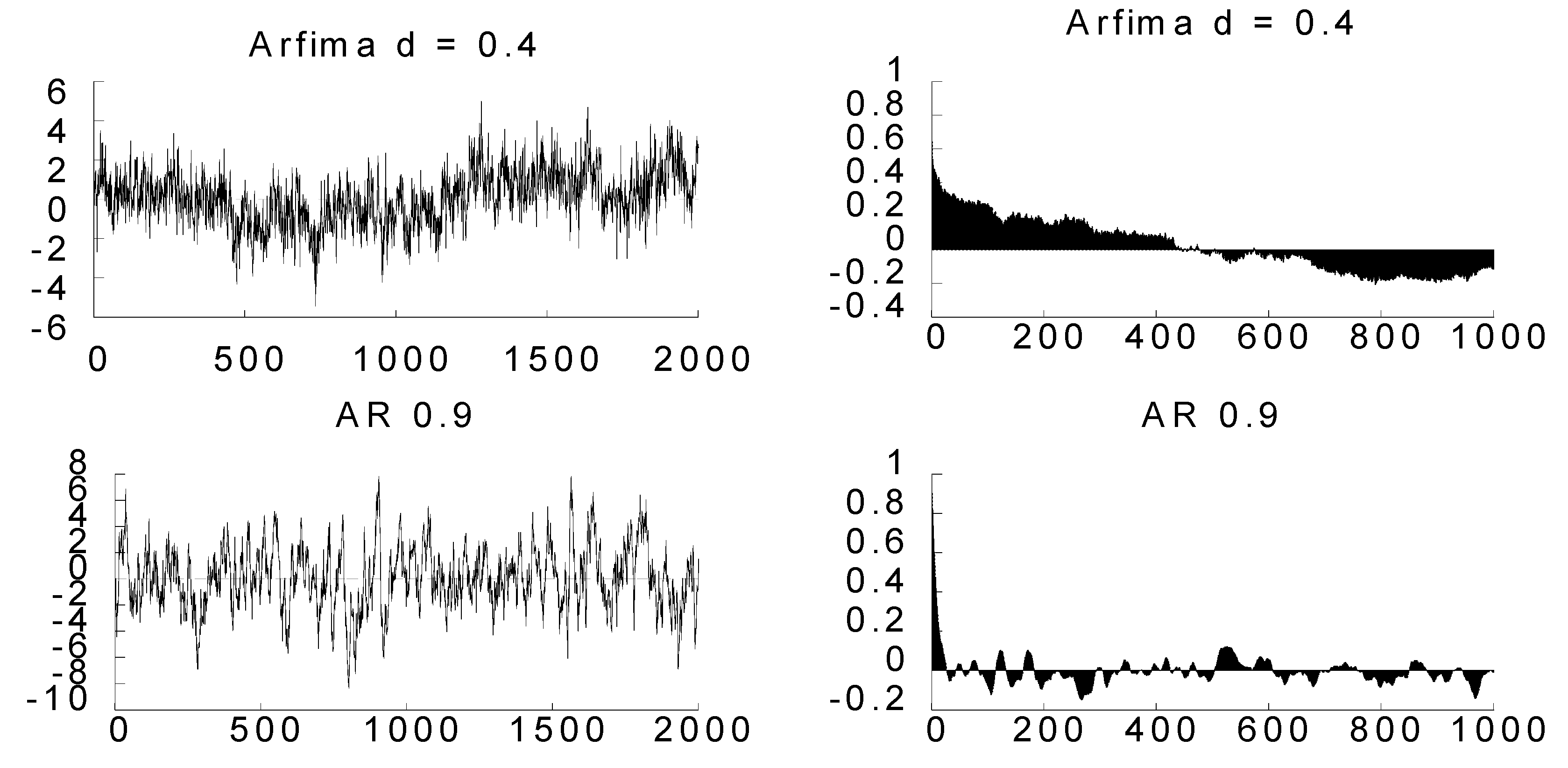
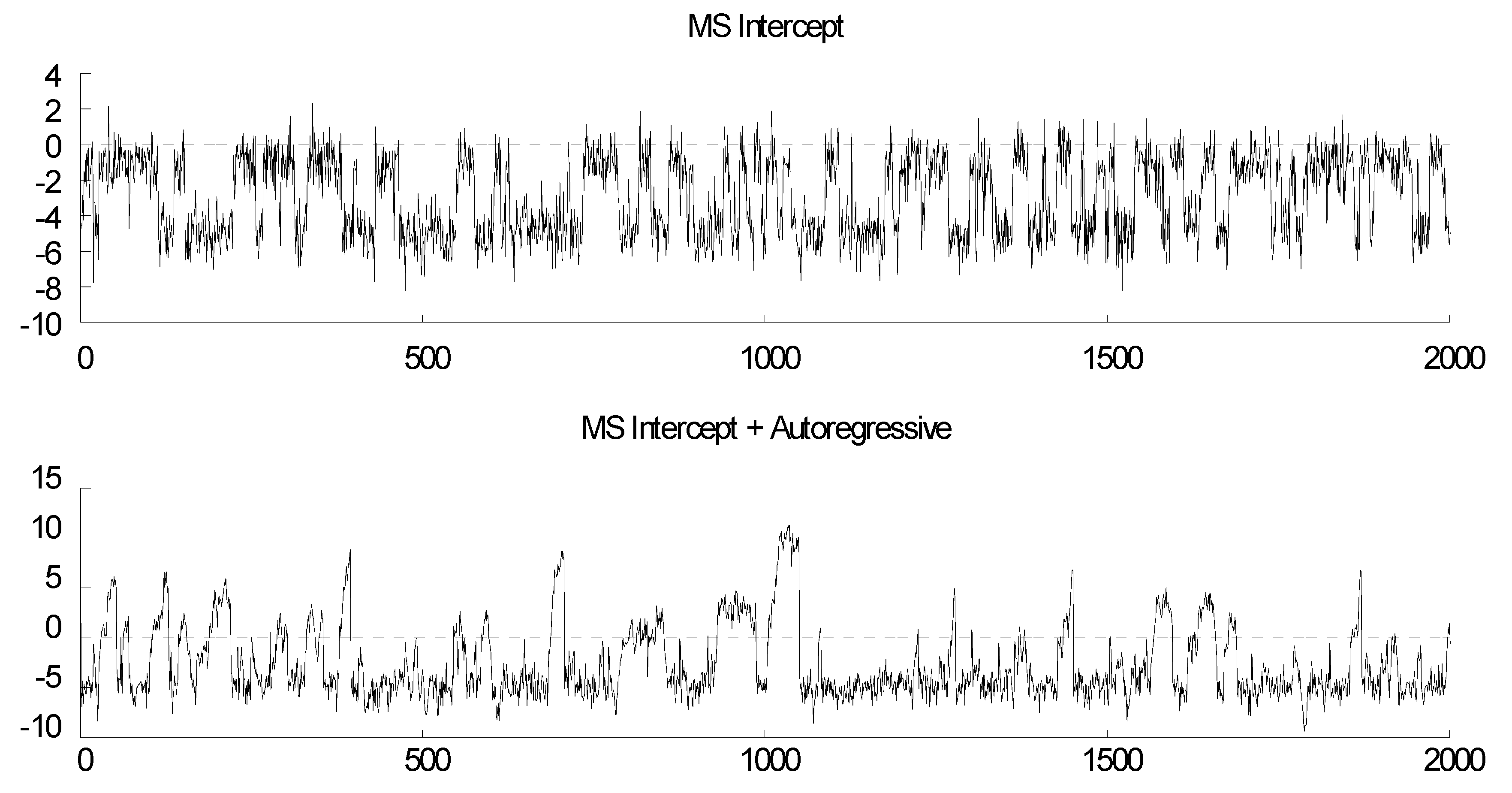
| 1 | Geometric decay would be easily discerned in the bottom right plot in Figure 1 if the number of lags was set at most at 30 (or at any low amount). |

| GPH (M = T0.5) | GPH (M = T0.8) | Fourier Estimations | Local Whittle | |
|---|---|---|---|---|
| Model 1 | 0.141 | 0.557 | 0.467 | 0.140 |
| (0.109) | (0.026) | (0.125) | (0.089) | |
| Model 2 | 0.284 | 0.741 | 0.447 | 0.282 |
| (0.147) | (0.051) | (0.168) | (0.135) |
| Bitcoin | Bitcoin Cash | XRP | Litecoin | Ethereum | |
|---|---|---|---|---|---|
| Mean | 0.00102 | −0.0007 | 0.00149 | 0.00098 | 0.00332 |
| Std dev | 0.03897 | 0.07881 | 0.07271 | 0.06444 | 0.06104 |
| Skewness | −0.340 | 0.612 | 2.076 | 1.720 | 0.271 |
| Kurtosis | 8.459 | 10.651 | 32.91 | 28.618 | 7.052 |
| Jarque–Bera | 2761 | 2206 | 88925 | 67783 | 1082 |
| N | 2190 | 882 | 2340 | 2435 | 1553 |
| Bitcoin | Ethereum | Litecoin | Bitcoin Cash | XRP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T = 2190 | T = 1553 | T = 2435 | T = 883 | T = 2340 | ||||||
| Estimate | p-Value | Estimate | p-Value | Estimate | p-Value | Estimate | p-Value | Estimate | p-Value | |
| Panel A: Return | ||||||||||
| GPH () | 0.153 | 0.165 | 0.259 ** | 0.036 | 0.170 | 0.111 | 0.121 | 0.405 | 0.057 | 0.589 |
| Bias Test | −0.454 | 0.675 | −1.407 | 0.920 | −0.122 | 0.549 | 0.806 | 0.210 | −0.886 | 0.812 |
| Skip-Sampling (h = 4) | −0.522 | 0.699 | −0.816 | 0.793 | 0.946 | 0.172 | −1.084 | 0.861 | 0.624 | 0.266 |
| Skip-Sampling (h = 8) | 0.378 | 0.353 | 0.168 | 0.433 | 0.044 | 0.482 | −0.486 | 0.686 | 0.544 | 0.293 |
| Panel B: Volatility | ||||||||||
| Volatility (LHR) | ||||||||||
| GPH () | 0.536 *** | 0.000 | 0.505 *** | 0.000 | 0.584 *** | 0.000 | 0.541 *** | 0.001 | 0.486 *** | 0.000 |
| Bias Test | −0.590 | 0.722 | 0.044 | 0.483 * | 0.084 | 0.467 | 0.322 | 0.374 | 2.356 *** | 0.009 |
| Skip-Sampling (h =4) | −0.073 | 0.529 | 0.431 | 0.333 | −0.768 | 0.779 | −0.451 | 0.674 | −0.406 | 0.658 |
| Skip-Sampling (h = 8) | 0.193 | 0.424 | 0.560 | 0.288 | −0.423 | 0.664 | −0.307 | 0.645 | −0.560 | 0.712 |
| Volatility (SR) | ||||||||||
| GPH () | 0.326 *** | 0.004 | 0.202* | 0.099 | 0.359 *** | 0.000 | 0.174 | 0.235 | 0.191 * | 0.077 |
| Bias Test | 1.524 * | 0.064 | −1.865 | 0.969 | 0.365 | 0.357 | 3.119 *** | 0.001 | 0.868 | 0.193 |
| Skip-Sampling (h = 4) | −0.860 | 0.805 | 0.637 | 0.262 | 0.142 | 0.443 | 0.585 | 0.279 | −0.737 | 0.770 |
| Skip-Sampling (h = 8) | −1.055 | 0.854 | 0.370 | 0.356 | 0.539 | 0.295 | 0.289 | 0.386 | −0.752 | 0.774 |
| Volatility (AR) | ||||||||||
| GPH () | 0.375 *** | 0.001 | 0.378 *** | 0.003 | 0.466 *** | 0.000 | 0.336 ** | 0.026 | 0.381 *** | 0.001 |
| Bias Test | −2.229 | 0.987 | −1.535 | 0.938 | 2.086 ** | 0.018 | 1.957 ** | 0.025 | −1.185 | 0.882 |
| Skip-Sampling (h = 4) | −1.027 | 0.848 | 0.423 | 0.336 | −1.229 | 0.890 | −0.013 | 0.505 | 0.070 | 0.472 |
| Skip-Sampling (h = 8) | −1.081 | 0.860 | 0.848 | 0.198 | −0.482 | 0.685 | −0.257 | 0.601 | −0.421 | 0.663 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rambaccussing, D.; Mazibas, M. True versus Spurious Long Memory in Cryptocurrencies. J. Risk Financial Manag. 2020, 13, 186. https://doi.org/10.3390/jrfm13090186
Rambaccussing D, Mazibas M. True versus Spurious Long Memory in Cryptocurrencies. Journal of Risk and Financial Management. 2020; 13(9):186. https://doi.org/10.3390/jrfm13090186
Chicago/Turabian StyleRambaccussing, Dooruj, and Murat Mazibas. 2020. "True versus Spurious Long Memory in Cryptocurrencies" Journal of Risk and Financial Management 13, no. 9: 186. https://doi.org/10.3390/jrfm13090186
APA StyleRambaccussing, D., & Mazibas, M. (2020). True versus Spurious Long Memory in Cryptocurrencies. Journal of Risk and Financial Management, 13(9), 186. https://doi.org/10.3390/jrfm13090186





