2.1. The CW-GARCH Specification
Consider a market with
assets traded at times
. At each time period
t an asset
s belongs to a volatility group
j, where
. Therefore it is assumed that the cross-sectional distribution of assets’ volatility exhibits a group structure. A volatility cluster is understood as a group of assets that, at time
t, have an “homogeneous” distribution in terms of volatility. The homogeneity concept underlying the cluster model is explained in the subsequent
Section 2.2. Volatility clusters are groups of assets with similar risk, therefore referred as “
risk groups”. We assume that there are
G fixed volatility clusters, where
G is not known to the researcher. Each asset
s can migrate from one cluster to another, but the number of clusters
G is assumed to be fixed for the entire time horizon. The class labels are arranged so that they induce a natural ordering in terms of the riskiness of their assets. That is, for any
, group
is riskier than group
. This ordering is not in generally necessary from the technical viewpoint since any asset is allowed to migrate from any group to any other group, however it is adopted to identify the group labels in terms of low-vs-high volatility.
Let
be the indicator function at the set
A, let
be the information set at time
, and let
denote the expectation conditional on
. Define the indicator variables
and assume that
. That is, at time
t the
j-th group is expected to contain a proportion of
assets. In other words
captures the expected size of the
j-th cluster at time
t. The vector
is a complete description of the class memberships of the
s-th asset at time
t. The elements of
are called “
hard memberships”, because these link each asset to a unique group inducing a partition at each
t.
Let
be the return of the asset
s at time
t. Let
be a sequence of random shocks where
. Consider the following returns’ generating process
where
and
are
G-dimensional model parameter vectors. In particular
,
,
The clustering information about the cross-sectional volatility enters the model for
via
.To see the connection with the classical GARCH(1,1) model (
Bollerslev 1986), note that
Therefore, conditional on the groups’ memberships at time
, the model (
1) specifies a GARCH(1,1) dynamic structure for all those assets within a given group
j. Based on this, model (
1) is referred as the “Clusterwise GARCH” (CW-GARCH) model. Within the
j-th cluster, the model parameters
and
can be interpreted as usual as the intercept, shock reaction and volatility decay coefficients of the
j-latent component. Therefore, we refer to
,
as the “within-group” GARCH(1,1) coefficients. The advantage of model (
1) is that it models the conditional variance dynamic in terms of an ordinal state variable so that the switch between
G different regimes is contingent to the overall market behavior. Volatility clusters are arranged in increasing order of risk from
to
, and in two different time periods
and
an asset
s may belong to the same risk group, i.e.,
, leading to the same GARCH regime although its volatility may have changed dramatically because the overall market volatility changed dramatically. The state variable
transforms a cardinal notion, i.e., volatility, into an ordinal notion induced by the memberships to ordered risk groups.
In order to see how the cluster dynamic interacts with the GARCH-type coefficients, define
The variance dynamic equation in (
1) can now be rewritten as
Equation (
2) resembles a GARCH(1,1) specification with time-varying coefficients obtained by weighting the within-groups classical GARCH(1,1) parameters by the class membership state variables. Although model (
2) leads to a convenient interpretation of the model, its formulation is not consistent with a model with dynamic parameters. In fact, the three model parameter vectors
do not depend on
t, and the dynamic of
is driven by the state variables
.
From (
2) it can be seen that the dynamic of
changes discontinuously because of the transition of an asset from a risk group to another. We introduce an alternative formulation of the model where the dynamic of
is smoothed by replacing the hard membership state variables
with a smooth version. There are situations where the membership of an asset is not totally clear (e.g., assets on the border of the transition between two risk groups), in this situation one may desire to smooth the transition between groups. Instead of assigning an asset to a risk group, one can attach a measure of the strength of the membership. In the classification literature these are called “
soft labels” or “
smooth memberships” (see
Hennig et al. 2016). There are various possibilities for defining a smooth assignment. The following choice will be motivated in
Section 2.2. Define
now
and
for all
. The quantity
gives the strength at which the asset
s is associated to the
j-th cluster at time
t based on the information at time
t. Define the vector
. We propose the following alternative version of model (
1) where the variance dynamic equation is replaced with the following
process
We call (
4) the “
Smooth CW-GARCH” (sCW-GARCH) model. For the sCW-GARCH the variance process can be written as a weighted sum of GARCH(1,1) models
As before, write the previous equation in terms of time varying GARCH components as follows
where
From the latter it can be easily seen that the sort of time varying GARCH(1,1) components of the sCW-GARCH change smoothly as assets migrate from one risk group to another. In this case, the formulation above gives also a better intuition about the role of the within-group GARCH parameters
. Note that
Therefore, each of the within-cluster GARCH parameter expresses the marginal variation of the corresponding GARCH component caused by a change in the degree of memberships with respect to the corresponding risk group.
From a different angle, it is worth noting that the sCW-GARCH model can be seen as a state-dependent dynamic volatility model with a continuous state space where, at time t, the current value of the state is determined by the smooth memberships . Differently, in the CW-GARCH models, the state space is discrete, since only G values are feasible, and the current value of the state is now determined by the hard memberships .
2.2. Cross-Sectional Cluster Model
In this section, we introduce a model for the cross-sectional distribution of assets’ volatility. While considerable research has investigated the time-series structure of the volatility process and its relationships with market and the expected returns (see, among others,
Campbell and Hentschel 1992;
Glosten et al. 1993), the question of how the distribution of assets’ volatility looks like at a given time point has received less attention. The key assumption in this work is that, at a given time point, there are groups of assets whose volatility cluster together to form groups of homogeneous risk. This assumption has been already explored in
Coretto et al. (
2011). This is empirically motivated by analyzing cross-sectional realized volatility data. From the data set studied in
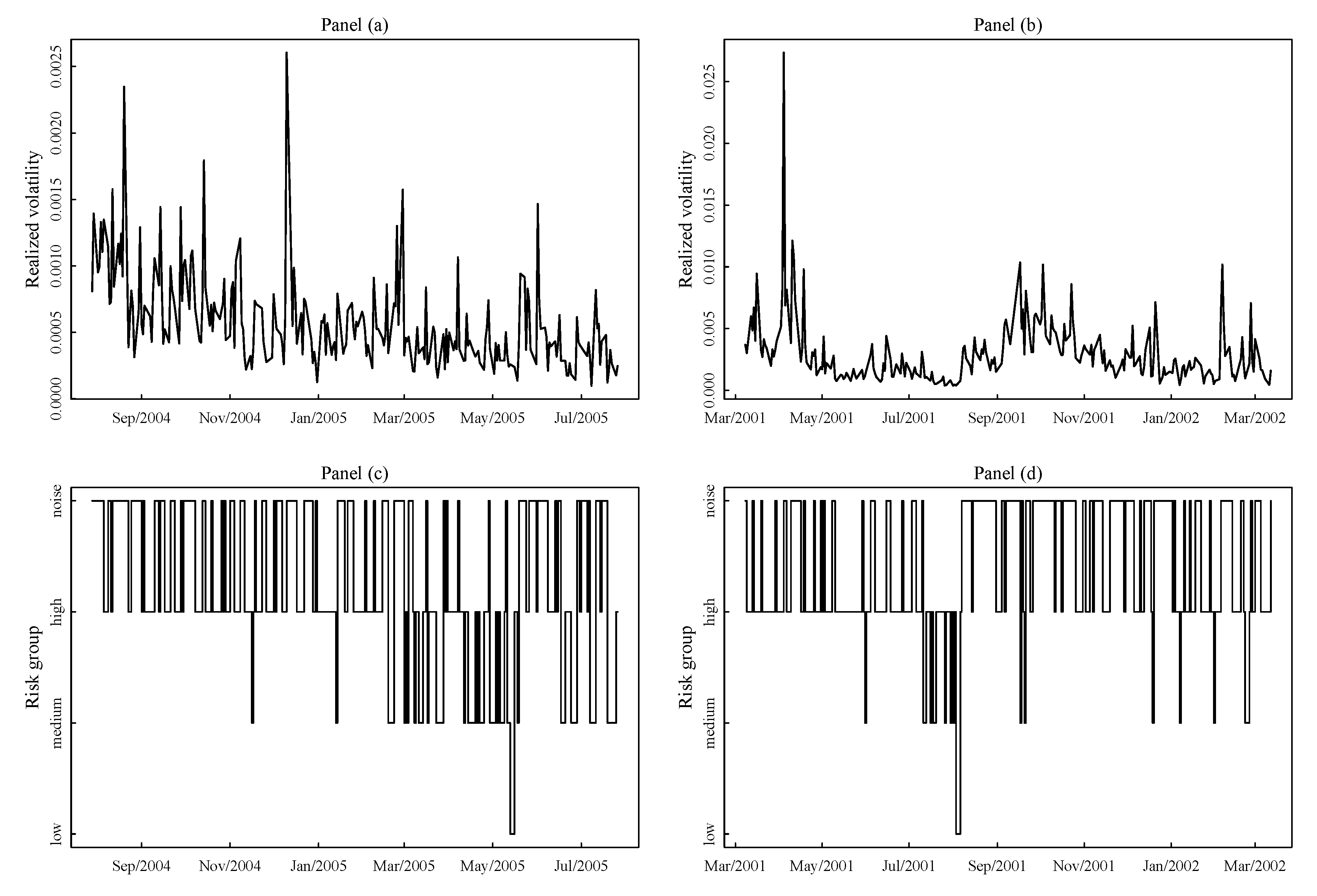
Section 4 including 123 stocks traded on the New York Stock Exchange market (NYSE), in
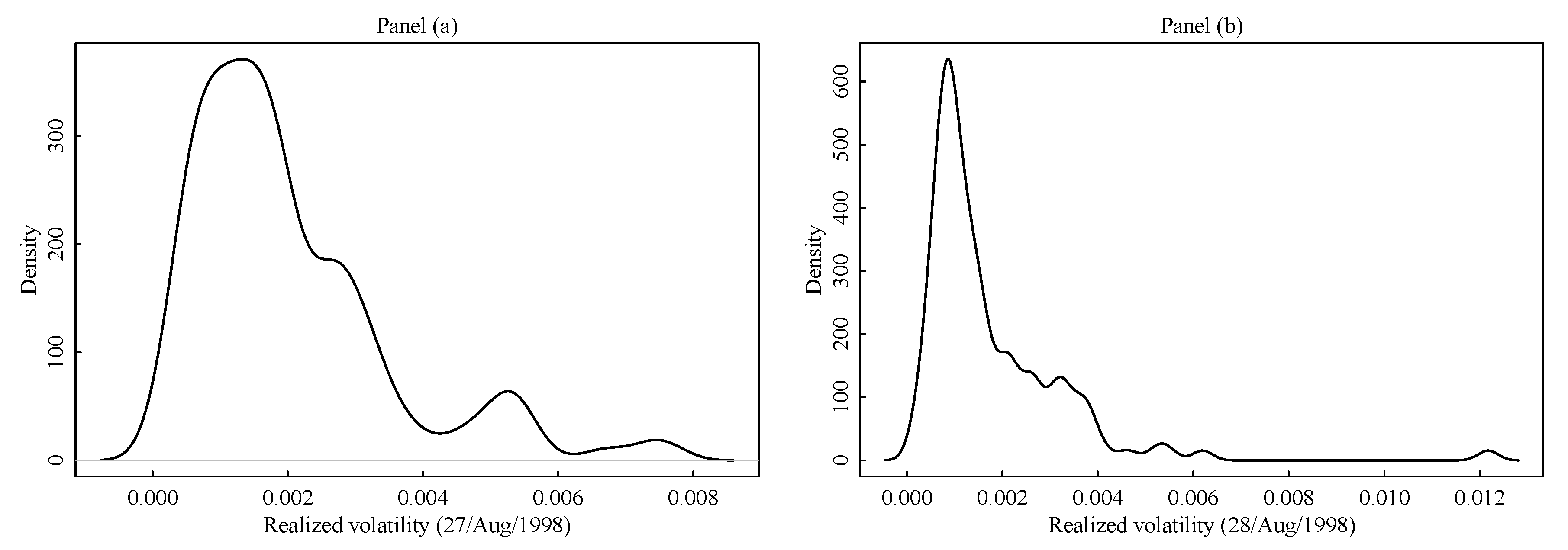
Figure 1 we show the kernel density estimate of the cross-sectional distribution of the realized volatility in two consecutive trading days.
Details on how the realized volatility is computed are postponed to
Section 4. In both panels of
Figure 1 there is evidence of multimodality, and this is consistent with the idea that there are groups of assets forming sub-populations with different average volatility levels. In panel (b) the kernel density estimate is corrupted by few assets exhibiting abnormal large realized volatility, this happens for a large number of trading days. In
Figure 1b the two rightmost density peaks close to 0.006 and 0.012 each capture just few scattered points, although the plot seems to suggest the presence of two symmetric components. Not the kernel density estimator itself, but the estimate of the optimal bandwidth of
Sheather and Jones (
1991) used in this case is heavily affected by this typical right-tail behavior of the distribution. This sort of artifacts are common to other kernel density estimators. Unless a large smoothing is introduced, in the presence of scattered points in low density regions the kernel density estimate is mainly driven by the shape of the kernel function. On the other hand, increasing the smoothing would tarnish the underlying multimodality structure.
The cross-sectional structure discussed above is consistent with mixture models. The idea is that each mixture component represents a group of assets that share similar risk behaviour. Let
be the realized volatility of the asset
s at time
t. We assume that at each
t there are
G groups of assets. Furthermore, conditional on
, the
jth group has a distribution
that is symmetric about the center
, has a variance
, and its expected size (proportion) is
. This implies that the the cross-sectional distribution of the realized volatility (unconditional on
) is represented by the finite location-scale mixture model
The idea is that each mixture component represents a group of assets that share similar risk behaviour. The parameter
represents the average within group realized volatility, while
represents its dispersion. Mixture models can reproduce clustered population, and it is a popular tool in model-based cluster analysis (see
Banfield and Raftery 1993;
McLachlan and Peel 2000, among others).
Coretto et al. (
2011) exploited the assumed mixture structure for using robust model-based cluster analysis to group asset with similar risk, and they proposed a parsimonious multivariate dynamic model where aggregate clusters’ volatility is modeled instead of individual assets’ volatility. The main goal of their work was to reduce the unfeasible large dimensionality of multivariate volatility models for large portfolios. Clustering methods applied to financial time series were also used in
Otranto (
2008), where the autoregressive metric (see
Corduas and Piccolo 2008) is applied to measure the distance between GARCH processes.
Finite mixtures of Gaussians, that is when
is the Gaussian density, are effective to model symmetrically shaped clusters also when clusters are not exactly normal. But in this case some more structure is needed to capture the effects of large variations in assets volatility that often show up for many trading days, e.g., the example shown in panel (b) of
Figure 1. In
Coretto et al. (
2011) it was proposed to adopt the approach of
Coretto and Hennig (
2016,
2017) where an improper constant density mixture component is introduced to catch points (interpreted as noise or contamination) in low density regions. This makes sense in all those situations where there are points extraneous to each clusters that have an unstructured behavior, and that can potentially appear everywhere in the data space. This is not exactly the cases studied in this paper. In fact, realized volatility is a positive quantity, and this heterogeneous component can only affect the right tail of the distribution. Here we assume that the group of few assets inflating the right tail of the distribution have a proper uniform distribution whose support is not overlapping with the other regular volatility clusters. Let
denote this group of asset exhibiting “abnormal” large volatility, we call this group of points “noise”. The term noise here is inherited from the robust clustering and classification literature (see
Ritter 2014), where it is understood as a “noisy cluster”, that is, a cluster of points with an unstructured shape compared with the main groups in the population. The uniform distribution is a convenient choice to capture atypical group of points not having a central location, and that are scattered in density regions somewhat separated from the main bulk of the data (
Banfield and Raftery 1993;
Coretto and Hennig 2016;
Hennig 2004).
We assume that
where
are respectively the lower and upper limit of the support of the uniform distribution. The previous implies that, without conditioning on the class labels
, the cross-sectional distribution of the assets’ volatility is represented by the following finite mixture model
where
is Gaussian density function. The unknown mixture parameter vector is
. This class of models where introduced in
Banfield and Raftery (
1993), and studied in
Coretto and Hennig (
2010,
2011) to perform robust clustering. The additional problem here is that if
is unrestricted one may have situations where the support of the noise group overlaps with one or more regular clusters if
is small enough. The latter would be inconsistent with the empirical evidence. To overcome this, we propose the following restriction, that is we assume that
is such that
The constant
controls the maximum degree of overlap between the support of the uniform distribution representing atypical observations and the closest regular Gaussian component. To see this, let
be the 99% quantile of the standard normal distribution, and take
. The restriction (
8) means that the uniform component can only overlap with the closest Gaussian component in its 1% tail probability. Restriction (
8) now ensures a well separation between regular and non-regular assets.
Although the mixture model introduced in this section is interesting for how it is able to fit the cross-sectional distribution of realized volatility at each time period, the main issue here is to obtain the hard class memberships variables
, and the smooth version
. Since
, here we have that
Quantities in (
8) are obtained simply applying the Bayes rule, this the reason why these are also called “
posterior weights” for class memberships. It can be easily shown (see
Velilla and Hernández 2005, and references therein) that the optimal partition of the points can be obtained by applying the following assignment rule also called “
Bayes classifier”
Basically the Bayes classifier assigns a point
to the group with largest posterior probability of membership. The assignment rule in (
10) is optimal in the sense that it achieves the lowest misclassification rate. Therefore, in order to obtain (
10) and (
9) from the data one needs to estimate
at each cross-section. Although we use the subscript
t to distinguish the
parameter in each cross-section, we do not assume any dependence in it. Here we treat the number of groups
G as fixed an known. While in some situation, including the one studied in this paper, a reasonable value of
G can be determined based on subject matter considerations, this is not always the case. In
Section 4 we will motivate our choice of
for this study and we will give some insights on how to fix in it in general.
In the next
Section 3 we introduce estimation methods for the quantities of interest, that are class memberships
and smooth weights
. But before to conclude this session we show how model (
7) under (
8) fits the data sets of the example of
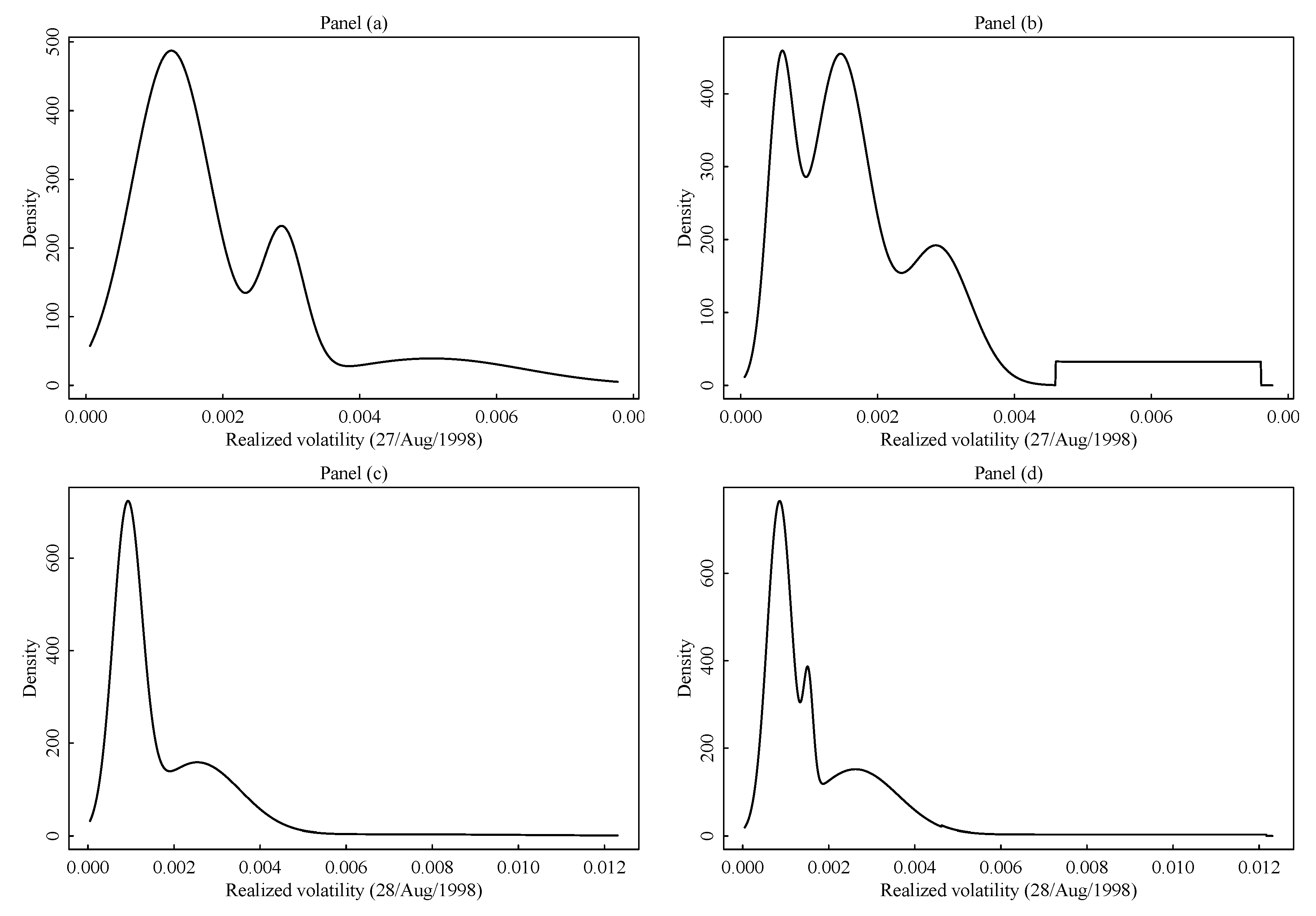
Figure 1. In this paper we are mainly interested in the cluster structure of the cross-sectional data, however, it is also of interest to investigate the fitting capability of the cross-sectional model. Estimated density of the two data sets of example in
Figure 1 are shown in
Figure 2. Panel (a) and (b) of
Figure 2 refers to the cross-section distribution of realized volatility on 27/Aug/1998 (compare with panel (a) in
Figure 1). Panel (c) and (d) of
Figure 2 refers to the cross-section distribution of realized volatility on 28/Aug/1998 (compare with panel (b) in
Figure 1). In panel (a) and (c) of
Figure 2 we show the fitted density based on model (
7) with
under (
8), and the additional restriction that
, i.e., there is no uniform noise. In panels (b) and (d) the same model is fitted with the uniform component active. Comparing panels (a) and (b) of
Figure 2 with panel (a) in
Figure 1 one can see how the proposed model can lead to well separated components. The comparison of panels (a) and (b) in
Figure 2 shows how the introduction of the uniform component completely modify the fitted regular components. In fact, in the case of panel (a) the absence of the uniform component causes a strong inflation of the variance of the rightmost Gaussian component so that the second component seen in panel (b) is completely eaten. A similar situation happen in panel (c) and (d) of
Figure 2. Because of the uniform density in model (
7) possible discontinuities at the boundaries of uniform support may arise in the final estimate. Compare Panel (d) vs. panel (b) in
Figure 2. When the group of noisy assets is reasonably concentrated, the corresponding support of the fitted uniform distribution becomes smaller, and the uniform density easily dominates the tail of the closest regular distribution (e.g., this happens in panel (b)). The discontinuity of the model density is less noticeable in cases like the one in panel (d) where the support of the uniform is rather large because of extremely scattered abnormal realized volatility. Although the discontinuity introduced by the uniform distribution adds some technical issues for the estimation theory (see
Coretto and Hennig 2011), it has two main advantages: (i) it allows to represent unstructured groups of points with a well defined, simple and proper probability model; (ii) the noisy cluster is understood as a group of points not having any particular shape, and that is different and distinguished from the regular clusters’ prototype model (the Gaussian density here). Therefore, a discontinuous transition between regular and non-regular density region obeys to the philosophy in robust statistic that in order to identify outliers/noise they need to arise in low density regions under the model for the regular points. Further discussions about the model-based treatment of noise/outliers in clustering can be found in
Hennig (
2004) and
Coretto and Hennig (
2016).