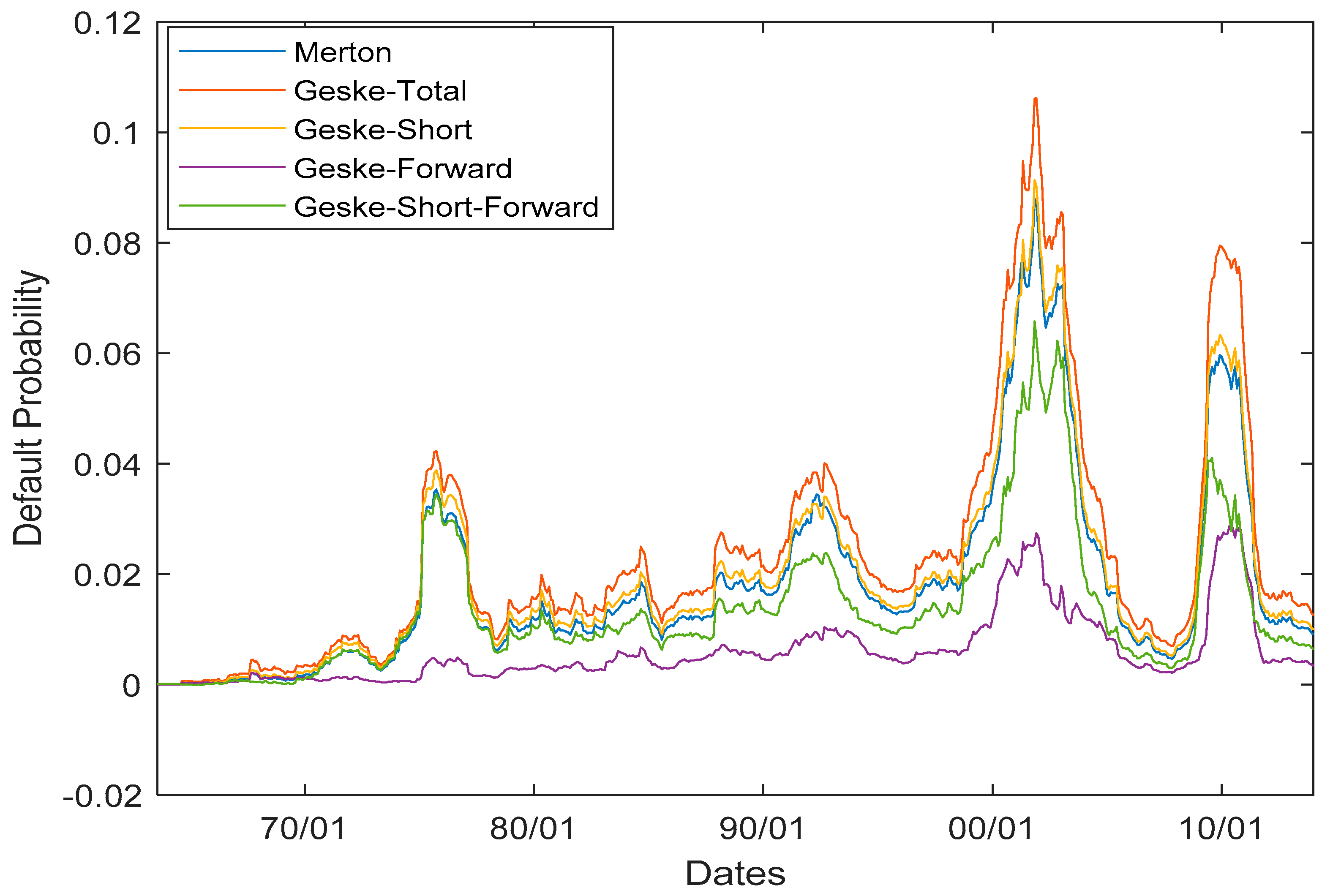
Figure 1.
Default probabilities.
Figure 1.
Default probabilities.
Table 1.
This table shows pairwise correlations between different measures of default probability, beta, size, and book-to-market ratio, for the period July 1963 to December 2013. M-Def. is Merton’s default probability, T-Def is the total default probability from Geske’s model, S-Def. is the short-term default probability, F-Def. is the forward default probability, S-F Def. is the short-term minus forward default probability from Geske’s model. Beta is the CAPM beta, size is the market value of equity, and bktmkt is the book-to-market ratio.
Table 1.
This table shows pairwise correlations between different measures of default probability, beta, size, and book-to-market ratio, for the period July 1963 to December 2013. M-Def. is Merton’s default probability, T-Def is the total default probability from Geske’s model, S-Def. is the short-term default probability, F-Def. is the forward default probability, S-F Def. is the short-term minus forward default probability from Geske’s model. Beta is the CAPM beta, size is the market value of equity, and bktmkt is the book-to-market ratio.
| | M-Def. | T-Def. | S-Def. | F-Def. | S-F Def. | Beta | Stdev | Size | bktmkt |
|---|
| M-Def. | 1.00 | 0.96 | 1.00 | 0.58 | 0.77 | −0.05 | 0.11 | 0.24 | 0.68 |
| T-Def. | 0.96 | 1.00 | 0.97 | 0.74 | 0.62 | −0.06 | 0.09 | 0.25 | 0.70 |
| S-Def. | 1.00 | 0.97 | 1.00 | 0.59 | 0.77 | −0.06 | 0.11 | 0.25 | 0.69 |
| F-Def. | 0.58 | 0.74 | 0.59 | 1.00 | 0.01 | −0.03 | 0.00 | 0.17 | 0.49 |
| S-F Def. | 0.77 | 0.62 | 0.77 | 0.01 | 1.00 | −0.05 | 0.13 | 0.18 | 0.49 |
| Beta | −0.05 | −0.06 | −0.06 | −0.03 | −0.05 | 1.00 | −0.07 | −0.05 | −0.16 |
| Stdev | 0.11 | 0.09 | 0.11 | 0.00 | 0.13 | −0.07 | 1.00 | −0.09 | −0.01 |
| Size | 0.24 | 0.25 | 0.25 | 0.17 | 0.18 | −0.05 | −0.09 | 1.00 | 0.47 |
| bktmkt | 0.68 | 0.70 | 0.69 | 0.49 | 0.49 | −0.16 | −0.01 | 0.47 | 1.00 |
Table 2.
Average returns from decile portfolios sorted by Merton’s default probability. From the data for July 1963 to December 2013, at the end of each month, we used the most recently calculated Merton’s default probability for each firm to sort all stocks into deciles. We then calculated the equally weighted and value-weighted returns over the next month. The returns are the average monthly returns over the sample period. Portfolio 1 is the portfolio with the lowest default risk and Portfolio 10 is the portfolio with the highest default risk. High-Low is the difference between the high and low default risk portfolios. t-values are calculated from Newey-West standard errors. Alphas are calculated using the CAPM, the three-factor Fama-French, and the four-factor model (Fama-French three-factor plus momentum).
Table 2.
Average returns from decile portfolios sorted by Merton’s default probability. From the data for July 1963 to December 2013, at the end of each month, we used the most recently calculated Merton’s default probability for each firm to sort all stocks into deciles. We then calculated the equally weighted and value-weighted returns over the next month. The returns are the average monthly returns over the sample period. Portfolio 1 is the portfolio with the lowest default risk and Portfolio 10 is the portfolio with the highest default risk. High-Low is the difference between the high and low default risk portfolios. t-values are calculated from Newey-West standard errors. Alphas are calculated using the CAPM, the three-factor Fama-French, and the four-factor model (Fama-French three-factor plus momentum).
| Deciles | ew_ret | vw_ret | Beta | Std | Size | bktmkt | MD | GTD | GSD | GF | GS-M | Nfirms |
|---|
| low | 1.05 | 0.89 | 0.58 | 6.16 | 6.43 | 0.51 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 2 | 1.11 | 0.99 | 0.79 | 7.67 | 6.01 | 0.59 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 3 | 1.20 | 0.99 | 0.93 | 8.80 | 5.59 | 0.63 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 4 | 1.20 | 1.07 | 1.03 | 9.88 | 5.19 | 0.67 | 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | 290 |
| 5 | 1.27 | 0.99 | 1.13 | 10.99 | 4.83 | 0.71 | 0.02 | 0.04 | 0.03 | 0.00 | −0.02 | 290 |
| 6 | 1.30 | 1.05 | 1.22 | 12.13 | 4.50 | 0.74 | 0.08 | 0.13 | 0.11 | 0.00 | −0.08 | 290 |
| 7 | 1.38 | 1.03 | 1.31 | 13.43 | 4.18 | 0.79 | 0.26 | 0.40 | 0.36 | 0.00 | −0.27 | 290 |
| 8 | 1.41 | 0.98 | 1.41 | 15.08 | 3.79 | 0.83 | 0.82 | 1.15 | 1.03 | 0.02 | −0.81 | 290 |
| 9 | 1.53 | 1.02 | 1.53 | 17.61 | 3.35 | 0.88 | 2.53 | 3.33 | 2.93 | 0.06 | −2.40 | 290 |
| high | 1.86 | 0.97 | 1.84 | 24.51 | 2.71 | 0.92 | 9.95 | 12.46 | 10.62 | 0.49 | −8.21 | 290 |
| dif | 0.81 | 0.08 | | | | | | | | | | |
| t-stat | 2.34 | 0.23 | | | | | | | | | | |
| Capm_alpha | 0.42 | | | | | | | | | | | |
| t-stat | 1.46 | | | | | | | | | | | |
| FF3-alpha | 0.16 | | | | | | | | | | | |
| t-stat | 0.73 | | | | | | | | | | | |
| FF4-alpha | 0.66 | | | | | | | | | | | |
| t-stat | 2.13 | | | | | | | | | | | |
Table 3.
Average returns from ddecile portfolios sorted by Geske’s total default probability. From the data for July 1963 to December 2013, at the end of each month, we used the most recently calculated Geske’s total default probability for each firm to sort all stocks into deciles. We then calculated the equally weighted and value-weighted returns over the next month. The returns are the average monthly returns over the sample period. Portfolio 1 is the portfolio with the lowest default risk and Portfolio 10 is the portfolio with the highest default risk. High-Low is the difference between the high and low default risk portfolios. t-values are calculated from Newey-West standard errors. Alphas are calculated using the CAPM, the three-factor Fama-French, and the four-factor model (Fama-French three-factor plus momentum).
Table 3.
Average returns from ddecile portfolios sorted by Geske’s total default probability. From the data for July 1963 to December 2013, at the end of each month, we used the most recently calculated Geske’s total default probability for each firm to sort all stocks into deciles. We then calculated the equally weighted and value-weighted returns over the next month. The returns are the average monthly returns over the sample period. Portfolio 1 is the portfolio with the lowest default risk and Portfolio 10 is the portfolio with the highest default risk. High-Low is the difference between the high and low default risk portfolios. t-values are calculated from Newey-West standard errors. Alphas are calculated using the CAPM, the three-factor Fama-French, and the four-factor model (Fama-French three-factor plus momentum).
| Deciles | ew_ret | vw_ret | Beta | Std | Size | bktmkt | MD | GTD | GSD | GF | GS-M | Nfirms |
|---|
| low | 1.09 | 0.94 | 0.63 | 6.35 | 6.37 | 0.53 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 2 | 1.16 | 0.91 | 0.79 | 7.80 | 5.84 | 0.58 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 3 | 1.19 | 0.98 | 0.91 | 8.71 | 5.50 | 0.65 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 4 | 1.20 | 0.97 | 1.01 | 9.70 | 5.16 | 0.68 | 0.00 | 0.01 | 0.01 | 0.00 | −0.01 | 290 |
| 5 | 1.27 | 0.97 | 1.10 | 10.73 | 4.81 | 0.71 | 0.02 | 0.04 | 0.03 | 0.00 | −0.03 | 290 |
| 6 | 1.28 | 0.99 | 1.21 | 11.87 | 4.53 | 0.74 | 0.09 | 0.16 | 0.13 | 0.00 | −0.12 | 290 |
| 7 | 1.42 | 1.08 | 1.29 | 13.21 | 4.19 | 0.78 | 0.31 | 0.47 | 0.39 | 0.01 | −0.37 | 290 |
| 8 | 1.41 | 0.97 | 1.42 | 14.96 | 3.84 | 0.81 | 0.91 | 1.31 | 1.09 | 0.04 | −1.00 | 290 |
| 9 | 1.55 | 0.91 | 1.55 | 17.67 | 3.41 | 0.85 | 2.65 | 3.60 | 3.02 | 0.15 | −2.74 | 290 |
| high | 1.72 | 0.74 | 1.88 | 24.77 | 2.84 | 0.86 | 9.92 | 12.77 | 10.63 | 1.38 | −8.08 | 290 |
| dif | 0.63 | −0.20 | | | | | | | | | | |
| t-stat | 1.90 | −0.64 | | | | | | | | | | |
| Capm_alpha | 0.25 | | | | | | | | | | | |
| t-stat | 0.90 | | | | | | | | | | | |
| FF3-alpha | 0.03 | | | | | | | | | | | |
| t-stat | 0.13 | | | | | | | | | | | |
| FF4-alpha | 0.48 | | | | | | | | | | | |
| t-stat | 1.63 | | | | | | | | | | | |
Table 4.
Average returns from decile portfolios sorted by Geske’s short-term default probability. From the data for July 1963 to December 2013, at the end of each month, we used the most recently calculated Geske’s short-term default probability for each firm to sort all stocks into deciles. We then calculated the equally weighted and value-weighted returns over the next month. The returns are the average monthly returns over the sample period. Portfolio 1 is the portfolio with the lowest default risk and Portfolio 10 is the portfolio with the highest default risk. High-Low is the difference between the high and low default risk portfolios. t-values are calculated from Newey-West standard errors. Alphas are calculated using the CAPM, the three-factor Fama-French, and the four-factor model (Fama-French three-factor plus momentum).
Table 4.
Average returns from decile portfolios sorted by Geske’s short-term default probability. From the data for July 1963 to December 2013, at the end of each month, we used the most recently calculated Geske’s short-term default probability for each firm to sort all stocks into deciles. We then calculated the equally weighted and value-weighted returns over the next month. The returns are the average monthly returns over the sample period. Portfolio 1 is the portfolio with the lowest default risk and Portfolio 10 is the portfolio with the highest default risk. High-Low is the difference between the high and low default risk portfolios. t-values are calculated from Newey-West standard errors. Alphas are calculated using the CAPM, the three-factor Fama-French, and the four-factor model (Fama-French three-factor plus momentum).
| Deciles | ew_ret | vw_ret | Beta | Std | Size | bktmkt | MD | GTD | GSD | GF | GS-M | Nfirms |
|---|
| low | 1.07 | 0.92 | 0.62 | 6.32 | 6.44 | 0.53 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 2 | 1.13 | 0.90 | 0.79 | 7.79 | 5.89 | 0.57 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 3 | 1.20 | 1.04 | 0.91 | 8.74 | 5.54 | 0.63 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 4 | 1.16 | 1.02 | 1.01 | 9.71 | 5.20 | 0.67 | 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | 290 |
| 5 | 1.27 | 0.95 | 1.11 | 10.82 | 4.83 | 0.71 | 0.02 | 0.04 | 0.03 | 0.00 | −0.02 | 290 |
| 6 | 1.30 | 1.02 | 1.21 | 11.95 | 4.52 | 0.74 | 0.08 | 0.14 | 0.12 | 0.00 | −0.09 | 290 |
| 7 | 1.38 | 1.07 | 1.30 | 13.28 | 4.20 | 0.78 | 0.26 | 0.43 | 0.36 | 0.01 | −0.29 | 290 |
| 8 | 1.40 | 0.99 | 1.41 | 14.95 | 3.82 | 0.83 | 0.82 | 1.22 | 1.03 | 0.03 | −0.84 | 290 |
| 9 | 1.53 | 1.00 | 1.54 | 17.55 | 3.39 | 0.87 | 2.52 | 3.43 | 2.93 | 0.09 | −2.43 | 290 |
| high | 1.84 | 0.93 | 1.85 | 24.51 | 2.74 | 0.91 | 9.93 | 12.59 | 10.63 | 0.57 | −8.22 | 290 |
| dif | 0.77 | 0.01 | | | | | | | | | | |
| t-stat | 2.27 | 0.02 | | | | | | | | | | |
| Capm_alpha | 0.38 | | | | | | | | | | | |
| t-stat | 1.36 | | | | | | | | | | | |
| FF3-alpha | 0.14 | | | | | | | | | | | |
| t-stat | 0.63 | | | | | | | | | | | |
| FF4-alpha | 0.63 | | | | | | | | | | | |
| t-stat | 2.08 | | | | | | | | | | | |
Table 5.
Average returns from decile portfolios sorted by Geske’s forward default probability. From the data for July 1963 to December 2013, at the end of each month, we used the most recently calculated Geske’s forward default probability for each firm to sort all stocks into deciles. We then calculated the equally weighted and value-weighted returns over the next month. The returns are the average monthly returns over the sample period. Portfolio 1 is the portfolio with the lowest default risk and Portfolio 10 is the portfolio with the highest default risk. High-Low is the difference between the high and low default risk portfolios. t-values are calculated from Newey-West standard errors. Alphas are calculated using the CAPM, the three-factor Fama-French, and the four-factor model (Fama-French three-factor plus momentum).
Table 5.
Average returns from decile portfolios sorted by Geske’s forward default probability. From the data for July 1963 to December 2013, at the end of each month, we used the most recently calculated Geske’s forward default probability for each firm to sort all stocks into deciles. We then calculated the equally weighted and value-weighted returns over the next month. The returns are the average monthly returns over the sample period. Portfolio 1 is the portfolio with the lowest default risk and Portfolio 10 is the portfolio with the highest default risk. High-Low is the difference between the high and low default risk portfolios. t-values are calculated from Newey-West standard errors. Alphas are calculated using the CAPM, the three-factor Fama-French, and the four-factor model (Fama-French three-factor plus momentum).
| Deciles | ew_ret | vw_ret | Beta | Std | Size | bktmkt | MD | GTD | GSD | GF | GS-M | Nfirms |
|---|
| low | 1.41 | 0.97 | 0.75 | 8.03 | 5.44 | 0.75 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 2 | 1.54 | 1.16 | 0.88 | 9.80 | 4.56 | 0.74 | 0.06 | 0.07 | 0.07 | 0.00 | −0.07 | 290 |
| 3 | 1.37 | 0.98 | 0.93 | 10.65 | 4.37 | 0.70 | 0.01 | 0.01 | 0.01 | 0.00 | −0.01 | 290 |
| 4 | 1.31 | 0.88 | 0.94 | 10.03 | 4.90 | 0.72 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 5 | 1.30 | 0.92 | 1.02 | 10.29 | 5.01 | 0.71 | 0.00 | 0.01 | 0.01 | 0.00 | −0.01 | 290 |
| 6 | 1.33 | 0.94 | 1.10 | 11.15 | 4.83 | 0.71 | 0.01 | 0.02 | 0.02 | 0.00 | −0.02 | 290 |
| 7 | 1.29 | 0.85 | 1.21 | 12.16 | 4.68 | 0.71 | 0.03 | 0.05 | 0.05 | 0.00 | −0.04 | 290 |
| 8 | 1.30 | 0.95 | 1.32 | 13.49 | 4.52 | 0.69 | 0.09 | 0.21 | 0.16 | 0.04 | −0.12 | 290 |
| 9 | 1.29 | 0.91 | 1.49 | 15.67 | 4.24 | 0.67 | 0.41 | 0.97 | 0.63 | 0.26 | −0.33 | 290 |
| high | 1.13 | 0.70 | 1.81 | 21.72 | 3.72 | 0.63 | 3.39 | 7.15 | 4.26 | 2.42 | −0.75 | 290 |
| dif | −0.29 | −0.27 | | | | | | | | | | |
| t-stat | −1.29 | −1.07 | | | | | | | | | | |
| Capm_alpha | −0.56 | | | | | | | | | | | |
| t-stat | −2.90 | | | | | | | | | | | |
| FF3-alpha | −0.59 | | | | | | | | | | | |
| t-stat | −3.94 | | | | | | | | | | | |
| FF4-alpha | −0.55 | | | | | | | | | | | |
| t-stat | −3.65 | | | | | | | | | | | |
Table 6.
Average returns from decile portfolios sorted by Geske’s short-term minus forward default probability. From the data for July 1963 to December 2013, at the end of each month, we used the most recently calculated Geske’s short-term minus forward default probability for each firm to sort all stocks into deciles. We then calculated the equally weighted and value-weighted returns over the next month. The returns are the average monthly returns over the sample period. Portfolio 1 is the portfolio with the lowest default risk and Portfolio 10 is the portfolio with the highest default risk. High-Low is the difference between the high and low default risk portfolios. t-values are calculated from Newey-West standard errors. Alphas are calculated using the CAPM, the three-factor Fama-French and the four-factor model (Fama-French three-factor plus momentum).
Table 6.
Average returns from decile portfolios sorted by Geske’s short-term minus forward default probability. From the data for July 1963 to December 2013, at the end of each month, we used the most recently calculated Geske’s short-term minus forward default probability for each firm to sort all stocks into deciles. We then calculated the equally weighted and value-weighted returns over the next month. The returns are the average monthly returns over the sample period. Portfolio 1 is the portfolio with the lowest default risk and Portfolio 10 is the portfolio with the highest default risk. High-Low is the difference between the high and low default risk portfolios. t-values are calculated from Newey-West standard errors. Alphas are calculated using the CAPM, the three-factor Fama-French and the four-factor model (Fama-French three-factor plus momentum).
| Deciles | ew_ret | vw_ret | Beta | Std | Size | bktmkt | MD | GTD | GSD | GF | GS-M | Nfirms |
|---|
| low | 0.88 | 0.72 | 1.41 | 14.81 | 4.91 | 0.50 | 0.07 | 0.64 | 0.17 | 0.46 | −0.21 | 290 |
| 2 | 0.93 | 0.76 | 0.87 | 8.42 | 6.06 | 0.55 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 3 | 1.15 | 0.98 | 0.71 | 6.94 | 6.12 | 0.58 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 4 | 1.24 | 1.10 | 0.84 | 8.15 | 5.59 | 0.63 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 290 |
| 5 | 1.30 | 1.18 | 0.96 | 9.50 | 5.09 | 0.70 | 0.01 | 0.01 | 0.01 | 0.00 | 0.01 | 290 |
| 6 | 1.33 | 1.07 | 1.09 | 10.89 | 4.61 | 0.76 | 0.04 | 0.06 | 0.06 | 0.00 | 0.05 | 290 |
| 7 | 1.45 | 1.15 | 1.22 | 12.34 | 4.25 | 0.81 | 0.17 | 0.23 | 0.22 | 0.00 | 0.19 | 290 |
| 8 | 1.44 | 1.03 | 1.33 | 14.08 | 3.84 | 0.86 | 0.61 | 0.77 | 0.74 | 0.00 | 0.66 | 290 |
| 9 | 1.57 | 1.13 | 1.47 | 16.71 | 3.37 | 0.91 | 2.09 | 2.48 | 2.38 | 0.02 | 2.10 | 290 |
| high | 1.98 | 1.25 | 1.75 | 23.05 | 2.66 | 0.96 | 8.78 | 9.87 | 9.38 | 0.05 | 8.22 | 290 |
| dif | 1.10 | 0.52 | | | | | | | | | | |
| t-stat | 4.56 | 2.07 | | | | | | | | | | |
| Capm_alpha | 0.98 | | | | | | | | | | | |
| t-stat | 4.51 | | | | | | | | | | | |
| FF3-alpha | 0.73 | | | | | | | | | | | |
| t-stat | 3.39 | | | | | | | | | | | |
| FF4-alpha | 1.24 | | | | | | | | | | | |
| t-stat | 4.61 | | | | | | | | | | | |
Table 7.
Average returns from double-sorted quantile portfolios (sorted by size and Merton’s default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on size and Merton’s default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
Table 7.
Average returns from double-sorted quantile portfolios (sorted by size and Merton’s default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on size and Merton’s default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
| Size | Low | 2 | 3 | 4 | High | High-Low | t-Stat |
|---|
| small | 1.36 | 1.53 | 1.59 | 1.91 | 2.37 | 1.02 | 3.27 |
| 2 | 1.23 | 1.26 | 1.31 | 1.28 | 1.09 | −0.15 | −0.52 |
| 3 | 1.08 | 1.23 | 1.25 | 1.26 | 1.07 | −0.01 | −0.03 |
| 4 | 1.18 | 1.20 | 1.24 | 1.20 | 0.99 | −0.19 | −0.73 |
| big | 0.97 | 1.05 | 1.08 | 0.98 | 1.07 | 0.09 | 0.34 |
| small-big | 0.38 | 0.48 | 0.51 | 0.93 | 1.31 | | |
| t-stat | 2.23 | 2.67 | 2.62 | 4.20 | 4.29 | | |
Table 8.
Average returns from double-sorted quantile portfolios (sorted by size and Geske’s total default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on size and Geske’s total default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
Table 8.
Average returns from double-sorted quantile portfolios (sorted by size and Geske’s total default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on size and Geske’s total default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
| Size | Low | 2 | 3 | 4 | High | High-Low | t-Stat |
|---|
| small | 1.42 | 1.51 | 1.61 | 2.00 | 2.35 | 0.93 | 3.18 |
| 2 | 1.28 | 1.28 | 1.30 | 1.26 | 1.07 | −0.20 | −0.76 |
| 3 | 1.16 | 1.27 | 1.26 | 1.25 | 1.05 | −0.11 | −0.45 |
| 4 | 1.20 | 1.23 | 1.20 | 1.21 | 0.98 | −0.22 | −0.89 |
| big | 1.00 | 1.06 | 1.06 | 1.03 | 0.81 | −0.19 | −0.73 |
| small-big | 0.42 | 0.46 | 0.56 | 0.98 | 1.55 | | |
| t-stat | 2.59 | 2.42 | 2.82 | 4.41 | 5.21 | | |
Table 9.
Average returns from double-sorted quantile portfolios (sorted by size and Geske’s short-term default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on size and Geske’s short-term default probability. The table shows average returns for each of 25 portfolios. Small–big is the return differential between the small and big firm portfolios within each default quantile. High–low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
Table 9.
Average returns from double-sorted quantile portfolios (sorted by size and Geske’s short-term default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on size and Geske’s short-term default probability. The table shows average returns for each of 25 portfolios. Small–big is the return differential between the small and big firm portfolios within each default quantile. High–low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
| Size | Low | 2 | 3 | 4 | High | High-Low | t-Stat |
|---|
| small | 1.38 | 1.49 | 1.63 | 1.92 | 2.38 | 1.00 | 3.35 |
| 2 | 1.26 | 1.26 | 1.32 | 1.27 | 1.08 | −0.17 | −0.65 |
| 3 | 1.11 | 1.24 | 1.28 | 1.26 | 1.08 | −0.04 | −0.14 |
| 4 | 1.19 | 1.23 | 1.23 | 1.20 | 0.99 | −0.20 | −0.78 |
| big | 0.98 | 1.10 | 1.06 | 0.98 | 0.98 | 0.00 | 0.01 |
| small-big | 0.40 | 0.39 | 0.57 | 0.95 | 1.40 | | |
| t-stat | 2.52 | 2.02 | 2.91 | 4.30 | 4.69 | | |
Table 10.
Average returns from double-sorted quantile portfolios (sorted by size and Geske’s forward default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on size and Geske’s forward default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
Table 10.
Average returns from double-sorted quantile portfolios (sorted by size and Geske’s forward default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on size and Geske’s forward default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
| Size | Low | 2 | 3 | 4 | High | High-Low | t-Stat |
|---|
| small | 2.15 | 2.31 | 2.05 | 1.96 | 1.88 | −0.27 | −2.13 |
| 2 | 1.36 | 1.36 | 1.32 | 1.19 | 0.97 | −0.39 | −2.61 |
| 3 | 1.27 | 1.29 | 1.25 | 1.29 | 1.00 | −0.27 | −1.90 |
| 4 | 1.22 | 1.37 | 1.20 | 1.16 | 1.05 | −0.17 | −1.07 |
| big | 1.10 | 1.01 | 1.01 | 1.01 | 0.82 | −0.28 | −1.43 |
| small-big | 1.05 | 1.30 | 1.05 | 0.94 | 1.06 | | |
| t-stat | 3.90 | 4.19 | 4.13 | 3.97 | 4.19 | | |
Table 11.
Average returns from double-sorted quantile portfolios (sorted by size and Geske’s short-term minus forward default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on size and Geske’s short-term minus forward default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
Table 11.
Average returns from double-sorted quantile portfolios (sorted by size and Geske’s short-term minus forward default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on size and Geske’s short-term minus forward default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
| Size | Low | 2 | 3 | 4 | High | High-Low | t-Stat |
|---|
| small | 1.20 | 1.55 | 1.52 | 1.91 | 2.44 | 1.24 | 5.20 |
| 2 | 0.86 | 1.41 | 1.38 | 1.34 | 1.15 | 0.29 | 1.47 |
| 3 | 0.91 | 1.22 | 1.35 | 1.36 | 1.11 | 0.19 | 0.97 |
| 4 | 1.04 | 1.23 | 1.30 | 1.27 | 1.11 | 0.07 | 0.33 |
| big | 0.82 | 1.11 | 1.19 | 1.05 | 1.39 | 0.57 | 2.04 |
| small-big | 0.38 | 0.44 | 0.33 | 0.86 | 1.06 | | |
| t-stat | 1.56 | 2.68 | 1.79 | 4.03 | 3.55 | | |
Table 12.
Average returns from double-sorted quantile portfolios (sorted by book-to-market ratio and Merton’s default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on the book-to-market ratio and Merton’s default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
Table 12.
Average returns from double-sorted quantile portfolios (sorted by book-to-market ratio and Merton’s default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on the book-to-market ratio and Merton’s default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
| | Low | 2 | 3 | 4 | High | High-Low | t-Stat |
|---|
| Low BM | 0.94 | 0.92 | 0.65 | 0.63 | 1.09 | 0.15 | 0.47 |
| 2 | 1.12 | 1.14 | 1.25 | 1.22 | 1.40 | 0.28 | 0.92 |
| 3 | 1.15 | 1.26 | 1.34 | 1.48 | 1.66 | 0.51 | 1.54 |
| 4 | 1.11 | 1.34 | 1.45 | 1.65 | 1.77 | 0.66 | 2.06 |
| High BM | 1.29 | 1.44 | 1.61 | 1.74 | 2.10 | 0.81 | 2.77 |
| High-low BM | 0.36 | 0.52 | 0.96 | 1.11 | 1.02 | | |
| t-stat | 2.06 | 2.58 | 4.93 | 5.64 | 4.64 | | |
Table 13.
Average returns from double-sorted quantile portfolios (sorted by book-to-market ratio and Geske’s total default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on the book-to-market ratio and Geske’s total default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
Table 13.
Average returns from double-sorted quantile portfolios (sorted by book-to-market ratio and Geske’s total default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on the book-to-market ratio and Geske’s total default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
| | Low | 2 | 3 | 4 | High | High-Low | t-Stat |
|---|
| Low BM | 0.95 | 0.93 | 0.69 | 0.73 | 0.96 | 0.01 | 0.03 |
| 2 | 1.19 | 1.09 | 1.20 | 1.22 | 1.41 | 0.22 | 0.78 |
| 3 | 1.22 | 1.28 | 1.30 | 1.48 | 1.61 | 0.39 | 1.26 |
| 4 | 1.18 | 1.37 | 1.43 | 1.67 | 1.74 | 0.56 | 1.86 |
| High BM | 1.31 | 1.49 | 1.65 | 1.75 | 2.10 | 0.79 | 2.75 |
| High-low BM | 0.36 | 0.56 | 0.96 | 1.02 | 1.14 | | |
| t-stat | 2.16 | 2.78 | 5.15 | 5.04 | 5.42 | | |
Table 14.
Average returns from double-sorted quantile portfolios (sorted by book-to-market ratio and Geske’s short-term default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on the book-to-market ratio and Geske’s short-term default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
Table 14.
Average returns from double-sorted quantile portfolios (sorted by book-to-market ratio and Geske’s short-term default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on the book-to-market ratio and Geske’s short-term default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
| | Low | 2 | 3 | 4 | High | High-Low | t-Stat |
|---|
| Low BM | 0.94 | 0.92 | 0.69 | 0.63 | 1.06 | 0.12 | 0.37 |
| 2 | 1.16 | 1.10 | 1.24 | 1.21 | 1.41 | 0.24 | 0.81 |
| 3 | 1.18 | 1.29 | 1.35 | 1.49 | 1.65 | 0.47 | 1.46 |
| 4 | 1.17 | 1.35 | 1.47 | 1.65 | 1.76 | 0.59 | 1.89 |
| High BM | 1.29 | 1.48 | 1.61 | 1.72 | 2.11 | 0.82 | 2.85 |
| High-low BM | 0.35 | 0.57 | 0.93 | 1.10 | 1.05 | | |
| t-stat | 2.05 | 2.75 | 4.65 | 5.50 | 4.86 | | |
Table 15.
Average returns from double-sorted quantile portfolios (sorted by book-to-market ratio and Geske’s forward default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on the book-to-market ratio and Geske’s forward default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
Table 15.
Average returns from double-sorted quantile portfolios (sorted by book-to-market ratio and Geske’s forward default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on the book-to-market ratio and Geske’s forward default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
| | Low | 2 | 3 | 4 | High | High-Low | t-Stat |
|---|
| Low BM | 1.01 | 1.08 | 0.85 | 0.83 | 0.62 | −0.39 | −2.11 |
| 2 | 1.38 | 1.24 | 1.19 | 1.15 | 1.09 | −0.30 | −1.94 |
| 3 | 1.51 | 1.53 | 1.27 | 1.32 | 1.25 | −0.26 | −1.52 |
| 4 | 1.54 | 1.39 | 1.46 | 1.43 | 1.53 | −0.01 | −0.05 |
| High BM | 1.92 | 1.73 | 1.73 | 1.76 | 1.72 | −0.20 | −1.37 |
| High-low BM | 0.91 | 0.65 | 0.87 | 0.92 | 1.10 | | |
| t-stat | 4.70 | 3.06 | 4.90 | 4.89 | 5.45 | | |
Table 16.
Average returns from double-sorted quantile portfolios (sorted by book-to-market ratio and Geske’s short-term minus forward default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on book-to-market and Geske’s short-term minus forward default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
Table 16.
Average returns from double-sorted quantile portfolios (sorted by book-to-market ratio and Geske’s short-term minus forward default probability). From the data for July 1963 to December 2013, at the end of each month, stocks are independently sorted into 5 × 5 portfolios based on book-to-market and Geske’s short-term minus forward default probability. The table shows average returns for each of 25 portfolios. Small-big is the return differential between the small and big firm portfolios within each default quantile. High-low is the return differential between the high and low default probability firms within each size quantile. t-statistics are calculated using Newey-West standard errors.
| | Low | 2 | 3 | 4 | High | High-Low | t-Stat |
|---|
| Low BM | 0.57 | 0.95 | 0.87 | 0.67 | 1.28 | 0.71 | 2.68 |
| 2 | 0.95 | 1.22 | 1.21 | 1.32 | 1.50 | 0.55 | 2.14 |
| 3 | 1.00 | 1.35 | 1.41 | 1.49 | 1.73 | 0.73 | 2.55 |
| 4 | 1.14 | 1.29 | 1.50 | 1.61 | 1.81 | 0.68 | 2.63 |
| High BM | 1.38 | 1.42 | 1.57 | 1.73 | 2.10 | 0.72 | 2.87 |
| High-low BM | 0.82 | 0.47 | 0.71 | 1.06 | 0.82 | | |
| t-stat | 4.15 | 2.42 | 3.53 | 5.33 | 3.65 | | |