Nonparametric Approach to Evaluation of Economic and Social Development in the EU28 Member States by DEA Efficiency
Abstract
:1. Introduction
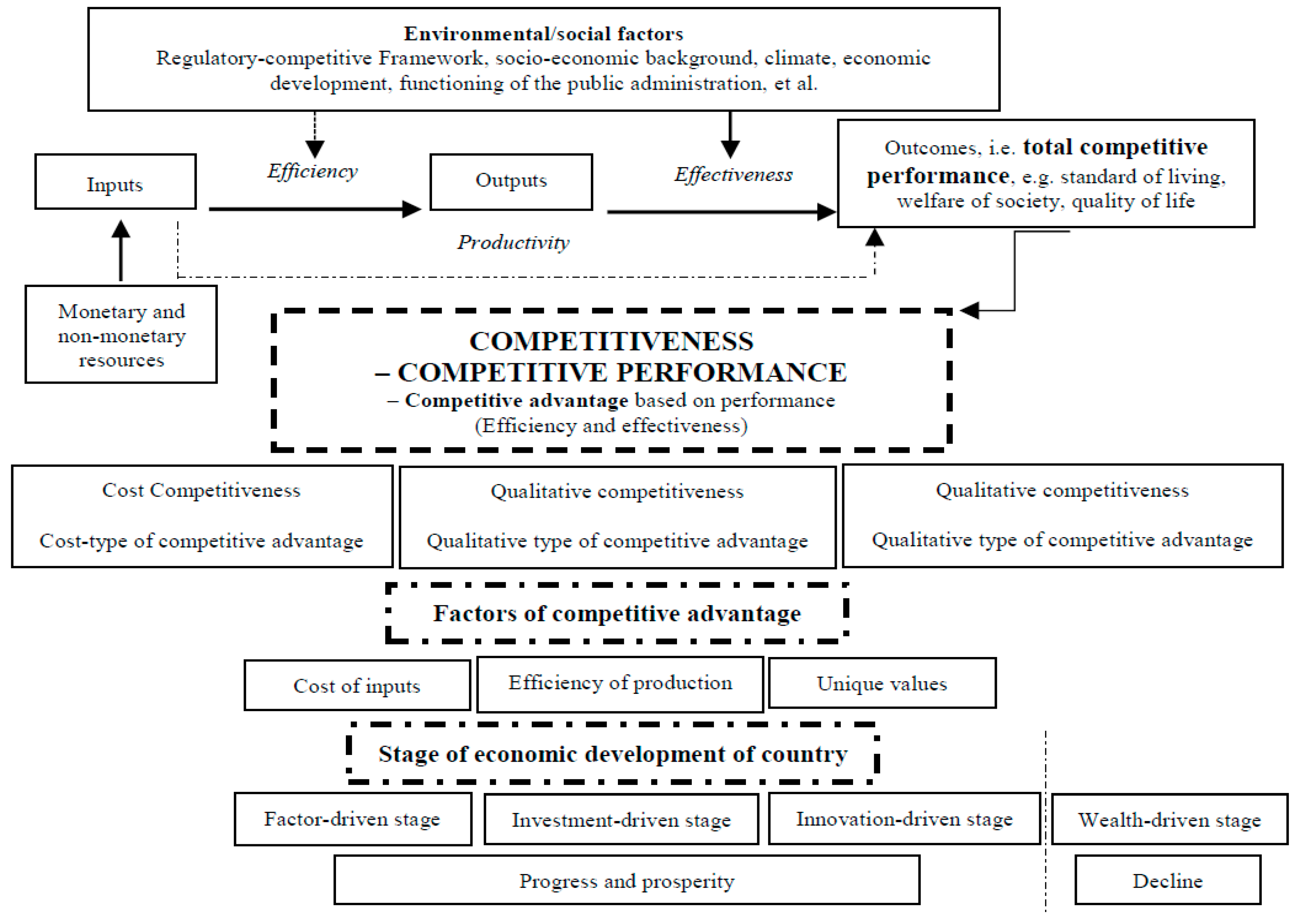
2. Theoretical Background
3. Materials and Methods
3.1. Factor Analysis
3.2. DEA-Based Malmquist Productivity Index
4. Results
Key Factors of Competitiveness at the EU National Level
5. Discussion
- The new EU member states constantly fall into the category of less developed and competitive states based on gross domestic product (GDP) per head in Purchasing Parity Standard (PPS), which is the reason for their inclusion in the appropriate categorization stage of development (see Annoni and Kozovska 2010; Annoni and Dijkstra 2013; or Annoni et al. 2017);
- The association of each country with the relevant stage of development testifies to its competitive advantages and disadvantages and determines its weaknesses. A medium stage of development is associated with economies primarily driven by factors such as lower skilled labor and basic infrastructures. Aspects related to good governance and quality of public health are considered basic inputs in this framework. An intermediate stage of development is characterized by labor market efficiency, quality of higher education, and market size, factors which contribute to a more sophisticated economy and more significant potential for competitiveness. In the high stage of development, factors related to innovation, business sophistication, and technological readiness are necessary inputs for innovation-driven economies (Annoni and Dijkstra 2013);
- The threshold defining the level of GDP as a percentage of EU average was taken as a reference as it is the criterion for identifying countries and their regions eligible for funding under the established criteria of the EU regional policy framework. European funds are an essential tool for regional development and reducing economic, social, and territorial disparities among European countries and their regions. Reducing disparities have a significant impact on competitiveness, and these two concepts are, thus, the EU complementary objectives. Of the total budget allocated to regional policy, a substantial part goes just to the NUTS 2 regions of EU13 countries (i.e., the basic regions for the application of regional policies classify based on the EU Nomenclature of Territorial Units for Statistics), where development is significantly supported;
- New EU member states are often considerably dependent on exports into the old EU member states and on the flow of money for this exchange shift.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Authors | Datasets | Inputs and Outputs Used in DEA | Key Results |
|---|---|---|---|
| Cheng Chen 2017 | 20 Taiwan counties/cities in the period 1999–2013 | Inputs and outputs: variables for the department of economic development, variables for the department of public security, variables for the department of social welfare, variables for the department of education | The police security department is the most efficient in most counties/cities in the period 1999–2013, and the economic development department is the second most efficient one in 2002–2005 and after 2009. There exist urban–rural gaps in the efficiency scores between counties and cities, between service-type and non-service type counties/cities, and among different regions. |
| Nurboja and Košak 2017 | 11 southeast European countries; 82 banks from EU member countries and 157 banks from non-EU countries; period 1999–2013 | Inputs: borrowed funds, labor, and physical Capital Outputs: loans, securities, and other earning assets, ratio of equity | Statistically significant cost efficiency gap between EU and non-EU banking systems in the region, where on average EU banking systems tend to be more cost efficient than their non-EU counterparts. |
| Wu et al. 2014 | 21 Organisation for Economic Co-Operation and Development (OECD) countries | Inputs: real physical capital per worker, real knowledge capital per worker Outputs: Real income per worker, real income per worker over unemployment rate, real income per worker over air pollutants | Research and development expenditures, the proxy variable for knowledge capital, can indeed improve countries’ efficiency scores, implying that the endogenous growth theory is supported in OECD countries. Whether the undesirable outputs are included in the DEA models and are properly treated is crucial in the evaluation of efficiency values. |
| Foddi and Usai 2013 | 271 regions in 29 European countries | Inputs: Total intramural R&D expenditure, Economically active population with tertiary education attainment Outputs: Number of the European Patent Office (EPO) patent applications per priority year and residence region of inventors | Malmquist index shows extremely differences in productivity dynamics across regions, important differences are between the core and periphery of Europe. |
| Rabar 2013 | Croatian regions, three-year period 2005–2007 | Inputs: registered unemployment rate, number of support allowance users Outputs: share of the secondary sector in Gross Valued Added (GVA), gross fixed capital formation in fixed assets, level of import coverage by export, number of graduate students, Gross Domestic Product (GDP) | Among 63 observed entities, 15 turned out to be efficient. The highest efficiency results were achieved in 2007 toward both orientations. None of the 21 counties was efficient during the entire period. The worst efficiency results were achieved in 2006, while the lowest average efficiency was achieved in 2005. Average efficiency scores for all three periods are greater in output orientation than in input orientation. |
| Goryushina and Mesropyan 2013 | Russian regional economy performance for the period from 2008 to 2010 | Inputs: number of cattle, organizations acreage under crops, average number of employees, power capacity, equipment parks Outputs: gross grain yield, production of milk, production of livestock and poultry | Agrarian production of the south of Russia shows the reserve of stability, and the southern regions belong to Pareto-efficient set of Russian regions. Only 4 regions among 13 of the south are estimated as having the stable decline. The economic development opportunities of this regions are significant, nevertheless, the considerable potential of regions is not used. |
| Afzal and Lawrey 2012 | Association of southeast Asian nations (ASEAN) in two years 1995 and 2010, World Development Indicators (WDI) and World Competitiveness Yearbook (WCY) | Inputs: Export/GDP, import/GDP, Foreign Direct Investment (FDI) inward flows, R&D expenditure, intellectual property rights, education expenditure, net enrolment ratio at secondary school, knowledge transfer rate (university to industry), FDI inflows Outputs: Real GDP growth, scientific and technical publications per 1000 population, computer users per 1000 population, high-tech export | Indonesia in knowledge acquisition; Singapore, South Korea and Thailand in knowledge production; Singapore in knowledge distribution; the Philippines, and South Korea in knowledge utilization are the most productive and 100% efficient countries in either one or both of the years investigated. |
| Deliktas and Balcilar 2005 | 25 transition economies (east European, Baltic, and other former Soviet Union countries) | Inputs: total labor force, gross capital formation Outputs: real GDP | No technological progress, but over the whole period 1991–2000 there was a technological regress, and also decline in the average annual total factor productivity. Results suggest that, on average, chance in technical efficiency is outweighed by the technical regress. |
| Tan et al. 2008 | WDI-2001 dataset for 54 developing countries | Inputs: Research and Development (R&D) expenditure, labor productivity, average schooling Outputs: mobile phone users, internet users, Personal Computer (PC) penetration, high-tech exports | India, Indonesia, Thailand, and China are inefficient countries due to the outflow of human resources. |
| Christopoulos 2007 | Selected OECD and non-OECD countries | Inputs: human capital, openness Output: real GDP | Movements towards openness increase the efficiency performance of non-OECD countries. |
| Mohamad 2007 | Selected Asia–Pacific countries. Datasets collected in 1996, 2000, and 2003 | Inputs: government expenditure as % of GDP Outputs: real GDP growth, real employment rate, inflation rate | Only seven of 25 selected countries are efficient. |
| Ramanathan 2006 | Selected Middle Eastern and north African countries, WDI-1999 | Inputs and outputs: ratio of labour to population, life expectancy, primary education teachers, GNP per capita, literacy rate, mortality rate, etc. | Bahrain, Jordan, Kuwait, and the United Arab Emirates (UAE) are the most efficient while Yemen is the least efficient country. |
| Malhotra and Malhotra 2006 | European Union (EU15) nations against one another from 1993 to 2006 | Seven economic variables: current account as % of GDP, current account as % of exports, GDP per head of population, inflation, international liquidity, real GDP growth, exchange rate stability | All the participating nations were not equally efficient at the beginning of the economic integration in 1993. Economic integration did help in achieving convergence in economic performance of EU15 nations because 13 of the 15 nations were efficient in 1998. After 1998, there is lack of convergence in the performance of EU 15 nations and some nations performed more efficiently in contrast to other nations. |
| Halkos and Tzeremes 2005 | 51 Greek prefectures, three decades (1980, 1990, 2000) | Inputs: Number of hospital beds per 1000 citizens, number of doctors per 1000 citizens, number of public schools per 1000 students, number of public buses per 1000 citizens Outputs: GDP as a percentage of the mean GDP of the country, difference of urban–rural population, number of new houses per 1000 citizens | Results of effect of fiscal policies on the Greek prefectures: the resources of a prefecture do not necessarily ensure the efficiency of this prefecture. |
| Hsu et al. 2008 | World Competitiveness Yearbook 2004 | WCY-2004 pillars used as input and output variables for OECD and non-OECD countries | Indonesia and Argentina outperform in all the efficiency scores and Turkey, Poland, and Mexico appear to have stable efficiencies. Twenty-nine countries are shown to be efficient. |
| Hseu and Shang 2005 | OECD countries, 1991-2000 | Inputs: wood pulp capacity, paper and paperboard capacity, number of employees Outputs: wood pulp, paper and paperboard | The productivity change of pulp and paper industry in OECD countries ranged from Switzerland’s 0.9% to Japan’s 2.4% over the sampled period. The Nordic nations (Finland, Norway, and Sweden) recorded 1.2–1.5% improvement in their performance. The productivity of the Canadian pulp and paper industry increased by 2%, while that of its United States counterpart increased only by 0.8%. The results also showed that the last decade’s productivity growth was attributed more to the technical change than efficiency change. |
| Breuss et al. 2000 | Central and eastern European candidate countries to the EU | Three Copenhagen criteria: (i) political criteria—i.e., the establishment of democracy and the protection of human rights and minorities; (ii) economic criteria—the building up of a functioning market economy able to withstand the competition on the single market; (iii) acquis criterion—i.e., the complete takeover of the legal status of the Union plus the acceptance of its targets (meaning monetary and political union) | Macroeconomic performance of most of the Central and Eastern European countries (CEEC) lies far behind the EU standards, in foreign trade some of the CEECs already perform better than some EU countries. Interestingly, authors find out that some CEECs were already better prepared for the European Monetary Union (EMU) than many EU member states. |
| Golany and Thore 1997 | Statistical department of 72 developed and developing countries in 1970–1985 | Inputs: real investment as % of GDP, real government consumption as % of GDP, education expenditure as % of GDP Outputs: real GDP growth, infant mortality, enrolment ratio for secondary schools, welfare payments | Japan, the United States of America (USA), Canada and the Asian tigers show increasing returns to scale (IRS); Scandinavian and very poor developing countries show decreasing returns to scale (DRS). |
References
- Adusei, Michael. 2016. Modelling the efficiency of universal banks in Ghana. Quantitative Finance Letters 4: 60–70. [Google Scholar] [CrossRef]
- Afzal, Munshi Naser Ibne, and Roger Lawrey. 2012. Evaluating the Comparative Performance of Technical and Scale Efficiencies in Knowledge-Based Economies (KBEs) in ASEAN: A Data Envelopment Analysis (DEA) Application. European Journal of Economics, Finance and Administrative Sciences 51: 81–95. [Google Scholar]
- Annoni, Paola, and Lewis Dijkstra. 2013. EU Regional Competitiveness Index 2013. Luxembourg: Publication Office of the European Union. [Google Scholar]
- Annoni, Paola, and Kornelia Kozovska. 2010. EU Regional Competitiveness Index 2010. Luxembourg: Publication Office of the European Union. [Google Scholar]
- Annoni, Paola, Lewis Dijkstra, and Nadia Gargano. 2017. EU Regional Competitiveness Index 2016. Working Paper WP 02/2017. Brussels: European Commission. [Google Scholar]
- Avkiran, Necmi K. 2006. Productivity Analysis in the Service Sector with Data Envelopment Analysis. SSRN Working Paper 2006. Brisbane: The University of Queensland. [Google Scholar]
- Bachtler, John, Joaquim Oliveira Martins, Peter Wostner, and Piotr Zuber. 2017. Towards Cohesion Policy 4.0: Structural Transformation and Inclusive Growth. Brussels: Regional Studies Association. [Google Scholar]
- Balcerowicz, Leszek, Andrzej Rzónca, Lech Kalina, and Aleksander Łaszek. 2013. Economic Growth in the European Union. Brussels: Lisbon Council asbl. [Google Scholar]
- Bansal, Pooja, and Aparna Mehra. 2018. Multi-period additive efficiency measurement in data envelopment analysis with non-positive and undesirable data. OPSEARCH 55: 642–61. [Google Scholar] [CrossRef]
- Barnum, Darold, Jason Coupet, John Gleason, Abagail McWilliams, and Annaleena Parhankangas. 2017. Impact of input substitution and output transformation on data envelopment analysis decisions. Applied Economics 49: 1543–56. [Google Scholar] [CrossRef]
- Breuss, Fritz, Mikulás Luptácik, and Bernhard Mahlberg. 2000. How far away are the CEECs from the EU economic standards? A data envelopment analysis of the economic performance of the CEECs. In EI Working Papers/Europainstitut, 35. Vienna: Vienna University of Economics and Business. [Google Scholar]
- Caves, Douglas W., Laurits R. Christensen, and W. Erwin Diewert. 1982. The Economic Theory of Index Numbers and the Measurement of Input, Output, and Productivity. Econometrica 50: 1393–414. [Google Scholar] [CrossRef]
- Chandola, Varun, Banerjee Arindam, and Vipin Kumar. 2009. Anomaly detection: A survey. ACM Computing Surveys 41: 1–58. [Google Scholar] [CrossRef]
- Charles, Vincent, and Luis Felipe Zegarra. 2014. Measuring regional competitiveness through Data Envelopment Analysis: A Peruvian case. Expert Systems with Applications 41: 5371–81. [Google Scholar] [CrossRef]
- Charnes, Abraham, William W. Cooper, and Edwardo L. Rhodes. 1978. Measuring the efficiency of decision making units. European Journal of Operational Research 2: 429–44. [Google Scholar] [CrossRef]
- Cheng Chen, Chih. 2017. Measuring departmental and overall regional performance: Applying the multi-activity DEA model to Taiwan’s cities/counties. Omega 67: 60–80. [Google Scholar] [CrossRef]
- Christopoulos, Dimitris K. 2007. Explaining country's efficiency performance. Economic Modelling 24: 224–35. [Google Scholar] [CrossRef]
- Chortirat, Thunyaporn, Boonorm Chomtee, and Juthaphorn Sinsomboonthong. 2011. Comparison of four data transformation methods for weibull distributed data. Kasetsart Journal-Natural Science 45: 366–83. [Google Scholar]
- Conte, Andrea, Philip Schweizer, Adriaan Dierx, and Fabienne Ilzkovitz. 2009. An Analysis of the Efficiency of Public Spending and National Policies in the Area of R&D. European Economy—Occassional Papers 54. Brussels: European Commission. [Google Scholar]
- Cooper, William W., Lawrence M. Seiford, and Kaoru Tone. 2007. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software. New York: Springer. [Google Scholar]
- Deliktas, Ertugrul, and Mehmet Balcilar. 2005. A Comparative Analysis of Productivity Growth, Catch-Up, and Convergence in Transition Economies. Emerging Markets Finance and Trade 41: 6–28. [Google Scholar] [CrossRef]
- Drucker, Peter. 2001. The Efficiency of the Decision Makers. Bucharest: Editura Destin. [Google Scholar]
- Easterly, William, and Ross Levine. 2012. The European Origins of Economic Development. NBER Working Paper Series 18162; Cambridge: National Bureau of Economic Research. [Google Scholar]
- Esser, Klaus, Wolfgang Hillebrand, Dirk Messner, and Jörg Meyer-Stamer. 1995. Systemic Competitiveness. New Governance Patterns for Industrial Development. London: Frank Cass. [Google Scholar]
- European Commission. 2019. 11 Trends for 11 Countries on EU Convergence: The EU Enlargement Countries in the Baltics, Balkans and Central and Eastern Europe. Available online: https://ec.europa.eu/info/conference-15th-anniversary-2004-eu-enlargement-looking-back-looking-forward/edited-volume_en (accessed on 1 April 2019).
- Färe, Rolf, Shawna Grosskopf, and C. A. Knox Lovell. 1994a. Production Frontiers. Cambridge: Cambridge University Press. [Google Scholar]
- Färe, Rolf, Shawna Grosskopf, Marry Norris, and Zhongyang Zhang. 1994b. Productivity Growth, Technical Progress and Efficiency Change in Industrialized Countries. The American Economic Review 84: 66–83. [Google Scholar]
- Farrell, Michael James. 1957. The measurement of productivity efficiency. Journal of the Royal Statistical Society 120: 253–90. [Google Scholar] [CrossRef]
- Foddi, Marta, and Stefano Usai. 2013. Technological catching up among European regions. Lessons from Data Envelopment Analysis. WP4/02 Search Working Paper. Brussels: European Commission. [Google Scholar]
- Gardiner, Ben, Ron Martin, and Peter Tyler. 2004. Competitiveness, Productivity and Economic Growth across the European Regions. Journal of Regional Studies 38: 1045–67. [Google Scholar] [CrossRef]
- Ghosh, Jayati, Peter Havlik, Marcos Poplawski-Ribeiro, and Waltraut Urban. 2009. Models of BRICs’ Economic Development and Challenges for EU Competitiveness. Vienna: The Vienna Institute for International Economics Studies. [Google Scholar]
- Golany, Boaz, and Sten Thore. 1997. Restricted best practice selection in DEA: An overview with a case study evaluating the socio-economic performance of nations. Annals of Operations Research 73: 117–40. [Google Scholar] [CrossRef]
- Goryushina, Evgenija, and Karine Mesropyan. 2013. Economic Inequality and Political Instability Measuring by DEA and Alternative Indices: State of the Art and Research Perspectives for Cross-Regional Studies. Der Donauraum 52: 445–64. [Google Scholar] [CrossRef]
- Hair, Joseph F., William C. Black, Barry J. Babin, and Roplh E. Anderson. 2009. Multivariate Data Analysis. Upper Saddle River: Prentice Hall. [Google Scholar]
- Halkos, George, and Nickolaos Tzeremes. 2005. A DEA Approach to Regional Development. MPRA Paper 3992. Available online: https://mpra.ub.uni-muenchen.de/id/eprint/3992 (accessed on 1 July 2007).
- Hseu, Jiing-Shyang, and Jui-Kou Shang. 2005. Productivity Changes of Pulp and Paper Industry in OECD Countries, 1991–2000: A Non-Parametric Malmquist Approach. Forest Policy and Economics 7: 411–22. [Google Scholar] [CrossRef]
- Hsu, Maxwell, Xueming Luo, and Gary H. Chao. 2008. The Fog of OECD and Non-OECD Country Efficiency: A Data Envelopment Analysis Approach. The Journal of Developing Areas 42: 81–93. [Google Scholar]
- Hwang, Yun-Gi, Soohyun Park, and Daecheol Kim. 2018. Efficiency Analysis of Official Development Assistance Provided by Korea. Sustainability 10: 2697. [Google Scholar] [CrossRef]
- Izadikhah, Mohammad, Reza Farzipoor Saen, and Razieh Roostaee. 2018. How to assess sustainability of suppliers in the presence of volume discount and negative data in data envelopment analysis? Annals of Operations Research 269: 241–67. [Google Scholar] [CrossRef]
- Jiang, Huichen, and Yifan He. 2018. Applying Data Envelopment Analysis in Measuring the Efficiency of Chinese Listed Banks in the Context of Macroprudential Framework. Mathematics 6: 184. [Google Scholar] [CrossRef]
- Lacko, Roman, and Zuzana Hajduová. 2018. Determinants of Environmental Efficiency of the EU Countries Using Two-Step DEA Approach. Sustainability 10: 3525. [Google Scholar] [CrossRef]
- Lambooy, Jan G., and Ron A. Boschma. 2001. Evolutionary economics and regional policy. The Annals of Regional Science 35: 113–31. [Google Scholar] [CrossRef]
- Lukovics, Miklos. 2009. Measuring Regional Disparities on Competitiveness Basis. In Regional Competitiveness, Innovation and Environment. Edited by Zoltán Bajmócy and Imre Lengyel. Szeged: JATE Press, pp. 39–53. [Google Scholar]
- MacGregor Pelikánová, Radka. 2017. European myriad of approaches to parasitic commercial practices. Oeconomia Copernicana 8: 167–80. [Google Scholar] [CrossRef]
- Makridou, Georgia, Kostas Andriosopoulos, Michael Doumpos, and Constantin Zopounidis. 2014. An Integrated Approach for Energy Efficiency Analysis in European Union Countries. Working Paper 2014.02. Chania: Technical University of Crete. [Google Scholar]
- Malhotra, Rashmi, and Davinder K. Malhotra. 2006. Evaluating the efficiency of European Union integration. International Journal of Commerce and Management 19: 233–52. [Google Scholar] [CrossRef]
- Mandl, Ulrike, Adriaan Dierx, and Fabienne Ilzkovitz. 2008. The Effectiveness and Efficiency of Public Spending. Brussels: European Commission-Directorate General for Economic and Financial Affairs. [Google Scholar]
- Martin, Ron. 2003. A Study on the Factors of Regional Competitiveness. Available online: http://ec.europa.eu/regional_policy/sources/docgener/studies/pdf/3cr/competitiveness.pdf (accessed on 1 September 2003).
- Melecký, Lukáš. 2018. The main achievements of the EU structural funds 2007–2013 in the EU member states: efficiency analysis of transport sector. Equilibrium. Quarterly Journal of Economics and Economic Policy 13: 285–306. [Google Scholar] [CrossRef]
- Mihaiu, Diana Marieta, Alin Opreana, and Marian Pompiliu Cristescu. 2010. Efficiency, effectiveness and performance of the public sector. Romanian Journal of Economic Forecasting 1: 132–47. [Google Scholar]
- Mohammad, Nordin. 2007. A Linear Programming Formulation of Macroeconomic Performance: The Case of Asia Pacific. Matematika 23: 29–40. [Google Scholar]
- Nurboja, Bashkim, and Marko Košak. 2017. Banking efficiency in South East Europe: Evidence for financial crises and the gap between new EU members and candidate countries. Economic Systems 41: 122–38. [Google Scholar] [CrossRef]
- Ocubo, Toshihiro. 2012. Antiagglomeration subsidies with heterogeneous firms. Journal of Regional Science 52: 285–87. [Google Scholar] [CrossRef]
- Otsuka, Akihiro. 2014. Analysis of Productive Efficiency in Japanese Regional Economies. Studies in Regional Science 44: 453–65. [Google Scholar] [CrossRef]
- Rabar, Danijela. 2013. Assessment of Regional Efficiency in Croatia using Data Envelopment Analysis. Croatian Operational Research Review 4: 76–88. [Google Scholar]
- Ramanathan, Ramakrishnan. 2006. Evaluating the comparative performance of countries of the Middle East and North Africa: A DEA Application. Socio-Economic Planning Sciences 40: 156–67. [Google Scholar] [CrossRef]
- Seiford, Lawrence M., and Joe Zhu. 1999. An investigation of returns to scale in data envelopment analysis. Omega 27: 1–11. [Google Scholar] [CrossRef]
- Shu, Guoping, Beiyan Zeng, Deanne Wright, and Oscar Smith. 2002. Impact of Data Transformation on the Performance of Different Clustering Methods and Cluster Number Determination Statistics for Analyzing Gene Expression Profile Data. Paper presented at 14th Annual Conference on Applied Statistics in Agriculture, Manhattan, Kansas, April 28–30; pp. 94–110. [Google Scholar]
- Staníčková, Michaela. 2017. Can the implementation of the Europe 2020 Strategy goals be efficient? The challenge for achieving social equality in the European Union. Equilibrium. Quarterly Journal of Economics and Economic Policy 12: 383–98. [Google Scholar]
- Stevens, James P. 1986. Applied Multivariate Statistics for the Social Sciences. Mahwah: Lawrence Erlbaum Associates. [Google Scholar]
- Tan, Hui-Boon, Chee-Wooi Hooy, Sardar M.N. Islam, and Alex Manzoni. 2008. Relative efficiency measures for the knowledge economies in the Asia Pacific region. Journal of Modelling in Management 3: 111–24. [Google Scholar]
- Toloo, Mehdi, Mona Barat, and Atefeh Masoumzadeh. 2015. Selective measures in data envelopment analysis. Annals of Operations Research 226: 523–642. [Google Scholar] [CrossRef]
- Tung, Shiue-Jen, Guo-Ya Gan, and Wen-Li Chyr. 2018. Efficiency Measures for VRM Models Dealing with Negative Data in DEA. Journal of Marine Science and Technology-Taiwan 26: 180–84. [Google Scholar]
- Watt, Andrew, and Andreas Botsch. 2010. After the Crisis: Towards a Sustainable Growth Model. Brussels: European Trade Union Institute. [Google Scholar]
- Wu, Po-Chin, Tzu-Hsien Huang, and Sheng-Chieh Pan. 2014. Country Performance Evaluation: The DEA Model Approach. Social Indicators Research 118: 835–49. [Google Scholar] [CrossRef]
- Zhu, Joe. 2011. Manual DEA Frontier—DEA Add-In for Microsoft Excel. Available online: http://www.deafrontier.net (accessed on 1 May 2011).
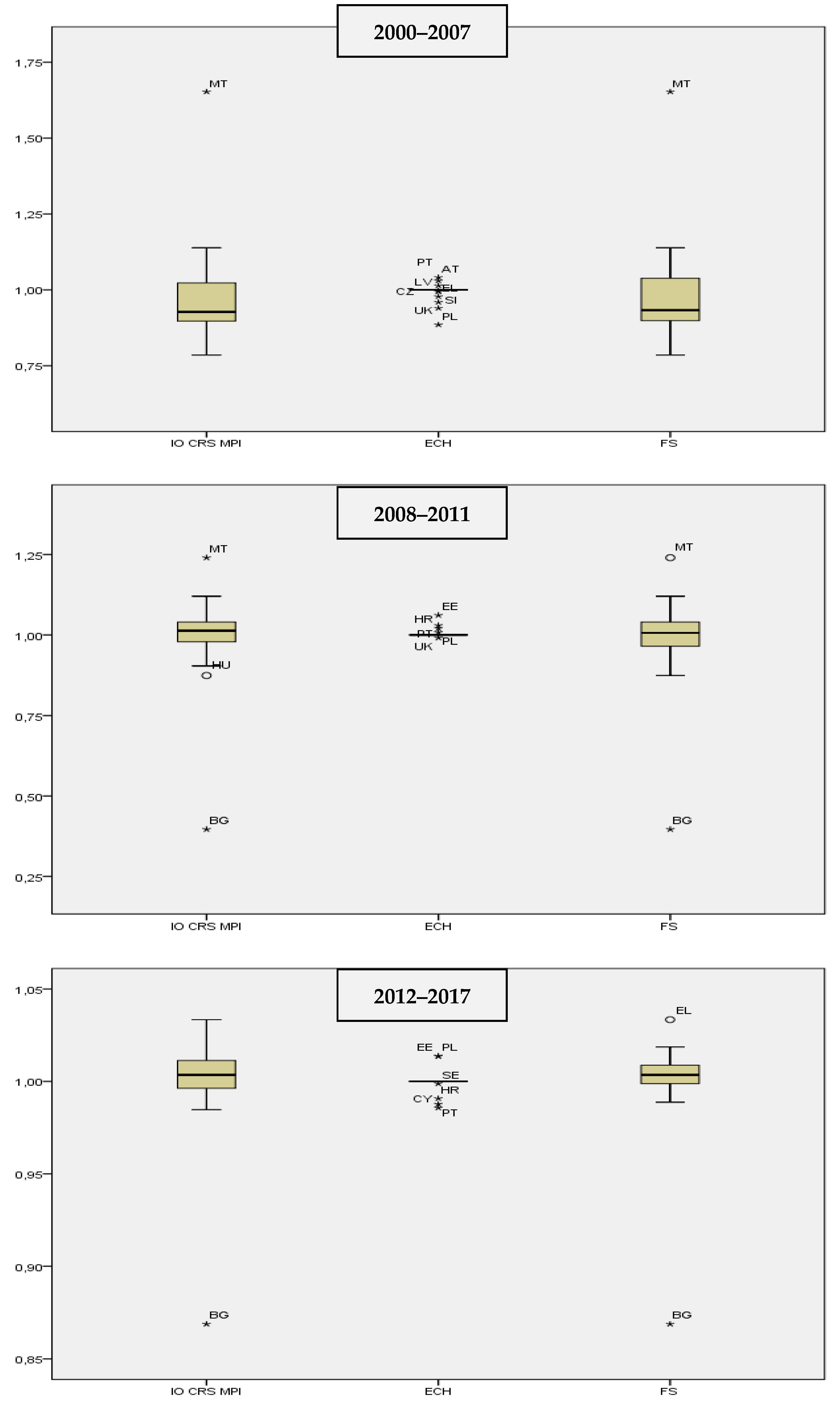
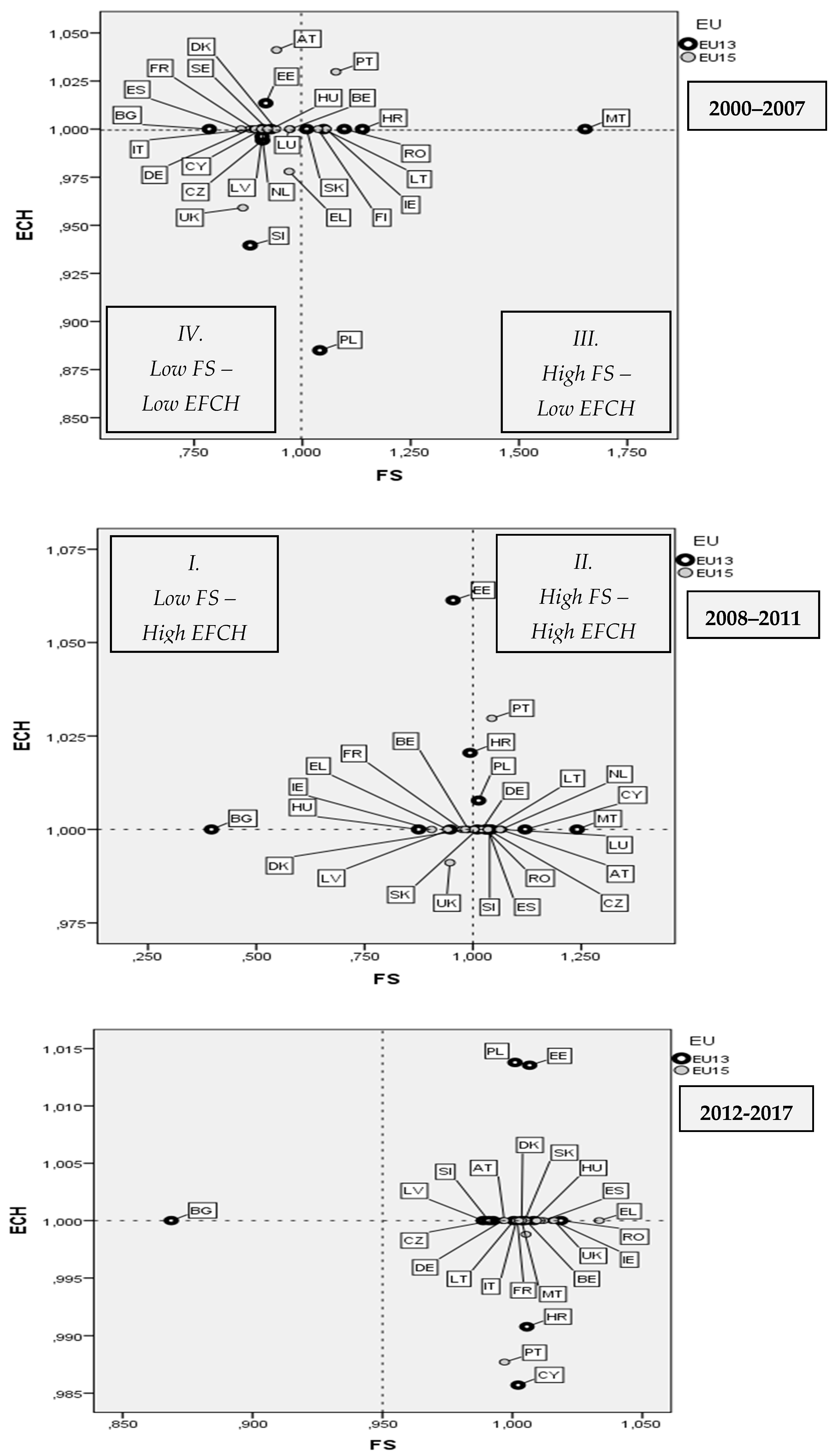
| MPI | Productivity | ECH | FS |
|---|---|---|---|
| MPI > 1 | Improving | Change >1, improving | Change >1, improving |
| MPI = 1 | Unchanging | Change = 1, unchanging | Change = 1, unchanging |
| MPI < 1 | Declining | Change <1, declining | Change <1, declining |
| Dimension | Pillar | Indicator of Input |
| Input | Institution | Political stability (PS), voice and accountability (VA), government effectiveness (GE), regulatory quality (RQ), rule of law (RL), control of corruption (CC) |
| Macroeconomic stability | Harmonized index of consumer prices (HICP), gross fixed capital formation (GFCF), income, saving, and net lending/net borrowing (ISLB), total intramural research and development expenditure (GERD), labor productivity per person employed (LPPE) | |
| Infrastructure | Railway transport—length of tracks (RTLT), air transport of passengers (ATP), volume of passenger transport (VPT), volume of freight transport (VFT), motorway transport—length of motorways (MTLM), air transport of freight (ATF) | |
| Health | Healthy life expectancy (HLE), infant mortality rate (IMR), cancer disease death rate (CDDR), heart disease death rate (HDDR), suicide death rate (SDR), hospital beds (HB), road fatalities (RF) | |
| Primary, secondary and tertiary education; training and lifelong learning | Mathematics, science, and technology enrolments and graduates (MSTEG), pupils to teachers ratio (PTR), financial aid to students (FAS), total public expenditure at primary level of education (TPEPLE), total public expenditure at secondary level of education (TPESLE), total public expenditure at tertiary level of education (TPETLE), participants in early education (PEE), participation in higher education (PHE), early leavers from education and training (ELET), accessibility to universities (AU), lifelong learning—participation in education and training (LLPET) | |
| Indicators for technological readiness | Level of internet access (LIA), E-government availability (EA) | |
| Dimension | Pillar | The Indicator of Output * |
| Output | Labor market efficiency | Labor productivity (LP), male employment (ME), female employment (FE), male unemployment (MU), female unemployment (FU), Public expenditure on labor market policies (PEoLMP), employment rate (15 to 64 years) (ER15to64), long-term unemployment (LtUR), unemployment rate (UR) |
| Market size | Gross domestic product (GDP), compensation of employees (CoE), disposable income (DI) | |
| Business sophistication | Gross value added in sophisticated sectors (GVA), employment in sophisticated sectors (EiSS) | |
| Innovation | Human resources in science and technology (HRST), total patent applications (TPAp), employment in technology and knowledge-intensive sectors by education (ETKIedu), employment in technology and knowledge-intensive sectors by gender (ETKIgen), employment in technology and knowledge-intensive sectors by type of occupation (ETKIocc), human resources in science and technology—core (HRSTcore), patent applications to the European Patent Office (EPO), high-tech patent applications to the EPO (HTI), Information and Communication Technologies (ICT) patent applications to EPO (ICT), biotechnology patent applications to the EPO (BioT) |
| Component | Initial Eigenvalues | Rotation Sums of Squared Loadings | ||||
|---|---|---|---|---|---|---|
| Total | % of Variance | Cumulative % | Total | % of Variance | Cumulative % | |
| 1 | 10.540 | 30.115 | 30.115 | 9.112 | 26.033 | 26.033 |
| 2 | 5.223 | 14.923 | 45.038 | 5.604 | 16.011 | 42.044 |
| 3 | 2.523 | 7.209 | 52.247 | 2.505 | 7.158 | 49.203 |
| 4 | 2.163 | 6.180 | 58.428 | 2.436 | 6.960 | 56.162 |
| 5 | 1.880 | 5.372 | 63.799 | 2.177 | 6.220 | 62.382 |
| 6 | 1.504 | 4.298 | 68.098 | 2.001 | 5.716 | 68.098 |
| 7 | 1.362 | 3.892 | 71.990 | |||
| 8 | 1.233 | 3.523 | 75.513 | |||
| 9 | 1.061 | 3.031 | 78.544 | |||
| Rotation Converged in 8 Iterations | Component | Group | Factor | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| Zscore(VA) | 0.922 | (1) | Factor 1 Economic growth and development | |||||
| Zscore(RL) | 0.917 | (1) | ||||||
| Zscore(CC) | 0.915 | (1) | ||||||
| Zscore(GE) | 0.913 | (1) | ||||||
| Zscore(GERD) | 0.873 | (2) | ||||||
| Zscore(LPPE) | 0.863 | (2) | ||||||
| Zscore(RQ) | 0.851 | (1) | ||||||
| Zscore(PS) | 0.765 | (1) | ||||||
| Zscore(GFCF) | 0.742 | −0.347 | (2) | |||||
| Zscore(LIA) | 0.735 | −0.431 | (3) | |||||
| Zscore(CDDR) | −0.696 | −0.315 | 0.470 | (4) | ||||
| Zscore(IMR) | −0.695 | 0.311 | (4) | |||||
| Zscore(RF) | −0.672 | 0.306 | (4) | |||||
| Zscore(LLPET) | 0.645 | 0.373 | (5) | |||||
| Zscore(TPETLE) | 0.553 | 0.318 | 0.521 | (5) | ||||
| Zscore(VFT) | −0.444 | −0.392 | (6) | |||||
| Zscore(ISLB) | 0.951 | (1) | Factor 2 Level of infrastructure | |||||
| Zscore(AU) | 0.914 | (2) | ||||||
| Zscore(ATP) | 0.879 | (3) | ||||||
| Zscore(MTLM) | 0.862 | (3) | ||||||
| Zscore(ATF) | 0.816 | (3) | ||||||
| Zscore(RTLT) | 0.735 | (3) | ||||||
| Zscore(HB) | 0.852 | (1) | Factor 3 Health phenomena in human life and | |||||
| Zscore(SDR) | 0.530 | 0.392 | (1) | |||||
| Zscore(TPEPLE) | −0.505 | (2) | ||||||
| Zscore(PTR) | 0.399 | 0.445 | (3) | |||||
| Zscore(HICP) | −0.312 | −0.732 | (1) | Factor 4 Inflation trends, transport, healthy lifestyle, the performance of educational institutions, and public administration | ||||
| Zscore(VPT) | 0.665 | (2) | ||||||
| Zscore(HLE) | 0.511 | (3) | ||||||
| Zscore(ELET) | 0.509 | −0.433 | (4) | |||||
| Zscore(FAS) | −0.457 | 0.334 | (4) | |||||
| Zscore(EA) | 0.369 | 0.423 | (5) | |||||
| Zscore(PEE) | 0.350 | −0.663 | (1) | Factor 5 Participation in education | ||||
| Zscore(PHE) | −0.326 | 0.627 | (1) | |||||
| Zscore(MSTEG) | 0.330 | 0.614 | (1) | |||||
| Zscore(TPESLE) | 0.811 | (1) | Factor 6 Expenditure on education and civilization diseases | |||||
| Zscore(HDDR) | −0.308 | −0.466 | (2) | |||||
| Component | Initial Eigenvalues | Rotation Sums of Squared Loadings | ||||
|---|---|---|---|---|---|---|
| Total | % of Variance | Cumulative % | Total | % of Variance | Cumulative % | |
| 1 | 11.807 | 45.412 | 45.412 | 6.547 | 25.182 | 25.182 |
| 2 | 3.517 | 13.526 | 58.939 | 6.088 | 23.415 | 48.597 |
| 3 | 2.943 | 11.320 | 70.258 | 5.632 | 21.662 | 70.258 |
| 4 | 2.314 | 8.899 | 79.157 | |||
| 5 | 1.874 | 7.210 | 86.367 | |||
| Rotation Converged in 5 Iterations | Component | Group | Factor | ||
|---|---|---|---|---|---|
| 1 | 2 | 3 | |||
| Zscore(EPO) | 0.871 | (1) | Factor 1 Economic performance and innovative potential | ||
| Zscore(DI) | 0.821 | 0.305 | (2) | ||
| Zscore(HTI) | 0.803 | (1) | |||
| Zscore(ICT) | 0.802 | (1) | |||
| Zscore(HRSTcore) | 0.801 | (1) | |||
| Zscore(GDP) | 0.778 | (2) | |||
| Zscore(HRST) | 0.776 | (1) | |||
| Zscore(PEoLMP) | 0.734 | (3) | |||
| Zscore(LP) | 0.726 | (3) | |||
| Zscore(BioT) | 0.683 | (1) | |||
| Zscore(FE) | 0.578 | 0.382 | (3) | ||
| Zscore(GVA) | 0.519 | (4) | |||
| Zscore(ETKIedu) | 0.982 | (1) | Factor 2 Knowledge-based economy | ||
| Zscore(EiSS) | 0.982 | (2) | |||
| Zscore(ETKIocc) | 0.982 | (1) | |||
| Zscore(ETKIgen) | 0.982 | (1) | |||
| Zscore(TPAp) | 0.852 | (1) | |||
| Zscore(CoE) | 0.843 | (3) | |||
| Zscore(UR) | −0.966 | (1) | Factor 3 Labor Market | ||
| Zscore(MU) | −0.937 | (1) | |||
| Zscore(LtUR) | −0.898 | (1) | |||
| Zscore(FU) | −0.890 | (1) | |||
| Zscore(ME) | 0.392 | 0.760 | (1) | ||
| Zscore(ER15to64) | 0.578 | 0.617 | (1) | ||
| Statistics | Period | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2000–2007 | 2008–2011 | 2012–2017 | ||||||||
| MPI | ECH | FS | MPI | ECH | FS | MPI | ECH | FS | ||
| N | Valid | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 | 28 |
| 0 | Missing | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Mean | 0.97235 | 0.99416 | 0.97789 | 0.99377 | 1.00394 | 0.98987 | 0.99961 | 0.99965 | 0.99996 | |
| SD | 0.159261 | 0.027815 | 0.155983 | 0.135679 | 0.013288 | 0.135008 | 0.027900 | 0.005487 | 0.027283 | |
| Variance | 0.025 | 0.001 | 0.024 | 0.018 | 0.000 | 0.018 | 0.001 | 0.000 | 0.001 | |
| Range | 0.867 | 0.156 | 0.867 | 0.844 | 0.070 | 0.844 | 0.165 | 0.028 | 0.165 | |
| Minimum | 0.785 | 0.885 | 0.785 | 0.396 | 0.991 | 0.396 | 0.869 | 0.986 | 0.869 | |
| Maximum | 1.653 | 1.041 | 1.653 | 1.240 | 1.061 | 1.240 | 1.033 | 1.014 | 1.033 | |
| No. | DMUs | IO CRS MPI | Efficiency Change | Frontier Shift | Rank | Group of Countries | ||
|---|---|---|---|---|---|---|---|---|
| 1 | BE | 0.972 | 1.000 | 0.972 | 1. | MT | 1.653 | 1st (3 EU15, 5 EU13) |
| 2 | BG | 0.785 | 1.000 | 0.785 | 2. | HR | 1.138 | |
| 3 | CZ | 0.903 | 0.994 | 0.908 | 3. | PT | 1.109 | |
| 4 | DK | 0.939 | 1.000 | 0.939 | 4. | RO | 1.097 | |
| 5 | DE | 0.880 | 1.000 | 0.880 | 5. | IE | 1.055 | |
| 6 | EE | 0.928 | 1.013 | 0.915 | 6. | LT | 1.049 | |
| 7 | IE | 1.055 | 1.000 | 1.055 | 7. | FI | 1.036 | |
| 8 | EL | 0.948 | 0.978 | 0.970 | 8. | SK | 1.010 | |
| 9 | ES | 0.858 | 1.000 | 0.858 | 9. | AT | 0.979 | 2nd (7 EU15, 6 EU13) |
| 10 | FR | 0.888 | 1.000 | 0.888 | 10. | BE | 0.972 | |
| 11 | IT | 0.892 | 1.000 | 0.892 | 11. | LU | 0.970 | |
| 12 | CY | 0.907 | 1.000 | 0.907 | 12. | EL | 0.948 | |
| 13 | LV | 0.904 | 0.996 | 0.907 | 13. | DK | 0.939 | |
| 14 | LT | 1.049 | 1.000 | 1.049 | 14. | EE | 0.928 | |
| 15 | LU | 0.970 | 1.000 | 0.970 | 15. | HU | 0.927 | |
| 16 | HU | 0.927 | 1.000 | 0.927 | 16. | PL | 0.920 | |
| 17 | MT | 1.653 | 1.000 | 1.653 | 17. | SE | 0.919 | |
| 18 | NL | 0.906 | 1.000 | 0.906 | 18. | CY | 0.907 | |
| 19 | AT | 0.979 | 1.041 | 0.940 | 19. | NL | 0.906 | |
| 20 | PL | 0.920 | 0.885 | 1.040 | 20. | LV | 0.904 | |
| 21 | PT | 1.109 | 1.030 | 1.077 | 21. | CZ | 0.903 | |
| 22 | RO | 1.097 | 1.000 | 1.097 | 22. | IT | 0.892 | 3rd (5 EU15, 1 EU13) |
| 23 | SI | 0.826 | 0.940 | 0.879 | 23 | FR | 0.888 | |
| 24 | SK | 1.010 | 1.000 | 1.010 | 24. | DE | 0.880 | |
| 25 | FI | 1.036 | 1.000 | 1.036 | 25. | ES | 0.858 | |
| 26 | SE | 0.919 | 1.000 | 0.919 | 26. | UK | 0.827 | |
| 27 | UK | 0.827 | 0.959 | 0.863 | 27. | SI | 0.826 | |
| 28 | HR | 1.138 | 1.000 | 1.138 | 28. | BG | 0.785 | 4th (1 EU13) |
| No. | DMUs | IO CRS MPI | Efficiency Change | Frontier Shift | Rank | Group of Countries | ||
|---|---|---|---|---|---|---|---|---|
| 1 | BE | 0.989 | 1.000 | 0.989 | 1. | MT | 1.240 | 1st (1 EU13) |
| 2 | BG | 0.396 | 1.000 | 0.396 | 2. | CY | 1.120 | 2nd (1 EU13) |
| 3 | CZ | 1.034 | 1.000 | 1.034 | 3. | PT | 1.075 | 3rd (8 EU15, 8 EU13) |
| 4 | DK | 0.987 | 1.000 | 0.987 | 4. | NL | 1.065 | |
| 5 | DE | 1.021 | 1.000 | 1.021 | 5. | LU | 1.065 | |
| 6 | EE | 1.013 | 1.061 | 0.954 | 6. | AT | 1.062 | |
| 7 | IE | 0.905 | 1.000 | 0.905 | 7. | LT | 1.042 | |
| 8 | EL | 0.942 | 1.000 | 0.942 | 8. | SI | 1.039 | |
| 9 | ES | 1.035 | 1.000 | 1.035 | 9. | ES | 1.035 | |
| 10 | FR | 0.975 | 1.000 | 0.975 | 10. | CZ | 1.034 | |
| 11 | IT | 1.002 | 1.000 | 1.002 | 11. | RO | 1.029 | |
| 12 | CY | 1.120 | 1.000 | 1.120 | 12. | PL | 1.021 | |
| 13 | LV | 0.948 | 1.000 | 0.948 | 13. | DE | 1.021 | |
| 14 | LT | 1.042 | 1.000 | 1.042 | 14. | HR | 1.014 | |
| 15 | LU | 1.065 | 1.000 | 1.065 | 15. | EE | 1.013 | |
| 16 | HU | 0.875 | 1.000 | 0.875 | 16. | SK | 1.010 | |
| 17 | MT | 1.240 | 1.000 | 1.240 | 17. | FI | 1.003 | |
| 18 | NL | 1.065 | 1.000 | 1.065 | 18. | IT | 1.002 | |
| 19 | AT | 1.062 | 1.000 | 1.062 | 19. | BE | 0.989 | 4th (7 EU15, 1 EU13) |
| 20 | PL | 1.021 | 1.008 | 1.013 | 20. | DK | 0.987 | |
| 21 | PT | 1.075 | 1.030 | 1.044 | 21. | SE | 0.982 | |
| 22 | RO | 1.029 | 1.000 | 1.029 | 22. | FR | 0.975 | |
| 23 | SI | 1.039 | 1.000 | 1.039 | 23 | LV | 0.948 | |
| 24 | SK | 1.010 | 1.000 | 1.010 | 24. | EL | 0.942 | |
| 25 | FI | 1.003 | 1.000 | 1.003 | 25. | UK | 0.938 | |
| 26 | SE | 0.982 | 1.000 | 0.982 | 26. | IE | 0.905 | |
| 27 | UK | 0.938 | 0.991 | 0.947 | 27. | HU | 0.875 | 5th (1 EU13) |
| 28 | HR | 1.014 | 1.020 | 0.993 | 28. | BG | 0.396 | 6th (1 EU13) |
| No. | DMUs | IO CRS MPI | Efficiency Change | Frontier Shift | Rank | Group of Countries | ||
|---|---|---|---|---|---|---|---|---|
| 1 | BE | 1.005 | 1.000 | 1.005 | 1. | EL | 1.033 | 1st (12 EU15, 7 EU13) |
| 2 | BG | 0.869 | 1.000 | 0.869 | 2. | EE | 1.020 | |
| 3 | CZ | 0.993 | 1.000 | 0.993 | 3. | RO | 1.019 | |
| 4 | DK | 1.004 | 1.000 | 1.004 | 4. | UK | 1.016 | |
| 5 | DE | 0.996 | 1.000 | 0.996 | 5. | IE | 1.015 | |
| 6 | EE | 1.020 | 1.014 | 1.007 | 6. | PL | 1.015 | |
| 7 | IE | 1.015 | 1.000 | 1.015 | 7. | ES | 1.012 | |
| 8 | EL | 1.033 | 1.000 | 1.033 | 8. | LU | 1.011 | |
| 9 | ES | 1.012 | 1.000 | 1.012 | 9. | FI | 1.009 | |
| 10 | FR | 1.002 | 1.000 | 1.002 | 10. | HU | 1.008 | |
| 11 | IT | 1.002 | 1.000 | 1.002 | 11. | BE | 1.005 | |
| 12 | CY | 0.988 | 0.986 | 1.002 | 12. | SK | 1.005 | |
| 13 | LV | 0.989 | 1.000 | 0.989 | 13. | SE | 1.004 | |
| 14 | LT | 1.001 | 1.000 | 1.001 | 14. | DK | 1.004 | |
| 15 | LU | 1.011 | 1.000 | 1.011 | 15. | MT | 1.004 | |
| 16 | HU | 1.008 | 1.000 | 1.008 | 16. | NL | 1.003 | |
| 17 | MT | 1.004 | 1.000 | 1.004 | 17. | FR | 1.002 | |
| 18 | NL | 1.003 | 1.000 | 1.003 | 18. | IT | 1.002 | |
| 19 | AT | 0.997 | 1.000 | 0.997 | 19. | LT | 1.001 | |
| 20 | PL | 1.015 | 1.014 | 1.001 | 20. | AT | 0.997 | 2nd (3 EU15, 5 EU13) |
| 21 | PT | 0.985 | 0.988 | 0.997 | 21. | DE | 0.996 | |
| 22 | RO | 1.019 | 1.000 | 1.019 | 22. | HR | 0.996 | |
| 23 | SI | 0.991 | 1.000 | 0.991 | 23 | CZ | 0.993 | |
| 24 | SK | 1.005 | 1.000 | 1.005 | 24. | SI | 0.991 | |
| 25 | FI | 1.009 | 1.000 | 1.009 | 25. | LV | 0.989 | |
| 26 | SE | 1.004 | 0.999 | 1.005 | 26. | CY | 0.988 | |
| 27 | UK | 1.016 | 1.000 | 1.016 | 27. | PT | 0.985 | |
| 28 | HR | 0.996 | 0.991 | 1.006 | 28. | BG | 0.869 | 3rd (1 EU13) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melecký, L.; Staníčková, M.; Hančlová, J. Nonparametric Approach to Evaluation of Economic and Social Development in the EU28 Member States by DEA Efficiency. J. Risk Financial Manag. 2019, 12, 72. https://doi.org/10.3390/jrfm12020072
Melecký L, Staníčková M, Hančlová J. Nonparametric Approach to Evaluation of Economic and Social Development in the EU28 Member States by DEA Efficiency. Journal of Risk and Financial Management. 2019; 12(2):72. https://doi.org/10.3390/jrfm12020072
Chicago/Turabian StyleMelecký, Lukáš, Michaela Staníčková, and Jana Hančlová. 2019. "Nonparametric Approach to Evaluation of Economic and Social Development in the EU28 Member States by DEA Efficiency" Journal of Risk and Financial Management 12, no. 2: 72. https://doi.org/10.3390/jrfm12020072
APA StyleMelecký, L., Staníčková, M., & Hančlová, J. (2019). Nonparametric Approach to Evaluation of Economic and Social Development in the EU28 Member States by DEA Efficiency. Journal of Risk and Financial Management, 12(2), 72. https://doi.org/10.3390/jrfm12020072





