Defined Contribution Pension Plans: Who Has Seen the Risk?
Abstract
1. Introduction
Sophisticated employers should choose their plan defaults carefully, since these defaults will strongly influence the retirement preparation of their employees. Policymakers should also recognize the role of defaults, since policymakers can facilitate, with laws and regulations, the socially optimal use of defaults.(Choi et al. 2002, p. 104)
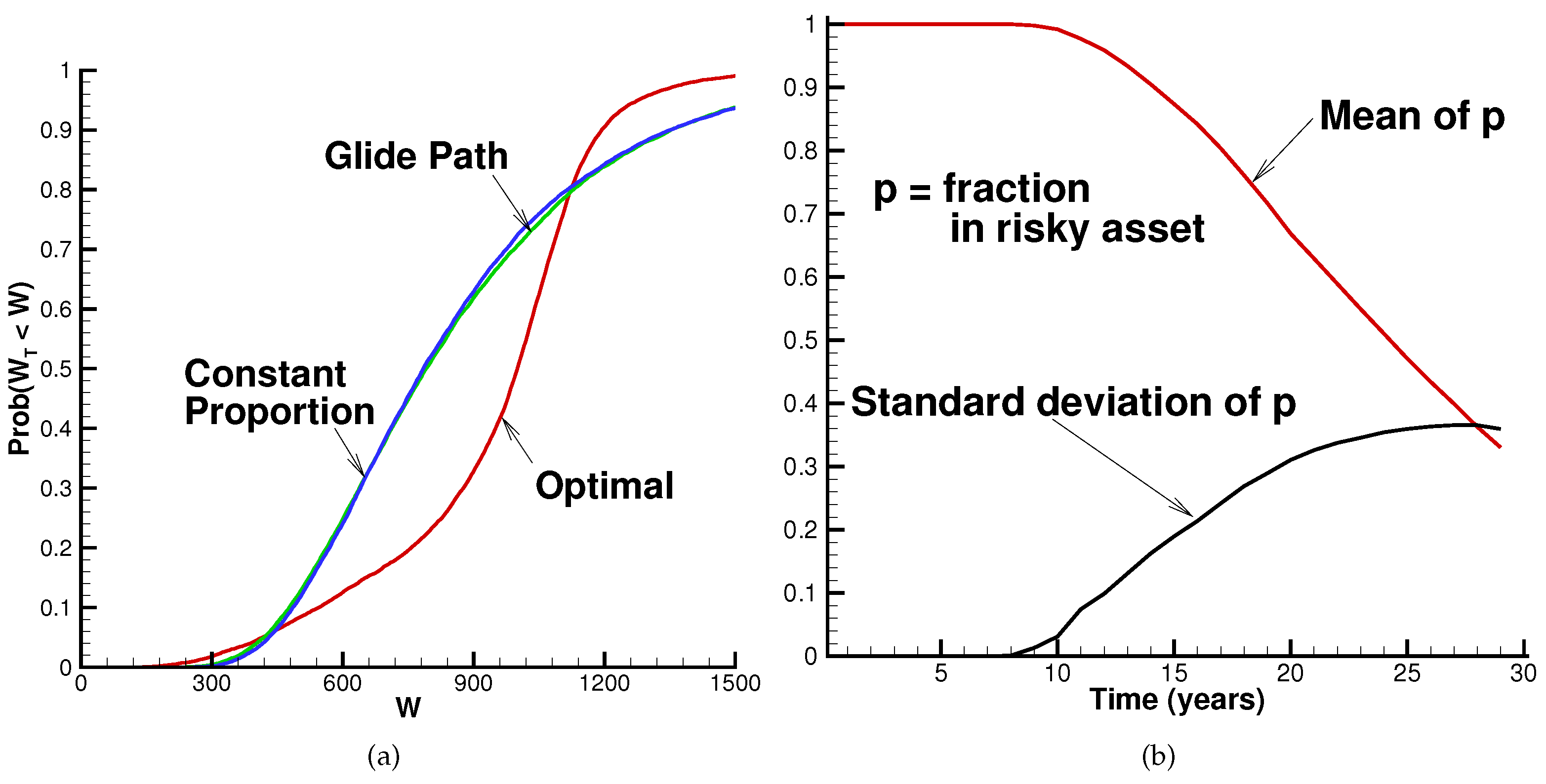
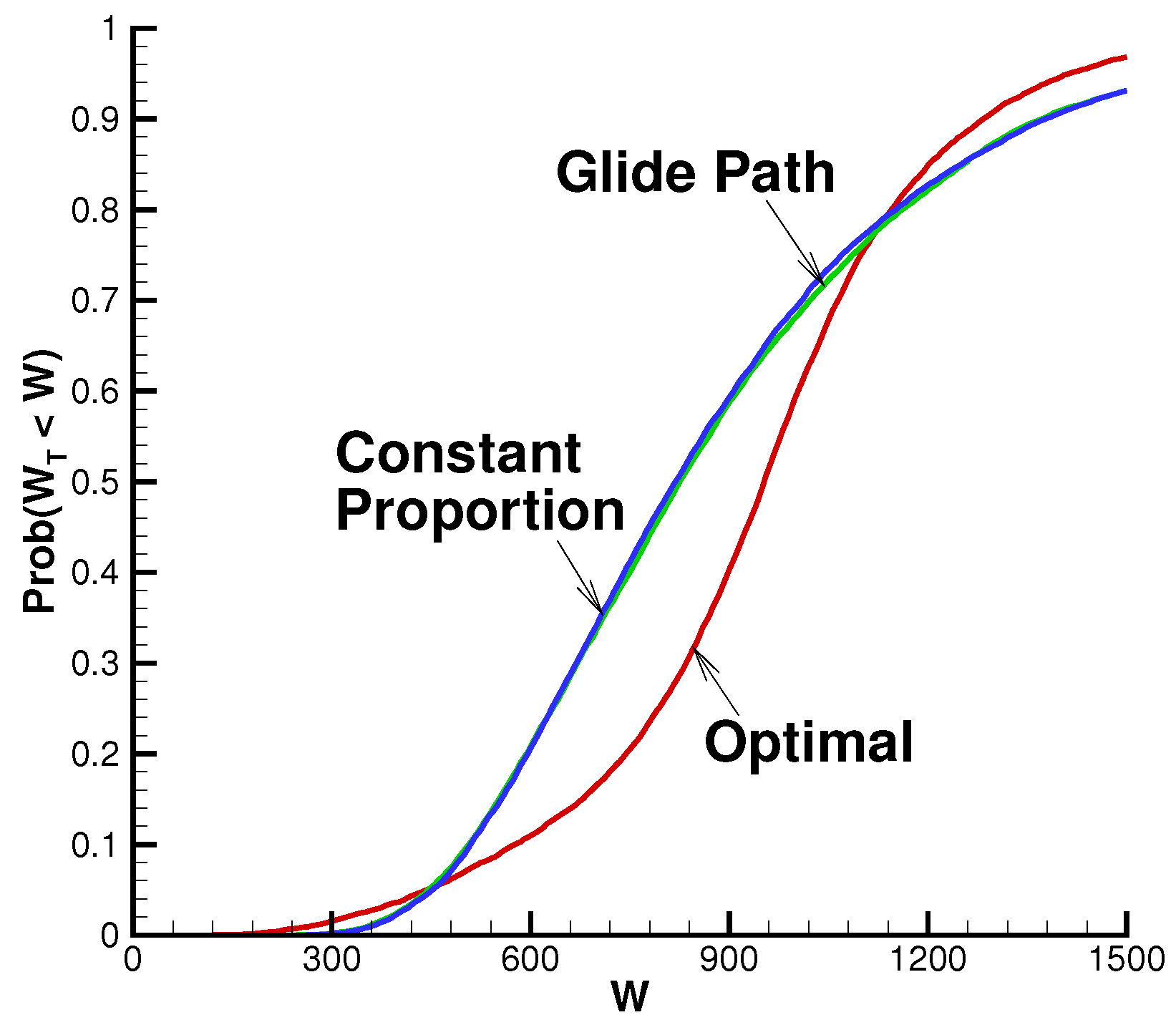
- With typical glide path or constant proportion strategies, there is an unacceptably large probability of shortfall in terms of meeting the target final wealth goal.
- Even with an optimal dynamic QS asset allocation strategy, there is still a fairly high probability of shortfall. This shortfall probability can be reduced to what we view as a reasonable level by increasing the total contribution rate or reducing the replacement ratio, compared to the base case. Another possibility is to substitute an equal-weighted equity index for the value-weighted index, but this may not work in practice due to higher costs associated with equal-weighted indexes, which are not recognized in our model.
2. Formulation
2.1. Deterministic Glide Paths
2.2. Adaptive Strategies
- (i)
- withdraw cash from the portfolio; and
- (ii)
- invest the remainder in the risk-free asset.
3. Data and Parameter Estimates
Robustness to Parameter Estimation
4. Base Case Scenario
- Constant proportion, i.e., .
- Linear glide path, as in Equation (5).
- Time consistent QS optimal strategy, as described in Section 2.2. Recall that this strategy is also multi-period pre-commitment MV optimal.
- When we change input parameters (e.g., invest in different assets, allow , etc.), we may need to recompute the expected wealth target , the equity weight for the constant proportion strategy, the glide path parameters , and the quadratic wealth target (along with the associated optimal control) in order to meet this target.
- The quadratic wealth target exceeds the target expected real terminal wealth . This is because the QS optimal strategy will de-risk if is attainable by investing only in the risk-free asset, so there is not much chance of exceeding this quadratic target by a significant amount. This implies that the average terminal wealth, factoring in paths where the accumulated savings does not ever reach , must be lower than .
5. Alternative Assumptions
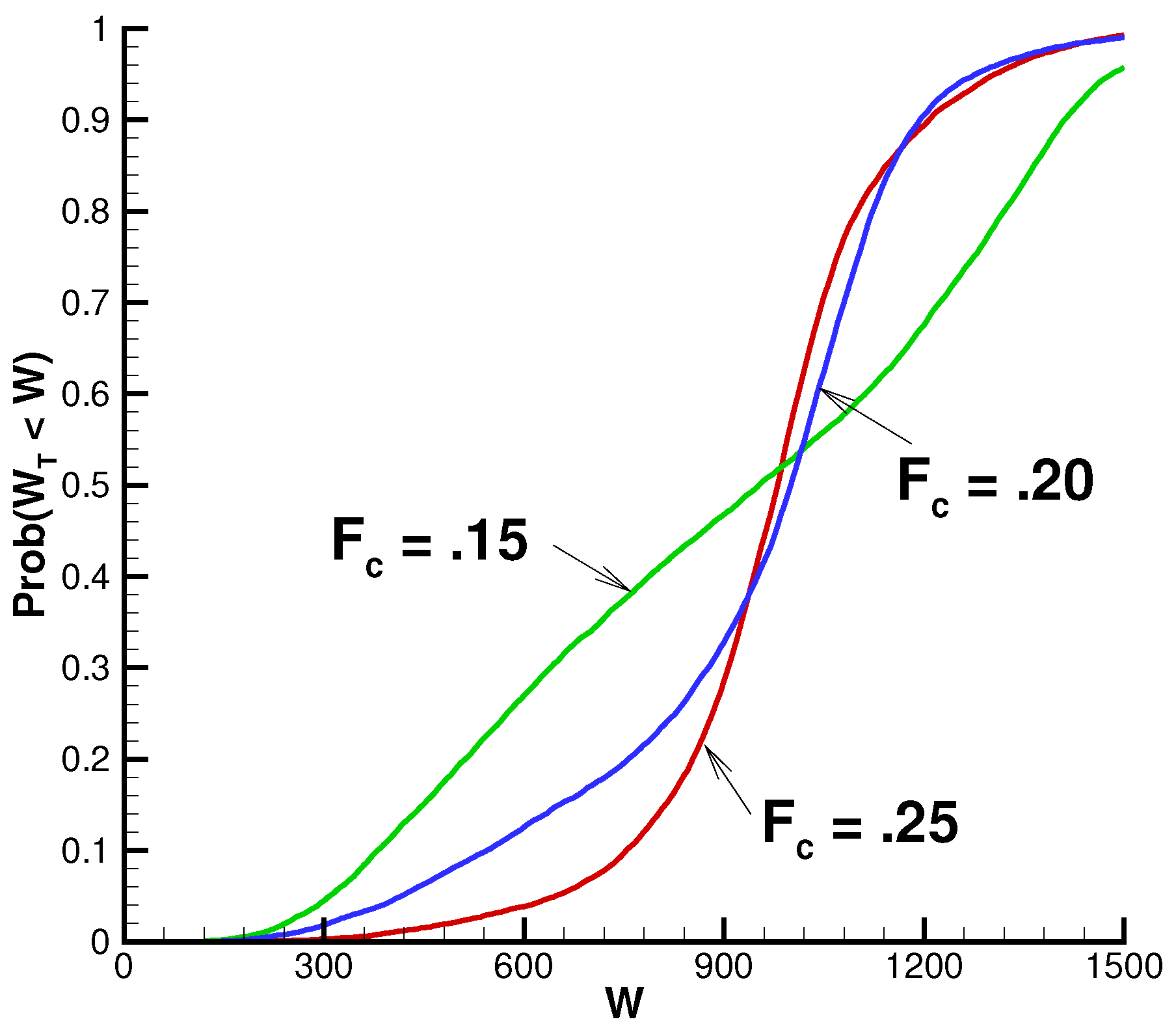
5.1. Effect of Contribution Fraction
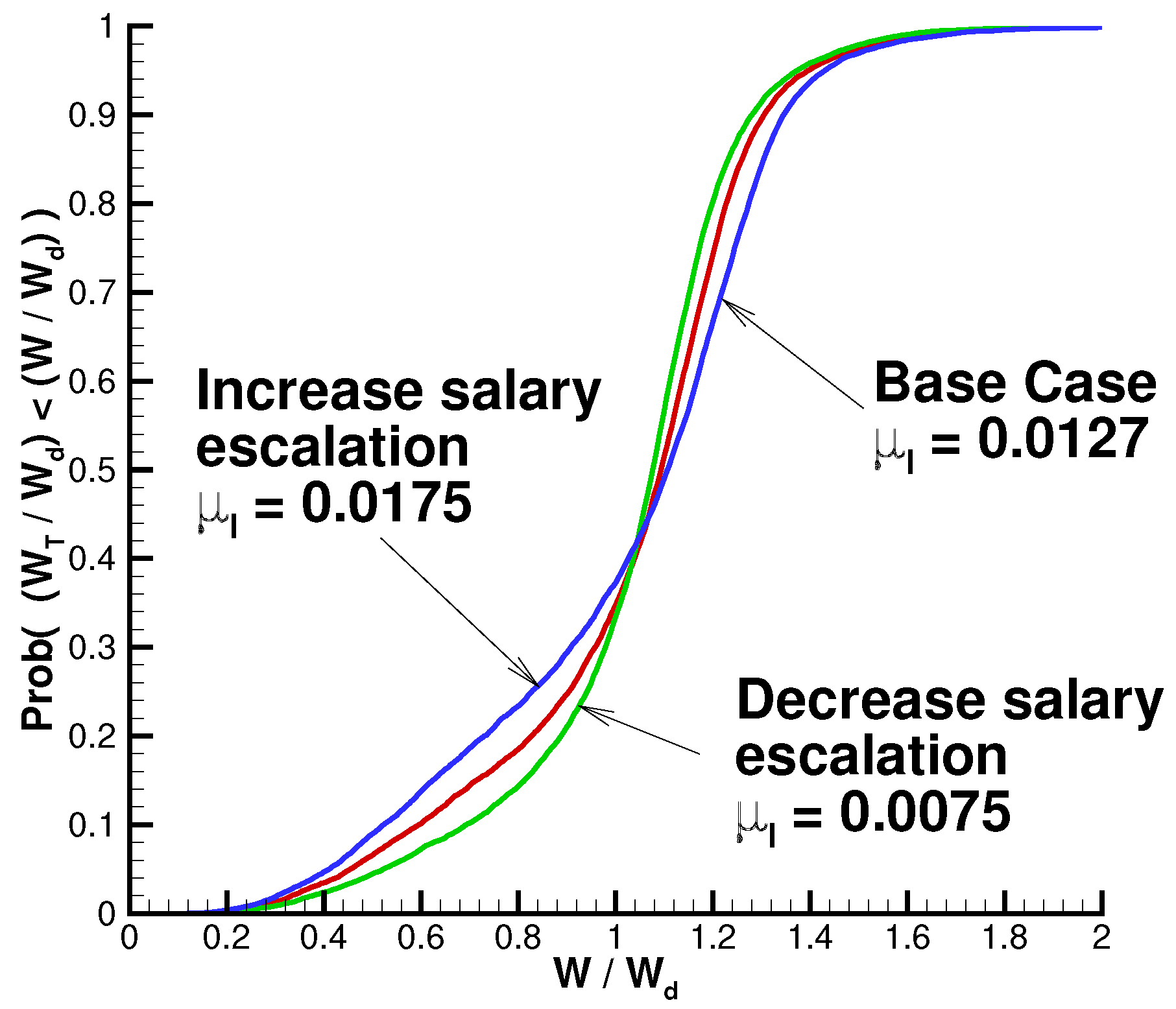
5.2. Effect of Salary Escalation Rate
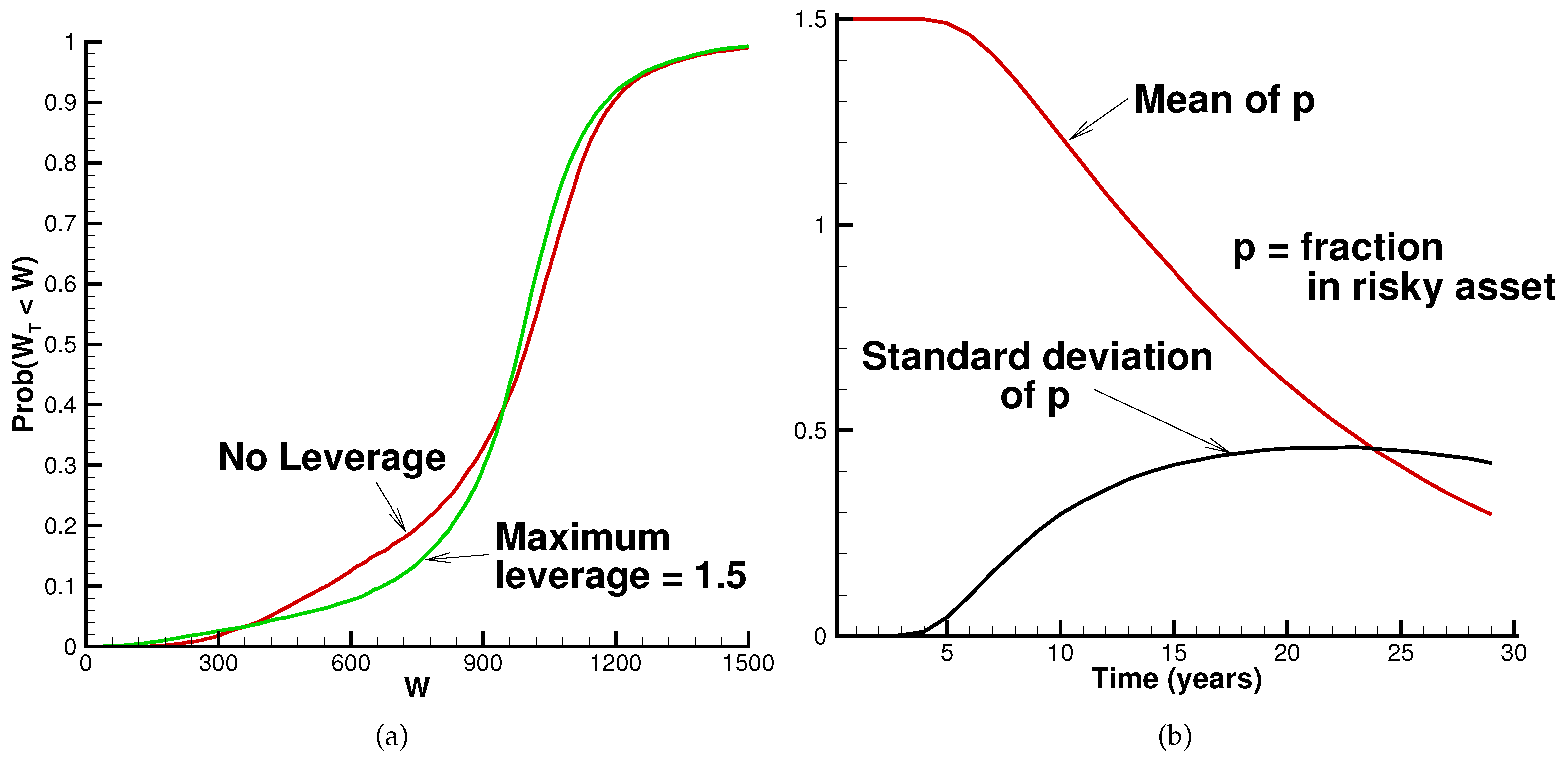
5.3. Effect of Leverage
5.4. Long-Term Bond Index
5.5. Equal-Weighted Equity Index
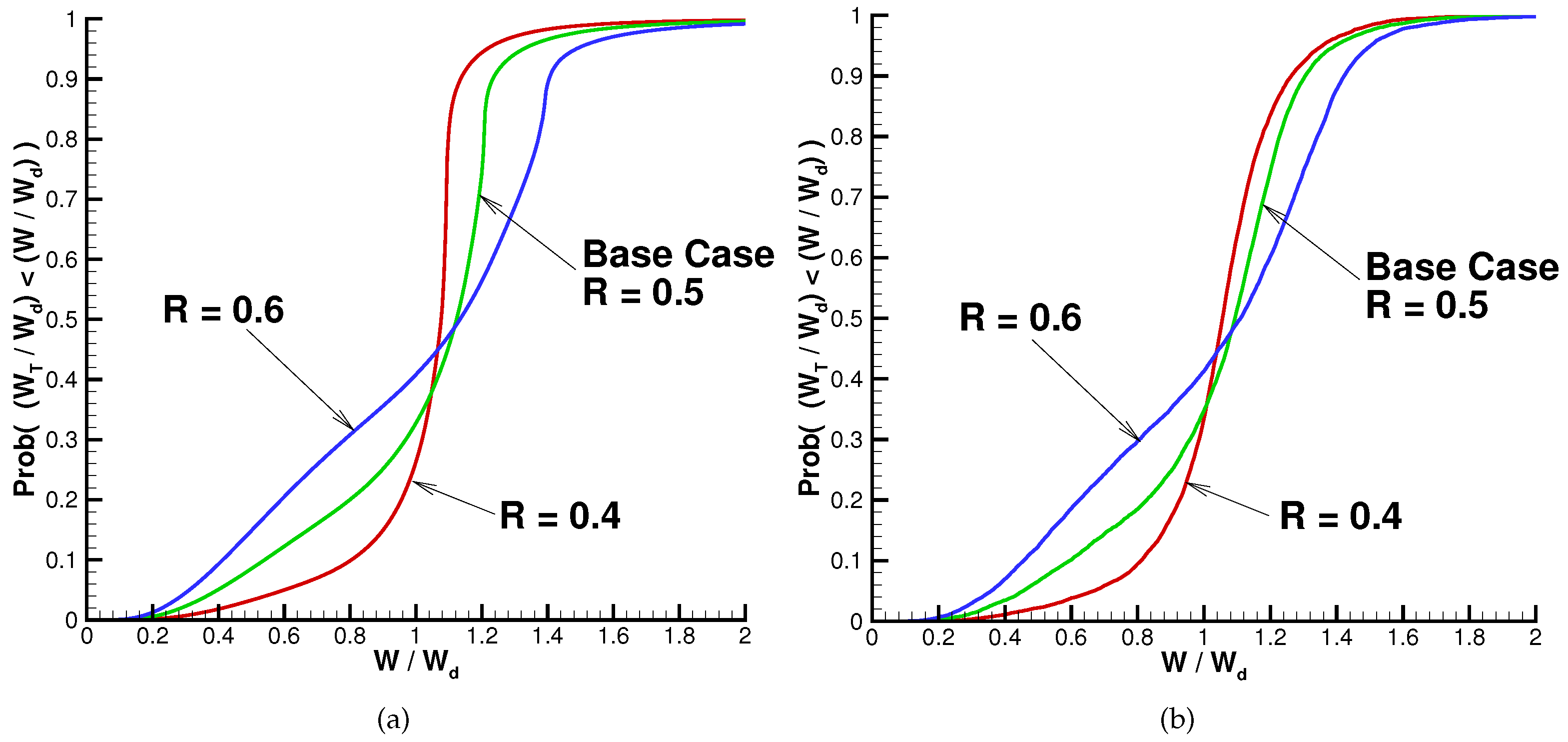
5.6. Effect of Replacement Ratio
5.7. Summary Regarding Alternative Assumptions
- varying the accumulation fraction , i.e., the investor saves at each rebalancing date;
- varying the real salary escalation rate ;
- use of leverage;
- alternative bond index: use of a 10 year T-bond index instead of a 3 month T-bill index;
- alternative stock index: use of an equal-weighted equity index instead of a value-weighted index; and
- varying the replacement ratio R.
6. Conclusions
- reducing the final salary target replacement ratio ( or less);
- increasing the total (employee and employer) contribution rate to per year;
- using alternative stock investment indices, such as an equal-weighted index. The backtests of an equal-weighted index perform well, but it is not clear that this will persist in the future. In addition, we have not factored in the additional costs of this type of index.
Author Contributions
Funding
Conflicts of Interest
References
- Arnott, Robert D., Katrina F. Sherrerd, and Lilian Wu. 2013. The glidepath illusion and potential solutions. The Journal of Retirement 1: 13–28. [Google Scholar] [CrossRef]
- Barber, Brad M., and Terrance Odean. 2013. The behavior of individual investors. In Handbook of Economics and Finance. Edited by George Constantinides, Milton Harris and Rene Stulz. Amsterdam: Elsevier, chp. 22. pp. 1533–69. [Google Scholar]
- Basak, Suleyman, and Georgy Chabakauri. 2010. Dynamic mean-variance asset allocation. Review of Financial Studies 23: 2970–3016. [Google Scholar] [CrossRef]
- Basu, Anup K., Alistair Byrne, and Michael E. Drew. 2011. Dynamic lifecycle strategies for target date retirement funds. Journal of Portfolio Management 37: 83–96. [Google Scholar] [CrossRef]
- Bengen, William. 1994. Determining withdrawal rates using historical data. Journal of Financial Planning 7: 171–180. [Google Scholar]
- Bensoussan, Alain, Kwok Chuen Wong, and Sheung Chi Phillip Yam. 2019. A paradox in time-consistency in the mean-variance problem? Finance and Stochastics 23: 173–207. [Google Scholar] [CrossRef]
- Björk, Tomas, and Agatha Murgoci. 2010. A General Theory of Markovian Time Inconsistent Stochastic Control Problems. SSRN 1694759. Rochester: Social Science Research Network. [Google Scholar]
- Björk, Tomas, and Agatha Murgoci. 2014. A theory of Markovian time inconsisent stochastic control in discrete time. Finance and Stochastics 18: 545–92. [Google Scholar] [CrossRef]
- Björk, Tomas, Agatha Murgoci, and Xun Yu Zhou. 2014. Mean-variance portfolio optimization with state-dependent risk aversion. Mathematical Finance 24: 1–24. [Google Scholar] [CrossRef]
- Bloom, David E., David Canning, and Michael Moore. 2014. Optimal retirement with increasing longevity. Scandinavian Journal of Economics 116: 838–58. [Google Scholar] [CrossRef]
- Choi, James J., David Laibson, Brigitte C. Madrian, and Andrew Metrick. 2002. Defined contribution pensions: Plan rules, participant choices, and the path of least resistance. Tax Policy and the Economy 16: 67–113. [Google Scholar] [CrossRef][Green Version]
- Cocco, João F., Franciso J. Goems, and Pascal J. Maenhout. 2005. Consumption and portfolio choice over the life cycle. Review of Financial Studies 18: 491–533. [Google Scholar] [CrossRef]
- Cogneau, Phillipe, and Valereiy Zakamouline. 2013. Block bootstrap methods and the choice of stocks for the long run. Quantitative Finance 13: 1443–57. [Google Scholar] [CrossRef]
- Cont, Rama, and Cecilia Mancini. 2011. Nonparametric tests for pathwise properties of semimartingales. Bernoulli 17: 781–813. [Google Scholar] [CrossRef]
- Cui, Xiangyu, Jianjun Gao, Xun Li, and Duan Li. 2014. Optimal multi-period mean variance policy under no-shorting constraint. European Journal of Operational Research 234: 459–68. [Google Scholar] [CrossRef]
- Cui, Xiangyu, Duan Li, Shouyang Wang, and Shushang Zhu. 2012. Better than dynamic mean-variance: Time inconsistency and free cash flow stream. Mathematical Finance 22: 346–78. [Google Scholar] [CrossRef]
- Dang, Duy-Minh, and Peter A. Forsyth. 2016. Better than pre-commitment mean-variance portfolio allocation strategies: A semi-self-financing Hamilton–Jacobi–Bellman equation approach. European Journal of Operational Research 250: 827–41. [Google Scholar] [CrossRef]
- Dang, Duy-Minh, Peter A. Forsyth, and Kenneth R. Vetzal. 2017. The 4% strategy revisited: A pre-commitment optimal mean-variance approach to wealth management data. Quantitative Finance 17: 335–51. [Google Scholar] [CrossRef]
- Dang, Duy-Minh, and Peter A. Forsyth. 2014. Continuous time mean-variance optimal portfolio allocation under jump diffusion: A numerical impulse control approach. Numerical Methods for Partial Differential Equations 30: 664–98. [Google Scholar] [CrossRef]
- Dang, Duy-Minh, Peter A. Forsyth, and Yuying Li. 2016. Convergence of the embedded mean-variance optimal points with discrete sampling. Numerische Mathematik 132: 271–302. [Google Scholar] [CrossRef]
- Dichtl, Hubert, Wolfgang Drobetz, and Martin Wambach. 2016. Testing rebalancing strategies for stock-bond portfolos across different asset allocations. Applied Economics 48: 772–88. [Google Scholar] [CrossRef]
- Dobrescu, Loretti I., Xiaodong Fan, Hazel Bateman, Ben R. Newell, A. Ortmann, and Susan Thorp. 2018. Retirement savings: A tale of decisions and defaults. Economic Journal 128: 1047–94. [Google Scholar] [CrossRef]
- Esch, David N., and Robert O. Michaud. 2014. The False Promise Of Target Date Funds. Working Paper. Boston: New Frontier Advisors, LLC. [Google Scholar]
- Estrada, Javier. 2014. The glidepath illusion: An international perspective. Journal of Portfolio Management 40: 52–64. [Google Scholar] [CrossRef]
- Forsyth, Peter A., and Kenneth R. Vetzal. 2017a. Dynamic mean variance asset allocation: Tests for robustness. International Journal of Financial Engineering 4: 1750021. [Google Scholar] [CrossRef]
- Forsyth, Peter A., and Kenneth R. Vetzal. 2017b. Robust asset allocation for long-term target-based investing. International Journal of Theoretical and Applied Finance 20: 1750017. [Google Scholar] [CrossRef]
- Forsyth, Peter A., and Kenneth R. Vetzal. 2019. Optimal asset allocation for retirement saving: Deterministic vs. time consistent adaptive strategies. Applied Mathematical Finance. forthcoming. [Google Scholar] [CrossRef]
- Gougeon, Phillipe. 2009. Shifting pensions. Statistics Canada: Perspectives on Labour and Income 10: 16–23. [Google Scholar]
- Hedesström, Ted M., Henrik Svedsäter, and Tommy Gärling. 2004. Identifying heuristic choice rules in the Swedish premium pension scheme. Journal of Behavioral Finance 5: 32–42. [Google Scholar] [CrossRef]
- Holt, Jeff. 2018. Target-Date Funds Keep Growing In Popularity. Available online: www.morningstar.com/videos/889903/targetdate-funds-keep-growing-in-popularity.html (accessed on 9 April 2019).
- Kou, Steven, and Hui Wang. 2004. Option pricing under a double exponential jump diffusion model. Management Science 50: 1178–92. [Google Scholar] [CrossRef]
- Li, Duan, and Wan-Lung Ng. 2000. Optimal dynamic portfolio selection: Multiperiod mean-variance formulation. Mathematical Finance 10: 387–406. [Google Scholar] [CrossRef]
- Lioui, Abrahan, and Patrice Poncet. 2016. Understanding dynamic mean variance asset allocation. European Journal of Operational Research 254: 320–37. [Google Scholar] [CrossRef]
- Ma, Kai, and Peter A. Forsyth. 2016. Numerical solution of the Hamilton–Jacobi–Bellman formulation for continuous time mean variance asset allocation under stochastic volatility. Journal of Computational Finance 20: 1–37. [Google Scholar] [CrossRef]
- MacDonald, Bonnie-Jean, Bruce Jones, Richaard J. Morrison, Robert L. Brown, and Mary Hardy. 2013. Research and reality: A literature review on drawing down retirement savings. North American Actuarial Journal 17: 181–215. [Google Scholar] [CrossRef]
- Madrian, Brigitte C., and Dennis F. Shea. 2001. The power of suggestion: Inertia in 401(k) participation and savings behavior. Quarterly Journal of Economics 116: 1149–87. [Google Scholar] [CrossRef]
- Menoncin, Francesco, and Elena Vigna. 2017. Mean-variance target based optimisation for defined contribution pension schemes in a stochastic framework. Insurance: Mathematics and Economics 76: 172–84. [Google Scholar] [CrossRef]
- O’Connell, Allison. 2009. Kiwisaver: A model scheme? Social Policy Journal of New Zealand 36: 130–41. [Google Scholar]
- Patton, Andrew, Dimitris Politis, and Halbert White. 2009. Correction to: Automatic block-length selection for the dependent bootstrap. Econometric Reviews 28: 372–375. [Google Scholar] [CrossRef]
- Pielichata, Paulina. 2018. Europeans seeing funds as solution to DC dilemma. Pensions & Investments, March 19. [Google Scholar]
- Plyakha, Yuliya, Raman Uppal, and Grigory Vilkov. 2014. Equal or Value Weighting? Implications For Asset-Pricing Tests. Working Paper. Lille, Nice and Paris: EDHEC Business School. [Google Scholar]
- Politis, Dimitris, and Halbert White. 2004. Automatic block-length selection for the dependent bootstrap. Econometric Reviews 23: 53–70. [Google Scholar] [CrossRef]
- Ruppert, Peter, and Giulio Zanella. 2015. Revisiting wage, earnings, and hours profiles. Journal of Monetary Economics 72: 114–30. [Google Scholar] [CrossRef]
- Tse, Shu-Tong, Peter A. Forsyth, and Yuying Li. 2014. Preservation of scalarization optimal points in the embedding technique for continuous time mean variance optimization. SIAM Journal on Control and Optimization 52: 1527–46. [Google Scholar] [CrossRef][Green Version]
- Vigna, Elena. 2014. On efficiency of mean-variance based portfolio selection in defined contribution pension schemes. Quantitative Finance 14: 237–58. [Google Scholar] [CrossRef]
- Vigna, Elena. 2017. Tail Optimality And Preferences Consistency For Intertemporal Optimization Problems. Working Paper No. 502. Collegio Carlo Alberto: Università Degli Studi di Torino. [Google Scholar]
- Wang, Jian, and Peter A. Forsyth. 2011. Continuous time mean variance asset allocation: A time-consistent strategy. European Journal of Operational Research 209: 184–201. [Google Scholar] [CrossRef]
- Zhou, Xun Yu, and Duan Li. 2000. Continuous-time mean-variance portfolio selection: A stochastic LQ framework. Applied Mathematics and Optimization 42: 19–33. [Google Scholar] [CrossRef]
| 1. | Statistics from the Thinking Ahead Institute’s “Global Pension Assets Study 2018”. Available online: www.thinkingaheadinstitute.org/-/media/Pdf/TAI/Research-Ideas/GPAS-2018.pdf. |
| 2. | In other words, the employee must explicitly decide to opt out of a TDF if she desires a different asset allocation strategy. |
| 3. | Although our focus in this article is on the US setting, we note that TDFs are now being marketed in various parts of Europe, in part due to regulatory developments (Pielichata, 2018). Major US vendors such as Vanguard and Fidelity have launched TDFs in Canada in recent years. In addition, some life-cycle products such as Time Pension which has been popular in Denmark are similar in some respects to TDFs. |
| 4. | See, for example, Hedesström et al. (2004) (Sweden), O’Connell (2009) (New Zealand), and Dobrescu et al. (2018) (Australia). |
| 5. | An obvious extension would be a GARCH/stochastic volatility model. However, Ma and Forsyth (2016) document that mean-reverting stochastic volatility effects for Heston-type stochastic volatility models are negligible for long-term investors. Since multivariate GARCH/stochastic volatility models are typically mean-reverting, this suggests that stochastic volatility may be unimportant for long-term investors under these models as well, but this has not been proven. |
| 6. | Recall the time consistent QS strategy has the same controls as the pre-commitment MV strategy. |
| 7. | As discussed below, in the case of an optimal QS strategy, the investor may also withdraw cash from the portfolio at an action time. |
| 8. | Since the investor rebalances her portfolio discretely, insolvency could also occur if in the special case of the model where jumps are ruled out (), i.e., the value of the risky asset follows geometric Brownian motion. |
| 9. | More precisely, suppose that insolvency occurs at time t, i.e., . Letting be the instant after t, then and . |
| 10. | For example, we can exogenously specify and find the value of which generates the desired expected terminal wealth via Newton iteration. Alternatively, we can exogenously set and numerically find the appropriate value of . |
| 11. | If problem (7) is not convex, there may be solutions to problem (8) that are not solutions to problem (7). However, these spurious solutions can be eliminated in a straightforward way (Dang et al., 2016; Tse et al., 2014). |
| 12. | More precisely, our calculations are based on data from Historical Indexes, ©2015 Center for Research in Security Prices (CSRP), The University of Chicago Booth School of Business. Wharton Research Data Services (WRDS) was used in preparing this work. This service and the data available thereon constitute valuable intellectual property and trade secrets of WRDS and/or its third-party suppliers. |
| 13. | As noted by Bloom et al. (2014), this rate has been used by the US Congressional Budget Office in its long-term projections. |
| 14. | This is a bit more aggressive in terms of taking on equity market risk than the strategy considered by Bengen (1994) which involved equal weights between the equity and bond markets. Keep in mind that here we are investing in a 3-month T-bill index, whereas Bengen used intermediate maturity Treasury bonds which offer somewhat higher average returns. |
| 15. | In other words, if the size of a block extends past the end of the sample in 2015:12, the return data resumes at the start of the sample in 1926:1 for the duration of the block. |
| 16. | In other words, the QS optimal strategy will appear riskier than the constant proportion or glide path strategies according to tail risk measures such as value-at-risk or conditional value-at-risk, provided that the risk measure is calculated using sufficiently low cumulative probabilities. |
| 17. | Of course, the equity allocation for the constant proportion and glide path cases is fixed in advance, being at most time-dependent and not varying at all in response to realized returns. |
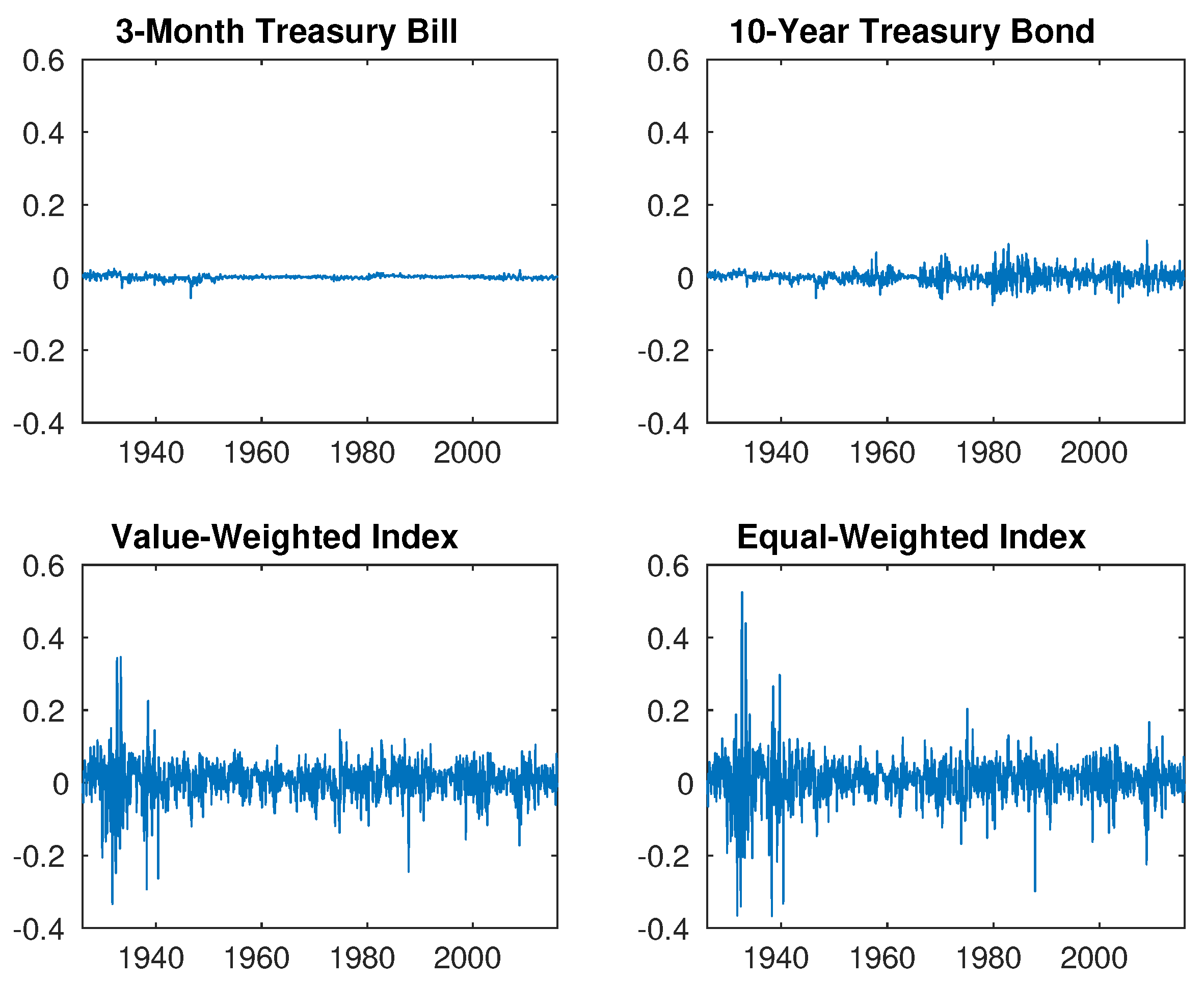
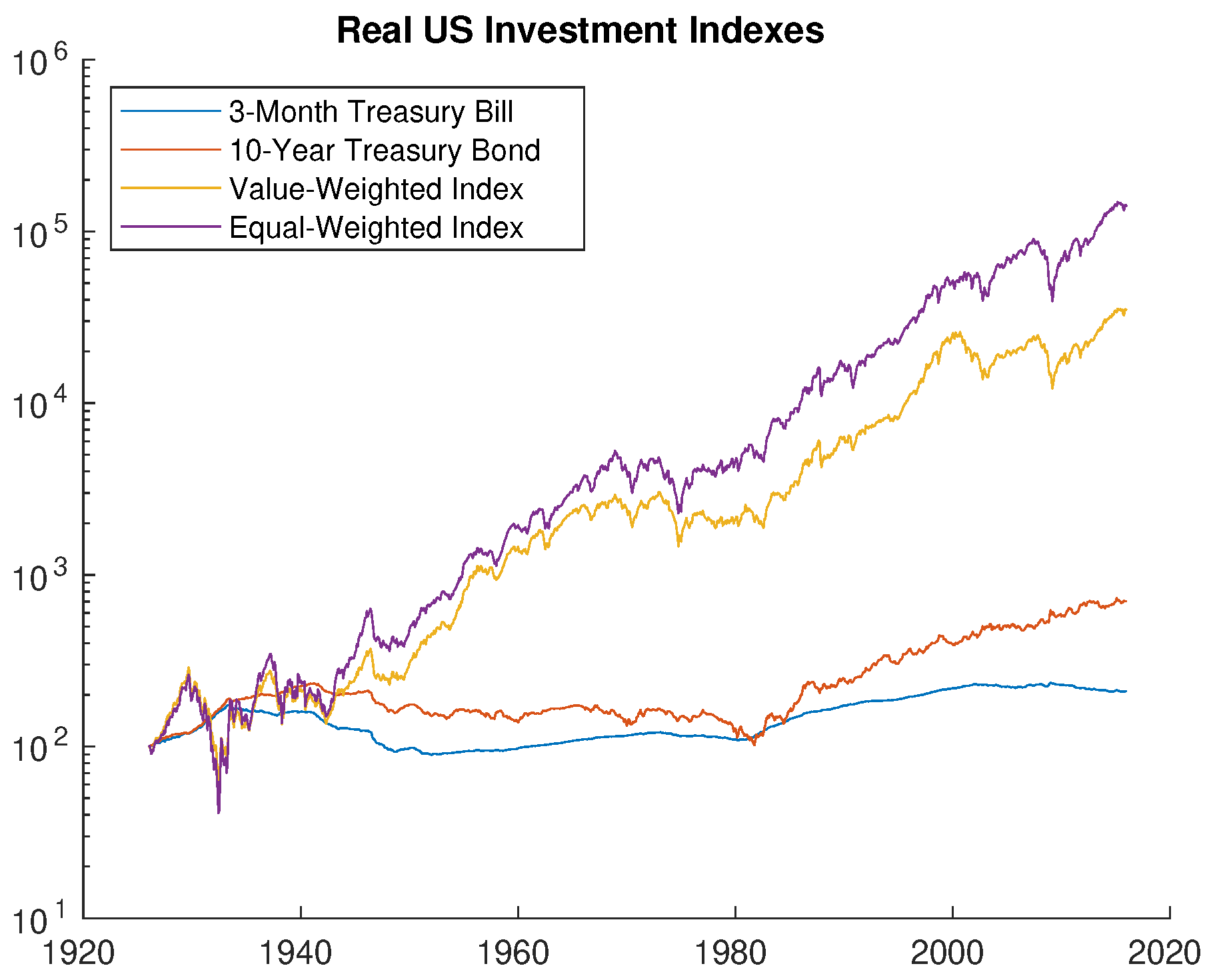

| Equity Market Index | ||||||
| Value-weighted | 0.0889 | 0.1477 | 0.3222 | 0.2759 | 4.4273 | 5.2613 |
| Equal-weighted | 0.1183 | 0.1663 | 0.4000 | 0.3333 | 3.6912 | 4.5409 |
| Bond Market Index | Average Return | |||||
| 3-month T-bill | 0.00827 | |||||
| 10-year T-bond | 0.02160 | |||||
| Initial salary | $50,000 |
| Salary escalation rate | 0.0127 (Bloom et al., 2014) |
| Contribution fraction | 0.20 |
| Accumulation period T | 30 years |
| Safe withdrawal rate | 0.04 |
| Equity index | Value-weighted |
| Bond index | 3-month T-bill |
| Investment strategies | Constant proportion, glide path, QS optimal |
| Rebalancing interval | 1 year |
| Maximum leverage indicator | 1.0 |
| If insolvent | Trading stops |
| Strategy | Expected Value | Standard Deviation | Expected Surplus Cash | ||
|---|---|---|---|---|---|
| Synthetic Market | |||||
| Constant proportion | 915 | 519 | 0.39 | 0.51 | NA |
| Glide path | 915 | 519 | 0.39 | 0.51 | NA |
| QS optimal | 915 | 244 | 0.19 | 0.24 | 21 |
| Historical Market (Expected blocksize year) | |||||
| Constant proportion | 876 | 402 | 0.38 | 0.51 | NA |
| Glide path | 872 | 398 | 0.39 | 0.52 | NA |
| QS optimal | 904 | 232 | 0.18 | 0.24 | 26 |
| Historical Market (Expected blocksize years) | |||||
| Constant proportion | 869 | 376 | 0.38 | 0.51 | NA |
| Glide path | 866 | 372 | 0.39 | 0.52 | NA |
| QS optimal | 911 | 221 | 0.17 | 0.23 | 31 |
| Historical Market (Expected blocksize years) | |||||
| Constant proportion | 862 | 349 | 0.37 | 0.50 | NA |
| Glide path | 861 | 347 | 0.38 | 0.51 | NA |
| QS optimal | 924 | 213 | 0.16 | 0.21 | 38 |
| Market Parameters | Expected Value | Standard Deviation | Expected Surplus Cash | ||
|---|---|---|---|---|---|
| Synthetic market | 915 | 244 | 0.19 | 0.24 | 21 |
| 916 | 245 | 0.19 | 0.24 | 21 | |
| 915 | 245 | 0.19 | 0.24 | 21 |
| Expected Value | Standard Deviation | Expected Surplus Cash | |||
|---|---|---|---|---|---|
| Synthetic Market | |||||
| 0.15 | 915 | 440 | 0.36 | 0.42 | 18 |
| 0.20 | 915 | 244 | 0.19 | 0.24 | 21 |
| 0.25 | 915 | 150 | 0.09 | 0.13 | 21 |
| Historical Market (Expected blocksize years) | |||||
| 0.15 | 916 | 380 | 0.34 | 0.41 | 12 |
| 0.20 | 911 | 221 | 0.17 | 0.23 | 31 |
| 0.25 | 909 | 126 | 0.07 | 0.14 | 67 |
| Wealth Target | Expected Value | Standard Deviation | Expected Surplus Cash | |||
|---|---|---|---|---|---|---|
| Synthetic Market | ||||||
| 0.0175 | 1056 | 1.0 | 0.31 | 0.25 | 0.30 | 0.02 |
| 0.0127 | 915 | 1.0 | 0.27 | 0.20 | 0.25 | 0.02 |
| 0.0075 | 783 | 1.0 | 0.22 | 0.15 | 0.21 | 0.02 |
| Historical Market (Expected blocksize years) | ||||||
| 0.0175 | 1056 | 0.99 | 0.29 | 0.23 | 0.29 | 0.03 |
| 0.0127 | 915 | 0.97 | 0.24 | 0.18 | 0.25 | 0.03 |
| 0.0075 | 783 | 0.99 | 0.19 | 0.14 | 0.21 | 0.04 |
| Expected Value | Standard Deviation | Expected Surplus Cash | |||
|---|---|---|---|---|---|
| Synthetic Market | |||||
| 1.0 | 915 | 244 | 0.19 | 0.24 | 21 |
| 1.5 | 915 | 205 | 0.12 | 0.17 | 24 |
| Historical Market (Expected blocksize years) | |||||
| 1.0 | 911 | 221 | 0.17 | 0.23 | 31 |
| 1.5 | 904 | 186 | 0.11 | 0.18 | 46 |
| Strategy | Expected Value | Standard Deviation | Expected Surplus Cash | ||
|---|---|---|---|---|---|
| Synthetic Market | |||||
| Constant proportion | 915 | 437 | 0.34 | 0.47 | NA |
| Glide path | 915 | 438 | 0.34 | 0.48 | NA |
| QS optimal | 915 | 222 | 0.16 | 0.21 | 19 |
| Historical Market (Expected blocksize years) | |||||
| Constant proportion | 900 | 374 | 0.34 | 0.47 | NA |
| Glide path | 897 | 376 | 0.34 | 0.48 | NA |
| QS optimal | 881 | 201 | 0.17 | 0.26 | 67 |
| Strategy | Expected Value | Standard Deviation | Expected Surplus Cash | ||
|---|---|---|---|---|---|
| Synthetic Market | |||||
| Constant proportion | 915 | 546 | 0.38 | 0.51 | NA |
| Glide path | 915 | 553 | 0.39 | 0.52 | NA |
| QS optimal | 915 | 185 | 0.11 | 0.16 | 44 |
| Historical Market (Expected blocksize year) | |||||
| Constant proportion | 837 | 327 | 0.39 | 0.54 | NA |
| Glide path | 831 | 319 | 0.39 | 0.55 | NA |
| QS optimal | 904 | 162 | 0.10 | 0.16 | 49 |
| Historical Market (Expected blocksize years) | |||||
| Constant proportion | 827 | 293 | 0.38 | .54 | NA |
| Glide path | 820 | 283 | 0.38 | 0.55 | NA |
| QS optimal | 915 | 139 | 0.07 | 0.13 | 51 |
| Historical Market (Expected blocksize years) | |||||
| Constant proportion | 815 | 248 | 0.36 | 0.53 | NA |
| Glide path | 808 | 242 | 0.37 | 0.55 | NA |
| QS optimal | 932 | 115 | 0.04 | 0.10 | 54 |
| R | Wealth Target | Expected Value | Standard Deviation | Expected Surplus Cash | ||
|---|---|---|---|---|---|---|
| Synthetic Market | ||||||
| 0.4 | 732 | 1.0 | 0.16 | 0.10 | 0.15 | 0.02 |
| 0.5 | 915 | 1.0 | 0.27 | 0.20 | 0.25 | 0.02 |
| 0.6 | 1098 | 1.0 | 0.37 | 0.31 | 0.36 | 0.02 |
| Historical Market (Expected blocksize years) | ||||||
| 0.4 | 732 | .99 | 0.15 | 0.09 | 0.17 | 0.0 |
| 0.5 | 915 | .97 | 0.24 | 0.18 | 0.25 | 0.03 |
| 0.6 | 1098 | 1.0 | 0.35 | 0.30 | 0.35 | 0.02 |
| Case | ||
|---|---|---|
| Base Case, Table 2 | ||
| Constant proportion | 0.43 | 0.54 |
| Glide path | 0.43 | 0.54 |
| QS optimal | 0.18 | 0.25 |
| QS Optimal | ||
| Contribution Fraction | ||
| 0.09 | 0.17 | |
| 0.37 | 0.43 | |
| Salary Escalation Rate | ||
| 0.23 | 0.29 | |
| 0.14 | 0.21 | |
| Leverage | ||
| 0.13 | 0.19 | |
| Alternative Bond Index | ||
| 10-year T-bond | 0.19 | 0.28 |
| Alternative Stock Index | ||
| Equal-weighted | 0.09 | 0.16 |
| Replacement Ratio | ||
| 0.09 | 0.17 | |
| 0.30 | 0.35 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forsyth, P.A.; Vetzal, K.R. Defined Contribution Pension Plans: Who Has Seen the Risk? J. Risk Financial Manag. 2019, 12, 70. https://doi.org/10.3390/jrfm12020070
Forsyth PA, Vetzal KR. Defined Contribution Pension Plans: Who Has Seen the Risk? Journal of Risk and Financial Management. 2019; 12(2):70. https://doi.org/10.3390/jrfm12020070
Chicago/Turabian StyleForsyth, Peter A., and Kenneth R. Vetzal. 2019. "Defined Contribution Pension Plans: Who Has Seen the Risk?" Journal of Risk and Financial Management 12, no. 2: 70. https://doi.org/10.3390/jrfm12020070
APA StyleForsyth, P. A., & Vetzal, K. R. (2019). Defined Contribution Pension Plans: Who Has Seen the Risk? Journal of Risk and Financial Management, 12(2), 70. https://doi.org/10.3390/jrfm12020070




