Positive Liquidity Spillovers from Sovereign Bond-Backed Securities
Abstract
:1. Introduction
2. Hedging, Arbitrage and Diversification
3. Microstructure Literature
4. Methodology
4.1. Derivation of SBBS Yields
4.2. Methodology for Optimal Hedge Selection
4.3. Measuring Out-Of-Sample Hedge Effectiveness
5. Results
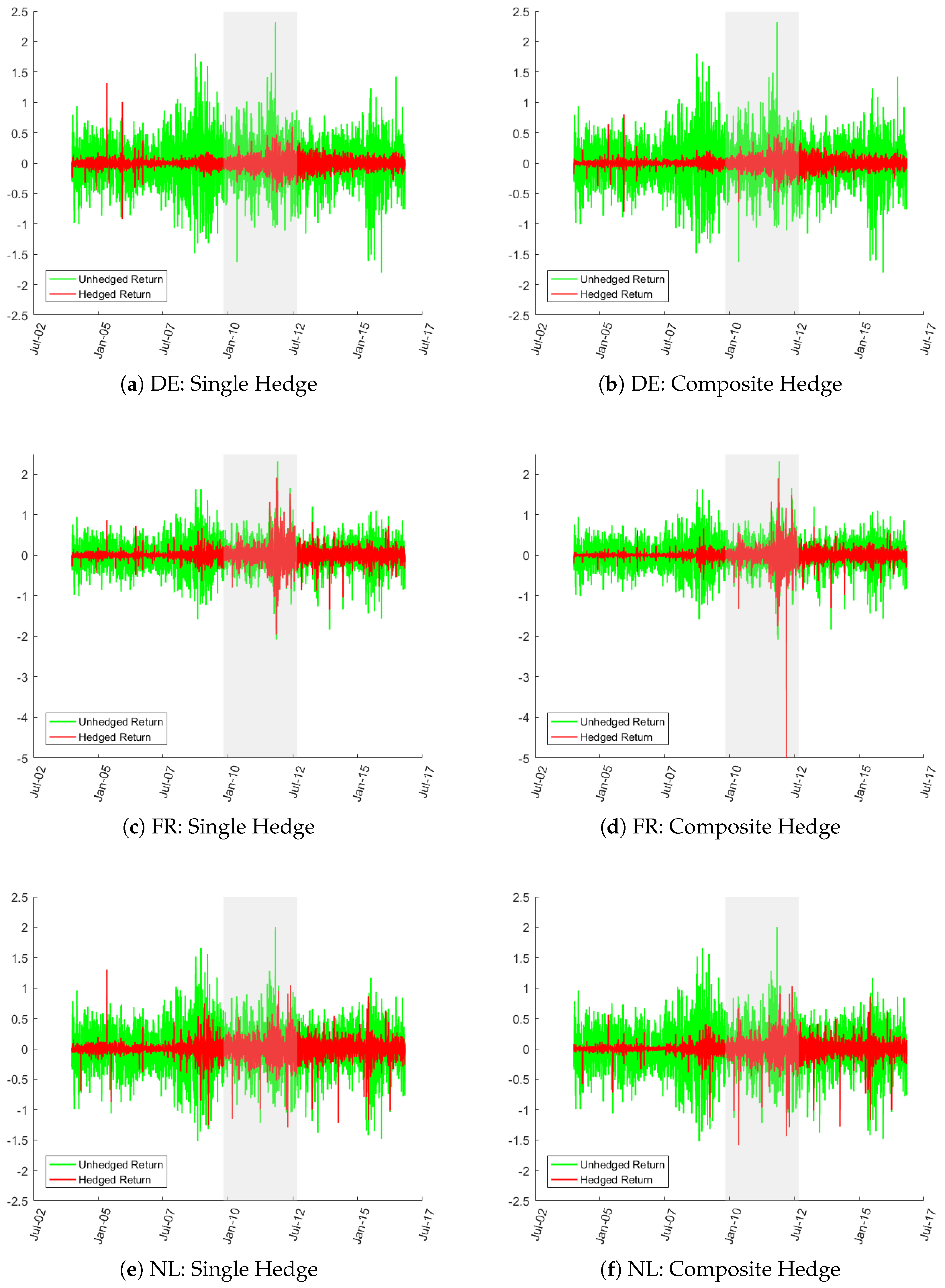
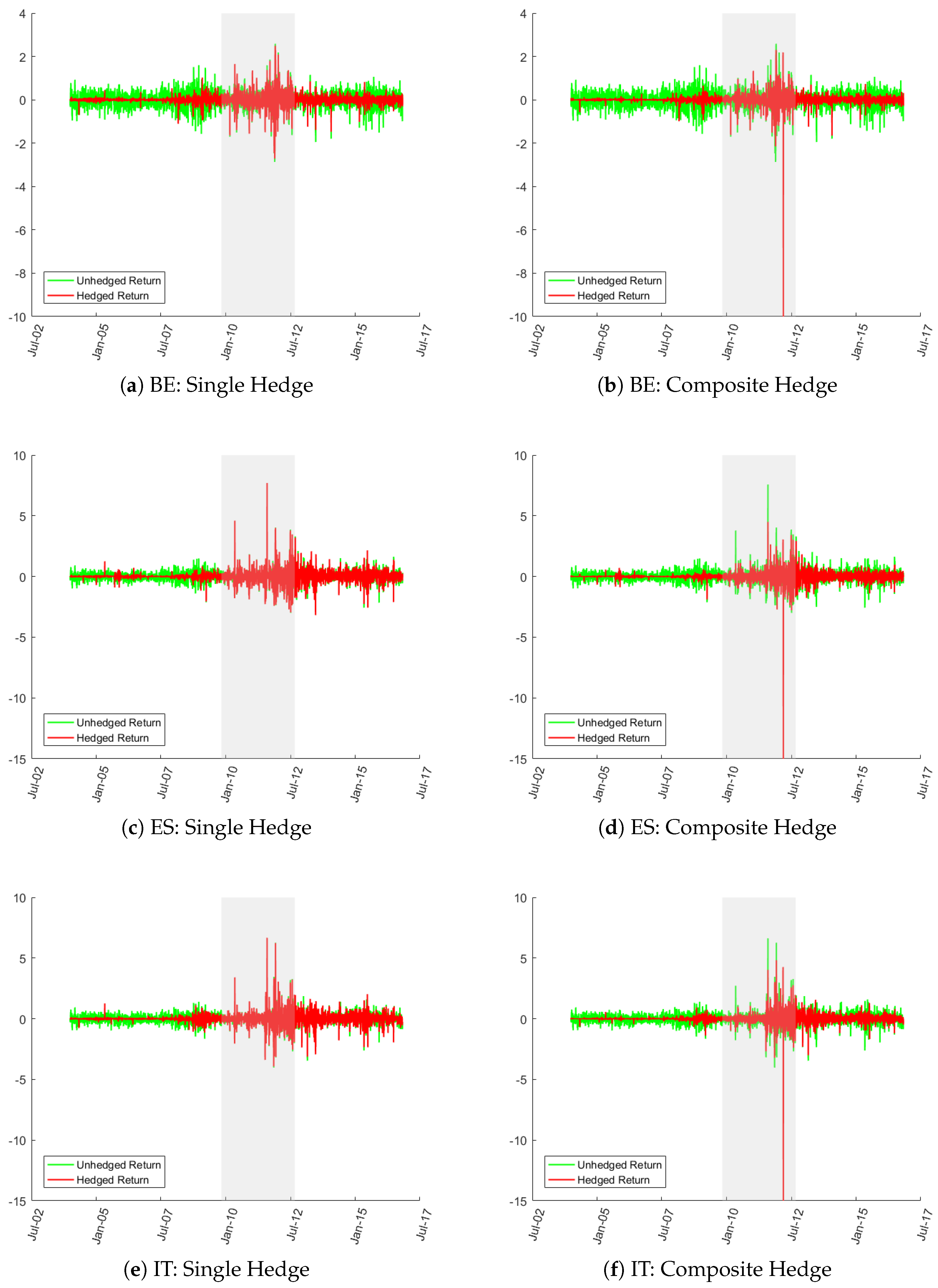
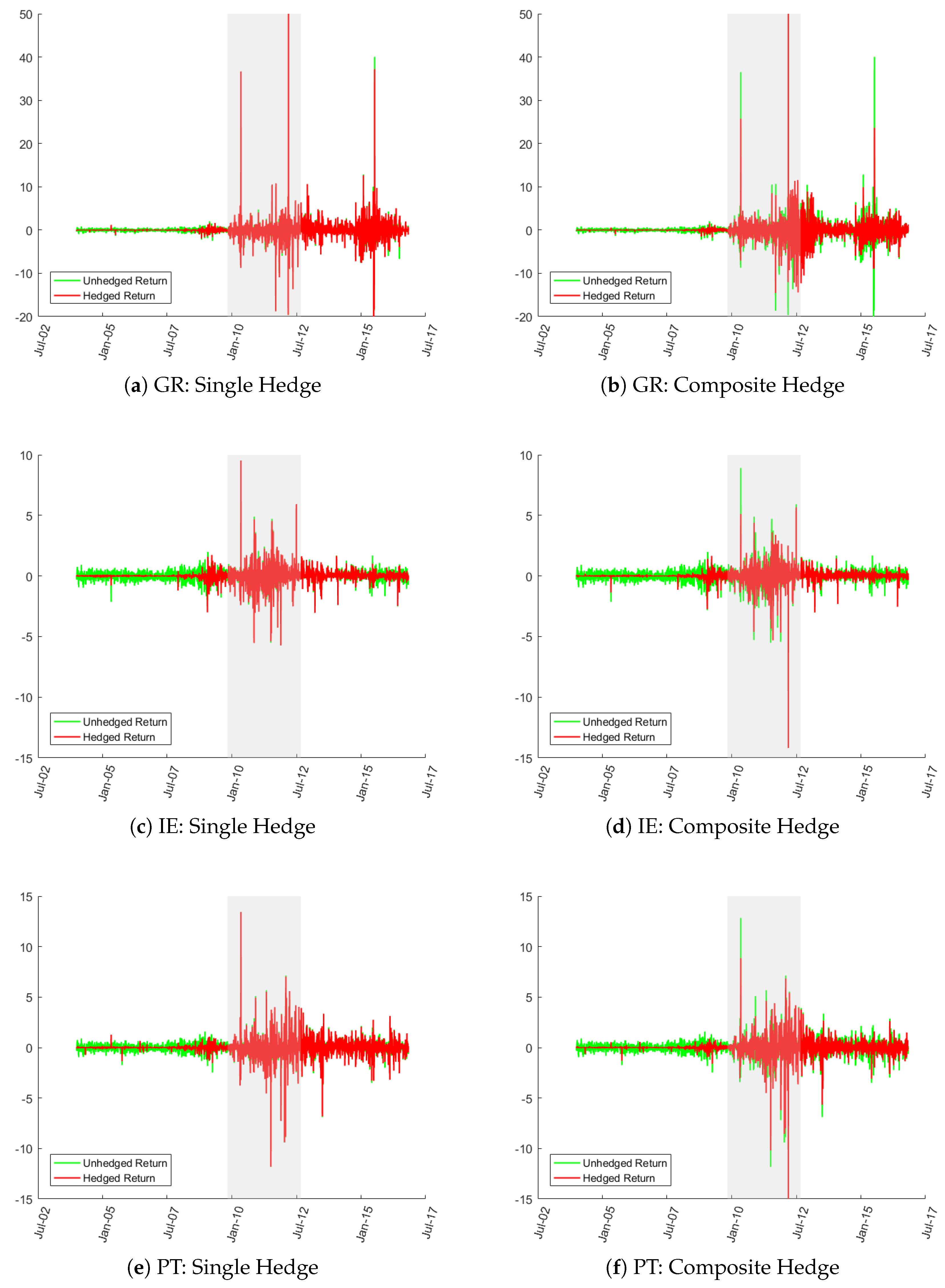
5.1. Effectiveness of Hedging without Diversification
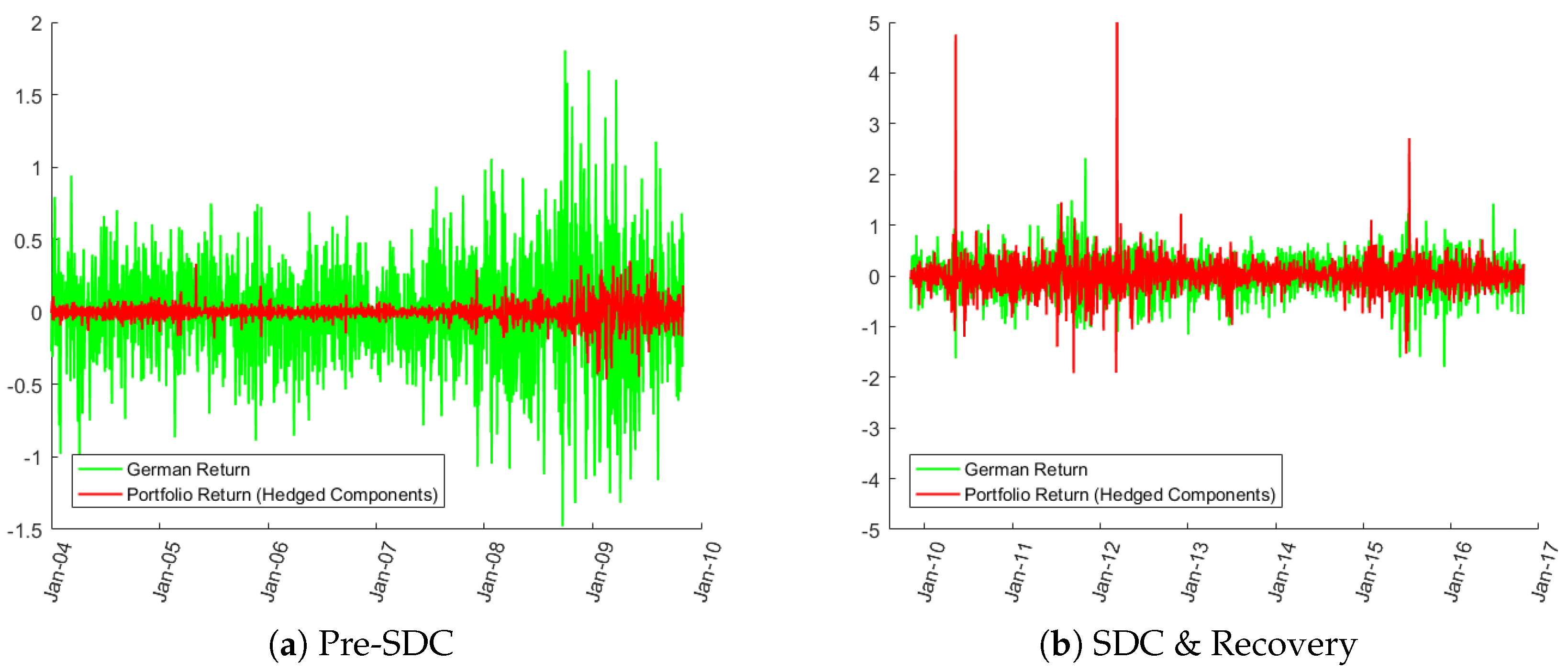
5.2. Post-Hedging Diversification of Risks
5.3. Summary of Results for Extensions
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Optimal Hedging
Appendix B. Robustness
Appendix B.1. Comparing with Futures as Hedge
| Sov Debt Crisis | Recovery | |||||
| Hedge = | BUND | BTP | BUND+BTP | BUND | BTP | BUND+BTP |
| AT(i) | −28 | 7 | −27 | −17 | −3 | −19 |
| AT(ii) | −26 | 13 | −24 | −23 | −7 | −29 |
| BE(i) | −1 | −11 | −19 | −10 | −6 | −16 |
| BE(ii) | 10 | 2 | −12 | −16 | −5 | −22 |
| DE(i) | −33 | 3 | −33 | −36 | −3 | −35 |
| DE(ii) | −32 | 6 | −32 | −44 | −4 | −44 |
| ES(i) | 2 | −36 | −33 | −2 | −24 | −23 |
| ES(ii) | −2 | −33 | −35 | −4 | −26 | −26 |
| FI(i) | −34 | 5 | −33 | −32 | −3 | −32 |
| FI(ii) | −38 | 0 | −38 | −41 | −7 | −44 |
| FR(i) | −22 | 6 | −21 | −16 | −4 | −19 |
| FR(ii) | −18 | 12 | −22 | −20 | −8 | −27 |
| GR(i) | 3 | 13 | 17 | 0 | 0 | 0 |
| GR(ii) | 3 | 18 | 19 | 3 | 0 | 2 |
| IE(i) | 0 | −5 | −6 | −1 | 0 | −1 |
| IE(ii) | −4 | −2 | −5 | −4 | −1 | −3 |
| IT(i) | 3 | −52 | −49 | −3 | −46 | −45 |
| IT(ii) | 7 | −57 | −59 | −5 | −59 | −58 |
| NL(i) | −33 | 5 | −32 | −29 | −2 | −29 |
| NL(ii) | −29 | 3 | −31 | −37 | −3 | −38 |
| PT(i) | 0 | −4 | −5 | 0 | −3 | −2 |
| PT(ii) | 3 | −8 | −5 | 1 | −5 | −6 |
Appendix B.2. Hedge Effectiveness at Other Maturities
| Pre-Crisis | Sov Debt Crisis | Recovery | |||||||
| Term = | 10 Year | 5 Year | 2 Year | 10 Year | 5 Year | 2 Year | 10 Year | 5 Year | 2 Year |
| AT(i) | −72 | −65 | −47 | −26 | −29 | −23 | −49 | −44 | −24 |
| AT(ii) | −84 | −80 | −58 | −41 | −40 | −30 | −56 | −51 | −24 |
| BE(i) | −77 | −67 | −56 | −20 | −23 | −15 | −52 | −35 | −15 |
| BE(ii) | −83 | −81 | −76 | −29 | −26 | −20 | −57 | −45 | −10 |
| DE(i) | −87 | −85 | −75 | −71 | −69 | −48 | −75 | −72 | −68 |
| DE(ii) | −89 | −88 | −82 | −73 | −69 | −55 | −74 | −73 | −67 |
| ES(i) | −69 | −67 | −62 | −28 | −44 | −42 | −43 | −50 | −43 |
| ES(ii) | −75 | −80 | −77 | −35 | −38 | −36 | −43 | −48 | −37 |
| FI(i) | −76 | −55 | −26 | −47 | −45 | −20 | −55 | −41 | −27 |
| FI(ii) | −84 | −80 | −30 | −55 | −56 | −26 | −62 | −56 | −24 |
| FR(i) | −83 | −81 | −75 | −31 | −33 | −29 | −59 | −49 | −31 |
| FR(ii) | −88 | −86 | −82 | −38 | −38 | −35 | −61 | −52 | −27 |
| GR(i) | −55 | −45 | −34 | −17 | 0 | 1 | −8 | ||
| GR(ii) | −67 | −60 | −61 | 23 | 31 | 42 | 12 | ||
| IE(i) | −52 | −40 | −17 | 1 | −13 | −27 | −14 | ||
| IE(ii) | −72 | −40 | −27 | −6 | −10 | −35 | −19 | ||
| IT(i) | −72 | −64 | −59 | −37 | −59 | −62 | −53 | −54 | −60 |
| IT(ii) | −77 | −70 | −73 | −44 | −51 | −61 | −54 | −55 | −57 |
| NL(i) | −81 | −71 | −54 | −43 | −42 | −25 | −56 | −47 | −39 |
| NL(ii) | −86 | −84 | −72 | −51 | −53 | −42 | −65 | −57 | −36 |
| PT(i) | −67 | −59 | −58 | 0 | −9 | −17 | −21 | −13 | −8 |
| PT(ii) | −77 | −76 | −69 | −9 | −5 | −3 | −26 | −11 | 1 |
| Avg(i) | −72 | −64 | −51 | −29 | −33 | −28 | −45 | −42 | −35 |
| Avg(ii) | −80 | −75 | −64 | −33 | −32 | −27 | −47 | −47 | −31 |
Appendix B.3. Hedge Effectiveness under Higher Incidence of Extreme Losses
| Pre-Crisis | Sov Debt Crisis | Recovery | ||||
| Gaussian | T-Dist | Gaussian | T-Dist | Gaussian | T-Dist | |
| AT(i) | −72 | −72 | −26 | −24 | −49 | −46 |
| AT(ii) | −84 | −83 | −41 | −38 | −56 | −52 |
| BE(i) | −77 | −77 | −20 | −19 | −52 | −49 |
| BE(ii) | −83 | −82 | −29 | −26 | −57 | −54 |
| DE(i) | −87 | −81 | −71 | −45 | −75 | −56 |
| DE(ii) | −89 | −83 | −73 | −48 | −74 | −53 |
| ES(i) | −69 | −68 | −28 | −34 | −43 | −40 |
| ES(ii) | −75 | −76 | −35 | −38 | −43 | −40 |
| FI(i) | −76 | −75 | −47 | −38 | −55 | −48 |
| FI(ii) | −84 | −83 | −55 | −44 | −62 | −55 |
| FR(i) | −83 | −84 | −31 | −26 | −59 | −57 |
| FR(ii) | −88 | −88 | −38 | −44 | −61 | −59 |
| GR(i) | −55 | −51 | −17 | −17 | −8 | 0 |
| GR(ii) | −67 | −63 | 23 | 29 | 12 | 27 |
| IE(i) | −52 | −50 | 1 | 0 | −27 | −26 |
| IE(ii) | −72 | −73 | −6 | −9 | −35 | −34 |
| IT(i) | −72 | −70 | −37 | −40 | −53 | −51 |
| IT(ii) | −77 | −71 | −44 | −40 | −54 | −55 |
| NL(i) | −81 | −81 | −43 | −37 | −56 | −51 |
| NL(ii) | −86 | −87 | −51 | −46 | −65 | −57 |
| PT(i) | −67 | −65 | 0 | 2 | −21 | −18 |
| PT(ii) | −77 | −76 | −9 | −14 | −26 | −21 |
| Avg(i) | −72 | −70 | −29 | −25 | −45 | −40 |
| Avg(ii) | −80 | −79 | −33 | −29 | −47 | −41 |
References
- Amihud, Yakov, and Haim Mendelson. 1980. Dealership Market: Market Making with Inventory. Journal of Financial Economics 8: 31–53. [Google Scholar] [CrossRef]
- Baillie, Richard T., and Robert J. Myers. 1991. Bivariate GARCH estimation of the optimal commodity futures hedge. Journal of Applied Econometrics 6: 109–24. [Google Scholar] [CrossRef]
- Basel Committee on Banking Supervision. 2017. Regulatory Treatment of Sovereign Exposures. Basel: Basel Committee on Banking Supervision. [Google Scholar]
- Bessler, Wolfgang, Alexander Leonhardt, and Dominik Wolff. 2016. Analyzing Hedging Strategies for Fixed Income Portfolios: A Bayesian Approach for Model Selection. International Review of Financial Analysis. Available online: http://dx.doi.org/10.2139/ssrn.2429344 (accessed on 8 April 2019).
- Brunnermeier, Markus K., and Lasse Heje Pedersen. 2009. Market Liquidity and Funding Liquidity. The Review of Financial Studies 22: 2201–38. [Google Scholar] [CrossRef]
- Brunnermeier, Markus K., Sam Langfield, Marco Pagano, Ricardo Reis, Stijn Van Nieuwerburgh, and Dimitri Vayanos. 2016. The sovereign-bank diabolic loop and ESBies. American Economic Review Papers and Proceedings 106: 508–12. [Google Scholar] [CrossRef]
- Brunnermeier, Markus K., Sam Langfield, Marco Pagano, Ricardo Reis, Stijn Van Nieuwerburgh, and Dimitri Vayanos. 2017. ESBies: Safety in the Tranches. Economic Policy 32: 175–219. [Google Scholar] [CrossRef]
- Chan, Joshua CC, and Angelia L. Grant. 2016. Modeling energy price dynamics: GARCH versus stochastic volatility. Energy Economics 54: 182–89. [Google Scholar] [CrossRef]
- Chen, Sheng-Syan, Cheng-few Lee, and Keshab Shrestha. 2003. Futures Hedge Ratios: A Review. Quarterly Review of Economics and Finance 43: 433–65. [Google Scholar] [CrossRef]
- Copeland, Thomas E., and Dan Galai. 1983. Information Effects on the Bid-Ask Spread. Journal of Finance 38: 1457–69. [Google Scholar] [CrossRef]
- Demsetz, Harold. 1968. The Cost of Transacting. Quarterly Journal of Economics 82: 33–53. [Google Scholar] [CrossRef]
- De Sola Perea, M., Peter G. Dunne, Martin Puhl, and Thomas Reininger. 2017. Sovereign Bond Backed Securities: A VAR-for-VaR & Marginal Expected Shortfall Assessment. ESRB Working Paper Series, Frankfurt, Germany: European Systemic Risk Board (ESRB). [Google Scholar]
- Dunne, Peter G., Michael J. Moore, and Richard Portes. 2007. Benchmark Status in Fixed-Income Asset Markets. Journal of Business, Finance & Accounting 34: 1615–34. [Google Scholar] [CrossRef]
- Easley, David, and Maureen O’hara. 1987. Price, Trade Size, and Information in Securities Markets. Journal of Financial Economics 19: 69–90. [Google Scholar] [CrossRef]
- Ederington, Louis. 1979. The Hedging Performance of the New Futures Markets. Journal of Finance 34: 157–70. [Google Scholar] [CrossRef]
- Engle, Robert. 2009. Anticipating Correlations. Princeton: Princeton University Press. [Google Scholar]
- ESRB High-Level Task Force on Safe Assets. 2018. Sovereign bond-backed securities: A feasibility study. Frankfurt: European Systemic Risk Board. [Google Scholar]
- Farhi, Emmanuel, and Jean Tirole. 2018. Deadly embrace: Sovereign and financial balance sheets Doom Loops. Review of Economic Studies 85: 1781–823. [Google Scholar] [CrossRef]
- Froot, Kenneth A., and Jeremy C. Stein. 1998. Risk management, capital budgeting and capital structure policy for financial institutions: An integrated approach. Journal of Financial Economics 47: 55–82. [Google Scholar] [CrossRef]
- Gao, Pengjie, Paul Schultz, and Zhaogang Song. 2017. Liquidity in a Market for Unique Assets: Specified Pool and To-Be-Announced Trading in the Mortgage-Backed Securities Market. The Journal of Finance 72: 1119–70. [Google Scholar] [CrossRef]
- Garbade, Kenneth. 1999. Fixed Income Analytics. Cambridge: MIT Press. [Google Scholar]
- Gibson, Heather D., Stephen G. Hall, and George S. Tavlas. 2017. A suggestion for constructing a large time-varying conditional covariance matrix. Economics Letters 156: 110–13. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., and Paul R. Milgrom. 1985. Bid, Ask and Transaction Prices in a Specialist Market with Heterogeneously Informed Traders. Journal of Financial Economics 14: 71–100. [Google Scholar] [CrossRef]
- Hagströmer, Björn, Richard Henricsson, and Lars L. Nordén. 2016. Components of the Bid—Ask Spread and Variance: A Unified Approach. Journal of Futures Markets 36: 545–63. [Google Scholar] [CrossRef]
- Ho, Thomas, and Hans R. Stoll. 1981. Optimal Dealer Pricing under Transactions and Return Uncertainty. Journal of Financial Economics 9: 47–73. [Google Scholar] [CrossRef]
- Ho, Thomas, and Hans R. Stoll. 1983. The Dynamics of Dealer Markets under Competition. Journal of Finance 38: 1053–74. [Google Scholar] [CrossRef]
- Huang, Roger D., and Hans R. Stoll. 1997. The Components of the Bid-Ask Spread: A General Approach. Review of Financial Studies 10: 995–1034. [Google Scholar] [CrossRef]
- Koutmos, Gregory, and Andreas Pericli. 2000. Are multiple hedging instruments better than one? Journal of Portfolio Management 26: 63–70. [Google Scholar] [CrossRef]
- Leandro, Álvaro, and Jeromin Zettelmeyer. 2018. Evaluating Proposals for a Euro Area Safe Asset. Working Paper. Washington, DC, USA: Peterson Institute for International Economics. [Google Scholar]
- Lien, Donald, and Yiu Kuen Tse. 2011. Some recent developments in Futures hedging. Journal of Economic Surveys 16: 359–96. [Google Scholar]
- Liu, Zijun, Yuliya Baranova, and Tamarah Shakir. 2017. Dealer Intermediation, Market Liquidity and the Impact of Regulatory Reform. Bank of England Staff Working Paper. London, UK: Bank of England, vol. 665. [Google Scholar]
- Lucas, André, Bernd Schwaab, and Xin Zhang. 2017. Modelling Financial Sector Tail Risk in the Euro Area. Journal of Applied Econometrics 32: 171–91. [Google Scholar] [CrossRef]
- Marcus, Alan J., and Evren Ors. 1996. Hedging corporate bond portfolios across the business cycle. Journal of Fixed Income 4: 56–60. [Google Scholar] [CrossRef]
- Morgan, Lawrence. 2008. Combination hedges applied to US markets. Financial Analysts Journal 64: 74–84. [Google Scholar] [CrossRef]
- Naik, Narayan Y., and Pradeep K. Yadav. 2003. Risk Management with Derivatives by Dealers and Market Quality in Government Bond Markets. Journal of Finance 58: 1873–904. [Google Scholar] [CrossRef]
- Schönbucher, Philipp J. 2003. Credit Derivatives Pricing Models: Models, Pricing and Implementation. London: Wiley. [Google Scholar]
- Stoll, Hans R. 1978. The Pricing of Security Dealer Services: An empirical study of Nasdaq stocks. Journal of Finance 33: 1153–72. [Google Scholar] [CrossRef]
- Stulz, René M. 1996. Rethinking risk management. Journal of Applied Corporate Finance 9: 8–24. [Google Scholar] [CrossRef]
- Tinic, Seha M., and Richard R. West. 1972. Competition and the Pricing of Dealer Services in the Over-the-Counter Market. Journal of Financial and Quantitative Analysis 7: 1707–27. [Google Scholar] [CrossRef]
- Yuan, Kathy. 2005. The Liquidity Service of Benchmark Securities. Journal of the European Economic Association 3: 1156–80. [Google Scholar] [CrossRef]
| 1. | A wider range of potential effects are considered in the report by the ESRB High-Level Task Force on Safe Assets (2018). |
| 2. | Gao et al. (2017) describe how, in that market, dealers typically hedge inventory risk in their Specific-Pool exposures with offsetting TBA trades and they show that impediments to hedging can reduce such liquidity. More interestingly, they conclude that the presence of TBA markets has very widespread beneficial effects on liquidity significantly beyond the mortgage pools that are cheapest to deliver. This is also traced to the ability to hedge inventory holding risk. |
| 3. | In a related paper, the acquisition of benchmark status in pre-crisis European sovereign bond markets is examined in Dunne et al. (2007). Benchmarks tend to become liquid as they are the location for discovery of the systematic component of the risk premium (in this case, it is envisaged that the different tranches of SBBS would be benchmarks for credit risks within different categories of the market). |
| 4. | Whether these bounds are sufficient to improve on current trading costs is moot. Even if the costs of hedging with SBBS were to exceed current trading costs in national markets, their use in this way would still be relevant in minimising the extent of any deterioration in trading costs due directly to reductions in the free float as a result of the securitisation. |
| 5. | This also relies, for simplicity, on the assumption that there is symmetry in the positioning of spreads relative to the underlying value. If not, then the proposition that follows applies on average across many trades. |
| 6. | It may also be supposed that this benign outcome would be compromised if the SBBS has a difficult-to-forecast correlation with the bond (i.e., if out of sample hedge ratios turn out to be less efficient than they could have been). This is really a type of operational risk and (assuming forecasts are as efficient as possible ex ante) this also gives rise to mostly idiosyncratic and diversifiable risks. |
| 7. | Bessler et al. (2016) point out that several futures markets for individual sovereign bonds existed pre-EMU and that the alignment of yields during the years of the Great Moderation was largely responsible for the disappearance of all but the German Bund futures. The Great Financial Crisis and the Sovereign Debt Crisis in Europe ultimately led to the reintroduction of futures on Italian BTPs and French OATs. Futures on Spanish Bonos only reappeared in 2015. Naik and Yadav (2003) examine the use of futures to hedge interest rate risk (undesirable duration) in sovereign bond portfolios of dealers and they find support for the propositions about hedging behaviour by Froot and Stein (1998). |
| 8. | For example, Naik and Yadav (2003) strongly reject the notion that dealers benefit from their information about orderflow even in the relatively concentrated UK Gilts market. |
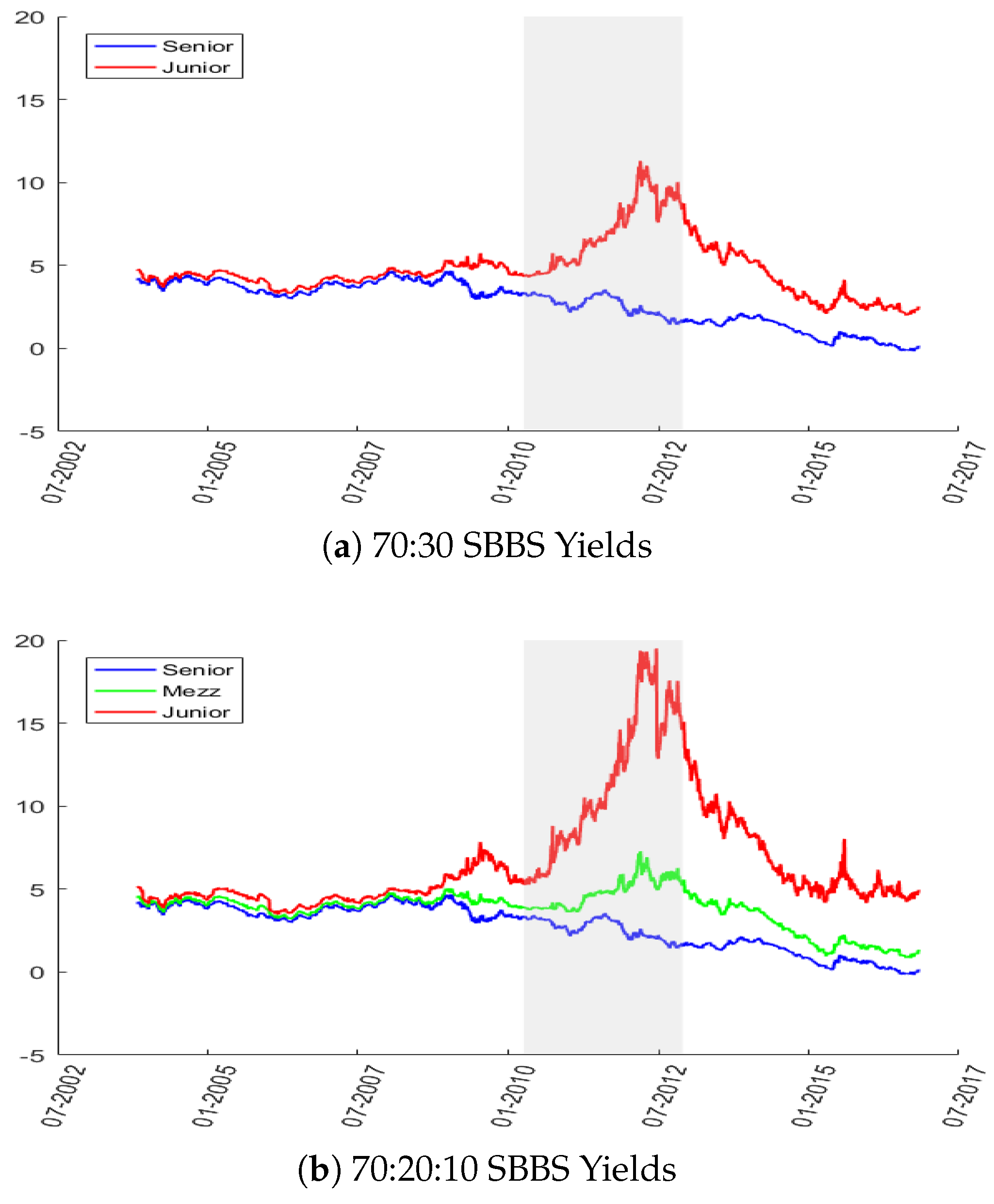
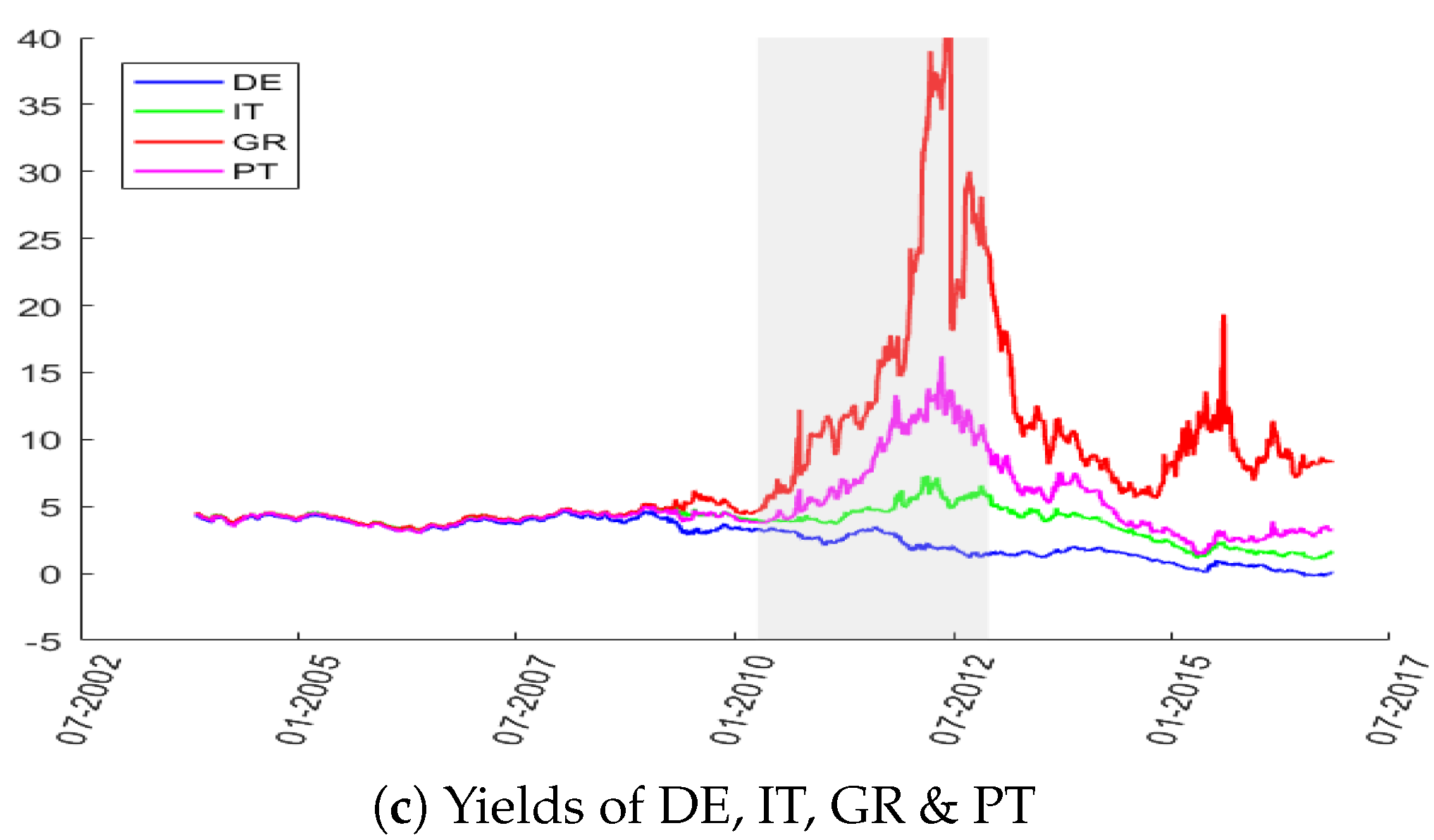
| 9. | The implied risk premium (i.e., yield above the risk-free rate) reflects the risk aversion of the representative market investor on any given day and, hence, may exceed the expected loss anticipated by a risk-neutral investor. This degree of risk aversion enters the simulation and is consequently also reflected consistently in the resulting estimated yields of senior, mezzanine and junior SBBS. |
| 10. | A similar analysis employing dynamic conditional correlation methods, compiling hedge ratios using conditional variances and covariances in line with the relations presented in Appendix A, did not in fact lead to significantly different hedge effectiveness ratios. In addition, the combined use of the methods of Gibson et al. (2017) and a stochastic volatility modelling approach designed to address the presence of isolated outliers, due to Chan and Grant (2016), also failed to change the conclusions drawn from the more straightforward application of a rolling linear regression approach. These alternative methods may however lead to improvements when used at higher frequency with regular updating. Extending the analysis to such a frequency is beyond the scope or needs of the present study. |
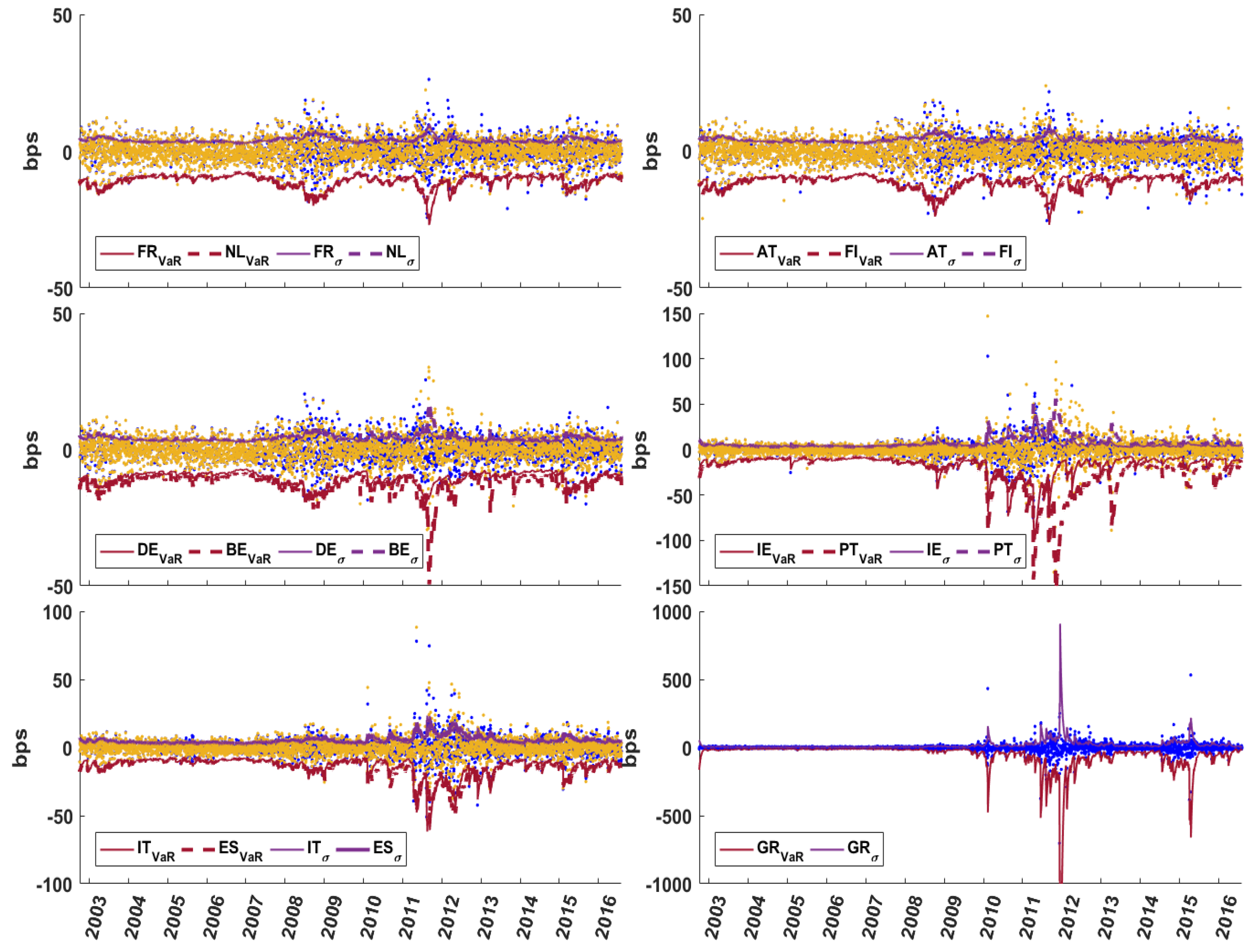
| 11. | The cases of Austria (AT) and Finland (FI) are not shown above but are quite similar to the case of NL. |
| 12. | The weights used in the analysis are related to the size of the individual sovereign float relative to that of the total of 11 sovereigns in the euro area market (weights are provided in the notes for Table 4). |
| 13. | It has been shown by Baranova et al. (2017) that recent tightening of capital and leverage requirements of financial intermediaries has damaged liquidity provision during calm markets’ conditions, but it has helped to protect liquidity during crises’ circumstances. Getting the balance right is therefore crucial. |

| 1 SBBS | 2-SBBS | 3-SBBS | |||||
| Hedge = | Snr | Mezz | Jnr | Snr-Mezz | Snr-Jnr | Mezz-Jnr | Snr-Mezz-Jnr |
| AT(i) | −62 | −61 | −35 | −67 | −70 | −50 | −72 |
| AT(ii) | −73 | −72 | −35 | −77 | −82 | −57 | −84 |
| BE(i) | −65 | −63 | −36 | −72 | −75 | −52 | −77 |
| BE(ii) | −71 | −70 | −37 | −76 | −80 | −58 | −83 |
| DE(i) | −79 | −78 | −32 | −84 | −84 | −46 | −87 |
| DE(ii) | −85 | −81 | −31 | −86 | −88 | −49 | −89 |
| ES(i) | −55 | −55 | −36 | −62 | −66 | −53 | −69 |
| ES(ii) | −62 | −61 | −36 | −69 | −73 | −58 | −75 |
| FI(i) | −70 | −69 | −35 | −72 | −75 | −46 | −76 |
| FI(ii) | −79 | −77 | −36 | −81 | −84 | −53 | −84 |
| FR(i) | −72 | −71 | −37 | −78 | −80 | −53 | −83 |
| FR(ii) | −76 | −75 | −37 | −81 | −84 | −59 | −88 |
| GR(i) | −36 | −33 | −27 | −46 | −51 | −49 | −55 |
| GR(ii) | −46 | −44 | −33 | −60 | −60 | −58 | −67 |
| IE(i) | −42 | −40 | −26 | −47 | −51 | −39 | −52 |
| IE(ii) | −66 | −62 | −33 | −70 | −72 | −52 | −72 |
| IT(i) | −50 | −47 | −35 | −63 | −65 | −59 | −72 |
| IT(ii) | −56 | −50 | −37 | −69 | −70 | −64 | −77 |
| NL(i) | −69 | −68 | −37 | −75 | −78 | −54 | −81 |
| NL(ii) | −77 | −75 | −36 | −80 | −83 | −58 | −86 |
| PT(i) | −50 | −48 | −34 | −59 | −63 | −54 | −67 |
| PT(ii) | −62 | −60 | −38 | −69 | −73 | −61 | −77 |
| 1 SBBS | 2-SBBS | 3-SBBS | |||||
| Hedge = | Snr | Mezz | Jnr | Snr-Mezz | Snr-Jnr | Mezz-Jnr | Snr-Mezz-Jnr |
| AT(i) | −24 | −11 | 0 | −32 | −16 | 4 | −26 |
| AT(ii) | −32 | −19 | −2 | −41 | −39 | −5 | −41 |
| BE(i) | −3 | −4 | −2 | −27 | 10 | −16 | −20 |
| BE(ii) | −2 | −2 | 0 | −27 | −10 | −17 | −29 |
| DE(i) | −68 | 0 | 7 | −72 | −67 | 4 | −71 |
| DE(ii) | −69 | 4 | 5 | −73 | −69 | −5 | −73 |
| ES(i) | 1 | 10 | 1 | −33 | 10 | −31 | −28 |
| ES(ii) | −3 | 15 | 5 | −29 | −13 | −34 | −35 |
| FI(i) | −52 | −7 | 3 | −52 | −49 | 6 | −47 |
| FI(ii) | −54 | −4 | 2 | −54 | −54 | 4 | −55 |
| FR(i) | −23 | −12 | 0 | −35 | −15 | 0 | −31 |
| FR(ii) | −30 | −12 | 2 | −38 | −32 | 2 | −38 |
| GR(i) | 0 | 1 | 0 | 0 | −15 | −15 | −17 |
| GR(ii) | −4 | 13 | 11 | 2 | 26 | 28 | 23 |
| IE(i) | 2 | 7 | 2 | −3 | 1 | −2 | 1 |
| IE(ii) | −1 | 6 | 3 | −5 | −8 | −7 | −6 |
| IT(i) | 0 | 10 | 1 | −44 | 18 | −39 | −37 |
| IT(ii) | 2 | 13 | 3 | −40 | −9 | −43 | −44 |
| NL(i) | −49 | −9 | 2 | −48 | −46 | 7 | −43 |
| NL(ii) | −53 | −6 | 5 | −52 | −52 | 3 | −51 |
| PT(i) | 1 | 5 | 1 | −1 | 1 | −2 | 0 |
| PT(ii) | 1 | 2 | 1 | −5 | −10 | −8 | −9 |
| 1 SBBS | 2-SBBS | 3-SBBS | |||||
| Hedge = | Snr | Mezz | Jnr | Snr-Mezz | Snr-Jnr | Mezz-Jnr | Snr-Mezz-Jnr |
| AT(i) | −45 | −22 | 0 | −47 | −49 | −10 | −49 |
| AT(ii) | −51 | −25 | 0 | −53 | −57 | −14 | −56 |
| BE(i) | −44 | −26 | −2 | −48 | −53 | −13 | −52 |
| BE(ii) | −50 | −28 | −3 | −53 | −57 | −15 | −57 |
| DE(i) | −73 | −13 | 4 | −74 | −73 | −8 | −75 |
| DE(ii) | −72 | −10 | 4 | −73 | −73 | −7 | −74 |
| ES(i) | −2 | 2 | −3 | −32 | −26 | −42 | −43 |
| ES(ii) | −4 | −6 | −4 | −29 | −28 | −41 | −43 |
| FI(i) | −52 | −16 | 1 | −53 | −55 | −9 | −55 |
| FI(ii) | −59 | −18 | 1 | −60 | −62 | −11 | −62 |
| FR(i) | −50 | −27 | −2 | −55 | −58 | −15 | −59 |
| FR(ii) | −54 | −28 | −2 | −56 | −61 | −16 | −61 |
| GR(i) | 0 | 7 | 7 | −8 | −8 | 2 | −8 |
| GR(ii) | 5 | 6 | 8 | 3 | 11 | 17 | 12 |
| IE(i) | −10 | −11 | −3 | −21 | −22 | −19 | −27 |
| IE(ii) | −14 | −17 | −5 | −29 | −28 | −23 | −35 |
| IT(i) | −3 | 1 | −4 | −41 | −28 | −50 | −53 |
| IT(ii) | −7 | −5 | −4 | −41 | −34 | −52 | −54 |
| NL(i) | −53 | −18 | 1 | −54 | −56 | −9 | −56 |
| NL(ii) | −60 | −18 | 0 | −61 | −64 | −11 | −65 |
| PT(i) | 0 | 2 | 0 | −13 | −15 | −21 | −21 |
| PT(ii) | −1 | 2 | 0 | −13 | −17 | −25 | −26 |
| Pre-Crisis | Sov Debt Crisis | Recovery | ||||
| Weighting = | Equal | Size | Equal | Size | Equal | Size |
| 10-Year | ||||||
| EA(Hedged)/EA (i) | −68 | −71 | 0 | −3 | −12 | −24 |
| EA(Hedged)/EA (ii) | −73 | −74 | −4 | −7 | −18 | −31 |
| EA(Hedged)/DE (i) | −71 | −73 | 8 | −1 | −4 | −24 |
| EA(Hedged)/DE (ii) | −76 | −76 | −2 | −14 | −11 | −29 |
| 5-Year | ||||||
| EA(Hedged)/EA (i) | −47 | −43 | 1 | −1 | −17 | −15 |
| EA(Hedged)/EA (ii) | −46 | −44 | 0 | 1 | −20 | −21 |
| EA(Hedged)/DE (i) | −50 | −46 | 52 | 25 | −21 | −3 |
| EA(Hedged)/DE (ii) | −50 | −46 | 34 | 12 | −27 | −10 |
| 2-Year | ||||||
| EA(Hedged)/EA (i) | −62 | −64 | 1 | −1 | −5 | −5 |
| EA(Hedged)/EA (ii) | −69 | −72 | 1 | 4 | −7 | −10 |
| EA(Hedged)/DE (i) | −70 | −67 | 252 | 81 | 21 | 47 |
| EA(Hedged)/DE (ii) | −76 | −74 | 186 | 64 | 15 | 38 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dunne, P.G. Positive Liquidity Spillovers from Sovereign Bond-Backed Securities. J. Risk Financial Manag. 2019, 12, 58. https://doi.org/10.3390/jrfm12020058
Dunne PG. Positive Liquidity Spillovers from Sovereign Bond-Backed Securities. Journal of Risk and Financial Management. 2019; 12(2):58. https://doi.org/10.3390/jrfm12020058
Chicago/Turabian StyleDunne, Peter G. 2019. "Positive Liquidity Spillovers from Sovereign Bond-Backed Securities" Journal of Risk and Financial Management 12, no. 2: 58. https://doi.org/10.3390/jrfm12020058
APA StyleDunne, P. G. (2019). Positive Liquidity Spillovers from Sovereign Bond-Backed Securities. Journal of Risk and Financial Management, 12(2), 58. https://doi.org/10.3390/jrfm12020058





