Instantaneous Volatility Seasonality of High-Frequency Markets in Directional-Change Intrinsic Time
Abstract
:1. Introduction
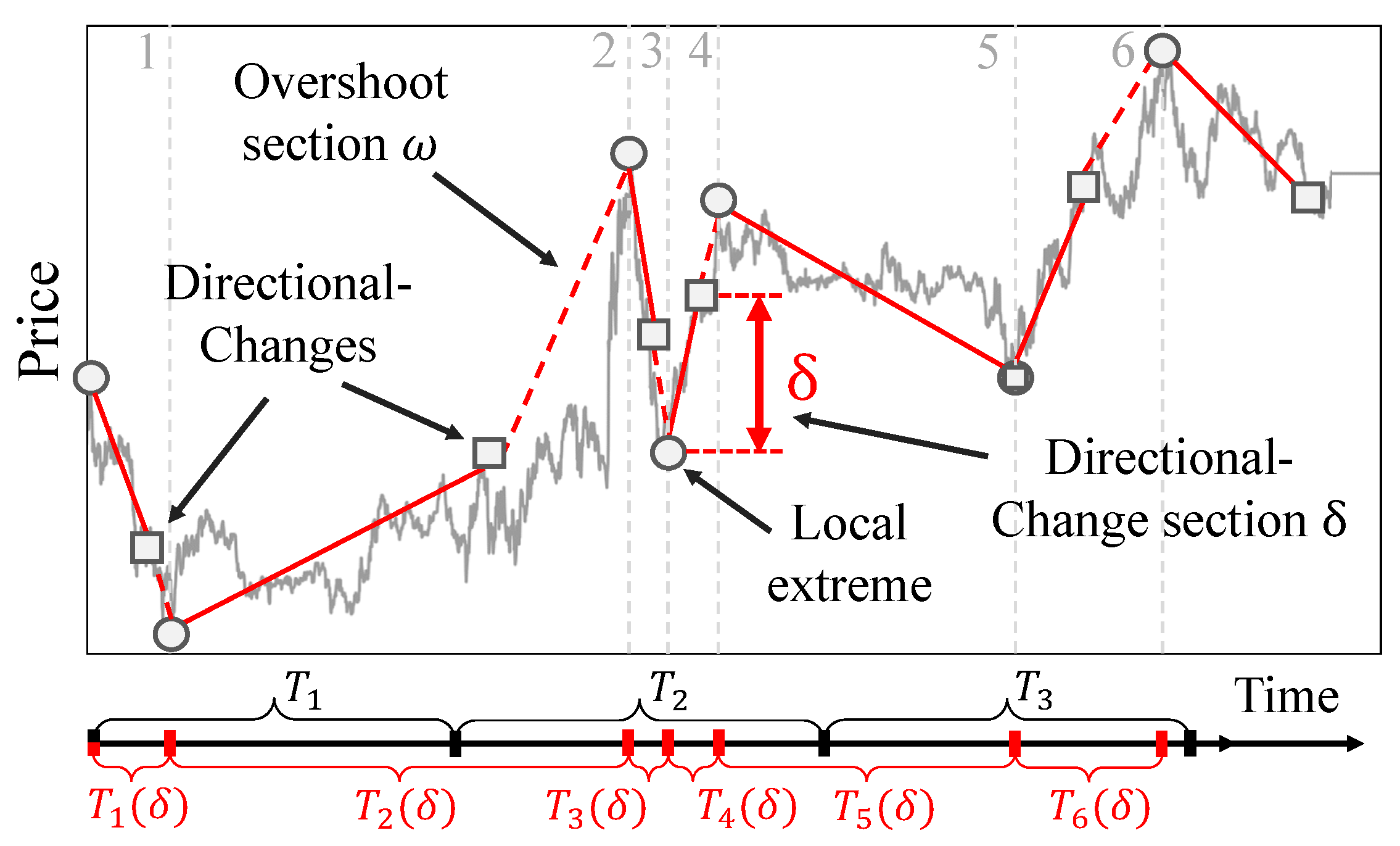
2. Drawdowns and Drawups: An Introduction
3. Directional-Change Intrinsic Time
4. Seasonality
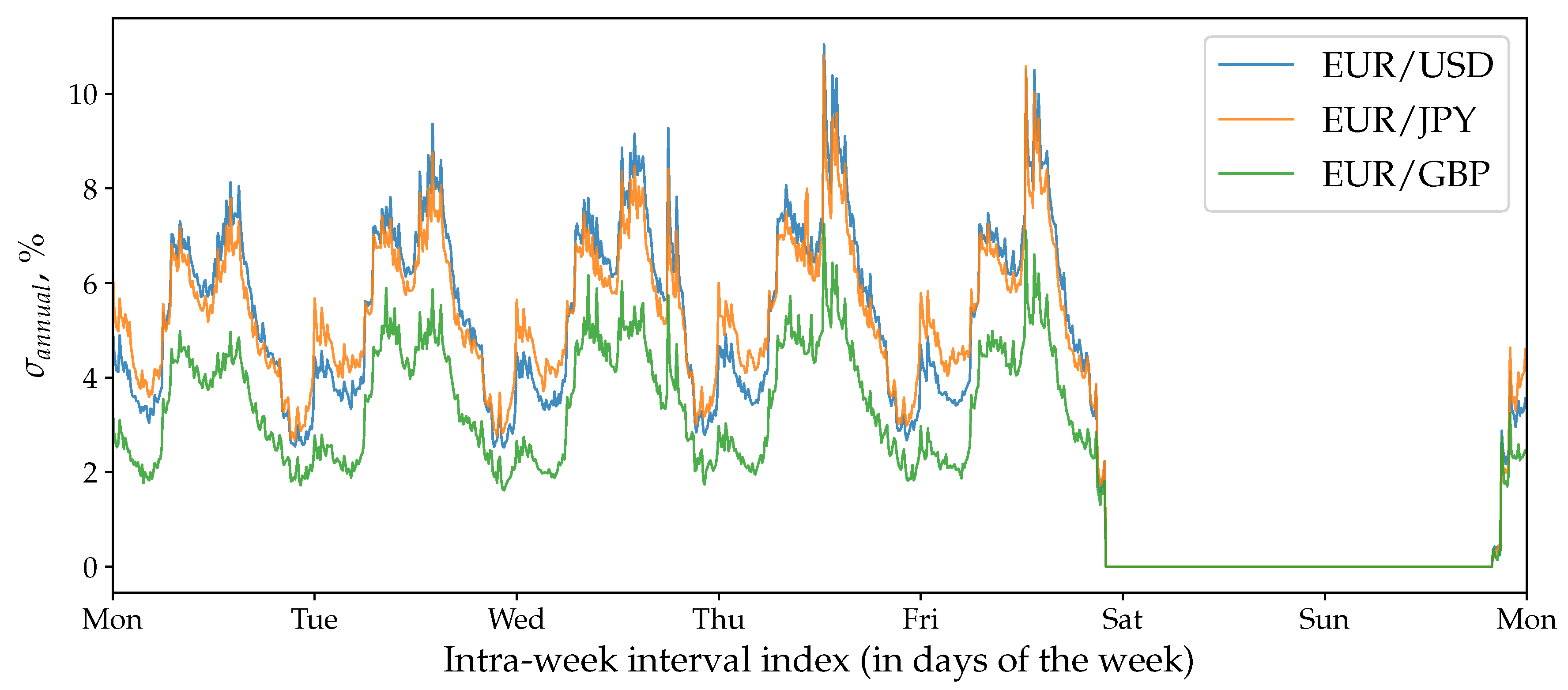
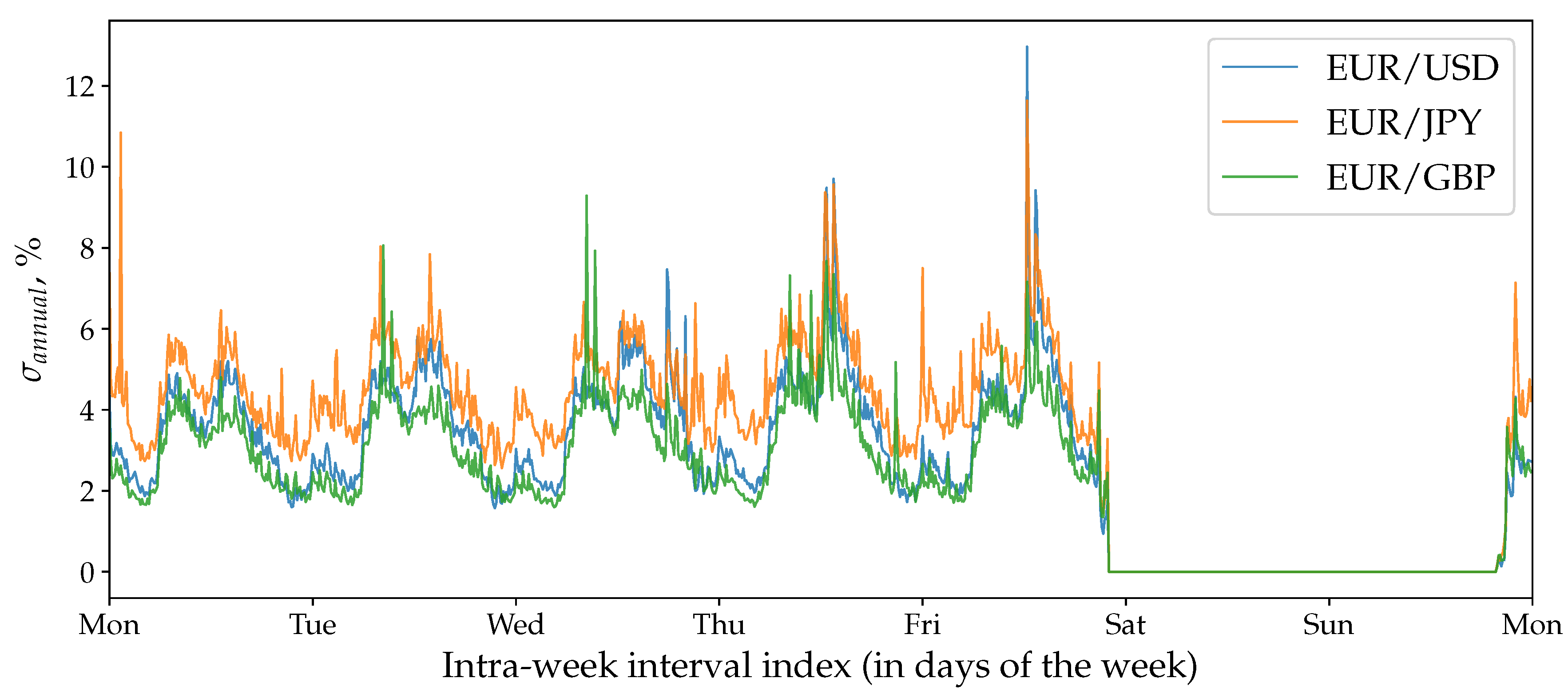
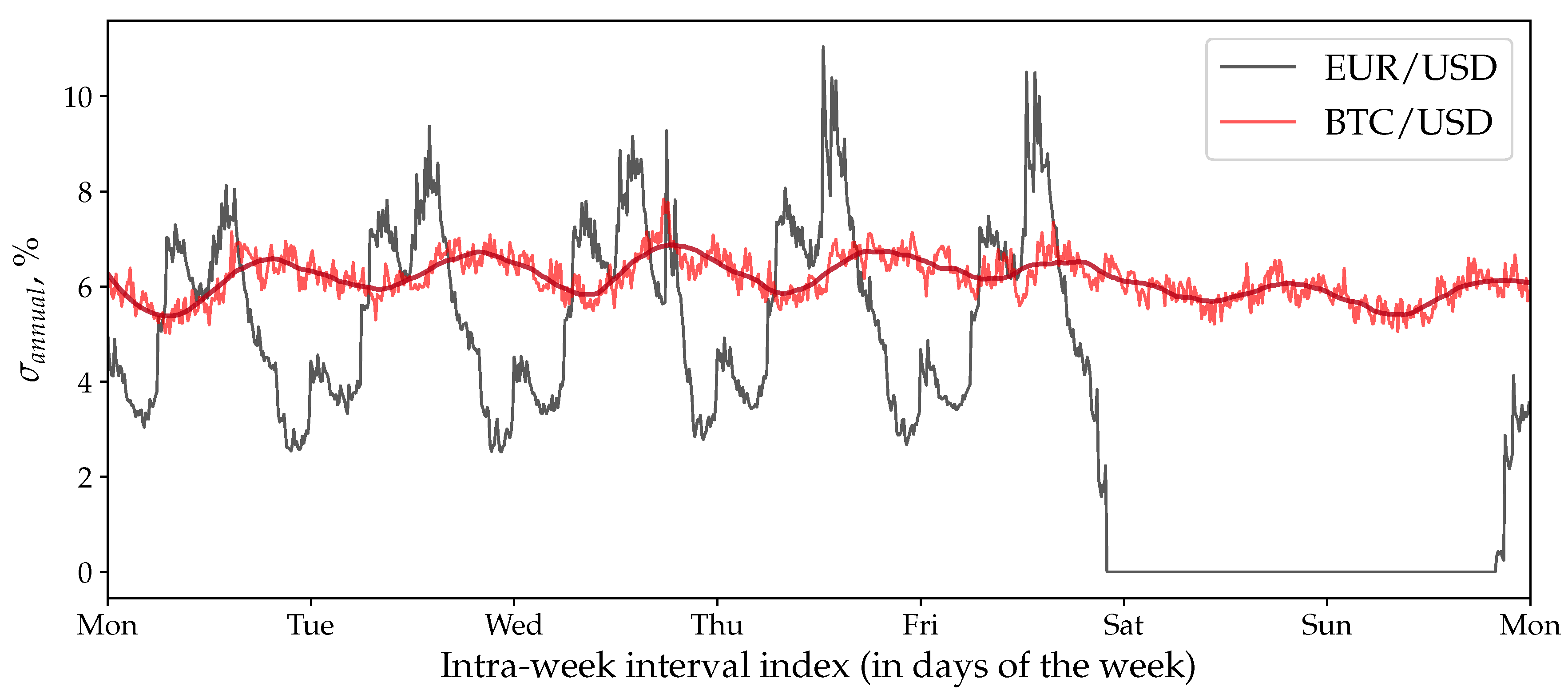
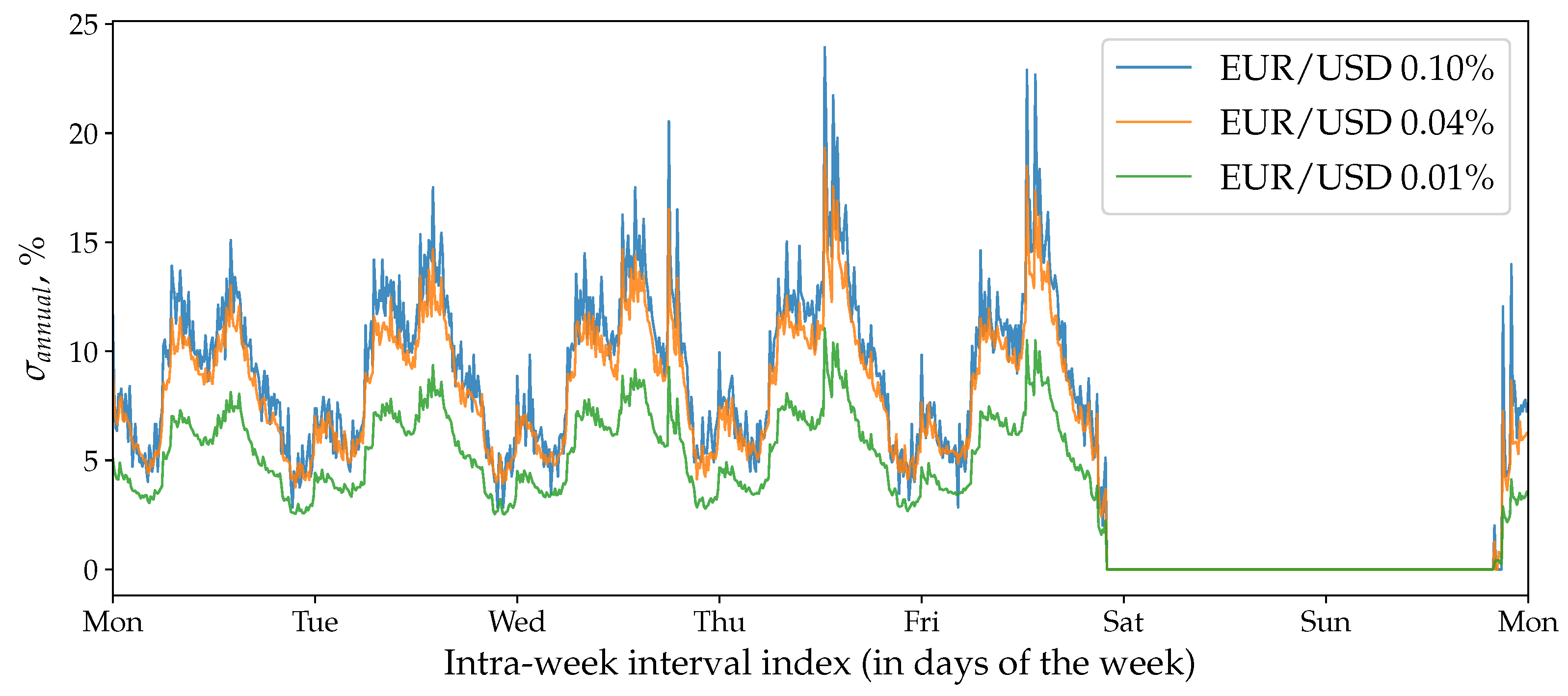
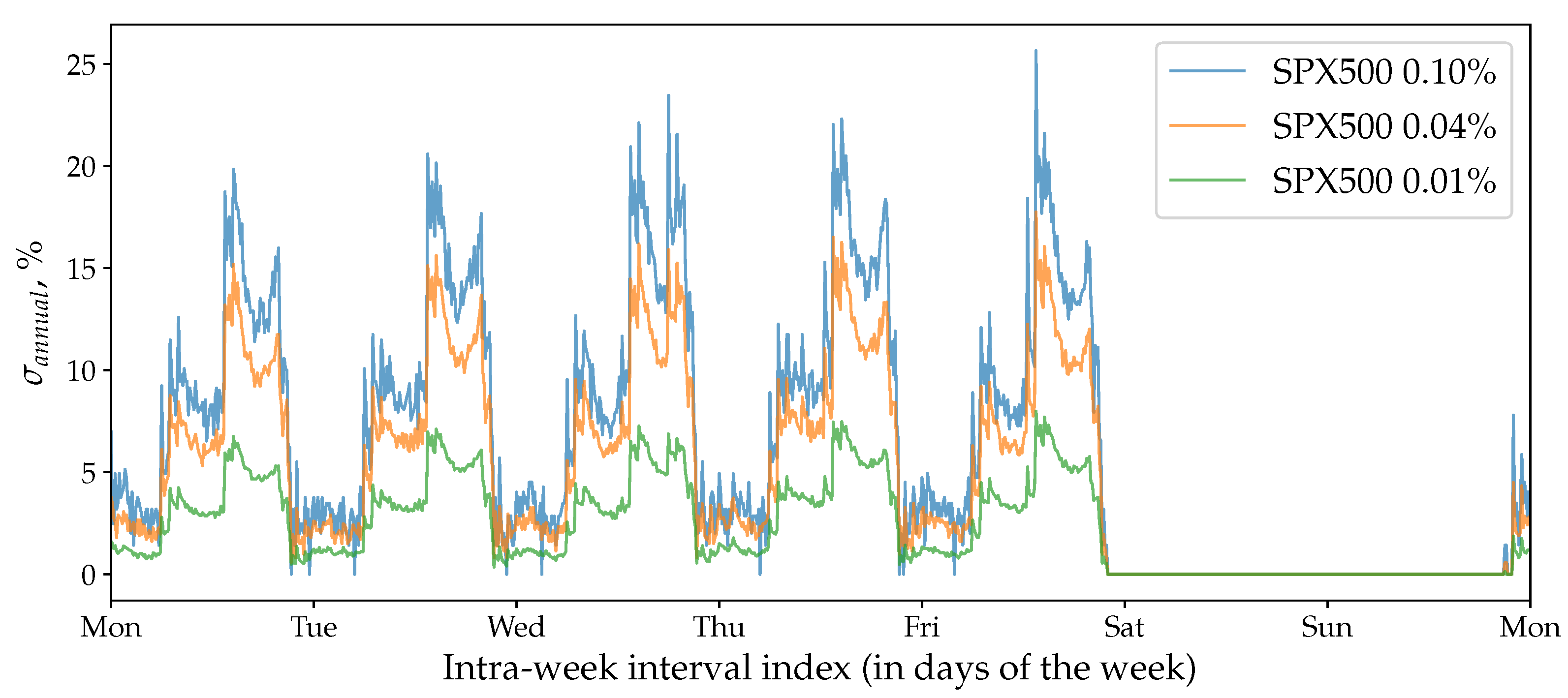
4.1. Traditional Markets
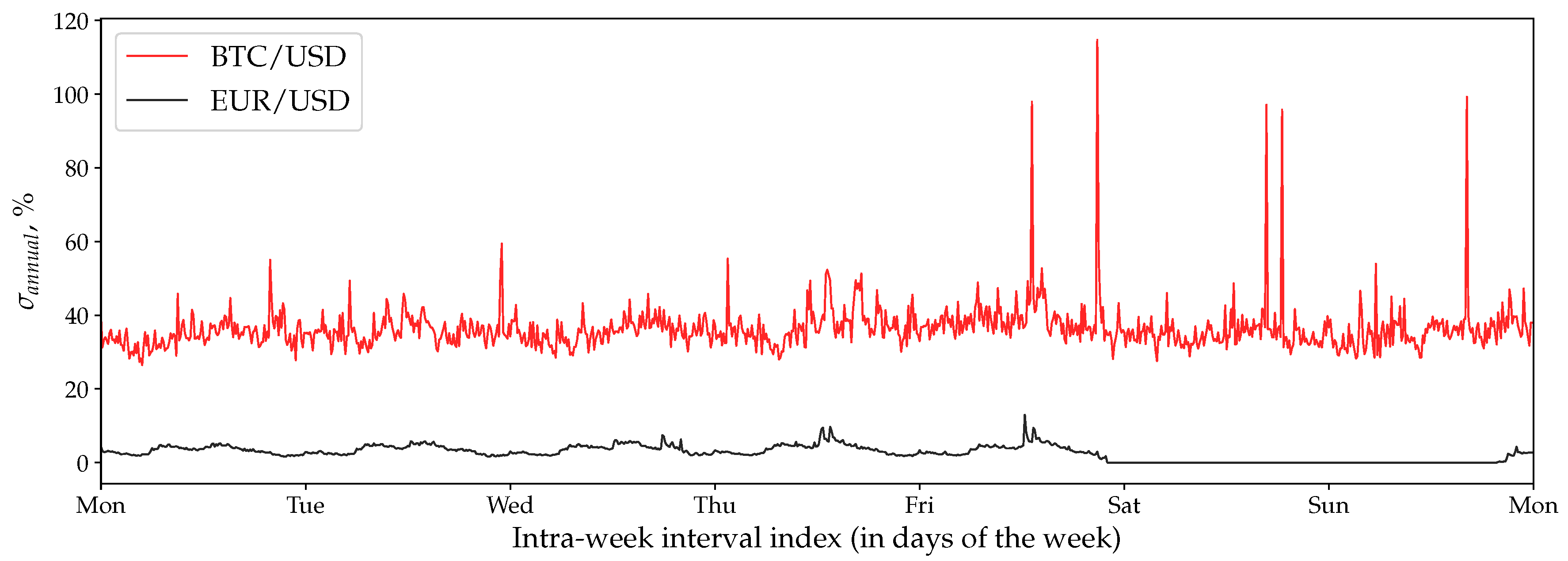
4.2. Bitcoin Seasonality
5. Data
Inner Price
6. Methods
6.1. Waiting Time
6.2. Number of Directional Changes
6.3. Instantaneous Volatility
7. Results
7.1. Number of Directional Changes
7.2. Realised versus Instantaneous Volatility
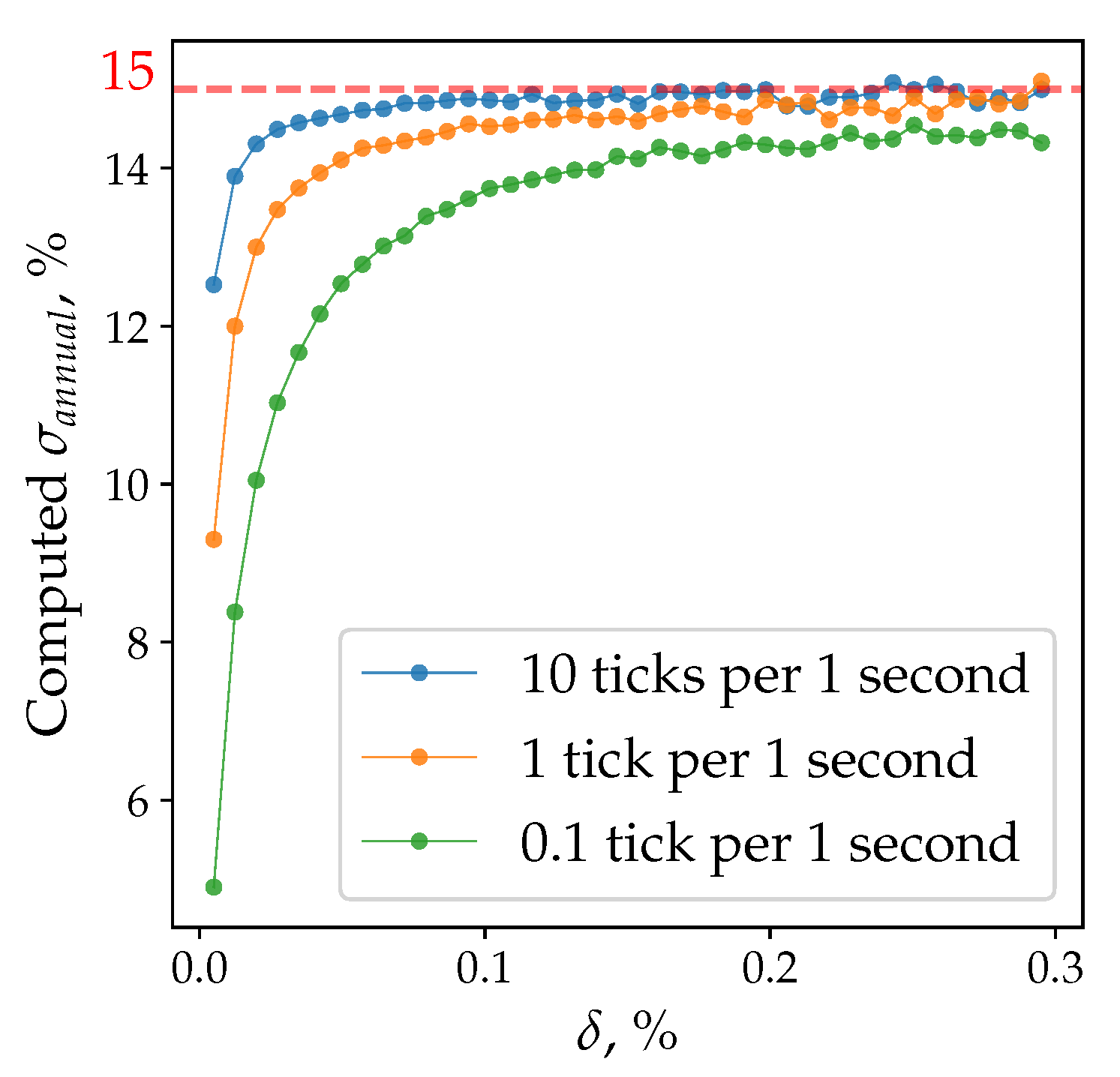
7.3. Discrete Price Effect
7.4. Volatility Seasonality
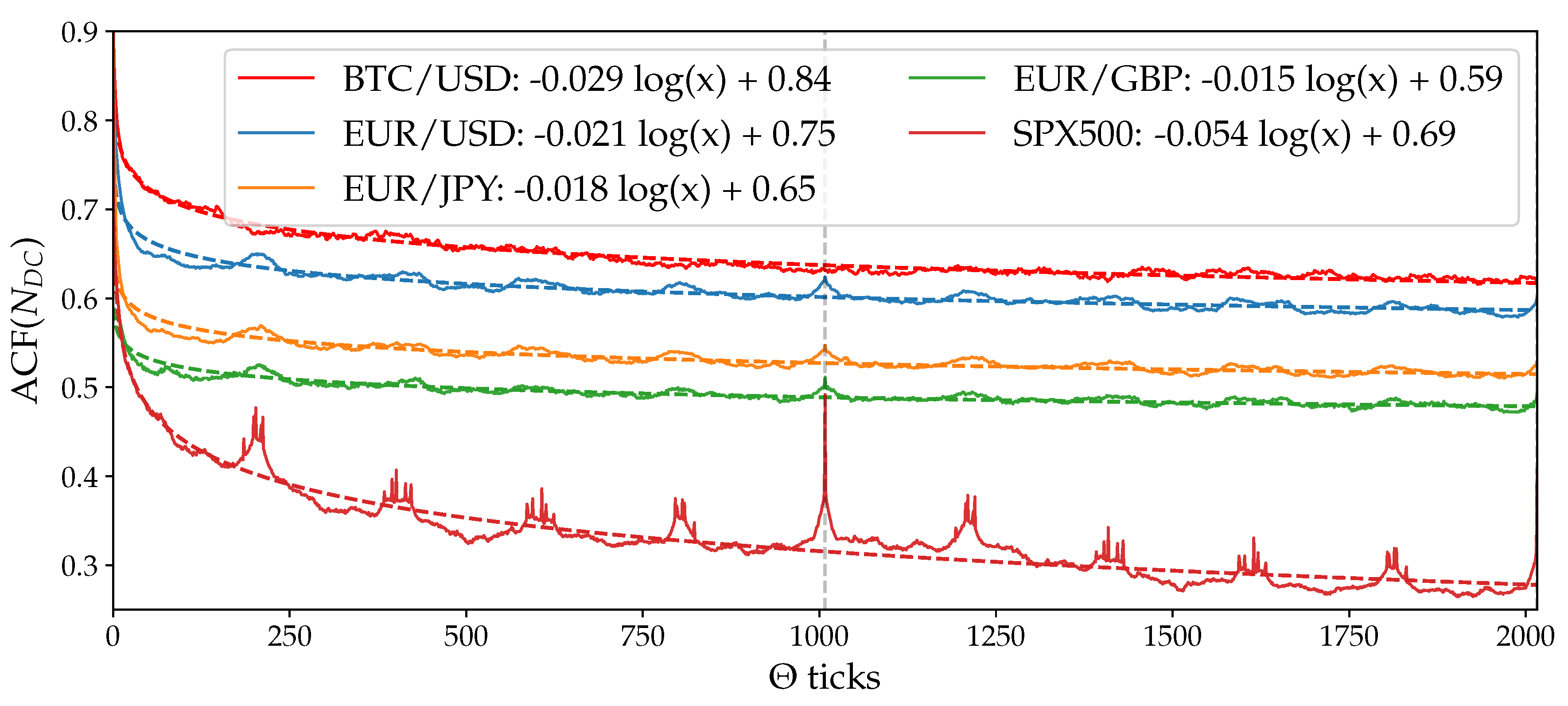
7.5. Volatility Autocorrelation and Theta Time
8. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Daily Seasonality
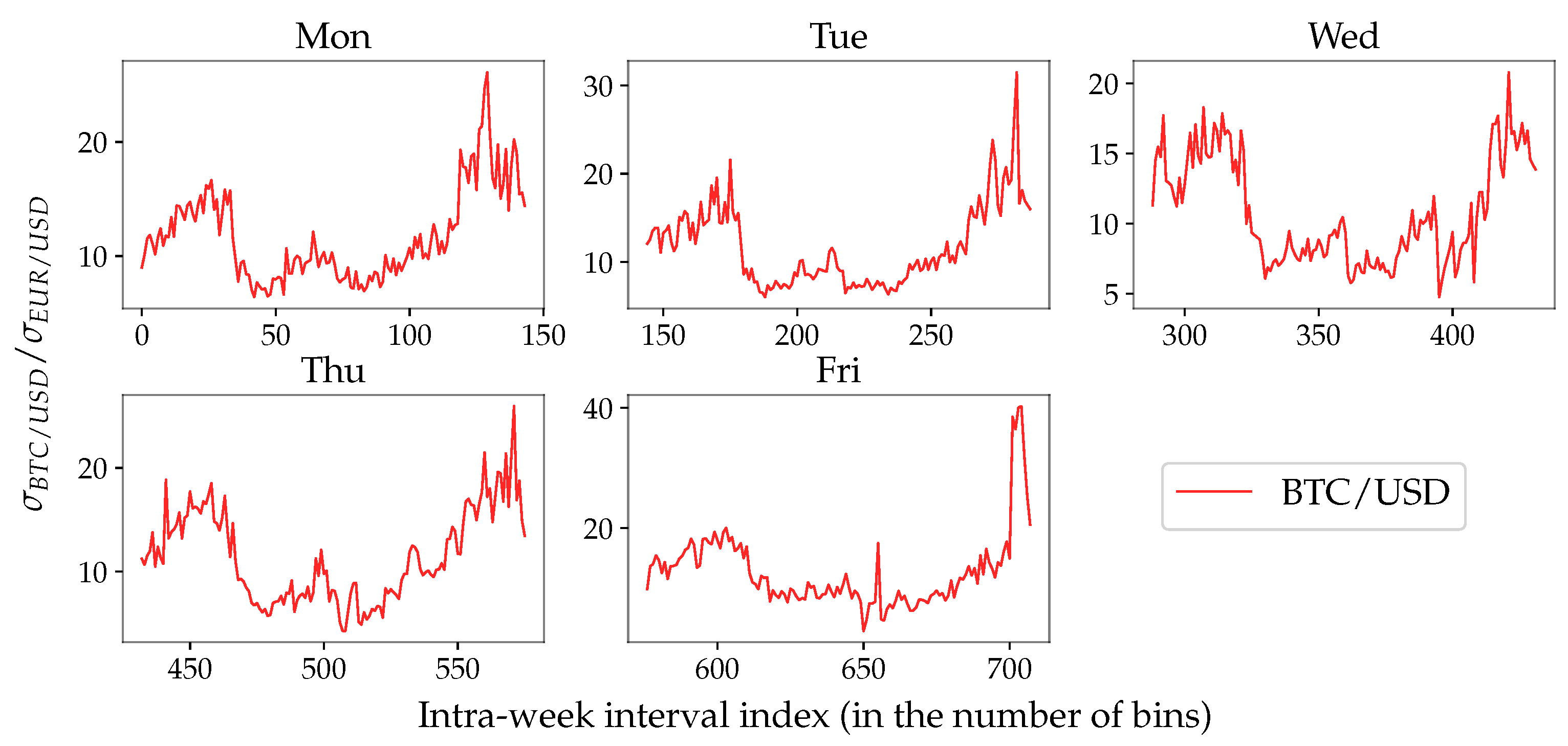

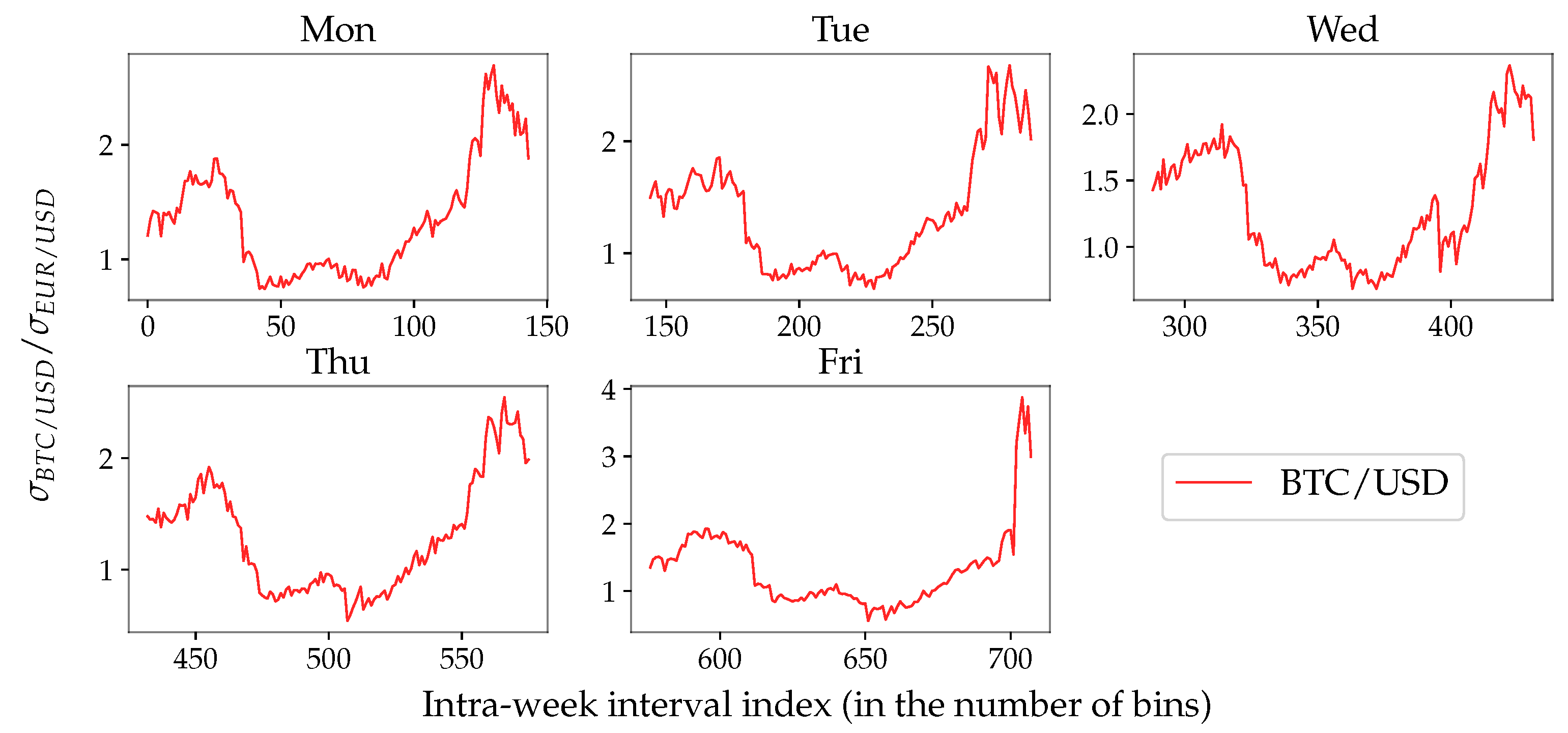

| Monday | EUR/JPY | 1.35 | 0.27 | 1.03 | 0.12 | 1.31 | 2.25 |
| EUR/GBP | 0.89 | 0.1 | 0.64 | 0.04 | 1.39 | 2.50 | |
| BTC/USD | 11.75 | 3.99 | 1.35 | 0.51 | 8.70 | 7.82 | |
| SPX500 | 0.97 | 0.51 | 0.57 | 0.29 | 1.70 | 1.76 | |
| Tuesday | EUR/JPY | 1.35 | 0.23 | 1.02 | 0.11 | 1.32 | 2.09 |
| EUR/GBP | 0.88 | 0.13 | 0.63 | 0.05 | 1.40 | 2.60 | |
| BTC/USD | 11.7 | 4.53 | 1.35 | 0.52 | 8.67 | 8.71 | |
| SPX500 | 0.95 | 0.47 | 0.57 | 0.3 | 1.67 | 1.57 | |
| Wednesday | EUR/JPY | 1.31 | 0.3 | 1.02 | 0.12 | 1.28 | 2.50 |
| EUR/GBP | 0.88 | 0.19 | 0.64 | 0.05 | 1.38 | 3.80 | |
| BTC/USD | 10.83 | 3.74 | 1.29 | 0.46 | 8.40 | 8.13 | |
| SPX500 | 0.93 | 0.42 | 0.53 | 0.26 | 1.75 | 1.62 | |
| Thursday | EUR/JPY | 1.34 | 0.22 | 1.03 | 0.12 | 1.30 | 1.83 |
| EUR/GBP | 0.89 | 0.18 | 0.64 | 0.05 | 1.39 | 3.60 | |
| BTC/USD | 11.42 | 4.42 | 1.29 | 0.5 | 8.85 | 8.84 | |
| SPX500 | 0.93 | 0.49 | 0.57 | 0.28 | 1.63 | 1.75 | |
| Friday | EUR/JPY | 1.35 | 0.28 | 1.03 | 0.12 | 1.31 | 2.33 |
| EUR/GBP | 0.9 | 0.17 | 0.64 | 0.06 | 1.41 | 2.83 | |
| BTC/USD | 11.81 | 4.93 | 1.3 | 0.54 | 9.08 | 9.13 | |
| SPX500 | 0.98 | 0.46 | 0.61 | 0.31 | 1.61 | 1.48 |
References
- Aı, Yacine, and Robert Kimmel. 2007. Maximum likelihood estimation of stochastic volatility models. Journal of Financial Economics 83: 413–52. [Google Scholar]
- Andersen, Torben G., and Jesper Lund. 1997. Estimating continuous-time stochastic volatility models of the short-term interest rate. Journal of Econometrics 77: 343–77. [Google Scholar] [CrossRef]
- Asmussen, Søren, and Hansjörg Albrecher. 2010. Ruin Probabilities. Singapore: World Scientific Publishing Co Pte Ltd. [Google Scholar]
- Bandt, Chstoph, and Faten Shiha. 2007. Order patterns in time series. Journal of Time Series Analysis 28: 646–65. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2002. Econometric analysis of realized volatility and its use in estimating stochastic volatility models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 64: 253–80. [Google Scholar] [CrossRef]
- Begušić, Stjepan, Zvonko Kostanjčar, H. Eugene Stanley, and Boris Podobnik. 2018. Scaling properties of extreme price fluctuations in bitcoin markets. Physica A: Statistical Mechanics and Its Applications 510: 400–6. [Google Scholar] [CrossRef]
- Bessembinder, Hendrik. 1994. Bid-ask spreads in the interbank foreign exchange markets. Journal of Financial Economics 35: 317–48. [Google Scholar] [CrossRef]
- BIS. 2016. Triennial Central Bank Survey: Foreign Exchange Turnover in April 2016. Basel: BIS. [Google Scholar]
- Black, Fischer, and Myron Scholes. 1973. The pricing of options and corporate liabilities. Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef]
- Bollerslev, Tim, and Ian Domowitz. 1993. Trading patterns and prices in the interbank foreign exchange market. The Journal of Finance 48: 1421–43. [Google Scholar] [CrossRef]
- Bollerslev, Tim, and Michael Melvin. 1994. Bid—Ask spreads and volatility in the foreign exchange market: An empirical analysis. Journal of International Economics 36: 355–72. [Google Scholar] [CrossRef]
- Campbell, John Y., Stefano Giglio, Christopher Polk, and Robert Turley. 2018. An intertemporal capm with stochastic volatility. Journal of Financial Economics 128: 207–33. [Google Scholar] [CrossRef]
- Carr, Peter, Hongzhong Zhang, and Olympia Hadjiliadis. 2011. Maximum drawdown insurance. International Journal of Theoretical and Applied Finance 14: 1195–30. [Google Scholar] [CrossRef]
- Chekhlov, Alexei, Stanislav Uryasev, and Michael Zabarankin. 2005. Drawdown measure in portfolio optimization. International Journal of Theoretical and Applied Finance 8: 13–58. [Google Scholar] [CrossRef]
- Cho, D Chinhyung, and Edward W Frees. 1988. Estimating the volatility of discrete stock prices. The Journal of Finance 43: 451–66. [Google Scholar] [CrossRef]
- Cont, Rama. 2001a. Empirical Properties of Asset Returns: Stylized Facts and Statistical Issues. Didcot: Taylor & Francis. [Google Scholar]
- Cont, Rama. 2011b. Statistical modeling of high-frequency financial data. IEEE Signal Processing Magazine 28: 16–25. [Google Scholar] [CrossRef]
- Cotter, John. 2005. Tail behaviour of the euro. Applied Economics 37: 827–40. [Google Scholar] [CrossRef]
- Dacorogna, Michael M., Ulrich A. Müller, Robert J. Nagler, Richard B. Olsen, and Olivier V. Pictet. 1993. A geographical model for the daily and weekly seasonal volatility in the foreign exchange market. Journal of International Money and Finance 12: 413–38. [Google Scholar] [CrossRef]
- Dacorogna, Michel M., Ulrich A. Müller, Olivier V. Pictet, and Casper G. De Vries. 2001. Extremal forex returns in extremely large data sets. Extremes 4: 105–27. [Google Scholar] [CrossRef]
- Dassios, Angelos, and Jia Wei Lim. 2018. An efficient algorithm for simulating the drawdown stopping time and the running maximum of a brownian motion. Methodology and Computing in Applied Probability 20: 189–204. [Google Scholar] [CrossRef]
- De Bondt, Werner F. M., and Richard H. Thaler. 1987. Further evidence on investor overreaction and stock market seasonality. The Journal of Finance 42: 557–81. [Google Scholar] [CrossRef]
- de Vries, Jon Erik, and Halvor Aarhus Aalborg. 2017. What Can Explain the Price, Volatility and Traded Volume of Bitcoin? Master’s dissertation, University of Stavanger, Stavanger, Norway. [Google Scholar]
- Dyhrberg, Anne Haubo. 2016. Bitcoin, gold and the dollar—A garch volatility analysis. Finance Research Letters 16: 85–92. [Google Scholar] [CrossRef]
- Dyhrberg, Anne H., Sean Foley, and Jiri Svec. 2018. How investible is bitcoin? Analyzing the liquidity and transaction costs of bitcoin markets. Economics Letters 171: 140–3. [Google Scholar] [CrossRef]
- Eross, Andrea, Frank Mcgroarty, Andrew Urquhart, and Simon Wolfe. 2017. The Intraday Dynamics of Bitcoin. SSRN Elecronic Journal. Available online: https://dx.doi.org/10.2139/ssrn.3013699 (accessed on 12 September 2018).
- Fang, Lily, Chunmei Lin, and Yuping Shao. 2018. School holidays and stock market seasonality. Financial Management 47: 131–57. [Google Scholar] [CrossRef]
- French, Kenneth R., and Richard Roll. 1986. Stock return variances: The arrival of information and the reaction of traders. Journal of Financial Economics 17: 5–26. [Google Scholar] [CrossRef]
- Gençay, Ramazan, Michel Dacorogna, Ulrich A. Muller, Olivier Pictet, and Richard Olsen. 2001. An Introduction to High-Frequency Finance. Amsterdam: Elsevier. [Google Scholar]
- Glattfelder, James B., Alexandre Dupuis, and Richard B. Olsen. 2011. Patterns in high-frequency fx data: Discovery of 12 empirical scaling laws. Quantitative Finance 11: 599–614. [Google Scholar] [CrossRef]
- Golub, Anton, Gregor Chliamovitch, Alexandre Dupuis, and Bastien Chopard. 2014. Multi-Scale Representation of High Frequency Market Liquidity. Available online: http://dx.doi.org/10.2139/ssrn.2393428 (accessed on 11 September 2018).
- Golub, Anton, James Glattfelder, and Richard B. Olsen. 2017. The Alpha Engine: Designing an Automated Trading Algorithm. Available online: http://dx.doi.org/10.2139/ssrn.2951348 (accessed on 11 September 2018).
- Gottlieb, Gary, and Avner Kalay. 1985. Implications of the discreteness of observed stock prices. The Journal of Finance 40: 135–53. [Google Scholar] [CrossRef]
- Grossman, Sanford J., and Zhongquan Zhou. 1993. Optimal investment strategies for controlling drawdowns. Mathematical Finance 3: 241–76. [Google Scholar] [CrossRef]
- Guillaume, Dominique M., Michel M. Dacorogna, Rakhal R. Davé, Ulrich A. Müller, Richard B. Olsen, and Olivier V. Pictet. 1997. From the bird’s eye to the microscope: A survey of new stylized facts of the intra-daily foreign exchange markets. Finance and Stochastics 1: 95–129. [Google Scholar] [CrossRef]
- Gultekin, Mustafa N., and N. Bulent Gultekin. 1983. Stock market seasonality: International evidence. Journal of Financial Economics 12: 469–81. [Google Scholar] [CrossRef]
- Hadjiliadis, Olympia, and Jan Večeř. 2006. Drawdowns preceding rallies in the brownian motion model. Quantitative Finance 6: 403–9. [Google Scholar] [CrossRef]
- Haferkorn, Martin, and Josué Manuel Quintana Diaz. 2014. Seasonality and interconnectivity within cryptocurrencies-an analysis on the basis of bitcoin, litecoin and namecoin. In International Workshop on Enterprise Applications and Services in the Finance Industry. Cham: Springer, pp. 106–20. [Google Scholar]
- Harris, Larry. 2003. Trading and Exchanges: Market Microstructure for Practitioners. Oxford: Oxford University Press. [Google Scholar]
- Hartmann, Philipp. 1999. Trading volumes and transaction costs in the foreign exchange market: Evidence from daily dollar–yen spot data. Journal of Banking & Finance 23: 801–24. [Google Scholar]
- Hasbrouck, Joel. 2018. High-frequency quoting: Short-term volatility in bids and offers. Journal of Financial and Quantitative Analysis 53: 613–41. [Google Scholar] [CrossRef]
- Ito, Takatoshi, and Yuko Hashimoto. 2006. Intraday seasonality in activities of the foreign exchange markets: Evidence from the electronic broking system. Journal of the Japanese and International Economies 20: 637–64. [Google Scholar] [CrossRef]
- Jondeau, Eric, and Michael Rockinger. 2003. Testing for differences in the tails of stock-market returns. Journal of Empirical Finance 10: 559–81. [Google Scholar] [CrossRef]
- Kaya, Orçun, Jan Schildbach, and Deutsche Bank Ag. 2016. High-frequency trading. Reaching the Limits, Automated Trader Magazine 41: 23–27. [Google Scholar]
- Keim, Donald B. 1983. Size-related anomalies and stock return seasonality: Further empirical evidence. Journal of Financial Economics 12: 13–32. [Google Scholar] [CrossRef]
- Kelly, John L., Jr. 2011. A new interpretation of information rate. In The Kelly Capital Growth Investment Criterion: Theory and Practice. Singapore: World Scientific, pp. 25–34. [Google Scholar]
- Koning, Nico, Daniel T. Cassidy, and Rachid Ouyed. 2018. Extended model of stock price behaviour. Journal of Mathematical Finance 8: 1. [Google Scholar] [CrossRef]
- Landriault, David, Bin Li, and Hongzhong Zhang. 2015. On the frequency of drawdowns for brownian motion processes. Journal of Applied Probability 52: 191–208. [Google Scholar] [CrossRef]
- Liu, Ruiping, Zhichao Shao, Guodong Wei, and Wei Wang. 2017. Garch model with fat-tailed distributions and bitcoin exchange rate returns. Journal of Accounting, Business and Finance Research 1: 71–75. [Google Scholar] [CrossRef]
- Lundberg, Filip. 1909. Uber die theorie der ruck-versicherung. In Trans VI International Congress Actuaries. pp. 877–955. Available online: https://ci.nii.ac.jp/naid/10004541215/ (accessed on 10 December 2018).
- Mancino, Maria Elvira, Maria Cristina Recchioni, and Simona Sanfelici. 2017. Estimation of instantaneous volatility. In Fourier-Malliavin Volatility Estimation. Cham: Springer, pp. 31–47. [Google Scholar]
- Menkhoff, Lukas, Lucio Sarno, Maik Schmeling, and Andreas Schrimpf. 2012. Carry trades and global foreign exchange volatility. The Journal of Finance 67: 681–718. [Google Scholar] [CrossRef]
- Mijatović, Aleksandar, and Martijn R. Pistorius. 2012. On the drawdown of completely asymmetric lévy processes. Stochastic Processes and their Applications 122: 3812–36. [Google Scholar] [CrossRef]
- Müller, Ulrich A., Michel M. Dacorogna, Rakhal D. Davé, Richard B. Olsen, Olivier V. Pictet, and Jacob E. von Weizsäcker. 1997. Volatilities of different time resolutions—Analyzing the dynamics of market components. Journal of Empirical Finance 4: 213–39. [Google Scholar] [CrossRef]
- Müller, Ulrich A., Michel M. Dacorogna, Richard B. Olsen, Olivier V. Pictet, Matthias Schwarz, and Claude Morgenegg. 1990. Statistical study of foreign exchange rates, empirical evidence of a price change scaling law, and intraday analysis. Journal of Banking & Finance 14: 1189–208. [Google Scholar]
- Nakamoto, Satoshi. 2008. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: http://bitcoin.org/bitcoin.pdf (accessed on 23 October 2018).
- Osborne, Maury F. M. 1959. Brownian motion in the stock market. Operations Research 7: 145–73. [Google Scholar] [CrossRef]
- Ponsford, Matthew P. 2015. A comparative analysis of bitcoin and other decentralised virtual currencies: Legal regulation in the people’s republic of china, canada, and the united states. HKJ Legal Studies 9: 29. [Google Scholar]
- Pospisil, Libor, Jan Vecer, and Olympia Hadjiliadis. 2009. Formulas for stopped diffusion processes with stopping times based on drawdowns and drawups. Stochastic Processes and their Applications 119: 2563–78. [Google Scholar] [CrossRef]
- Rachev, Svetlozar T., Christian Menn, and Frank J. Fabozzi. 2005. Fat-Tailed and Skewed Asset Return Distributions: Implications for Risk Management, Portfolio Selection, and Option Pricing. Hoboken: John Wiley & Sons, vol. 139. [Google Scholar]
- Rolski, Tomasz, Hanspeter Schmidli, Volker Schmidt, and Jozef L. Teugels. 2009. Stochastic Processes for Insurance and Finance. Hoboken: John Wiley & Sons, vol. 505. [Google Scholar]
- Roy, Souvik, and P. Venkateswaran. 2014. Online payment system using steganography and visual cryptography. Paper presented at 2014 IEEE Students’ Conference on Electrical, Electronics and Computer Science, Bhopal, India, March 1–2; Lakes-Bhopal: IEEE, pp. 1–5. [Google Scholar]
- Rozeff, Michael S., and William R. Kinney Jr. 1976. Capital market seasonality: The case of stock returns. Journal of Financial Economics 3: 379–402. [Google Scholar] [CrossRef]
- Sapuric, Svetlana, and Angelika Kokkinaki. 2014. Bitcoin is volatile! Isn’t that right? Paper presented at International Conference on Business Information Systems, Larnaca, Cyprus, May 22–23; Cham: Springer, pp. 255–65. [Google Scholar]
- Schuhmacher, Frank, and Martin Eling. 2011. Sufficient conditions for expected utility to imply drawdown-based performance rankings. Journal of Banking & Finance 35: 2311–18. [Google Scholar]
- Seif, Mostafa, Paul Docherty, and Abul Shamsuddin. 2017. Seasonal anomalies in advanced emerging stock markets. The Quarterly Review of Economics and Finance 66: 169–81. [Google Scholar] [CrossRef]
- Shintate, Takuya, and Lukáš Pichl. 2019. Trend prediction classification for high frequency bitcoin time series with deep learning. Journal of Risk and Financial Management 12: 17. [Google Scholar] [CrossRef]
- Taylor, Howard M. 1975. A stopped brownian motion formula. The Annals of Probability 3: 234–46. [Google Scholar] [CrossRef]
- Zarowin, Paul. 1990. Size, seasonality, and stock market overreaction. Journal of Financial and Quantitative Analysis 25: 113–25. [Google Scholar] [CrossRef]
- Zhang, Hongzhong. 2015. Occupation times, drawdowns, and drawups for one-dimensional regular diffusions. Advances in Applied Probability 47: 210–30. [Google Scholar] [CrossRef]
- Zhang, Hongzhong, and Olympia Hadjiliadis. 2012. Drawdowns and the speed of market crash. Methodology and Computing in Applied Probability 14: 739–52. [Google Scholar] [CrossRef]
| 1. | A basic polynomial functional relationship where a change in input results in a proportional change in output. |
| 2. | A growing list of records containing information on the ownership of all existing Bitcoins. |
| 3. | Information on all cryptocurrencies and trading venues can be found at Coinmarketcap.com. |
| 4. | At the moment of writing the paper, Wall Street and other big financial hubs are considering trading cryptocurrencies, which will potentially result in the higher segregation level. |
| 5. | According to the Bank for International Settlements the daily average FX trading volume in April 2016 was $5.1 trillion (BIS 2016) when the highest registered volume in the crypto market is to the date only $45.8 billion (https://coinmarketcap.com/charts/). |
| 6. | |
| 7. | |
| 8. | |
| 9. | The expression is known in the insurance industry as “adjustment coefficient” or “the Lundberg exponent” (Asmussen and Albrecher 2010). It finds its application in the ruin theory dating back to 1909 (Lundberg 1909). It is also described as the optimal information theoretical betting size called Kelly Criterion (Kelly 2011). |
| 10. | The work Cho and Frees (1988) is particularly interesting due to the analysis the authors did to compare volatilities computed by “natural” and “temporal” estimators. The latter employs time intervals measured between consequent and alternating price moves of fixed relative size and thus is very close to the approach presented in the current paper. |
| 11. | The type of mathematical analysis applied to identify patterns or cycles in a normalised time series data. |
| 12. | It had a minimum at $230 per Bitcoin, temporary maximum at about $20,000, and then a drop to $6000. |
| 13. | The evidence that the distribution of returns approaches the normal one measured over longer timescales. |
| 14. | According to the Table 2. |

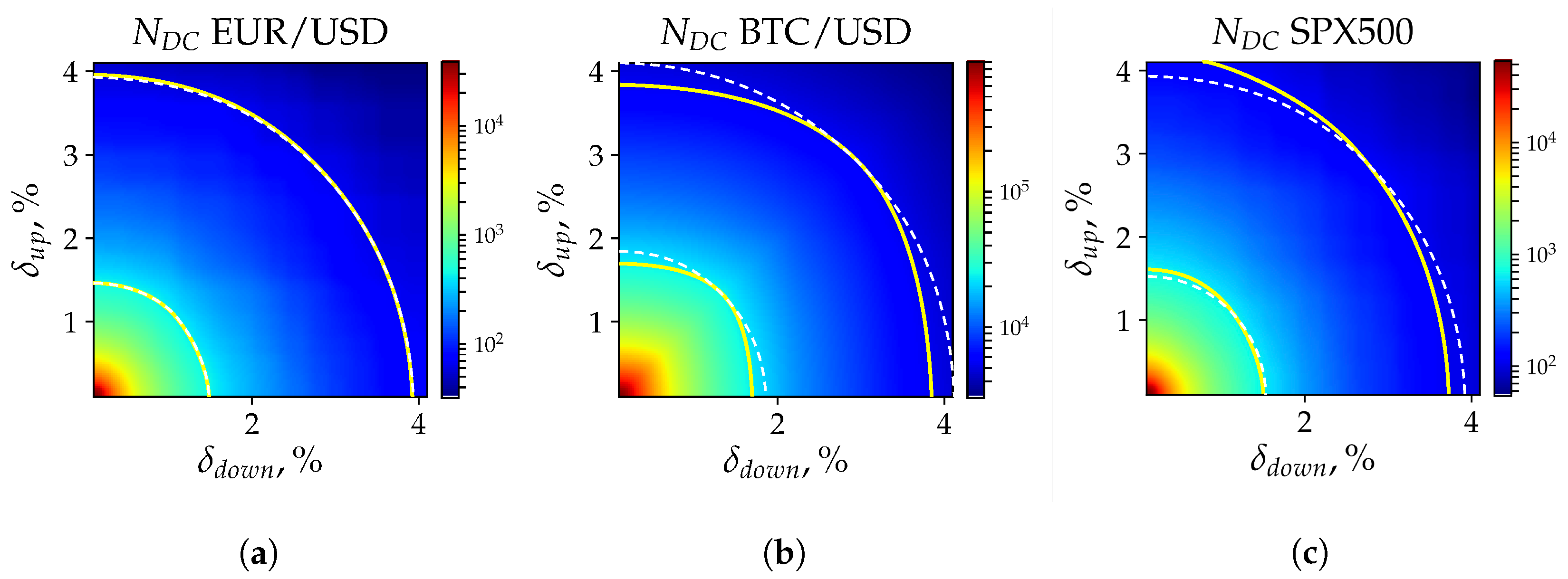



| , % | , % | |||||
|---|---|---|---|---|---|---|
| 1 | 10 | 1.028 | 0.968 | 2.54 × 10−5 | 1.019 | 2.53 × 10−6 |
| 20 | 1.009 | 0.989 | 2.78 × 10−6 | 1.012 | 3.32 × 10−7 | |
| 30 | 1.001 | 0.995 | 8.79 × 10−7 | 1.033 | 9.58 × 10−8 | |
| 6 | 10 | 1.021 | 0.971 | 2.29 × 10−5 | 1.043 | 2.59 × 10−6 |
| 20 | 1.005 | 0.993 | 2.94 × 10−6 | 1.019 | 3.29 × 10−7 | |
| 30 | 0.987 | 1.011 | 8.84 × 10−7 | 1.034 | 9.98 × 10−8 | |
| 11 | 10 | 1.029 | 0.968 | 2.20 × 10−5 | 1.011 | 2.78 × 10−6 |
| 20 | 0.994 | 1.006 | 2.72 × 10−6 | 0.997 | 3.30 × 10−7 | |
| 30 | 0.986 | 1.014 | 8.82 × 10−7 | 1.017 | 1.02 × 10−7 |
| Name | ||||||
|---|---|---|---|---|---|---|
| EUR/USD | 9.72 | 0.03 | 7.53 | 1.38 | 1.29 | 0.02 |
| EUR/JPY | 11.93 | 0.12 | 8.55 | 2.07 | 1.40 | 0.06 |
| EUR/GBP | 8.04 | 0.23 | 5.81 | 1.43 | 1.38 | 0.16 |
| BTC/USD | 84.76 | 8.67 | 80.87 | 22.21 | 1.05 | 0.39 |
| SPX500 | 13.19 | 0.67 | 6.63 | 3.24 | 1.99 | 0.21 |
| Name | ||
|---|---|---|
| BTC/USD | −0.029 | 0.84 |
| EUR/USD | −0.021 | 0.75 |
| EUR/JPY | −0.018 | 0.65 |
| EUR/GBP | −0.015 | 0.59 |
| SPX500 | −0.054 | 0.69 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrov, V.; Golub, A.; Olsen, R. Instantaneous Volatility Seasonality of High-Frequency Markets in Directional-Change Intrinsic Time. J. Risk Financial Manag. 2019, 12, 54. https://doi.org/10.3390/jrfm12020054
Petrov V, Golub A, Olsen R. Instantaneous Volatility Seasonality of High-Frequency Markets in Directional-Change Intrinsic Time. Journal of Risk and Financial Management. 2019; 12(2):54. https://doi.org/10.3390/jrfm12020054
Chicago/Turabian StylePetrov, Vladimir, Anton Golub, and Richard Olsen. 2019. "Instantaneous Volatility Seasonality of High-Frequency Markets in Directional-Change Intrinsic Time" Journal of Risk and Financial Management 12, no. 2: 54. https://doi.org/10.3390/jrfm12020054
APA StylePetrov, V., Golub, A., & Olsen, R. (2019). Instantaneous Volatility Seasonality of High-Frequency Markets in Directional-Change Intrinsic Time. Journal of Risk and Financial Management, 12(2), 54. https://doi.org/10.3390/jrfm12020054






