Sentiment-Induced Bubbles in the Cryptocurrency Market
Abstract
:1. Introduction
2. Cryptocurrencies and a Sentiment Index
2.1. StockTwits Data
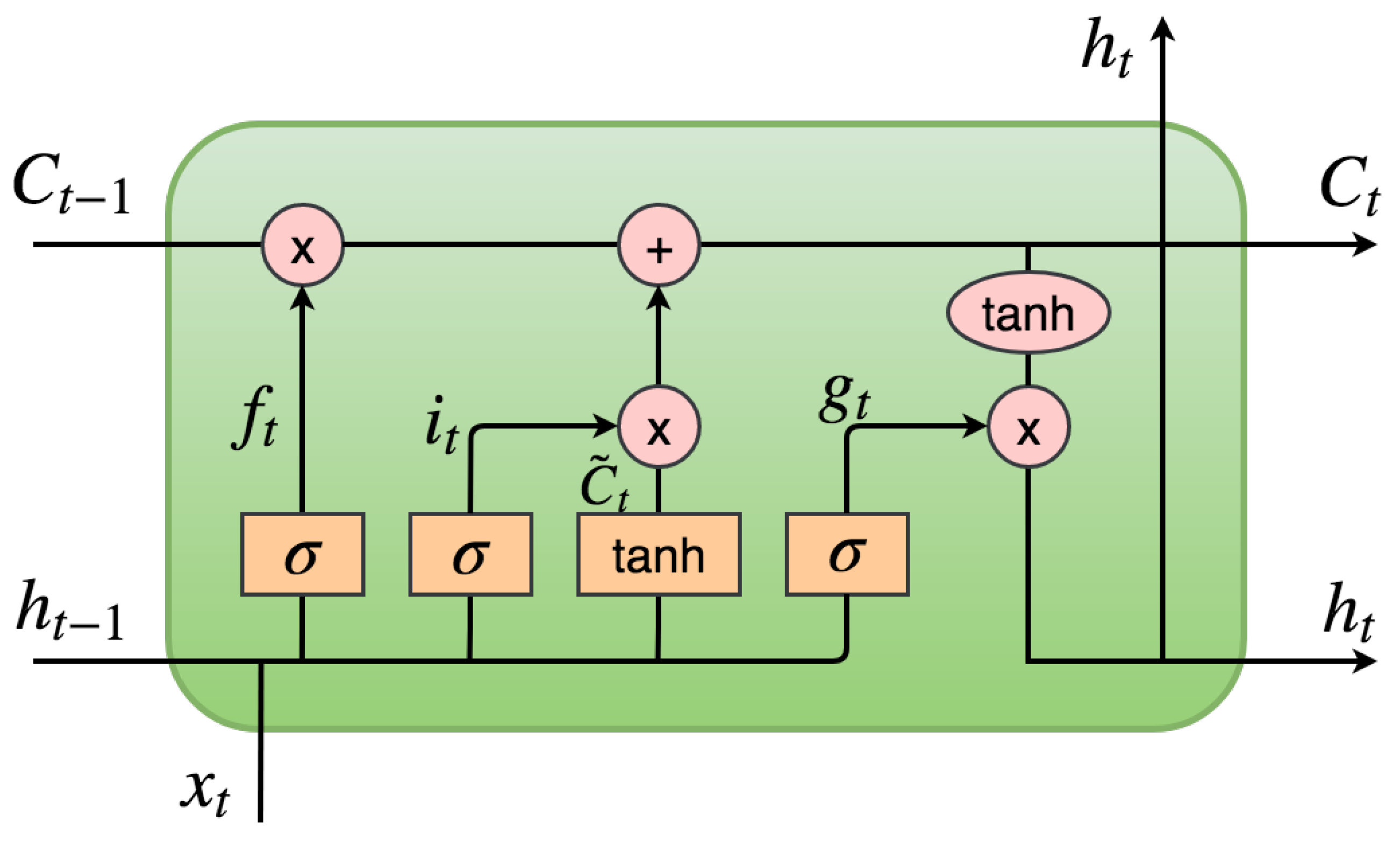
2.2. Sentiment Prediction
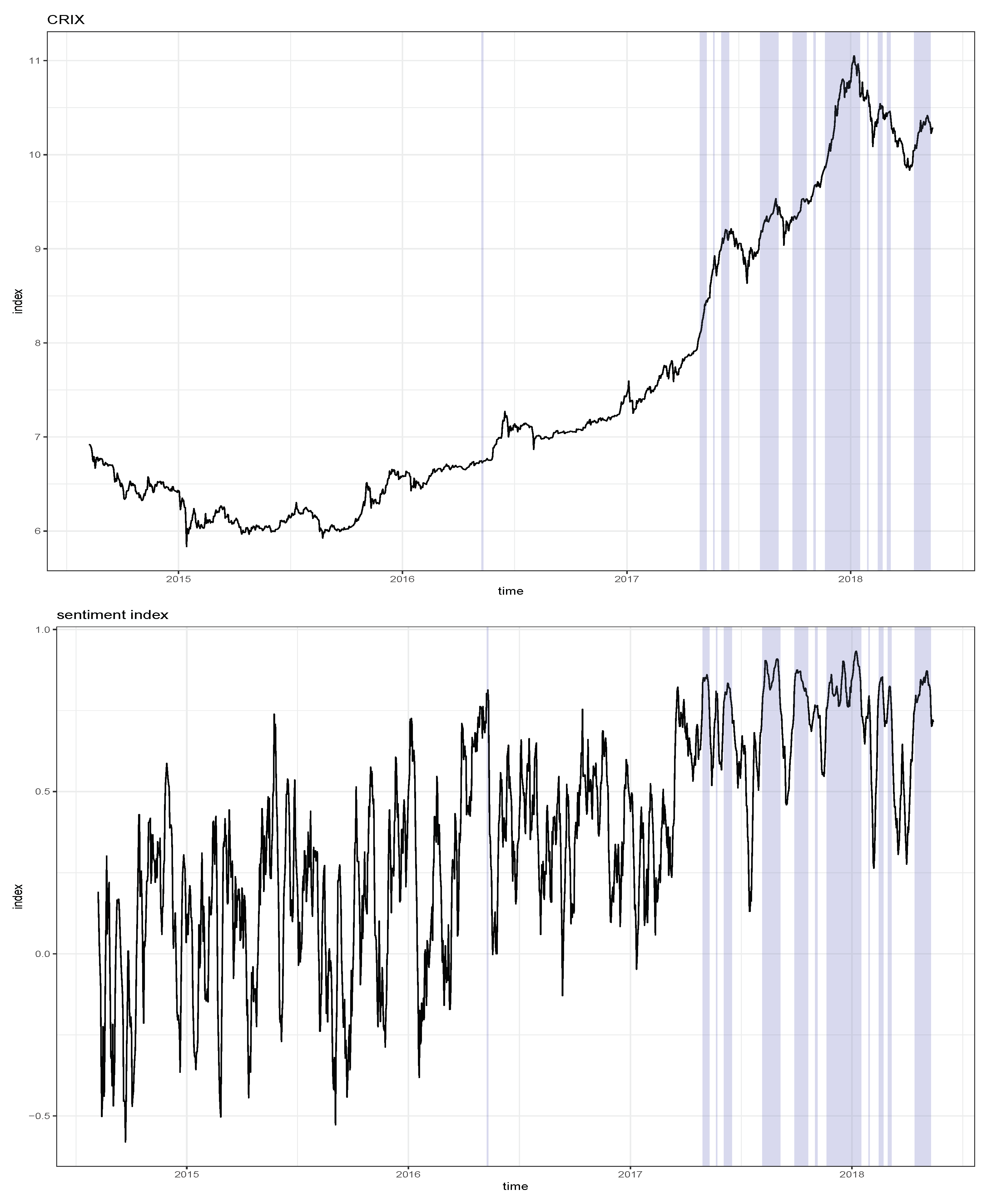
2.3. Sentiment Index and Cryptocurrency Index
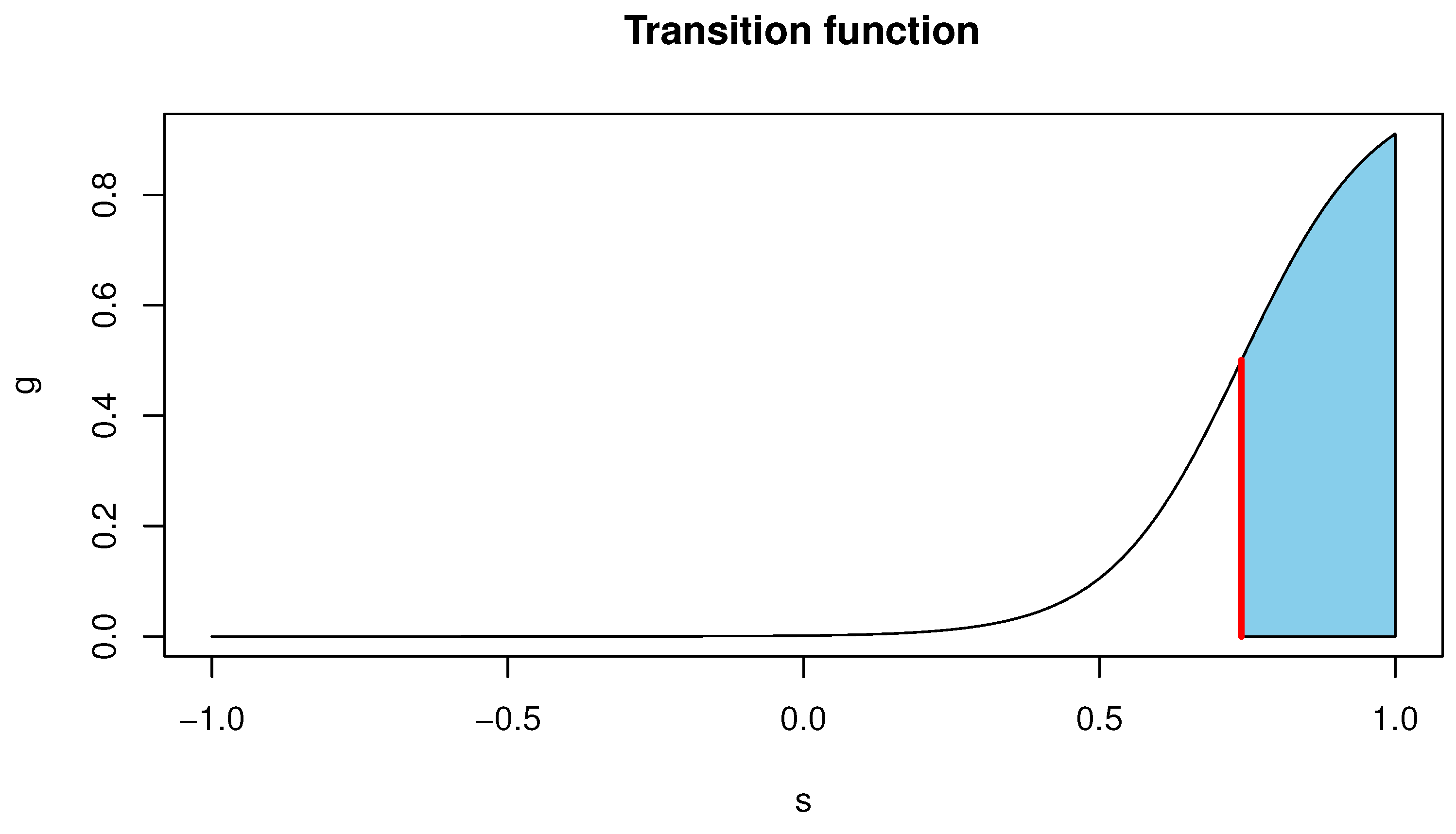
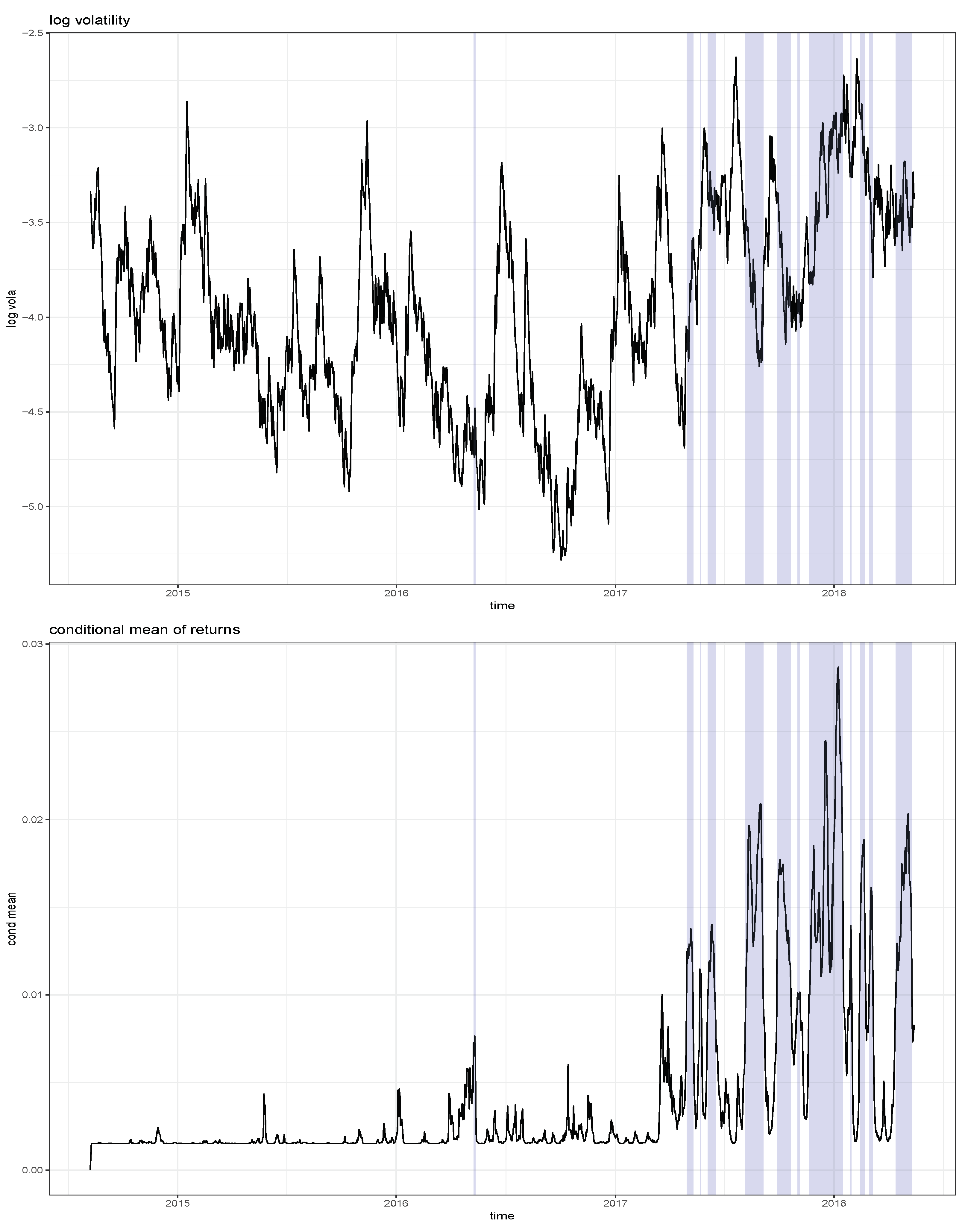
3. A Sentiment-Based Model for Locally Explosive Crypto Prices
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Avery, Christopher N., Judith A. Chevalier, and Richard J. Zeckhauser. 2016. The “caps” prediction system and stock market returns. Review of Finance 20: 1363–81. [Google Scholar] [CrossRef]
- Bauwens, Luc, Christian M Hafner, and Sébastien Laurent. 2012. Volatility models. In Handbook of Volatility Models and Their Applications. Edited by Luc Bauwens, Christian M. Hafner and Sébastien Laurent. New York: John Wiley& Sons, chp. 1. pp. 1–50. [Google Scholar]
- Black, Fischer. 1976. Studies in stock price volatility changes. In Proceedings of the American Statistical Association, Business and Economic Statistics Section. Washington, DC: American Statistical Association, pp. 177–81. [Google Scholar]
- Cheah, Eng-Tuck, and John Fry. 2015. Speculative bubbles in bitcoin markets? An empirical investigation into the fundamental value of bitcoin. Economics Letters 130: 32–36. [Google Scholar] [CrossRef]
- Chen, Cathy Y. H., Romeo Després, Li Guo, and Thomas Renault. 2018. What Makes Cryptocurrencies Special? Investor Sentiment and Price Predictability in the Absence of Fundamental Value, Discussion Paper Sfb 649. Unpublished work.
- Cheung, Adrian, Eduardo Roca, and Jen-Je Su. 2015. Crypto-currency bubbles: An application of the Phillips-Shi-Yu (2013) methodology on Mt.Gox bitcoin prices. Applied Economics 47: 2348–58. [Google Scholar] [CrossRef]
- Christie, Andrew A. 1982. The stochastic behavior of common stock variances: Value, leverage and interest rate effects. Journal of Financial Economics 10: 407–32. [Google Scholar] [CrossRef]
- Conrad, Christian, Anessa Custovic, and Eric Ghysels. 2018. Long- and short-term cryptocurrency volatility components: A GARCH-MIDAS analysis. Journal of Risk and Financial Management 11: 23. [Google Scholar] [CrossRef]
- Corbet, Shaen, Brian Lucey, and Larisa Yarovaya. 2018. Datestamping the bitcoin and ethereum bubbles. Finance Research Letters 26: 81–88. [Google Scholar] [CrossRef]
- Creal, Drew, Siem Jan Koopman, and André Lucas. 2011. A dynamic multivariate heavy-tailed model for time-varying volatilities and correlations. Journal of Business & Economic Statistics 29: 552–63. [Google Scholar]
- De Long, J. Bradford, Andrei Shleifer, Lawrence H. Summers, and Robert J. Waldmann. 1990. Positive feedback investment strategies and destabilizing rational speculation. The Journal of Finance 45: 379–95. [Google Scholar] [CrossRef]
- Fry, John, and Eng-Tuck Cheah. 2016. Negative bubbles and shocks in cryptocurrency markets. International Review of Financial Analysis 47: 343–52. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., and Paul R. Milgrom. 1985. Bid, ask and transaction prices in a specialist market with heterogeneously informed traders. Journal of Financial Economics 14: 71–100. [Google Scholar] [CrossRef]
- Granger, Clive W. J., and Timo Teräsvirta. 1993. Modelling Nonlinear Economic Relationships. Oxford: Oxford University Press. [Google Scholar]
- Gürkaynak, Refet S. 2008. Econometric tests of asset price bubbles: Taking stock. Journal of Economic Survey 22: 166–86. [Google Scholar] [CrossRef]
- Hafner, Christian. 2018. Testing for bubbles in cryptocurrencies with time-varying volatility. Journal of Financial Econometrics. [Google Scholar] [CrossRef]
- Harvey, Andrew C. 2013. Dynamic Models for Volatility and Heavy Tails. Cambridge: Cambridge University Press. [Google Scholar]
- Kim, Soon-Ho, and Dongcheol Kim. 2014. Investor sentiment from internet message postings and the predictability of stock returns. Journal of Economic Behavior & Organization 107: 708–29. [Google Scholar]
- Kjaerland, Frode, Aras Khazal, Erlend A. Krogstad, Frans B. G. Nordstroem, and Are Oust. 2018. An analysis of bitcoin’s price dynamics. Journal of Risk and Financial Management 11: 63. [Google Scholar] [CrossRef]
- Kruse, Robinson, and Christoph Wegener. 2019. Time-varying persistence in real oil prices and its determinant. Energy Economics. [Google Scholar] [CrossRef]
- Luukkonen, Saikkonen, and Teräsvirta. 1988. Testing linearity against smooth transition autoregressive models. Biometrika 75: 491–99. [Google Scholar] [CrossRef]
- Nasekin, Sergey, and Cathy Yi-Hsuan Chen. 2018. Deep Learning-Based Cryptocurrency Sentiment Construction. Available at SSRN 3310784. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3310784 (accessed on 29 March 2019).
- Nelson, Daniel B. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica 59: 347–70. [Google Scholar] [CrossRef]
- Pavlidis, Efthymios G., Ivan Paya, and David A. Peel. 2017. Testing for speculative bubbles using spot and forward prices. International Economic Review 58: 1191–226. [Google Scholar] [CrossRef]
- Pavlidis, Efthymios G., Ivan Paya, and David A. Peel. 2018. Using market expectations to test for speculative bubbles in the crude oil market. Journal of Money, Credit and Banking 50: 833–56. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, and Ida Johnsson. 2018. Double-question survey measures for the analysis of financial bubbles and crashes. Journal of Business & Economic Statistics, 1–15. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., Shuping Shi, and Jun Yu. 2015. Testing for multiple bubbles: Historical episodes of exuberance and collapse in the s&p 500. International Economic Review 56: 1043–78. [Google Scholar]
- Phillips, Peter C. B., Yangru Wu, and Jun Yu. 2011. Explosive behavior in the 1990s nasdaq: When did exuberance escalate asset values? International Economic Review 52: 201–26. [Google Scholar] [CrossRef]
- Teräsvirta, Timo. 1994. Specification, estimation, and evaluation of smooth transition autoregressive models. Journal of the American Statistical Association 89: 208–18. [Google Scholar]
- Trimborn, Simon, and Wolfgang Karl Härdle. 2018. Crix an index for cryptocurrencies. Journal of Empirical Finance 49: 107–22. [Google Scholar] [CrossRef]
- van Dijk, Dick, Timo Teräsvirta, and Philip Hans Franses. 2002. Smooth transition autoregressive models—A survey of recent developments. Econometric Reviews 21: 1–47. [Google Scholar] [CrossRef]
- Yang, Fuyu, and Alasdair Brown. 2016. The Role of Speculative Trade in Market Efficiency: Evidence from a Betting Exchange. Review of Finance 21: 583–603. [Google Scholar]
| 1 | |
| 2 | This list can be found at https://api.stocktwits.com/symbol-sync/symbols.csv. |
| Parameter | Model M0 | Model M1 | ||
|---|---|---|---|---|
| −0.0929 | (0.0323) | −0.0972 | (0.0085) | |
| 0.1193 | (0.0155) | 0.1183 | (0.0153) | |
| 0.9759 | (0.0081) | 0.9709 | (0.0000) | |
| 0.3716 | (0.0325) | 0.3872 | (0.0330) | |
| 0.0025 | (0.0005) | 0.0015 | (0.0006) | |
| −0.0222 | (0.0392) | |||
| 0.7461 | (0.1461) | |||
| 0.0061 | (0.0012) | |||
| −0.2740 | (0.1289) | |||
| 2820.45 | 2838.78 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.Y.-H.; Hafner, C.M. Sentiment-Induced Bubbles in the Cryptocurrency Market. J. Risk Financial Manag. 2019, 12, 53. https://doi.org/10.3390/jrfm12020053
Chen CY-H, Hafner CM. Sentiment-Induced Bubbles in the Cryptocurrency Market. Journal of Risk and Financial Management. 2019; 12(2):53. https://doi.org/10.3390/jrfm12020053
Chicago/Turabian StyleChen, Cathy Yi-Hsuan, and Christian M. Hafner. 2019. "Sentiment-Induced Bubbles in the Cryptocurrency Market" Journal of Risk and Financial Management 12, no. 2: 53. https://doi.org/10.3390/jrfm12020053
APA StyleChen, C. Y.-H., & Hafner, C. M. (2019). Sentiment-Induced Bubbles in the Cryptocurrency Market. Journal of Risk and Financial Management, 12(2), 53. https://doi.org/10.3390/jrfm12020053




