Entropy Minimization for Generalized Newtonian Fluid Flow between Converging and Diverging Channels
Abstract
:1. Introduction
2. Description and Formulation of the Problem
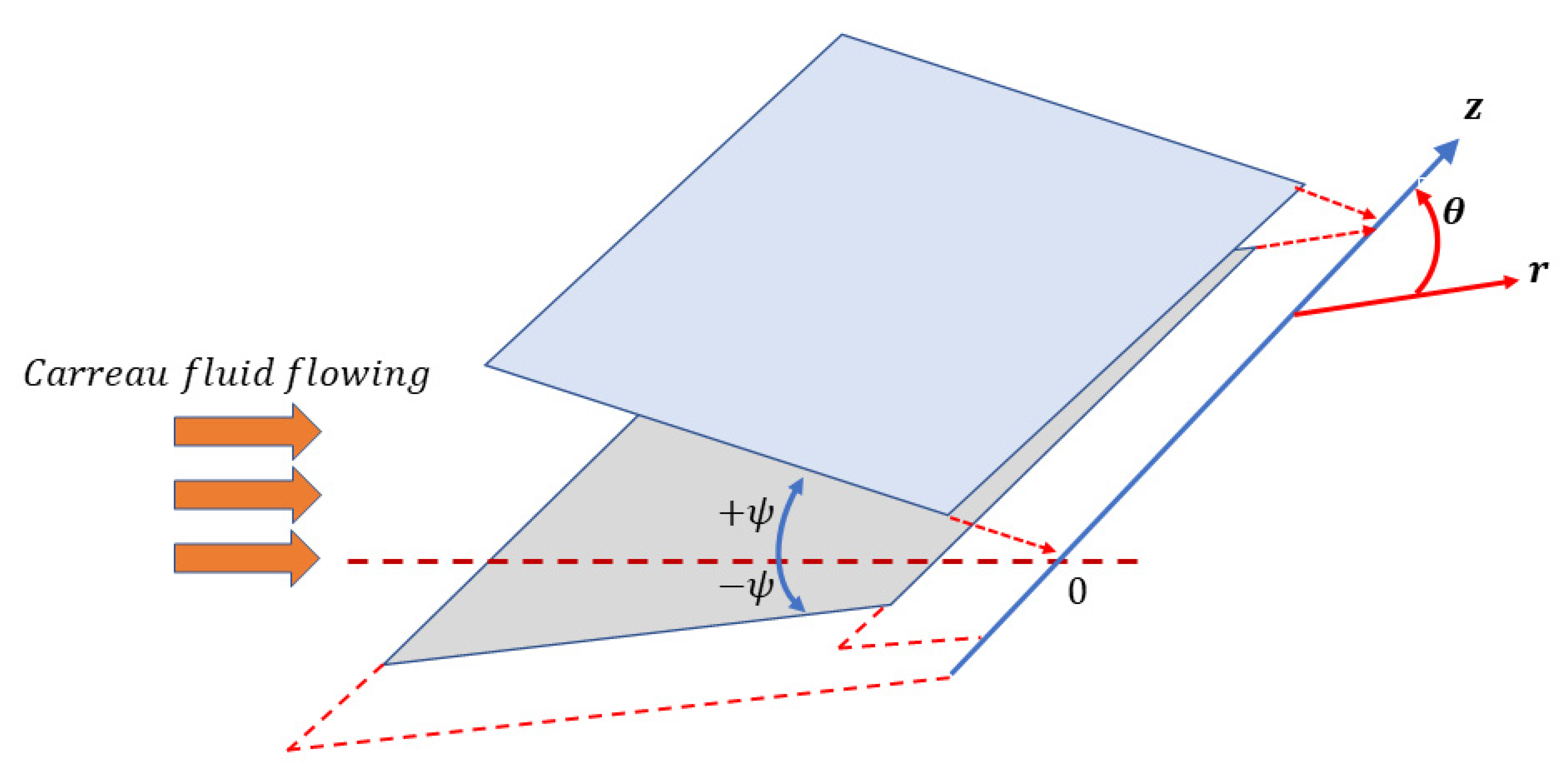
2.1. Physical Configuration
2.2. Similarity Solutions
2.3. Entropy Generation within the System
2.4. Irreversibility Distribution Ratio
2.5. Curiosity in Physical Measurements
3. Numerical Scheme for the Solution
4. Results and Discussion
4.1. Consequences of the Reynolds Number
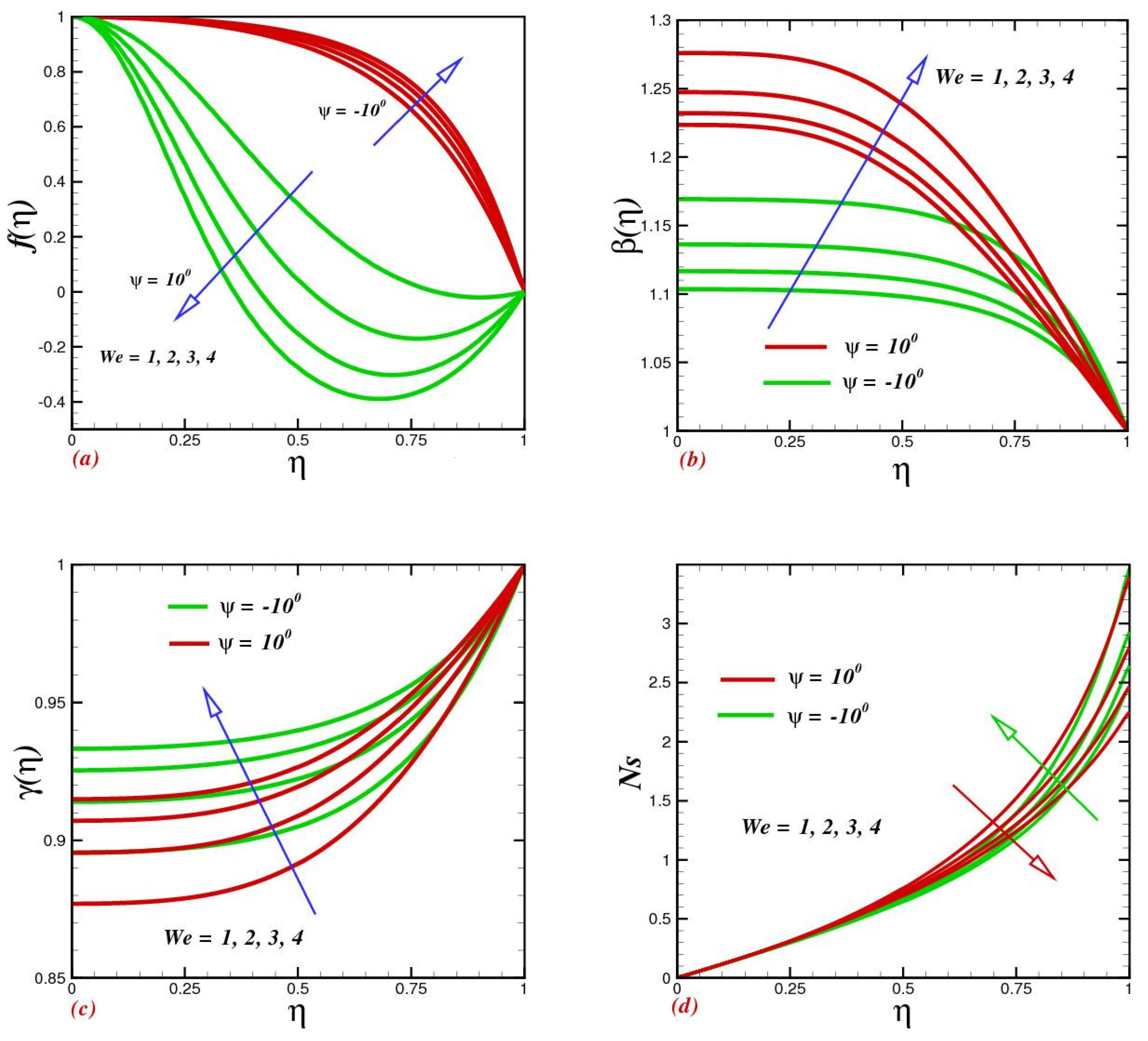
4.2. Consequences of the Weissenberg Number
4.3. Consequences of Indexed Power
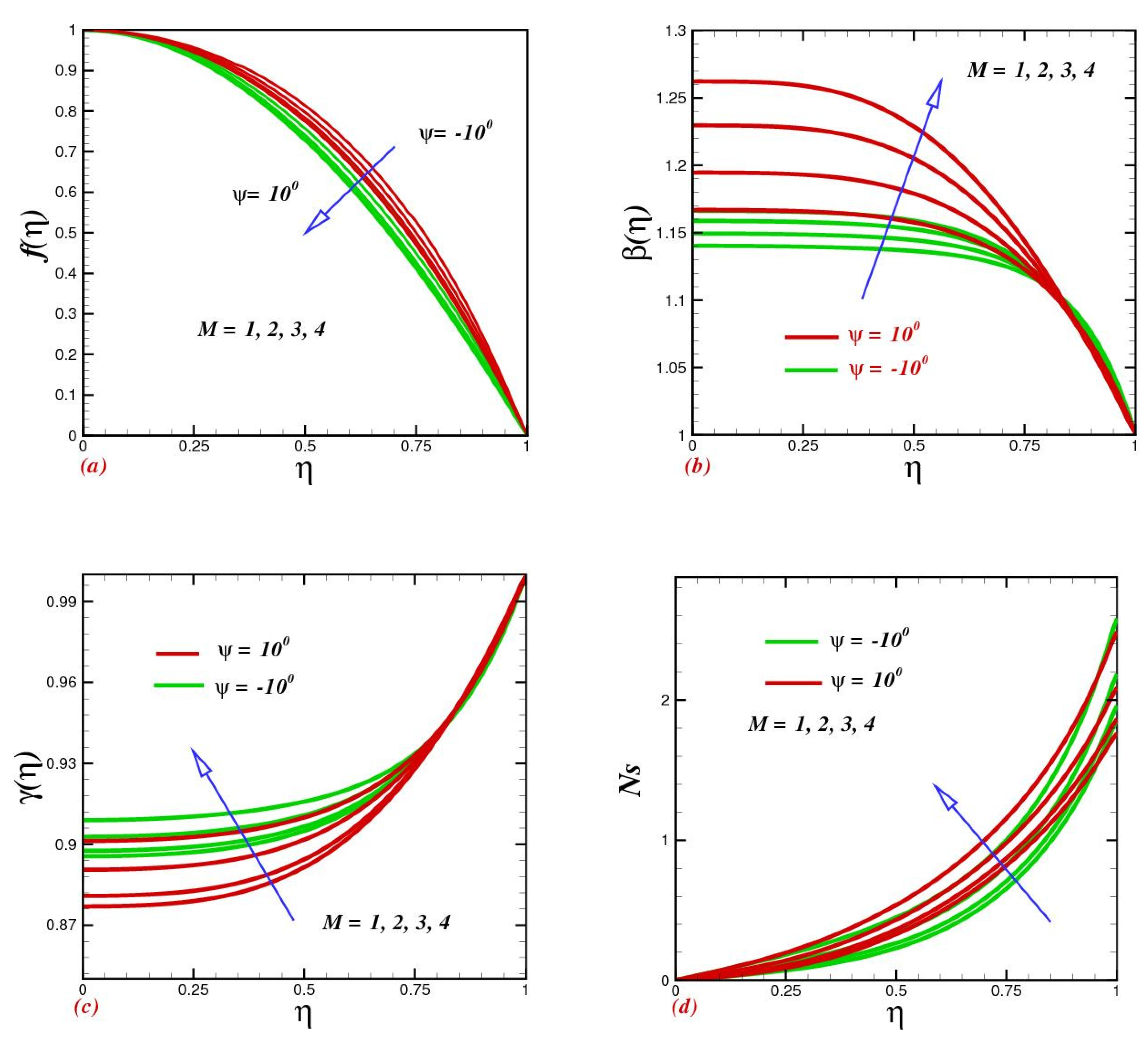
4.4. Consequences of Magnetic Parameter
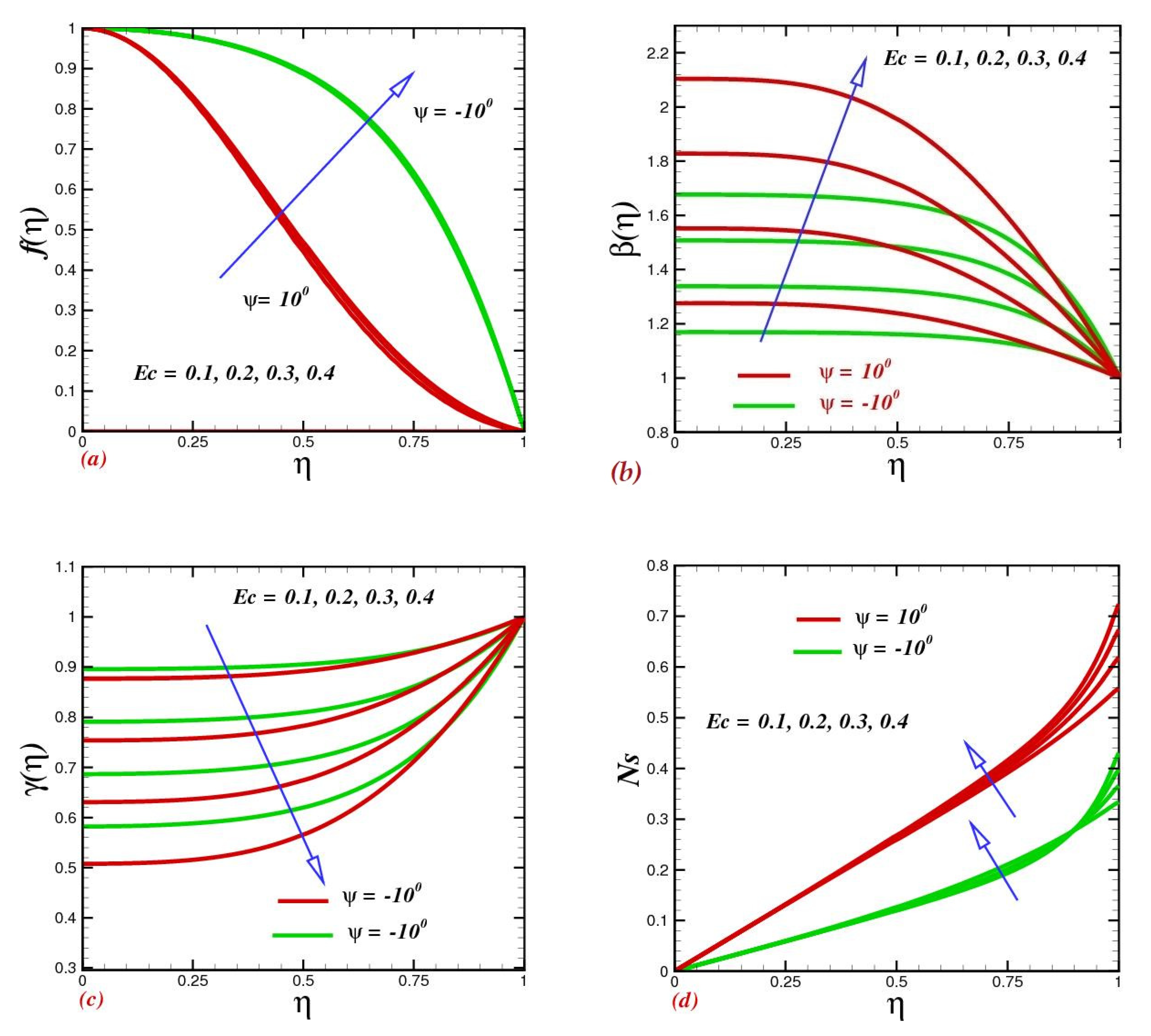
4.5. Effect of the Eckert Number
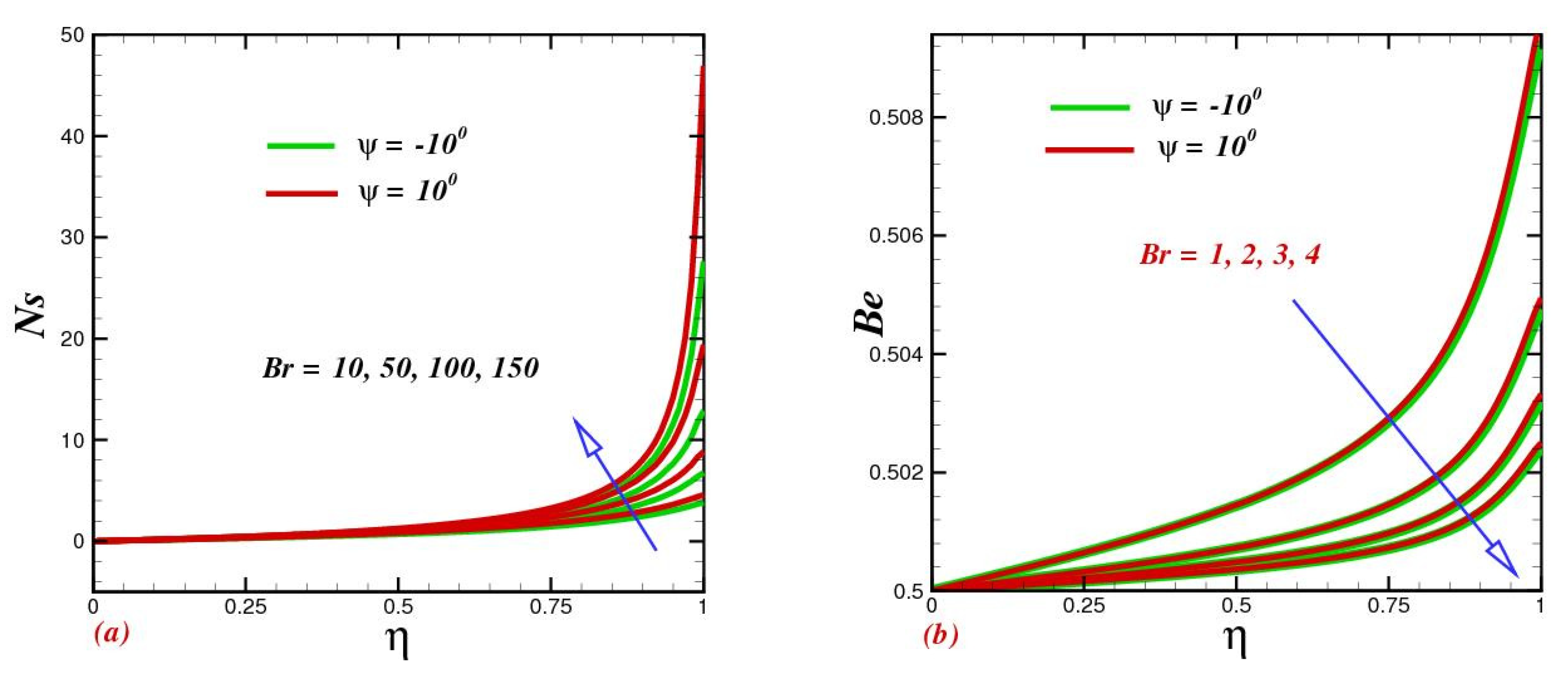
4.6. Effect of the Brinkman Number on Entropy Generation Rate and the Bejan Number
4.7. Influence of Various Physical Parameters on the Bejan Number
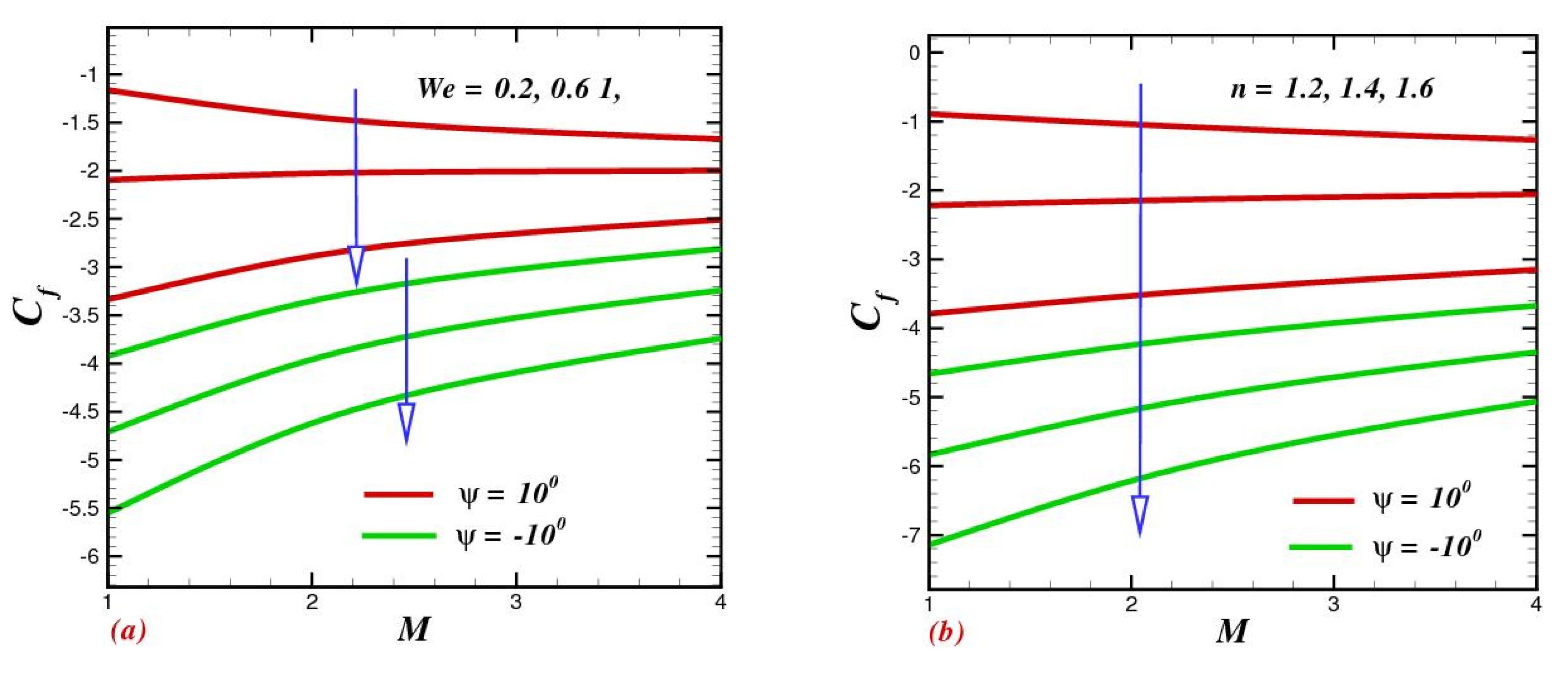
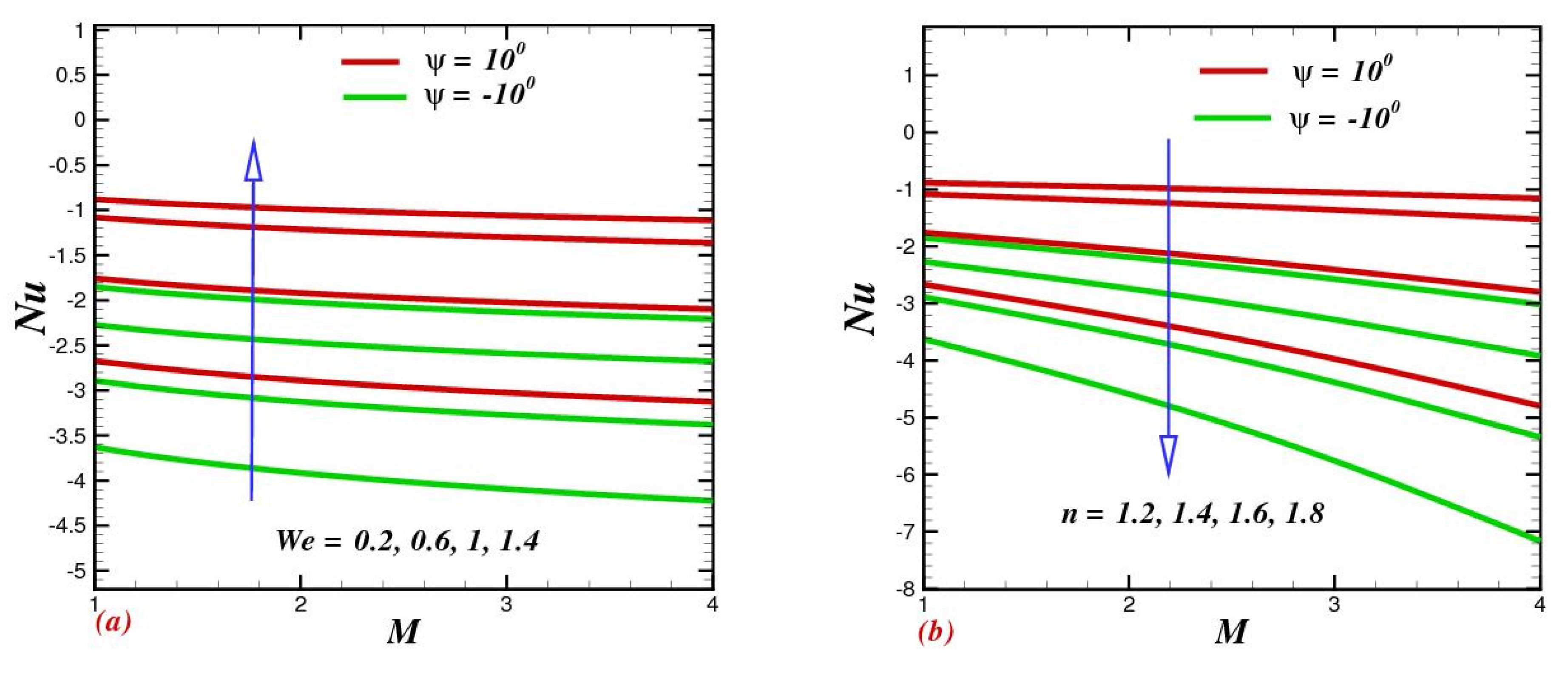
4.8. Influence of Physical Parameters on Skin-Drag Force and Heat-Transfer Rate
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef] [Green Version]
- Natalini, G.; Sciubba, E. Minimization of the Local Rates of Entropy Production in the Design of Air-Cooled Gas Turbine Blades. J. Eng. Gas Turbines Power 1999, 121, 466–475. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Andreozzi, A.; Auletta, A.; Manca, O. Entropy generation in natural convection in a symmetrically and uniformly heated vertical channel. Int. J. Heat Mass Transf. 2006, 49, 3221–3228. [Google Scholar] [CrossRef]
- Makinde, O.D. Entropy-generation analysis for variable-viscosity channel flow with non-uniform wall temperature. Appl. Energy 2008, 85, 384–393. [Google Scholar] [CrossRef]
- Makinde, O.D.; Bég, O.A. On inherent irreversibility in a reactive hydromagnetic channel flow. J. Therm. Sci. 2010, 19, 72–79. [Google Scholar] [CrossRef]
- Weigand, B.; Birkefeld, A. Similarity solutions of the entropy transport equation. Int. J. Therm. Sci. 2009, 48, 1863–1869. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A. Entropy analysis of magnetohydrodynamic flow and heat transfer over a convectively heated radially stretching surface. J. Taiwan Inst. Chem. Eng. 2014, 45, 1197–1203. [Google Scholar] [CrossRef]
- Aksoy, Y. Effects of couple stresses on the heat transfer and entropy generation rates for a flow between parallel plates with constant heat flux. Int. J. Therm. Sci. 2016, 107, 1–12. [Google Scholar] [CrossRef]
- Alam, S.; Khan, A.H.; Makinde, O.D. Magneto-Nanofluid Dynamics in Convergent-Divergent Channel and its Inherent Irreversibility. Defect Diffus. Forum 2017, 377, 95–110. [Google Scholar] [CrossRef]
- Aliabadi, M.A.F.; Jahangiri, A.; Khazaee, I.; Lakzian, E. Investigating the effect of water nano-droplets injection into the convergent-divergent nozzle inlet on the wet steam flow using entropy generation analysis. Int. J. Therm. Sci. 2019, 149, 106181. [Google Scholar] [CrossRef]
- Shukla, N.; Rana, P.; Pop, I. Second law thermodynamic analysis of thermo-magnetic Jeffery–Hamel dissipative radiative hybrid nanofluid slip flow: Existence of multiple solutions. Eur. Phys. J. Plus 2020, 135, 849. [Google Scholar] [CrossRef]
- Riaz, A.; Zeeshan, A.; Bhatti, M.M. Entropy Analysis on a Three-Dimensional Wavy Flow of Eyring–Powell Nanofluid: A Comparative Study. Math. Probl. Eng. 2021, 2021, 6672158. [Google Scholar] [CrossRef]
- Basha, H.; Sivaraj, R. Entropy generation of peristaltic Eyring–Powell nanofluid flow in a vertical divergent channel for biomedical applications. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2021, 235, 1575–1586. [Google Scholar] [CrossRef]
- He, Y.; Wang, L.; Wu, T.; Wu, Z.; Chen, Y.; Yin, K. Facile fabrication of hierarchical textures for substrate-independent and durable superhydrophobic surfaces. Nanoscale 2022, 14, 9392–9400. [Google Scholar] [CrossRef]
- Jeffery, G.L. The two-dimensional steady motion of a viscous fluid. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1915, 29, 455–465. [Google Scholar] [CrossRef] [Green Version]
- Hamel, G. Spiralförmige Bewegungen zäher Flüssigkeiten. Jahresber. Dtsch. Math.-Ver. 1917, 25, 34–60. [Google Scholar]
- Hooper, A.; Duffy, B.R.; Moffatt, H.K. Flow of fluid of non-uniform viscosity in converging and diverging channels. J. Fluid Mech. 1982, 117, 283–304. [Google Scholar] [CrossRef]
- Makinde, O.; Mhone, P. Hermite–Padé approximation approach to MHD Jeffery–Hamel flows. Appl. Math. Comput. 2006, 181, 966–972. [Google Scholar] [CrossRef]
- Makinde, O.; Mhone, P. Temporal stability of small disturbances in MHD Jeffery–Hamel flows. Comput. Math. Appl. 2007, 53, 128–136. [Google Scholar] [CrossRef] [Green Version]
- Alam, S.; Khan, M.; Alim, M. Critical Analysis of Magnetohydrodynamic Jeffery-Hamel Flow Using Cu-Water Nanofluid. GANIT J. Bangladesh Math. Soc. 2016, 34, 111–126. [Google Scholar] [CrossRef]
- Usman, M.; Haq, R.U.; Hamid, M.; Wang, W. Least square study of heat transfer of water based Cu and Ag nanoparticles along a converging/diverging channel. J. Mol. Liq. 2018, 249, 856–867. [Google Scholar] [CrossRef]
- Meher, R.; Patel, N.D. Numerical study of magnetohydrodynamics Jeffery–Hamel flow with cu-water nanofluid between two rectangular smooth walls with transverse magnetic field. Int. J. Comput. Mater. Sci. Eng. 2020, 9, 2050010. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles. Argonne National Lab. (ANL), Argonne, IL (United States), ANL/MSD/CP-84938; CONF-951135-29, Oct. 1995. Available online: https://www.osti.gov/biblio/196525 (accessed on 12 May 2022).
- Moradi, A.; Alsaedi, A.; Hayat, T. Investigation of heat transfer and viscous dissipation effects on the Jeffery-Hamel flow of nanofluids. Therm. Sci. 2015, 19, 563–578. [Google Scholar] [CrossRef]
- Dogonchi, A.; Ganji, D. Investigation of MHD nanofluid flow and heat transfer in a stretching/shrinking convergent/divergent channel considering thermal radiation. J. Mol. Liq. 2016, 220, 592–603. [Google Scholar] [CrossRef]
- Abbasi, A.; Farooq, W.; Tag-ElDin, E.S.M.; Khan, S.U.; Khan, M.I.; Guedri, K.; Elattar, S.; Waqas, M.; Galal, A.M. Heat Transport Exploration for Hybrid Nanoparticle (Cu, Fe3O4)—Based Blood Flow via Tapered Complex Wavy Curved Channel with Slip Features. Micromachines 2022, 13, 1415. [Google Scholar] [CrossRef]
- Waqas, H.; Oreijah, M.; Guedri, K.; Khan, S.U.; Yang, S.; Yasmin, S.; Khan, M.I.; Bafakeeh, O.T.; Tag-ElDin, E.S.M.; Galal, A.M. Gyrotactic Motile Microorganisms Impact on Pseudoplastic Nanofluid Flow over a Moving Riga Surface with Exponential Heat Flux. Crystals 2022, 12, 1308. [Google Scholar] [CrossRef]
- Shahid, M.; Javed, H.M.A.; Ahmad, M.I.; Qureshi, A.A.; Khan, M.I.; Alnuwaiser, M.A.; Ahmed, A.; Khan, M.A.; Tag-ElDin, E.S.M.; Shahid, A.; et al. A Brief Assessment on Recent Developments in Efficient Electrocatalytic Nitrogen Reduction with 2D Non-Metallic Nanomaterials. Nanomaterials 2022, 12, 3413. [Google Scholar] [CrossRef]
- Manzoor, N.; Qasim, I.; Khan, M.I.; Ahmed, M.W.; Guedri, K.; Bafakeeh, O.T.; Tag-Eldin, E.S.M.; Galal, A.M. Antibacterial Applications of Low-Pressure Plasma on Degradation of Multidrug Resistant V. cholera. Appl. Sci. 2022, 12, 9737. [Google Scholar] [CrossRef]
- Mamatha, S.U.; Devi, R.L.V.R.; Ahammad, N.A.; Shah, N.A.; Rao, B.M.; Raju, C.S.K.; Khan, M.I.; Guedri, K. Multi-linear regression of triple diffusive convectively heated boundary layer flow with suction and injection: Lie group transformations. Int. J. Mod. Phys. B, 2022, in press. [CrossRef]
- Carreau, P.J. Rheological Equations from Molecular Network Theories. Trans. Soc. Rheol. 1972, 16, 99–127. [Google Scholar] [CrossRef]
- Hayat, T.; Nawaz, M.; Sajid, M. Effect of heat transfer on the flow of a second-grade fluid in divergent/convergent channel. Int. J. Numer. Methods Fluids 2009, 64, 761–776. [Google Scholar] [CrossRef]
- Al-Saif, A.-S.J.A.; Jasim, A.M. New Analytical Study of the Effects Thermo-Diffusion, Diffusion-Thermo and Chemical Reaction of Viscous Fluid on Magneto Hydrodynamics Flow in Divergent and Convergent Channels. Appl. Math. 2019, 10, 268–300. [Google Scholar] [CrossRef] [Green Version]
- Gahgah, M.; Sari, M.R.; Kezzar, M.; Eid, M.R. Duan–Rach modified Adomian decomposition method (DRMA) for viscoelastic fluid flow between nonparallel plane walls. Eur. Phys. J. Plus 2020, 135, 250. [Google Scholar] [CrossRef]
- Rehman, S.; Hashim; Shah, S.I.A. Numerical simulation for heat and mass transport of non-Newtonian Carreau rheological nanofluids through convergent/divergent channels. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 6025–6039. [Google Scholar] [CrossRef]



| Al-Saif and Jasim [34] | Ghagha et al. [35] | Present Study | |
|---|---|---|---|
| 0.0 | 1 | 1 | 1 |
| 0.1 | 0.98901 | 0.98953 | 0.98953 |
| 0.3 | 0.95626 | 0.95819 | 0.95991 |
| 0.4 | 0.90917 | 0.90619 | 0.90998 |
| 0.5 | 0.84124 | 0.83386 | 0.84001 |
| 0.6 | 0.75123 | 0.741635 | 0.74887 |
| 0.7 | 0.64012 | 0.630019 | 0.63981 |
| 0.8 | 0.51324 | 0.499554 | 0.51018 |
| 0.9 | 0.36129 | 0.350769 | 0.35918 |
| 1.0 | 0.19913 | 0.184134 | 0.19023 |
| 0.3 | 0 | 0 | 0 |
| Alam et al. [21] | Rehman et al. [36] | Present Study | |
|---|---|---|---|
| 5.13092 | −5.13092 | 5.13094 | |
| 4.65216 | −4.65215 | 4.65216 | |
| 2.83395 | −2.83391 | 2.83393 | |
| 0 | 0 | 0 | |
| 3.66971 | 3.66971 | 3.66963 | |
| 3.50810 | −3.50810 | 3.50831 | |
| 1.10933 | −1.10932 | 1.10941 | |
| 0 | 0 | 0 | |
| Alam et al. [21] | Hayat et al. [33] | Present Study | |
|---|---|---|---|
| 0.03157 | 0.03157 | 0.03156 | |
| 0.03734 | 0.03732 | 0.03735 | |
| 0.04214 | 0.04215 | 0.04217 | |
| 0.04214 | 0.04215 | 0.04213 | |
| 0.05052 | 0.05024 | 0.05053 | |
| 0.034751 | 0.03477 | 0.03474 | |
| 0.039993 | 0.03998 | 0.03999 | |
| 0.046401 | 0.04640 | 0.04541 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, S.; Hashim; Nasr, A.; Eldin, S.M.; Malik, M.Y. Entropy Minimization for Generalized Newtonian Fluid Flow between Converging and Diverging Channels. Micromachines 2022, 13, 1755. https://doi.org/10.3390/mi13101755
Rehman S, Hashim, Nasr A, Eldin SM, Malik MY. Entropy Minimization for Generalized Newtonian Fluid Flow between Converging and Diverging Channels. Micromachines. 2022; 13(10):1755. https://doi.org/10.3390/mi13101755
Chicago/Turabian StyleRehman, Sohail, Hashim, Abdelaziz Nasr, Sayed M. Eldin, and Muhammad Y. Malik. 2022. "Entropy Minimization for Generalized Newtonian Fluid Flow between Converging and Diverging Channels" Micromachines 13, no. 10: 1755. https://doi.org/10.3390/mi13101755






