Conservation Laws and Travelling Wave Solutions for a Negative-Order KdV-CBS Equation in 3+1 Dimensions
Abstract
1. Introduction
2. Lie Point Symmetries
3. Conservation Laws
4. Travelling Wave Reduction and First Integrals
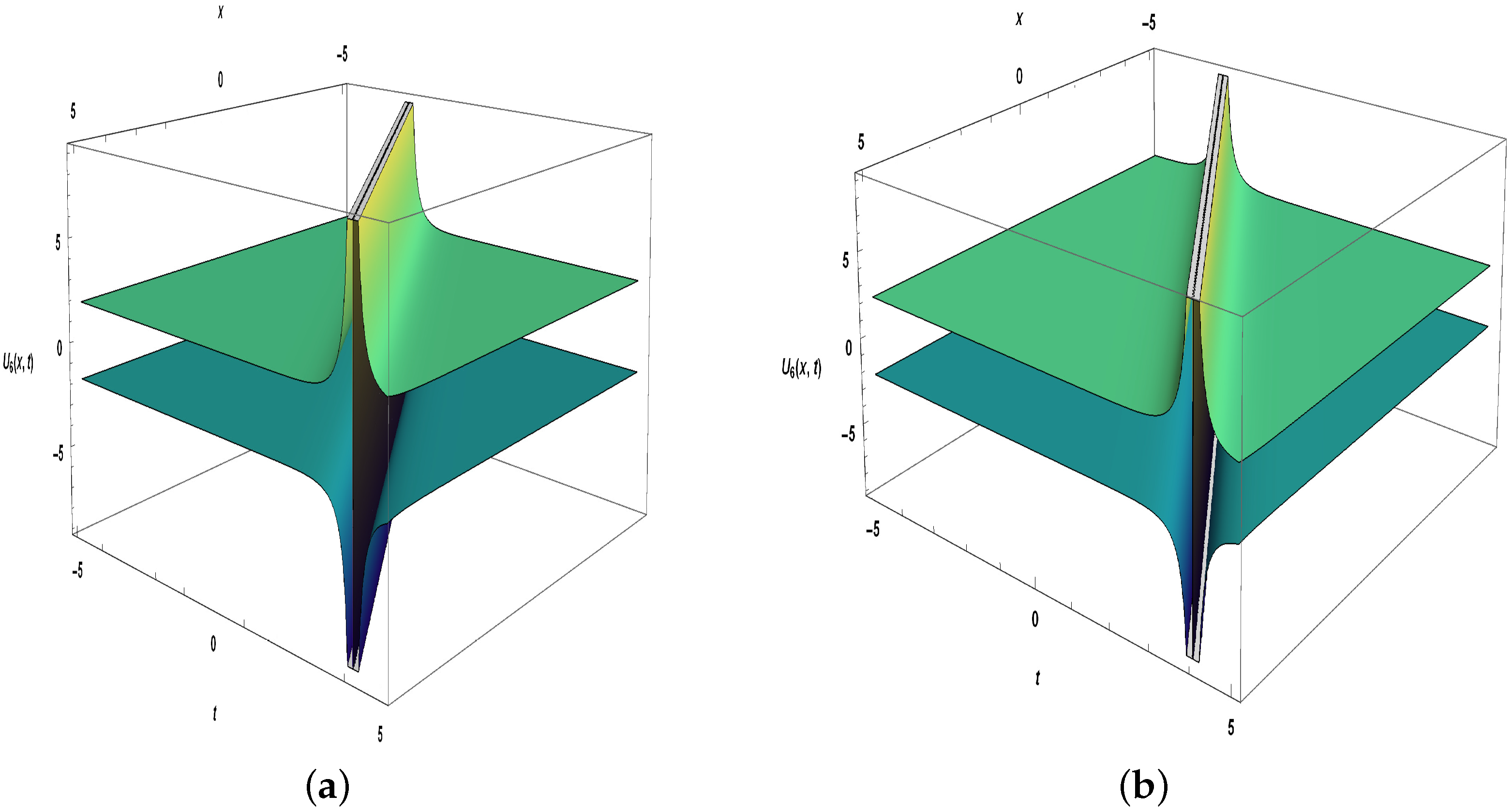
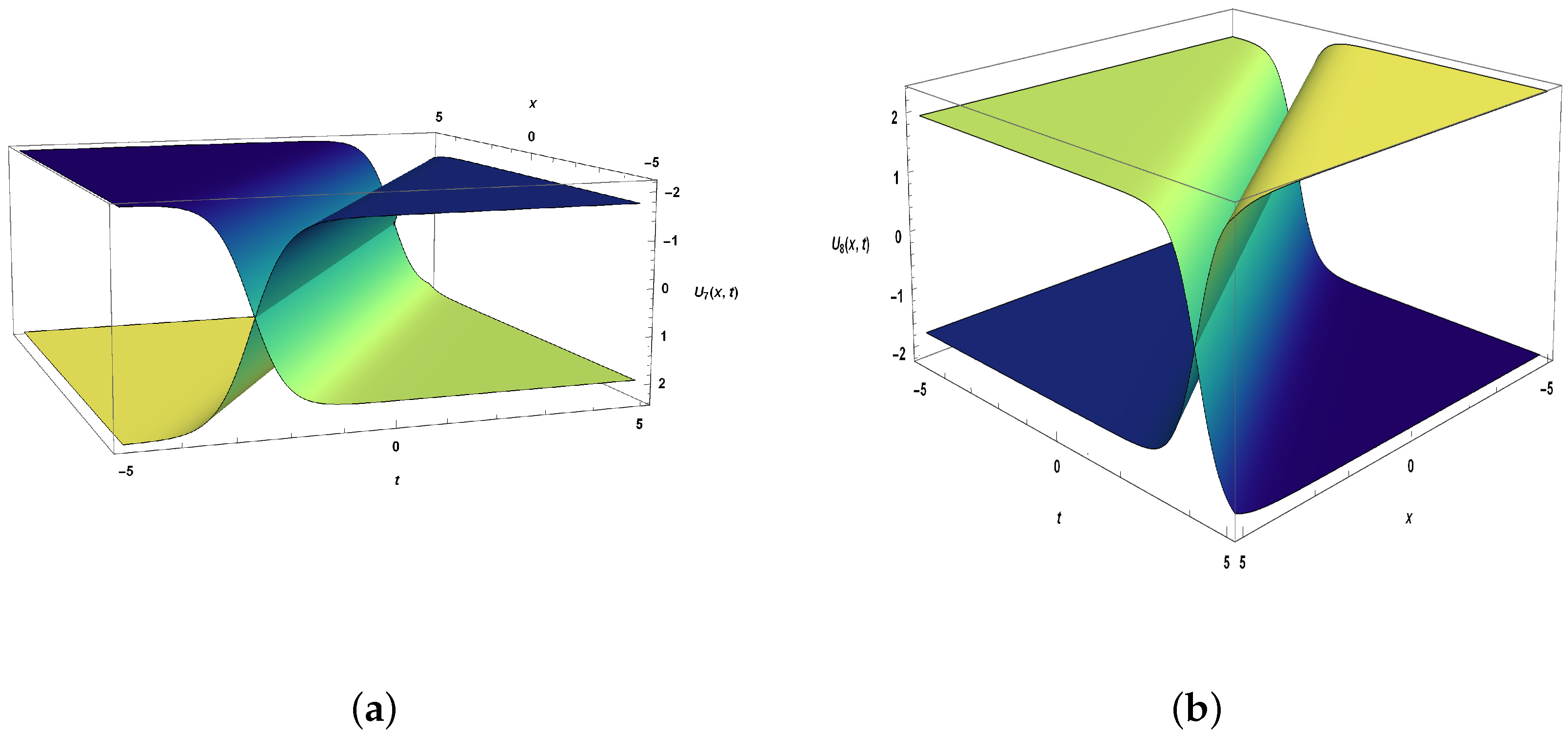
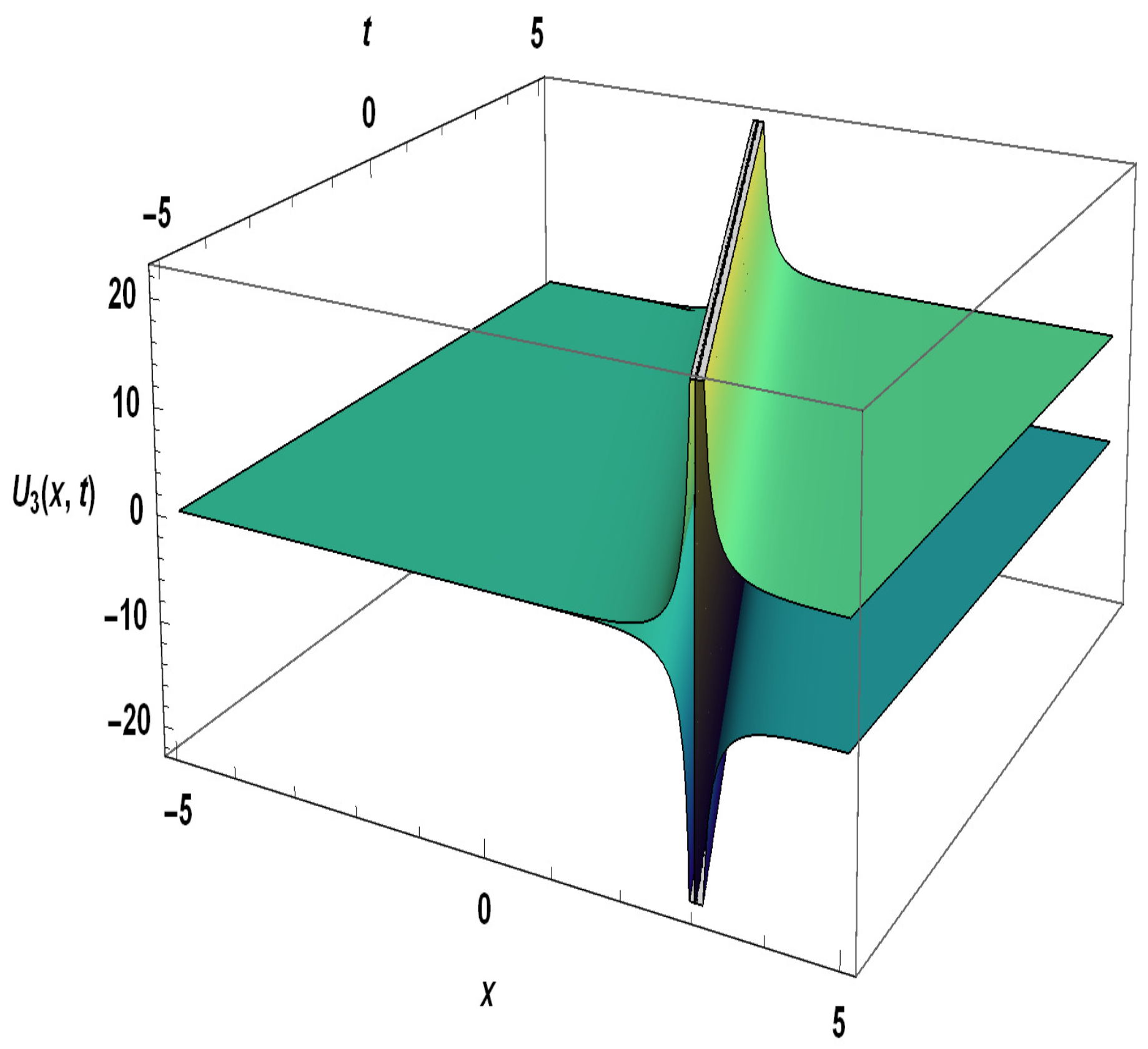
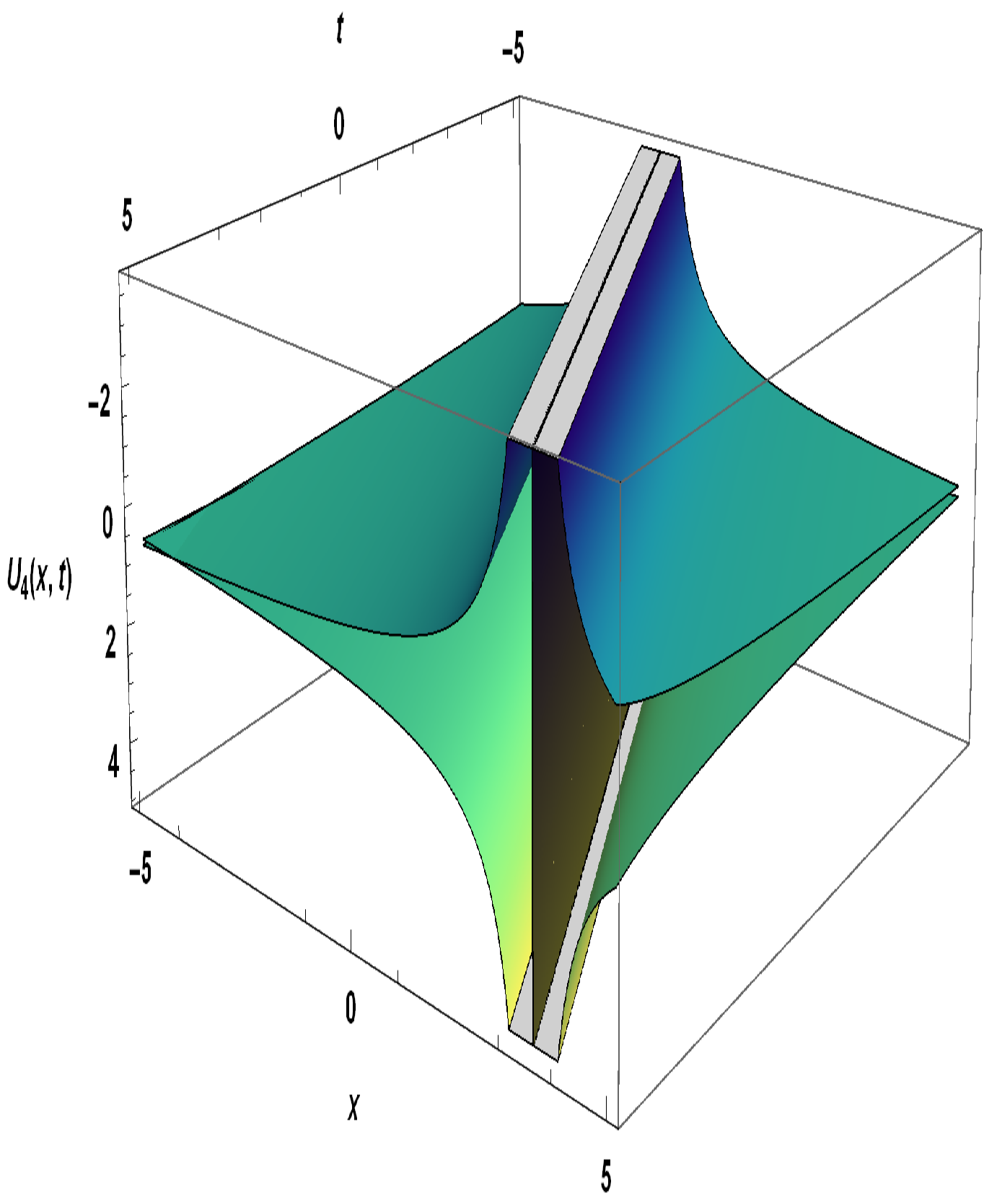
5. Extraction of Solitons from a Negative-Order KdV-CBS Equation
- Case 1. When ,
- Case 2. When ,
- Case 3. When ,
- Case 4.
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wazwaz, A.M. A new (2+ 1)-dimensional Korteweg-de Vries equation and its extension to a new (3+ 1)-dimensional Kadomtsev-Petviashvili equation. Phys. Scr. 2011, 84, 035010. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Abundant solutions of various physical features for the (2+ 1)-dimensional modified KdV-Calogero–Bogoyavlenskii–Schiff equation. Nonlinear Dyn. 2017, 89, 1727–1732. [Google Scholar] [CrossRef]
- El-Kalaawy, O.H.; Ibrahim, R.S. Solitary Wave Solution of the Two-Dimensional Regularized Long-Wave and Davey-Stewartson Equations in Fluids and Plasmas. Appl. Math. 2012, 3, 833–843. [Google Scholar] [CrossRef]
- Al-Amr, M.O. New applications of reduced differential transform method. Alex. Eng. J. 2014, 53, 243–247. [Google Scholar] [CrossRef][Green Version]
- Helal, M.A.; Seadawy, A.R. Variational method for the derivative nonlinear Schrödinger equation with computational applications. Phys. Scr. 2009, 80, 350–360. [Google Scholar] [CrossRef]
- Salman, F.; Raza, N.; Basendwah, G.A.; Jaradat, M.M. Optical solitons and qualitative analysis of nonlinear Schrodinger equation in the presence of self steepening and self frequency shift. Results Phys. 2022, 39, 105753. [Google Scholar] [CrossRef]
- Jhangeer, A.; Raza, N.; Rezazadeh, H.; Seadawy, A. Nonlinear self-adjointness, conserved quantities, bifurcation analysis and travelling wave solutions of a family of long-wave unstable lubrication model. Pramana 2020, 94, 1–9. [Google Scholar] [CrossRef]
- Taghizadeh, N.; Mirzazadeh, M. The modified extended tanh method with the Riccati equation for solving nonlinear partial differential equations. Math. Aeterna 2012, 2, 145–153. [Google Scholar]
- Cheemaa, N.; Chen, S.; Seadawy, A.R. Propagation of isolated waves of coupled nonlinear (2+ 1)-dimensional Maccari system in plasma physics. Results Phys. 2020, 17, 102987. [Google Scholar] [CrossRef]
- Lu, D.; Seadawy, A. R.; Iqbal, M. Mathematical methods via construction of traveling and solitary wave solutions of three coupled system of nonlinear partial differential equations and their applications. Results Phys. 2018, 11, 1161–1171. [Google Scholar] [CrossRef]
- Yang, X.F.; Deng, Z.C.; Wei, Y. A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Differ. Equ. 2015, 2015, 1–17. [Google Scholar] [CrossRef]
- Jiong, S. Auxiliary equation method for solving nonlinear partial differential equations. Phys. Lett. A 2003, 309, 387–396. [Google Scholar]
- Zhang, H. New application of the (G′/G)-expansion method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3220–3225. [Google Scholar] [CrossRef]
- Liao, S. Comparison between the homotopy analysis method and homotopy perturbation method. Appl. Math. Comput. 2005, 169, 1186–1194. [Google Scholar] [CrossRef]
- Raza, N.; Rafiq, M.H.; Kaplan, M.; Kumar, S.; Chu, Y. The unified method for abundant soliton solutions of local time fractional nonlinear evolution equations. Results Phys. 2021, 22, 103979. [Google Scholar] [CrossRef]
- Wazwaz, A.M.; Osman, M.S. Analyzing the combined multi-waves polynomial solutions in a two-layer-liquid medium. Comput. Math. Appl. 2018, 76, 276–283. [Google Scholar] [CrossRef]
- Javid, A.; Raza, N. Singular and dark optical solitons to the well posed Lakshamanan-Porsezian-Daniel model. Optik 2018, 171, 120–129. [Google Scholar] [CrossRef]
- Ekici, M.; Sonmezoglu, A.; Zhou, Q.; Biswas, A.; Ullah, M.Z.; Asma, M.; Moshokoa, S.P.; Belic, M. Optical solitons in DWDM system by extended trial equation method. Optik 2017, 141, 157–167. [Google Scholar] [CrossRef]
- Wang, M.L.; Zhou, Y.B.; Li, Z.B. Application of homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 1996, 216, 67–75. [Google Scholar] [CrossRef]
- Vahidi, J.; Zabihi, A.; Rezazadeh, H.; Ansari, R. New extended direct algebraic method for the resonant nonlinear Schrödinger equation with Kerr law nonlinearity. Optik 2021, 227, 165936. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D. Optical soliton solutions of the generalized higher-order nonlinear Schrödinger equations and their applications. Opt. Quantum Electron. 2018, 5, 1–6. [Google Scholar] [CrossRef]
- Alhussain, Z.A.; Raza, N. New Optical Solitons with Variational Principle and Collective Variable Strategy for Cold Bosons in Zig-Zag Optical Lattices. J. Math. 2022, 2022. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, R.; Kumar, A. On similarity solutions of Zabolotskaya-Khokhlov equation. Comput. Math. Appl. 2014, 68, 454–463. [Google Scholar] [CrossRef]
- Ray, S.S. Lie symmetry analysis and reduction for exact solution of (2+ 1)-dimensional Bogoyavlensky-Konopelchenko equation by geometric approach. Mod. Phys. Lett. B 2018, 32, 1850127. [Google Scholar] [CrossRef]
- Vinita; Ray, S.S. Optical soliton group invariant solutions by optimal system of Lie subalgebra with conservation laws of the resonance nonlinear Schrödinger equation. Mod. Phys. Lett. B 2020, 34, 2050402. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Exact solutions of compact and noncompact structures for the KP-BBM equation. Appl. Math. Comput. 2005, 169, 700–712. [Google Scholar] [CrossRef]
- Olver, P.J. Application of Lie Groups to Differential Equations; Springer: NewYork, NY, USA, 1993. [Google Scholar]
- Kumar, S.; Kumar, D.; Wazwaz, A.M. Group invariant solutions of (3+ 1)-dimensional generalized B-type Kadomstsev Petviashvili equation using optimal system of Lie subalgebra. Phys. Scr. 2019, 94, 065204. [Google Scholar] [CrossRef]
- Bai, Y.; Bilige, S.; Chaolu, T. Potential symmetries, one-dimensional optimal system and invariant solutions of the coupled Burgers? equations. J. Appl. Math. Phys. 2018, 6, 1825. [Google Scholar] [CrossRef][Green Version]
- Kara, A.H.; Biswas, A.; Zhou, Q.; Moraru, L.; Moshokoa, S.P.; Belic, M. Conservation laws for optical solitons with Chen?Lee?Liu equation. Optik 2018, 174, 195–198. [Google Scholar] [CrossRef]
- Jafari, H.; Kadkhoda, N.; Azadi, M.; Yaghobi, M. Group classification of the time-fractional Kaup-Kupershmidt equation. Sci. Iran. 2017, 24, 302–307. [Google Scholar] [CrossRef][Green Version]
- Kadkhoda, N.; Jafari, H.; Moremedi, G.M.; Baleanu, D.; Qaenat, I.R.; Babolsar, I.R. Optimal system and symmetry reduction of the (1+ 1) dimensional Sawada–Kotera equation. Int. J. Pure Appl. Math. 2016, 103, 215–226. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Two new Painlevé integrable KdV-Calogero–Bogoyavlenskii–Schiff (KdV-CBS) equation and new negative-order KdV-CBS equation. Nonlinear Dyn. 2021, 104, 4311–4315. [Google Scholar] [CrossRef]
- Anco, S.C.; Gandarias, M. Symmetry multi-reduction method for partial differential equations with conservation laws. Commun. Nonlin. Sci. Numer. Simul. 2020, 91, 105349. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Bluman, G.W.; Cheviakov, A.; Anco, S.C. Applications of Symmetry Methods to Partial Differential Equations; Springer: New York, NY, USA, 2009. [Google Scholar]
- Anco, S.C. Generalization of Noether’s theorem in modern form to non-variational partial differential equations. In Recent Progress and Modern Challenges in Applied Mathematics, Modeling and Computational Science; Springer: New York, NY, USA, 2017; pp. 119–182. [Google Scholar]
- Anco, S.C.; Gandarias, M.L.; Recio, E. Line-solitons, line-shocks, and conservation laws of a universal KP-like equation in 2+1 dimensions. J. Math. Anal. Appl. 2021, 504, 125319. [Google Scholar] [CrossRef]
- Sjöberg, A. Double reduction of PDEs from the association of symmetries with conservation laws with applications. Appl. Math. Comput. 2007, 184, 608–616. [Google Scholar] [CrossRef]
- Sjöberg, A. On double reduction from symmetries and conservation laws. Nonlin. Analysis Real World Appl. 2009, 10, 3472–3477. [Google Scholar] [CrossRef]
- Bokhari, A.H.; Dweik, A.Y.; Zaman, F.D.; Kara, A.H.; Mahomed, F.M. Generalization of the double reduction theory. Nonlin. Analysis Real World Appl. 2010, 11, 3763–3769. [Google Scholar] [CrossRef]
- Whittaker, E.E.; Watson, G.M. Modern Analysis, 4th ed.; Cambridge University Press: Cambridge, UK, 1927. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Tables; Dover: New York, NY, USA, 1965. [Google Scholar]
- Lu, D.; Seadawy, A.; Arshad, M. Applications of extended simple equation method on unstable nonlinear Schrödinger equations. Optik 2017, 140, 136–144. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gandarias, M.L.; Raza, N. Conservation Laws and Travelling Wave Solutions for a Negative-Order KdV-CBS Equation in 3+1 Dimensions. Symmetry 2022, 14, 1861. https://doi.org/10.3390/sym14091861
Gandarias ML, Raza N. Conservation Laws and Travelling Wave Solutions for a Negative-Order KdV-CBS Equation in 3+1 Dimensions. Symmetry. 2022; 14(9):1861. https://doi.org/10.3390/sym14091861
Chicago/Turabian StyleGandarias, Maria Luz, and Nauman Raza. 2022. "Conservation Laws and Travelling Wave Solutions for a Negative-Order KdV-CBS Equation in 3+1 Dimensions" Symmetry 14, no. 9: 1861. https://doi.org/10.3390/sym14091861
APA StyleGandarias, M. L., & Raza, N. (2022). Conservation Laws and Travelling Wave Solutions for a Negative-Order KdV-CBS Equation in 3+1 Dimensions. Symmetry, 14(9), 1861. https://doi.org/10.3390/sym14091861