Modelling of Irreversible Homogeneous Reaction on Finite Diffusion Layers
Abstract
:1. Introduction
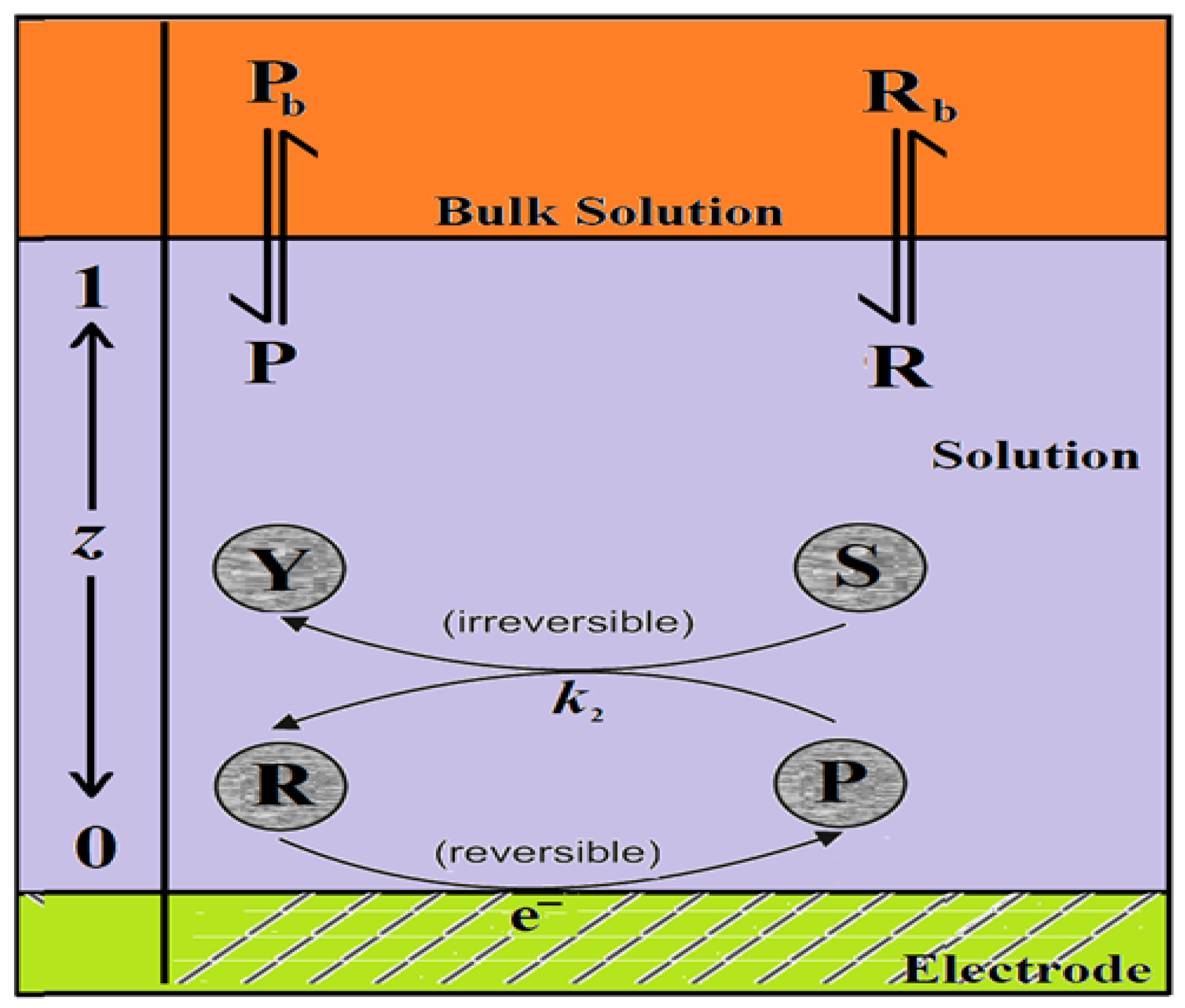
2. Mathematical Formulation
3. Analytical Expression of Concentrations
3.1. Analytical Expression of Concentrations Using the Akbari-Ganji Method (AGM)
3.2. Analytical Expression of Concentrations Using the Differential Transform Method (DTM)
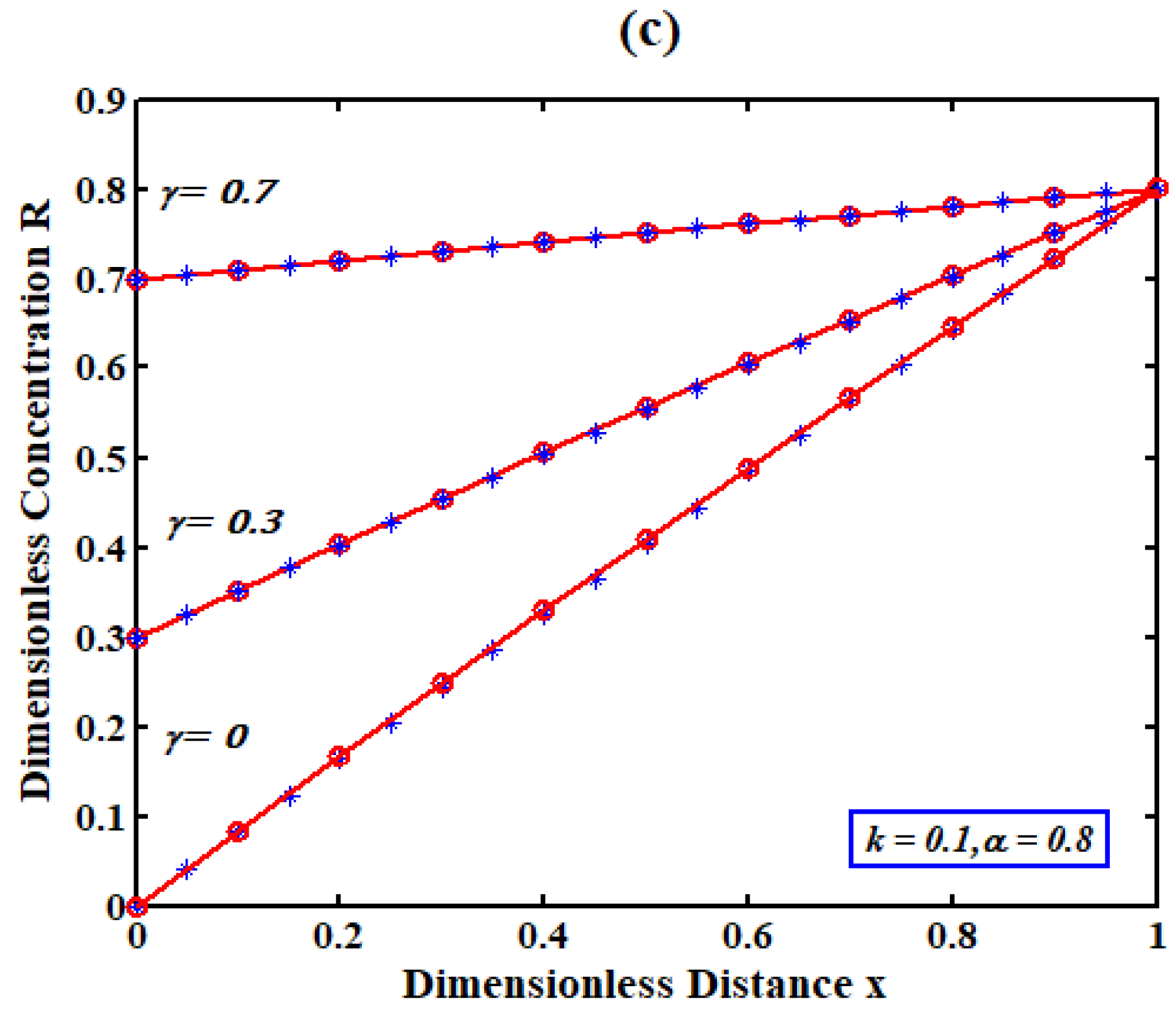
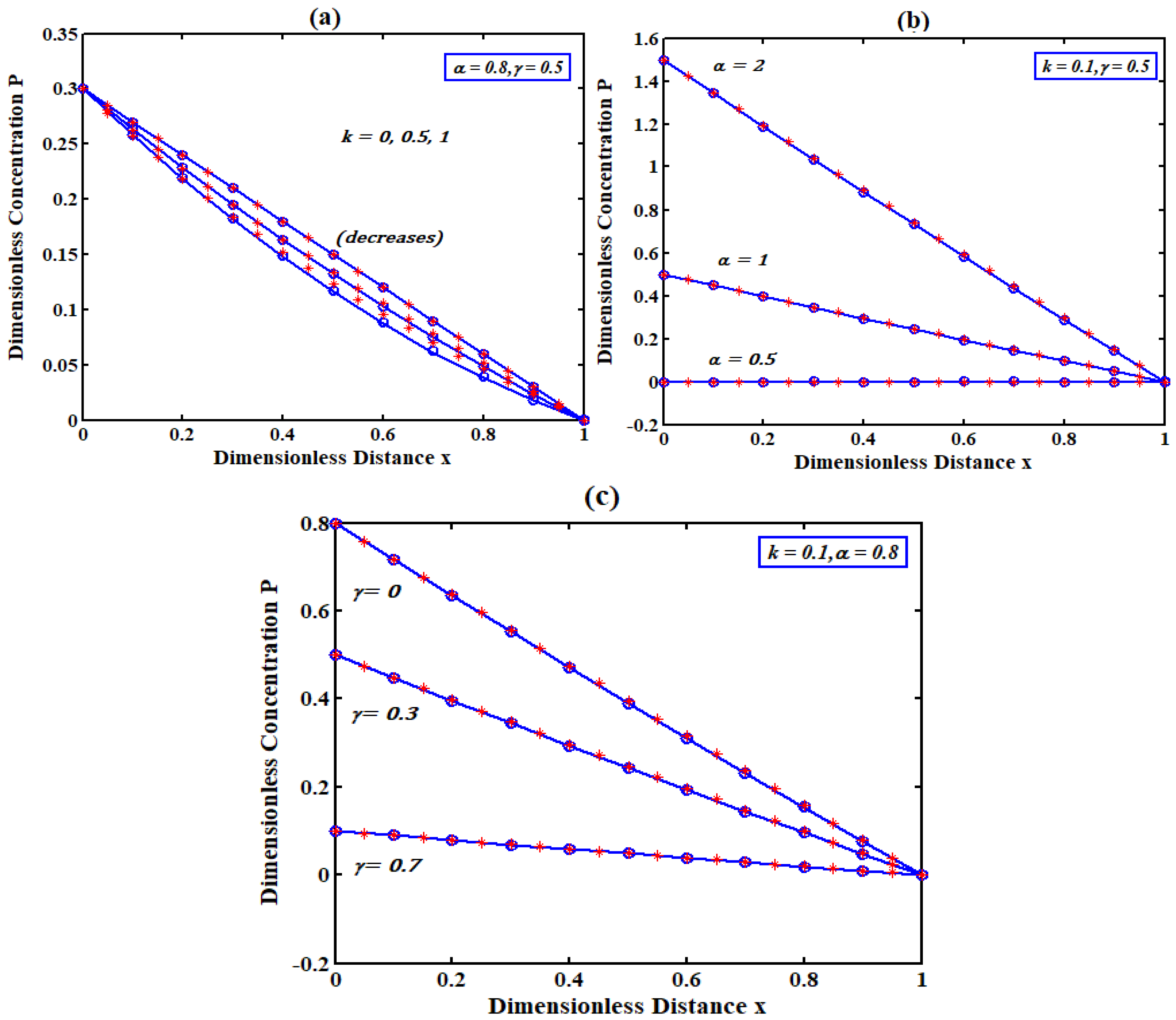
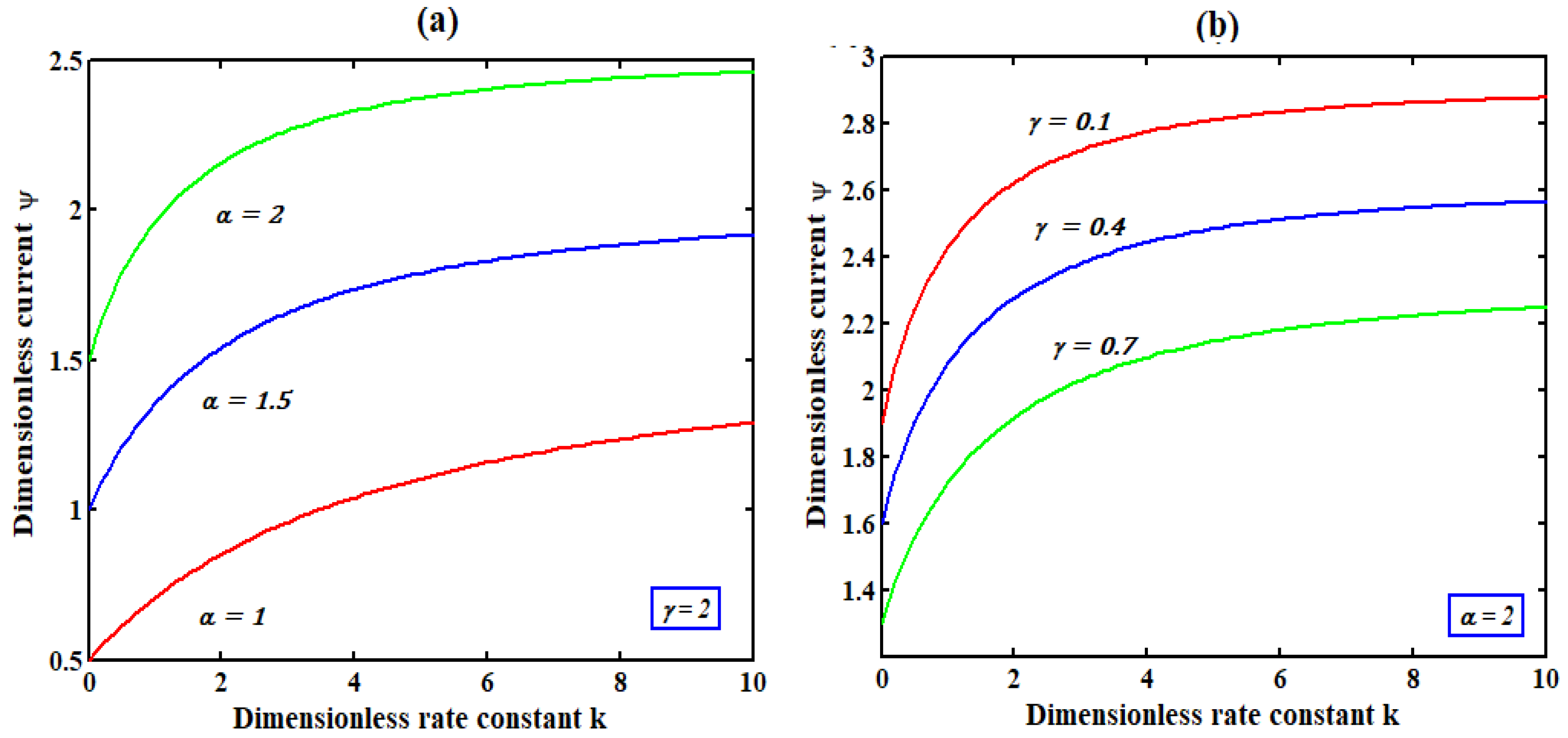
4. Validation of Analytical Results with Numerical Simulation
5. Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | Name | Unit |
| CR | Concentration of reactant | Mol cm−3 |
| CP | Concentration of product | Mol cm−3 |
| CS | Concentration of solute | Mol cm−3 |
| CRb, CSb | Bulk concentration | Mol cm−3 |
| CR0,SS | Concentration of R at the electrode in steady-state | Mol cm−3 |
| δ | Diffusion layer thickness | cm |
| D | Diffusion coefficient | cm2s−1 |
| k2 | Reaction-rate constant | Mol cm−3s |
| z | Distance from the electrode surface | cm |
| R | Dimensionless concentration of reactant | None |
| P | Dimensionless concentration of product | None |
| S | Dimensionless concentration of solute | None |
| x | Dimensionless distance | None |
| k | Dimensionless rate constant | None |
| α, γ | Concentration ratio | None |
| ψ | Dimensionless current | None |
| n | Number of electrons transferred | None |
Appendix A. The Relationship between Concentrations of Species
Appendix B. Analytical Solution of the Equations (3)–(5) Using AGM
Appendix C. Approximate Analytical Solution of Nonlinear Differential Equations (3)–(5) Using the DTM
Appendix D. Numerical Solution of Nonlinear Equations (3)–(5)
References
- Thomas, W.; Chapman, T.W.; Antano, R. The effect of an irreversible homogeneous reaction on finite-layer diffusion impedance. Electrochim. Acta 2010, 56, 128. [Google Scholar]
- Orazem, M.E.; Tribollet, B. Electrochemical Impedance Spectroscopy, Theory; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Lasia, A. Electrochemical Impedance Spectroscopy and its applications. In Modern Aspects of Electrochemistry; Conway, B.E., Bockris, J.O.M., White, R.E., Eds.; Plenum Press: New York, NY, USA, 1999; Volume 32, p. 143. [Google Scholar]
- Lasia, A. Applications of Electrochemical Impedance Spectroscopy to Hydrogen Adsorption, Evolution and Absorption into Metals. In Modern Aspects of Electrochemistry; Conway, B.E., White, R.E., Eds.; Kluwer Springer: New York, NY, USA, 2002; Volume 35, p. 1. [Google Scholar]
- Montella, C. Review and theoretical analysis of ac–av methods for the investigation of hydrogen insertion I. Diffusion formalism. J. Electroanal. Chem. 1999, 462, 73. [Google Scholar] [CrossRef]
- Montella, C. Review and theoretical analysis of ac–av methods for the investigation of hydrogen insertion: Part III. Comparison of entry side impedance, transfer function and transfer impedance methods. J. Electroanal. Chem. 2000, 480, 150. [Google Scholar] [CrossRef]
- Drossbach, P.; Schultz, J. Elektrochemischeuntersuchungen an kohleelektroden—I: Die überspannung des wasserstoffs. Electrochim. Acta 1964, 9, 1391. [Google Scholar] [CrossRef]
- Franceschetti, D.R.; Macdonald, J.R.; Buck, R.P. Interpretation of finite-length-warburg-type impedances in supported and unsupported electrochemical cells with kinetically reversible electrodes. J. Electrochem. Soc. 1991, 138, 1368. [Google Scholar] [CrossRef]
- Diard, J.P.; le Gorrec, B.; Montella, C. Linear diffusion impedance. General expression and applications. J. Electroanal. Chem. 1999, 471, 126. [Google Scholar] [CrossRef]
- Franceschetti, D.R.; Macdonald, J.R. Diffusion of neutral and charged species under small-signal a.c. conditions. J. Electroanal. Chem. 1979, 101, 307. [Google Scholar] [CrossRef]
- Macdonald, J.R. Impedance Spectroscopy, Emphasizing Solid Materials and Systems, Theory; John Wiley and Sons Inc.: New York, NY, USA, 1987; p. 45. [Google Scholar]
- Bisquert, J. Theory of the impedance of electron diffusion and recombination in a thin layer. J. Phys. Chem. B 2002, 106, 325. [Google Scholar] [CrossRef]
- Maheswari, M.U.; Rajendran, L. Analytical expressions of concentrations of substrate and hydroquinone in an amperometric glucose biosensor. Int. Sch. Res. Not. 2012, 3, 2089. [Google Scholar] [CrossRef]
- Vijayalakshmi, T.; Senthamarai, R. Analytical approach to a three species food chain model by applying homotopy perturbation method. Int. J. Adv. Sci. Technol. 2020, 29, 2853. [Google Scholar]
- Umadevi, R.; Venugopal, K.; Jeyabarathi, P.; Rajendran, L.; Abukhaled, M. Analytical study of nonlinear roll motion of ships: A homotopy perturbation approach. Palest. J. Math. 2022, 11, 316. [Google Scholar]
- Manimegalai, B.; Lyons, M.E.G.; Rajendran, L. Transient chronoamperometric current at rotating disc electrode for second-order ECE reactions. J. Electroanal. Chem. 2021, 902, 115775. [Google Scholar] [CrossRef]
- Salomi, R.J.; Sylvia, S.V.; Rajendran, L.; Lyons, M.E.G. Lyons, Transient current, sensitivity and resistance of biosensors acting in a trigger mode: Theoretical study. J. Electroanal. Chem. 2021, 895, 115421. [Google Scholar] [CrossRef]
- Manimegalai, B.; Rajendran, L.; Lyons, M.E.G. Theory of the transient current response for the homogeneous mediated enzyme catalytic mechanism at the rotating disc electrode. Int. J. Electrochem. Sci. 2021, 16, 41. [Google Scholar] [CrossRef]
- Swaminathan, R.; Saravanakumar, R.; Venugopal, K.; Rajendran, L. Analytical solution of non linear problems in homogeneous reactions occur in the mass-transfer boundary layer: Homotopy Perturbation Method. Int. J. Electrochem. Sci. 2021, 16, 115421. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Nonlinear Mech. 2000, 35, 37. [Google Scholar] [CrossRef]
- Saravanakumar, R.; Pirabaharan, P.; Abukhaled, M.; Rajendran, L. Theoretical analysis of voltammetry at a rotating disk electrode in the absence of supporting electrolyte. J. Phys. Chem. B 2020, 124, 443. [Google Scholar] [CrossRef]
- He, J.H. Variational iteration method for autonomous ordinary differential systems. Appl. Math. Comput. 2000, 114, 115. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. A generalized differential transform method for linear partial differential equations of fractional order. Appl. Math. Lett. 2008, 21, 194. [Google Scholar] [CrossRef]
- Saranya, K.; Mohan, V.; Rajendran, L. Steady-state concentrations of carbon dioxide absorbed into phenyl glycidyl ether solutions by residual method. J. Math. Chem. 2020, 58, 1230. [Google Scholar] [CrossRef]
- Nirmala, K.; Manimegalai, B.; Rajendran, L. Steady-State substrate and product concentrations for non michaelis-menten kinetics in an amperometric biosensor–hyperbolic function and Padé approximants method. Int. J. Electrochem. Sci. 2020, 15, 5682. [Google Scholar] [CrossRef]
- Mallikarjuna, M.; Senthamarai, R. Analytical solution of enzyme catalysis in calcium alginate. In Proceedings of the 6th International Conference on Materials Technology and Applications (ICMTA 2021) AIPCP22-AR-ICMTA, Fukuoka, Japan, 30 October–2 November 2021. [Google Scholar]
- Rajendran, L.; Rahamathunissa, G. Application of He’s variational iteration method in nonlinear boundary value problems in enzyme–substrate reaction diffusion processes: Part 1. The steady-state amperometric response. J. Math. Chem. 2008, 44, 849. [Google Scholar]
- Eswari, A.; Rajendran, L. Application of variational iteration method and electron transfer mediator/catalyst composites in modified electrodes. Nat. Sci. 2010, 2, 612. [Google Scholar] [CrossRef] [Green Version]
- Loghambal, S.; Rajendran, L. Analysis of amperometric enzyme electrodes in the homogeneous mediated mechanism using variational iteration method. Int. J. Electrochem. Sci. 2010, 5, 327. [Google Scholar]
- Devi, M.R.; Rajendran, L. A new mathematical modelling using homotopy perturbation method to solve nonlinear equations in enzymatic glucose fuel cells. Int. J. Math. Arch. 2014, 5, 142. [Google Scholar]
- Ibrahim, M.S.; Pavithra, S.; Saravanakumar, R.; Ashokan, R.; Rajendran, L. Modelling of Non Linear Enzyme Reaction Process Using Variational Iteration Method. Int. J. Comp. Eng. Res. 2016, 6, 2250. [Google Scholar]
- Suganya, G.; Senthamarai, R. Mathematical modeling and analysis of the effect of the rugose spiraling whitefly on coconut trees. AIMS Math. 2022, 7, 13053. [Google Scholar]
- Adomian, G. A review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 1988, 135, 501. [Google Scholar] [CrossRef]
- Liao, S.J. A kind of approximate solution technique which does not depend upon small parameters (II): An application in fluid mechanics. Int. J. Nonlinear Mech. 1997, 32, 815. [Google Scholar] [CrossRef]
- Liao, S.J. Homotopy analysis method for heat radiation equations. Appl. Math. Comput. 2007, 147, 499. [Google Scholar]
- Liao, S.J. Comparison between the homotopy analysis method and homotopy perturbation method. Appl. Math. Comput. 2005, 169, 1186. [Google Scholar] [CrossRef]
- Akbari, M.R.; Ganji, D.D.; Nimafar, M.; Ahmadi, A.R. Significant progress in solution of nonlinear equations at displacement of structure and heat transfer extended surface by new AGM approach. Front. Mech. Eng. 2014, 9, 390–401. [Google Scholar] [CrossRef]
- Pirabaharan, P.; Devi, M.C.; Swaminathan, R.; Rajendran, L.; Lyons, M.E.G. Modelling the current response and sensitivity of oxidase enzyme electrodes, Monitored Amperometrically by the Consumption of Oxygen. Electrochem 2022, 3, 309–321. [Google Scholar] [CrossRef]
- Shanthi, R.; Devi, M.C.; Abukhaled, M.; Lyons, M.E.G.; Rajendran, L. Mathematical modeling of ph-based potentiometric biosensor using Akbari-Ganji method. Int. J. Electrochem. Sci. 2022, 17, 2. [Google Scholar] [CrossRef]
- Padma, S.; Jeyabarathi, P.; Rajendran, L.; Lyons, M.E.G. A kinetic model for amperometric immobilized enzymes at planar, cylindrical and spherical electrodes: The Akbari-Ganji Method. Int. J. Electrochem. Sci. 2022, 17, 114921. [Google Scholar]
- Manimegalai, B.; Lyons, M.E.; Rajendran, L. Mathematical modeling of substrate consumption in a biofilm: Solutions arrived using Akbari-Ganji method. J. Electroanal. Chem. 2021, 880, 114921. [Google Scholar] [CrossRef]
- Vanaja, R.; Jeyabarathi, P.; Rajendran, L.; Lyons, M.E.G. The Analytical Expression of Steady-State Concentration of Mixture of Toluene and N- Propanol in the Biofilm: Akbari-Ganji’s method. Int. J. Electrochem. Sci. 2022, 17, 2. [Google Scholar] [CrossRef]
- Sivasundari, S.A.S.; Rani, R.U.; Lyons, M.E.G.; Rajendran, L. Transport and Kinetics in Biofiltration Membranes: New analytical expressions for concentration profiles of hydrophilic and hydrophobic VOCs Using Taylor’s Series and Akbari-Ganji methods. Int. J. Electrochem. Sci. 2022, 17, 2. [Google Scholar]
- Umadevi, R.; Devi, M.C.; Venugopal, K.; Rajendran, L.; Lyons, M.E. Theoretical analysis of reaction-diffusion process in biocatalyst modified electrodes: Solutions derived via Akbari-Ganji method and Taylor’s series with Ancient Chinese algorithms. Int. J. Electrochem. Sci. 2022, 17, 2. [Google Scholar] [CrossRef]
- Lilly Clarance Mary, M.; Chitra Devi, M.; Meena, A.; Rajendran, L.; Abukhaled, M. A reliable Taylor series solution to the nonlinear reaction-diffusion model representing the steady-state behaviour of a cationic glucose-sensitive membrane. J. Math. Comput. Sci. 2021, 11, 8354. [Google Scholar]
- Vinolyn Sylvia, S.; Joy Salomi, R.; Rajendran, L.; Abukhaled, M. Solving nonlinear reaction–diffusion problem in electrostatic interaction with reaction-generated pH change on the kinetics of immobilized enzyme systems using Taylor series method. J. Math. Chem. 2021, 59, 1332. [Google Scholar] [CrossRef]
- Jalili, B.; Aghaee, N.; Jalili, P.; Ganji, D.D. Novel usage of the curved rectangular fin on the heat transfer of a double-pipe heat exchanger with a nanofluid. Case Stud. Therm. Eng. 2022, 35, 102086. [Google Scholar] [CrossRef]
- Jalili, B.; Ghafoori, H.; Jalili, P. Investigation of carbon nano-tube (CNT) particles effect on the performance of a refrigeration cycle. Int. J. Mater. Sci. Innov. 2014, 2, 8–17. [Google Scholar]
- Jalili, P.; Kazerani, K.; Jalili, B.; Ganji, D.D. Investigation of thermal analysis and pressure drop in non-continuous helical baffle with different helix angles and hybrid nano-particles. Case Stud. Therm. Eng. 2022, 36, 102209. [Google Scholar] [CrossRef]

| Substrate Concentration S | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NUM | AGM Equation (12) | DTM Equation (17) | Error % for AGM | Error % for DTM | NUM | AGM Equation (12) | DTM Equation (17) | Error % for AGM | Error % for DTM | NUM | AGM Equation (12) | DTM Equation (17) | Error % for AGM | Error % for DTM | |
| 0 | 1 | 1 | 1 | 0 | 0 | 0.9535 | 0.9294 | 0.9302 | 2.53 | 2.44 | 0.913 | 0.8667 | 0.8696 | 5.07 | 4.75 |
| 0.25 | 1 | 1 | 1 | 0 | 0 | 0.9576 | 0.9338 | 0.9346 | 2.49 | 2.40 | 0.9206 | 0.8748 | 0.8777 | 4.98 | 4.66 |
| 0.5 | 1 | 1 | 1 | 0 | 0 | 0.9681 | 0.9469 | 0.9477 | 2.19 | 2.11 | 0.9405 | 0.8994 | 0.9022 | 4.37 | 4.07 |
| 0.75 | 1 | 1 | 1 | 0 | 0 | 0.9830 | 0.9689 | 0.9695 | 1.43 | 1.37 | 0.9683 | 0.9409 | 0.9429 | 2.83 | 2.62 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1.0000 | 1.0000 | 1.0000 | 0.00 | 0.00 | 1.0000 | 1.0000 | 1.0000 | 0.00 | 0.00 |
| Average Error % | 0 | 0 | Average Error % | 1.7274 | 1.6652 | Average Error % | 3.4481 | 3.2220 | |||||||
| Substrate Concentration S | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NUM | AGM Equation (12) | DTM Equation (17) | Error % for AGM | Error % for DTM | NUM | AGM Equation (12) | DTM Equation (17) | Error % for AGM | Error % for DTM | NUM | AGM Equation (12) | DTM Equation (17) | Error % for AGM | Error % for DTM | |
| 0 | 1 | 1 | 1 | 0 | 0 | 0.9837 | 0.9755 | 0.9756 | 0.83 | 0.82 | 0.9524 | 0.9294 | 0.9302 | 2.41 | 2.33 |
| 0.25 | 1 | 1 | 1 | 0 | 0 | 0.9851 | 0.9770 | 0.9771 | 0.82 | 0.81 | 0.9565 | 0.9338 | 0.9346 | 2.37 | 2.29 |
| 0.5 | 1 | 1 | 1 | 0 | 0 | 0.9888 | 0.9816 | 0.9817 | 0.73 | 0.72 | 0.9673 | 0.9469 | 0.9477 | 2.11 | 2.03 |
| 0.75 | 1 | 1 | 1 | 0 | 0 | 0.9940 | 0.9893 | 0.9893 | 0.47 | 0.47 | 0.9825 | 0.9689 | 0.9695 | 1.38 | 1.32 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1.0000 | 1.0000 | 1.0000 | 0.00 | 0.00 | 1.0000 | 1.0000 | 1.0000 | 0.00 | 0.00 |
| Average Error % | 0 | 0 | Average Error % | 0.5714 | 0.5653 | Average Error % | 1.6563 | 1.5940 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sivasundari, S.A.S.; Senthamarai, R.; Devi, M.C.; Rajendran, L.; Lyons, M.E.G. Modelling of Irreversible Homogeneous Reaction on Finite Diffusion Layers. Electrochem 2022, 3, 479-491. https://doi.org/10.3390/electrochem3030033
Sivasundari SAS, Senthamarai R, Devi MC, Rajendran L, Lyons MEG. Modelling of Irreversible Homogeneous Reaction on Finite Diffusion Layers. Electrochem. 2022; 3(3):479-491. https://doi.org/10.3390/electrochem3030033
Chicago/Turabian StyleSivasundari, Singaravel Anandhar Salai, Rathinam Senthamarai, Mohan Chitra Devi, Lakshmanan Rajendran, and Michael E. G. Lyons. 2022. "Modelling of Irreversible Homogeneous Reaction on Finite Diffusion Layers" Electrochem 3, no. 3: 479-491. https://doi.org/10.3390/electrochem3030033
APA StyleSivasundari, S. A. S., Senthamarai, R., Devi, M. C., Rajendran, L., & Lyons, M. E. G. (2022). Modelling of Irreversible Homogeneous Reaction on Finite Diffusion Layers. Electrochem, 3(3), 479-491. https://doi.org/10.3390/electrochem3030033







