Lung Cancer Prevalence in Virginia: A Spatial Zipcode-Level Analysis via INLA
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethics Statement
2.2. Data Description
2.2.1. Demographics
2.2.2. Prevalence of Binge Drinking, Smoking, and Obesity
2.2.3. Percent Population below Poverty
2.2.4. Social Deprivation Index (SDI)
2.2.5. Average Daily Air Quality PM2.5 Concentration
2.3. Spatial Statistical Model for LC Counts
2.4. Extension to the Negative Binomial Regression Model
2.5. Spatial Imputation of Missing Covariates
2.6. Model Fitting and Model Comparison Using R-INLA
3. Results
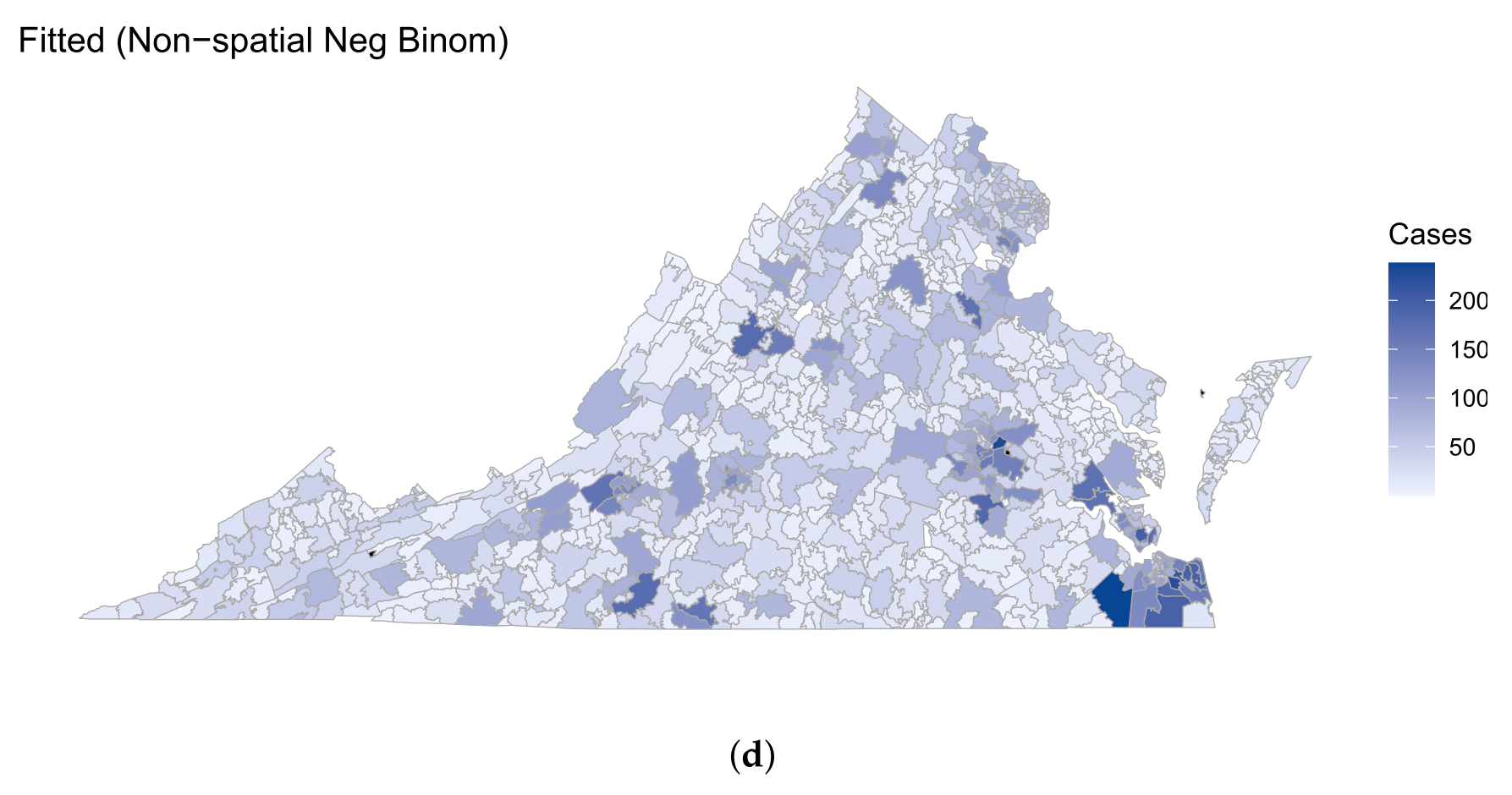
3.1. Model Comparison
3.2. Findings
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Siegel, R.L.; Miller, K.D.; Wagle, N.S.; Jemal, A. Cancer statistics, 2023. CA Cancer J. Clin. 2023, 73, 17–48. [Google Scholar] [CrossRef]
- Cruz, C.S.D.; Tanoue, L.T.; Matthay, R.A. Lung cancer: Epidemiology, etiology, and prevention. Clin. Chest Med. 2011, 32, 605–644. [Google Scholar] [CrossRef] [PubMed]
- Alberg, A.J.; Brock, M.V.; Samet, J.M. Epidemiology of lung cancer: Looking to the future. J. Clin. Oncol. 2005, 23, 3175–3185. [Google Scholar] [CrossRef] [PubMed]
- Powell, H.A.; Iyen-Omofoman, B.; Hubbard, R.B.; Baldwin, D.R.; Tata, L.J. The association between smoking quantity and lung cancer in men and women. Chest 2013, 143, 123–129. [Google Scholar] [CrossRef]
- Lucas, R.M.; Rodney Harris, R.M. On the nature of evidence and ‘proving’causality: Smoking and lung cancer vs. sun exposure, vitamin D and multiple sclerosis. Int. J. Environ. Res. Public Health 2018, 15, 1726. [Google Scholar] [CrossRef] [PubMed]
- O’Keeffe, L.M.; Taylor, G.; Huxley, R.R.; Mitchell, P.; Woodward, M.; Peters, S.A. Smoking as a risk factor for lung cancer in women and men: A systematic review and meta-analysis. BMJ Open 2018, 8, e021611. [Google Scholar] [CrossRef] [PubMed]
- Remen, T.; Pintos, J.; Abrahamowicz, M.; Siemiatycki, J. Risk of lung cancer in relation to various metrics of smoking history: A case-control study in Montreal. BMC Cancer 2018, 18, 1275. [Google Scholar] [CrossRef]
- Pierce, J.P.; Messer, K.; White, M.M.; Kealey, S.; Cowling, D.W. Forty Years of Faster Decline in Cigarette Smoking in California Explains Current Lower Lung Cancer RatesSmoking Trends in California and Rest of Nation. Cancer Epidemiol. Biomarkers Prev. 2010, 19, 2801–2810. [Google Scholar] [CrossRef]
- United States. Public Health Service. Office of the Surgeon General; Center for Chronic Disease Prevention and Health Promotion (U.S.). Office on Smoking and Health; Centers for Disease Control (U.S.). Reducing the Health Consequences of Smoking: 25 Years of Progress. A Report of the Surgeon General. 1989. Available online: https://stacks.cdc.gov/view/cdc/13240/cdc_13240_DS1.pdf (accessed on 14 January 2024).
- Centers for Disease Control and Prevention (CDC). State-specific trends in lung cancer incidence and smoking–United States, 1999–2008. MMWR. Morb. Mortal. Wkly. Rep. 2011, 60, 1243–1247. [Google Scholar]
- Bailey-Wilson, J.E.; Sellers, T.A.; Elston, R.C.; Evens, C.C.; Rothschild, H. Evidence for a major gene effect in early-onset lung cancer. J. La. State Med. Soc. Off. Organ La. State Med. Soc. 1993, 145, 157–162. [Google Scholar]
- Sinha, R.; Kulldorff, M.; Curtin, J.; Brown, C.C.; Alavanja, M.C.; Swanson, C.A. Fried, well-done red meat and riskof lung cancer in women (United States). Cancer Causes Control 1998, 9, 621–630. [Google Scholar] [CrossRef]
- Bandera, E.V.; Freudenheim, J.L.; Vena, J.E. Alcohol consumption and lung cancer: A review of the epidemiologic evidence. Cancer Epidemiol. Biomarkers Prev. 2001, 10, 813–821. [Google Scholar] [PubMed]
- Korte, J.E.; Brennan, P.; Henley, S.J.; Boffetta, P. Dose-specific meta-analysis and sensitivity analysis of the relation between alcohol consumption and lung cancer risk. Am. J. Epidemiol. 2002, 155, 496–506. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Hu, J.; Ugnat, A.M.; Semenciw, R.; Fincham, S. Socioeconomic status and lung cancer risk in Canada. Int. J. Epidemiol. 2001, 30, 809–817. [Google Scholar] [CrossRef] [PubMed]
- Uguen, M.; Dewitte, J.D.; Marcorelles, P.; Loddé, B.; Pougnet, R.; Saliou, P.; De Braekeleer, M.; Uguen, A. Asbestos-related lung cancers: A retrospective clinical and pathological study. Mol. Clin. Oncol. 2017, 7, 135–139. [Google Scholar] [CrossRef]
- Wei, S.; Zhang, H.; Tao, S. A review of arsenic exposure and lung cancer. Toxicol. Res. 2019, 8, 319–327. [Google Scholar] [CrossRef]
- Brüske-Hohlfeld, I. Environmental and Occupational Risk Factors for Lung Cancer. In Cancer Epidemiology: Modifiable Factors; Verma, M., Ed.; Humana Press: Totowa, NJ, USA, 2009; pp. 3–23. [Google Scholar]
- Yu, X.Q.; Luo, Q.; Hughes, S.; Wade, S.; Caruana, M.; Canfell, K.; O’Connell, D.L. Statistical projection methods for lung cancer incidence and mortality: A systematic review. BMJ Open 2019, 9, e028497. [Google Scholar] [CrossRef]
- Hu, L.; Griffith, D.A.; Chun, Y. Space-time statistical insights about geographic variation in lung cancer incidence rates: Florida, USA, 2000–2011. Int. J. Environ. Res. Public Health 2018, 15, 2406. [Google Scholar] [CrossRef]
- Block, R. Software review: Scanning for clusters in space and time: A tutorial review of SatScan. Soc. Sci. Comput. Rev. 2007, 25, 272–278. [Google Scholar] [CrossRef]
- Shi, X. A geocomputational process for characterizing the spatial pattern of lung cancer incidence in New Hampshire. Ann. Assoc. Am. Geogr. 2009, 99, 521–533. [Google Scholar] [CrossRef]
- Christian, W.J.; Vanderford, N.L.; McDowell, J.; Huang, B.; Durbin, E.B.; Absher, K.J.; Walker, C.J.; Arnold, S.M. Spatiotemporal analysis of lung cancer histological types in Kentucky, 1995–2014. Cancer Control 2019, 26, 1073274819845873. [Google Scholar] [CrossRef] [PubMed]
- Moraga, P.; Cramb, S.M.; Mengersen, K.L.; Pagano, M. A geostatistical model for combined analysis of point-level and area-level data using INLA and SPDE. Spat. Stat. 2017, 21, 27–41. [Google Scholar] [CrossRef]
- Moraga, P. Geospatial Health Data: Modeling and Visualization with R-INLA and Shiny; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Besag, J.; York, J.; Mollié, A. Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991, 43, 1–20. [Google Scholar] [CrossRef]
- Leroux, B.G.; Lei, X.; Breslow, N. Estimation of disease rates in small areas: A new mixed model for spatial dependence. In Proceedings of the Statistical Models in Epidemiology, the Environment, and Clinical Trials; Springer: New York, NY, USA, 2000; pp. 179–191. [Google Scholar]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, M.; Ji, M.; Fan, J.; Xie, J.; Wei, X.; Jiang, X.; Xu, J.; Chen, L.; Yin, R.; et al. Air pollution, genetic factors, and the risk of lung cancer: A prospective study in the UK Biobank. Am. J. Respir. Crit. Care Med. 2021, 204, 817–825. [Google Scholar] [CrossRef]
- Gómez-Rubio, V.; Cameletti, M.; Blangiardo, M. Missing data analysis and imputation via latent Gaussian Markov random fields. SORT-Stat. Oper. Res. Trans. 2022, 46, 217–244. [Google Scholar]
- Rue, H.; Held, L. Gaussian Markov Random Fields: Theory and Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2005. [Google Scholar]
- Moran, P.A. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Butler, D.C.; Petterson, S.; Phillips, R.L.; Bazemore, A.W. Measures of social deprivation that predict health care access and need within a rational area of primary care service delivery. Health Serv. Res. 2013, 48, 539–559. [Google Scholar] [CrossRef]
- Phillips, R.L.; Liaw, W.; Crampton, P.; Exeter, D.J.; Bazemore, A.; Vickery, K.D.; Petterson, S.; Carrozza, M. How other countries use deprivation indices—And why the United States desperately needs one. Health Aff. 2016, 35, 1991–1998. [Google Scholar] [CrossRef]
- Holland, D. Fused Air Quality Predictions Using Downscaling. Research Triangle Park, NC US Environmental Protection Agency. 2012. Available online: https://www.epa.gov/sites/default/files/2016-07/documents/data_fusion_meta_file_july_2016.pdf (accessed on 17 January 2024).
- Yirga, A.A.; Melesse, S.F.; Mwambi, H.G.; Ayele, D.G. Negative binomial mixed models for analyzing longitudinal CD4 count data. Sci. Rep. 2020, 10, 16742. [Google Scholar] [CrossRef]
- Hilbe, J.M. Negative Binomial Regression; Cambridge University Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Hilbe, J.M. Modeling Count Data; Cambridge University Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Gschlößl, S.; Czado, C. Modelling count data with overdispersion and spatial effects. Stat. Pap. 2008, 49, 531–552. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Vounatsou, P. Proper multivariate conditional autoregressive models for spatial data analysis. Biostatistics 2003, 4, 11–15. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Rubio, V. Bayesian Inference with INLA; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Lindgren, F.; Rue, H. Bayesian spatial modelling with R-INLA. J. Stat. Softw. 2015, 63, 1–25. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 721–741. [Google Scholar] [CrossRef] [PubMed]
- Bakka, H.; Rue, H.; Fuglstad, G.A.; Riebler, A.; Bolin, D.; Illian, J.; Krainski, E.; Simpson, D.; Lindgren, F. Spatial modeling with R-INLA: A review. Wiley Interdiscip. Rev. Comput. Stat. 2018, 10, e1443. [Google Scholar] [CrossRef]
- Ugarte, M.D.; Adin, A.; Goicoa, T.; Militino, A.F. On fitting spatio-temporal disease mapping models using approximate Bayesian inference. Stat. Methods Med. Res. 2014, 23, 507–530. [Google Scholar] [CrossRef] [PubMed]
- Bivand, R.; Gómez-Rubio, V.; Rue, H. Spatial data analysis with R-INLA with some extensions. J. Stat. Softw. 2015, 63, 1–31. [Google Scholar] [CrossRef]
- Gelman, A.; Hwang, J.; Vehtari, A. Understanding predictive information criteria for Bayesian models. Stat. Comput. 2014, 24, 997–1016. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Practical Use of the Information-Theoretic Approach; Springer: New York, NY, USA, 1998. [Google Scholar]
- Sayani, A.; Vahabi, M.; O’Brien, M.A.; Liu, G.; Hwang, S.; Selby, P.; Nicholson, E.; Giuliani, M.; Eng, L.; Lofters, A. Advancing health equity in cancer care: The lived experiences of poverty and access to lung cancer screening. PLoS ONE 2021, 16, e0251264. [Google Scholar] [CrossRef]
- Jemal, A.; Miller, K.D.; Ma, J.; Siegel, R.L.; Fedewa, S.A.; Islami, F.; Devesa, S.S.; Thun, M.J. Higher lung cancer incidence in young women than young men in the United States. N. Engl. J. Med. 2018, 378, 1999–2009. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Yang, X.; Huang, Y.; Zhao, M.; Li, M.; Ma, K.; Yin, J.; Zhan, C.; Wang, Q. Trends in the incidence, treatment, and survival of patients with lung cancer in the last four decades. Cancer Manag. Res. 2019, 11, 943–953. [Google Scholar] [CrossRef]
- Venuta, F.; Diso, D.; Onorati, I.; Anile, M.; Mantovani, S.; Rendina, E.A. Lung cancer in elderly patients. J. Thorac. Dis. 2016, 8, S908–S914. [Google Scholar] [CrossRef]
- Redondo-Sánchez, D.; Petrova, D.; Rodríguez-Barranco, M.; Fernández-Navarro, P.; Jiménez-Moleón, J.J.; Sánchez, M.J. Socio-economic inequalities in lung cancer outcomes: An overview of systematic reviews. Cancers 2022, 14, 398. [Google Scholar] [CrossRef] [PubMed]
- Krist, A.H.; Davidson, K.W.; Mangione, C.M.; Barry, M.J.; Cabana, M.; Caughey, A.B.; Davis, E.M.; Donahue, K.E.; Doubeni, C.A.; Kubik, M.; et al. Screening for lung cancer: US Preventive Services Task Force recommendation statement. J. Am. Med. Assoc. 2021, 325, 962–970. [Google Scholar]
- Papadogeorgou, G.; Samanta, S. Spatial causal inference in the presence of unmeasured confounding and interference. arXiv 2023, arXiv:2303.08218. [Google Scholar]

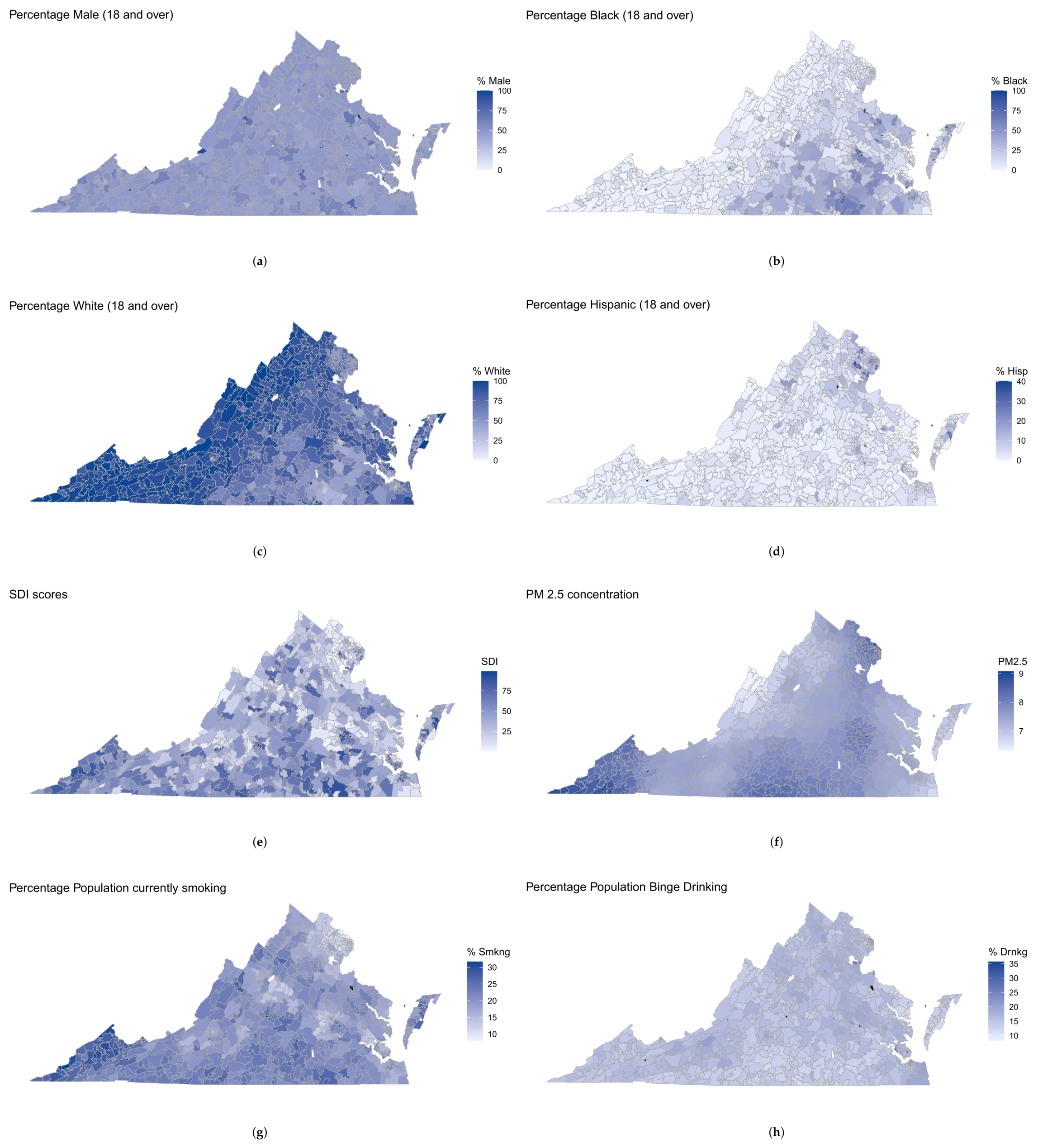

| Zip Code | City | County | LC Counts |
|---|---|---|---|
| 23803 | Petersburg | Petersburg (City) | 234 |
| 23452 | VA Beach | VA Beach (City) | 230 |
| 23464 | VA Beach | VA Beach (City) | 218 |
| 23462 | VA Beach | VA Beach (City) | 202 |
| 23455 | VA Beach | VA Beach (City) | 199 |
| 23454 | VA Beach | VA Beach (City) | 197 |
| 23434 | Suffolk | Suffolk (City) | 196 |
| 23320 | Chesapeake | Cheasapeake (City) | 194 |
| 22407 | Fredericksburg | Spotsylavnia | 194 |
| 23451 | VA Beach | VA Beach (City) | 193 |
| 23223 | Richmond | Richmond (City) | 189 |
| 22980 | Waynesboro | Waynesboro (City) | 188 |
| 23322 | Chesapeake | Cheasapeake (City) | 181 |
| 24153 | Salem | Salem (City) | 180 |
| 23666 | Hampton | Hampton (City) | 177 |
| Variables | Mean (SD) |
|---|---|
| Gender (percent) | |
| Female | 50.94 (8.80) |
| Male | 49.06 (8.80) |
| Race (percent) | |
| Black | 16.38 (18.84) |
| White | 77.95 (20.24) |
| Other (Asian, NHPI, two or more races, etc.) | 5.67 (7.84) |
| Ethnicity (percent) | |
| Hispanic or Latino | 4.05 (5.83) |
| Not Hispanic or Latino | 95.95 (5.83) |
| Percent population with age | 24.43 (13.16) |
| Percent population currently smoking | 19.87 (4.40) |
| Percent population binge drinking | 15.99 (2.80) |
| Percent population obese | 33.92 (5.40) |
| Percent population below poverty | 11.46 (9.80) |
| Social Deprivation Index (SDI) | 38.09 (24.95) |
| Daily Air Quality PM2.5 Concentration | 7.58 (0.48) |
| Model | DIC | WAIC | RMSE | RSE |
|---|---|---|---|---|
| MCAR Imputation model | ||||
| Spatial Poisson GLM | 5007.13 | 5010.27 | 3.55 | 0.0072 |
| Spatial NB GLM | 5062.60 | 5057.44 | 4.06 | 0.0095 |
| Linear regression Imputation model | ||||
| Non-spatial Poisson GLM | 5446.90 | 5465.77 | 8.94 | 0.046 |
| Non-spatial NB GLM | 5205.08 | 5207.39 | 9.56 | 0.052 |
| No Imputation model | ||||
| Spatial Poisson GLM | 5011.08 | 5012.52 | 3.56 | 0.0073 |
| Spatial NB GLM | 5041.98 | 5040.88 | 3.85 | 0.0085 |
| Non-spatial Poisson GLM | 5446.34 | 5464.33 | 8.94 | 0.046 |
| Non-spatial NB GLM | 5207.47 | 5210.06 | 9.55 | 0.052 |
| Covariates | Posterior Mean | Posterior SD | 95% Credible Interval |
|---|---|---|---|
| SDI score | 0.050 | 0.014 | (0.021, 0.076) |
| PM2.5 | −0.089 | 0.015 | (−0.118, −0.059) |
| Race (w.r.t. Others) | |||
| % black | 0.212 | 0.046 | (0.122, 0.301) |
| % white | 0.255 | 0.046 | (0.165, 0.345) |
| Ethnicity (w.r.t. non-hispanic) | |||
| % hispanic | −0.039 | 0.015 | (−0.068, −0.009) |
| Gender (w.r.t. female) | |||
| % male | −0.096 | 0.020 | (−0.137, −0.056) |
| Age (w.r.t. < 65 years) | |||
| % over 65 years | 0.211 | 0.022 | (0.167, 0.254) |
| Binge drinking idx | −0.103 | 0.023 | (−0.150, −0.058) |
| Smoking idx | 0.136 | 0.030 | (0.075, 0.192) |
| Obesity idx | 0.046 | 0.030 | (−0.011, 0.108) |
| Poverty idx | −0.083 | 0.026 | (−0.135, −0.031) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahoo, I.; Zhao, J.; Deng, X.; Cockburn, M.G.; Tossas, K.; Winn, R.; Bandyopadhyay, D. Lung Cancer Prevalence in Virginia: A Spatial Zipcode-Level Analysis via INLA. Curr. Oncol. 2024, 31, 1129-1144. https://doi.org/10.3390/curroncol31030084
Sahoo I, Zhao J, Deng X, Cockburn MG, Tossas K, Winn R, Bandyopadhyay D. Lung Cancer Prevalence in Virginia: A Spatial Zipcode-Level Analysis via INLA. Current Oncology. 2024; 31(3):1129-1144. https://doi.org/10.3390/curroncol31030084
Chicago/Turabian StyleSahoo, Indranil, Jinlei Zhao, Xiaoyan Deng, Myles Gordon Cockburn, Kathy Tossas, Robert Winn, and Dipankar Bandyopadhyay. 2024. "Lung Cancer Prevalence in Virginia: A Spatial Zipcode-Level Analysis via INLA" Current Oncology 31, no. 3: 1129-1144. https://doi.org/10.3390/curroncol31030084
APA StyleSahoo, I., Zhao, J., Deng, X., Cockburn, M. G., Tossas, K., Winn, R., & Bandyopadhyay, D. (2024). Lung Cancer Prevalence in Virginia: A Spatial Zipcode-Level Analysis via INLA. Current Oncology, 31(3), 1129-1144. https://doi.org/10.3390/curroncol31030084





