Traumatic Impact Assessment of CPR Load on a Human Ribcage
Abstract
:1. Introduction
2. Materials and Methods
3. Numerical Procedure
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Agnew, A.; Kang, Y.; Moorhouse, K.; Herriott, R. Age-Related changes in stiffness in human ribs. In Proceedings of the International Research Council on Biomechanics of Injury Conference, Gothenburg, Sweden, 11–13 September 2013. [Google Scholar]
- Augenstein, J.; Perdeck, E.; Martin, P.; Bowen, J.; Stratton, J.; Horton, T.; Singer, M.; Digges, K.; Steps, J. Injuries to restrained occupants in far-side crashes. In Proceedings of the Annual Meetings/Association for the Advancement of Automotive Medicine, Chicago, IL, USA, 2–4 October 2000. [Google Scholar]
- Schmitt, K.; Niederer, P.; Muser, M.; Walz, F. Trauma Biomechanics: Accidental Injury in Traffic and Sports, Zurich, Switzerland; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Baudrit, P.; Leport, T. Rib strain fields corridors inside and oblique impact based on PMHS tests. In Proceedings of the Thirty-Eight International Workshop, Scottsdale, AZ, USA, 24–29 October 2010. [Google Scholar]
- Cavanaugh, J.; Jepsen, K.; King, A. Quasi-static frontal loading of the thorax of human cadavers and the Hybrid III dummy. In Proceedings of the 16th Annual International Workshop on Human Subjects for Biomechanical Research, Atlanta, GA, USA, 16 October 1988. [Google Scholar]
- Duma, S.; Kemper, A.; Stitzel, J.; McNally, C.; Kennedy, E.; Matsuoka, F. Rib fracture timing in dynamic belt tests with human cadavers. Clin. Anat. 2011, 24, 327–338. [Google Scholar] [CrossRef]
- Perz, R.; Toczyski, J.; Kindig, M.; Ito, D.; Ejima, S.; Yasuki, T.; Crandall, J. Evaluation of the geometrical properties distribution along the human ribs using different x-ray imaging methods. In Proceedings of the International Research Council on Biomechanics of Injury Conference, Gothenburg, Sweden, 11–13 September 2013. [Google Scholar]
- Holcombe, S.; Ejima, S.; Huhdanpaa, H.; Jones, A.; Wang, S. Ribcage characterization for FE using automatic CT processing. In Proceedings of the 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Paris, France, 14–17 May 2008. [Google Scholar]
- Mohr, M.; Engel, C.; Bottlang, M.; Abrams, E. Cross-sectional geometry of human ribs. Cortex 2003, 80, 2–10. [Google Scholar]
- Aguilar-Perez, L.; Torres-San-Miguel, C.; Ceccarelli, M. Design of a methodology for the determination of the mechanical rib stiffness as injury index. In New Trends in Medical and Service Robotics; Rauter, G., Cattin, P.C., Zam, A., Riener, R., Carbone, G., Pisla, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 62–69. [Google Scholar]
- Boresi, A.; Schmidt, R. Advanced Mechanics of Materials, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Devon, A.; Kang, Y.; Agnew, A.; Kemper, A. The effect of injurious whole rib loading on ribcortical bone material properties. In Proceedings of the International Research Council on the Biomechanics of Injury Conference, Athens, Greece, 12–14 September 2018. [Google Scholar]
- Yoganandan, N.; Pintar, F. Biomechanics of human thoracic ribs. J. Biomech. Eng. 1998, 120, 100–104. [Google Scholar] [CrossRef] [PubMed]
- Roth, S.; Torres, F.; Feuerstein, P.; Thoral-Pierre, K. Anthropometric dependence of the response of a thorax FE model under high speed loading: Validation and real world accident replication. Comput. Methods Programs Biomed. 2013, 110, 160–170. [Google Scholar] [CrossRef]
- Currey, J. The structure and mechanics of bone. J. Mater. Sci. 2012, 47, 41–54. [Google Scholar] [CrossRef]
- Kieser, J.; Weller, S.; Swain, M.; Neil, W.; Das, R. Compressive rib fracture: Peri-mortem and post-mortem trauma patterns in a pig model. Leg. Med. 2013, 15, 193–201. [Google Scholar] [CrossRef] [PubMed]
- Pezowics, C.; Glowacki, M. The mechanical properties of human ribs in young adult. Acta Bioeng. Biomech. 2012, 14, 53–60. [Google Scholar]
- Gilchrist, M. IUTAM Symposium on Impact Biomechanics: From Fundamental Insights to Applications; Springer: Dublin, Ireland, 2005. [Google Scholar]
- Forbes, A. Development of a Human Body Model for the Analysis of Side Impact. Master’s Thesis, Department of Mechanical Engineering, Waterloo, ON, Canada, 2005. [Google Scholar]
- Stein, I.; Granik, G. Rib structure and bending strength: An autopsy study. Calcif. Tissue Res. 1976, 20, 61–73. [Google Scholar] [CrossRef] [PubMed]
- Abellán, D.; Sánchez, M.; Martínez, L. Frontal crashworthiness characterization of a vehicle segment using curve comparison metrics. Accid. Anal. Prev. 2018, 117, 136–144. [Google Scholar] [CrossRef] [PubMed]
- Awoukeng, G.; Thoral, K.; Roth, S. Biomechanical model of the thorax under blast loading: A three-dimensional numerical study. Int. J. Numer. Methods Biomed. Eng. 2014, 12, 1667–1678. [Google Scholar]
- Moerman, K. GIBBON: The geometry and image-based bioengineering add-on. J. Open-Source Softw. 2018, 3, 506. [Google Scholar] [CrossRef]
- Mohr, M.; Abrams, E.; Engel, C.; Long, W.; Bottlang, M. Geometry of humans ribs pertinent to orthopedic chest wall reconstruction. J. Biomech. 2007, 40, 1310–1317. [Google Scholar] [CrossRef] [PubMed]
- Roberts, S.; Chen, P. Global geometric characteristics of typical human ribs. J. Biomech. 1972, 5, 191–201. [Google Scholar] [CrossRef]
- Si, H. TetGen, a delaunay-Based quality tetrahedral mesh generator. ACM Trans. Math. Softw. 2015, 41, 1–36. [Google Scholar] [CrossRef]
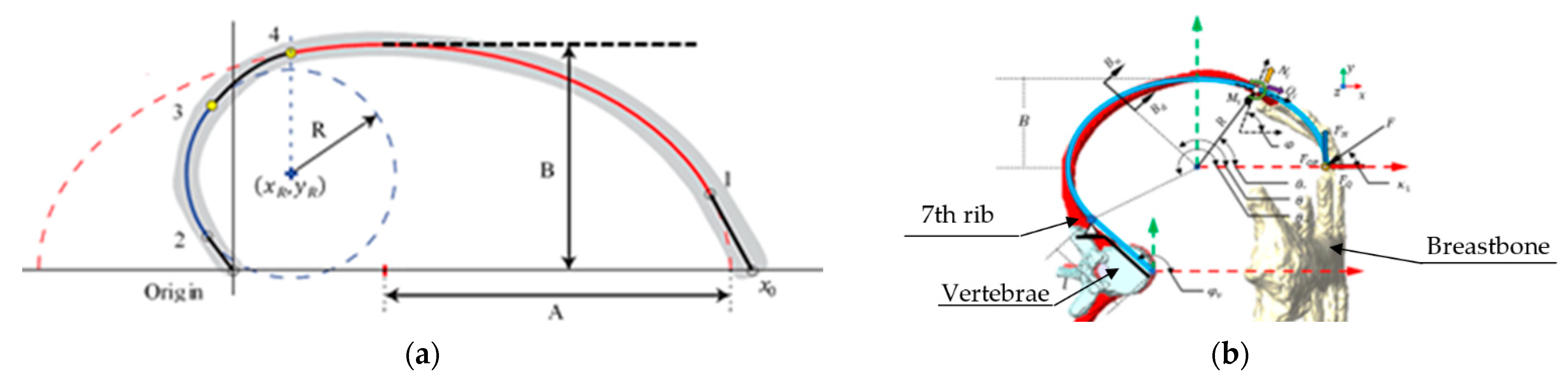
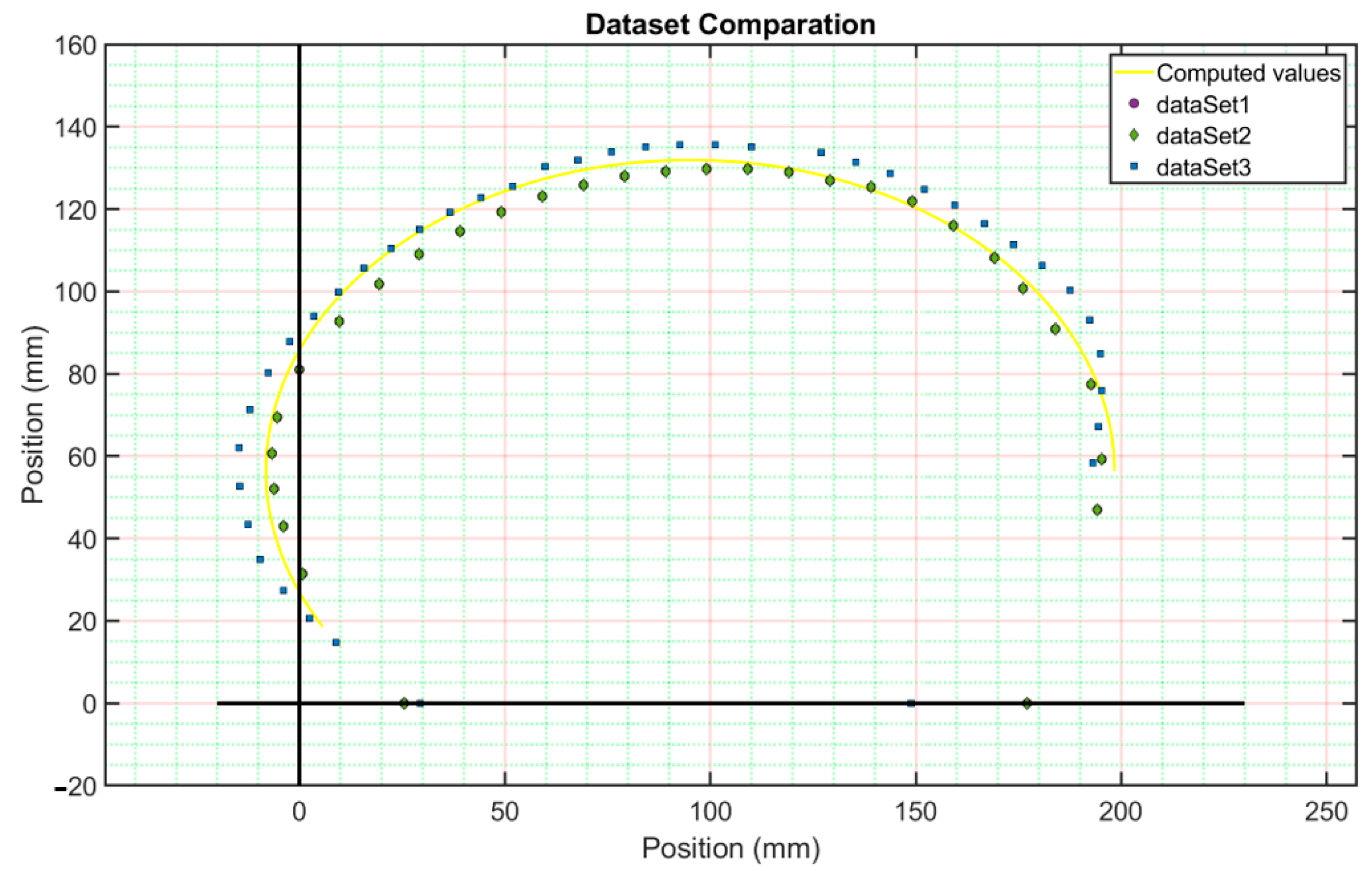

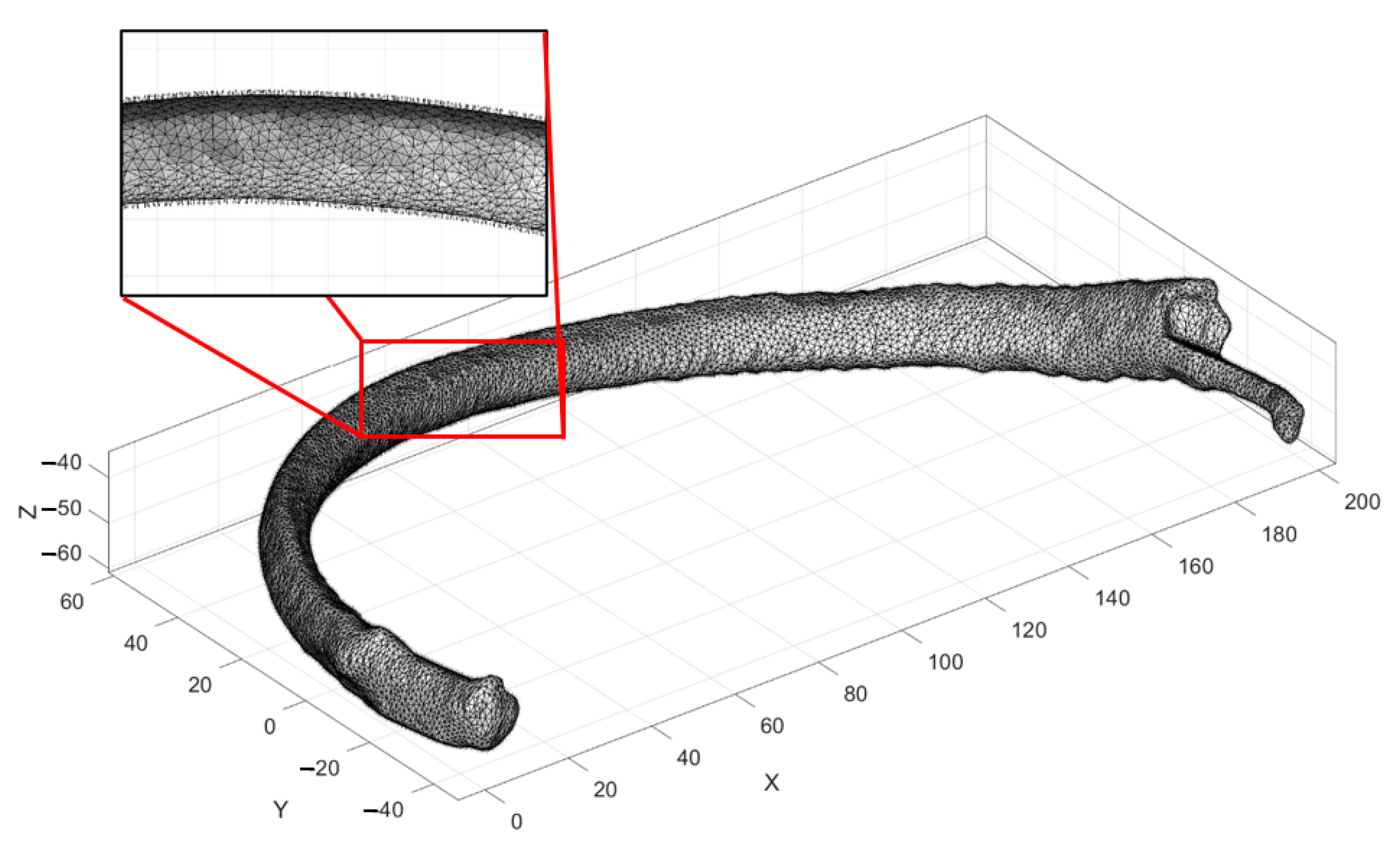
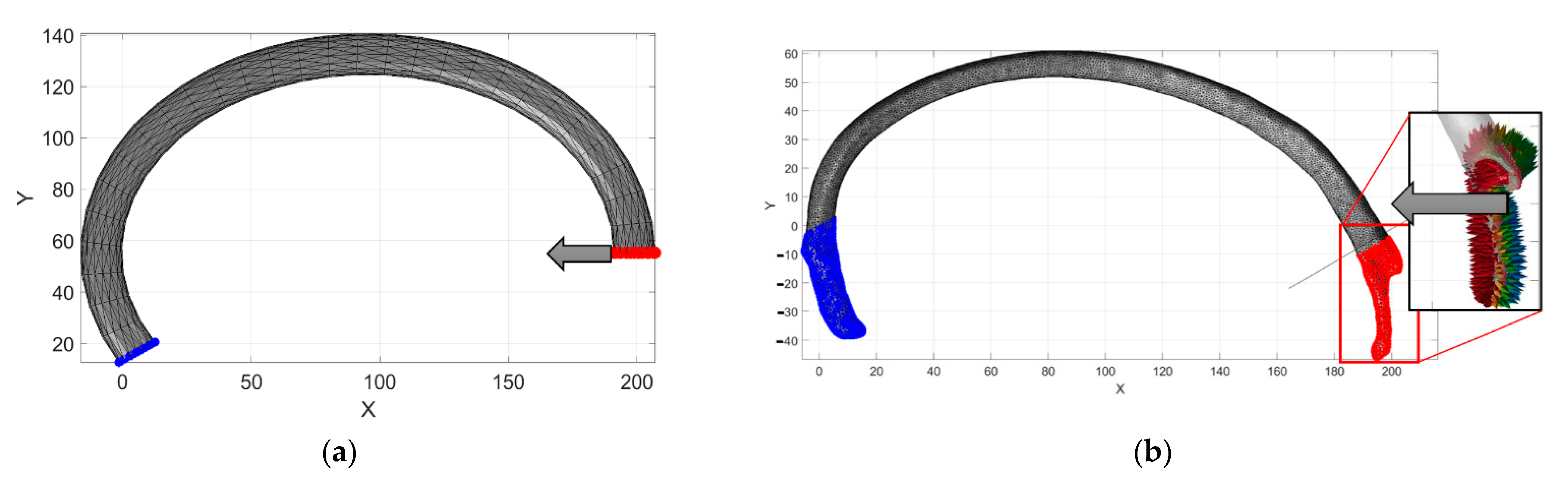
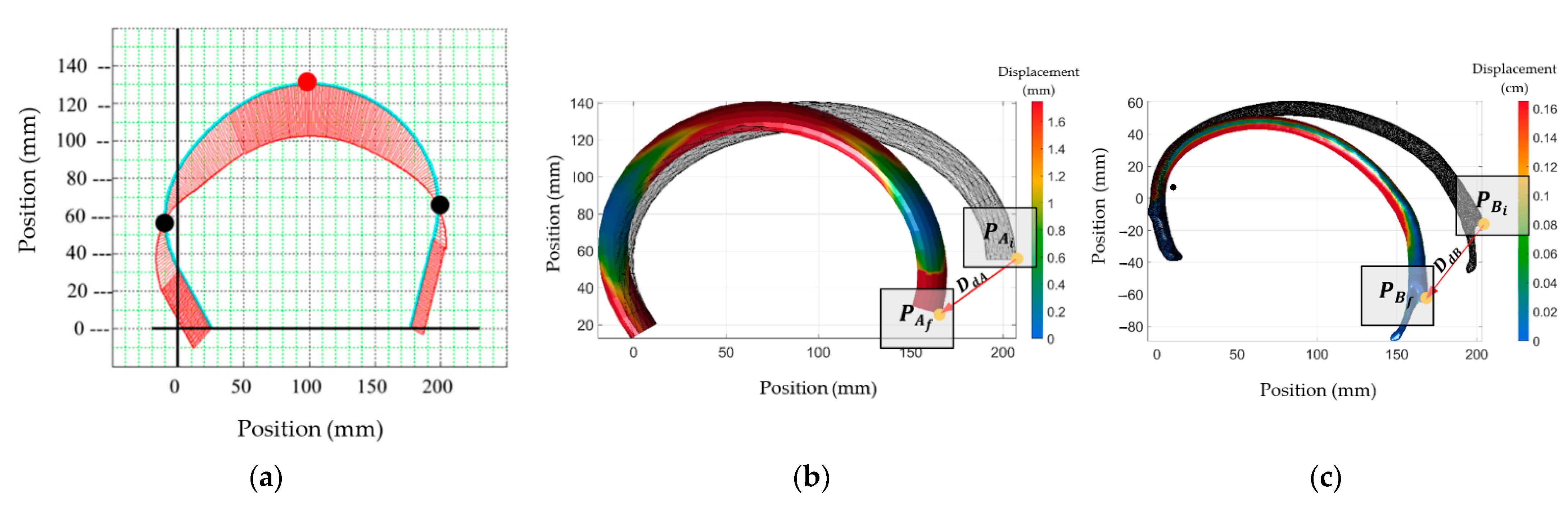
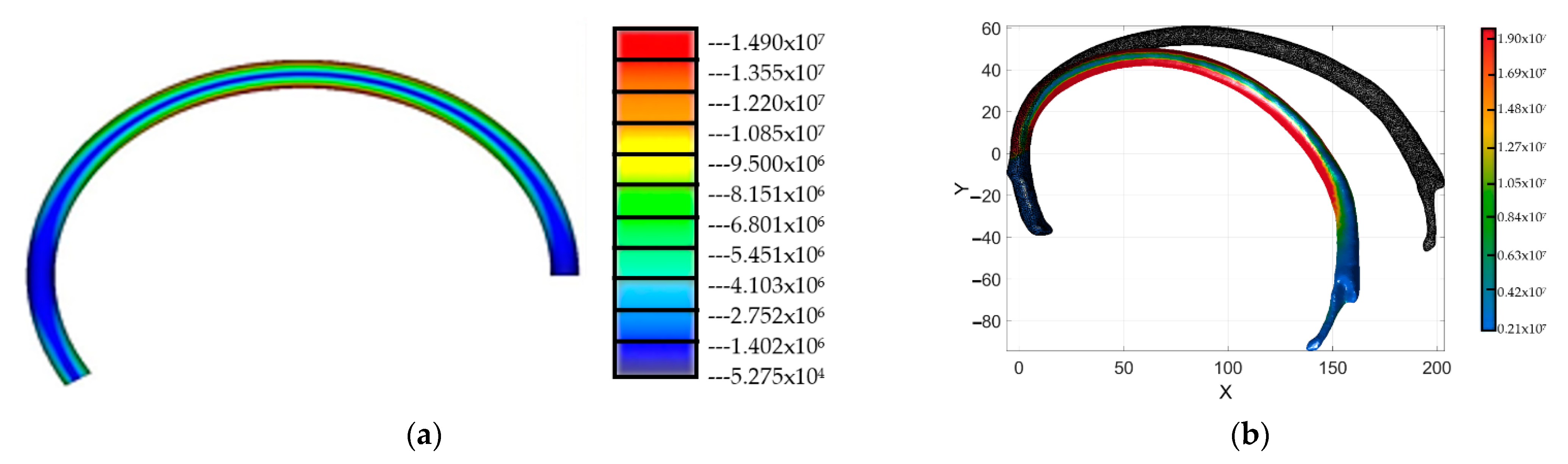

| Dataset 1 | Dataset 2 | Dataset 3 | Dataset 4 | |
|---|---|---|---|---|
| Age | 75 | 21 | 43 | 22 |
| Genre | M | M | F | M |
| Voxel size | ||||
| Z (mm) | 1.5 | 2 | 4 | 1 |
| X (mm) | 0.68 | 0.97 | 0.68 | 0.97 |
| Y (mm) | 0.68 | 0.97 | 0.68 | 0.97 |
| Wide side (W, mm) | 96.04 | 106 | 93.5 | 99 |
| Short side (H, mm) | 63.00 | 73.5 | 74.5 | 73 |
| The Radius of the Cross-Section | ||||
| Z1 (mm) | 16.22 | 20.70 | 19 | 17.7 |
| Z2 (mm) | 11.02 | 12.80 | 7.34 | 8.56 |
| Y1 (mm) | 10.48 | 11.50 | 10.5 | 11.6 |
| Y2 (mm) | 4.88 | 4.40 | 2.51 | 3.79 |
| Author | Maximum Payload Application Reported before Breaking | Young’s Module (E, GPa) | Velocity (mm/min) | σu (MPa) |
|---|---|---|---|---|
| Yoganandan [13] | 153 | 2.37 | 2.50 | 2.102 |
| Roth [14] | --- | 14.00 | --- | 70.00 |
| Currey [15] | --- | 13.00 | --- | 110.00 |
| Kieser [16] | 150 | 4.70 | 10.00 | 53.33 |
| Pezowics [17] | --- | 5.97 | --- | --- |
| Gilchrist [18] | --- | 11.50 | --- | --- |
| Forbes [19] | --- | 26.00 | --- | --- |
| Stein y Granik [20] | 226.80 | 11.50 | 2.54 | 106.00 |
| Martínez-Sáez [21] | --- | 7.50 | 1.70 | --- |
| Goumtcha [22] | --- | 14.00 | --- | 70.00 |
| Payload (N) | δx (mm) | Ut (J) | k | ||
|---|---|---|---|---|---|
| The main vertical axis of the rib cross-section | BONE | 15 | 1.5266 | 0.2149 | 0.1844 |
| 30 | 3.0532 | 0.8597 | |||
| 45 | 4.5797 | 1.9343 | |||
| 90 | 9.1595 | 7.7372 | |||
| 180 | 18.319 | 30.949 | |||
| 200 | 20.3544 | 38.2086 | |||
| 220 | 22.3899 | 46.2324 | |||
| 240 | 24.4253 | 55.0204 | |||
| PLASTIC | 15 | 7.3866 | 0.8321 | 0.0305 | |
| 30 | 14.7732 | 3.3284 | |||
| 45 | 22.1598 | 7.4889 | |||
| 90 | 44.3195 | 29.9554 | |||
| 180 | 88.6391 | 119.8217 | |||
| 200 | 98.4879 | 147.928 | |||
| 220 | 108.3366 | 178.9929 | |||
| 240 | 118.1854 | 213.0164 | |||
| STEEL | 15 | 0.1294 | 0.0157 | 1.8734 | |
| 30 | 0.2588 | 0.0628 | |||
| 45 | 0.3882 | 0.1412 | |||
| 90 | 0.7765 | 0.5648 | |||
| 180 | 1.553 | 2.2591 | |||
| 200 | 1.7255 | 2.789 | |||
| 220 | 1.8981 | 3.3747 | |||
| 240 | 2.0706 | 4.0162 | |||
| PLASTIC 2 × the cross-section | 15 | 0.4641 | 0.0846 | 0.786 | |
| 30 | 0.9282 | 0.3386 | |||
| 45 | 1.3923 | 0.7618 | |||
| 90 | 2.7847 | 3.0473 | |||
| 180 | 5.5693 | 12.1892 | |||
| 200 | 6.1882 | 15.0484 | |||
| 220 | 6.807 | 18.2086 | |||
| 240 | 7.4258 | 21.6697 | |||
| Horizontal main axis of the cross rib section | PLASTIC | 15 | 1.5917 | 15.9855 | 0.0125 |
| 30 | 6.3667 | 31.9709 | |||
| 45 | 14.325 | 47.9564 | |||
| 90 | 57.3 | 95.9128 | |||
| 180 | 229.1999 | 191.8256 | |||
| 200 | 282.9628 | 213.1396 | |||
| 220 | 342.385 | 234.4535 | |||
| 240 | 407.4664 | 255.7675 | |||
| STEEL | 15 | 0.029 | 0.2799 | 0.7399 | |
| 30 | 0.1159 | 0.5598 | |||
| 45 | 0.2608 | 0.8397 | |||
| 90 | 1.0433 | 1.6794 | |||
| 180 | 4.1732 | 3.3588 | |||
| 200 | 5.1521 | 3.7319 | |||
| 220 | 6.2341 | 4.1051 | |||
| 240 | 7.419 | 4.4783 | |||
| PLASTIC 2 × the cross-section | 15 | 0.1321 | 1.0015 | 0.2634 | |
| 30 | 0.5285 | 2.0031 | |||
| 45 | 1.1891 | 3.0046 | |||
| 90 | 4.7563 | 6.0093 | |||
| 180 | 19.0254 | 12.0185 | |||
| 200 | 23.4881 | 13.3539 | |||
| 220 | 28.4206 | 14.6893 | |||
| 240 | 33.8229 | 16.0247 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar-Pérez, L.A.; Torres-SanMiguel, C.R.; Ceccarelli, M.; Urriolagoitia-Calderón, G.M. Traumatic Impact Assessment of CPR Load on a Human Ribcage. Int. J. Environ. Res. Public Health 2022, 19, 3414. https://doi.org/10.3390/ijerph19063414
Aguilar-Pérez LA, Torres-SanMiguel CR, Ceccarelli M, Urriolagoitia-Calderón GM. Traumatic Impact Assessment of CPR Load on a Human Ribcage. International Journal of Environmental Research and Public Health. 2022; 19(6):3414. https://doi.org/10.3390/ijerph19063414
Chicago/Turabian StyleAguilar-Pérez, Luis Antonio, Christopher René Torres-SanMiguel, Marco Ceccarelli, and Guillermo Manuel Urriolagoitia-Calderón. 2022. "Traumatic Impact Assessment of CPR Load on a Human Ribcage" International Journal of Environmental Research and Public Health 19, no. 6: 3414. https://doi.org/10.3390/ijerph19063414
APA StyleAguilar-Pérez, L. A., Torres-SanMiguel, C. R., Ceccarelli, M., & Urriolagoitia-Calderón, G. M. (2022). Traumatic Impact Assessment of CPR Load on a Human Ribcage. International Journal of Environmental Research and Public Health, 19(6), 3414. https://doi.org/10.3390/ijerph19063414








