Long-Term Variations of Global Solar Radiation and Its Potential Effects at Dome C (Antarctica)
Abstract
1. Introduction
2. Data and Methodology
2.1. Measurements and Data Selection
2.2. Model Formulation, Development and Evaluation
3. Results
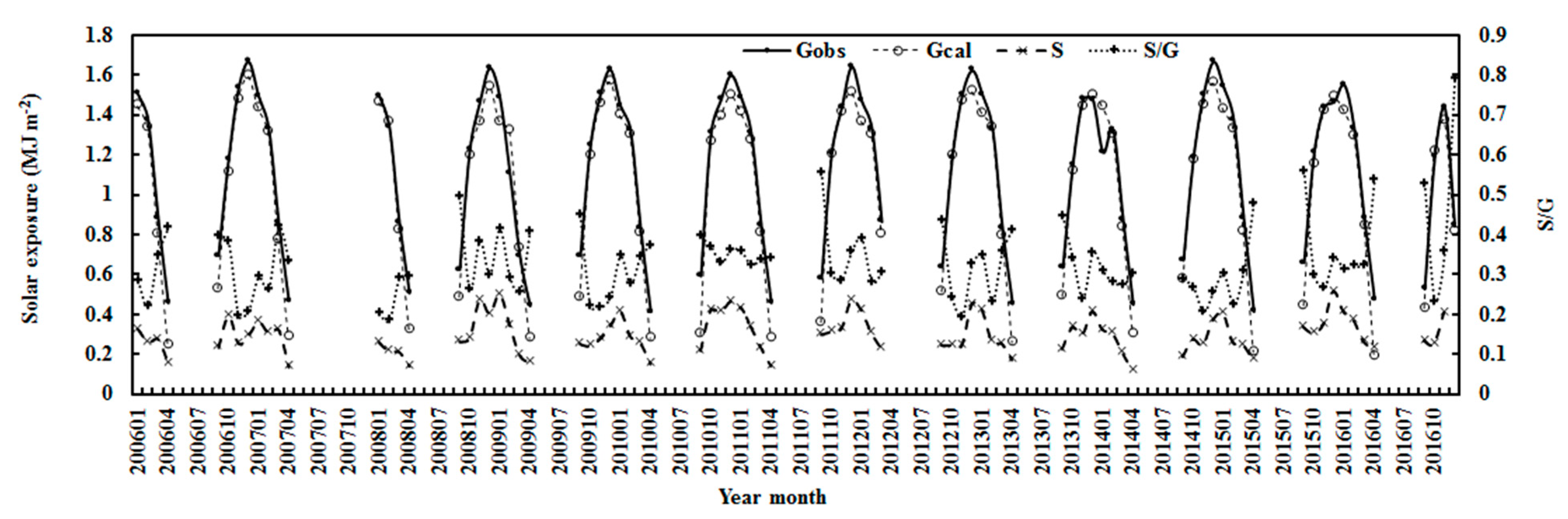
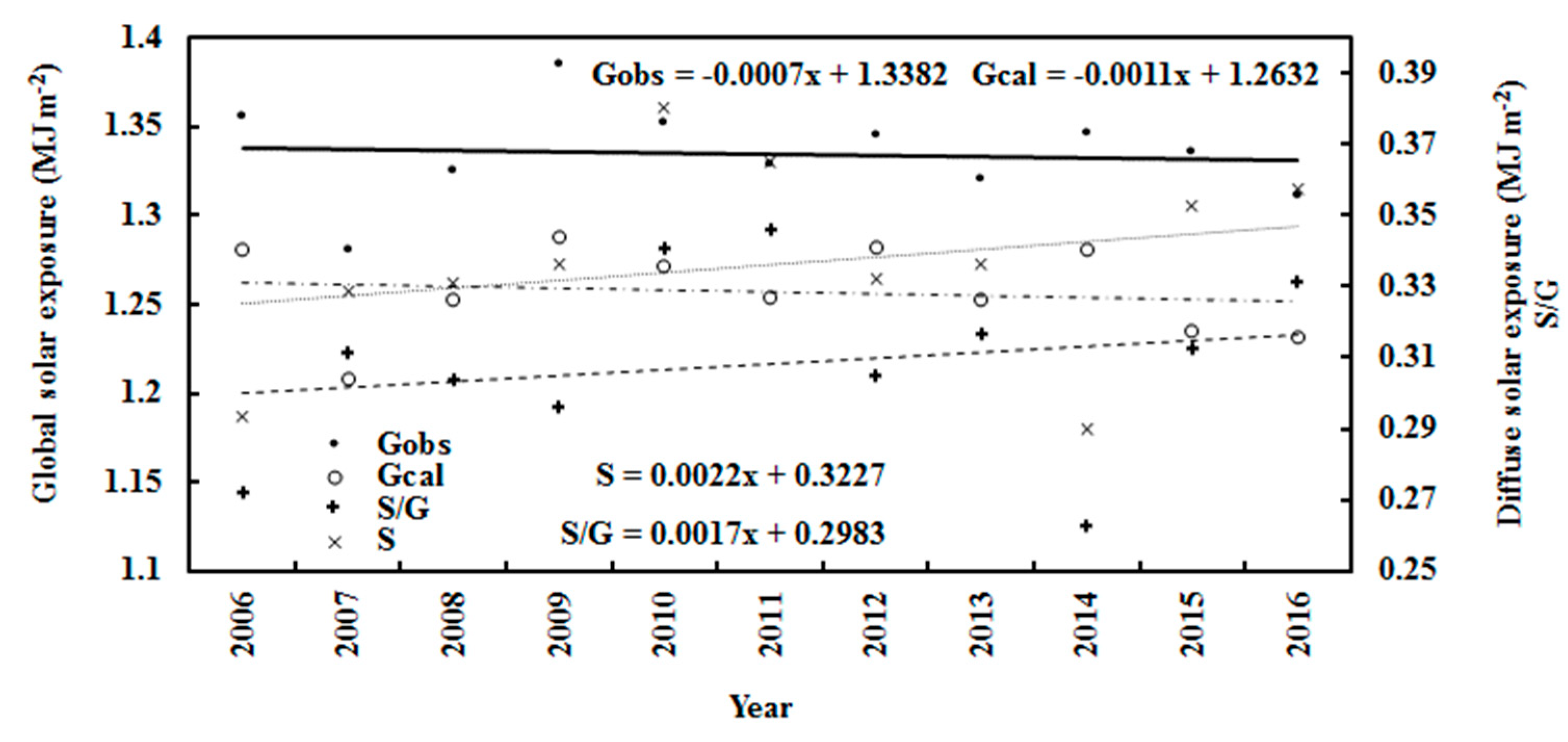
3.1. Global Solar Radiation during 2006–2016
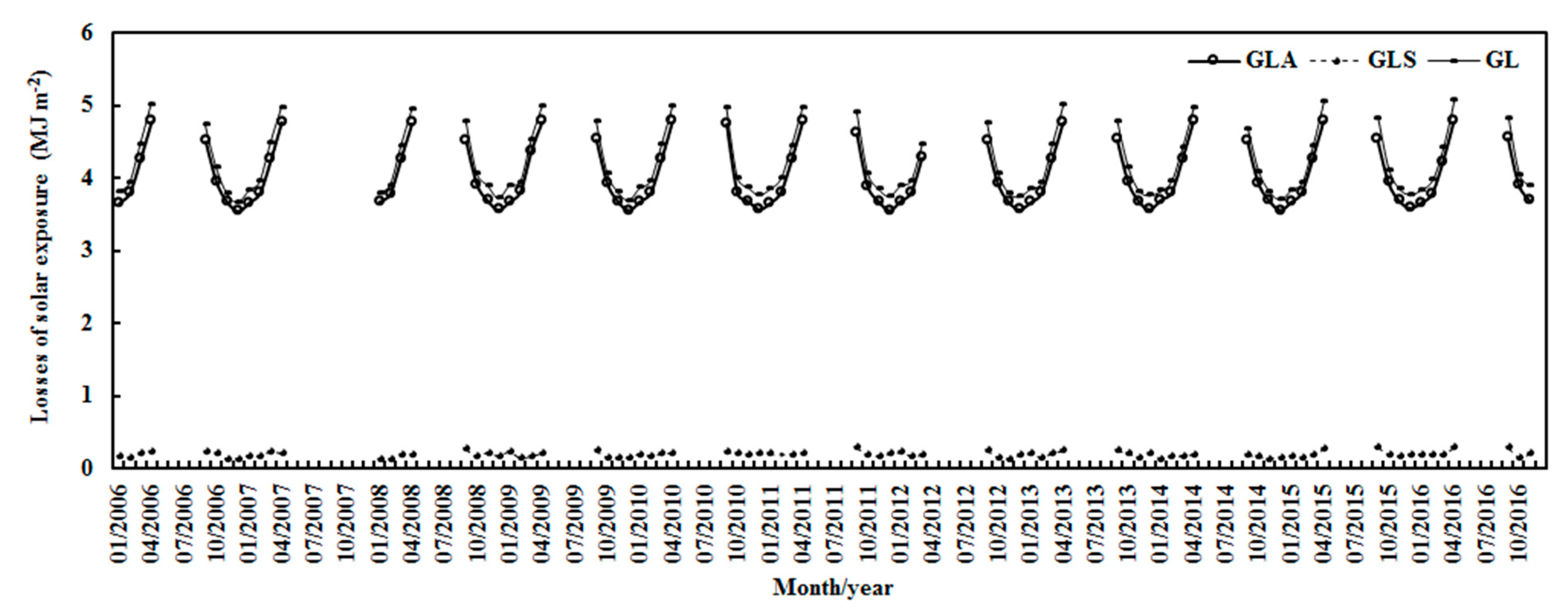
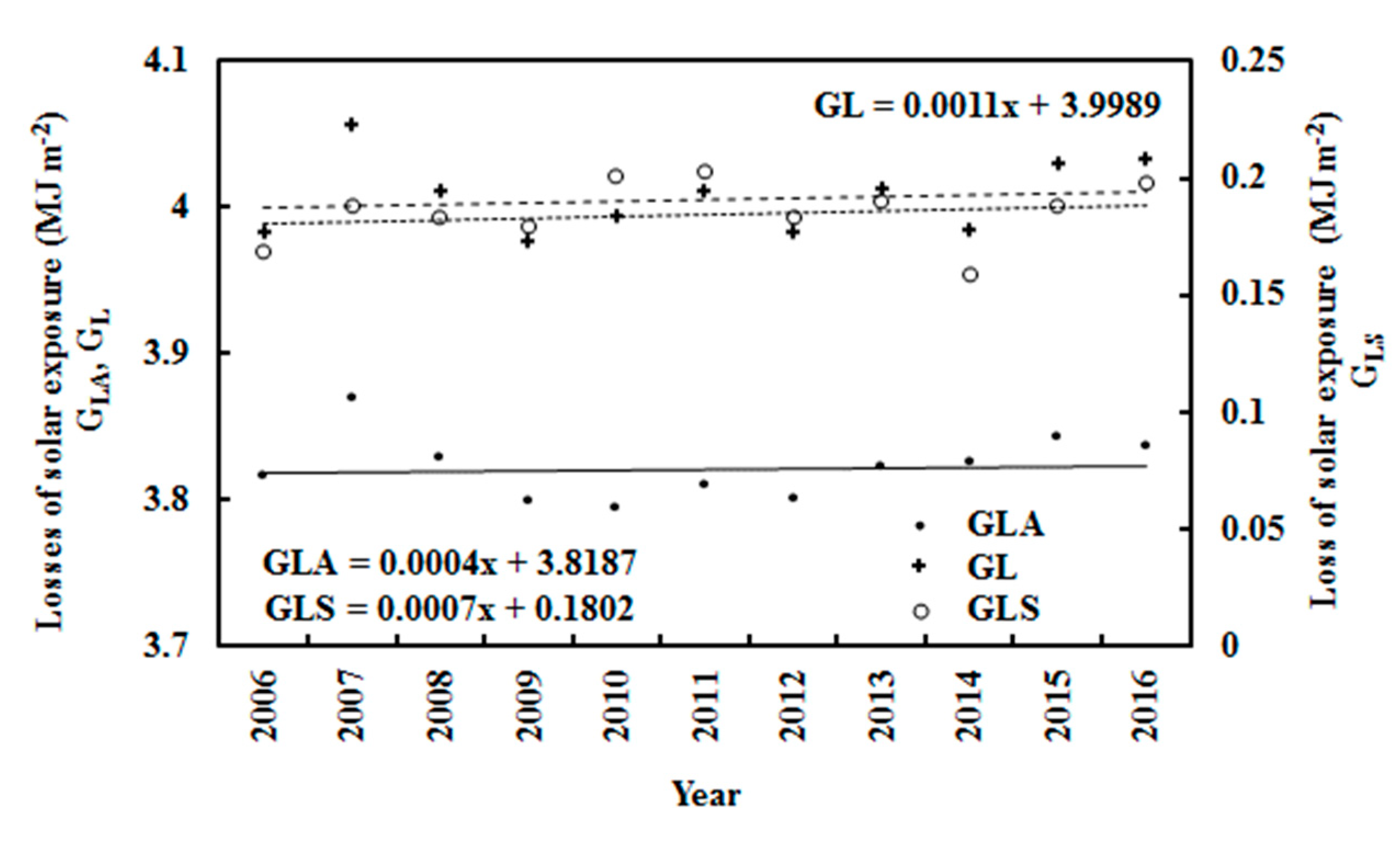
3.2. The Losses of Global Solar Radiation in the Atmosphere during 2006–2016
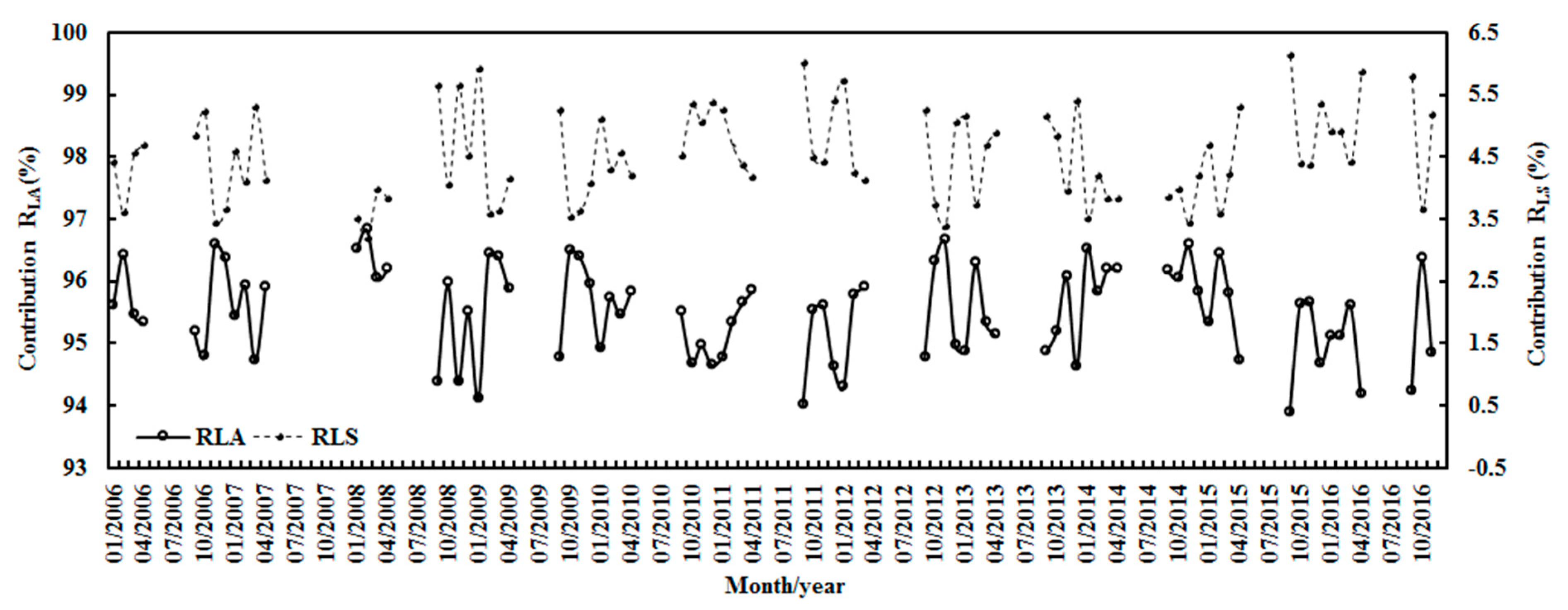
3.3. Global Solar Radiation and Its Loss in the Atmosphere in the Period from October to March (2006–2016)
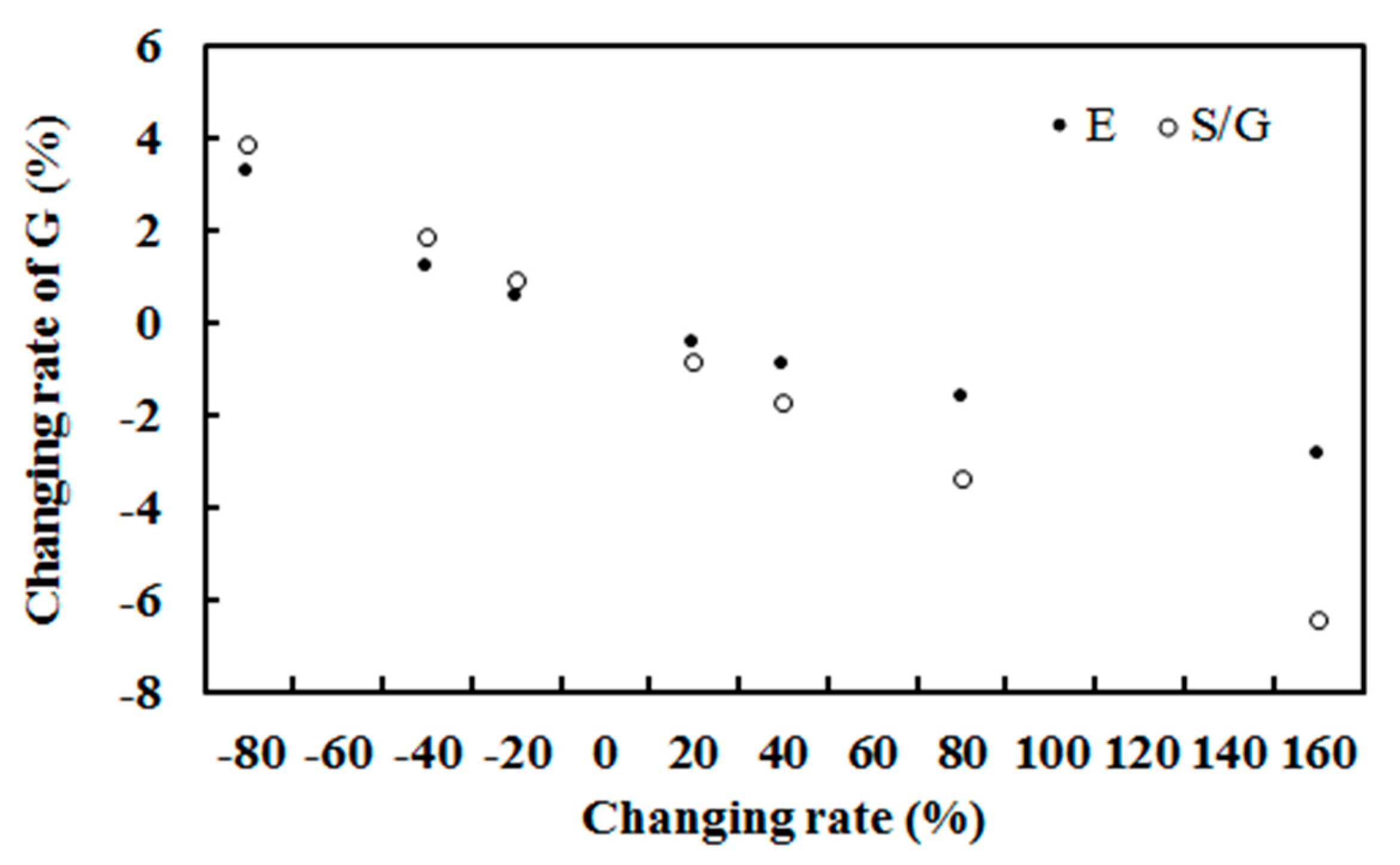
3.4. Sensitivity Study
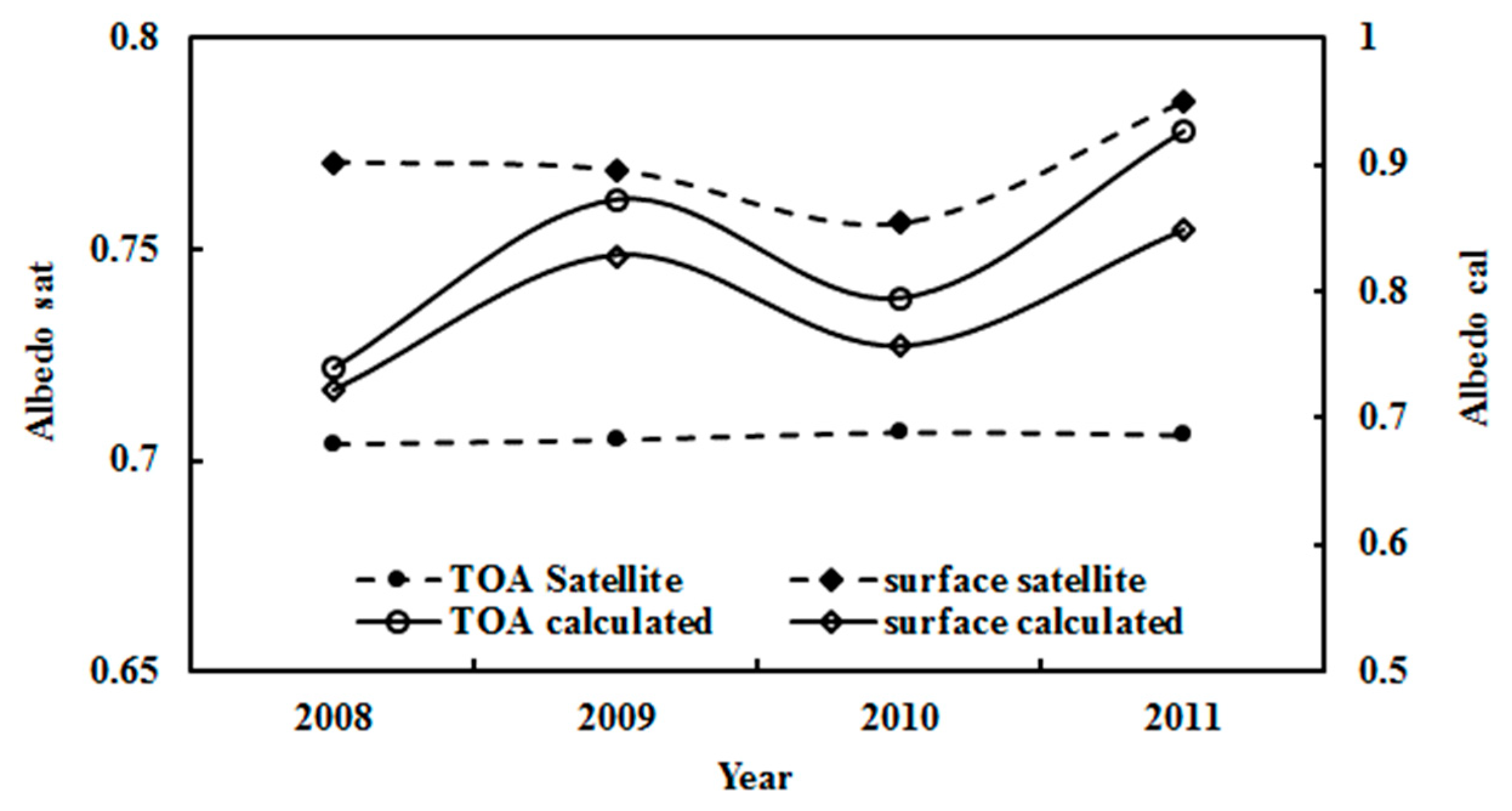
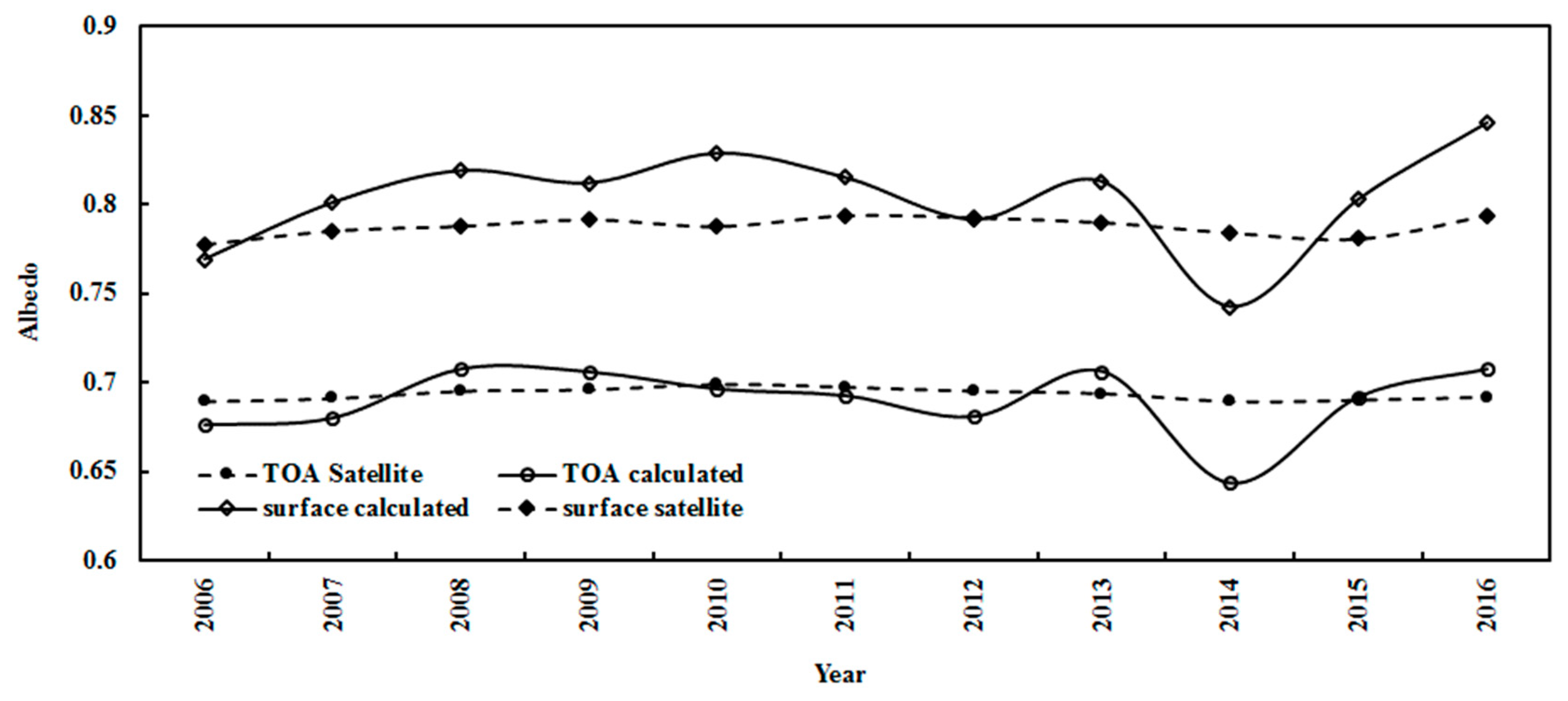
3.5. Albedos at the TOA and the Surface
4. Discussion
4.1. Application of the Empirical Model for Global Solar Radiation
4.2. Analysis of the Interactions between Changes in Air Temperature and Solar Radiation
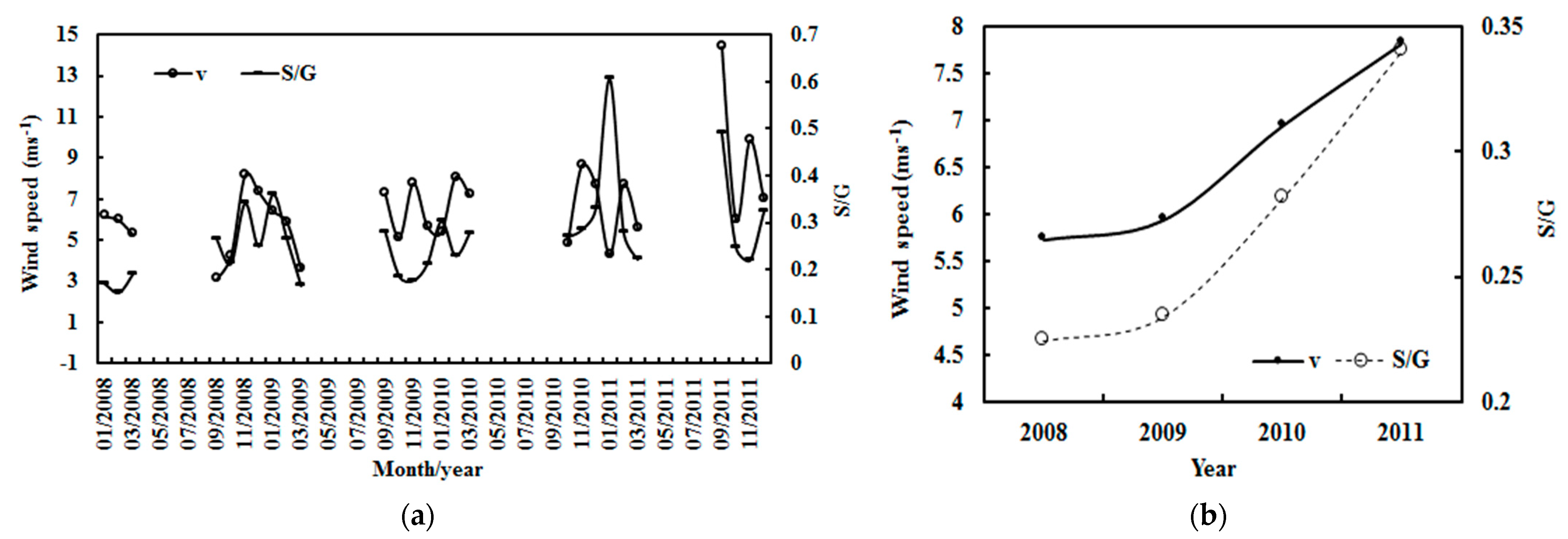
4.3. Relationship between Wind Speed and S/G
4.4. Comparisons of Global Solar Radiation at Two Pole Sites and a Mid-Latitude Site in 2013–2016
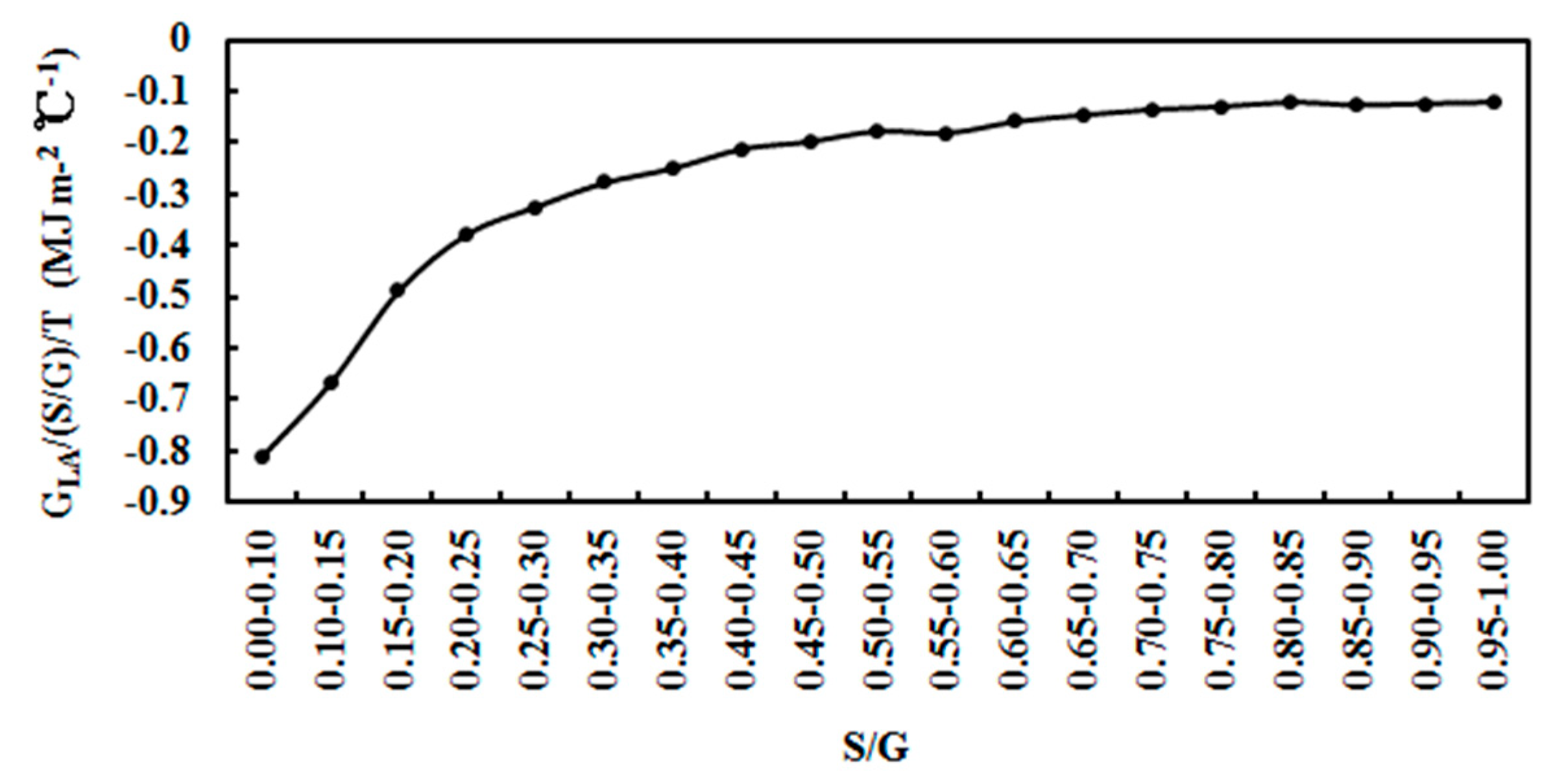
4.5. Normalized Absorbing Energy and Its Potential Effects
GLA/(S/G) = −0.856T−20.077
4.6. Biogenic Secondary Organic Aerosols and Their Potential Roles
4.7. Further Evaluation of the Empirical Model of Global Solar Irradiance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vaughan, D.; Marshall, G.J.; Connolley, W.M.; Parkinson, C.; Mulvaney, R.; Hodgson, D.A.; King, J.C.; Pudsey, C.J.; Turner, J. Recent Rapid Regional Climate Warming on the Antarctic Peninsula. Clim. Chang. 2003, 60, 243–274. [Google Scholar] [CrossRef]
- Turner, J.; Colwell, S.R.; Marshall, G.J.; Lachlan-Cope, T.A.; Carleton, A.M.; Jones, P.D.; Lagun, V.; Reid, P.A.; Iagovkina, S.V. Antarctic climate change during the last 50 years. Int. J. Climatol. 2005, 25, 279–294. [Google Scholar] [CrossRef]
- Vaughan, D.G.; Marshall, G.J.; Connolley, W.M.; King, J.C.; Mulvaney, R. Climate Change: Devil in the Detail. Science 2001, 293, 1777–1779. [Google Scholar] [CrossRef] [PubMed]
- Vaughan, D.G. British Antarctic Survey; Natural Environment Research Council, Madingley Road, Cambridge CB3 0ET, United Kingdom. 2007. Available online: http://www.homepages.ed.ac.uk/shs/Climatechange/Data%20sources/antarctic_peninsula.php.htm (accessed on 17 January 2022).
- Turner, J.; Lu, H.; White, I.; King, J.C.; Phillips, T.; Scott Hosking, J.; Bracegirdle, T.J.; Marshall, G.J.; Mulvaney, R.; Deb, P. Absence of 21st century warming on Antarctic Peninsula consistent with natural variability. Nature 2016, 535. [Google Scholar] [CrossRef]
- Cao, Y.F.; Liang, S.L. Recent advances in driving mechanisms of the Arctic amplification: A review. Chin. Sci. Bull. 2018, 63, 2757–2771. [Google Scholar] [CrossRef]
- Cohen, J.; Screen, J.A.; Furtado, J.; Barlow, M.; Whittleston, D.; Coumou, D.; Francis, J.A.; Dethloff, K.; Entekhabi, D.; Overland, J.E.; et al. Recent Arctic amplification and extreme mid-latitude weather. Nat. Geosci. 2014, 7, 627–637. [Google Scholar] [CrossRef]
- Liu, S.Y.; Wang, B.Y.; Xie, Y.X.; Hu, S.H.; Wang, Z.Y.; Yue, L.Y. The Variation Characteristics of Temperature in Barrow Alaska during 1925–2018. Clim. Chang. Res. Lett. 2019, 8, 769–774. [Google Scholar] [CrossRef]
- Solanki, S.K. Solar variability and climate change: Is there a link. Astron. Geophys. 2002, 43, 5–9. [Google Scholar] [CrossRef]
- Elminir, H.K. Relative influence of weather conditions and air pollutants on solar radiation—Part 2: Modification of solar radiation over urban and rural sites. Meteorol. Atmos. Phys. 2007, 96, 257–264. [Google Scholar] [CrossRef]
- Lean, J.; Rind, D. Climate forcing by changing solar radiation. J. Clim. 1998, 11, 3069–3094. [Google Scholar] [CrossRef]
- Andreae, M.O.; Ramanathan, V. Climate’s Dark Forcings. Sciences 2013, 340, 280–281. [Google Scholar] [CrossRef] [PubMed]
- García, R.D.; Cuevas, E.; García, O.E.; Cachorro, V.E.; Pallé, P.; Bustos, J.J.; Romero-Campos, P.M.; de Frutos, A.M. Reconstruction of global solar radiation time series from 1933 to 2013 at the Izaña Atmospheric Observatory. Atmos. Meas. Tech. 2014, 7, 3139–3150. [Google Scholar] [CrossRef][Green Version]
- Rosenfeld, D.; Sherwood, S.; Wood, R.; Donner, L. Climate Effects of Aerosol-Cloud Interactions. Sciences 2014, 343, 379–380. [Google Scholar] [CrossRef] [PubMed]
- Williamson, C.E.; Zepp, R.G.; Lucas, R.M.; Madronich, S.; Austin, A.T.; Ballaré, C.L.; Norval, M.; Sulzberger, B.; Bais, A.F.; McKenzie, R.L.; et al. Solar ultraviolet radiation in a changing climate. Nat. Clim. Chang. 2014, 4, 434–441. [Google Scholar] [CrossRef]
- Calabrò, E.; Magazù, S. Correlation between Increases of the Annual Global Solar Radiation and the Ground Albedo Solar Radiation due to Desertification-A Possible Factor Contributing to Climatic Change. Climate 2016, 4, 64. [Google Scholar] [CrossRef]
- Bai, J.H.; Zong, X.M. Global solar radiation transfer and its loss in the atmosphere. Appl. Sci. 2021, 11, 2651. [Google Scholar] [CrossRef]
- Glower, J.; McGulloch, J.S.G. The empirical relation between solar radiation and hours of sunshine. Q. J. R. Meteorol. Soc. 1958, 84, 172–175. [Google Scholar]
- Zhang, J.; Zhao, L.; Deng, S.; Xu, W.; Zhang, Y. A critical review of the models used to estimate solar radiation. Renew. Sustain. Energy Rev. 2017, 70, 314–329. [Google Scholar] [CrossRef]
- Gueymard, C.A. Critical analysis and performance assessment of clear sky solar irradiance models using theoretical and measured data. Sol. Energy 1993, 51, 121–138. [Google Scholar] [CrossRef]
- Gueymard, C.A. Clear-sky solar irradiance predictions for large-scale applications using 18 radiative models: Improved validation methodology and detailed performance analysis. Sol. Energy 2012, 86, 2145–2169. [Google Scholar] [CrossRef]
- Badescu, V.; Gueymard, C.A.; Cheval, S.; Oprea, C.; Baciu, M.; Dumitrescu, A.; Iacobescu, F.; Milos, I.; Rada, C. Accuracy analysis for fifty-four clear-sky solar radiation models using routine hourly global irradiance measurements in Romania. Renew. Energy 2013, 55, 85–103. [Google Scholar] [CrossRef]
- Bayrakc, H.C.; Demircan, C.; Keceba, A. The development of empirical models for estimating global solar radiation on horizontal surface: A case study. Renew. Sustain. Energy Rev. 2018, 81, 2771–2782. [Google Scholar] [CrossRef]
- Antonanzas-Torres, F.; Urraca, R.; Polo, J.; Perpinan-Lamigueiro, O.; Escobar, R. Clear sky solar irradiance models: A review of seventy models. Renew. Sustain. Energy Rev. 2019, 107, 374–387. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Wang, M.; Wei, Z.; Sun, G. Estimation and validation of daily global solar radiation by day of the year-based models for different climates in China. Renew. Energy 2019, 135, 984–1003. [Google Scholar] [CrossRef]
- Psiloglou, B.; Kambezidis, H.; Kaskaoutis, D.; Karagiannis, D.; Polo, J. Comparison between MRM simulations, CAMS and PVGIS databases with measured solar radiation components at the Methoni station, Greece. Renew. Energy 2020, 146, 1372–1391. [Google Scholar] [CrossRef]
- Bai, J.; Heikkilä, A.; Zong, X. Long-Term Variations of Global Solar Radiation and Atmospheric Constituents at Sodankylä in the Arctic. Atmos 2021, 12, 749. [Google Scholar] [CrossRef]
- Ohmura, A.; Dutton, E.G.; Forgan, B.; Frohlich, C.; Gilgen, H.; Hegner, H.; Heimo, A.; König-Langlo, G.; McArthur, B.; Muller, G.; et al. Baseline Surface Radiation Network (BSRN/WCRP): New Precision Radiometry for Climate Research. Bull. Amer. Meteor. Soc. 1998, 79, 2115–2136. [Google Scholar] [CrossRef]
- Driemel, A.; Augustine, J.; Behrens, K.; Colle, S.; Cox, C.; Cuevas-Agulló, E.; Denn, F.M.; Duprat, T.; Fukuda, M.; Grobe, H.; et al. Baseline Surface Radiation Network (BSRN): Structure and data description (1992–2017). Earth Syst. Sci. Data 2018, 10, 1491–1501. [Google Scholar] [CrossRef]
- Lupi, A.; Lanconelli, C.; Vitale, V. Basic and Other Measurements of Radiation at Concordia Station (2006-01 et seq.); Institute of Atmospheric Sciences and Climate of the Italian National Research Council: Bologna, Italy, 2021. [Google Scholar] [CrossRef]
- Lanconelli, C.; Busetto, M.; Dutton, E.G.; ¨onig-Langlo, G.K.; Maturilli, M.; Sieger, R.; Vitale1, V.; Yamanouchi4, T. Polar baseline surface radiation measurements during the international polar year 2007–2009. Earth Syst. Sci. Data 2011, 3, 1–8. [Google Scholar] [CrossRef]
- Busetto, M.; Lanconelli, C.; Mazzola, M.; Lupi, A.; Petkov, B.; Vitale, V.; Tomasi, C.; Grigioni, P.; Pellegrini, A. Parameterization of clear sky effective emissivity under surface-based temperature inversion at Dome C and South Pole, Antarctica. Antarct. Sci. 2013, 25, 697–710. [Google Scholar] [CrossRef]
- Grigioni, P.; Antonelli, A.; Camporeale, G.; Ciardini, V.; De Silvestri, L.; Dolci, S.; Iaccarino, A.; Proposito, M.; Scarchilli, C. Radiosonde and AWS Data from Italian Antarctic Meteo-Climatological Observatory during Southern Hemisphere YOPP Special Observing Period (16-Nov-2018 15-Feb-2019); Institute of Atmospheric Sciences and Climate of the Italian National Research Council: Bologna, Italy, 2019. [Google Scholar] [CrossRef]
- Petkov, B.H.; Láska, K.; Vitale, V.; Lanconelli, C.; Lupi, A.; Mazzola, M.; Budíková, M. Variability in solar irradiance observed at two contrasting Antarctic sites. Atmos. Res. 2016, 172, 126–135. [Google Scholar] [CrossRef]
- Sixa, D.; Filya, M.; Alvainb, S.; Henryc, P.; Benoist, J. Surface characterisation of the Dome Concordia area (Antarctica) as a potential satellite calibration site, using Spot 4 Vegetation instrument. Remote Sens. Environ. 2004, 89, 83–94. [Google Scholar]
- Candidi, M.; Lori, A. Status of the Antarctic Base at Dome C. Mem. Della Soc. Astron. Ital. 2003, 74, 29–36. [Google Scholar]
- Scambos, T.A.; Campbell, G.G.; Pope, A.; Haran, T.; Muto, A.; Lazzara, M.; Reijmer, C.H.; Broeke, M.R.V.D. Ultralow surface temperatures in East Antarctica from satellite thermal infrared mapping: The coldest places on Earth. Geophys. Res. Lett. 2018, 45, 6124–6133. [Google Scholar] [CrossRef]
- Argentini, S.; Pietroni, I.; Mastrantonio, G.; Viola, A.P.; Dargaud, G.; Petenko, I. Observations of near surface wind speed, temperature and radiative budget at Dome C, Antarctic Plateau during 2005. Antarct. Sci. 2014, 26, 104–112. [Google Scholar] [CrossRef][Green Version]
- Sakerin, S.M.; Vlasov, N.I.; Kabanov, D.M.; Lubo_Lesnichenko, K.E.; Prakhov, A.N.; Radionov, V.F.; Turchinovich, Y.S.; Holben, B.N.; Smirnov, A. Results of spectral measurements of atmospheric aerosol optical depth with sun photometers in the 58th Russian Antarctic Expedition. Atmos. Ocean. Opt. 2014, 27, 393–402. [Google Scholar] [CrossRef]
- Yang, Y.K.; Zhao, C.F.; Wang, Q.; Cong, Z.Y.; Yang, X.C.; Fan, H. Aerosol characteristics at the three poles of the Earth as characterized by Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observations. Atmos. Chem. Phys. 2021, 21, 4849–4868. [Google Scholar] [CrossRef]
- Tomasi, C.; Vitale, V.; Lupi, A.; Di Carmine, C.; Campanelli, M.; Herber, A.; Treffeisen, R.; Stone, R.S.; Andrews, E.; Sharma, S.; et al. Aerosols in polar regions: A historical overview based on optical depth and in situ observations. J. Geophys. Res. 2007, 112, D16205. [Google Scholar] [CrossRef]
- Bilbao, J.; Mateos, D.; De Miguel, A. Analysis and cloudiness influence on UV total irradiation. J. Climatol. 2011, 31, 451–460. [Google Scholar]
- Koo, J.H.; Choi, T.; Cho, Y.; Lee, H.; Kim, J.; Ahn, D.H.; Kim, J.; Lee, Y.G. The Variation in Aerosol Optical Depth over the Polar Stations of Korea. Aerosol Air Qual. Res. 2018, 18, 3202–3210. [Google Scholar] [CrossRef]
- Kondratyev, K.Y.A. Solar Energy; Science Press: Beijing, China, 1962; pp. 123–132. [Google Scholar]
- Gueymard, C.A. A reevaluation of the solar constant based on a 42-year total solar irradiance time series and a reconciliation of spaceborne observations. Sol. Energy 2018, 168, 2–9. [Google Scholar] [CrossRef]
- Roesch, A.; Wild, M.; Ohmura, A.; Dutton, E.G.; Long, C.N.; Zhang, T. Assessment of BSRN radiation records for the computation of monthly means. Atmos. Meas. Tech. 2011, 4, 339–354. [Google Scholar] [CrossRef]
- Myers, D.R. Solar radiation modeling and measurements for renewable energy applications data and model quality. Energy 2005, 30, 1517–1531. [Google Scholar] [CrossRef]
- Post, E.; Alley, R.B.; Christensen, T.R.; Macias-Fauria, M.; Forbes, B.; Gooseff, M.N.; Iler, A.; Kerby, J.T.; Laidre, K.L.; Mann, M.E.; et al. The polar regions in a 2 °C warmer world. Sci. Adv. 2019, 5, eaaw9883. [Google Scholar] [CrossRef]
- Dickinson, R.E. Land surface processes and climate surface albedos and energy balance. Adv. Geophys. 1983, 25, 305–353. [Google Scholar]
- Li, Z.Q.; Garand, L. Estimation of Surface Albedo from Surface-A Parameterization for Global Application. J. Geophys. Res. 1994, 99, 8335–8350. [Google Scholar] [CrossRef]
- Hudson, S.R.; Warren, S.G.; Brandt, R.E.; Grenfell, T.C.; Six, D. Spectral bidirectional reflectance of Antarctic snow: Measurements and parameterization. J. Geophys. Res. 2006, 111, D18106. [Google Scholar] [CrossRef]
- Psiloglou, B.E.; Kambezidis, H.D. Estimation of the ground albedo for the Athens area, Greece. J. Atmos. Sol.-Terr. Phys. 2009, 71, 943–954. [Google Scholar] [CrossRef]
- Loeb, N.G.; Doelling, D.R.; Wang, H.; Su, W.; Nguyen, C.; Corbett, J.G.; Liang, L.; Mitrescu, C.; Rose, F.G.; Kato, S. Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) Top-of-Atmosphere (TOA) Edition 4.0 Data Product. J. Clim. 2018, 31, 895–918. [Google Scholar] [CrossRef]
- Kato, S.; Rose, F.G.; Rutan, D.A.; Thorsen, T.J.; Loeb, N.G.; Doelling, D.R.; Huang, X.; Smith, W.L.; Su, W.; Ham, S.H. Surface Irradiances of Edition 4.0 Clouds and the Earth’s Radiant Energy System (CERES) Energy Balanced and Filled (EBAF) Data Product. J. Clim. 2018, 31, 4501–4527. [Google Scholar] [CrossRef]
- Sun, Y.J.; Wang, Z.H.; Qin, Q.M.; Han, G.H.; Ren, H.Z.; Huang, J.F. Retrieval of surface albedo based on GF-4geostationary satellite image data. J. Remote Sens. 2018, 22, 220–233. [Google Scholar]
- Bai, J.H. Photosynthetically active radiation loss in the atmosphere in North China. Atmos. Pollut. Res. 2013, 4, 411–419. [Google Scholar] [CrossRef]
- Shindell, D.T.; Chin, M.; Dentener, F.; Doherty, R.M.; Faluvegi, G.; Fiore, A.M.; Hess, P.; Koch, D.M.; MacKenzie, I.A.; Sanderson, M.G.; et al. A multi-model assessment of pollution transport to the Arctic. Atmos. Chem. Phys. 2008, 8, 5353–5372. [Google Scholar] [CrossRef]
- Arnold, S.; Law, K.; Brock, C.; Thomas, J.; Starkweather, S.; Von Salzen, K.; Stohl, A.; Sharma, S.; Lund, M.; Flanner, M.; et al. Arctic air pollution: Challenges and opportunities for the next decade. Elem. Sci. Anth. 2016, 4, 104. [Google Scholar] [CrossRef]
- Qiu, J.Y.; Huang, Q.; Tian, W.S.; Xie, F.; Liu, X.R.; Wang, F.Y. Numerical simulation study on the transport of pollution from China to the Arctic region. Plateau Meteorol. 2019, 38, 887–900. [Google Scholar]
- Valero, F.P.J.; Pope, S.K.; Bush, B.C.; Nguyen, Q.; Marsden, D.; Cess, R.D.; Simpson-Leitner, A.S.; Bucholtz, A.; Udelhofen, P.M. Absorption of solar radiation by the clear and cloudy atmosphere during the Atmospheric Radiation Measurement Enhanced Shortwave Experiments (ARESE) I and II: Observations and models. J. Geophys. Res. 2003, 108, 4016. [Google Scholar] [CrossRef]
- Bai, J.H. O3 Concentration and its relation with BVOC emissions in a subtropical plantation. Atmosphere 2021, 12, 711. [Google Scholar] [CrossRef]
- Bai, J.H. UV extinction in the atmosphere and its spatial variation in North China. Atmos. Environ. 2017, 154, 318–330. [Google Scholar] [CrossRef]
- Jacobson, M. Isolating nitrated and aromatic aerosols and nitrated aromatic gases as sources of ultraviolet light absorption. J. Geophys. Res. 1999, 104, 3527–3542. [Google Scholar] [CrossRef]
- Kulmala, M.; Suni, T.; Lehtinen, K.E.J.; Maso, M.D.; Boy, M.; Reissell, A.; Rannik, U.; Aalto, P.; Keronen, P.; Hakola, H.; et al. A new feedback mechanism linking forests, aerosols, and climate. Atmos. Chem. Phys. 2004, 4, 557–562. [Google Scholar] [CrossRef]
- Li, S.; Matthews, J.; Sinha, A. Atmospheric Hydroxyl Radical Production from Electronically Excited NO2 and H2O. Science 2008, 319, 1657–1660. [Google Scholar] [CrossRef] [PubMed]
- Law, K.S.; Stohl, A.; Quinn, P.K.; Brock, C.A.; Burkhart, J.F.; Paris, J.-D.; Ancellet, G.; Singh, H.B.; Roiger, A.; Schlager, H.; et al. Arctic Air Pollution: New Insights from POLARCAT-IPY. Bull. Am. Meteorol. Soc. 2014, 95, 1873–1895. [Google Scholar] [CrossRef]
- Virkkula, A.; Grythe, H.; Backman, J.; Petaja, T.; Busetto, M.; Lanconelli, C.; Lupi, A.; Becagli, S.; Traversi, R.; Severi, M.; et al. Aerosol optical properties calculated from size distributions, filter samples and absorption photometer data at Dome C, Antarctica and their relationships between seasonal cycles of sources. Atmos. Chem. Phys. Discuss. 2021, 1–63. [Google Scholar] [CrossRef]
- Crutzen, P.J.; Heidt, L.E.; Krasnec, J.P.; Pollock, W.H.; Seiler, W. Biomass burning as a source of atmospheric gases CO, H2, N2O, NO, CH3Cl and COS. Nature 1979, 282, 253–256. [Google Scholar] [CrossRef]
- Andreae, M.O. Biomass burning: Its history, use, and distribution and its impact. In Global Biomass Burning: Atmospheric, Climatic and Biospheric Implications; Levine, J.S., Ed.; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Andreae, M.O.; Fishman, J.; Garstang, M.; Goldammer, J.G.; Justice, C.O.; Levine, J.S.; Scholes, R.J.; Stocks, B.J.; Thompson, A.M.; van Wilgen, B. Biomass Burning in the Global Environment: First Results from the IGAC/BIBEX Field Campaign STARE/TRACE-A/SAFARI-92. In Global Atmospheric-Biospheric Chemistry; Prinn, R.G., Ed.; Springer: Boston, MA, USA, 1994; pp. 83–101. [Google Scholar]
- Andreae, M.O.; Metlet, P. Emission of trace gases and aerosols from biomass burning. Glob. Biogeochem. Cycles 2001, 15, 955–966. [Google Scholar] [CrossRef]
- Claeys, M.; Graham, B.; Vas, G.; Wang, W.; Vermeylen, R.; Pashynska, V.; Cafmeyer, J.; Guyon, P.; Andreae, M.O.; Artaxo, P.; et al. Formation of Secondary Organic Aerosols Through Photooxidation of Isoprene. Science 2004, 303, 1173–1176. [Google Scholar] [CrossRef]
- Carlton, A.G.; Wiedinmyer, C.; Kroll, J.H. A review of secondary organic aerosol (SOA) formation from isoprene. Atmos. Chem. Phys. 2009, 9, 4987–5005. [Google Scholar] [CrossRef]
- Riccobono, F.; Schobesberger, S.; Scott, C.E.; Dommen, J.; Ortega, I.K.; Rondo, L.; Almeida, J.; Amorim, A.; Bianchi, F.; Breitenlechner, M.; et al. Oxidation Products of Biogenic Emissions Contribute to Nucleation of Atmospheric Particles. Science 2014, 344, 717–721. [Google Scholar] [CrossRef]
- Jokinen, T.; Berndt, T.; Makkonen, R.; Kerminen, V.M.; Junninen, H.; Paasonen, P.; Stratmann, F.; Herrmann, H.; Guenther, A.B.; Worsnop, D.R.; et al. Production of extremely low volatile organic compounds from biogenic emissions Measured yields and atmospheric implications. Proc. Natl. Acad. Sci. USA 2015, 112, 7123–7128. [Google Scholar] [CrossRef]
- Bai, J.H.; Guenther, A.; Turnipseed, A.; Duhl, T.; Greenberg, J. Seasonal and interannual variations in whole-ecosystem BVOC emissions from a subtropical plantation in China. Atmos. Environ. 2017, 161, 176–190. [Google Scholar] [CrossRef]
- Santos, F.; Longo, K.; Guenther, A.; Kim, S.W.; Gu, D.S.; Oram, D.; Forster, G.; Lee, J.; Hopkins, J.; Brito, J.; et al. Biomass burning emission disturbances of isoprene oxidation. Atmos. Chem. Phys. 2018, 18, 12715–12734. [Google Scholar] [CrossRef]
- Chu, B.; Kerminen, V.M.; Bianchi, F.; Yan, C.; Petäjä, T.; Kulmala, M. Atmospheric new particle formation in China. Atmos. Chem. Phys. 2019, 19, 115–138. [Google Scholar] [CrossRef]
- Ramanathan, V.; Feng, Y. Air pollution, greenhouse gases and climate change: Global and regional perspectives. Atmos. Environ. 2009, 43, 37–50. [Google Scholar] [CrossRef]
- Von Schneidemesser, E.; Monks, P.S.; Allan, J.D.; Bruhwiler, L.; Forster, P.; Fowler, D.; Lauer, A.; Morgan, W.T.; Paasonen, P.; Righi, M.; et al. Chemistry and the linkages between air quality and climate change. Chem. Rev. 2015, 115, 3856–3897. [Google Scholar] [CrossRef]
- Bai, J.H.; Duhl, T. A primary generalized empirical model of BVOC emissions for some typical forests in China. Atmos. Pollut. Res. 2021, 12, 101126. [Google Scholar] [CrossRef]
- Lee, J.D.; Drysdale, W.S.; Finch, D.P.; Wilde, S.E.; Palmer, P.I. UK surface NO2 levels dropped by 42% during the COVID-19 lockdown: Impact on surface O3. Atmos. Chem. Phys. 2020, 20, 15743–15759. [Google Scholar] [CrossRef]
- Bai, J.H. A calibration method of solar radiometers. Atmos. Pollut. Res. 2019, 10, 1365–1373. [Google Scholar] [CrossRef]
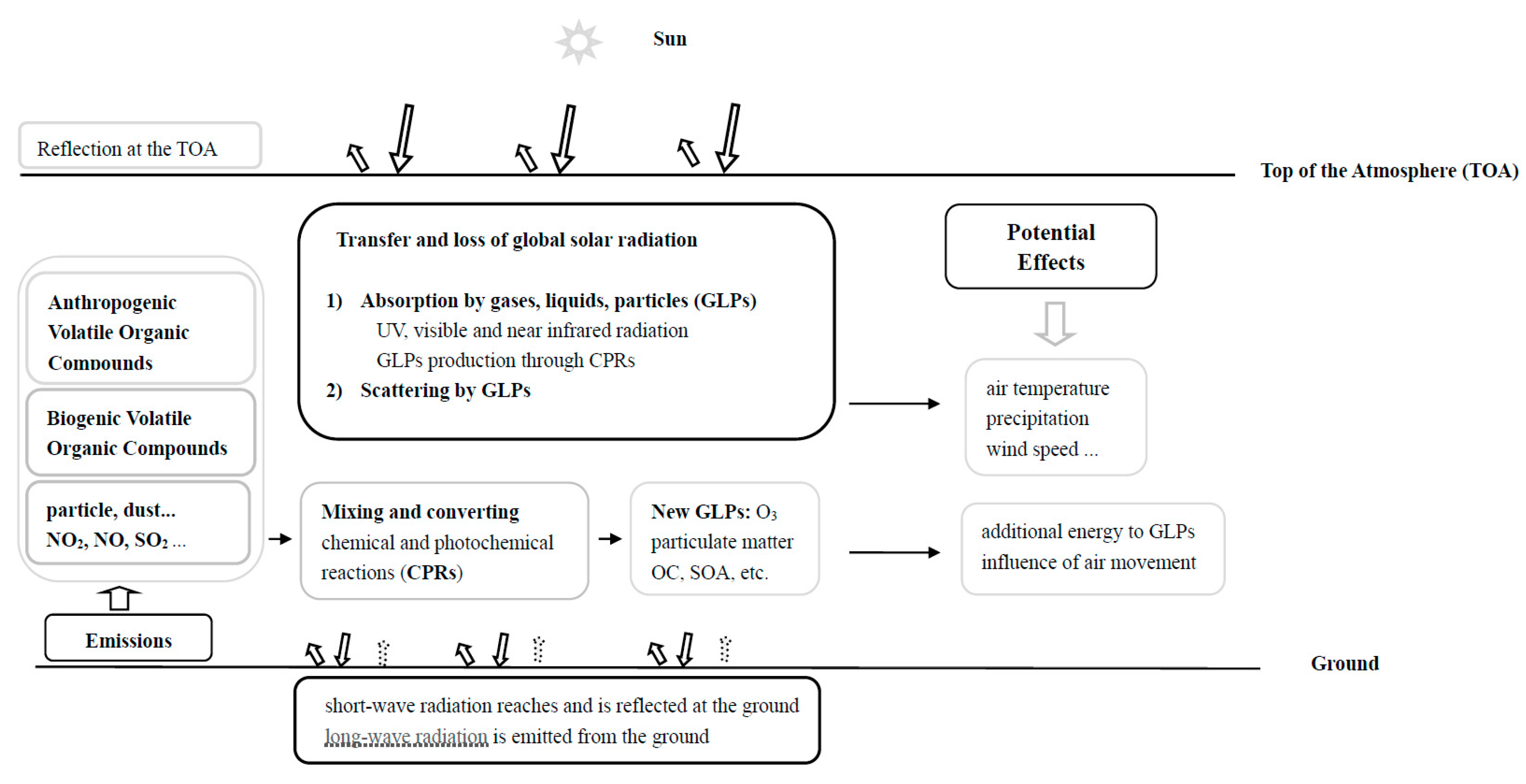
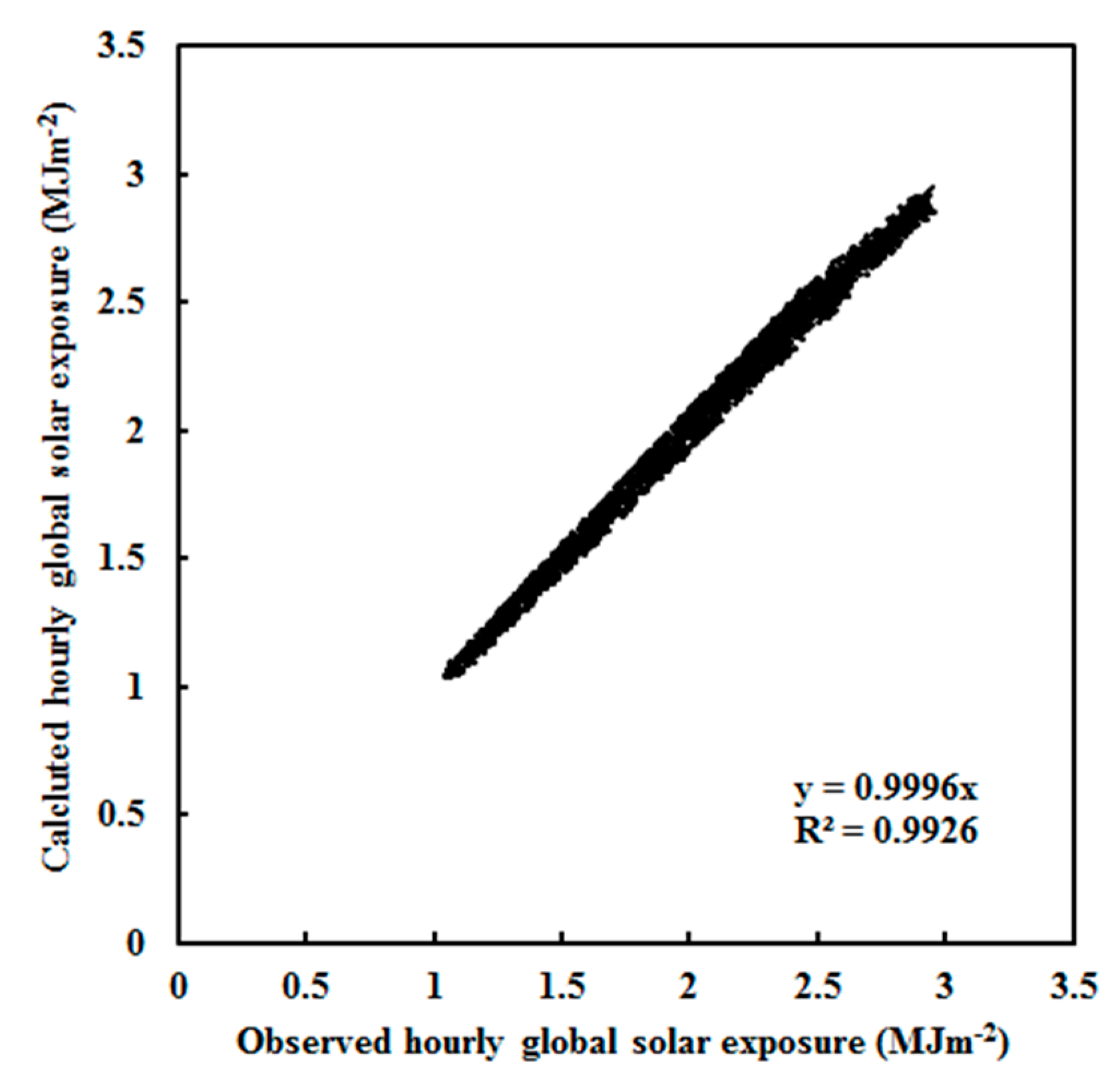
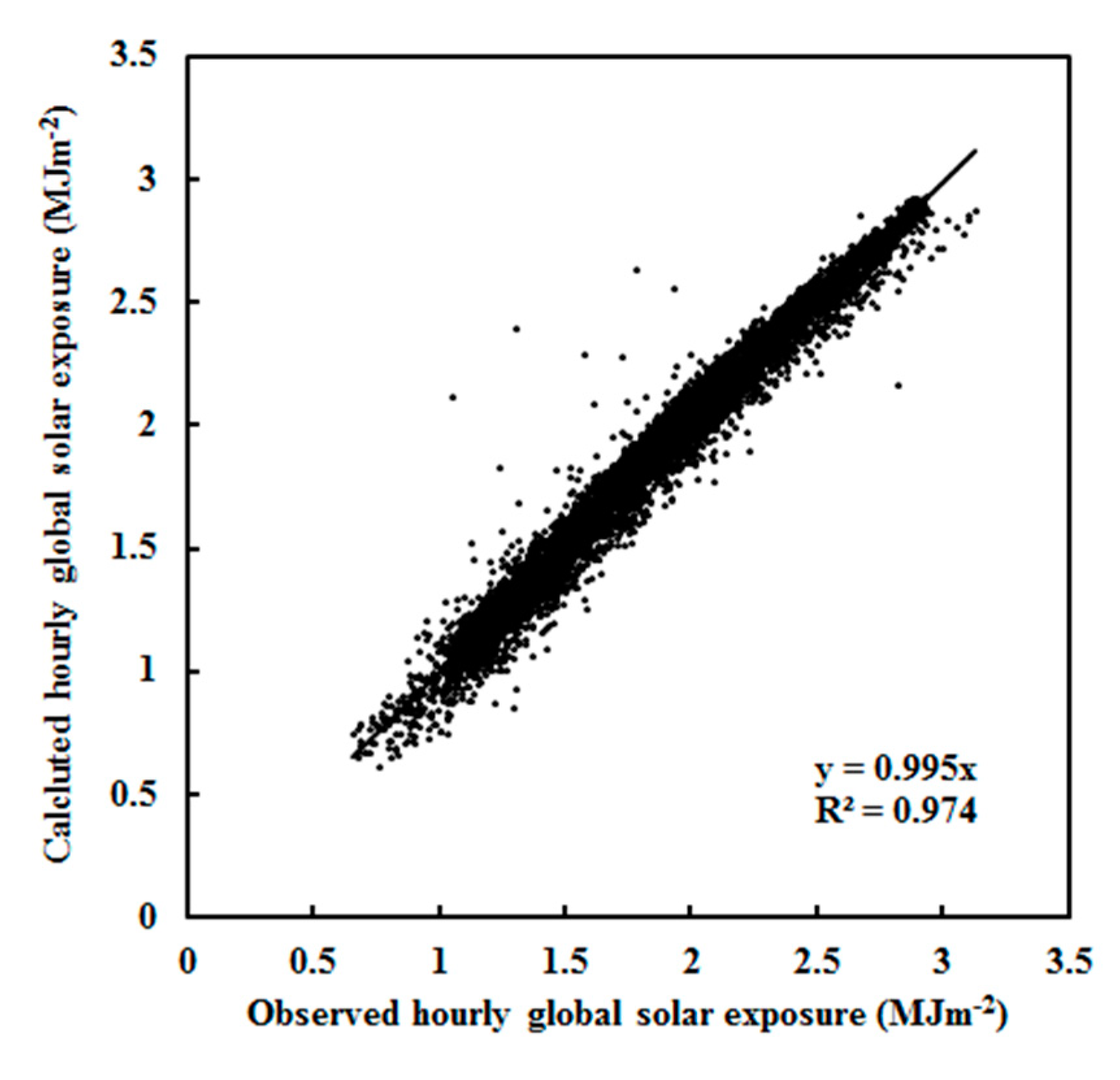

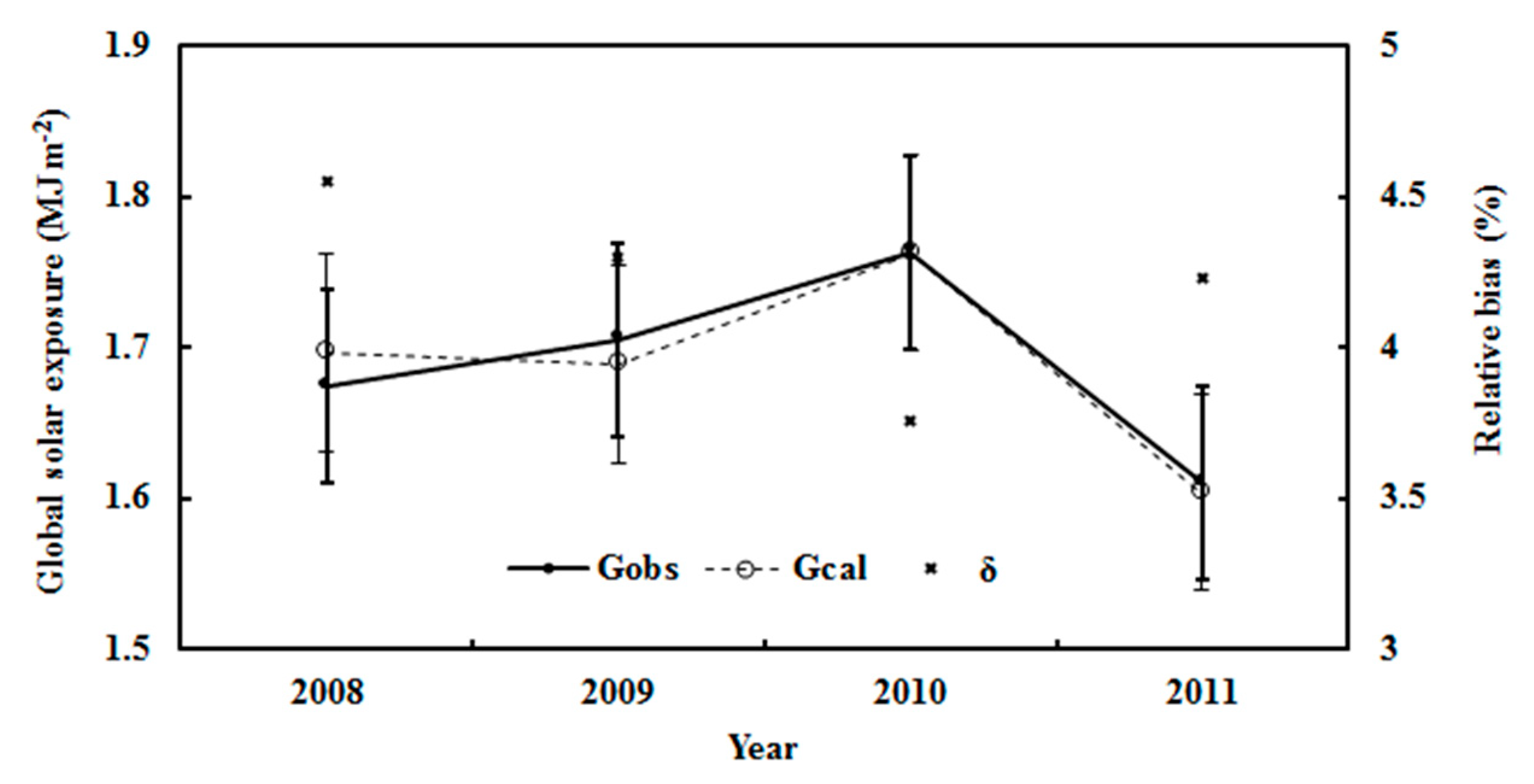





| Parameter | Instrument | Protocols | Surroundings |
|---|---|---|---|
| G | CM22, Kipp & Zonen Inc. | BSRN | homogeneous snow surface |
| S | CM22, Kipp & Zonen Inc. | BSRN | temperature: −80 °C to −20 °C |
| D | CH1, Kipp & Zonen Inc. | BSRN | cold, dry, clear and clean atmosphere |
| T, RH, v | automatic weather station | http://www.climantartide.it (accessed on 17 January 2022) | very low AOD |
| A1 | A2 | A0 | R2 | δavg | δmax | NMSE | σcal | σobs | MAD | RMSE | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (MJ m−2) | (%) | (MJ m−2) | (%) | |||||||||
| 5.607 | 0.752 | −1.097 | 0.993 | 1.76 | 5.23 | 0.0004 | 0.500 | 0.502 | 0.036 | 1.68 | 0.043 | 2.02 |
| h | Gobs | Gcal | δavg | δmax | NMSE | σcal | σobs | MAD | RMSE | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (MJ m−2) | (%) | (MJ m−2) | (%) | ||||||||
| ≥5° | 1.333 | 1.270 | 4.86 | 11.07 | 0.00003 | 0.836 | 0.750 | 0.064 | 4.81 | 0.007 | 0.56 |
| ≥10° | 1.555 | 1.533 | 2.15 | 6.05 | 0.00001 | 0.280 | 0.296 | 0.034 | 2.21 | 0.004 | 0.23 |
| h | Gobs | Gcal | S | T | ΔT (°C) | RH | E | S/G | GLA | GLS | GL |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ≥5° | 0.002 | 0.006 | 0.132 | 0.04 | 0.78 | 0.19 | 0.48 | 0.07 | −0.004 | 0.039 | −0.002 |
| ≥10° | 0.013 | 0.003 | 0.135 | 0.05 | 1.07 | 0.18 | 0.54 | 0.04 | −0.003 | 0.040 | −0.001 |
| T-Gobs | T-Gcal | T-GLA | T-GLS | T-GL | T-S/G | GLA-E | GLS-E | GL-E | GLA-S/G | GLS-S/G | GL-S/G | P-S/G | v-S/G | P-E | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ≥5° | 0.844 | 0.797 | −0.829 | 0.042 | −0.797 | 0.145 | 0.717 | 0.147 | 0.676 | 0.147 | 0.985 | 0.256 | 0.098 | 0.020 | 0.730 |
| ≥10° | 0.864 | 0.826 | −0.852 | 0.050 | −0.826 | 0.155 | 0.739 | 0.162 | 0.704 | 0.114 | 0.986 | 0.210 | 0.040 | 0.044 | 0.726 |
| Average | h Degree | Gobs MJ m−2 | Gcal MJ m−2 | S MJ m−2 | T °C | RH % | E hPa | S/G | GLA MJ m−2 | GLS MJ m−2 | GL MJ m−2 | RLA % | RLS % |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAVG | ≥5° | 1.333 | 1.270 | 0.332 | −41.84 | 56.86 | 0.120 | 0.296 | 3.889 | 0.149 | 4.038 | 95.58 | 4.42 |
| MAVG | ≥10° | 1.555 | 1.533 | 0.373 | −41.06 | 57.32 | 0.129 | 0.268 | 3.564 | 0.164 | 3.729 | 95.64 | 4.39 |
| AAVG | ≥5° | 1.328 | 1.265 | 0.332 | −41.77 | 56.93 | 0.120 | 0.297 | 3.818 | 0.180 | 3.997 | 95.56 | 4.44 |
| AAVG | ≥10° | 1.549 | 1.528 | 0.374 | −40.99 | 57.40 | 0.129 | 0.270 | 3.569 | 0.165 | 3.374 | 95.62 | 4.38 |
| E (%) | S/G (%) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| +20 | +40 | +80 | +160 | −20 | −40 | −80 | +20 | +40 | +80 | +160 | −20 | −40 | −80 | −100 |
| −0.48 | −0.91 | −1.66 | −1.85 | 0.56 | 1.22 | 3.28 | −0.89 | −1.76 | −3.42 | −6.48 | 0.92 | 1.86 | 3.84 | 4.87 |
| Gobs | Gcal | GLA | GLS | GL | T | E | S/G | n |
|---|---|---|---|---|---|---|---|---|
| 1.4 × 10−3 | 1.4 × 10−3 | −1.0 × 10−4 | −1.1 × 10−3 | −1.0 × 10−3 | 2.9 × 10−3 | 6.0 × 10−3 | 1.4 × 10−3 | 2771 |
| 5.4 × 10−4 | 3.8 × 10−4 | −3.4 × 10−4 | 3.0 × 10−3 | −2.0 × 10−4 | 2.8 × 10−3 | 3.0 × 10−5 | 3.9 × 10−3 | 6356 |
| 1.5 × 10−5 | 1.6 × 10−6 | −5.2 × 10−6 | 5.6 × 10−5 | −5.0 × 10−7 | 1.6 × 10−4 | 5.7 × 10−4 | 9.9 × 10−5 | 33311 |
| Gobs | Gcal | GLA | GLS | GL | T (% and °C) | E | S/G | n |
|---|---|---|---|---|---|---|---|---|
| −0.06 | −0.19 | 0.03 | 1.50 | 0.09 | 0.58 (2.12 °C) | 3.56 | 2.10 | 2771 |
| Gobs (MJ m−2) | T (°C) | E (hPa) | S/G | n | Situation |
|---|---|---|---|---|---|
| 2.14 | −35.94 | 0.188 | 0.135 | 2771 | 1 |
| 1.87 | −37.32 | 0.184 | 0.261 | 6356 | 2 |
| 1.34 | −41.55 | 0.135 | 0.308 | 33311 | 3 |
| Site | Gcal MJ m−2 | T °C | RH % | E hPa | S/G | GLA MJ m−2 | GLS MJ m−2 | GL MJ m−2 | GLA Wm−2 | GLS Wm−2 | GL Wm−2 | RLA % | RLS % | alb TOA | alb sur |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sod | 0.65 | 3.05 | 76.00 | 6.83 | 0.59 | 1.94 | 1.23 | 3.18 | 539.65 | 342.54 | 882.19 | 61.96 | 38.04 | 0.36 | 0.22 |
| QYZ | 1.42 | 22.71 | 75.76 | 22.38 | 0.83 | 1.68 | 0.27 | 1.95 | 466.37 | 75.35 | 541.71 | 89.31 | 13.69 | 0.29 | 0.22 |
| Dome | 1.25 | −41.39 | 58.23 | 0.13 | 0.31 | 3.83 | 0.18 | 4.01 | 1064.06 | 50.61 | 1114.85 | 95.51 | 4.49 | 0.69 | 0.80 |
| Ratio1 | 0.46 | 0.13 | 1.00 | 0.30 | 0.71 | 1.15 | 4.56 | 1.63 | 1.16 | 4.55 | 1.63 | 0.69 | 2.77 | 1.24 | 0.99 |
| Ratio2 | 0.88 | −1.82 | 0.37 | 0.006 | 0.37 | 2.28 | 0.67 | 2.06 | 2.28 | 0.67 | 2.06 | 1.07 | 0.33 | 2.38 | 3.64 |
| Site | Gcal | Gobs | T | RH | E | S/G | GLA | GLS | GL | alb TOA | alb sur |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sod | −0.54 | −2.45 | −3.79 | 0.17 | 1.13 | 0.86 | 0.03 | 0.25 | 0.11 | −1.20 | −0.11 |
| QYZ | −3.93 | −5.55 | −1.96 | 4.34 | 0.50 | 6.08 | 0.01 | −9.71 | −1.72 | 11.73 | −0.81 |
| Dome | −1.25 | −0.85 | −1.25 | 0.87 | −5.88 | 3.34 | 0.15 | 3.13 | 0.27 | 0.77 | 2.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, J.; Zong, X.; Lanconelli, C.; Lupi, A.; Driemel, A.; Vitale, V.; Li, K.; Song, T. Long-Term Variations of Global Solar Radiation and Its Potential Effects at Dome C (Antarctica). Int. J. Environ. Res. Public Health 2022, 19, 3084. https://doi.org/10.3390/ijerph19053084
Bai J, Zong X, Lanconelli C, Lupi A, Driemel A, Vitale V, Li K, Song T. Long-Term Variations of Global Solar Radiation and Its Potential Effects at Dome C (Antarctica). International Journal of Environmental Research and Public Health. 2022; 19(5):3084. https://doi.org/10.3390/ijerph19053084
Chicago/Turabian StyleBai, Jianhui, Xuemei Zong, Christian Lanconelli, Angelo Lupi, Amelie Driemel, Vito Vitale, Kaili Li, and Tao Song. 2022. "Long-Term Variations of Global Solar Radiation and Its Potential Effects at Dome C (Antarctica)" International Journal of Environmental Research and Public Health 19, no. 5: 3084. https://doi.org/10.3390/ijerph19053084
APA StyleBai, J., Zong, X., Lanconelli, C., Lupi, A., Driemel, A., Vitale, V., Li, K., & Song, T. (2022). Long-Term Variations of Global Solar Radiation and Its Potential Effects at Dome C (Antarctica). International Journal of Environmental Research and Public Health, 19(5), 3084. https://doi.org/10.3390/ijerph19053084







