1. Introduction
The emergence of the SARS-CoV-2 virus (COVID-19) has dramatically impacted the world over the last two and half years. Since the first cases were reported in the Chinese province of Wuhan in late 2019, the virus has been rapidly spreading across the globe. In March 2020, the situation was declared a pandemic by the World Health Organization (WHO) when the worldwide death count was 4291 and more than 118,000 cases were distributed across 114 countries. By mid November 2022, 633 million cases and 6.6 million deaths have been officially reported. The United States alone accounts for 97.5 million cases and 1.07 million deaths [
1].
The COVID-19 pandemic caught most of the western countries devoid of answers. The still remaining large number of unanswered questions and the need to contain the impact of the pandemic forced most of them to adopt policies aiming to keep social distances and to restrict human mobility. Since the disease caused by the coronavirus is a type of respiratory disease, primary policies were based on two main
non-pharmaceutical interventions (NPIs): mobility restrictions and mask mandates [
2,
3,
4]. The forced restriction on human mobility aimed to minimize the number and frequency of interactions among people by suggesting to shelter at home except for essential reasons such as commuting to work, attendance to medical appointments, or basic shopping. Such policies were followed by closing non-essential businesses and limiting the capacity of essential ones in order to leave enough space for customers to keep social distance. Mask adoption mandates were enforced by most states since the emergence of COVID-19 virus and were adopted by almost all businesses and organizations. Even after the COVID-19 vaccine was majorly available after 2021, mask adoption was extremely encouraged by healthcare officials in the event of a rise in confirmed cases.
Many studies have evaluated the effectiveness of such interventions and their impact on urban agglomerations, where people live more concentrated. These studies have mostly used statistical modeling techniques to show the effectiveness of lockdown policies in mitigating the disease spread by reducing human mobility [
3,
4,
5,
6,
7,
8,
9,
10]. Although these studies indicate that adherence to social distancing is crucial in controlling the disease spread, Holtz et al. [
11] show that ignoring the effects of social and geographical spillovers could negatively impact the effectiveness of such policies. This is followed by another line of research that pertains to modeling and predicting the disease spread across several scenarios [
7,
8,
9,
10,
11,
12]. These studies have made important contributions to improve and to implement more efficient responses.
Although all mentioned studies agree on the benefits of social distancing during the pandemic, they also indicate that the compliance with such policies shows significant differences among various socio-demographic groups, confirming the disproportionate impact of COVID-19 on some of them [
7,
13,
14,
15]. For instance, neighborhoods with lower income have been suffering from both higher infection rates as well as more negative impact on the employment rates. In addition to income, some social factors such as education levels and political belief explain differences in adherence to social distancing measures [
16,
17,
18], although they are less important in comparison to the poverty level. For example, Painter and Qiu [
17] showed that American residents in Republican counties were less likely to completely shelter at home after a state order. They also found that Democrats were less likely to respond to a state-level order when it was issued by a Republican governor relative to one issued by a Democratic one. Some other studies checked the effectiveness of face covering to prevent the spread of the coronavirus, showing significant differences among neighborhoods in adherence to mask adoption mandates [
19,
20,
21].
Initially, we expected that NPIs were eventually adopted until until the implementation of a permanent solution in the form of vaccination took place. The eventual adoption of NPIs helped to minimize infection rates and to improve the response capacity of health system. The crucial objective was to massively reduce the number of deaths caused directly by the virus, but also to avoid the collapse of the healthcare system by keeping an optimal attention to all the people affected by the virus and/or any other ailments [
1]. The successive approval of vaccines since the end of 2020 helped with minimizing the impact of the virus by reducing its severity.
Most of the western countries have experienced many difficulties in containing the virus. From the very beginning, various national strategies ranging from coexisting with the virus to its total suppression, the so-called
Zero COVID strategy, initially adopted by Sweden and China, which are the most significant examples in both policies, respectively [
22]. The unequal spatial patterns related to the spread and severity of COVID-19 were very noticeable over different geographies, but also considering the socio-demographic attributes of each community [
23,
24,
25]. Significant differences were evident across continents, nations, regions, cities, and even neighborhoods. This has revealed the great territorial complexity associated with the virus and the emergence of vast territorial inequalities across multiple scales.
The actual impact of the virus goes far beyond the health issues, causing a great uncertainty about its effects in other sectors as well [
26]. Thus, some scholars anticipate the impoverishment of large sections of communities, further emphasizing social inequalities. Beyond the great differences in terms of wealth (i.e., social coverage policies) and resources (i.e., health response capacity) with which different countries face this pandemic, the official number of infections reveals a precise indicator related to the impact of the virus across communities. The social dynamics behind the collective behavior help to understand understand the unequal distribution of the virus effects across the globe [
27,
28,
29].
Regardless of the particular interventions and policies enforced by health authorities in each region, a crucial factor relates to the level of compliance with rules and recommendations by the people. Thus, adherence of citizens to the rules and their social behavior must be evaluated in order to better understand the real impact of policies. Collective responses should be investigated considering multiple factors and variables, which allows us to address the socio-spatial complexity behind the compliance with mandates. Among these factors, aspects related to individuals’ ideological and political preferences, level of income, educational levels, and socio-spatial determinants (rural vs. urban) must be considered as potential factors behind the virus spreading and people’s compliance with mandates.
From a spatial perspective, the virus impact was predominantly concentrated in cities during the first wave. According to the United Nations [
30], urban regions became
ground zero of the COVID-19 pandemic by allocating around 90 percent of the reported cases during the first weeks. In the United States, the impact of the virus in the central states, which are less populated, was delayed and more contained in the first months. There, compliance with the official rules was initially laxer because the virus was perceived as a distant threat.
In this paper, we analyze the association between a group of socioeconomic variables and the people’s response to three main governmental policies enforced by the American authorities for containing the pandemic: (a) mobility restrictions, (b) mask adoption, and (c) vaccine participation. Our aim is to isolate what were the most influential variables impacting people’s responses to these policies. The study results give us a better understanding of the collective behavior within human communities in the United States. Estimating the importance level of such factors is crucial for the design and implementation of more efficient policies in case of any other eventual emergency or threat in the future. This paper is structured as follows:
Section 2 details material and methods,
Section 3 presents the analysis and results, and
Section 4 discusses the most significant findings.
3. Analysis and Results
In this section, we carry out a multiple regression analysis to discover significant variables associated with people’s response to each of the three individual interventions, namely: mask adoptions, mobility restrictions, and vaccine participation. While the causal processes that produce the results are complex, in order to get more meaningful results we then add an instrumental variable to the regression models. The analyses results provided in this section are organized as follows: Multiple Linear Regression (
Section 3.1), Instrumental Variable Regression (
Section 3.2), and comparison between both methods (
Section 3.3).
In the following subsections, we introduce all the variables considered in both regression models (multiple and instrumental). After that, we show which ones are the more significant ones for the respective models. We briefly discuss about if these results present some logic by providing some arguments.
3.1. Multiple Linear Regression
Multiple linear regression (MLR) is a well-known and broadly applied ordinary least squares (OLS) based statistical technique that uses several explanatory variables to predict the outcome of a response variable. The goal of multiple linear regression is to model the linear relationship between the explanatory (independent) variables and a response (dependent) variable. This model has been utilized by many recent research works aiming to understand the dynamics of social behavior and collective response to public health policies in the context of the COVID-19 pandemic [
11,
17,
19].
The regression models we implemented are based on the following equations (Equations (1)–(3)):
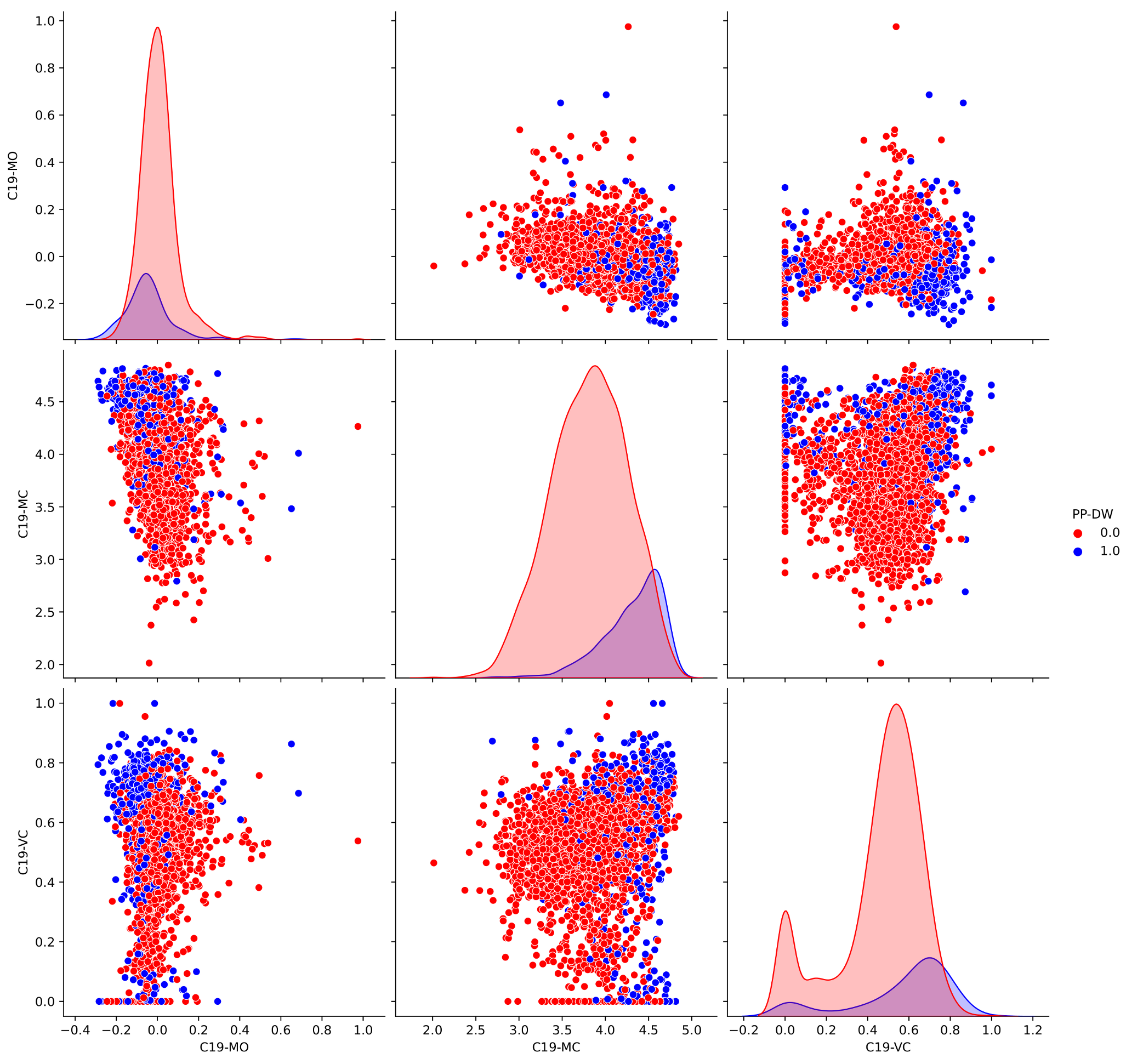
In these equations, CONTROLS refer to the controlling variables in each regression model. These variables are used to account for hidden effects and confounding variables so the final analysis of results has a low bias level. The following variables are used as CONTROLS: C19-CC, HC-PW, HC-HO, EC-PO, EC-UN, and PS-PD. Since, these are not the target variables of this study, they are included in the models to control for their effects. The parameter refers to the intercept value in each regression equation, refers to the coefficient of the PP-DW variable, refers to the coefficient of the EC-MC variable, and finally refers to the aggregate of controlling variables’ coefficients in each regression. It is important to note that all the variables used represent a collective response at a county level.
The results of all three multiple regressions are displayed in
Table 3,
Table 4 and
Table 5. There, rows show the different explanatory variables with regard to the dependent variable discussed in that specific table. In order to understand the effect and significance of each independent variable of interest on the outcome, we use the step-wise variable addition approach. We create three different models for each dependent variable and we add controls and variables of interest incrementally to evaluate their contribution to the analyses. In the regression tables, each column refers to a model used for analysis.
For each regression analysis, we included independent variables: PP-DW, PS-PD, and EC-PO in Model 1. In Model 2, we added EL-MC to the list of predictors. In Model 3, all the independent variables and controls were included. The reason for this step-wise addition of variables is that we implement a forward selection algorithm in model selection. We first start with a null model and then add the independent variables to the model one-by-one. We estimate the R
2 for each resulting regression. If after addition of a variable, R
2 of the regression was not improved, then we eliminate that variable from the regression. For each regression model, only the most significant variables that provide the best R
2 were selected, resulting in Models 1, 2, and 3. There are exceptions to this general rule as in
Table 3, where the incorporation of EL-MC did not result in a significant improvement in the R
2 of Model 2. However, since EL-MC is the main variable of analyses here, we refrained from eliminating it being included in Models 2 and 3.
For discussion purposes, coefficients in Model 3 of each regression table are considered. The coefficients in Models 1 and 2 are provided just to show the process through which the step-wise addition of variables took place and final models’ variables were selected.
3.1.1. Mobility Restrictions (C19-MO)
As shown in
Table 3, political preference (PP-DW) is statistically significant in all three models after controlling for several socioeconomic factors and COVID-19 related variables. This means the counties with more democratic leaning political preference show less movement under all three regression models. This is in line with previous studies by confirming how those regions with higher political preference towards the Democratic party showed more adherence to the social distancing and shelter at home orders [
17].
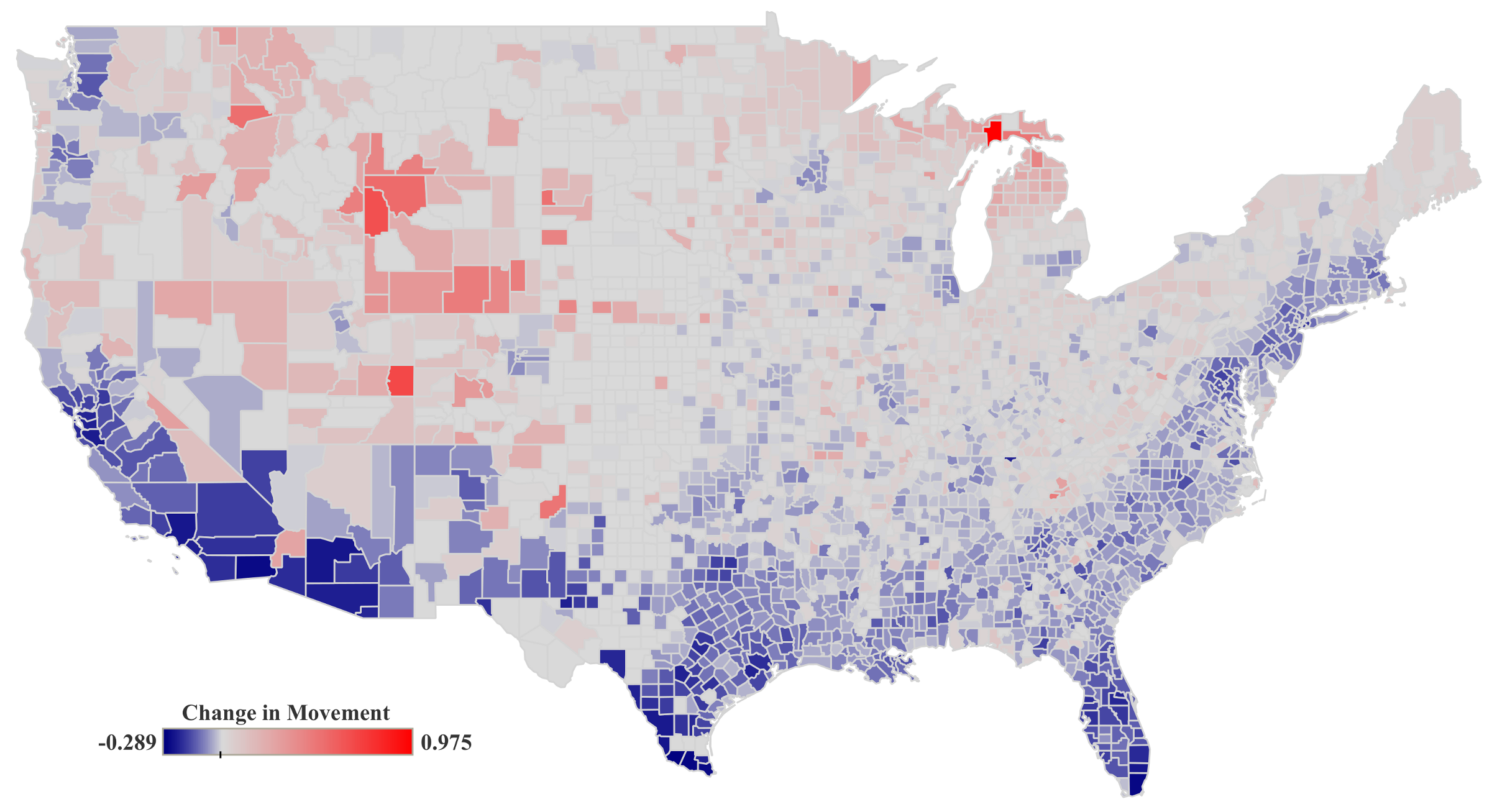
Education level (EL-MC) is introduced in Models 2 and 3. While it is not statistically significant in Model 2, after adding control variables in Model 3 it becomes statistically significant which shows that the counties with higher levels of education, would have been expected to observe more movement during the studied time frame with respect to the baseline before the pandemic started. Moreover, from the resulting coefficients for population density (PS-PD), it is evident that the people living in more densely populated regions reduced substantially their mobility much more than the rest of the people. In addition to negative association of the confirmed COVID-19 cases (C19-CC), this positive adherence could arguably be a result of differences in their higher perceived risk of exposure and infection.
In short, regarding the significance of each variable in Model 3, results show that all variables considered are statistically significant, with PS-PD, PP-DW, C19-CC, EC-PO, and HC-HO having a negative association with the change in movement of individuals (C19-MO), and EL-MC, HC-PW, and EC-UN having a positive association.
3.1.2. Mask Adoption (C19-MC)
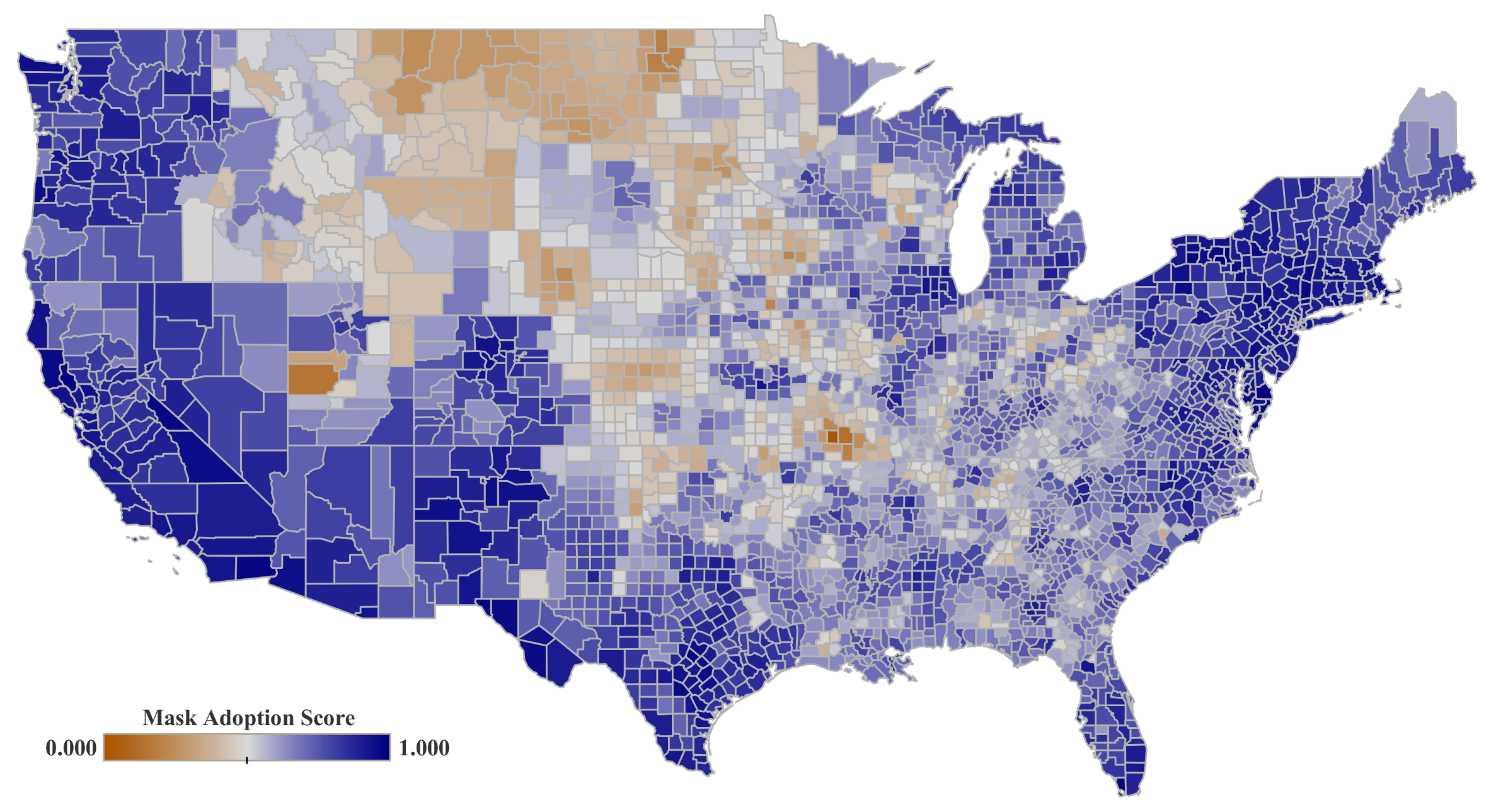
The results in
Table 4, show that political preference (PP-DW) and education level (EL-MC) are statistically significant showing a positive association with mask adoption (C19-MA), indicating that in the counties that voted for the Democratic party in 2020 and/or have higher levels of education, residents wear masks more frequently.
Based on the resulting coefficients for population density (PS-PD), similar to the change in movement (C19-MO), it is evident that the people living in areas with higher population density, used their masks more to protect themselves as they had a higher chance of encounters with other infected residents. This is also true about the variable representing the COVID-19 confirmed cases (C19-CC). As the number of infected people in a county increase, rate of mask usage increases, which can be associated with their perception of higher risk of infection.
3.1.3. Vaccine Participation (C19-VC)
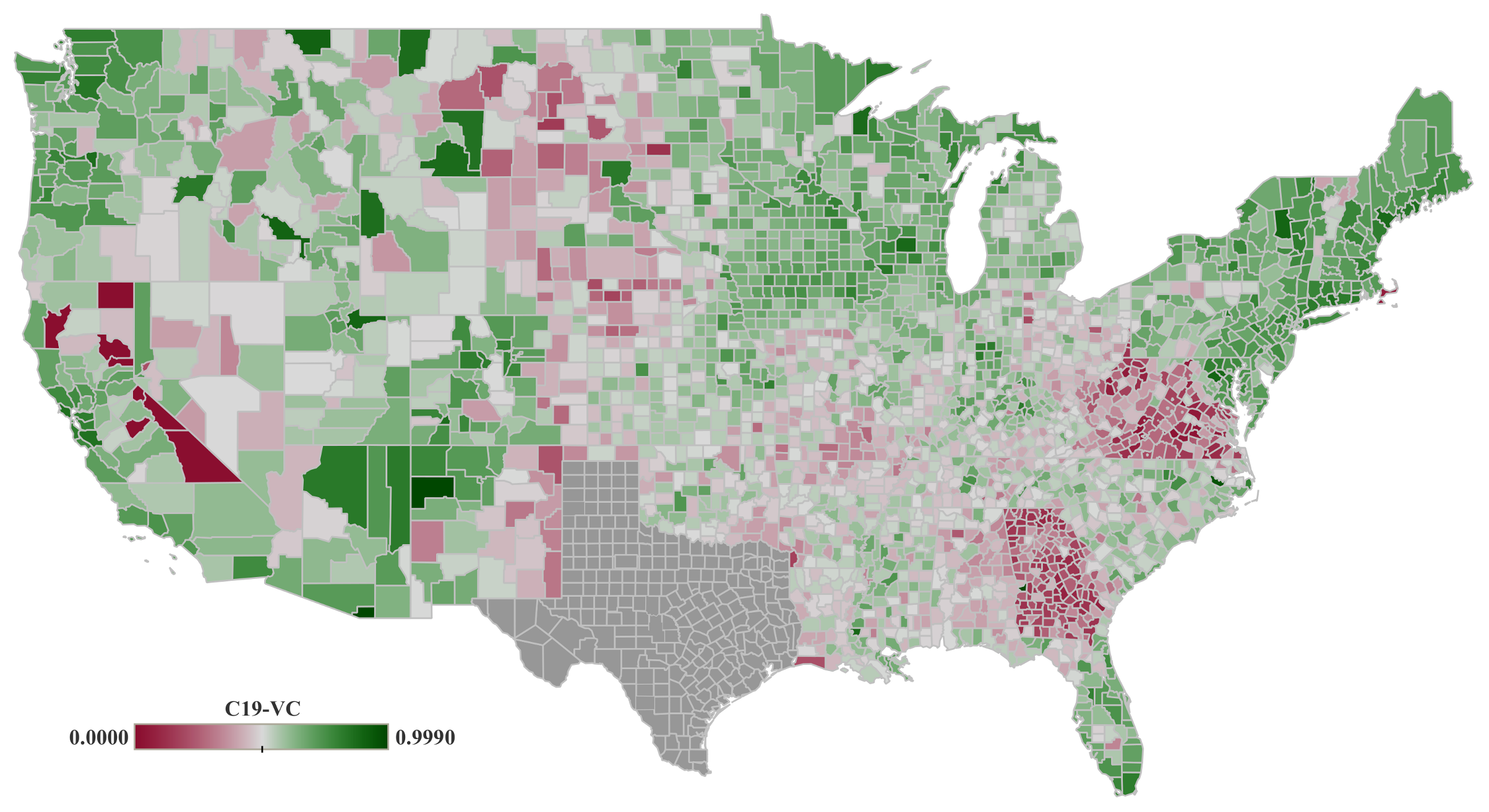
The results shown in
Table 5 indicate that political preference (PP-DW) and education level (EL-MC) are statistically significant showing a positive association with vaccine participation rate (C19-VC). Similar to the mask adoption rate (C19-MC), the counties that voted for the Democratic party in the 2020 Presidential election, would have been expected to observe higher vaccine participation rates (C19-VC). This is also true for counties with higher level of education (EL-MC), which were more responsive to participate in the vaccination during the first months.
3.2. Instrumental Variable Analysis
Analysis based on instrumental variables (IV) is a method for uncovering causality in socioeconomic research. This is a powerful tool for finding out whether there exists a causal relationship between two variables by considering an instrument. In the previous subsection, the outcome variables C19-MC, C19-MO, and C19-VC were analyzed using multiple linear regression.
In this subsection, we investigate the role of higher education on each of the dependent variables. Specifically, we aim to investigate if there is a causal relationship between the level of education and complying with governmental mandates during the pandemic. With this in mind, we used the Federal Investment in Education (EL-FI) as an instrument in our analysis to form Instrumental Variable regression. EL-FI satisfies the relevance and validity assumptions in our study (see
Appendix B). It satisfies the relevance assumption because it is highly associated with the endogenous variable EL-MC. It satisfies the validity assumption because it passes the Wu–Hausman for weak instruments, which shows that EL-FI and hidden variables impacting the outcome of interest (compliance with mandates) are not correlated. Additional explanations with more details regarding the causal diagram of the IV regression, equations, and assumptions are provided in
Appendix B.
We use the three following regression models:
where Z is the instrument for each of the IV regression models.
The main reason for conducting IV regression analysis is to isolate the causal impact of education level (EL-MC) on each of the three mandates. We conduct a step-wise IV regression for Equations (4)–(6). The results of all three multiple IV regressions are displayed in
Table 6,
Table 7 and
Table 8. In each IV regression table, Model 1 is the simplest, capturing merely the causal impact of EL-MC without any control variables considering EL-FI as an instrument. Model 2 adds the PP-DW variable to the existing IV regression of EL-MC on target mandates to better understand its impact on the causal relationship of interest. Model 3 includes all non-explicit control variables in addition to EL-MC, PP-DW, still considering EL-FI as the instrument.
3.2.1. Mobility Restrictions (C19-MO)
As
Table 6 indicates, PP-DW has a negative impact on C19-MO in Model 3, and it is statistically significant. Since Model 3 is the only model wherein we introduced all controls in addition to PP-DW and EL-MC variables in the IV regression, the results can be accepted with more confidence compared to Models 1 and 2. The results are similar to those of OLS regression estimation. More details about this are discussed in
Section 3.3.
EL-MC is introduced in all of the models and it is initially statistically significant in Models 1 and 2. Once PP-DW is introduced along with all control variables in Model 3, the estimated value loses its significance, discarding the notion that EL-MC has a causal impact on the outcome variable C19-MO using EL-FI as the instrumental variable.
In summary, the results suggest that political preference (PP-DW) had a causal impact on mobility and the resulting movement patterns (C19-MO) as well as compliance with social distancing orders. On the other hand, education level (EL-MC) did not have a causal impact on mobility (C19-MO).
3.2.2. Mask Adoption (C19-MC)
Table 7 shows the IV regression’s results for the variable C19-MC. The results show that PP-DW has a positive impact on C19-MC in Model 3, being statistically significant. Since PP-DW is introduced in Models 2 and 3, and all the control variables are present in Model 3, we can accept such statistically significant and positive results for its coefficient in Model 3. According to this, the counties that voted for the Democratic party are expected to have higher rates of mask adoption during the time period here considered. These results are similar to the results of OLS regression. More details about this are discussed in
Section 3.3.
EL-MC is introduced in all models. It is initially statistically significant in Models 1 and 2, but after the introduction of PP-DW and all control variables in Model 3, the estimated value loses its significance, discarding the notion that education level (EL-MC) has a significant causal impact on the mask adoption of individuals (C19-MC).
3.2.3. Vaccine Participation (C19-VC)
Table 8 shows the results of IV regression for the vaccine participation as the target variable (C19-VC). In Models 2 and 3, we can observe how PP-DW has no impact on C19-VC. This finding is different from the results produced by OLS regression in
Table 5. More details about this are discussed in
Section 3.3.
EL-MC is introduced in all of the models, being statistically significant (although not at the same level) in Models 1 and 3. After PP-DW is introduced in Model 2, the estimated value for the EL-MC coefficient loses its significance. However, after the introduction of all control variables along with PP-DW and EL-MC in Model 3, a positive and statistically significant coefficient for EL-MC is estimated. These results indicate that the education level (EL-MC) had a causal impact on vaccine participation (C19-VC), such as was mentioned before.
3.3. Comparison between OLS and IV Regression Results
In this section we conduct a comparison study of the results obtained by both OLS and IV methods for the three target variables.
Table 9 shows a summarized view of the results of analyses only for Model 3 as it includes the most complete set of the control and independent variables.
The Wu–Hausman’s test [
43,
44] evaluates the consistency of an estimator when compared to an alternative—less efficient estimator—which is already known to be consistent. It helps one evaluate if a statistical model corresponds to the data. In case of rejection, as is the case in all IV regressions in this study, the results obtained in the OLS regressions with the same dependent and independent variables are more reliable and should be accepted. In the following, more explanations regarding comparisons between OLS and IV regression for each target variable are provided.
3.3.1. Mobility Restrictions (C19-MO)
Table 9 shows that the PP-DW’s coefficients in both OLS and IV regressions are statistically significant. The slightly negative values confirms an inverse—but minimal in magnitude—association between PP-DW and C19-MO. Since the Wu–Hausman’s test is rejected for the IV regression, the OLS results will be accepted.
The EL-MC’s coefficient is statistically significant in the OLS regression in contrast to the one obtained in the IV regression for Model 3. However, since the Wu–Hausman’s test is rejected, it can be inferred that the OLS results can be accepted. Although there seems to be no causal relationship between education level (EL-MC) and change in movements (C19-MO), we can argue there is a strong association between these both variables.
3.3.2. Mask Adoption (C19-MC)
According to
Table 9, the PP-DW’s coefficients in both OLS and IV regression are statistically significant and very close to each other in terms of magnitude. However, since the Wu–Hausman’s test is rejected, the OLS result will be accepted and considered as final when determining the association between mask usage (C19-MC) and political preference (PP-DW) at a county level.
The EL-MC’s coefficient is not statistically significant in the IV regression, but it is in the OLS regression methods after the control variables are introduced. Since Wu–Hausman’s test in IV regression is rejected, OLS result will be accepted, which means that although education level (EL-MC) does not have a causal impact on mask usage (C19-MC), there is a strong correlation between the two variables.
3.3.3. Vaccine Participation (C19-VC)
Based on the results shown in
Table 9, the PP-DW’s coefficient is statistically significant in the OLS regression, in contrast to the IV regression. However, the association between PP-DW and C19-VC in the OLS regression is relatively small in terms of its magnitude. On the other hand, the EL-MC’s coefficient in both OLS and IV regression against C19-VC shows a strong relationship between both variables and some causality effects, indicating that the education level (EL-MC) is positively correlated with vaccination participation (C19-VC).
In summary, in all regression models, we included education level (EL-MC) and political preference (PP-DW) as the main independent variables to identify their association with behavioral response variables. In order to improve the explanatory power of the models, we additionally included relevant socioeconomic and healthcare infrastructure related variables before and during the COVID-19 pandemic. Although not all independent variables are statistically significant, the presence of such controlling variables significantly helped to check the true impact of the main independent variables and to minimize the bias effect. In addition, we used an IV regression approach to better understand the relationship among variables and to raise our confidence in capturing the causal impact of education on compliance with public health related mandates. Therefore, although some regression models might not possess significantly high values, integrating their results with the IV regression approach enriches the insights presented in this study.
4. Discussion and Conclusions
We divide this section into three minor sub-sections as follows: (
Section 4.1) Summary, (
Section 4.2) Limitations, and (
Section 4.3) Implications and future directions.
4.1. Summary
In order to better understand the COVID-19 pandemic, one must analyze its incidence and impact using statistical tools and analytical approaches. Noticeably, the large variability in the virus impact across regions requires the consideration of a vast number of variables related to the physical mechanisms behind the virus spread and the complex behavior of human societies.
In this study, we attempt to deal with this social complexity by conducting a multivariate research of the uneven spatial impact of COVID-19 across the United States. For that, we analyze the correlation between the COVID-19 incidence and a diverse group of variables related to the healthcare system in addition to other socioeconomical variables such as people’s educational level and political preferences. These variables are jointly analyzed with people’s responses to the three major interventions adopted by the U.S. health authorities for containing the pandemic: (a) mobility restrictions, (b) mask adoption, and (c) vaccine participation.
According to our results (summarized in
Table 9), investigating socioeconomical factors is crucial for understanding spatial differences in the COVID-19 pandemic. Factors related to people’s political preferences (PP-DW) were one of the most influential variables for understanding the responses to mask adoption (C19-MC) and mobility restrictions (C19-MO), whereas educational level (EL-MC) was more important for understanding the uneven engagement in the vaccine participation (C19-VC). Other variables such as the relative severity of the COVID-19 impact, which can be estimated using proxies such as the level of hospital occupancy by COVID-19 patients (HC-HO) in relation to the percentage of essential workers in hospitals (HC-PW) were also significant, but much smaller in magnitude than the education level (EL-MC).
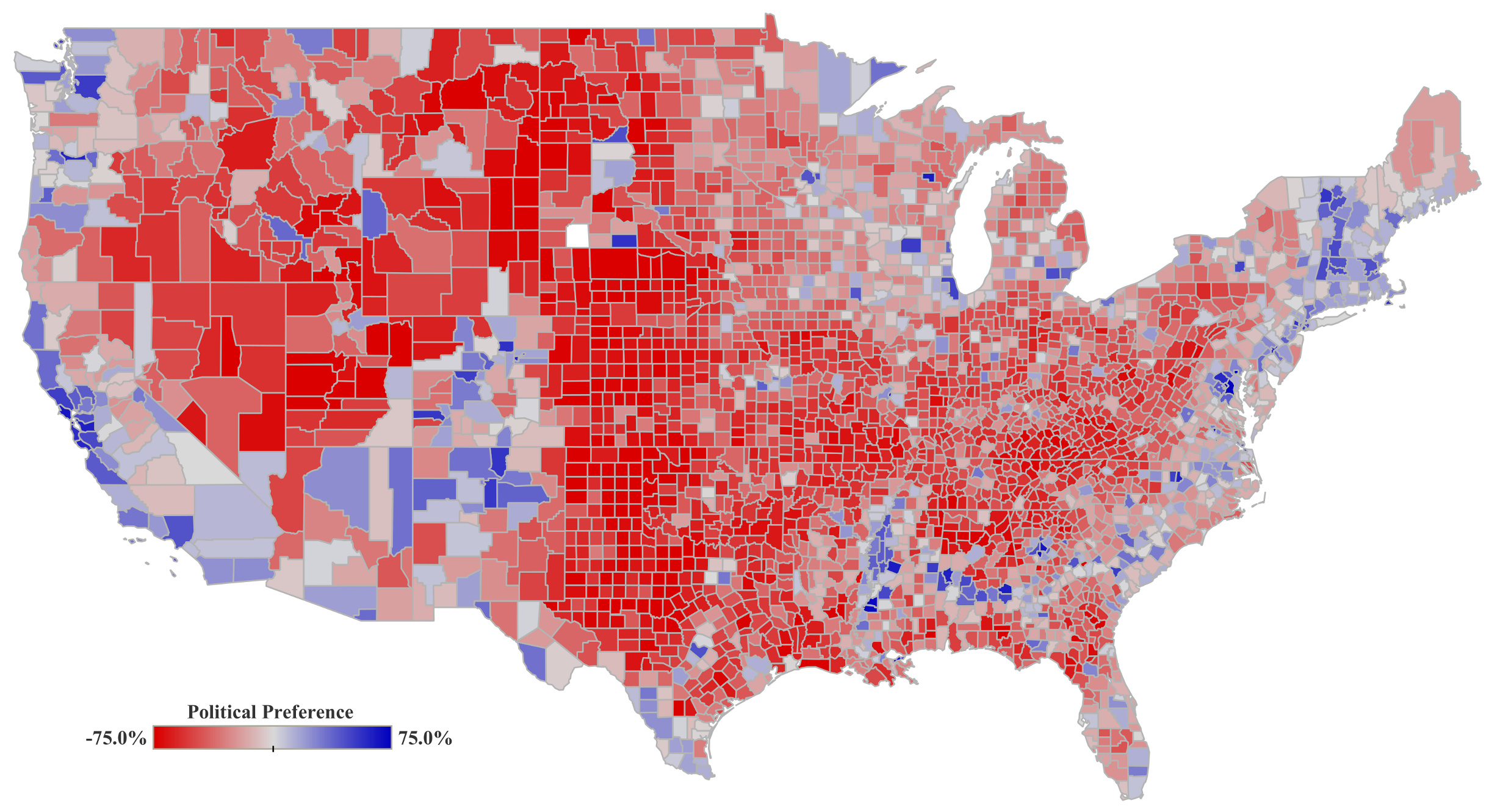
Political preference (PP-DW) demonstrates significant differences in people’s responses to COVID-19 mandates across the US counties. Republican counties tend to register higher mobility and lower intention for mask adoption. However, unlike what has been reported before [
45], political preference alone did not explain variations in vaccine participation rates in our models. This might be explained by the fact that we accounted for a wider range of control variables and emphasized on education levels using federal investment on education (EL-FI) as instruments in our analyses. The results we obtained demonstrate that although political preferences changed the perception of the pandemic, it only did so to a limited extent.
Some population setting attributes such as population density (PS-PD) were also relevant.
Table 9 shows how population density and mask adoption are significantly associated (0.835). Obviously, the particular COVID-19 transmission mechanism could have led to a heightened perception of the disease in urban regions, at least during the first months when the vast majority of the infections were located in dense urban areas.
People’s educational level was found to be a decisive factor for understanding the spatial variation in the engagement in the vaccination against the virus. We found a strong relationship (0.654) between those counties with a larger predominance of highly educated residents (EL-MC) and the rate of vaccinated people (C19-VC) according to the OLS regressions shown in
Table 9. This was further confirmed by an IV analysis where an increase of one unit in educational level caused an increase of 1.774 units in vaccine participation.
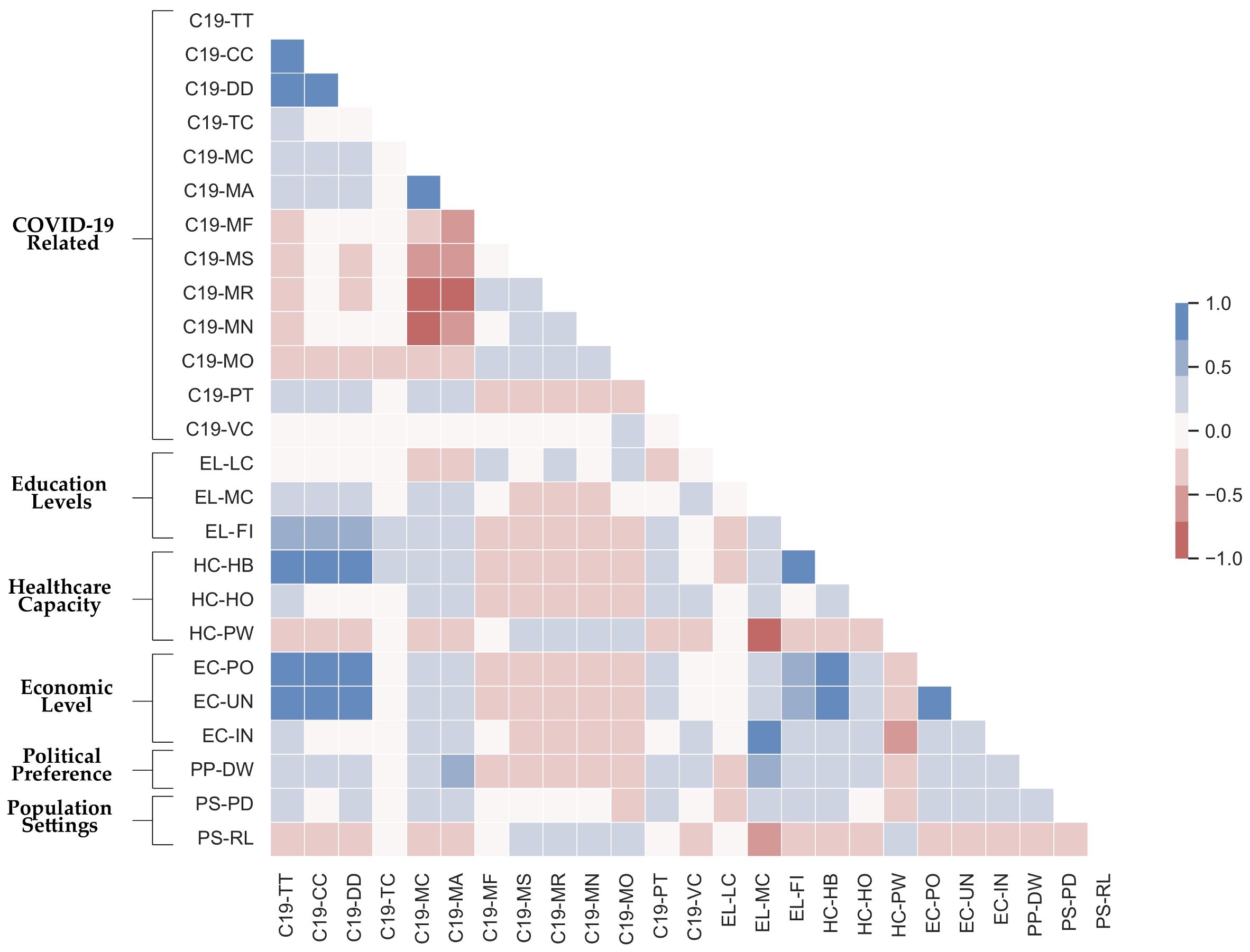
In this multi-factorial analysis, we also investigate and analyze the correlation between variables. For instance, according to results presented as a pairwise correlation table in Figure
Figure A1, the Republican counties present higher rurality rates and, therefore, lower population densities. Also in these counties, the reported average household incomes and education levels are lower. These counties tend to present lower COVID-19 vaccine participation rates [
46,
47] and higher rates of COVID-9 incidence, at least during the time period here considered. On the other hand, we find that the Democratic counties experienced on average less harm from COVID-19 which is confirmed by other research as well [
41].
4.2. Limitations
This study presents some limitations. The most important refers to the number of indicators considered. We attempted to reduce the social complexity related to the social behavior within communities to a short number of indicators. This is determined by the data availability during the time window considered. We collect relevant data related to collective behavior in relation to vaccine participation, mask usage, and mobility patterns in the first months of the pandemic. Although this approach could lead to an oversimplification of the human behavior, our results shed light onto the most basic relationships between different socio-economic variables and the response to the main interventions adopted by US authorities. In this way, we conduct a optimal trade-off between the number of variables and the significance of the models implemented.
We must note that our data were retrieved from different data sources. These data were collected using different methodologies. Most of these data were constrained to a very short time window at the beginning of the pandemic. Thus, people’s responses to the COVID-19 pandemic must be contextualized within the early months. This limitation is common among early studies trying to model people’s behavior during the first months of the pandemic [
11,
12,
21].
It is also important to note that performing behavioral analyses and modeling collective behavior requires more detailed microscopic data. Access to such detailed datasets at the individual level would potentially enhance the accuracy and interpretation of our results. That being said, macroscopic datasets like the ones used in this study are still extremely useful in identifying general patterns (e.g., in mobility [
48,
49]). Moreover, although many governments and institutions offered open datasets during the pandemic, many data presented important limitations and restrictions related to spatio-temporal resolution, privacy concerns, etc. Our analysis was conducted at a county level by merging information collected from different data sources. Our results are in accordance with other research studies, but we also observed some divergences with other ones conducted at different spatial scales [
37].
4.3. Implications and Future Directions
In this study, we investigated the causal relationship between social context and the level of adherence to the COVID-19 interventions in the United States. The results are of high relevance for better understanding social behaviors and to implement more efficient policies in emergency situations such as the current pandemic and future ones. Our findings help to explain the heterogeneous impact of COVID-19 on different communities, and thus to adopt policy implications for encouraging the public to comply with the public health policies. Our results are especially significant regarding the vaccination programs and may help public health authorities to adopt more efficient policies in order to increase the vaccination rates through educational programs.
This study progresses in line of some recent requests [
50]. Our results can be extrapolated to other regions. Similar studies were already implemented in other countries [
2,
3,
4,
9,
24]. For instance, Flaxman et al. [
9] show that non-pharmaceutical interventions such as social distancing encouragement, banning public events, ordering school closures, and ordering lockdowns had a significant impact on preventing or slowing the spread of COVID-19 in 12 European countries including Austria, Belgium, Switzerland, Spain, Italy, etc., in early 2020. The number of deaths as a result of COVID-19 was significantly reduced in countries with such policies compared to other countries with no such mandates in place. Carballosa et al. [
24] simulated the impact of mobility restrictions among municipalities in Spain. They observed that the confinement of the economically non-active individuals (elderly and children) may result in a significant reduction of risk, showing quite similar effects to the lockdown of the total population.
This research can be expanded by increasing the number of variables in the model. Another possible extension is to apply spatial econometric models to the current data in order to better understand underlying relationships among the variables used in this study.