Predicting Groundwater Indicator Concentration Based on Long Short-Term Memory Neural Network: A Case Study
Abstract
1. Introduction
2. Related Works
3. Materials and Methods
3.1. Study Area
3.2. Index Selection
3.3. Data Sources and Monitoring Methods
3.4. Data Preparation
3.5. Long Short-Term Memory Neural Network
4. Results and Discussion
4.1. Rainfall Data
4.2. Monitoring Results of Groundwater
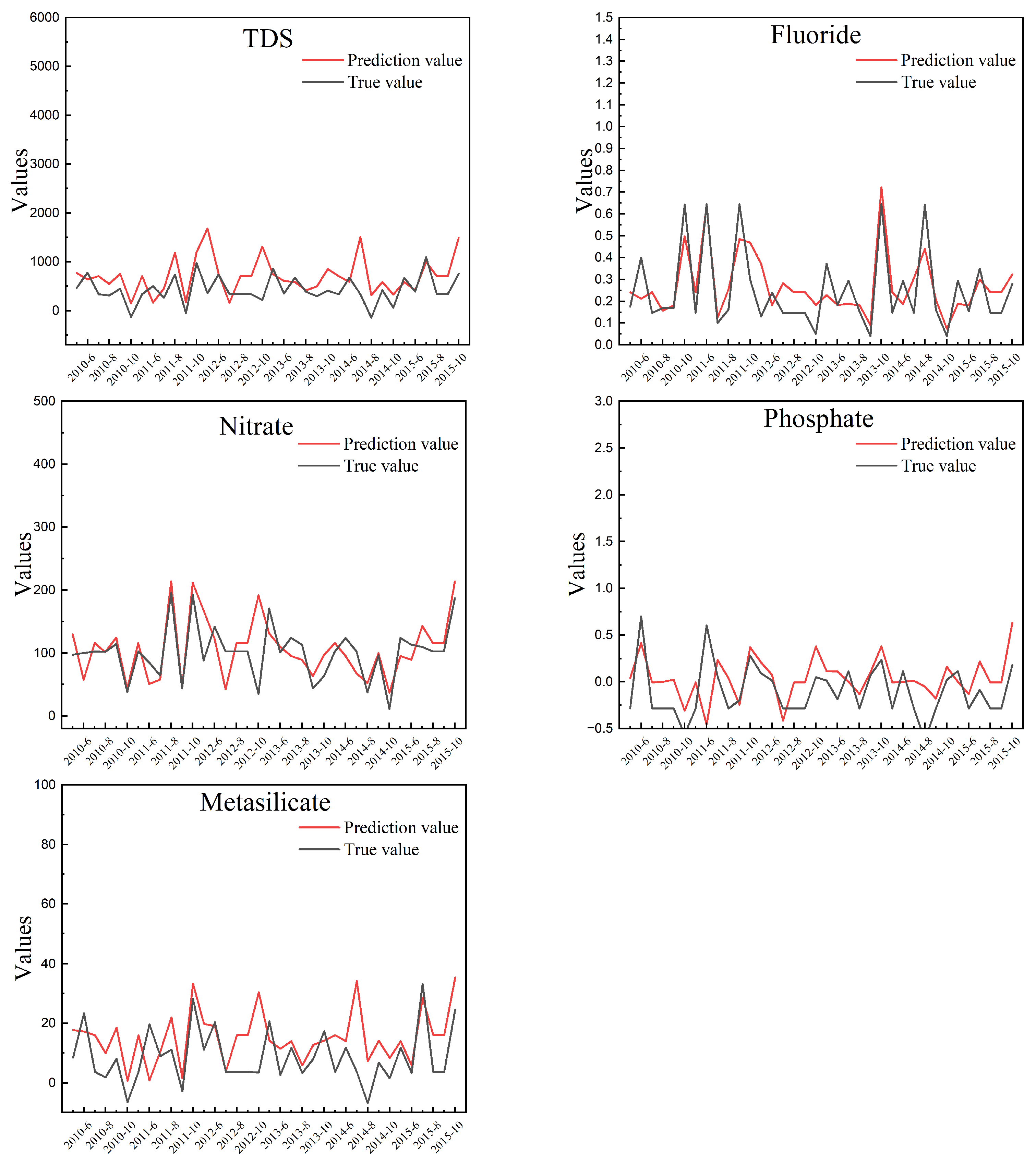
4.3. Modeling Result
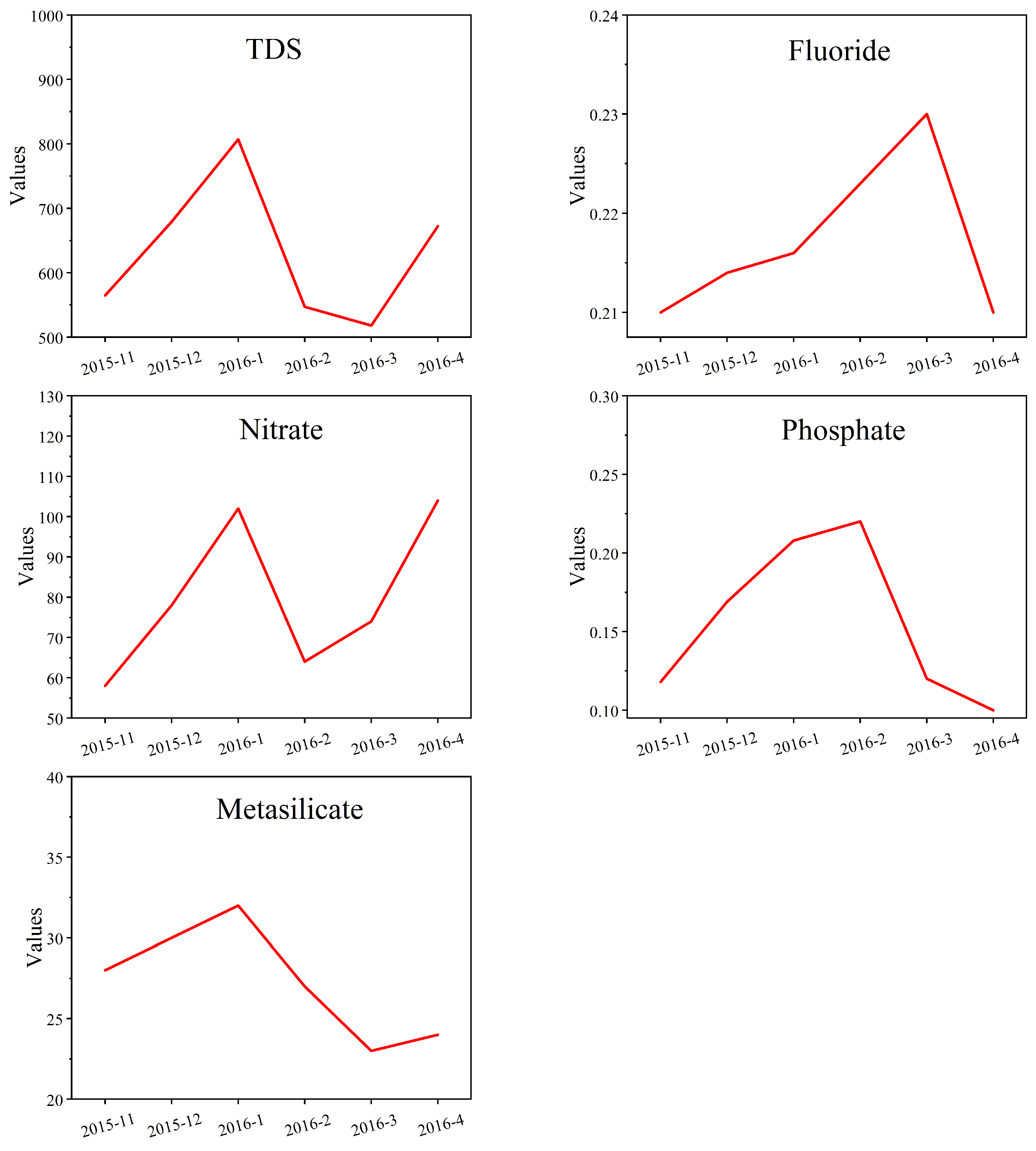
4.4. Application of the Concentration Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, M.; Tao, W.; Shang, Y.; Zhao, X. Spatiotemporal characteristics and influencing factors of China’s urban water resource utilization efficiency from the perspective of sustainable development. J. Clean. Prod. 2022, 338, 130649. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Z.; Yin, L.; Duan, L.; Huang, J. Topical Collection: Groundwater recharge and discharge in arid and semi-arid areas of China. Hydrogeol. J. 2021, 29, 521–524. [Google Scholar] [CrossRef]
- Bouimouass, H.; Fakir, Y.; Tweed, S.; Sahraoui, H.; Leblanc, M.; Chehbouni, A. Traditional irrigation practices sustain groundwater quality in a semiarid piedmont. Catena 2022, 210, 105923. [Google Scholar] [CrossRef]
- Kitterod, N.O.; Kvaerner, J.; Aagaard, P.; Arustien, J.; Biks, J.; Dagestad, A.; Gundersen, P.; Hansen, B.; Hjartarson, A.; Karro, E.; et al. Hydrogeology and groundwater quality in the Nordic and Baltic countries. Hydrol. Res. 2022, 53, 958–982. [Google Scholar] [CrossRef]
- Ha, K.; Lee, E.; An, H.; Kim, S.; Park, C.; Kim, G.B.; Ko, K.S. Evaluation of Seasonal Groundwater Quality Changes Associated with Groundwater Pumping and Level Fluctuations in an Agricultural Area, Korea. Water 2021, 13, 51. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, R.; Wu, J.; Wang, H.; Luo, Z. Uncertain in WQI-based groundwater quality assessment methods: A case study in east of Beijing, China. Environ. Earth Sci. 2022, 81, 1–16. [Google Scholar] [CrossRef]
- Aladejana, J.A.; Kahn, R.M.; Sentenac, P.; Hassan, I. Assessing the Impact of Climate Change on Groundwater Quality of the Shallow Coastal Aquifer of Eastern Dahomey Basin, Southwestern Nigeria. Water 2020, 12, 224. [Google Scholar] [CrossRef]
- Yan, R.; Liao, J.; Yang, J.; Sun, W.; Nong, M.; Li, F. Multi-hour and multi-site air quality index forecasting in Beijing using CNN, LSTM, CNN-LSTM, and spatiotemporal clustering. Expert Syst. Appl. 2021, 169, 114513. [Google Scholar] [CrossRef]
- Xie, W.; Ren, B.; Hursthouse, A.; Wang, Z.; Luo, X. Simulation of Manganese Transport in Groundwater Using Visual MODFLOW: A Case Study from Xiangtan Manganese Ore Area in Central China. Pol. J. Environ. Stud. 2021, 30, 1409–1420. [Google Scholar] [CrossRef]
- Bierkens, M.F.P.; Wada, Y. Non-renewable groundwater use and groundwater depletion: A review. Environ. Res. Lett. 2019, 14, 063002. [Google Scholar] [CrossRef]
- Ostad-Ali-Askari, K.; Shayannejad, M. Quantity and quality modelling of groundwater to manage water resources in Isfahan-Borkhar Aquifer. Environ. Dev. Sustain. 2021, 23, 15943–15959. [Google Scholar] [CrossRef]
- Haghnazar, H.; Johannesson, K.H.; Gonzalez-Pinzon, R.; Pourakbar, M.; Aghayani, E.; Rajabi, A.; Hashemi, A.A. Groundwater geochemistry, quality, and pollution of the largest lake basin in the Middle East: Comparison of PMF and PCA-MLR receptor models and application of the source-oriented HHRA approach. Chemosphere 2022, 288, 132489. [Google Scholar] [CrossRef]
- Koh, E.H.; Hyun, B.S.; Lee, E.; Kim, M.C.; Kang, B.R.; Park, W.B.; Jun, S.C. Crop Field Level Estimation of Nitrogen Input from Fertilizer Use in Jeju Island, South Korea: Management Methods to Prevent Groundwater NO3-N Contamination. Water 2021, 13, 2715. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Zhan, H.; Yang, S. Effect of long-term saline mulched drip irrigation on soil-groundwater environment in arid Northwest China. Sci. Total. Environ. 2022, 820, 153222. [Google Scholar] [CrossRef]
- Liu, G.; Ye, J.; Chen, Y.; Yang, X.; Gu, Y. Analysis of Water Pollution Causes and Control Countermeasures in Liaohe Estuary via Support Vector Machine Particle Swarm Optimization under Deep Learning. CMES Comput. Model. Eng. Sci. 2022, 130, 315–329. [Google Scholar] [CrossRef]
- El Mountassir, O.; Bahir, M.; Ouazar, D.; Chehbouni, A.; Carreira, P.M. Temporal and spatial assessment of groundwater contamination with nitrate using nitrate pollution index (NPI), groundwater pollution index (GPI), and GIS (case study: Essaouira basin, Morocco). Environ. Sci. Pollut. Res. 2022, 29, 17132–17149. [Google Scholar] [CrossRef] [PubMed]
- Yafouz, A.; AlDahoul, N.; Birima, A.H.; Ahmed, A.N.; Sherif, M.; Sefelnasr, A.; Allawi, M.F.; Elshafie, A. Comprehensive comparison of various machine learning algorithms for short-term ozone concentration prediction. Alex. Eng. J. 2022, 61, 4607–4622. [Google Scholar] [CrossRef]
- Shi, L.; Zhang, H.; Xu, X.; Han, M.; Zuo, P. A balanced social LSTM for PM2.5 concentration prediction based on local spatiotemporal correlation. Chemosphere 2022, 291, 133124. [Google Scholar] [CrossRef]
- Moghaddam, H.K.; Rajaei, A.; Rahimzadeh kivi, Z.; Moghaddam, H.K. Prediction of qualitative parameters concentration in the groundwater resources using the Bayesian approach. Groundw. Sustain. Dev. 2022, 17, 100758. [Google Scholar] [CrossRef]
- Orellana-Macias, J.M.; Perles Rosello, M.J. Assessment of Risk and Social Impact on Groundwater Pollution by Nitrates. Implementation in the Gallocanta Groundwater Body (NE Spain). Water 2022, 14, 202. [Google Scholar] [CrossRef]
- Cao, L.; Huang, L.; Zhao, P.; Liu, Y. Study on the Whole Process Simulation and Regulation Mechanism of Urban Green Ecological Rainwater Drainage System. CMES Comput. Model. Eng. Sci. 2021, 129, 787–803. [Google Scholar] [CrossRef]
- Jenifer, M.A.; Jha, M.K.; Khatun, A. Assessing Multi-Criteria Decision Analysis Models for Predicting Groundwater Quality in a River Basin of South India. Sustainability 2021, 13, 6719. [Google Scholar] [CrossRef]
- Abba, S.I.; Hadi, S.J.; Sammen, S.S.; Salih, S.Q.; Abdulkadir, R.A.; Pham, Q.B.; Yaseen, Z.M. Evolutionary computational intelligence algorithm coupled with self-tuning predictive model for water quality index determination. J. Hydrol. 2020, 587, 124974. [Google Scholar] [CrossRef]
- Bayatvarkeshi, M.; Imteaz, M.A.; Kisi, O.; Zarei, M.; Yaseen, Z.M. Application of M5 model tree optimized with Excel Solver Platform for water quality parameter estimation. Environ. Sci. Pollut. Res. 2021, 28, 7347–7364. [Google Scholar] [CrossRef] [PubMed]
- Tiyasha; Tung, T.M.; Yaseen, Z.M. A survey on river water quality modelling using artificial intelligence models: 2000–2020. J. Hydrol. 2020, 585, 124670. [Google Scholar] [CrossRef]
- Al-Sulttani, A.O.; Al-Mukhtar, M.; Roomi, A.B.; Farooque, A.A.; Khedher, K.M.; Yaseen, Z.M. Proposition of New Ensemble Data-Intelligence Models for Surface Water Quality Prediction. IEEE Access 2021, 9, 108527–108541. [Google Scholar] [CrossRef]
- Tiyasha; Tung, T.M.; Yaseen, Z.M. Deep Learning for Prediction of Water Quality Index Classification: Tropical Catchment Environmental Assessment. Nat. Resour. Res. 2021, 30, 4235–4254. [Google Scholar] [CrossRef]
- Deng, Y.; Zhou, X.; Shen, J.; Xiao, G.; Hong, H.; Lin, H.; Wu, F.; Liao, B.Q. New methods based on back propagation (BP) and radial basis function (RBF) artificial neural networks (ANNs) for predicting the occurrence of haloketones in tap water. Sci. Total. Environ. 2021, 772, 145534. [Google Scholar] [CrossRef]
- Huang, X.; Gao, L.; Crosbie, R.S.; Zhang, N.; Fu, G.; Doble, R. Groundwater Recharge Prediction Using Linear Regression, Multi-Layer Perception Network, and Deep Learning. Water 2019, 11, 1879. [Google Scholar] [CrossRef]
- Vijay, S.; Kamaraj, K. Prediction of Water Quality Index in Drinking Water Distribution System Using Activation Functions Based Ann. Water Resour. Manag. 2021, 35, 535–553. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, C.; Zhou, Y.; Xu, X. Modeling of Vapor-Liquid Equilibrium for Electrolyte Solutions Based on COSMO-RS Interaction. J. Chem. 2022, 2022, 1–13. [Google Scholar] [CrossRef]
- Siarkos, I.; Sevastas, S.; Mallios, Z.; Theodossiou, N.; Ifadis, I. Investigating groundwater vulnerability variation under future abstraction scenarios to estimate optimal pumping reduction rates. J. Hydrol. 2021, 598, 126297. [Google Scholar] [CrossRef]
- Miranda-Rius, J.; Brunet-Llobet, L.; Lahor-Soler, E.; Mrina, O.; Mashala, E.I.; Mahande, M.J. Periodontal and dental conditions of a school population in a volcanic region of Tanzania with highly fluoridated community drinking water. Afr. Health Sci. 2020, 20, 476–487. [Google Scholar] [CrossRef]
- Liu, W.; Xu, X.; Lu, F.; Cao, J.; Li, P.; Fu, T.; Chen, G.; Su, Q. Three-dimensional mapping of soil salinity in the southern coastal area of Laizhou Bay, China. Land Degrad. Dev. 2018, 29, 3772–3782. [Google Scholar] [CrossRef]
- Hu, Y.; You, M.; Liu, G.; Dong, Z. Distribution and potential health risk of nitrate in centralized groundwater sources of Wanbei Plain, Central China. Aqua Water Infrastruct. Ecosyst. Soc. 2021, 70, 684–695. [Google Scholar] [CrossRef]
- Temkin, A.; Evans, S.; Manidis, T.; Campbell, C.; Naidenko, O.V. Exposure-based assessment and economic valuation of adverse birth outcomes and cancer risk due to nitrate in United States drinking water. Environ. Res. 2019, 176, 108442. [Google Scholar] [CrossRef]
- Li, Y.; Bian, J.; Li, J.; Ma, Y.; Auguiano, J.H.H. Hydrochemistry and stable isotope indication of natural mineral water in Changbai Mountain, China. J. Hydrol. Reg. Stud. 2022, 40, 101047. [Google Scholar] [CrossRef]

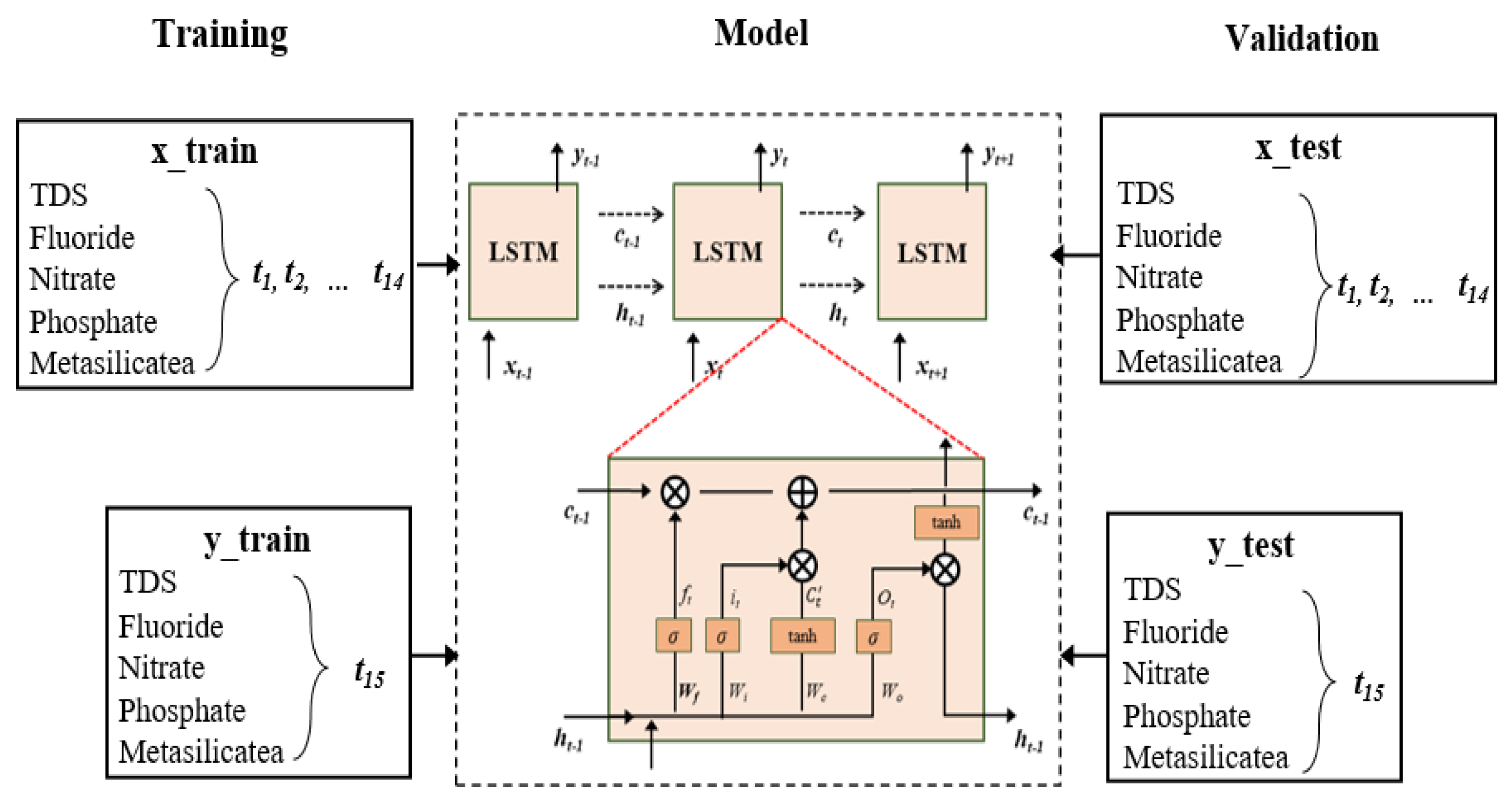


| No. | Indicators | Standards | Measurement Method |
|---|---|---|---|
| 1 | TDS | ”Standard examination methods for drinking water—Organoleptic and physical parameters”(GB/T5750.4-2006) | Gravimetric method |
| 2 | Fluoride | ”Water Quality-Determination of Fluoride-Ion Selective Elec-trode Method”(GB7484-87) | Ion selective electrode method |
| 3 | Nitrate | ”Water quality—Determination of nitrate-nitrogen—Ultraviolet spectrophotometry” (HJ/T346-2007) | Ultraviolet spectro- photometry |
| 4 | Phosphate | ”Standard examination methods for drinking water—Nonmental parameters” (GB/T 5750.5-2006) | Molybdenum blue spectrophotometric method |
| 5 | Metasilicate | ”Drinking natural mineral water test method” (GB8538-2016) | Molybdosilicate blue photometry |
| Methods | TDS | Fluoride | Nitrate | Phosphate | Metasilicate |
|---|---|---|---|---|---|
| Kolmogorov–Sminov (KS test) | 0.030 | 0.000 | 0.000 | 0.000 | 0.013 |
| Shapiro–Wilk (SW test) | 0.000 | 0.000 | 0.000 | 0.000 | 0.039 |
| Year | 1# | 2# | 3# | |||
|---|---|---|---|---|---|---|
| Dry Period | Wet Period | Dry Period | Wet Period | Dry Period | Wet Period | |
| 2000 | 0.20 | 0.80 | 0.21 | 0.79 | 0.20 | 0.80 |
| 2001 | 0.24 | 0.96 | 0.20 | 0.80 | 0.24 | 0.76 |
| 2002 | 0.16 | 0.84 | 0.17 | 0.83 | 0.17 | 0.84 |
| 2003 | 0.21 | 0.79 | 0.19 | 0.81 | 0.22 | 0.79 |
| 2004 | 0.15 | 0.84 | 0.15 | 0.85 | 0.15 | 0.84 |
| 2005 | 0.16 | 0.84 | 0.22 | 0.78 | 0.16 | 0.84 |
| 2006 | 0.14 | 0.86 | 0.10 | 0.89 | 0.13 | 0.86 |
| 2007 | 0.05 | 0.95 | 0.07 | 0.93 | 0.05 | 0.95 |
| 2008 | 0.29 | 0.72 | 0.27 | 0.73 | 0.28 | 0.72 |
| 2009 | 0.21 | 0.79 | 0.18 | 0.82 | 0.21 | 0.79 |
| 2010 | 0.08 | 0.92 | 0.11 | 0.89 | 0.07 | 0.92 |
| 2011 | 0.27 | 0.73 | 0.28 | 0.72 | 0.27 | 0.73 |
| 2012 | 0.20 | 0.80 | 0.21 | 0.78 | 0.20 | 0.80 |
| 2013 | 0.25 | 0.75 | 0.30 | 0.70 | 0.25 | 0.75 |
| 2014 | 0.26 | 0.74 | 0.30 | 0.71 | 0.26 | 0.74 |
| Average | 0.19 | 0.82 | 0.20 | 0.80 | 0.19 | 0.81 |
| Names of Wells | Geographical Location | Statistical Indicators | TDS (mg/L) | Fluoride (mg/L) | Nitrate (mg/L) | Phosphate (mg/L) | Metasilicate (mg/L) |
|---|---|---|---|---|---|---|---|
| 1 | 121.831 °E /36.985 °N | Avg Std. CV (%) | 421.44 81.02 19.22 | 93.64 51.05 54.52 | 0.17 0.12 73.40 | 0.04 0.03 64.75 | 30.86 5.11 16.55 |
| 2 | 121.882 °E /37.063 °N | Avg Std. CV (%) | 918.52 351.12 38.23 | 139.60 126.21 90.41 | 0.18 0.11 63.05 | 0.09 0.08 94.91 | 23.75 6.83 28.74 |
| 3 | 121.886 °E /37.093 °N | Avg Std. CV (%) | 698.09 196.32 28.12 | 100.42 60.81 60.55 | 0.25 0.09 34.51 | 0.30 0.19 62.23 | 21.53 7.37 34.23 |
| Names of Wells | Longitute/ Latitude | Statistical Indicators | TDS (mg/L) | Fluoride (mg/L) | Nitrate (mg/L) | Phosphate (mg/L) | Metasilicate (mg/L) |
|---|---|---|---|---|---|---|---|
| 1 | 121.831 °E /36.985 °N | Avg Std. CV (%) | 516.90 195.35 37.79 | 132.22 101.35 76.65 | 0.25 0.11 44.30 | 0.04 0.01 40.54 | 34.84 2.41 6.91 |
| 2 | 121.882 °E /37.063 °N | Avg Std. CV (%) | 934.70 359.17 38.43 | 186.93 135.35 72.41 | 0.14 0.14 100.56 | 0.18 0.09 47.17 | 26.68 4.29 16.08 |
| 3 | 121.886 °E /37.093 °N | Avg Std. CV (%) | 764.94 81.64 10.67 | 138.57 38.90 28.07 | 0.28 0.21 77.26 | 0.28 0.14 48.46 | 26.68 4.71 17.67 |
| Indicators (mg/L) | MAE (Rainy Period) | MAE (Dry Period) |
|---|---|---|
| TDS | 89.45 | 76.35 |
| Fluoride | 0.09 | 0.06 |
| Nitrate | 10.32 | 5.47 |
| Phosphate | 0.23 | 0.17 |
| Metasilicate | 4.21 | 2.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Xu, M.; Liu, Y.; Li, X.; Pang, Z.; Miao, S. Predicting Groundwater Indicator Concentration Based on Long Short-Term Memory Neural Network: A Case Study. Int. J. Environ. Res. Public Health 2022, 19, 15612. https://doi.org/10.3390/ijerph192315612
Liu C, Xu M, Liu Y, Li X, Pang Z, Miao S. Predicting Groundwater Indicator Concentration Based on Long Short-Term Memory Neural Network: A Case Study. International Journal of Environmental Research and Public Health. 2022; 19(23):15612. https://doi.org/10.3390/ijerph192315612
Chicago/Turabian StyleLiu, Chao, Mingshuang Xu, Yufeng Liu, Xuefei Li, Zonglin Pang, and Sheng Miao. 2022. "Predicting Groundwater Indicator Concentration Based on Long Short-Term Memory Neural Network: A Case Study" International Journal of Environmental Research and Public Health 19, no. 23: 15612. https://doi.org/10.3390/ijerph192315612
APA StyleLiu, C., Xu, M., Liu, Y., Li, X., Pang, Z., & Miao, S. (2022). Predicting Groundwater Indicator Concentration Based on Long Short-Term Memory Neural Network: A Case Study. International Journal of Environmental Research and Public Health, 19(23), 15612. https://doi.org/10.3390/ijerph192315612






