Injury Metrics for Assessing the Risk of Acute Subdural Hematoma in Traumatic Events
Abstract
1. Introduction
2. Data and Methods
2.1. Materials and Data
2.2. Injury Metrics
2.3. Proposed Injury Metric
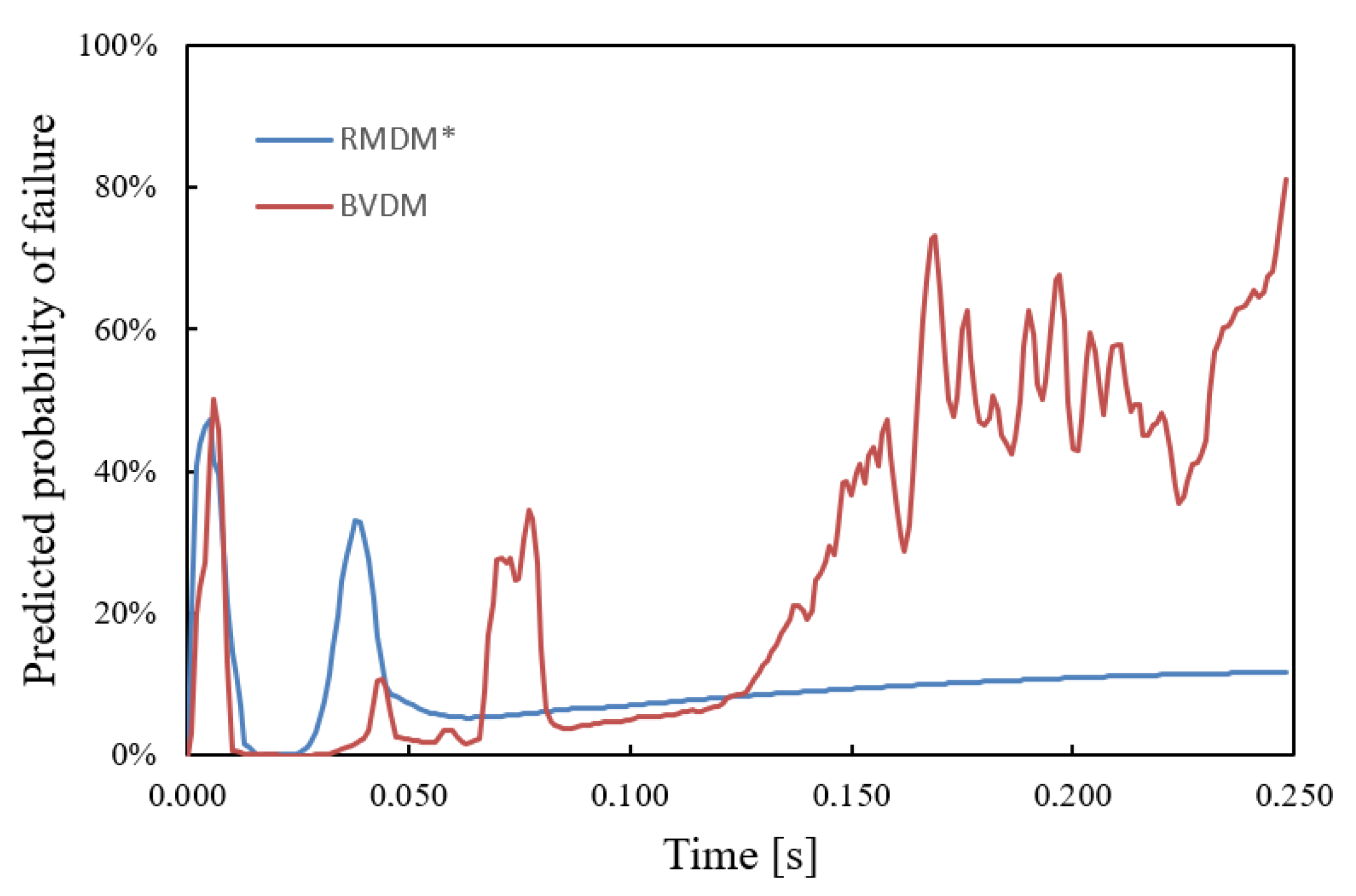
3. Results
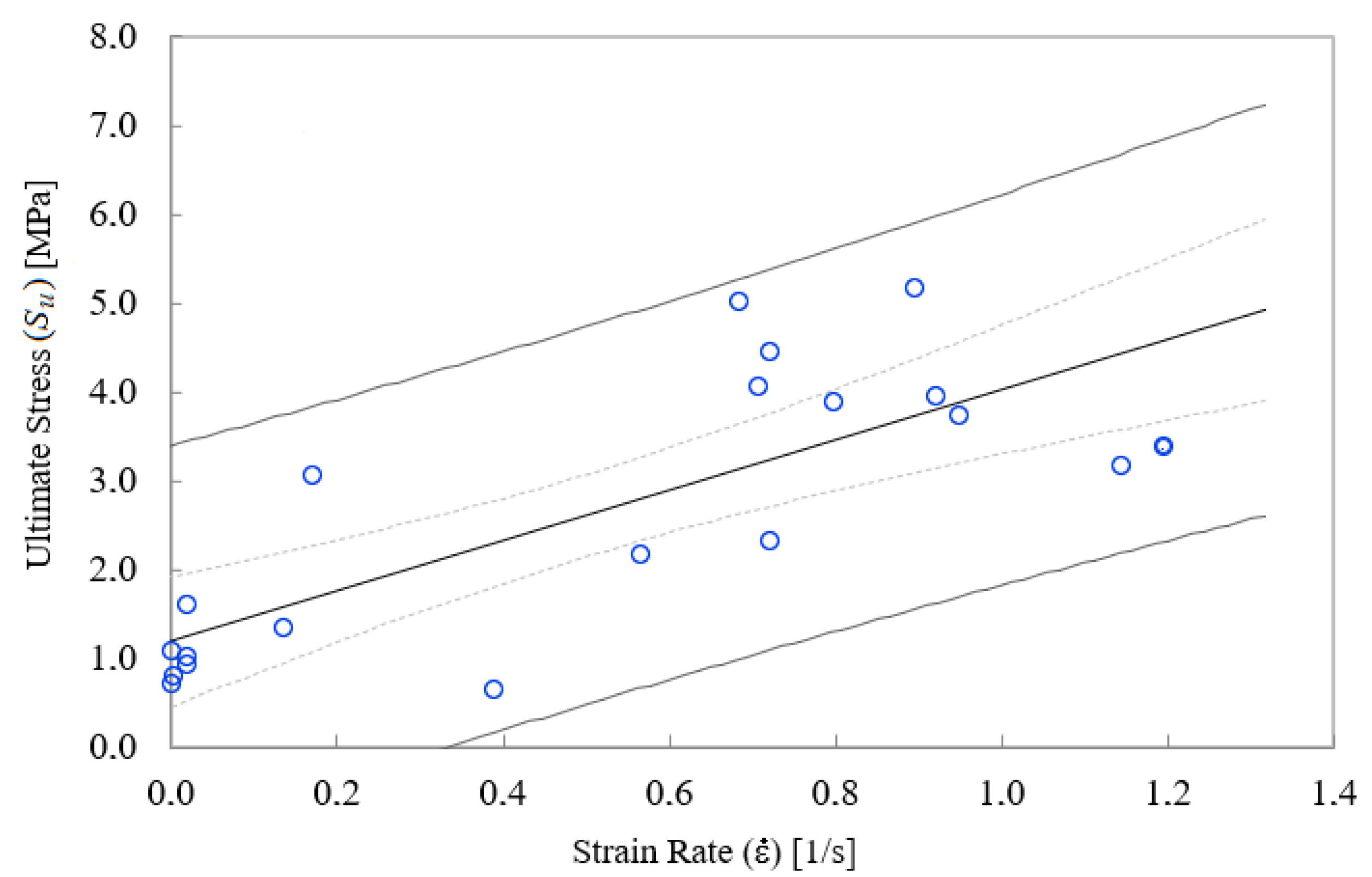
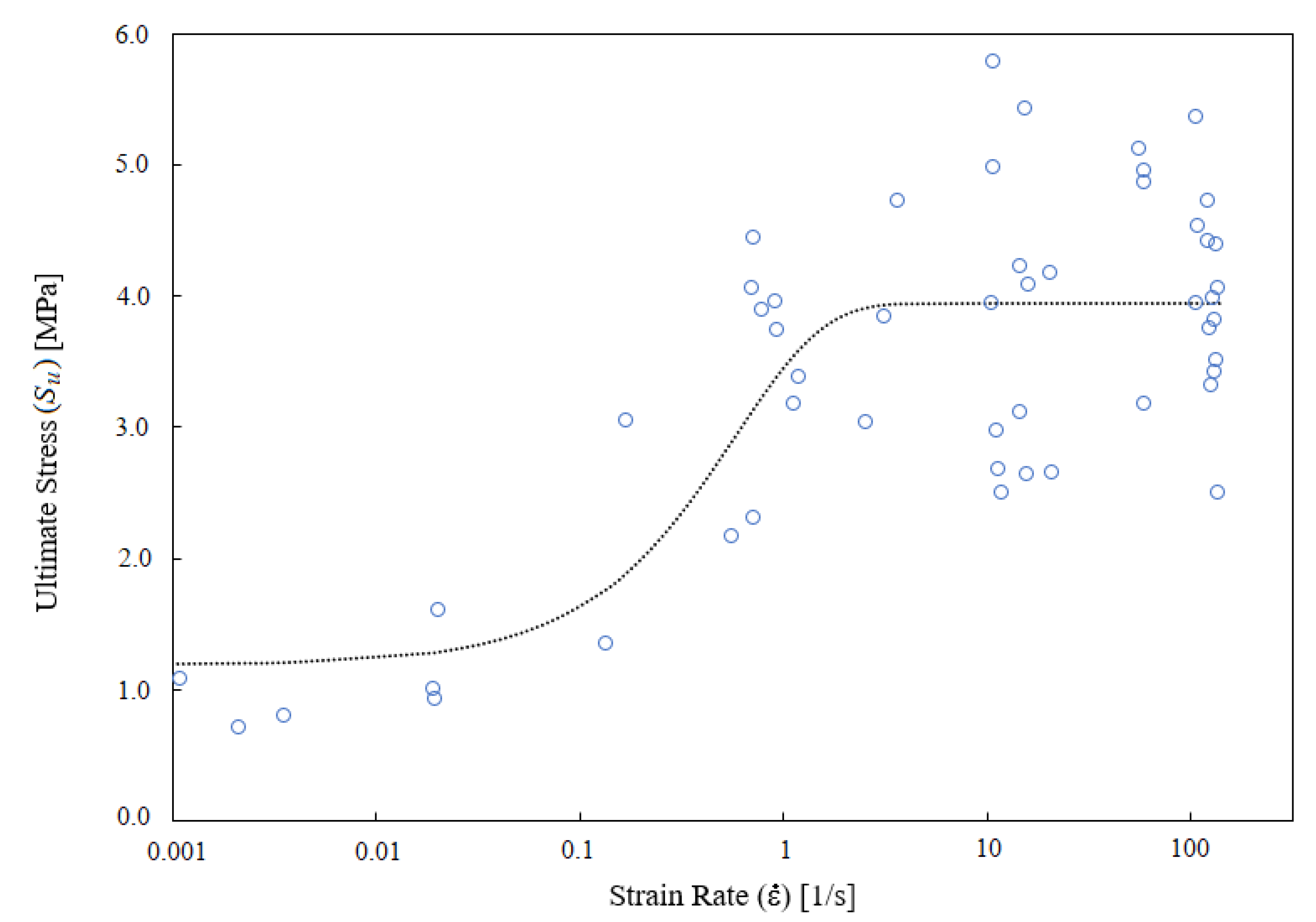
3.1. Dependence of Ultimate Stress on Strain Rate
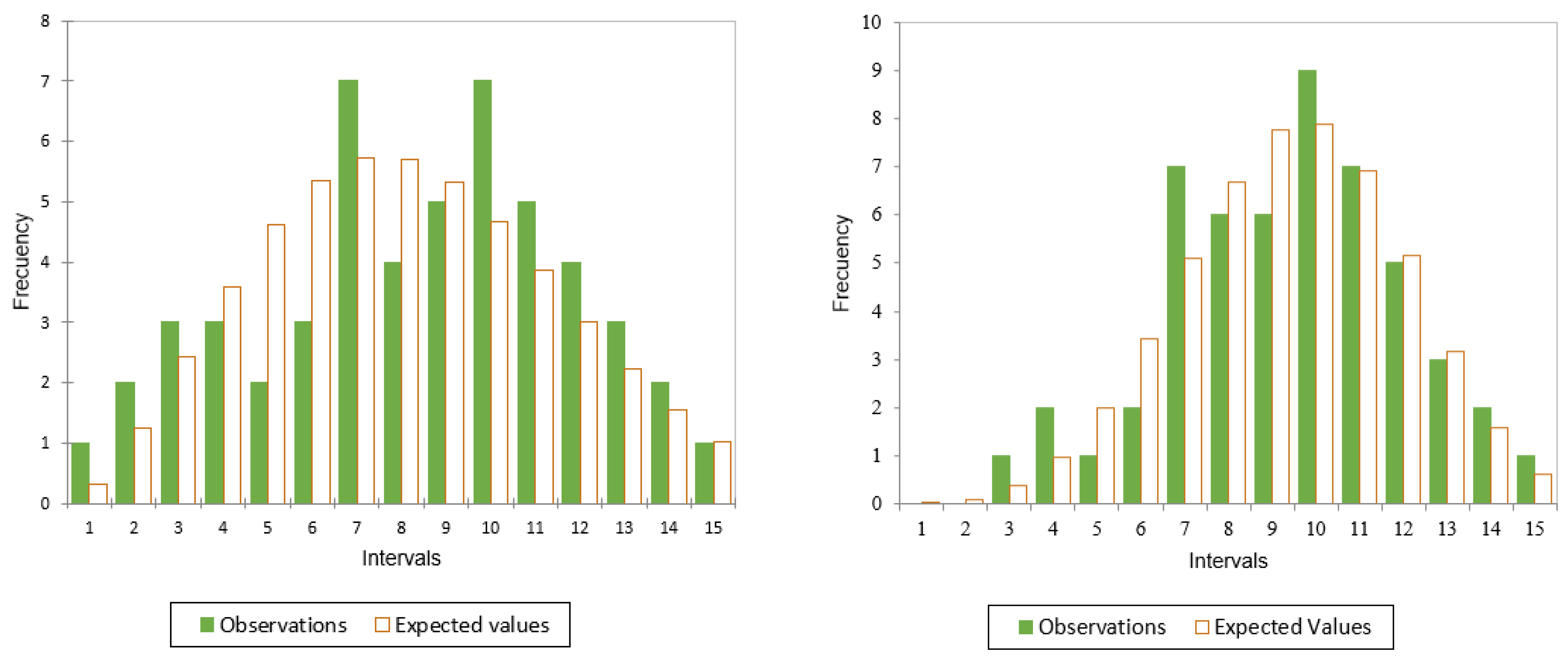
3.2. Distribution of the Intrinsic Ultimate Stress
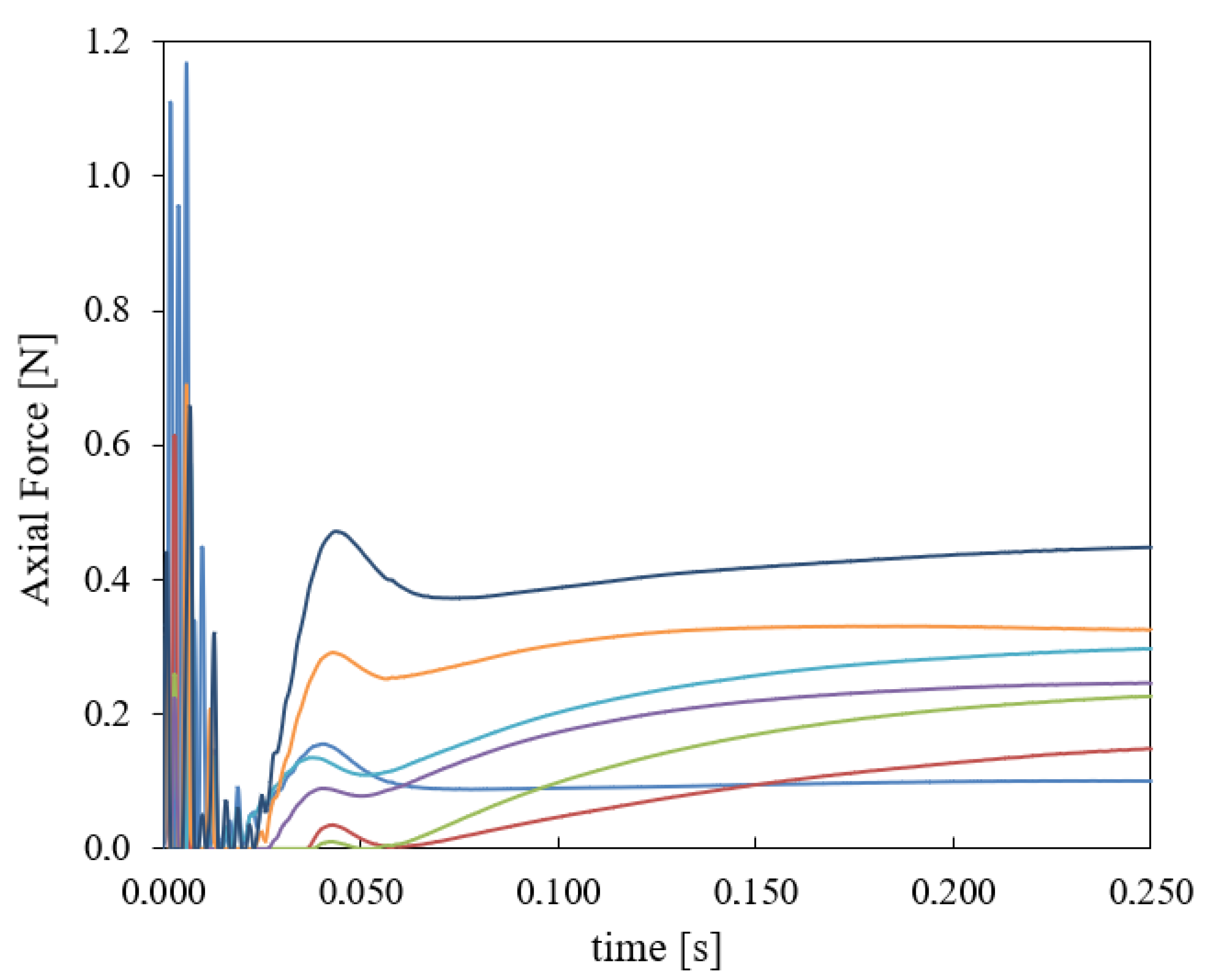
3.3. Comparison of the Metrics in a Fall from a Height
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASDH | Acute Subdural Hematoma |
| BVDM | Bridging Vein Damage Metric |
| CBV(s) | Cerebral Bridging Vein(s) |
| CDF(s) | Cumulative Distribution Function(s) |
| EVT | Extreme Value Theory |
| FEHM | Finite Element Head Model |
| GEV | Generalized Extreme Value |
| PMHS | Post-Mortem Human Subject |
| RMDM | Relative Motion Damage Measure |
| SRDF | Strain Rate Dependence Function |
| TBI | Traumatic Brain Injury |
Appendix A. Suitability of BVDM
References
- Yang, B.Z.; Loo, B.P. Land use and traffic collisions: A link-attribute analysis using Empirical Bayes method. Accid. Anal. Prev. 2016, 95, 236–249. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Global Status Report on Road Safety 2018: Summary; WHO: Geneva, Switzerland, 2018. [Google Scholar]
- Dewan, M.C.; Rattani, A.; Gupta, S.; Baticulon, R.E.; Hung, Y.C.; Punchak, M.; Agrawal, A.; Adeleye, A.O.; Shrime, M.G.; Rubiano, A.M.; et al. Estimating the global incidence of traumatic brain injury. J. Neurosurg. 2018, 130, 1080–1097. [Google Scholar] [CrossRef]
- Miller, J.D.; Nader, R. Acute subdural hematoma from bridging vein rupture: A potential mechanism for growth. J. Neurosurg. 2014, 120, 1378–1384. [Google Scholar] [CrossRef] [PubMed]
- Gennarelli, T.A.; Thibault, L.E. Biomechanics of acute subdural hematoma. J. Trauma 1982, 22, 680–686. [Google Scholar] [CrossRef]
- Graham, D.I.; Adams, J.H.; Nicoll, J.A.R.; Maxwell, W.L.; Gennarelli, T.A. The nature, distribution and causes of traumatic brain injury. Brain Pathol. 1995, 5, 397–406. [Google Scholar] [CrossRef] [PubMed]
- Depreitere, B.; Van Lierde, C.; Vander Sloten, J.; Van Audekercke, R.; Van Der Perre, G.; Plets, C.; Goffin, J. Mechanics of acute subdural hematomas resulting from bridging vein rupture. J. Neurosurg. 2006, 104, 950–956. [Google Scholar] [CrossRef] [PubMed]
- Migueis, G.F.J.; Fernandes, F.A.O.; Ptak, M.; Ratajczak, M.; de Sousa, R.A. Detection of bridging veins rupture and subdural haematoma onset using a finite element head model. Clin. Biomech. 2019, 63, 104–111. [Google Scholar] [CrossRef]
- Costa, J.M.; Fernandes, F.A.; de Sousa, R.J.A. Prediction of subdural haematoma based on a detailed numerical model of the cerebral bridging veins. J. Mech. Behav. Biomed. Mater. 2020, 111, 103976. [Google Scholar] [CrossRef]
- Arregui-Dalmases, C.; Rebollo-Soria, M.C.; Sanchez-Molina, D.; Velazquez-Ameijide, J.; Alvarez, T. Pedestrian head injury biomechanics and damage mechanism. Pedestrian protection automotive regulation assessment. Neurocirugía 2017, 28, 41–46. (In English) [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sánchez-Molina, D.; García-Vilana, S.; Llumà, J.; Galtés, I.; Velázquez-Ameijide, J.; Rebollo-Soria, M.C.; Arregui-Dalmases, C. Mechanical behaviour of blood vessels during a Traumatic Brain Injury: Elastic and viscoelastic contributions. Biology 2021, 10, 831. [Google Scholar] [CrossRef]
- Monea, A.G.; Baeck, K.; Verbeken, E.; Verpoest, I.; Vander Sloten, J.; Goffin, J.; Depreitere, B. The biomechanical behaviour of the bridging vein–superior sagittal sinus complex with implications for the mechanopathology of acute subdural haematoma. J. Mech. Behav. Biomed. Mater. 2014, 32, 155–165. [Google Scholar] [CrossRef] [PubMed]
- Takhounts, E.G.; Eppinger, R.H.; Campbell, J.Q.; Tannous, R.E.; Power, E.D.; Shook, L.S. On the development of the SIMon finite element head model. Stapp. Car. Crash. J. 2003, 47, 107–133. [Google Scholar]
- Takhounts, E.G.; Ridella, S.A.; Hasija, V.; Tannous, R.E.; Campbell, J.Q.; Malone, D.; Duma, S. Investigation of traumatic brain injuries using the next generation of simulated injury monitor (SIMon) finite element head model. Stapp. Car. Crash. J. 2008, 52, 1–31. [Google Scholar]
- Sánchez-Molina, D.; Arregui-Dalmases, C.; Velázquez-Ameijide, J.; Angelini, M.; Kerrigan, J.; Crandall, J. Traumatic brain injury in pedestrian–vehicle collisions: Convexity and suitability of some functionals used as injury metrics. Comput. Methods Programs Biomed. 2016, 136, 55–64. [Google Scholar] [CrossRef]
- Sanchez-Molina, D.; Velazquez-Ameijide, J.; Arregui-Dalmases, C.; Crandall, J.R.; Untaroiu, C.D. Minimization of analytical injury metrics for head impact injuries. Traffic Inj. Prev. 2012, 13, 278–285. [Google Scholar] [CrossRef] [PubMed]
- Löwenhielm, P. Dynamic properties of the parasagittal bridging veins. Z. Rechtsmed. 1974, 74, 55–62. [Google Scholar] [CrossRef]
- Ott, K.A.; Wiechel, J.F.; Guenther, D.A.; Stammen, J.; Mallory, A.E. Assessment of the simulated injury monitor (SIMon) in analyzing head injuries in pedestrian crashes. Int. J. Passeng. Cars-Mech. Syst. 2012, 5, 487–505. [Google Scholar] [CrossRef]
- Bartsch, A.J.; Benzel, E.C.; Miele, V.J.; Morr, D.R.; Prakash, V. Boxing and mixed martial arts: Preliminary traumatic neuromechanical injury risk analyses from laboratory impact dosage data. J. Neurosurg. 2012, 116, 1070–1080. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, F.A.O.; Alves de Sousa, R.J.; Ptak, M. Finite element head modelling and head injury predictors. In Head Injury Simulation in Road Traffic Accidents; Springer Briefs in Applied Sciences and Technology; Springer: Cham, Switzerland; Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Hazay, M.; Bojtár, I. The probability of traumatic brain injuries based on tissue-level reliability analysis. Acta Bioeng. Biomech. 2019, 21, 1. [Google Scholar]
- Famaey, N.; Cui, Z.Y.; Musigazi, G.U.; Ivens, J.; Depreitere, B.; Verbeken, E.; Vander Sloten, J. Structural and mechanical characterisation of bridging veins: A review. J. Mech. Behav. Biomed. Mater. 2015, 41, 222–240. [Google Scholar] [CrossRef]
- Delye, H.; Goffin, J.; Verschueren, P.; Vander Sloten, J.; Van der Perre, G.; Alaerts, H.; Verpoest, I.; Berckmans, D. Biomechanical properties of the superior sagittal sinus-bridging vein complex. Stapp. Car. Crash. J. 2006, 50, 625–636. [Google Scholar] [PubMed]
- Monson, K.L.; Goldsmith, W.; Barbaro, N.M.; Manley, G.T. Axial mechanical properties of fresh human cerebral blood vessels. J. Biomech. Eng. 2003, 125, 288–294. [Google Scholar] [CrossRef] [PubMed]
- García-Vilana, S.; Sánchez-Molina, D.; Llumà, J.; Galtés, I.; Velázquez-Ameijide, J.; Rebollo-Soria, M.C.; Arregui-Dalmases, C. Viscoelastic Characterization of Parasagittal Bridging Veins and Implications for Traumatic Brain Injury: A pilot study. Bioengineering 2021, 8, 145. [Google Scholar] [CrossRef]
- Gnedenko, B.V. Sur la distribution limite du terme maximum d’une serie aleatoire. Ann. Math. 1943, 44, 423–453. [Google Scholar] [CrossRef]
- Tippett, L.H.C. Statistics in research and management in the cotton industry. Inc. Stat. 1954, 5, 147–159. [Google Scholar] [CrossRef]
- Tippett, L.H.C. A restrospect of mathematics in textile technology. J. Text. Inst. Proc. 1960, 51, 413–422. [Google Scholar] [CrossRef]
- García-Vilana, S.; Sánchez-Molina, D.; Llumà, J.; Fernández-Osete, I.; Veláquez-Ameijide, J.; Martínez-González, E. A predictive model for fracture in human ribs based on in vitro acoustic emission data. Med. Phys. 2021, 48, 5540–5548. [Google Scholar] [CrossRef]
- Basu, B.; Tiwari, D.; Kundu, D.; Prasad, R. Is Weibull distribution the most appropriate statistical strength distribution for brittle materials? Ceram. Int. 2009, 35, 237–246. [Google Scholar] [CrossRef]
- Bertalan, Z.; Shekhawat, A.; Sethna, J.P.; Zapperi, S. Fracture strength: Stress concentration, extreme value statistics, and the fate of the Weibull distribution. Phys. Rev. Appl. 2014, 2, 034008. [Google Scholar] [CrossRef]
- Sánchez-Molina, D.; Martínez-González, E.; Velázquez-Ameijide, J.; Llumà, J.; Soria, M.R.; Arregui-Dalmases, C. A stochastic model for soft tissue failure using acoustic emission data. J. Mech. Behav. Biomed. Mater. 2015, 51, 328–336. [Google Scholar] [CrossRef][Green Version]
- Fernandes, F.A.; Sousa, R.J.A.D. Head injury predictors in sports trauma–a state-of-the-art review. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2015, 229, 592–608. [Google Scholar] [CrossRef] [PubMed]
- Gabler, L.F.; Crandall, J.R.; Panzer, M.B. Assessment of kinematic brain injury metrics for predicting strain responses in diverse automotive impact conditions. Ann. Biomed. Eng. 2016, 44, 3705–3718. [Google Scholar] [CrossRef] [PubMed]
- Gabler, L.F.; Crandall, J.R.; Panzer, M.B. Development of a metric for predicting brain strain responses using head kinematics. Ann. Biomed. Eng. 2018, 46, 972–985. [Google Scholar] [CrossRef]
- Kim, T.; Poplin, G.; Bollapragada, V.; Daniel, T.; Crandall, J. Monte Carlo method for estimating whole-body injury metrics from pedestrian impact simulation results. Accid. Anal. Prev. 2020, 147, 105761. [Google Scholar] [CrossRef] [PubMed]
- Hajiaghamemar, M.; Wu, T.; Panzer, M.B.; Margulies, S.S. Embedded axonal fiber tracts improve finite element model predictions of traumatic brain injury. Biomech. Model. Mechanobiol. 2020, 19, 1109–1130. [Google Scholar] [CrossRef]
- Levy, Y.; Bian, K.; Patterson, L.; Ouckama, R.; Mao, H. Head Kinematics and Injury Metrics for Laboratory Hockey-Relevant Head Impact Experiments. Ann. Biomed. Eng. 2021, 49, 2914–2923. [Google Scholar] [CrossRef] [PubMed]
- Rowson, B.; Duma, S.M. A review of on-field investigations into the biomechanics of concussion in football and translation to head injury mitigation strategies. Ann. Biomed. Eng. 2020, 48, 1044–1055. [Google Scholar] [CrossRef] [PubMed]
- Golman, A.J.; Danelson, K.A.; Gaewsky, J.P.; Stitzel, J.D. Implementation and validation of thoracic side impact injury prediction metrics in a human body model. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 1044–1055. [Google Scholar] [CrossRef]
- Dickey, G.J.; Bian, K.; Khan, H.R.; Mao, H. Developing commotio cordis injury metrics for baseball safety: Unravelling the connection between chest force and rib deformation to left ventricle strain and pressure. Comput. Methods Biomech. Biomed. Eng. 2021, 24, 1–10. [Google Scholar] [CrossRef]
- Jones, D.A.; Gaewsky, J.P.; Kelley, M.E.; Weaver, A.A.; Miller, A.N.; Stitzel, J.D. Lumbar vertebrae fracture injury risk in finite element reconstruction of CIREN and NASS frontal motor vehicle crashes. Traffic Inj. Prev. 2016, 17 (Suppl. 1), 109–115. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Molina, D.; García-Vilana, S.; Velázquez-Ameijide, J.; Arregui-Dalmases, C. Probabilistic assessment for clavicle fracture under compression loading: Rate-dependent behavior. Biomed. Eng. Appl. Basis Commun. 2020, 32, 2050040. [Google Scholar] [CrossRef]
- Mao, H.; Zhang, L.; Jiang, B.; Genthikatti, V.V.; Jin, X.; Zhu, F.; Yang, K.H. Development of a finite element human head model partially validated with thirty five experimental cases. J. Biomech. Eng. 2013, 135, 111002. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Ji, S. Incorporation of vasculature in a head injury model lowers local mechanical strains in dynamic impact. J. Biomech. 2020, 104, 109732. [Google Scholar] [CrossRef] [PubMed]
- Kleiven, S. Predictors for traumatic brain injuries evaluated through accident reconstructions. Stapp. Car. Crash. J. 2007, 51, 81–114. [Google Scholar] [PubMed]
- Doorly, M.C. Investigations into Head Injury Criteria Using Numerical Reconstruction of Real Life Accident Cases. Ph.D. Thesis, University College Dublin, Dublin, Ireland, 2007. [Google Scholar]
- Yan, W.; Pangestu, O.D. A modified human head model for the study of impact head injury. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 1049–1057. [Google Scholar] [CrossRef] [PubMed]
- Viano, D.C.; Casson, I.R.; Pellman, E.J.; Zhang, L.; King, A.I.; Yang, K.H. Concussion in professional football: Brain responses by finite element analysis: Part 9. Neurosurgery 2005, 57, 891–916. [Google Scholar] [CrossRef]
- Fernandes, F.A.; de Sousa, R.J.A.; Ptak, M. Validation of YEAHM. In Head Injury Simulation in Road Traffic Accidents; Springer: Cham, Switzerland, 2018; pp. 41–58. [Google Scholar]
- Pasquesi, S.A.; Margulies, S.S. Failure and fatigue properties of immature human and porcine parasagittal bridging veins. Ann. Biomed. Eng. 2017, 45, 1877–1889. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Vilana, S.; Sánchez-Molina, D.; Velázquez-Ameijide, J.; Llumà, J. Injury Metrics for Assessing the Risk of Acute Subdural Hematoma in Traumatic Events. Int. J. Environ. Res. Public Health 2021, 18, 13296. https://doi.org/10.3390/ijerph182413296
García-Vilana S, Sánchez-Molina D, Velázquez-Ameijide J, Llumà J. Injury Metrics for Assessing the Risk of Acute Subdural Hematoma in Traumatic Events. International Journal of Environmental Research and Public Health. 2021; 18(24):13296. https://doi.org/10.3390/ijerph182413296
Chicago/Turabian StyleGarcía-Vilana, Silvia, David Sánchez-Molina, Juan Velázquez-Ameijide, and Jordi Llumà. 2021. "Injury Metrics for Assessing the Risk of Acute Subdural Hematoma in Traumatic Events" International Journal of Environmental Research and Public Health 18, no. 24: 13296. https://doi.org/10.3390/ijerph182413296
APA StyleGarcía-Vilana, S., Sánchez-Molina, D., Velázquez-Ameijide, J., & Llumà, J. (2021). Injury Metrics for Assessing the Risk of Acute Subdural Hematoma in Traumatic Events. International Journal of Environmental Research and Public Health, 18(24), 13296. https://doi.org/10.3390/ijerph182413296





