Sample Size Requirements for Calibrated Approximate Credible Intervals for Proportions in Clinical Trials
Abstract
1. Introduction
2. Methodology
2.1. Exact and Approximate Intervals
2.2. A Measure of Discrepancy and Predictive Analysis
- (i)
- draw N samples from ;
- (ii)
- compute and , for ;
- (iii)
- compute , for ;
- (iv)
- set ;with a large number of draws, e.g., .
3. Examples: The Beta-Binomial Model
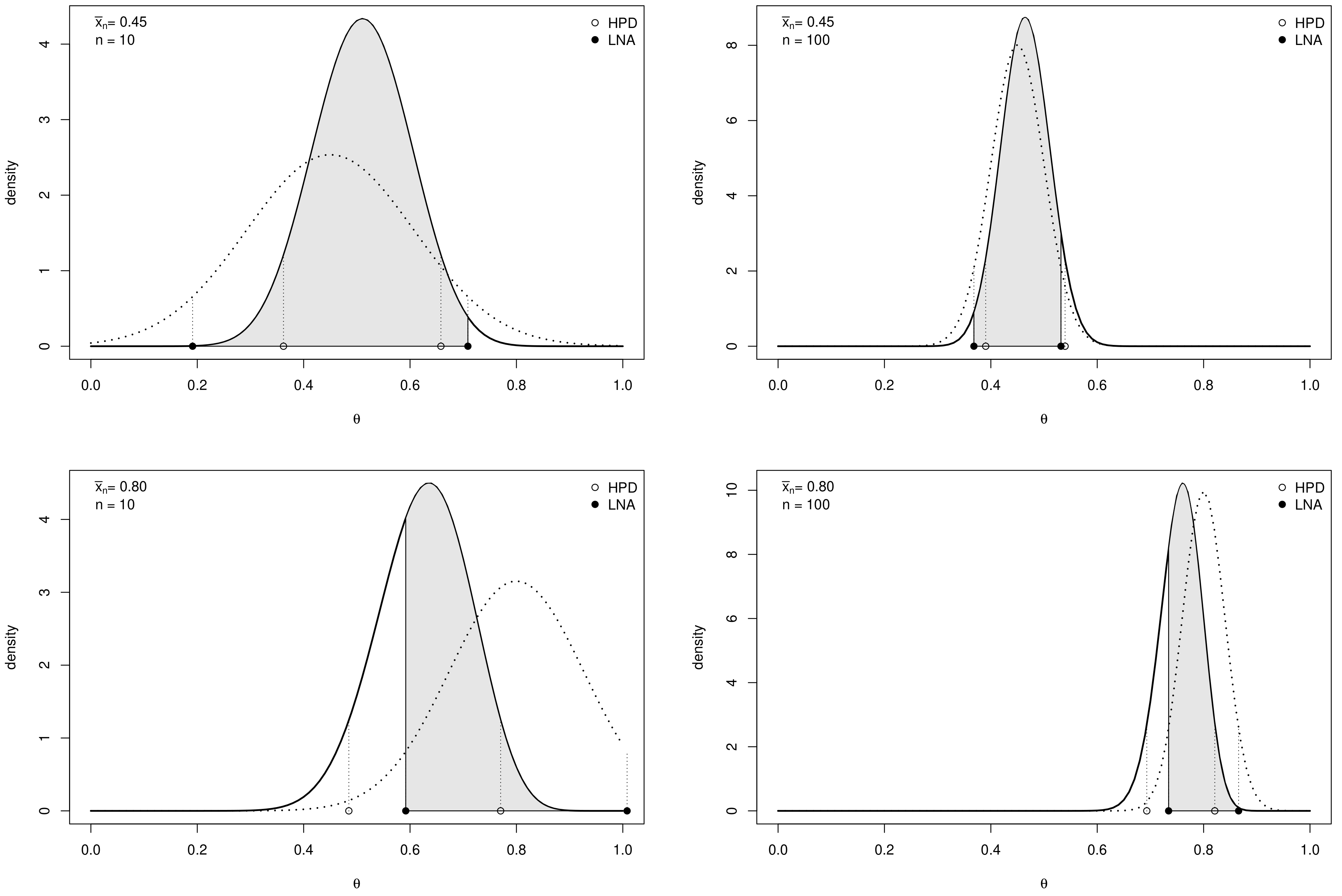
3.1. Credible Intervals for a Proportion
3.2. Credible Intervals for the Log-Odds
- (i)
- draw from the posterior Beta density, where M is a large number;
- (ii)
- compute , for ;
- (iii)
- use the R function HDInterval::hdi with the MC draws in input.
4. Application to Clinical Trials
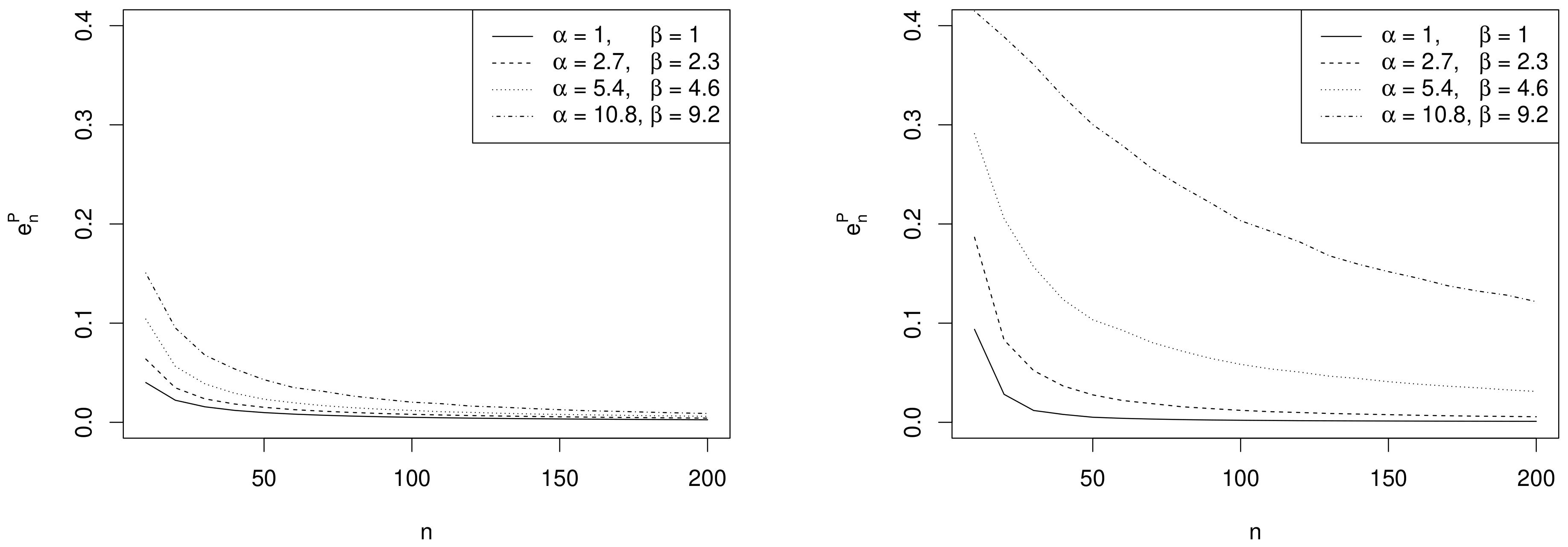
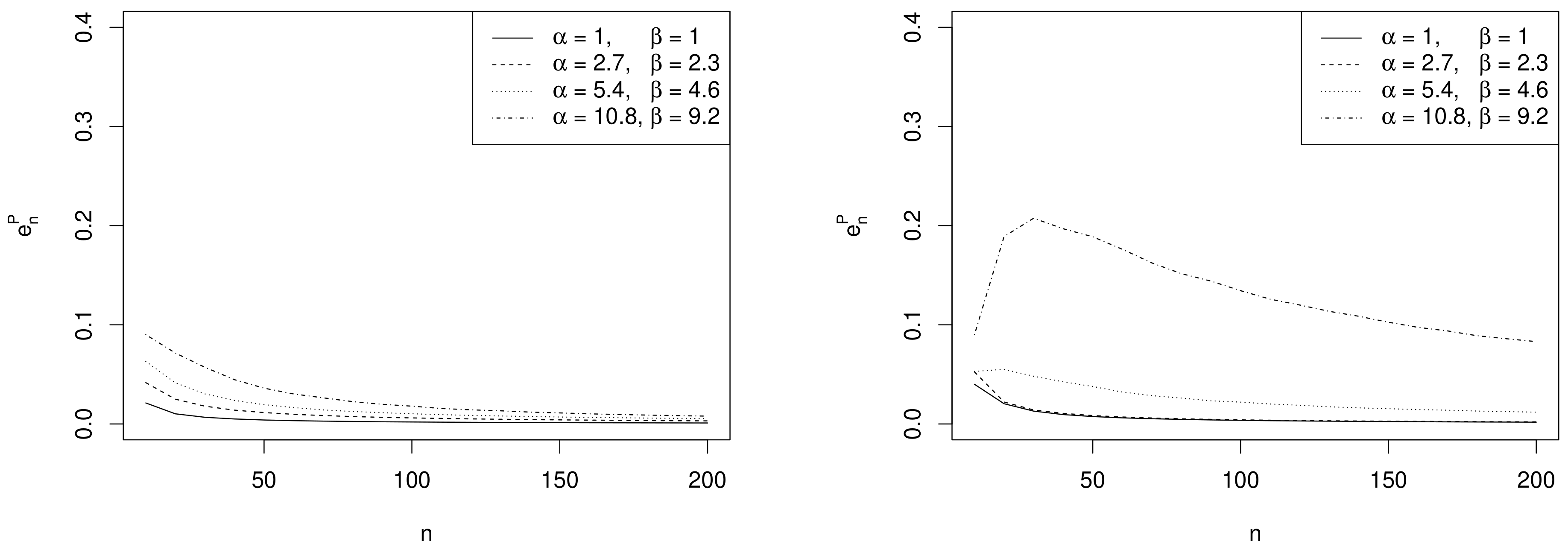
- Effect of sample size. As expected, the values of decrease as n increases and depend on the specific choices of , and as commented in the following remarks.
- Effect of prior sample size. For each value of n, the larger , the greater the values of . In fact, as the prior becomes more and more concentrated around the prior mean , the weight of the prior in the posterior distribution increases with respect to the role of the likelihood. This makes the discrepancy between Bayesian exact intervals and their likelihood approximation more striking. Moreover, when the uniform non-informative prior is considered, the smallest values of are observed (see solid line in Figure 2). As a consequence, larger values of the prior sample size imply greater values of , as shown in Table 1.
- Effect of the difference between design value and prior mean. When the distance between and the prior mean is relatively large and, at the same time, the prior sample size dominates n, the posterior mode and the maximum likelihood estimate are well separated. In other words, Equation (4) does not provide a good approximation of the posterior density of . This explains the larger values of , in the right panel of Figure 2, where , with respect to those observed in the left panel, where . As before, the effect of the difference between design value and prior mean on also reflects on the values of the optimal sample sizes reported in Table 1. For instance, under the most informative prior, if , then ; conversely, when , a huge number of experimental units (e.g., ) is required to have a sufficiently small expected discrepancy.
- Comparison with . As expected, the trend of w.r.t. to and is consistent with that of .
- Comparison with ALC. For each , becomes slightly smaller when the prior sample size gets larger and the corresponding posterior is more concentrated (see Table 1). Conversely, since approximate intervals do not depend on the prior, is not affected by the choice of prior hyperparameters. Furthermore, when the design value is closer to the boundary of the parameter space, the posterior distribution and, consequently, its approximation, become more concentrated, yielding shorter intervals. Hence the values of and of are uniformly smaller for than for .It is interesting to note the opposite impact of the prior sample size on and on the one hand, and on on the other hand. In fact, larger values of determine shorter intervals and smaller values of . On the contrary, when , a more concentrated prior implies a more remarkable discrepancy between the posterior and its likelihood approximation and, consequently, yields greater values of and .
5. Conclusions
- Other models. The methodology proposed in the paper can be easily extended to other models and setups relevant to clinical trials applications. A natural extension is to two-arms designs for the comparison of two proportions (difference or log odds ratio), in which the additional issue of units allocation arises [32]. For a predictive approach to allocation based on the control of posterior variances, see for instance [33]. See also [5] for related ideas in the Poisson model.
- Probability vs. Expectation. In Section 2.2 we propose to summarize the predictive distribution of the discrepancy using the expected value w.r.t. . An alternative is to take into account the whole probability distribution of P and to determine the smallest n such that is sufficiently small.
- Decision-theoretic approach. The approach proposed in the paper is performance-based. Alternatively one could follow some previous works and rephrase the problem in a decision-theoretic framework and define a measure of discrepancy based on the posterior expected loss of C and . We will elaborate on this in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, J.; Chu, C.T. Bayesian clinical trials in action. Stat. Med. 2012, 31, 2955–2972. [Google Scholar] [PubMed]
- Yin, G.; Lam, C.K.; Shi, H. Bayesian randomized clinical trials: From fixed to adaptive design. Contemp. Clin. Trials 2017, 59, 77–86. [Google Scholar] [CrossRef] [PubMed]
- Bittl, J.A.; He, Y. Bayesian analysis. A practical approach to interpret clinical trials and create clinical practice guidelines. Circ. Cardiovasc. Qual. Outcomes 2017, 10, e003563. [Google Scholar] [CrossRef] [PubMed]
- Spiegelhalter, D.J.; Abrams, K.R.; Myles, J.P. Bayesian Approaches to Clinical Trials and Health-Care Evaluation; Statistics in Practice; Wiley: Chichester, UK, 2004. [Google Scholar]
- De Santis, F.; Gubbiotti, S. A note on the progressive overlap of two alternative Bayesian intervals. Commun. Stat. Theory Methods 2019, 1–18. [Google Scholar] [CrossRef]
- Lesaffre, E.; Lawson, A.B. Bayesian Biostatistics; Wiley: Chichester, UK, 2012. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; Chapman & Hall/CRC Texts in Statistical Science; Taylor & Francis: Boca Raton, FL, USA, 2013. [Google Scholar]
- Kalbfleisch, J.G. Probability and Statistical Inference. Volume 2: Statistical Inference, 2nd ed.; Springer: New York, NY, USA, 1985. [Google Scholar]
- Robert, C.P. The Bayesian Choice: From Decision-Theoretic Foundations to Computational Implementation, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Meeker, W.Q.; Hahn, G.J.; Escobar, L.A. Statistical Intervals: A Guide for Practitioners and Researchers; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Brutti, P.; De Santis, F.; Gubbiotti, S. Bayesian—Frequentist sample size determination: A game of two priors. Metron 2014, 72, 133–151. [Google Scholar] [CrossRef]
- Adcock, C.J. Sample size determination: A review. J. R. Stat. Soc. Ser. D Stat. 1997, 46, 261–283. [Google Scholar] [CrossRef]
- Joseph, L.; du Berger, R.; Belisle, P. Bayesian and mixed Bayesian/likelihood criteria for sample size determination. Stat. Med. 1997, 16, 769–781. [Google Scholar] [CrossRef]
- Joseph, L.; Wolfson, D. Interval-based versus decision theoretic criteria for the choice of sample size. J. R. Stat. Soc. Ser. Stat. 1997, 46, 145–149. [Google Scholar] [CrossRef]
- Brutti, P.; De Santis, F. Robust Bayesian sample size determination for avoiding the range of equivalence in clinical trials. J. Stat. Plan. Inference 2008, 138, 1577–1591. [Google Scholar] [CrossRef]
- Cao, J.; Lee, J.J.; Alber, S. Comparison of Bayesian sample size criteria: ACC, ALC, and WOC. J. Stat. Plan. Inference 2009, 139, 4111–4122. [Google Scholar] [CrossRef]
- Gubbiotti, S.; De Santis, F. A Bayesian method for the choice of the sample size in equivalence trials. Aust. New Zealand J. Stat. 2011, 53, 443–460. [Google Scholar] [CrossRef]
- Joseph, L.; Wolfson, D.B.; Berger, R.D. Sample Size Calculations for Binomial Proportions via Highest Posterior Density Intervals. J. R. Stat. Soc. Ser. D Stat. 1995, 44, 143–154. [Google Scholar] [CrossRef]
- M’Lan, C.E.; Joseph, L.; Wolfson, D.B. Bayesian sample size determination for binomial proportions. Bayesian Anal. 2008, 3, 269–296. [Google Scholar] [CrossRef]
- De Santis, F.; Fasciolo, M.C.; Gubbiotti, S. Predictive control of posterior robustness for sample size choice in a Bernoulli model. Stat. Methods Appl. 2013, 22, 319–340. [Google Scholar] [CrossRef]
- De Santis, F. Sample size determination for robust Bayesian analysis. J. Am. Stat. Assoc. 2006, 101, 278–291. [Google Scholar] [CrossRef]
- Brutti, P.; De Santis, F.; Gubbiotti, S. Robust Bayesian sample size determination in clinical trials. Stat. Med. 2008, 27, 2290–2306. [Google Scholar] [CrossRef] [PubMed]
- Joseph, L.; Belisle, P. Bayesian consensus-based sample size criteria for binomial proportions. Stat. Med. 2019, 38, 4566–4573. [Google Scholar] [CrossRef] [PubMed]
- Brutti, P.; De Santis, F.; Gubbiotti, S. Predictive measures of the conflict between frequentist and Bayesian estimators. J. Stat. Plan. Inference 2014, 148, 111–122. [Google Scholar] [CrossRef]
- De Santis, F.; Gubbiotti, S. A decision-theoretic approach to sample size determination under several priors. Appl. Stoch. Model. Bus. Ind. 2017, 33, 282–295. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R. Statistical Inference; Duxbury: Belmont, CA, USA, 2001. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Sacchi, S.; Marcheselli, R.; Bari, A.; Buda, G.; Molinari, A.L.; Baldini, L.; Vallisa, D.; Cesaretti, M.; Musto, P.; Ronconi, S.; et al. Safety and efficacy of lenalidomide in combination with rituximab in recurrent indolent non-follicular lymphoma: Final results of a phase II study conducted by the Fondazione Italiana Linfomi. Haematologica 2016, 101, e196–e199. [Google Scholar] [CrossRef]
- Zhou, H.; Lee, J.J.; Yuan, Y. BOP2: Bayesian optimal design for phase II clinical trials with simple and complex endpoints. Stat. Med. 2017, 36, 3302–3314. [Google Scholar] [CrossRef] [PubMed]
- Sambucini, V. Bayesian predictive monitoring with bivariate binary outcomes in phase II clinical trials. Comput. Stat. Data Anal. 2019, 132, 18–30. [Google Scholar] [CrossRef]
- Morita, S.; Thall, P.F.; Muller, P. Determining the effective sample size of a parametric prior. Biometrics 2008, 64, 595–602. [Google Scholar] [CrossRef] [PubMed]
- M’Lan, C.E.; Joseph, L.; Wolfson, D.B. Bayesian Sample Size Determination for Case-Control Studies. J. Am. Stat. Assoc. 2006, 101, 760–772. [Google Scholar] [CrossRef]
- De Santis, F.; Perone Pacifico, M.; Sambucini, V. Optimal predictive sample size for case-control studies. Appl. Stat. 2004, 53, 427–441. [Google Scholar] [CrossRef]
- Wang, F.; Gelfand, A.E. A simulation-based approach to Bayesian sample size determination for performance under a given model and for separating models. Statist. Sci. 2002, 17, 193–208. [Google Scholar] [CrossRef]
| 49 | 80 | 119 | 182 | ||
| 42 | 96 | 180 | 347 | ||
| 265 | 262 | 257 | 247 | ||
| 267 | 267 | 267 | 267 | ||
| 35 | 118 | 646 | 2911 | ||
| 91 | 228 | 482 | 992 | ||
| 170 | 169 | 169 | 167 | ||
| 172 | 172 | 172 | 172 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Santis, F.; Gubbiotti, S. Sample Size Requirements for Calibrated Approximate Credible Intervals for Proportions in Clinical Trials. Int. J. Environ. Res. Public Health 2021, 18, 595. https://doi.org/10.3390/ijerph18020595
De Santis F, Gubbiotti S. Sample Size Requirements for Calibrated Approximate Credible Intervals for Proportions in Clinical Trials. International Journal of Environmental Research and Public Health. 2021; 18(2):595. https://doi.org/10.3390/ijerph18020595
Chicago/Turabian StyleDe Santis, Fulvio, and Stefania Gubbiotti. 2021. "Sample Size Requirements for Calibrated Approximate Credible Intervals for Proportions in Clinical Trials" International Journal of Environmental Research and Public Health 18, no. 2: 595. https://doi.org/10.3390/ijerph18020595
APA StyleDe Santis, F., & Gubbiotti, S. (2021). Sample Size Requirements for Calibrated Approximate Credible Intervals for Proportions in Clinical Trials. International Journal of Environmental Research and Public Health, 18(2), 595. https://doi.org/10.3390/ijerph18020595




