Modeling Community Health with Areal Data: Bayesian Inference with Survey Standard Errors and Spatial Structure
Abstract
1. Introduction
2. The American Community Survey
2.1. A Systematic Spatial Sampling Design
2.2. ACS Standard Errors
- SEs contain systematic spatial patterns;
- Data reliability is not constant across variables;
- Data describing affluent areas is often of higher reliability than that of impoverished areas; and,
- Data describing areas estimated to be majority Black, Hispanic, or American Indian tends to be lower quality than that of majority White areas.
2.3. Implications
- Additive error tends to increase sample variance, leading to exaggerated confidence in regression estimates;
- the additional variability tends to attenuate bivariate correlations and mask non-linear relations; and,
- in multivariate models, observational error may result in a change of sign, attenuation, or exaggeration of coefficient estimates at any sample size.
- 4.
- Observational error tends to decrease the degree of observed SA; and,
- 5.
- Spatial variation in data quality tends to produce spatial variation in the analytical consequences of observational error.
3. Spatial HBMs for Survey Data
3.1. Prior Information and Model Specification
- Polarization, such that relatively extreme values are not unexpected; and,
- Segregation, such that most social and economic variables display moderate to strong SA.
3.2. Model Evaluation
3.3. Examining Implications
4. Modeling U.S. County Mid-Life Mortality
4.1. Data and Prior Information
4.2. Process and Parameter Models
4.3. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACS | American Community Survey |
| CAR | Conditional autoregressive |
| CI | Credible interval |
| CV | Coefficient of variation |
| ICAR | Intrinsic conditional autoregressive |
| ICE | Index of Concentration at the Extremes |
| HBM | Hierarchical Bayesian model |
| HH | Household |
| MAD | Median absolute deviation |
| Markov chain Monte Carlo | MCMC |
| RII | Relative index of inequality |
| SA | Spatial autocorrelation |
| SE | Standard error |
Appendix A. Inference from Uncertain Observation
Appendix A.1. Plausibility
Appendix A.2. Probability
Appendix A.3. HBMs
Appendix B. Between-County Inequality: Prior Knowledge
| Source | Outcome | Period | Comparison | Findings |
|---|---|---|---|---|
| [47] | Age-adjusted mortality, 0–19 yo. | 1968–1992 | Bottom v. top quintile by deprivation index | y. 1992 RR = 1.52; RR range: 1.45–1.65 |
| [48] | Age-standardized mortality, 0–65 yo. | 1960–2002 | Bottom v. top quintile of median HH income | RR = 1.6 [1.6, 1.7] |
| [45] | Age- and sex-adjusted mortality | 1988–1992 | Lowest inequality, highest income v. highest inequality, lowest income; by quartile of each measure | RR = 1.22 |
| [50] | Mortality, 15–24 yo. | 1999–2007 | Bottom v. top decile by deprivation index | ; Female RR = 1.62 [1.56, 1.67] |
| [51] | Age-adjusted mortality | 1999–2013 | Highest v. lowest of 8 county classes, grouped by mortality | RR increased each year from 2.1 (1999) to 2.7 (2013) |
| [49] | Age-standardized mortality, 25–64 yo. | 2000–2003 | Quintiles of education (% bachelors degree+) and median HH income | Education RR = 1.64; Income RR = 1.78 |
| [46] | Age-adjusted mortality, 0–75 yo. | 2002–2006 | Bottom v. top quartile of median HH income | RR = 1.41 |
| [52] | Mortality, 45–64 yo. | 2005–2009 | Metropolitan areas with <5% poverty vs. non-metro. areas with >20% poverty | RR = 2.22 [2.20, 2.24] |
References
- Du Bois, W.E.B. The Philadelphia Negro: A Social Study; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Battle-Baptiste, W.; Rusert, B. (Eds.) W.E.B. Du Bois’s Data Portraits: Visualizing Black American; Princeton Architectural Press: New York, NY, USA, 2018. [Google Scholar]
- Jones-Eversley, S.D.; Dean, L.T. After 121 years, it’s time to recognize WEB Du Bois as a founding father of social epidemiology. J. Negro Educ. 2018, 87, 230–245. [Google Scholar] [CrossRef]
- Stockwell, E.G. Socioeconomic status and mortality in the United States: Review of the Literature. Public Health Rep. 1961, 76, 1081–1086. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kitagawa, E.M.; Hauser, P.M. Differential Mortality in the United States; Harvard University Press: Cambridge, MA, USA, 1973. [Google Scholar]
- Center for International Earth Science Information Network, Columbia University. Gridded Population of the World, Version 4 (GPWv4): Basic Demographic Characteristics; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2018. [Google Scholar] [CrossRef]
- Griffith, D.A.; Chun, Y.; Lee, M. Deeper spatial statistical insights into small geographic area data uncertainty. Int. J. Environ. Res. Public Health 2021, 18, 231. [Google Scholar] [CrossRef] [PubMed]
- Spielman, S.E.; Folch, D.; Nagle, N. Patterns and causes of uncertainty in the American Community Survey. Appl. Geogr. 2014, 46, 147–157. [Google Scholar] [CrossRef] [PubMed]
- Folch, D.C.; Arribas-Bel, D.; Koschinsky, J.; Spielman, S.E. Spatial Variation in the Quality of American Community Survey Estimates. Demography 2016, 53, 1535–1554. [Google Scholar] [CrossRef]
- Carroll, R.J.; Ruppert, D.; Stefanski, L.A.; Crainiceanu, C.M. Measurement Error in Nonlinear Models: A Modern Perspective; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Cressie, N. Statistics for Spatial Data, revised edition ed.; Wiley Classics: New York, NY, USA, 2015. [Google Scholar]
- Griffith, D.A. Effective geographic sample size in the presence of spatial autocorrelation. Ann. Assoc. Am. Geogr. 2005, 95, 740–760. [Google Scholar] [CrossRef]
- Clayton, D. Models for the longitudinal analysis of cohort and case-control studies with inaccurately measured exposures. In Statistical Models for Longitudinal Studies of Health; Dwyer, J.H., Feinleib, M., Lippert, P., Hoffmeister, H., Eds.; Oxford University Press: Oxford, UK, 1992; pp. 301–331. [Google Scholar]
- Richardson, S.; Gilks, W.R. A Bayesian approach to measurement error problems in epidemiology using conditional independent models. Am. J. Epidemiol. 1993, 138, 430–442. [Google Scholar] [CrossRef]
- Richardson, S.; Gilks, W.R. Conditional independence models for epidemiological studies with covariate measurement error. Stat. Med. 1993, 12, 1703–1722. [Google Scholar] [CrossRef]
- Richardson, S.; Leblond, L. Some comments on misspecification of priors in Bayesian modelling of measurement error problems. Stat. Med. 1997, 16, 203–213. [Google Scholar] [CrossRef]
- Berliner, L.M. Hierarchical Bayesian time-series models. In Maximum Entropy and Bayesian Methods; Hanson, K.M., Silver, R.N., Eds.; Springer: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Wikle, C.K.; Berliner, L.M.; Cressie, N. Hierarchical Bayesian space-time models. Environ. Ecol. Stat. 1998, 5, 117–154. [Google Scholar] [CrossRef]
- Kang, E.L.; Liu, D.; Cressie, N. Statistical analysis of small-area data based on independence, spatial, non-hierarchical, and hierarchical models. Comput. Stat. Data Anal. 2009, 53, 3016–3032. [Google Scholar] [CrossRef]
- Cressie, N.; Wikle, C.K. Statistics for Spatio-Temporal Data; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Weinberg, D.H.; Abowd, J.M.; Belli, R.F.; Cressie, N.; Folch, D.C.; Holan, S.H.; Levenstein, M.C.; Olson, K.M.; Reiter, J.P.; Shapiro, M.D.; et al. Effects of a Government-Academic Partnership: Has the NSF-Census Bureau Research Network Helped Improve the US Statistical System? J. Surv. Stat. Methodol. 2019, 7, 589–619. [Google Scholar] [CrossRef]
- Krieger, N.; Kim, R.; Feldman, J.; Waterman, P.D. Using the Index of Concentration at the Extremes at multiple geographical levels to monitor health inequities in an era of growing spatial social polarization: Massachusetts, USA (2010-2014). Int. J. Epidemiol. 2018, 47, 788–819. [Google Scholar] [CrossRef] [PubMed]
- Massey, D. The prodigal paradigm returns: Ecology comes back to sociology. In Does it Take a Village? Community Effects on Children, Adolescents, and Families; Booth, A., Crouter, A., Eds.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2001; pp. 41–48. [Google Scholar]
- United States Census Bureau. American Community Survey Design and Methodology (January 2014); Technical Report; U.S. Department of Commerce Bureau of the Census: Suitland, MD, USA, 2014.
- Chun, Y.; Griffith, D.A. Spatial Statistics and Geostatistics; Sage: Thousand Oaks, CA, USA, 2013. [Google Scholar]
- Wolter, K.M. An investigation of some estimators of variance for systematic sampling. J. Am. Stat. Assoc. 1984, 79, 781–790. [Google Scholar] [CrossRef]
- Judkins, D.R. Fay’s method for variance estimation. J. Off. Stat. 1990, 6, 223–239. [Google Scholar]
- Fay, R.E.; Train, G.F. Aspects of survey and model-based postcensal estimation of income and poverty characteristics for states and counties. In Proceedings of the Section on Government Statistics; American Statistical Association: Alexandria, VA, USA, 1995; pp. 154–159. [Google Scholar]
- United States Census Bureau. 2015–2019 Variance Replicate Tables Documentation; Technical Report; U.S. Department of Commerce Bureau of the Census: Suitland, MD, USA, 2019.
- Westfall, J.; Yarkoni, T. Statistically controlling for confounding constructs is harder than you think. PLoS ONE 2016, 11, e0152719. [Google Scholar] [CrossRef]
- Loken, E.; Gelman, A. Measurement error and the replication crisis. Science 2017, 355, 584–585. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Sivia, D.S. Data Analysis: A Bayesian Tutorial; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Haining, R.P.; Li, G. Modelling Spatial and Spatio-Temporal Data: A Bayesian Approach; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Bivand, R.S.; Pebesma, E.; Gomez-Rubio, V. Applied Spatial Data Analysis with R, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Griffith, D.; Chun, Y.; Li, B. Spatial Regression Analysis Using Eigenvector Spatial Filtering; Academic Press: London, UK, 2019. [Google Scholar]
- Donegan, C.; Chun, Y.; Hughes, A.E. Bayesian estimation of spatial filters with Moran’s eigenvectors and hierarchical shrinkage priors. Spatial Stat. 2020, 38, 100450. [Google Scholar] [CrossRef]
- Carpenter, B.; Gelman, A.; Hoffman, M.D.; Lee, D.; Goodrich, B.; Betancourt, M.; Brubaker, M.; Guo, J.; Li, P.; Riddell, A. Stan: A probabilistic programming language. J. Stat. Softw. 2017, 76. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Clifford, P.; Richardson, S.; Hémon, D. Assessing the significance of the correlation between two spatial processes. Biometrics 1989, 45, 123–134. [Google Scholar] [CrossRef] [PubMed]
- Haining, R. Bivariate correlation with spatial data. Geogr. Anal. 1991, 23, 210–227. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Wong, D.W.S. The modifiable areal unit problem in multivariate statistical analysis. Environ. Plan. A 1991, 23, 1025–1044. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention, National Center for Health Statistics. Underlying Cause of Death 1999-2018 on CDC Wonder Online Database. 2020. Available online: http://wonder.cdc.gov/ucd-iid10.html (accessed on 19 October 2020).
- McLaughlin, D.K.; Stokes, C.S. Income inequality and mortality in US counties: Does minority racial concentration matter? Am. J. Public Health 2002, 92, 99–104. [Google Scholar] [CrossRef]
- Cheng, E.R.; Kindig, D.A. Disparities in premature mortality between high- and low-income US counties. Prev. Chronic Dis. 2012, 9. [Google Scholar] [CrossRef]
- DiLiberti, J.H. The relationship between social stratification and all-cause mortality among children in the United States: 1968–1992. Pediatrics 2000, 105, e2. [Google Scholar] [CrossRef]
- Krieger, N.; Rehkopf, D.H.; Chen, J.T.; Waterman, P.D.; Marcelli, E.; Kennedy, M. The fall and rise of US inequities in premature mortality: 1960–2002. PLoS Med. 2008, 5, e46. [Google Scholar] [CrossRef]
- Shiels, M.S.; de González, A.B.; Best, A.F.; Chen, Y.; Chernyavskiy, P.; Hartge, P.; Khan, S.Q.; Pérez-Stable, E.; Rodriquez, E.J.; Spillane, S.; et al. Premature mortality from all causes and drug poisonings in the USA according to socioeconomic status and rurality: An analysis of death certificate data by county from 2000-15. Lancet Public Health 2019, 4, e97–e106. [Google Scholar] [CrossRef]
- Singh, G.K.; Azuine, R.E.; Siahpush, M.; Kogan, M.D. All-cause and cause-specific mortality among US youth: Socioeconomic and rural-urban disparities and international patterns. J. Urban Health 2013, 90, 388–405. [Google Scholar] [CrossRef]
- Baltrus, P.; Malhotra, K.; Levine, R.; Li, C.; Gaglioti, A. Identifying county-level all-cause mortality rate trajectories and their spatial distribution across the United States. Prev. Chronic Dis. 2019, 16. [Google Scholar] [CrossRef]
- Singh, G.K.; Siahpush, M. Widening rural-urban disparities in all-cause mortality and mortality from major causes of death in the USA, 1969-2009. J. Urban Health 2009, 91, 272–292. [Google Scholar] [CrossRef]
- Besag, J.; York, J.; Mollié, A. Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Vol. 1991, 43, 1–20. [Google Scholar] [CrossRef]
- Morris, M.; Wheeler-Martin, K.; Simpson, D.; Mooney, S.J.; Gelman, A.; DiMaggio, C. Bayesian hierarchical spatial models: Implementing the Besag York Mollié model in stan. Spat. Spatio-Temporal Epidemiol. 2019, 31, 100301. [Google Scholar] [CrossRef] [PubMed]
- Donegan, C. Flexible Functions for ICAR, BYM, and BYM2 Models in Stan. Code Repository. 2021. Available online: https://github.com/ConnorDonegan/Stan-IAR (accessed on 15 May 2021).
- Freni-Sterrantino, A.; Ventrucci, M.; Rue, H. A note on intrinsic conditional autoregressive models for disconnected graphs. Spat. Spatio-Temporal Epidemiol. 2018, 26, 25–34. [Google Scholar] [CrossRef] [PubMed]
- Riebler, A.; Sørbye, S.H.; Simpson, D.; Rue, H. An intuitive Bayesian spatial model for disease mapping that accounts for scaling. Stat. Methods Med Res. 2016, 25, 1145–1165. [Google Scholar] [CrossRef] [PubMed]
- Gausset, W.S. The elimination of spurious correlation due to position in time and space. Biometrika 1914, 10, 179–180. [Google Scholar]
- Clayton, D.G.; Bernardinelli, L.; Montomoli, C. Spatial correlation in ecological analysis. Int. J. Epidemiol. 1993, 22, 1193–1202. [Google Scholar] [CrossRef] [PubMed]
- Box, G.E.; Tiao, G.C. Bayesian Inference in Statistical Analysis; John Wiley & Sons: New York, NY, USA, 1992. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Gabry, J.; Češnovar, R. cmdstanr: R Interface to ‘CmdStan’. 2020. Available online: https://mc-stan.org/cmdstanr (accessed on 15 June 2021).
- Lynch, S.M.; Wiese, D.; Ortiz, A.; Sorice, K.A.; Nguyen, M.; González, E.T.; Henry, K.A. Towards precision public health: Geospatial analytics and sensitivity/specificity assessments to inform liver cancer prevention. SSM Popul. Health 2020, 12, 100640. [Google Scholar] [CrossRef]
- Cupido, K.; Fotheringham, A.S.; Jevtic, P. Local modelling of US mortality rates: A multiscale geographically weighted regression approach. Popul. Space Place 2021, 27, e2379. [Google Scholar] [CrossRef]
- Hoffman, M.D.; Gelman, A. The no-U-turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Betancourt, M.; Girolami, M. Hamiltonian Monte Carlo for hierarchical models. In Current Trends in Bayesian Methodology with Applications; Upadhyay, S.K., Singh, U., Dey, D.K., Loganathan, A., Eds.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Betancourt, M. A Conceptual Introduction to Hamiltonian Monte Carlo. arXiv 2018, arXiv:stat.ME/1701.02434. [Google Scholar]
- Polya, G. Mathematics and Plausible Reasoning, 2nd ed.; Vol. II: Patterns of Plausible Inference; Princeton University Press: Princeton, NJ, USA, 1990. [Google Scholar]
- Laplace, P.S. A Philosophical Essay on Probabilities; Dover Publications, Inc.: New York, NY, USA, 1952. [Google Scholar]
- Keynes, J.M. A Treatise on Probability; Harper & Row: New York, NY, USA, 1962. [Google Scholar]
- Jeffreys, H. Theory of Probability; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Cox, R.T. The Algebra of Probable Inference; The Johns Hopkins Press: Baltimore, MD, USA, 1961. [Google Scholar]
- Jeffreys, S.H. Scientific Inference, 3rd ed.; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. Lond. Ser. A, Contain. Pap. A Math. Phys. Character 1922, 222, 309–368. [Google Scholar]
- Fisher, R.A. Theory of statistical estimation. Math. Proc. Camb. Philos. Soceity 1925, 22, 700–725. [Google Scholar] [CrossRef]
- Lipton, P. Inference to the Best Explanation; Routledge: Abingdon-on-Thames, UK, 1991. [Google Scholar]
- Bretthorst, G.L. An introduction to parameter estimation using Bayesian probability theory. In Maximum Entropy and Bayesian Methods; Fougère, P.F., Ed.; Springer: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Loredo, T.J. The promise of Bayesian inference for astrophysics. In Statistical Challenges in Modern Astronomy; Springer: Dordrecht, The Netherlands, 1992; pp. 275–297. [Google Scholar]
- MacKay, D. Information Theory, Inference, and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Greenland, S. Probability logic and probabilistic induction. Epidemiology 1998, 9, 322–332. [Google Scholar] [CrossRef]
- Bayes, T. An essay toward solving a problem in the doctrine of chances. Philos. Trans. R. Soc. Lond. 1764, 53, 370–418. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana/Chicago, IL, USA, 1998. [Google Scholar]
- Alexeeff, S.E.; Carroll, R.J.; Coull, B. Spatial measurement error and correction by spatial SIMEX in linear regression models when using predicted air pollution exposures. Biostatistics 2016, 17, 377–389. [Google Scholar] [CrossRef] [PubMed]
- Navarro, V. Race or class versus race and class: Mortality differentials in the United States. Lancet 1990, 336, 1238–1240. [Google Scholar] [CrossRef]
- Meara, E.R.; Richards, S.; Culer, D.M. The gap gets bigger: Changes in mortality and life expectancy, by education, 1981–2000. Health Aff. 2008, 27, 350–360. [Google Scholar] [CrossRef]
- Rehkopf, D.H.; Berkman, L.F.; Coull, B.; Krieger, N. The non-linear risk of mortality by income level in a healthy population: US National Health and Nutrition Examination Survey mortality follow-up cohort, 1988–2001. BMC Public Health 2008, 8, 383. [Google Scholar] [CrossRef]
- Julia, C.; Valleron, A.J. Louis-René Villermé (1782–1863), a pioneer in social epidemiology: Re-analysis of his data on comparative mortality in Paris in the early 19th century. J. Epidemiol. Community Health 2011, 65, 666–670. [Google Scholar] [CrossRef] [PubMed]
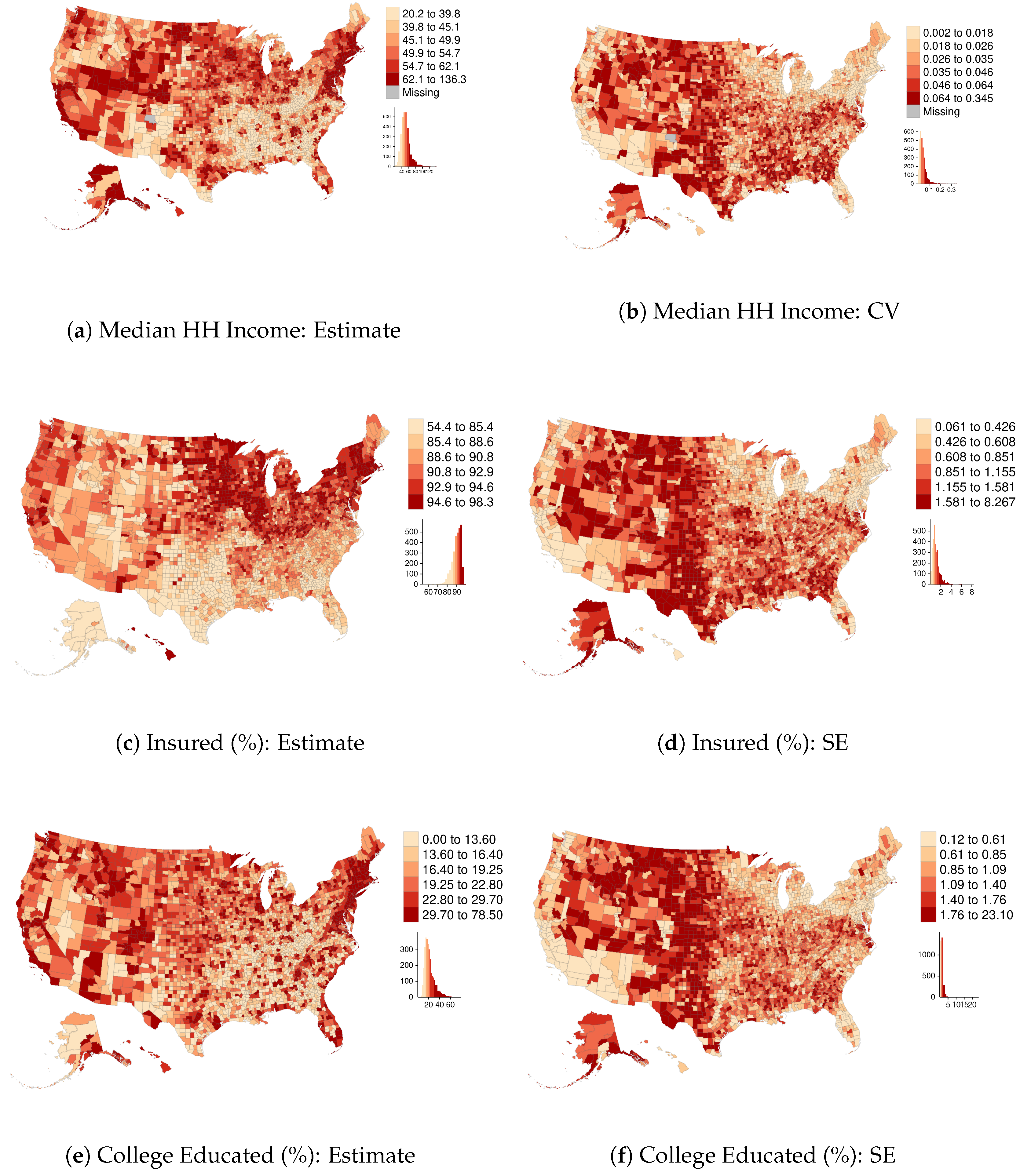
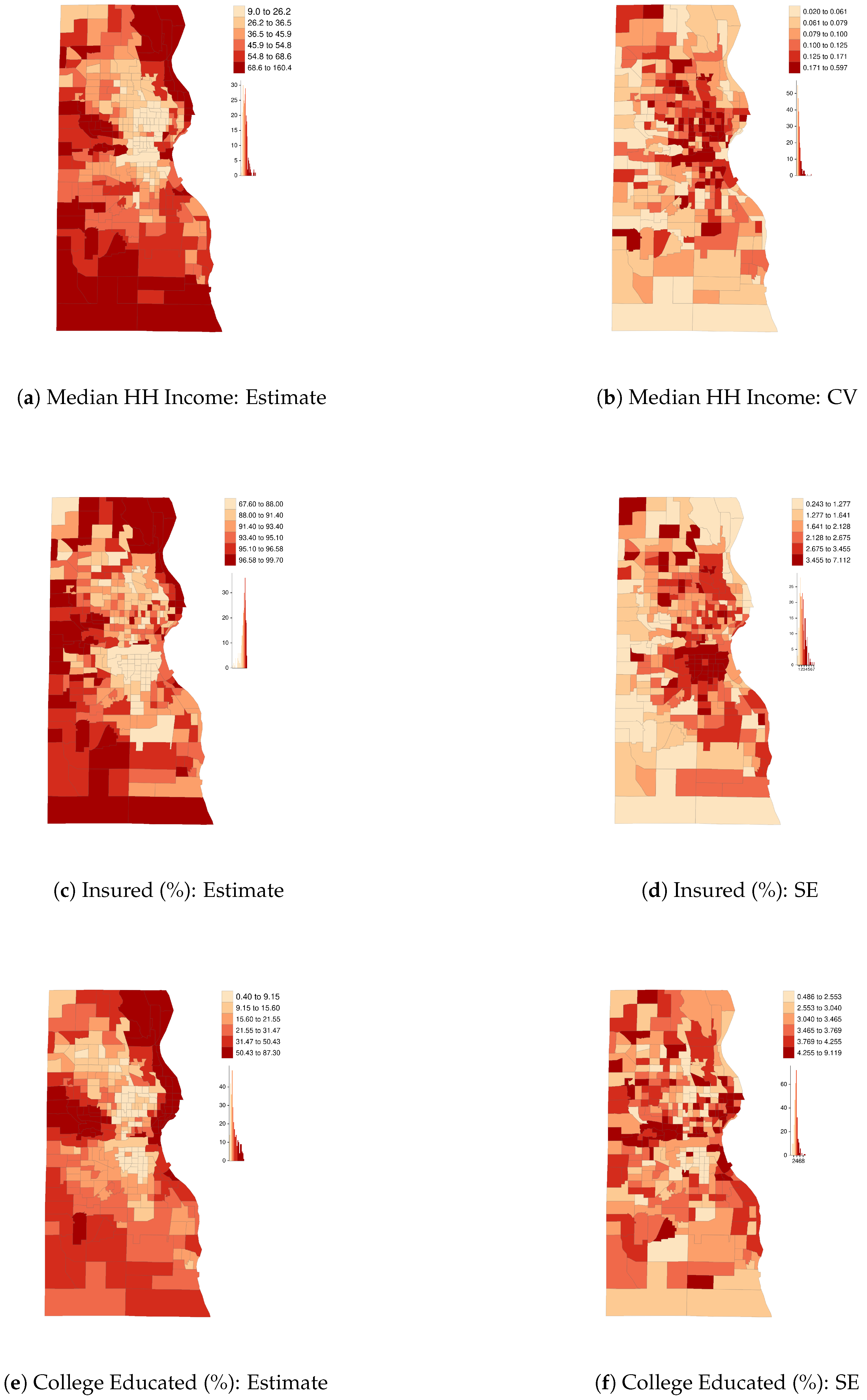

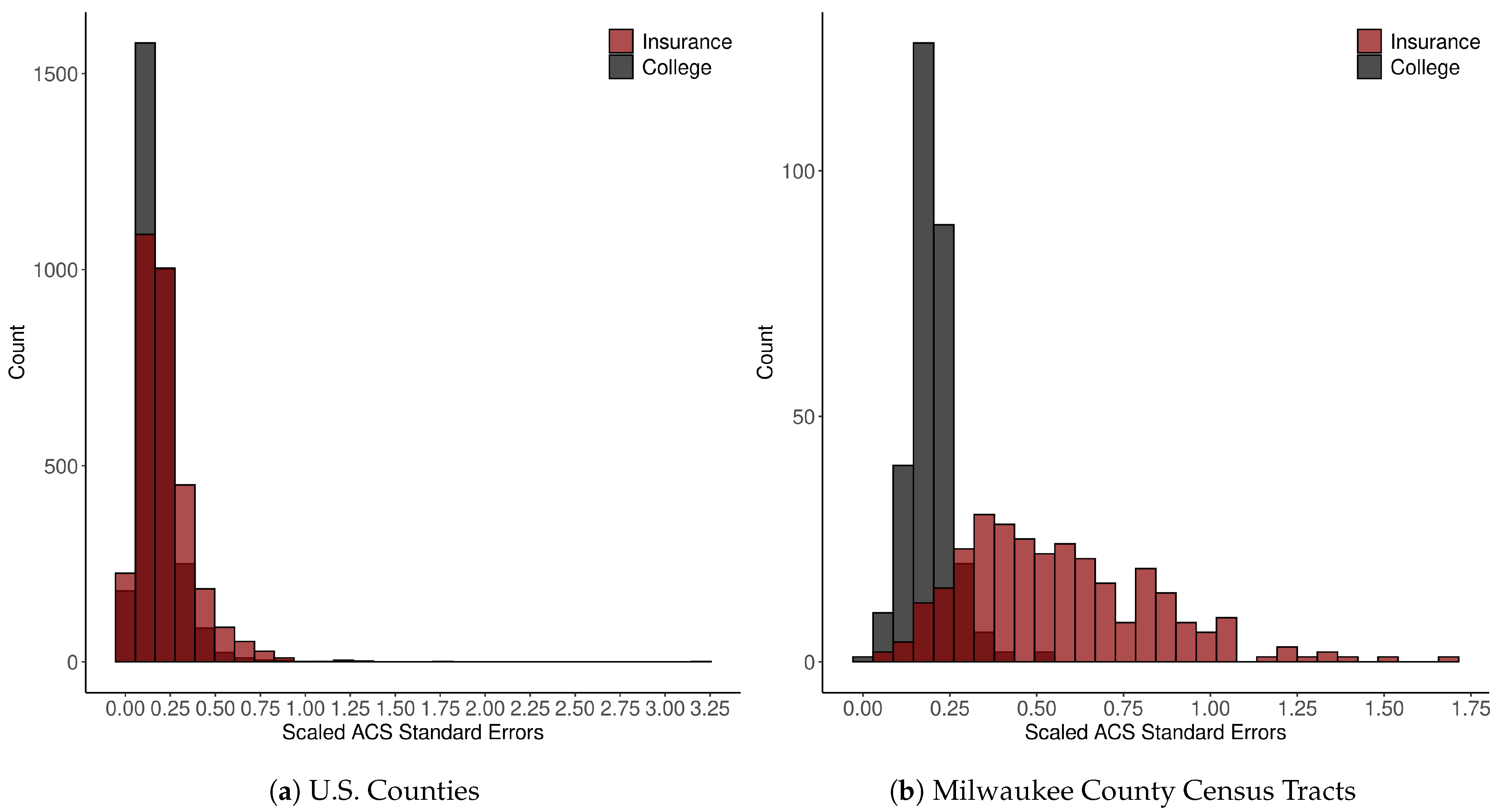
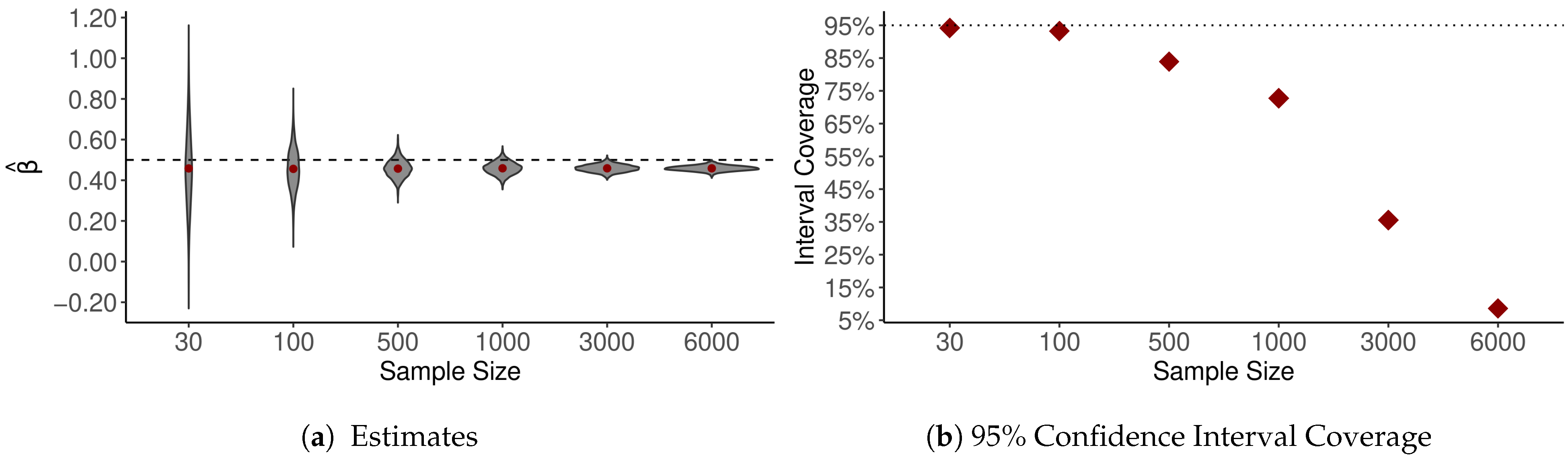
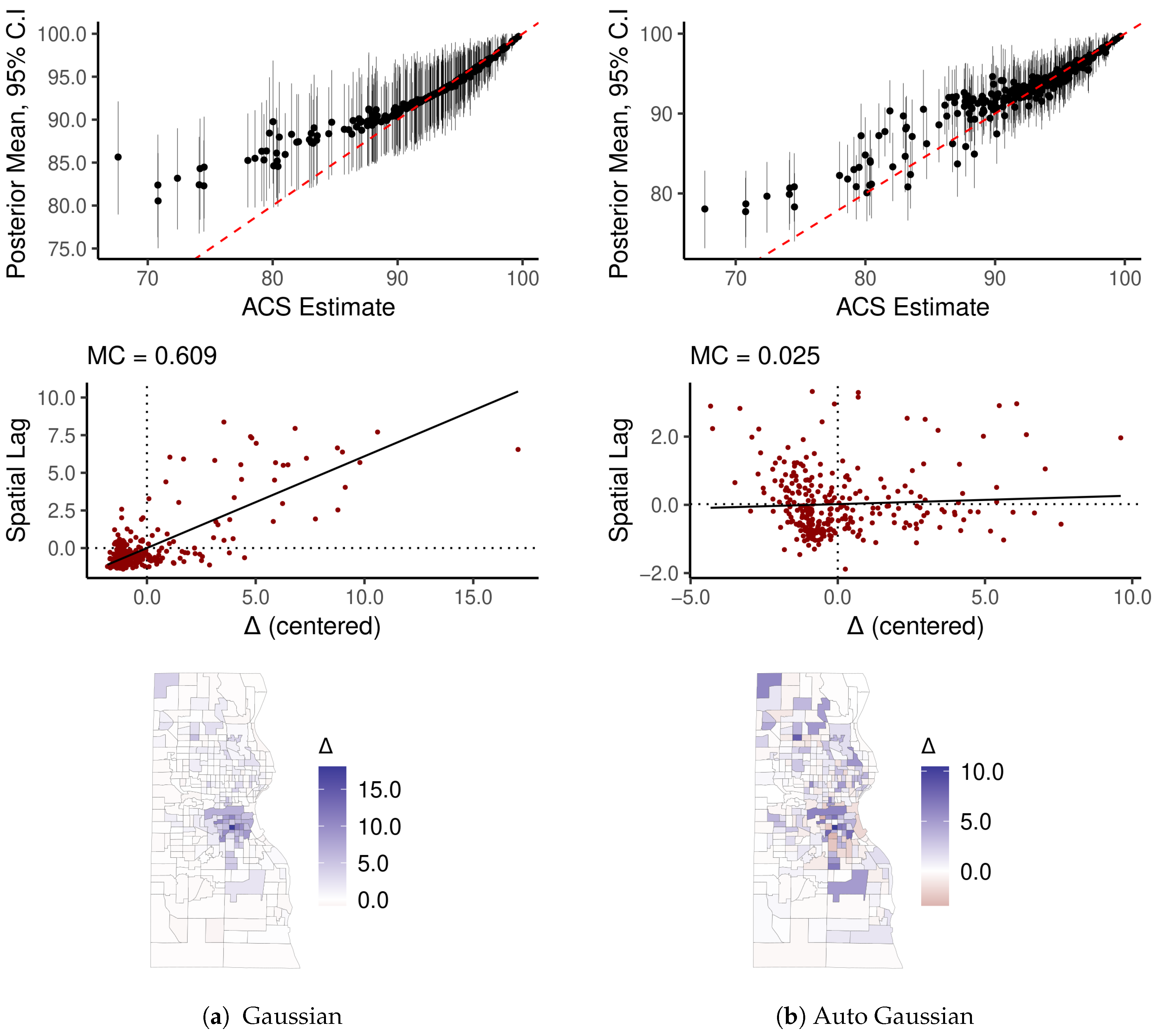
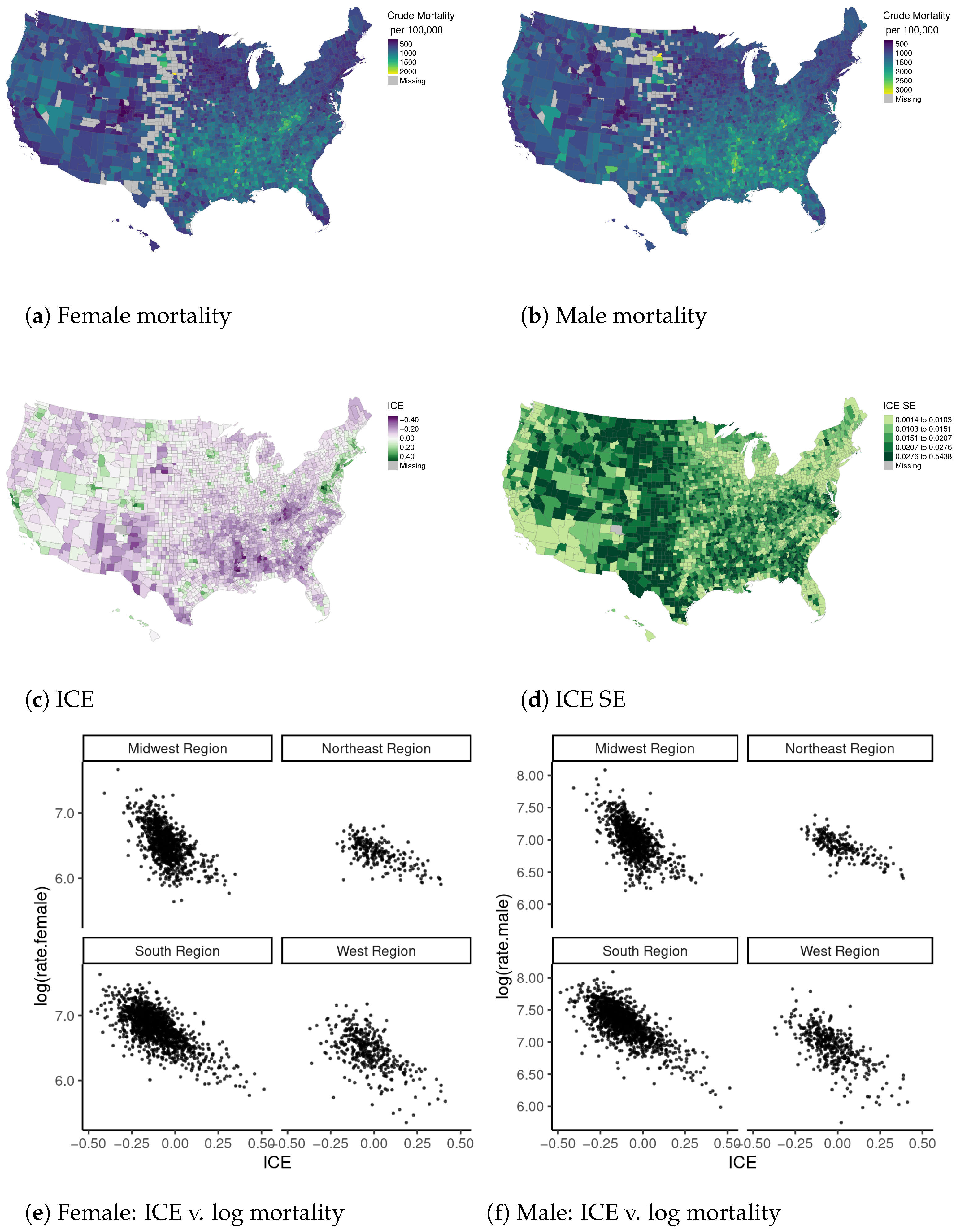
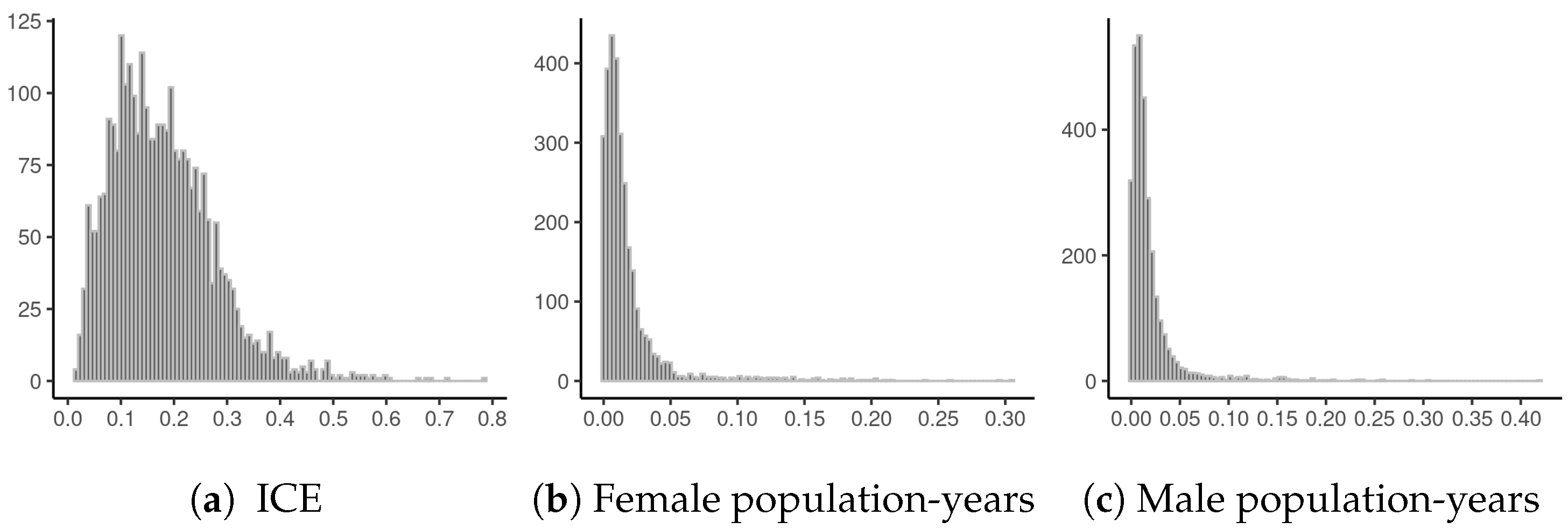
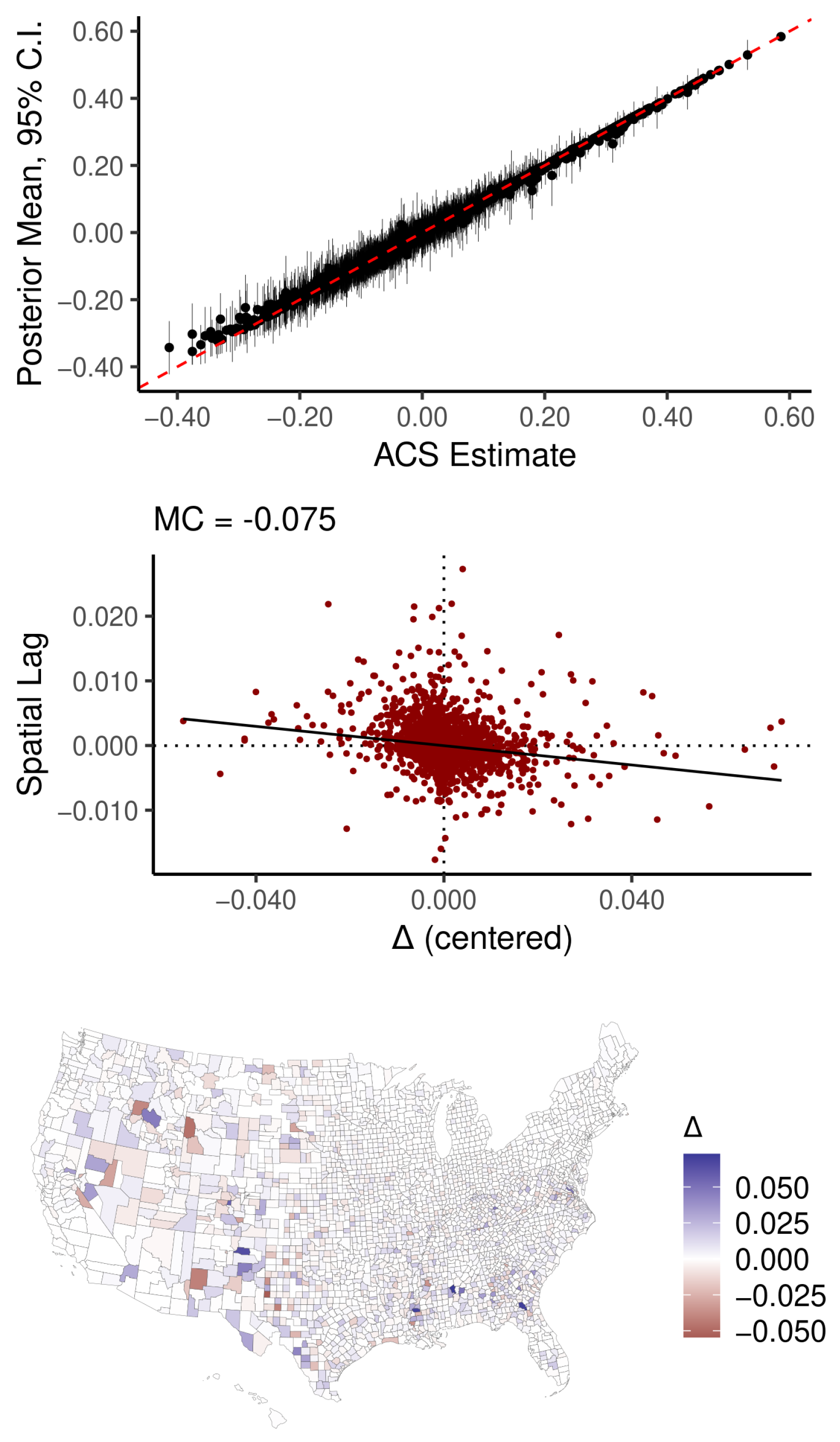
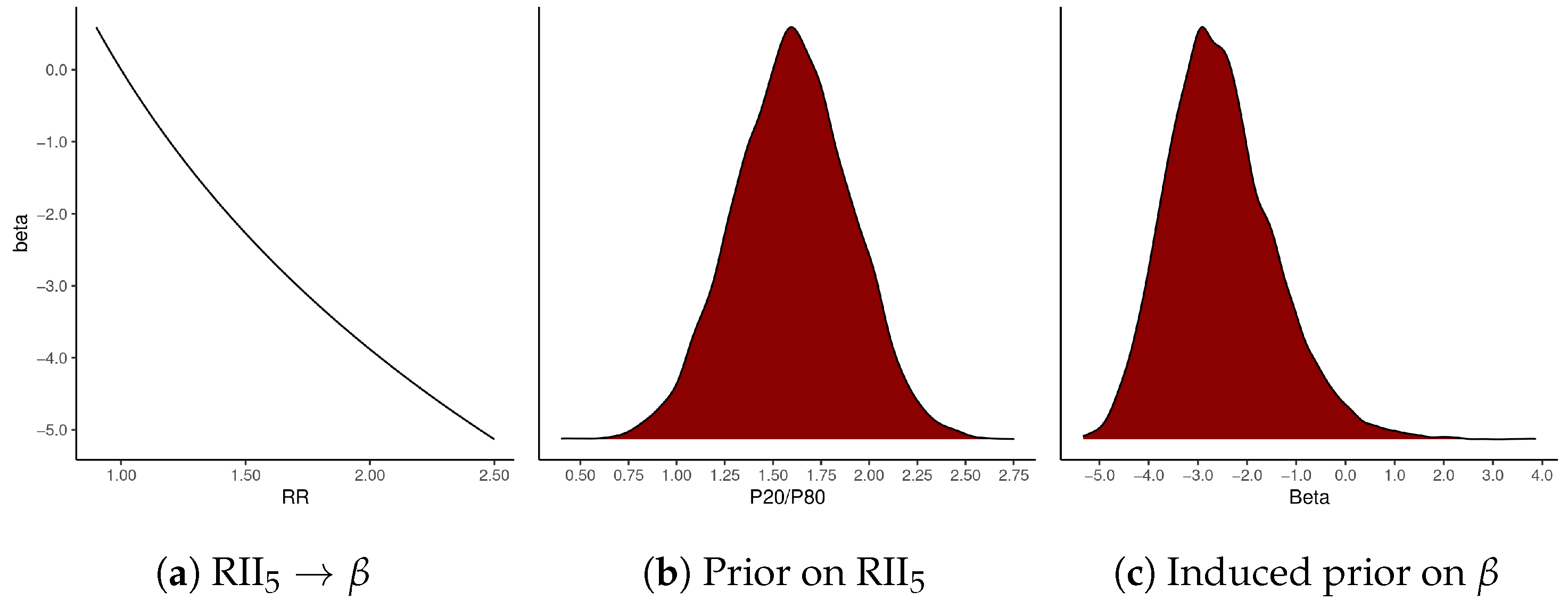
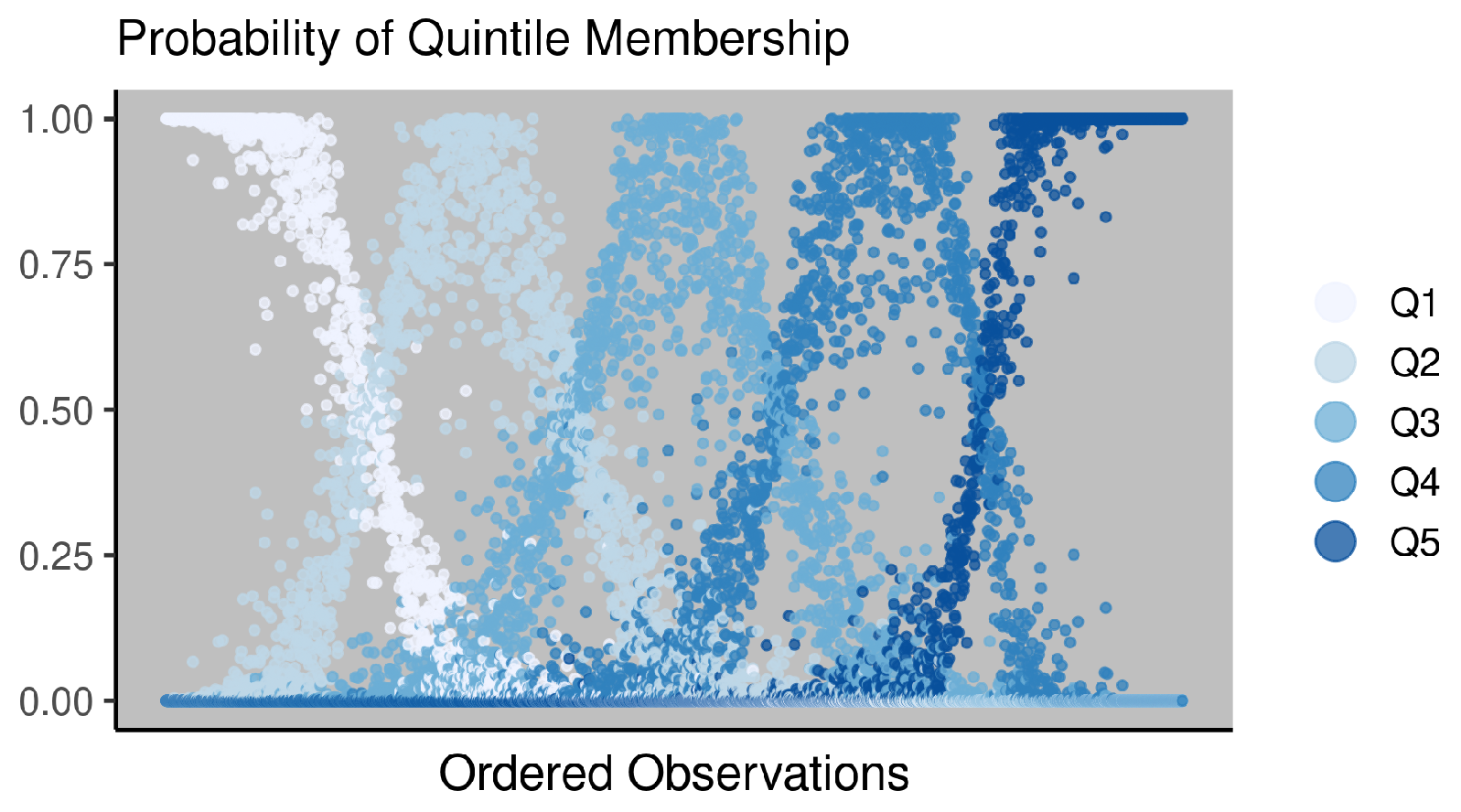
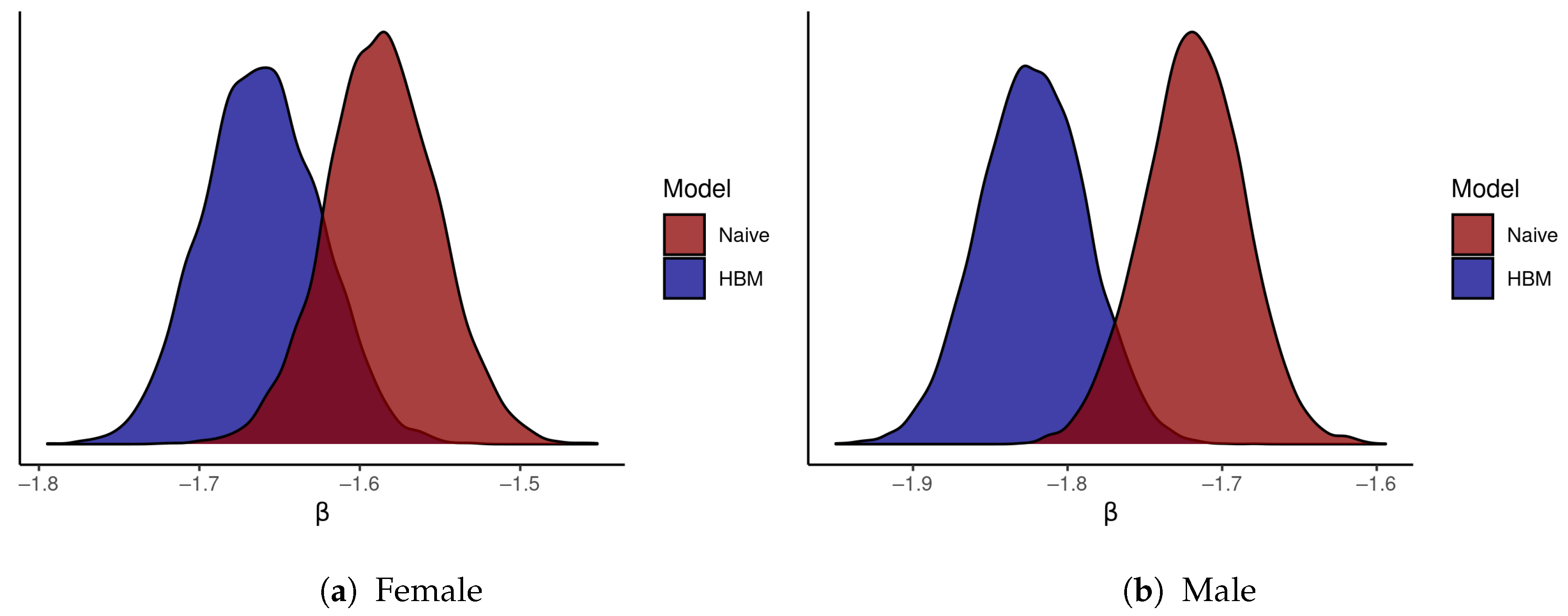
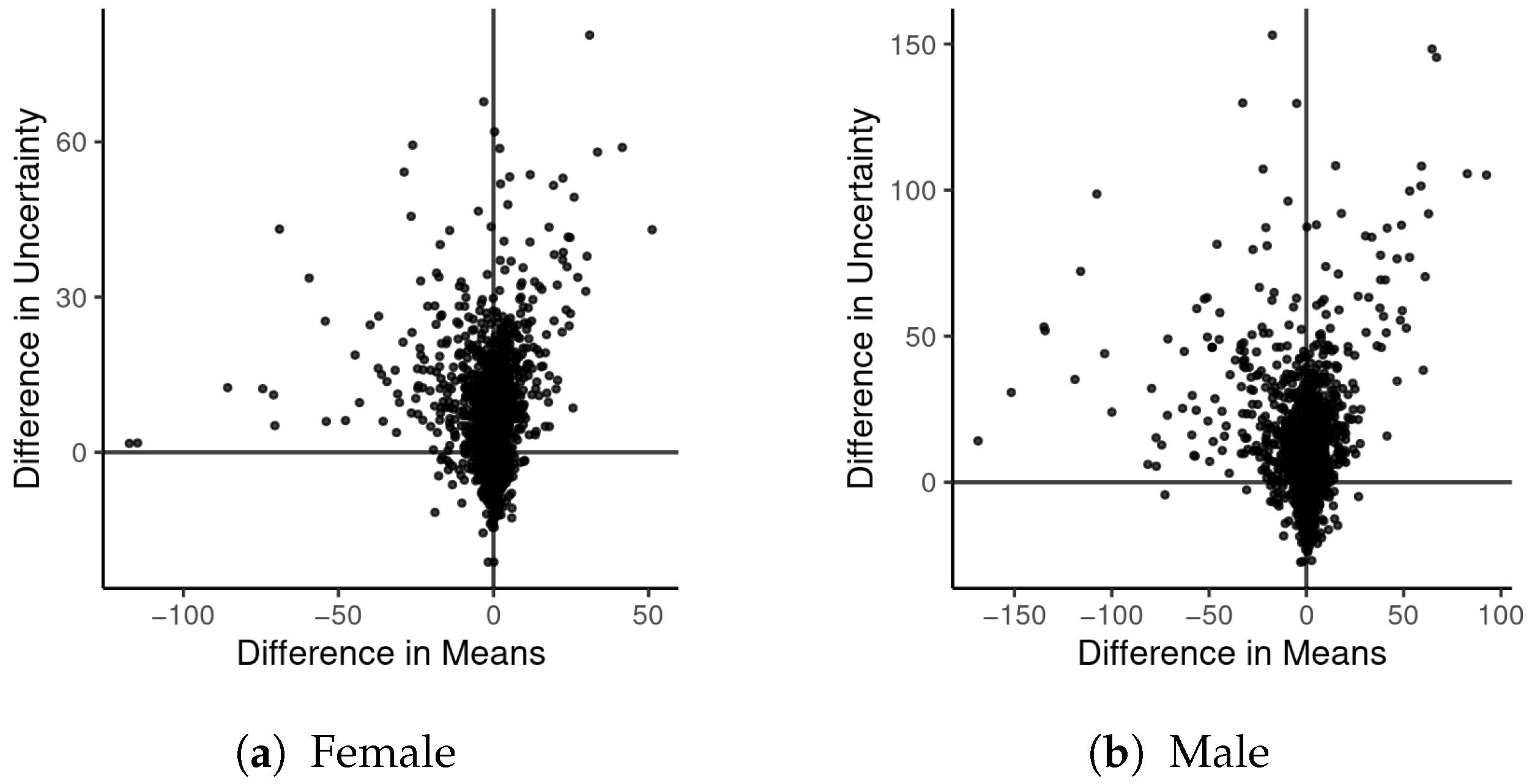
| U.S. Counties | Milwaukee County Census Tracts | |||||
|---|---|---|---|---|---|---|
| Income | Insurance (%) | College Ed. (%) | Income | Insurance (%) | College Ed. (%) | |
| black Estimates | 0.80 | 0.76 | 0.69 | 0.84 | 0.82 | 0.93 |
| Data reliability | 0.56 | 0.69 | 0.57 | 0.46 | 0.59 | 0.52 |
| Income | Insurance (%) | College Ed. (%) | |
|---|---|---|---|
| U.S. Counties | |||
| White | 1 | 1 | 1 |
| Black | 2 | 1.36 | 1.17 |
| Hispanic | 1.67 | 1.72 | 1.11 |
| Native American | 1.67 | 1.85 | 1.22 |
| Milwaukee County Census Tracts | |||
| White | 1 | 1 | 1 |
| Black | 1.625 | 1.5 | 0.85 |
| Hispanic | 1.38 | 2.39 | 0.59 |
| Native American | - | - | - |
| Mean | Standard Deviation | SA () | ||
|---|---|---|---|---|
| Log-income | ACS | 10.69 | 0.49 | 0.88 |
| Model | 10.7 [10.68, 10.71] | 0.46 [0.45, 0.48] | 0.90 [0.88, 0.91] | |
| Insurance (%) | ACS | 91.96 | 5.67 | 0.82 |
| Model | 92.81 [92.52, 93.09] | 4.59 [4.22, 4.96] | 0.89 [0.86, 0.92] | |
| College (%) | ACS | 28.31 | 20.87 | 0.93 |
| Model | 28.1 [27.69, 28.51] | 20.63 [20.23, 21.02] | 0.94 [0.93, 0.95] |
| Female | Male | |||||
|---|---|---|---|---|---|---|
| Mean | 2.5% | 97.5% | Mean | 2.5% | 97.5% | |
| −4.863 | −4.867 | −4.859 | −4.375 | −4.379 | −4.371 | |
| −0.163 | −0.236 | −0.090 | 0.005 | −0.068 | 0.077 | |
| 0.333 | 0.218 | 0.449 | 0.443 | 0.341 | 0.549 | |
| −1.661 | −1.720 | −1.601 | −1.823 | −1.879 | −1.766 | |
| 0.167 | 0.153 | 0.180 | 0.149 | 0.137 | 0.163 | |
| 0.223 | 0.058 | 0.553 | 0.200 | 0.028 | 0.537 | |
| 0.059 | 0.047 | 0.070 | 0.067 | 0.056 | 0.076 | |
| −0.001 | −0.042 | 0.038 | −0.001 | −0.043 | 0.039 | |
| 0.996 | 0.992 | 0.999 | 0.996 | 0.993 | 0.999 | |
| 0.173 | 0.169 | 0.177 | 0.173 | 0.169 | 0.177 | |
| a. Mortality Per 100,000 | ||||||
|---|---|---|---|---|---|---|
| 1% | 10% | 20% | 80% | 90% | 99% | |
| F | 391 [382, 400] | 529 [523, 536] | 602 [596, 607] | 1001 [993, 1010] | 1116 [1105, 1128] | 1408 [1,375, 1,444] |
| M | 627 [612, 641] | 865 [855, 874] | 980 [972, 989] | 1631 [1619, 1644] | 1823 [1807, 1840] | 2,309 [2261, 2361] |
| b. Relative Index of Inequality | ||||||
| F | 1.66 [1.64, 1.68] | 2.11 [2.08, 2.14] | 3.60 [3.48,3.72] | |||
| M | 1.66 [1.64, 1.68] | 2.11 [2.08, 2.14] | 3.68 [3.57, 3.81] | |||
| F | 1.35 [1.33, 1.36] | 1.62 [1.59, 1.65] | 2.84 [2.72, 2.97] |
| M | 1.38 [1.37, 1.40] | 1.70 [1.66, 1.73] | 3.14 [3.01, 3.28] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Donegan, C.; Chun, Y.; Griffith, D.A. Modeling Community Health with Areal Data: Bayesian Inference with Survey Standard Errors and Spatial Structure. Int. J. Environ. Res. Public Health 2021, 18, 6856. https://doi.org/10.3390/ijerph18136856
Donegan C, Chun Y, Griffith DA. Modeling Community Health with Areal Data: Bayesian Inference with Survey Standard Errors and Spatial Structure. International Journal of Environmental Research and Public Health. 2021; 18(13):6856. https://doi.org/10.3390/ijerph18136856
Chicago/Turabian StyleDonegan, Connor, Yongwan Chun, and Daniel A. Griffith. 2021. "Modeling Community Health with Areal Data: Bayesian Inference with Survey Standard Errors and Spatial Structure" International Journal of Environmental Research and Public Health 18, no. 13: 6856. https://doi.org/10.3390/ijerph18136856
APA StyleDonegan, C., Chun, Y., & Griffith, D. A. (2021). Modeling Community Health with Areal Data: Bayesian Inference with Survey Standard Errors and Spatial Structure. International Journal of Environmental Research and Public Health, 18(13), 6856. https://doi.org/10.3390/ijerph18136856







