Nonparametric Limits of Agreement in Method Comparison Studies: A Simulation Study on Extreme Quantile Estimation
Abstract
1. Introduction
2. Materials and Methods
2.1. Nonparametric Quantile Estimators
2.1.1. Sample Quantile Estimator
2.1.2. Harrell–Davis Estimator
2.1.3. Bernstein Polynomial Estimator
2.1.4. HD Estimator Using a Level Crossing Empirical Distribution
2.1.5. Sfakianakis–Verginis Estimator
2.1.6. Navruz–Özdemir Estimator
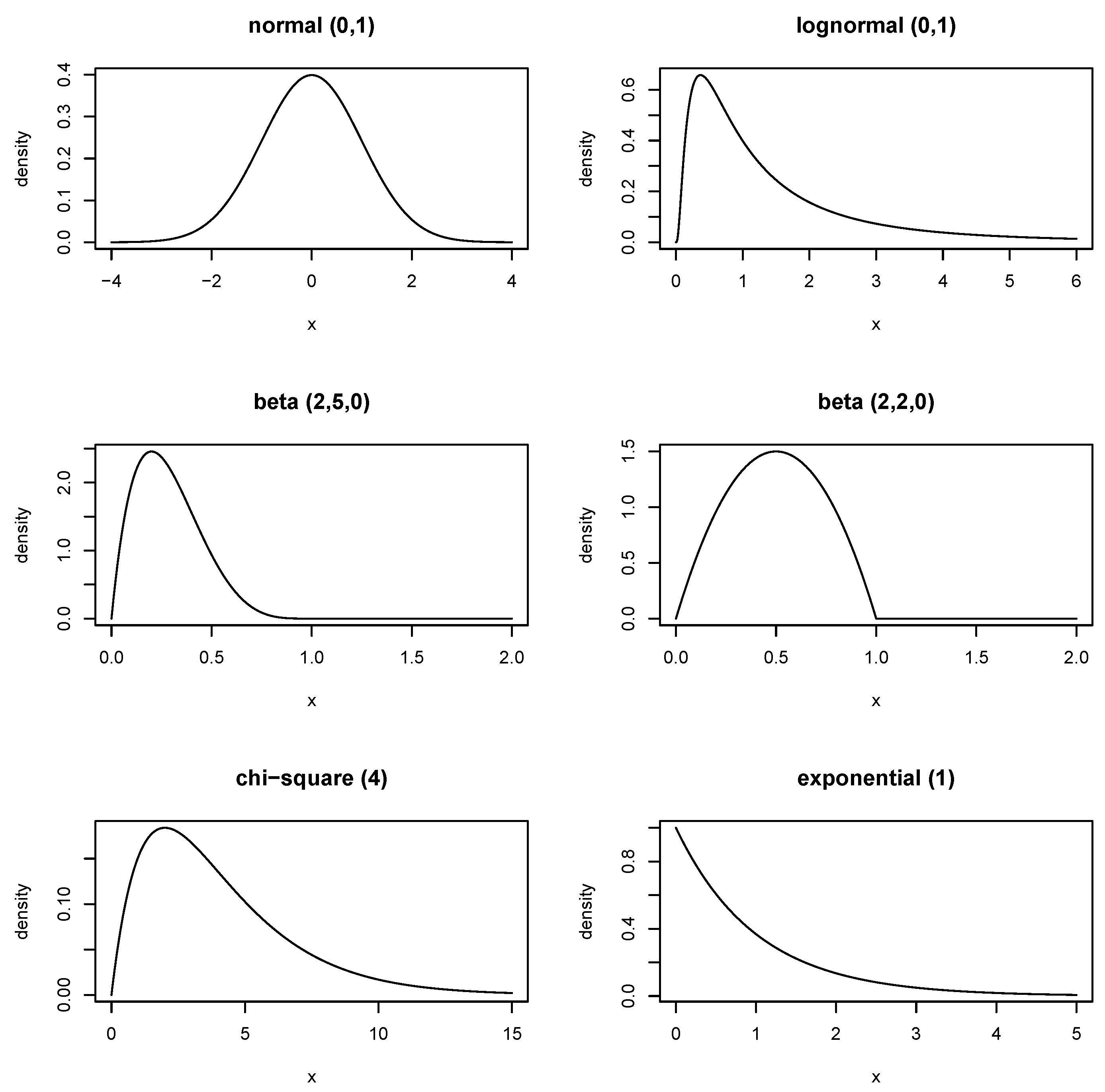
2.2. Simulation Setup
- the standard normal distribution;
- a lognormal distribution with meanlog = 1 and sdlog = 1;
- a beta distribution with shape parameters and (non-centrality parameter );
- a beta distribution with shape parameters and ();
- a chi-squared distribution with 4 degrees of freedom; and
- an exponential distribution with rate parameter 1.
3. Results
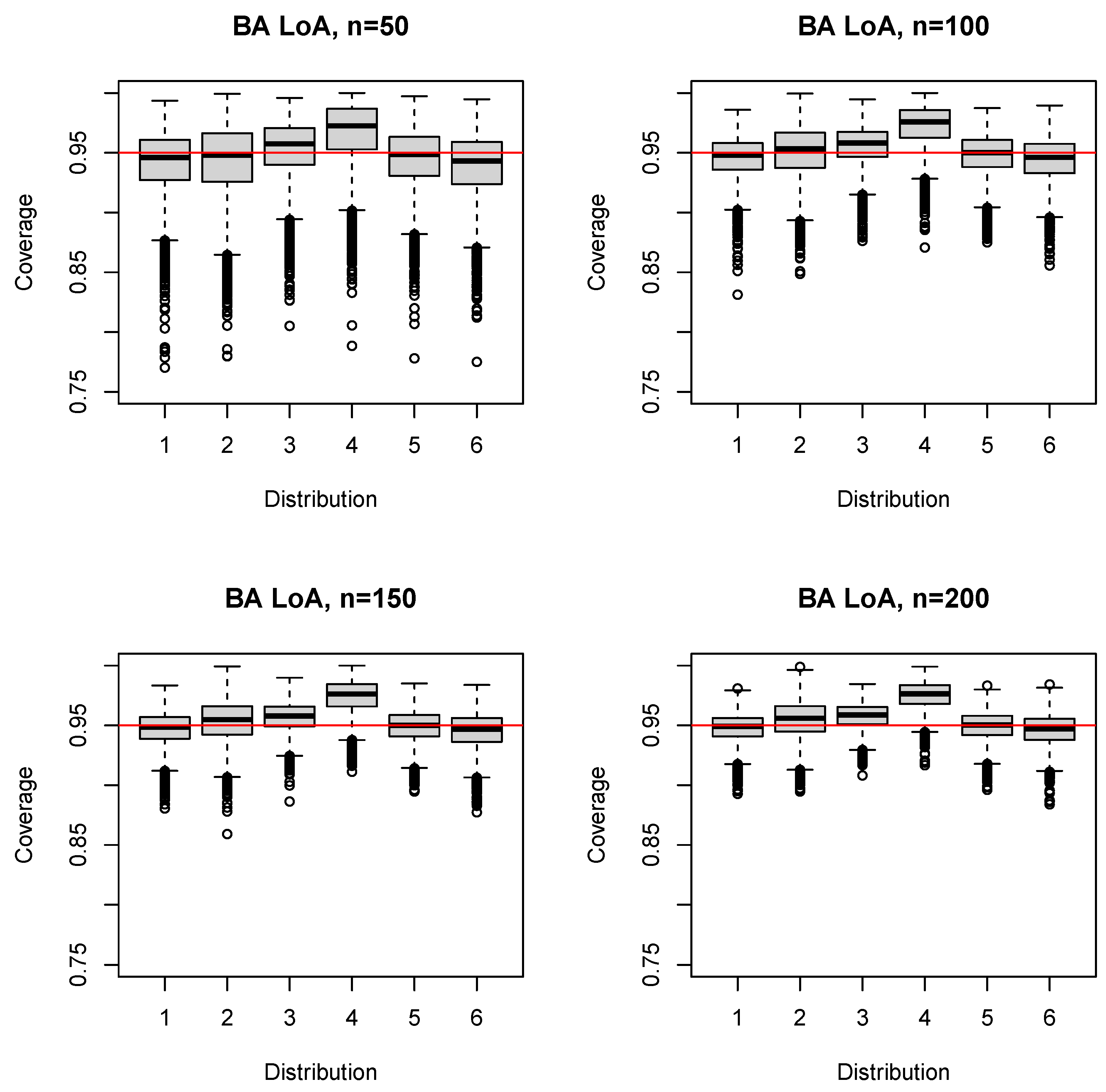
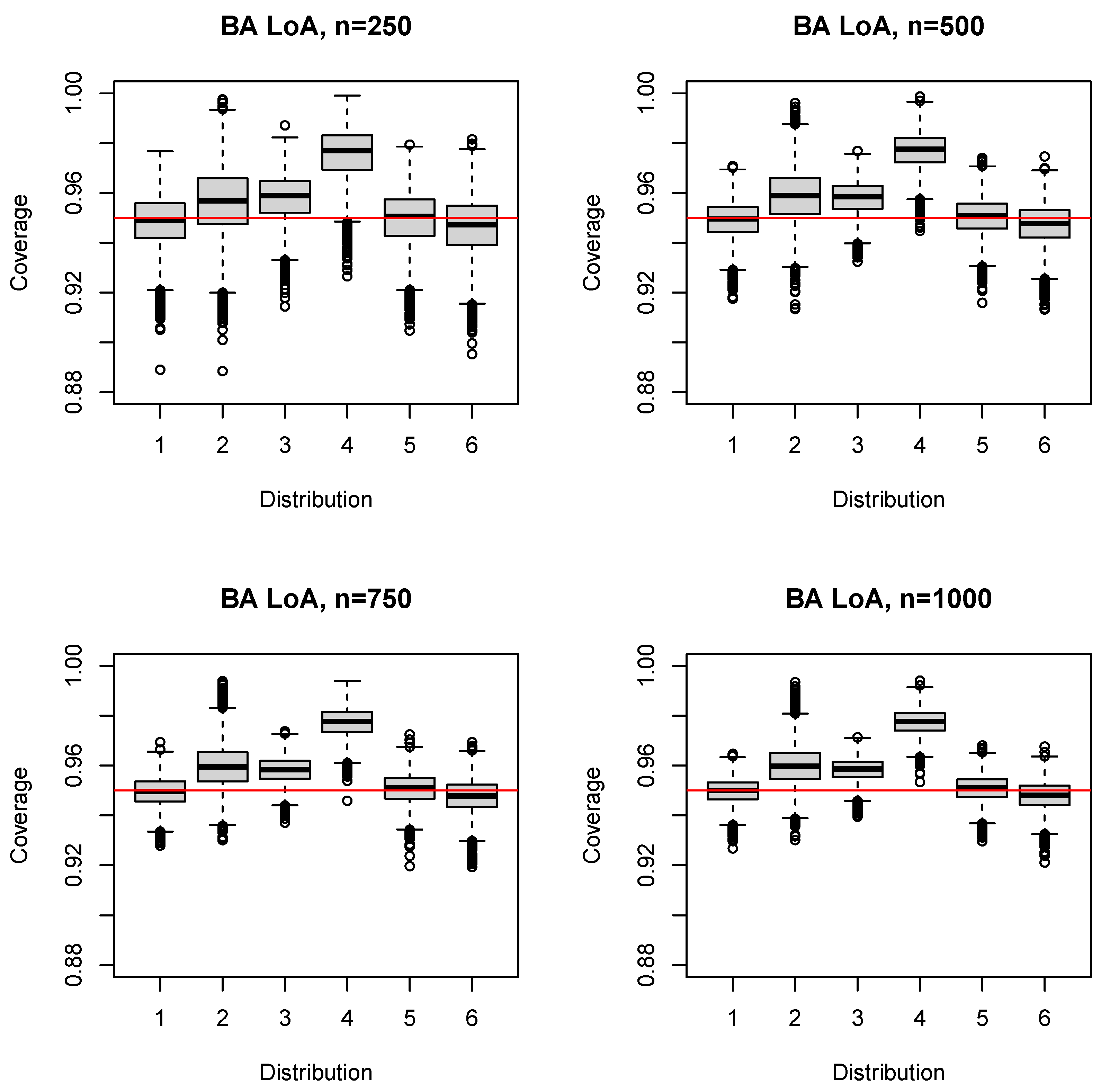
3.1. BA LoA
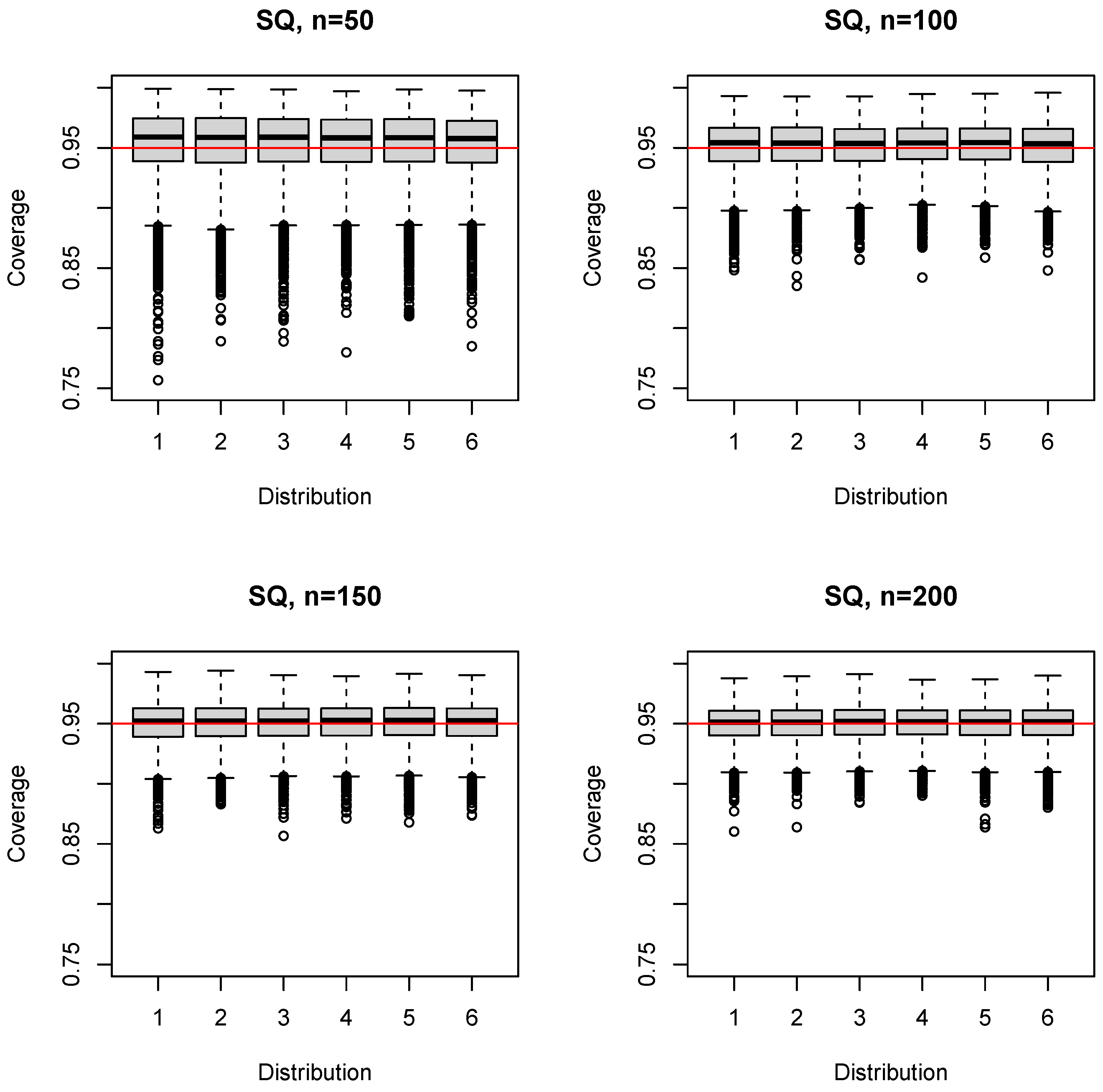
3.2. Nonparametric Quantile Estimators
3.2.1. SQ Estimator
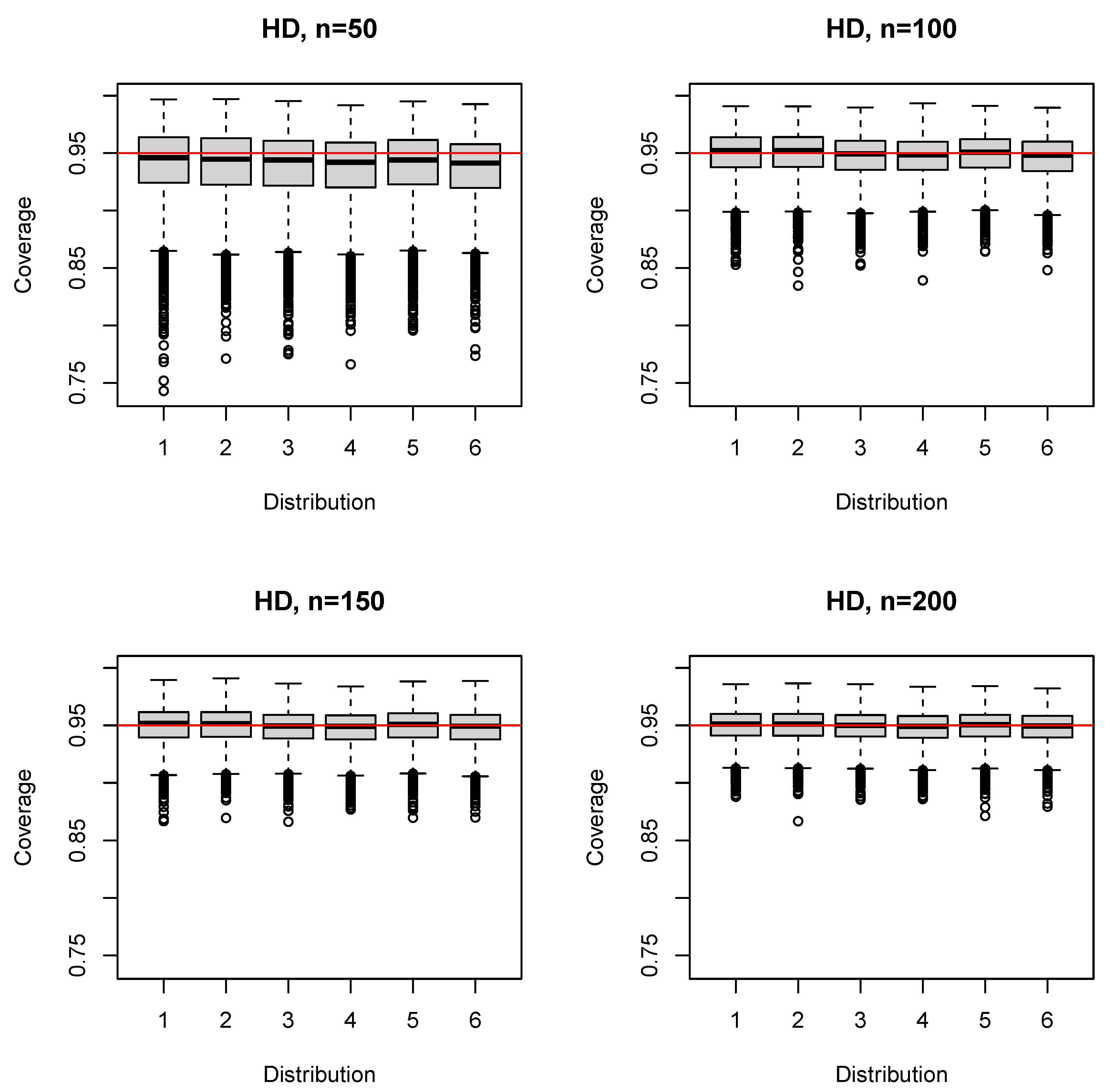
3.2.2. HD Estimator
3.2.3. BP Estimator
3.2.4. HD lc Estimator
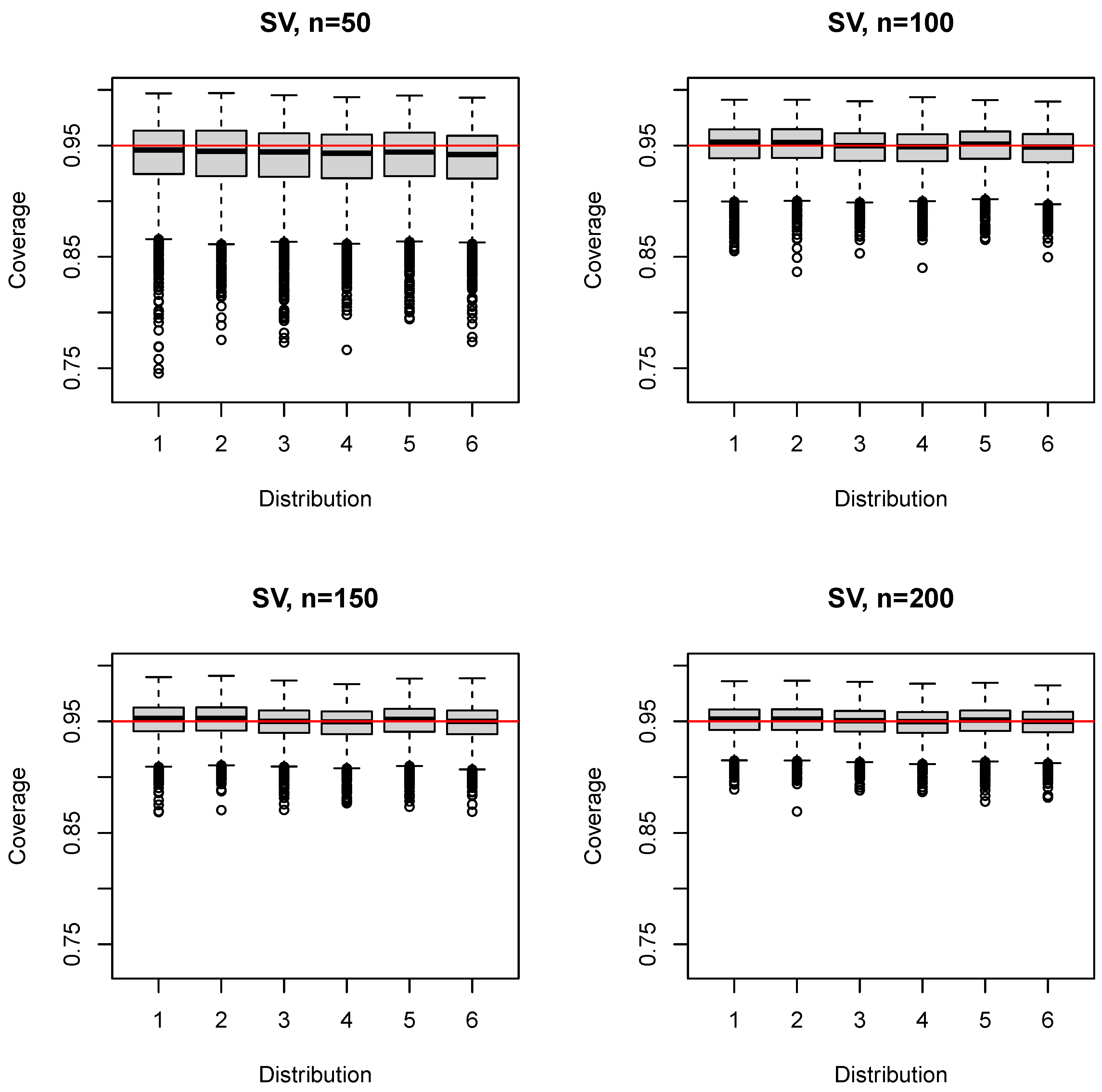
3.2.5. SV Estimator
3.2.6. NO Estimator
4. Discussion
4.1. Key Finding
4.2. What Does This Add to What Is Known
4.3. What Is the Implication, and What Should Change Now?
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BA | Bland–Altman |
| BP | Bernstein Polynomial |
| HD | Harrell–Davis |
| HD lc | Harrell–Davis level crossing |
| LoAs | Limits of Agreement |
| NO | Navruz–Özdemir |
| RMSE | Root Mean Squared Error |
| SQ | Sample Quantile |
| SV | Sfakianakis–Verginis |
References
- Altman, D.G.; Bland, J.M. Measurement in medicine: The analysis of method comparison studies. Statistician 1983, 32, 307–317. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
- Carkeet, A. Exact parametric confidence intervals for Bland–Altman limits of agreement. Optom. Vis. Sci. 2015, 92, e71–e80. [Google Scholar] [CrossRef] [PubMed]
- Carkeet, A.; Goh, Y.T. Confidence and coverage for Bland–Altman limits of agreement and their approximate confidence intervals. Stat. Methods Med. Res. 2018, 27, 1559–1574. [Google Scholar] [CrossRef] [PubMed]
- Abu-Arafeh, A.; Jordan, H.; Drummond, G. Reporting of method comparison studies: A review of advice, an assessment of current practice, and specific suggestions for future reports. Br. J. Anaesth. 2016, 117, 569–575. [Google Scholar] [CrossRef] [PubMed]
- Gerke, O. Reporting standards for a Bland–Altman agreement analysis: A review of methodological reviews. Diagnostics 2020, 10, 334. [Google Scholar] [CrossRef]
- Ludbrook, J. Confidence in Altman-Bland plots: A critical review of the method of differences. Clin. Exp. Pharmacol. Physiol. 2010, 37, 143–149. [Google Scholar] [CrossRef]
- Steinberg, S.M.; Davis, C.E. Comparison of nonparametric point estimators for interquantile differences in moderate sized samples. Commun. Stat. Theory Methods 1987, 16, 1607–1616. [Google Scholar] [CrossRef]
- Parrish, R.S. Comparision of quantile estimators in normal sampling. Biometrics 1990, 46, 247–257. [Google Scholar] [CrossRef]
- Sheather, S.J.; Marron, J.S. Kernel quantile estimators. J. Am. Stat. Assoc. 1990, 85, 410–416. [Google Scholar] [CrossRef]
- Dielman, T.; Lowry, C.; Pfaffenberger, R. A comparision of quantile estimators. Commun. Stat. Simul. Comput. 1994, 23, 355–371. [Google Scholar] [CrossRef]
- Frey, M.E.; Petersen, H.C.; Gerke, O. Nonparametric limits of agreement for small to moderate sample sizes: A simulation study. Stats 2020, 3, 343–355. [Google Scholar] [CrossRef]
- Harrell, F.E.; Davis, C.E. A new distribution-free quantile estimator. Biometrika 1982, 69, 635–640. [Google Scholar] [CrossRef]
- Sfakianakis, M.E.; Verginis, D.G. A new family of nonparametric quantile estimators. Commun. Stat. Simul. Comput. 2008, 37, 337–345. [Google Scholar] [CrossRef]
- Serfling, R.J. Approximation Theorems of Mathematical Statistics; John Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Cheng, C. The Bernstein polynomial estimator of a smooth quantile function. Stat. Probab. Lett. 1995, 24, 321–330. [Google Scholar] [CrossRef]
- Huang, M.L. On a distribution-free quantile estimator. Comput. Stat. Data Anal. 2001, 37, 477–486. [Google Scholar] [CrossRef]
- Navruz, G.; Özdemir, A.F. A new quantile estimator with weights based on a subsampling approach. Br. J. Math. Stat. Psychol. 2020, 73. [Google Scholar] [CrossRef]
- Dekkers, I.A.; de Heer, P.; Bizino, M.B.; de Vries, A.P.J.; Lamb, H.J. 1 H-MRS for the assessment of renal triglyceride content in humans at 3T: A primer and reproducibility study. J. Magn. Reson. Imaging 2018, 48, 507–513. [Google Scholar] [CrossRef]
- Sadler, W.A. Using the variance function to generalize Bland–Altman analysis. Ann. Clin. Biochem. 2019, 56, 198–203. [Google Scholar] [CrossRef]
- Simonsen, J.A.; Thilsing-Hansen, K.; Høilund-Carlsen, P.F.; Gerke, O.; Andersen, T.L. Glomerular filtration rate: Comparison of simultaneous plasma clearance of 99mTc-DTPA and 51Cr-EDTA revisited. Scand. J. Clin. Lab. Investig. 2020, 80, 408–411. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.J.; Zhong, W.H.; Liu, Y.X.; Miao, H.Z.; Li, Y.C.; Ji, M.H. Sample size for assessing agreement between two methods of measurement by Bland–Altman method. Int. J. Biostat. 2016, 12, 20150039. [Google Scholar] [CrossRef] [PubMed]
- Jan, S.L.; Shieh, G. The Bland–Altman range of agreement: Exact interval procedure and sample size determination. Comput. Biol. Med. 2018, 100, 247–252. [Google Scholar] [CrossRef] [PubMed]
- Shieh, G. The appropriateness of Bland–Altman’s approximate confidence intervals for limits of agreement. BMC Med. Res. Methodol. 2018, 18, 45. [Google Scholar] [CrossRef] [PubMed]
- Shieh, G. Assessing agreement between two methods of quantitative measurements: Exact test procedure and sample size calculation. Stat. Biopharm. Res. 2020, 12, 352–359. [Google Scholar] [CrossRef]
- Drummond, G.B. Limits of Agreement with confidence intervals are necessary to assess comparability of measurement devices. Anesth. Analg. 2017, 125, 1075. [Google Scholar] [CrossRef]
- Drummond, G.B. Limits of agreement may have large confidence intervals. Br. J. Anaesth. 2016, 116, 430–431. [Google Scholar] [CrossRef][Green Version]
| Estimator | 50 | 100 | 150 | 200 | 250 | 500 | 750 | 1000 |
|---|---|---|---|---|---|---|---|---|
| BA LoA | 0.893 | 0.914 | 0.922 | 0.927 | 0.929 | 0.936 | 0.939 | 0.941 |
| SQ | 0.896 | 0.913 | 0.919 | 0.922 | 0.925 | 0.933 | 0.936 | 0.938 |
| HD | 0.880 | 0.910 | 0.919 | 0.922 | 0.926 | 0.933 | 0.936 | 0.938 |
| BP | 0.859 | 0.897 | 0.911 | 0.917 | 0.921 | 0.931 | 0.935 | 0.937 |
| HDlc | 0.871 | 0.903 | 0.914 | 0.920 | 0.923 | 0.932 | 0.936 | 0.938 |
| SV | 0.880 | 0.911 | 0.920 | 0.923 | 0.926 | 0.933 | 0.936 | 0.939 |
| NO | 0.491 | 0.728 | 0.858 | 0.903 | 0.920 | 0.934 | 0.936 | 0.938 |
| n | Estimator | Normal (0,1) | Lognormal (0,1) | Beta (2,5,0) | Beta (2,2,0) | Chi-Squared (4) | Exponential (1) |
|---|---|---|---|---|---|---|---|
| 50 | BA LoA | 0.20 | 2.34 | 0.070 | 0.045 | 1.97 | 0.94 |
| SQ | 0.34 | 0.040 | 0.015 | 0.031 | 0.17 | 0.015 | |
| HD | 0.28 | 0.037 | 0.014 | 0.028 | 0.16 | 0.017 | |
| BP | 0.26 | 0.043 | 0.016 | 0.032 | 0.18 | 0.023 | |
| HD lc | 0.26 | 0.039 | 0.014 | 0.029 | 0.17 | 0.019 | |
| SV | 0.27 | 0.038 | 0.014 | 0.029 | 0.16 | 0.017 | |
| NO | 0.28 | 0.049 | 0.018 | 0.037 | 0.21 | 0.024 | |
| 100 | BA LoA | 0.14 | 2.48 | 0.070 | 0.038 | 2.00 | 0.96 |
| SQ | 0.22 | 0.029 | 0.011 | 0.023 | 0.124 | 0.012 | |
| HD | 0.20 | 0.026 | 0.010 | 0.021 | 0.11 | 0.012 | |
| BP | 0.18 | 0.028 | 0.010 | 0.022 | 0.12 | 0.014 | |
| HD lc | 0.19 | 0.027 | 0.010 | 0.021 | 0.12 | 0.013 | |
| SV | 0.20 | 0.026 | 0.009 | 0.020 | 0.11 | 0.012 | |
| NO | 0.19 | 0.029 | 0.011 | 0.022 | 0.13 | 0.014 | |
| 150 | BA LoA | 0.11 | 2.52 | 0.070 | 0.035 | 2.01 | 0.97 |
| SQ | 0.18 | 0.024 | 0.009 | 0.019 | 0.104 | 0.010 | |
| HD | 0.16 | 0.022 | 0.008 | 0.017 | 0.093 | 0.009 | |
| BP | 0.15 | 0.023 | 0.009 | 0.018 | 0.098 | 0.011 | |
| HD lc | 0.16 | 0.022 | 0.008 | 0.017 | 0.095 | 0.010 | |
| SV | 0.16 | 0.022 | 0.008 | 0.017 | 0.092 | 0.009 | |
| NO | 0.15 | 0.023 | 0.009 | 0.018 | 0.099 | 0.011 | |
| 200 | BA LoA | 0.095 | 2.55 | 0.070 | 0.034 | 2.01 | 0.98 |
| SQ | 0.16 | 0.021 | 0.008 | 0.017 | 0.092 | 0.009 | |
| HD | 0.14 | 0.019 | 0.007 | 0.015 | 0.082 | 0.008 | |
| BP | 0.14 | 0.020 | 0.007 | 0.016 | 0.085 | 0.009 | |
| HD lc | 0.14 | 0.019 | 0.007 | 0.015 | 0.083 | 0.008 | |
| SV | 0.14 | 0.019 | 0.007 | 0.015 | 0.081 | 0.008 | |
| NO | 0.14 | 0.020 | 0.008 | 0.016 | 0.085 | 0.009 | |
| 250 | BA LoA | 0.086 | 2.59 | 0.071 | 0.034 | 2.02 | 0.98 |
| SQ | 0.14 | 0.019 | 0.007 | 0.015 | 0.080 | 0.008 | |
| HD | 0.13 | 0.017 | 0.006 | 0.014 | 0.073 | 0.007 | |
| BP | 0.12 | 0.018 | 0.007 | 0.014 | 0.074 | 0.008 | |
| HD lc | 0.12 | 0.017 | 0.007 | 0.014 | 0.073 | 0.008 | |
| SV | 0.13 | 0.017 | 0.006 | 0.014 | 0.072 | 0.007 | |
| NO | 0.12 | 0.018 | 0.007 | 0.014 | 0.075 | 0.008 | |
| 500 | BA LoA | 0.062 | 2.65 | 0.070 | 0.033 | 2.03 | 0.98 |
| SQ | 0.096 | 0.013 | 0.005 | 0.011 | 0.059 | 0.006 | |
| HD | 0.091 | 0.012 | 0.005 | 0.010 | 0.055 | 0.005 | |
| BP | 0.090 | 0.012 | 0.005 | 0.010 | 0.056 | 0.006 | |
| HD lc | 0.090 | 0.012 | 0.005 | 0.010 | 0.056 | 0.006 | |
| SV | 0.091 | 0.012 | 0.005 | 0.010 | 0.055 | 0.005 | |
| NO | 0.090 | 0.012 | 0.005 | 0.010 | 0.056 | 0.006 | |
| 750 | BA LoA | 0.050 | 2.68 | 0.071 | 0.033 | 2.02 | 0.98 |
| SQ | 0.077 | 0.011 | 0.004 | 0.009 | 0.048 | 0.005 | |
| HD | 0.073 | 0.010 | 0.004 | 0.009 | 0.045 | 0.004 | |
| BP | 0.073 | 0.010 | 0.004 | 0.009 | 0.046 | 0.005 | |
| HD lc | 0.073 | 0.010 | 0.004 | 0.009 | 0.046 | 0.004 | |
| SV | 0.073 | 0.010 | 0.004 | 0.009 | 0.045 | 0.004 | |
| NO | 0.073 | 0.010 | 0.004 | 0.009 | 0.046 | 0.005 | |
| 1000 | BA LoA | 0.043 | 2.68 | 0.071 | 0.033 | 2.02 | 0.99 |
| SQ | 0.068 | 0.010 | 0.004 | 0.008 | 0.042 | 0.004 | |
| HD | 0.065 | 0.009 | 0.003 | 0.007 | 0.040 | 0.004 | |
| BP | 0.064 | 0.009 | 0.004 | 0.007 | 0.040 | 0.004 | |
| HD lc | 0.064 | 0.009 | 0.003 | 0.007 | 0.040 | 0.004 | |
| SV | 0.065 | 0.009 | 0.003 | 0.007 | 0.040 | 0.004 | |
| NO | 0.064 | 0.009 | 0.003 | 0.007 | 0.040 | 0.004 |
| n | Estimator | Normal (0,1) | Lognormal (0,1) | Beta (2,5,0) | Beta (2,2,0) | Chi-Squared (4) | Exponential (1) |
|---|---|---|---|---|---|---|---|
| 50 | BA LoA | 0.20 | 2.16 | 0.052 | 0.046 | 1.75 | 0.81 |
| SQ | 0.34 | 3.40 | 0.059 | 0.032 | 2.06 | 0.87 | |
| HD | 0.28 | 2.60 | 0.049 | 0.029 | 1.62 | 0.68 | |
| BP | 0.26 | 2.01 | 0.048 | 0.033 | 1.40 | 0.59 | |
| HD lc | 0.26 | 2.30 | 0.047 | 0.030 | 1.49 | 0.63 | |
| SV | 0.28 | 2.54 | 0.049 | 0.029 | 1.61 | 0.68 | |
| NO | 0.73 | 2.81 | 0.23 | 0.33 | 4.05 | 1.38 | |
| 100 | BA LoA | 0.14 | 1.83 | 0.046 | 0.039 | 1.63 | 0.76 |
| SQ | 0.22 | 1.85 | 0.039 | 0.023 | 1.27 | 0.54 | |
| HD | 0.20 | 1.87 | 0.034 | 0.020 | 1.16 | 0.49 | |
| BP | 0.19 | 1.47 | 0.033 | 0.022 | 1.02 | 0.43 | |
| HD lc | 0.19 | 1.60 | 0.033 | 0.021 | 1.07 | 0.45 | |
| SV | 0.20 | 1.95 | 0.034 | 0.020 | 1.18 | 0.50 | |
| NO | 0.38 | 1.62 | 0.13 | 0.18 | 2.05 | 0.70 | |
| 150 | BA LoA | 0.11 | 1.69 | 0.044 | 0.036 | 1.63 | 0.74 |
| SQ | 0.18 | 1.37 | 0.031 | 0.019 | 0.99 | 0.43 | |
| HD | 0.16 | 1.36 | 0.028 | 0.017 | 0.92 | 0.40 | |
| BP | 0.16 | 1.17 | 0.027 | 0.018 | 0.84 | 0.36 | |
| HD lc | 0.16 | 1.23 | 0.028 | 0.017 | 0.87 | 0.38 | |
| SV | 0.16 | 1.45 | 0.028 | 0.017 | 0.94 | 0.41 | |
| NO | 0.18 | 1.24 | 0.048 | 0.074 | 0.99 | 0.39 | |
| 200 | BA LoA | 0.096 | 1.60 | 0.043 | 0.034 | 1.62 | 0.74 |
| SQ | 0.16 | 1.18 | 0.028 | 0.017 | 0.87 | 0.37 | |
| HD | 0.14 | 1.14 | 0.025 | 0.015 | 0.79 | 0.34 | |
| BP | 0.14 | 1.02 | 0.025 | 0.016 | 0.75 | 0.32 | |
| HD lc | 0.14 | 1.07 | 0.025 | 0.016 | 0.77 | 0.33 | |
| SV | 0.14 | 1.19 | 0.025 | 0.015 | 0.80 | 0.34 | |
| NO | 0.14 | 1.18 | 0.026 | 0.026 | 0.79 | 0.34 | |
| 250 | BA LoA | 0.088 | 1.55 | 0.042 | 0.033 | 1.62 | 0.74 |
| SQ | 0.14 | 1.02 | 0.024 | 0.015 | 0.76 | 0.33 | |
| HD | 0.13 | 0.99 | 0.023 | 0.014 | 0.71 | 0.30 | |
| BP | 0.13 | 0.91 | 0.022 | 0.014 | 0.68 | 0.29 | |
| HD lc | 0.13 | 0.94 | 0.022 | 0.014 | 0.69 | 0.30 | |
| SV | 0.13 | 1.02 | 0.022 | 0.014 | 0.71 | 0.31 | |
| NO | 0.13 | 1.10 | 0.022 | 0.014 | 0.74 | 0.32 | |
| 500 | BA LoA | 0.062 | 1.39 | 0.043 | 0.032 | 1.61 | 0.73 |
| SQ | 0.097 | 0.69 | 0.018 | 0.011 | 0.53 | 0.22 | |
| HD | 0.091 | 0.67 | 0.017 | 0.010 | 0.50 | 0.21 | |
| BP | 0.090 | 0.64 | 0.016 | 0.010 | 0.49 | 0.21 | |
| HD lc | 0.090 | 0.65 | 0.016 | 0.010 | 0.49 | 0.21 | |
| SV | 0.091 | 0.67 | 0.017 | 0.010 | 0.50 | 0.21 | |
| NO | 0.094 | 0.72 | 0.017 | 0.010 | 0.53 | 0.22 | |
| 750 | BA LoA | 0.050 | 1.34 | 0.043 | 0.033 | 1.60 | 0.73 |
| SQ | 0.079 | 0.57 | 0.014 | 0.009 | 0.44 | 0.18 | |
| HD | 0.075 | 0.55 | 0.014 | 0.008 | 0.42 | 0.17 | |
| BP | 0.074 | 0.53 | 0.014 | 0.008 | 0.41 | 0.17 | |
| HD lc | 0.075 | 0.54 | 0.014 | 0.008 | 0.41 | 0.17 | |
| SV | 0.075 | 0.55 | 0.014 | 0.008 | 0.42 | 0.17 | |
| NO | 0.076 | 0.57 | 0.014 | 0.008 | 0.43 | 0.18 | |
| 1000 | BA LoA | 0.043 | 1.31 | 0.042 | 0.032 | 1.60 | 0.73 |
| SQ | 0.068 | 0.48 | 0.012 | 0.008 | 0.37 | 0.16 | |
| HD | 0.065 | 0.47 | 0.012 | 0.007 | 0.36 | 0.15 | |
| BP | 0.064 | 0.46 | 0.012 | 0.007 | 0.35 | 0.15 | |
| HD lc | 0.065 | 0.46 | 0.012 | 0.007 | 0.35 | 0.15 | |
| SV | 0.065 | 0.47 | 0.012 | 0.007 | 0.36 | 0.15 | |
| NO | 0.066 | 0.48 | 0.012 | 0.007 | 0.36 | 0.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerke, O. Nonparametric Limits of Agreement in Method Comparison Studies: A Simulation Study on Extreme Quantile Estimation. Int. J. Environ. Res. Public Health 2020, 17, 8330. https://doi.org/10.3390/ijerph17228330
Gerke O. Nonparametric Limits of Agreement in Method Comparison Studies: A Simulation Study on Extreme Quantile Estimation. International Journal of Environmental Research and Public Health. 2020; 17(22):8330. https://doi.org/10.3390/ijerph17228330
Chicago/Turabian StyleGerke, Oke. 2020. "Nonparametric Limits of Agreement in Method Comparison Studies: A Simulation Study on Extreme Quantile Estimation" International Journal of Environmental Research and Public Health 17, no. 22: 8330. https://doi.org/10.3390/ijerph17228330
APA StyleGerke, O. (2020). Nonparametric Limits of Agreement in Method Comparison Studies: A Simulation Study on Extreme Quantile Estimation. International Journal of Environmental Research and Public Health, 17(22), 8330. https://doi.org/10.3390/ijerph17228330





