The Role of Specific Warm-up during Bench Press and Squat Exercises: A Novel Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Approach to the Problem
2.2. Subjects
2.3. Procedures
2.4. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- McGowan, C.J.; Pyne, D.B.; Thompson, K.G.; Rattray, B. Warm-up strategies for sport and exercise: Mechanisms and applications. Sports Med. 2015, 45, 1523–1546. [Google Scholar] [CrossRef] [PubMed]
- Bishop, D. Warm up I: Potential mechanisms and the effects of passive warm up on exercise performance. Sports Med. 2003, 33, 439–454. [Google Scholar] [CrossRef] [PubMed]
- Bishop, D. Warm up II: Performance changes following active warm up and how to structure the warm up. Sports Med. 2003, 33, 483–498. [Google Scholar] [CrossRef] [PubMed]
- Gourgoulis, V.; Aggeloussis, N.; Kasimatis, P.; Mavromatis, G.; Garas, A. Effect of a submaximal half-squats warm-up program on vertical jumping ability. J. Strength Cond. Res. 2003, 17, 342–344. [Google Scholar] [PubMed]
- Pojskić, H.; Pagaduan, J.C.; Babajić, F.; Užičanin, E.; Muratović, M.; Tomljanović, M. Acute effects of prolonged intermittent low-intensity isometric warm-up schemes on jump, sprint, and agility performance in collegiate soccer players. Biol Sport 2015, 32, 129–134. [Google Scholar] [CrossRef] [PubMed]
- Silva, L.M.; Neiva, H.P.; Marques, M.C.; Izquierdo, M.; Marinho, D.A. Effects of warm-up, post-warm-up, and re-warm-up strategies on explosive efforts in team sports: A systematic review. Sports Med. 2018, 48, 2285–2299. [Google Scholar] [CrossRef]
- Junior, D.; Junor, A.; Serpa, É.; Gomes, W.; Soares, E.; Lopes, C.; Teixeira, L.; Marchetti, P. Different warm-ups on the maximum repetition performance in resistance training. Rev. Bras. Med. Esporte 2014, 20, 461–464. [Google Scholar]
- Ribeiro, A.; Romanzini, M.; Schoenfeld, B.; Souza, M.F.; Avelar, A.; Cyrino, E.S. Effect of different warm-up procedures on the performance of resistance training exercises. Percept. Mot. Skills 2014, 119, 133–145. [Google Scholar] [CrossRef]
- Alves, R.R.; Viana, R.B.; Silva, M.H.; Guimarães, T.C.; Vieira, C.A.; Santos, D.A.T.; Gentil, P.R.V. Postactivation potentiation improves performance in a resistance training session in trained men. J. Strength Cond. Res. 2019. [Google Scholar] [CrossRef]
- Neiva, H.P.; Marques, M.C.; Barbosa, T.M.; Izquierdo, M.; Viana, J.L.; Teixeira, A.; Marinho, D.A. Warm-up volume affects the 100 m swimming performance: A randomized crossover study. J. Strength Cond. Res. 2015, 29, 3026–3036. [Google Scholar] [CrossRef]
- Evans, A.K.; Durham, M.P.; Hodgkins, T.D.; Sinclair, D.R.; Adams, K.J. Acute effect of bench press on power output during a subsequent ballistic bench throw. Med. Sci Sports 2001, 33, 325. [Google Scholar] [CrossRef]
- Gil, M.H.; Neiva, H.P.; Sousa, A.C.; Marques, M.C.; Marinho, D.A. Current approaches on warming up for sports performance: A critical review. Strength Cond. J. 2019, 41, 70–79. [Google Scholar] [CrossRef]
- Conrado de Freitas, M.; Rossi, F.E.; Colognesi, L.A.; de Oliveira, J.V.N.S.; Zanchi, N.E.; Lira, F.S.; Cholewa, J.M.; Gobbo, L.A. Postactivation potentiation improves acute resistance exercise performance and muscular force in trained men. J. Strength Cond. Res. 2018. [Google Scholar] [CrossRef] [PubMed]
- Abad, C.C.; Prado, M.L.; Ugrinowitsch, C.; Tricoli, V.; Barroso, R. Combination of general and specific warm-ups improves leg-press one repetition maximum compared with specific warm-up in trained individuals. J. Strength Cond. Res. 2011, 25, 2242–2245. [Google Scholar] [CrossRef]
- Kilduff, L.P.; Bevan, H.R.; Kingsley, M.I.C.; Owen, N.J.; Bennett, M.A.; Bunce, P.J.; Hore, A.M.; Maw, J.R.; Cunningham, D.J. Postactivation potentiation in professional rugby players: Optimal recovery. J. Strength Cond. Res. 2007, 21, 1134–1138. [Google Scholar] [CrossRef]
- Kilduff, L.P.; Owen, N.; Bevan, H.; Bennett, M.; Kingsley, M.I.C.; Cunningham, D. Influence of recovery time on post-activation potentiation in professional rugby players. J. Sports Sci. 2008, 26, 795–802. [Google Scholar] [CrossRef]
- Sale, D.G. Postactivation potentiation: Role in human performance. Exerc. Sport Sci Rev. 2002, 30, 138–143. [Google Scholar] [CrossRef]
- Barroso, R.; Silva-Batista, C.; Tricoli, V.; Roschel, H.; Ugrinowitsch, C. The effects of different intensities and durations of the general warm-up on leg press 1RM. J. Strength Cond. Res. 2013, 27, 1009–1013. [Google Scholar] [CrossRef]
- Brandenburg, J. The acute effects of prior dynamic resistance exercise using different loads on subsequent upper-body explosive performance in resistance-trained men. J. Strength Cond. Res. 2005, 19, 427–432. [Google Scholar]
- González-Badillo, J.J.; Marques, M.C.; Sánchez-Medina, L. The importance of movement velocity as a measure to control resistance training intensity. J. Hum. Kinet. 2011, 29, 15–19. [Google Scholar] [CrossRef]
- González-Badillo, J.J.; Sánchez-Medina, L. Movement velocity as a measure of loading intensity in resistance training. Int. J. Sports Med. 2010, 31, 347–352. [Google Scholar]
- Jovanović, M.; Flanagan, E.P. Researched applications of velocity-based strength training. J. Aust. Strength Cond. 2014, 22, 58–69. [Google Scholar]
- Pareja-Blanco, F.; Rodríguez-Rosell, D.; Sánchez-Medina, L.; Sanchis-Moysi, J.; Dorado, C.; Mora-Custodio, R.; Yáñez-García, J.M.; Morales-Alamo, D.; Pérez-Suárez, I.; Calbet, J.; et al. Effects of velocity loss during resistance training on athletic performance, strength gains and muscle adaptations. Scand J. Med. Sci Sports 2017, 27, 724–735. [Google Scholar] [CrossRef] [PubMed]
- González-Badillo, J.J.; Sánchez-Medina, L.; Pareja Blanco, F.; Rodríguez Rosell, D. La Velocidad de Ejecución como Referencia Para la Programación, Control y Evaluación del Entrenamiento de la Fuerza; Ergotech Consulting: Pamplona, Navarra, Spain, 2017. [Google Scholar]
- Sanchez-Medina, L.; González-Badillo, J.J. Velocity loss as an indicator of neuromuscular fatigue during resistance training. Med. Sci. Sport Exer. 2011, 43, 1725–1734. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Medina, L.; Pallarés, J.G.; Pérez, C.E.; Morán-Navarro, R.; González-Badillo, J.J. Estimation of relative load from bar velocity in the full back squat exercise. Sports Med. Int Open. 2017, 1, 80–88. [Google Scholar] [CrossRef]
- Garnacho-Castaño, M.V.; Muñoz-González, A.; Garnacho-Castaño, M.A.; Maté-Muñoz, J.L. Power–and velocity–load relationships to improve resistance exercise performance. Proc. Inst. Mech. Eng. Part. P: J. Sports Eng. Technol. 2018, 232, 349–359. [Google Scholar] [CrossRef]
- Pallarés, J.G.; Sánchez-Medina, L.; Pérez, C.E.; De La Cruz-Sánchez, E.; Mora-Rodriguez, R. Imposing a pause between the eccentric and concentric phases increases the reliability of isoinertial strength assessments. J. Sports Sci. 2014, 32, 1165–1175. [Google Scholar] [CrossRef]
- Sánchez-Medina, L.; González-Badillo, J.J.; Pérez, C.E.; Pallarés, J.G. Velocity- and power-load relationships of the bench pull vs. bench press exercises. Int. J. Sports Med. 2014, 35, 209–216. [Google Scholar] [CrossRef]
- Adams, K. Progression models in resistance training for healthy adults. Med. Sci. Sports Exerc. 2002, 34, 364–380. [Google Scholar]
- Kraemer, W.J.; Ratamess, N.A. Fundamentals of resistance training: Progression and exercise prescription. Med. Sci. Sports Exerc. 2004, 36, 674–688. [Google Scholar] [CrossRef]
- García-Ramos, A.; Pestaña-Melero, F.L.; Pérez-Castilla, A.; Rojas, F.J.; Haff, G.G. Mean velocity vs. mean propulsive velocity vs. peak velocity: Which variable determines bench press relative load with higher reliability? J. Strength Cond. Res. 2018, 32, 1273–1279. [Google Scholar] [CrossRef] [PubMed]
- Borg, G. Borg’s Perceived Exertion and Pain Scales; Human Kinetics: Champaign, IL, USA, 1998. [Google Scholar]
- Lakens, D. Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Front. Psychol. 2013, 4, 1–12. [Google Scholar] [CrossRef]
- Hopkins, M.G.; Marshall, S.W.; Batterham, A.M.; Hanin, J. Progressive statistics for studies in sports medicine and exercise science. Med. Sci Sports Exerc. 2009, 41, 3–12. [Google Scholar] [CrossRef] [PubMed]
- Xenofondos, A.; Laparidis, K.; Kyranoudis, A.; Galazoulas, C.; Bassa, E.; Kotzamanidis, C. Post-activation potentiation: Factors affecting it and the effect on performance. J. Phys. Educ. Sport 2010, 28, 32–38. [Google Scholar]
- Albuquerque, C.; Maschio, J.; Gruber, C.; Souza, R.; Hernandez, S. Efeito agudo de diferentes formas de aquecimento sobre a força muscular. Fisioter Mov. 2011, 24, 221–229. [Google Scholar] [CrossRef]
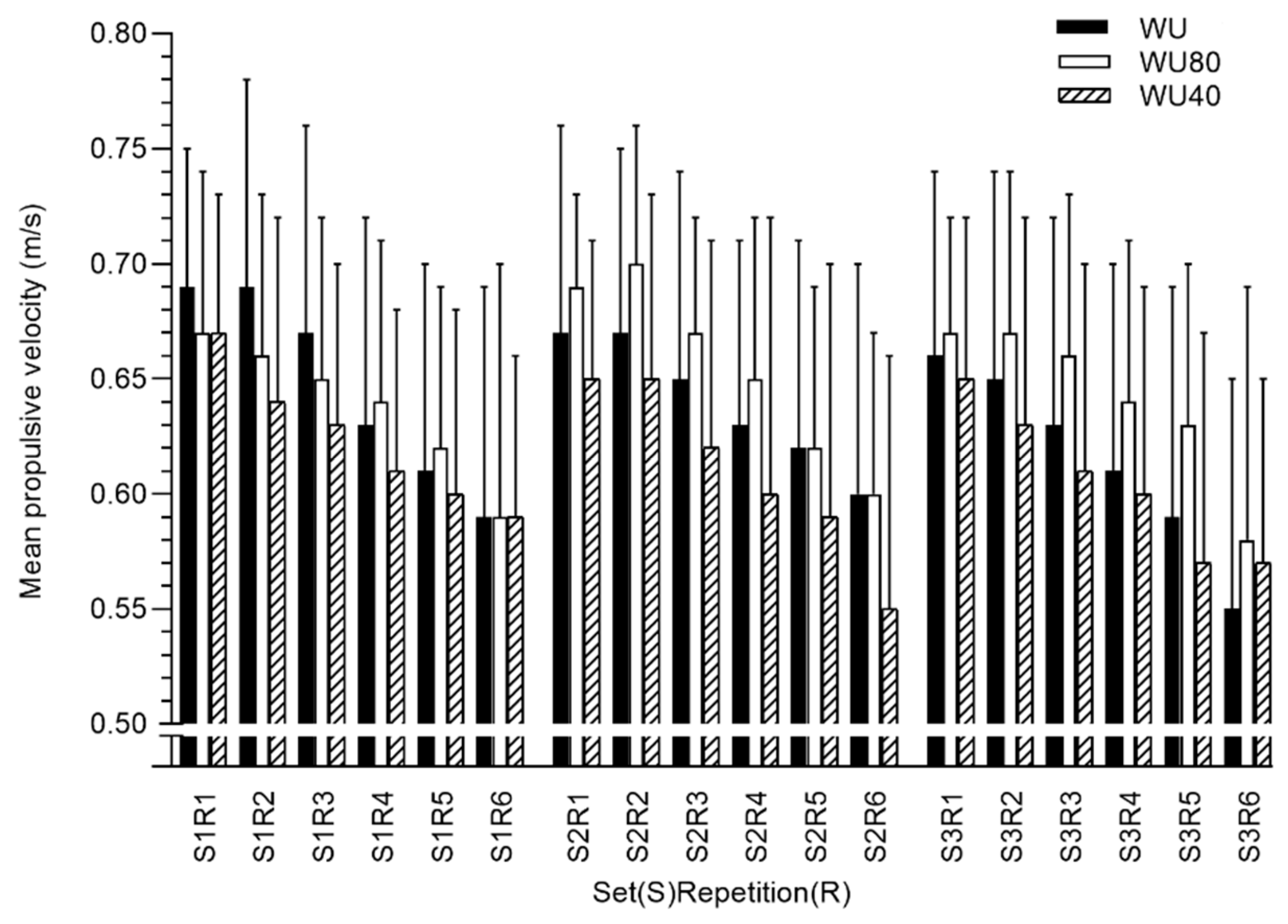

| WU | WU80 | WU40 | WU vs. WU80 | WU vs. WU40 | WU80 vs. WU40 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Difference (±95% CI) | p-Value (ES) | Difference (±95% CI) | p-Value (ES) | Difference (±95% CI) | p-Value (ES) | ||||
| MPV [set 1] (m.s−1) | 0.71 ± 0.08 | 0.69 ± 0.07 | 0.68 ± 0.06 | 0.02 (±0.02) | 0.10 (0.48) | 0.03 (±0.04) | 0.21 (0.40) | 0.01 (±0.03) | 0.71 (0.15) |
| MPV [set 2] (m.s−1) | 0.69 ± 0.09 | 0.71 ± 0.05 | 0.67 ± 0.06 | −0.01 (±0.04) | 0.46 (0.27) | 0.02 (±0.04) | 0.15 (0.34) | 0.04 (±0.03) | 0.02 * (0.80) |
| MPV [set 3] (m.s−1) | 0.68 ± 0.09 | 0.69 ± 0.07 | 0.66 ± 0.07 | −0.02 (±0.05) | 0.41 (0.13) | 0.02 (±0.01) | 0.08 (0.58) | 0.03 (±0.04) | 0.05 * (0.51) |
| MPVmin [set 1] (m.s−1) | 0.58 ± 0.10 | 0.58 ± 0.10 | 0.58 ± 0.08 | 0.01 (±0.06) | 0.88 (<0.01) | 0.01 (±0.04) | 0.79 (<0.01) | 0.00 (±0.05) | 0.98 (<0.01) |
| MPVmin [set 2] (m.s−1) | 0.58 ± 0.09 | 0.59 ± 0.07 | 0.54 ± 0.11 | −0.01 (±0.05) | 0.69 (0.12) | 0.04 (±0.04) | 0.01 ** (0.70) | 0.05 (±0.05) | 0.04 * (0.60) |
| MPVmin [set 3] (m.s−1) | 0.54 ± 0.09 | 0.57 ± 0.09 | 0.55 ± 0.09 | −0.03 (±0.06) | 0.31 (0.34) | −0.01 (±0.04) | 0.58 (0.16) | 0.02 (±0.06) | 0.62 (0.18) |
| VL [set 1] (%) | 17.56 ± 9.14 | 16.31 ± 10.35 | 15.11 ± 7.44 | 1.26 (±8.47) | 0.75 (0.09) | 2.45 (±6.06) | 0.40 (0.23) | 1.19 (±5.85) | 0.67 (0.12) |
| VL [set 2] (%) | 16.35 ± 5.63 | 16.32 ± 6.07 | 20.57 ± 10.89 | 0.03 (±3.16) | 0.99 (0.01) | −4.22 (±4.75) | 0.08 (0.51) | −4.25 (±5.66) | 0.13 (0.43) |
| VL [set 3] (%) | 19.99 ± 7.11 | 18.44 ± 9.94 | 16.86 ± 8.57 | 1.55 (±6.21) | 0.60 (0.14) | 3.14 (±5.45) | 0.24 (0.33) | 1.59 (±8.21) | 0.68 (0.11) |
| VL [total] (%) | 26.59 ± 8.58 | 26.83 ± 10.58 | 26.09 ± 10.40 | −0.24 (±5.40) | 0.93 (0.03) | 0.50 (±5.53) | 0.85 (0.05) | 0.74 (±8.33) | 0.85 (0.05) |
| WU | WU80 | WU40 | WU vs. WU80 | WU vs. WU40 | WU80 vs. WU40 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Difference (±95% CI) | p-Value (ES) | Difference (±95% CI) | p-Value (ES) | Difference (±95% CI) | p-Value (ES) | ||||
| PV [total] (m.s−1) | 1.33 ± 0.11 | 1.32 ± 0.07 | 1.30 ± 0.08 | 0.01 (±0.05) | 0.76 (0.11) | 0.03 (±0.05) | 0.16 (0.38) | 0.03 (±0.04) | 0.20 (0.29) |
| Time to PV [set1] (ms) | 586.21 ± 109.87 | 589.93 ± 133.11 | 638.00 ± 163.28 | −3.71 (±60.23) | 0.90 (0.04) | −51.79 (±53.18) | 0.06 (0.56) | −48.07 (±50.85) | 0.06 (0.55) |
| Time to PV [set2] (ms) | 601.64 ± 110.91 | 565.86 ± 106.87 | 623.50 ± 136.80 | 35.79 (±54.94) | 0.18 (0.38) | −21.86 (±45.19) | 0.32 (0.28) | −57.64 (±51.25) | 0.03 * (0.65) |
| Time to PV [set3] (ms) | 606.93 ± 114.53 | 582.57 ± 129.29 | 619.36 ± 191.00 | 24.36 (±48.06) | 0.29 (0.29) | −12.43 (±69.26) | 0.71 (0.10) | −36.79 (±76.09) | 0.32 (0.28) |
| WU | WU80 | WU40 | WU vs. WU80 | WU vs. WU40 | WU80 vs. WU40 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Difference (±95% CI) | p-Value (ES) | Difference (±95% CI) | p-Value (ES) | Difference (±95% CI) | p-Value ES | ||||
| MPP [set 1] (W) | 528.78 ± 107.18 | 519.29 ± 90.75 | 510.86 ± 101.92 | 9.49 (±25.06) | 0.43 (0.22) | 17.92 (±33.82) | 0.27 (0.31) | 8.43 (±31.71) | 0.58 (0.15) |
| MPP [set 2] (W) | 521.09 ± 98.87 | 532.53 ± 102.09 | 501.25 ± 83.04 | −11.44 (±41.70) | 0.56 (0.16) | 19.84 (±3 1.58) | 0.20 (0.36) | 31.28 (±36.39) | 0.09 (0.50) |
| MPP [set 3] (W) | 501.46 ± 96.06 | 523.07 ± 107.75 | 492.48 ± 91.46 | −21.61 (±42.53) | 0.29 (0.29) | 8.99 (±17.00) | 0.27 (0.31) | 30.59 (±33.19) | 0.07 (0.53) |
| MPPmin [set1] (W) | 430.41 ± 85.19 | 428.86 ± 99.11 | 424.17 ± 94.14 | 1.56 (±42.27) | 0.94 (0.02) | 6.24 (±34.24) | 0.70 (0.11) | 4.69 (±33.51) | 0.77 (0.08) |
| MPPmin [set 2] (W) | 425.78 ± 82.25 | 440.29 ± 90.33 | 391.97 ± 91.33 | −14.51 (±51.24) | 0.45 (0.21) | 33.81 (±33.38) | 0.02 * (0.74) | 48.32 (±54.31) | 0.03 * (0.65) |
| MPPmin [set 3] (W) | 398.86 ± 88.74 | 422.53 ± 111.28 | 406.07 ± 99.94 | −23.66 (±43.26) | 0.29 (0.32) | −7.21 (±24.25) | 0.53 (0.17) | 16.46 (±46.57) | 0.46 (0.20) |
| Work [set 1] (J) | 2405.81 ± 532.92 | 2322.21 ± 493.88 | 2385.81 ± 549.18 | 83.59 (±107.05) | 0.12 (0.45) | 19.99 (±159.89) | 0.79 (0.07) | −63.60 (±163.90) | 0.42 (0.22) |
| Work [set 2] (J) | 2388.63 ± 488.98 | 2342.16 ± 506.69 | 2377.38 ± 490.31 | 46.47 (±87.76) | 0.27 (0.31) | 11.25 (±96.19) | 0.80 (0.07) | −35.22 (±94.29) | 0.43 (0.22) |
| Work [set 3] (J) | 2361.30 ± 502.87 | 2319.56 ± 504.58 | 2368.65 ± 493.40 | 41.74 (±77.47) | 0.27 (0.31) | −7.35 (±116.55) | 0.89 (0.04) | −49.09 (±133.67) | 0.44 (0.21) |
| Work [total] (J) | 7155.73 ± 1517.62 | 6983.94 ± 1489.85 | 7131.84 ± 1509.67 | 171.79 (±200.29) | 0.09 (0.50) | 23.89 (±338.94) | 0.88 (0.04) | −147.90 (±328.57) | 0.35 (0.26) |
| WU | WU80 | WU40 | WU vs. WU80 | WU vs. WU40 | WU80 vs. WU40 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Difference (±95% CI) | p-Value (ES) | Difference (±95% CI) | p-Value (ES) | Difference (±95% CI) | p-Value ES | ||||
| MPV [set 1] (m.s−1) | 0.53 ± 0.07 | 0.52 ± 0.11 | 0.50 ± 0.10 | 0.01 (±0.05) | 0.74 (0.09) | 0.02 (±0.04) | 0.15 (0.35) | 0.02 (±0.04) | 0.44 (0.19) |
| MPV [set 2] (m.s−1) | 0.48 ± 0.09 | 0.48 ± 0.10 | 0.48 ± 0.08 | 0.00 (±0.06) | 0.97 (<0.01) | 0.00 (±0.03) | 0.98 (<0.01) | 0.00 (±0.04) | 0.94 (<0.01) |
| MPV [set 3] (m.s−1) | 0.50 ± 0.08 | 0.47 ± 0.11 | 0.47 ± 0.10 | 0.03 (±0.05) | 0.18 (0.26) | 0.03 (±0.03) | 0.09 (0.40) | 0.00 (±0.04) | 0.89 (<0.01) |
| MPVmin [set 1] (m.s−1) | 0.37 ± 0.11 | 0.36 ± 0.11 | 0.36 ± 0.09 | 0.01 (±0.06) | 0.74 (0.07) | 0.01 (±0.04) | 0.73 (0.09) | 0.00 (±0.04) | 0.94 (<0.01) |
| MPVmin [set 2] (m.s−1) | 0.33 ± 0.11 | 0.32 ± 0.13 | 0.33 ± 0.11 | 0.01 (±0.08) | 0.85 (0.05) | 0.00 (±0.04) | 0.91 (<0.01) | −0.01 (±0.05) | 0.70 (0.08) |
| MPVmin [set 3] (m.s−1) | 0.32 ± 0.12 | 0.31 ± 0.12 | 0.31 ± 0.11 | 0.01 (±0.06) | 0.61 (0.07) | 0.01 (±0.05) | 0.53 (0.09) | 0.00 (±0.05) | 0.99 (<0.01) |
| VL [set 1] (%) | 30.65 ± 13.83 | 30.96 ± 12.23 | 28.19 ± 9.32 | −0.31 (±6.33) | 0.92 (0.02) | 2.46 (±6.74) | 0.46 (0.15) | 2.77 (±5.17) | 0.28 (0.22) |
| VL [set 2] (%) | 33.42 ± 14.35 | 35.69 ± 16.73 | 32.81 ± 13.43 | −2.27 (±9.87) | 0.64 (0.09) | 0.62 (±6.05) | 0.84 (0.04) | 2.89 (±6.81) | 0.39 (0.17) |
| VL [set 3] (%) | 35.96 ± 15.76 | 35.35 ± 13.66 | 35.54 ± 14.48 | 0.62 (±7.23) | 0.86 (0.03) | 1.42 (±7.90) | 0.71 (0.02) | 0.81 (±7.06) | 0.82 (0.01) |
| VL [total] (%) | 44.86 ± 12.98 | 43.81 ± 13.80 | 45.12 ± 13.11 | 1.04 (±6.79) | 0.76 (0.06) | −0.27 (±5.78) | 0.92 (0.02) | −1.31 (±5.34) | 0.62 (0.10) |
| WU | WU80 | WU40 | WU vs. WU80 | WU vs. WU40 | WU80 vs. WU40 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Difference (±95% CI) | p-Value (ES) | Difference (±95% CI) | p-Value (ES) | Difference (±95% CI) | p-Value ES | ||||
| PV [total] (m.s−1) | 0.82 ± 0.11 | 0.80 ± 0.15 | 0.82 ± 0.12 | 0.02 (±0.05) | 0.43 (0.17) | 0.00 (±0.04) | 0.95 (<0.01) | −0.02 (±0.05) | 0.45 (0.17) |
| Time to PV [set1] (ms) | 574.77 ± 233.46 | 588.62 ± 334.46 | 694.50 ± 211.71 | −13.85 (±137.71) | 0.84 (0.04) | −119.73 (±70.36) | <0.01 ** (0.69) | −105.89 (±144.22) | 0.14 (0.30) |
| Time to PV [set2] (ms) | 533.19 ± 272.22 | 549.58 ± 293.34 | 662.31 ± 257.51 | −16.39 (±96.37) | 0.73 (0.07) | −129.12 (±120.81) | 0.04 * (0.43) | −112.73 (±128.65) | 0.08 (0.35) |
| Time to PV [set3] (ms) | 583.19 ± 272.04 | 609.19 ± 334.18 | 575.61 ± 303.09 | −26.00 (±119.23) | 0.66 (0.09) | 7.58 (±130.52) | 0.91 (0.02) | 33.58 (±171.65) | 0.69 (0.08) |
| WU | WU80 | WU40 | WU vs. WU80 | WU vs. WU40 | WU80 vs. WU40 | ||||
|---|---|---|---|---|---|---|---|---|---|
| Difference (±95% CI) | p-Value (ES) | Difference (±95% CI) | p-Value (ES) | Difference (±95% CI) | p-Value ES | ||||
| MPP [set 1] (W) | 309.30 ± 89.35 | 303.68 ± 87.97 | 292.25 ± 77.90 | 5.61 (±30.05) | 0.70 (0.08) | 17.04 (±20.09) | 0.09 (0.34) | 11.43 (±25.60) | 0.37 (0.18) |
| MPP [set 2] (W) | 288.13 ± 103.95 | 283.09 ± 82.62 | 286.45 ± 93.54 | 5.04 (±29.87) | 0.73 (0.07) | 1.68 (±18.47) | 0.85 (0.04) | −3.35 (±22.28) | 0.76 (0.06) |
| MPP [set 3] (W) | 293.65 ± 97.98 | 279.92 ± 86.21 | 277.43 ± 98.77 | 13.74 (±47.49) | 0.56 (0.12) | 16.22 (±18.07) | 0.08 (0.36) | 2.48 (±48.18) | 0.92 (0.02) |
| MPPmin [set 1] (W) | 213.86 ± 79.99 | 211.38 ± 83.48 | 209.95 ± 66.28 | 2.48 (±33.78) | 0.88 (0.03) | 3.91 (±25.34) | 0.75 (0.06) | 1.43 (±26.28) | 0.91 (0.02) |
| MPPmin [set 2] (W) | 195.27 ± 94.72 | 184.76 ± 81.72 | 194.44 ± 85.96 | 10.51 (±42.15) | 0.61 (0.10) | 0.83 (±24.40) | 0.95 (0.01) | −9.68 (±30.93) | 0.53 (0.13) |
| MPPmin [set 3] (W) | 184.26 ± 58.27 | 179.75 ± 79.56 | 183.65 ± 94.00 | 4.50 (±32.70) | 0.78 (0.06) | 0.61 (±29.79) | 0.97 (0.01) | −3.89 (±32.57) | 0.81 (0.05) |
| Work [set 1] (J) | 1600.42 ± 448.60 | 1587.83 ± 427.57 | 1555.32 ± 440.22 | 12.59 (±44.22) | 0.56 (0.12) | 45.10 (±34.99) | 0.01 ** (0.52) | 32.51 (±37.61) | 0.09 (0.35) |
| Work [set 2] (J) | 1580.15 ± 453.53 | 1550.15 ± 421.00 | 1542.10 ± 461.30 | 30.00 (±43.32) | 0.16 (0.28) | 38.05 (±30.84) | 0.02 * (0.49) | 8.04 (±40.15) | 0.68 (0.08) |
| Work [set 3] (J) | 1569.33 ± 418.91 | 1534.35 ± 417.90 | 1534.38 ± 456.36 | 34.98 (±57.36) | 0.22 (0.25) | 34.95 (±41.02) | 0.09 (0.35) | −0.03 (±45.16) | 0.99 (<0.01) |
| Work [total] (J) | 4749.90 ± 1312.99 | 4672.32 ± 1261.93 | 4631.80 ± 1355.01 | 77.59 (±125.19) | 0.21 (0.25) | 118.11 (±87.65) | 0.01 ** (0.54) | 40.52 (±111.54) | 0.46 (0.15) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ribeiro, B.; Pereira, A.; Neves, P.P.; Sousa, A.C.; Ferraz, R.; Marques, M.C.; Marinho, D.A.; Neiva, H.P. The Role of Specific Warm-up during Bench Press and Squat Exercises: A Novel Approach. Int. J. Environ. Res. Public Health 2020, 17, 6882. https://doi.org/10.3390/ijerph17186882
Ribeiro B, Pereira A, Neves PP, Sousa AC, Ferraz R, Marques MC, Marinho DA, Neiva HP. The Role of Specific Warm-up during Bench Press and Squat Exercises: A Novel Approach. International Journal of Environmental Research and Public Health. 2020; 17(18):6882. https://doi.org/10.3390/ijerph17186882
Chicago/Turabian StyleRibeiro, Bruno, Ana Pereira, Pedro P. Neves, António C. Sousa, Ricardo Ferraz, Mário C. Marques, Daniel A. Marinho, and Henrique P. Neiva. 2020. "The Role of Specific Warm-up during Bench Press and Squat Exercises: A Novel Approach" International Journal of Environmental Research and Public Health 17, no. 18: 6882. https://doi.org/10.3390/ijerph17186882
APA StyleRibeiro, B., Pereira, A., Neves, P. P., Sousa, A. C., Ferraz, R., Marques, M. C., Marinho, D. A., & Neiva, H. P. (2020). The Role of Specific Warm-up during Bench Press and Squat Exercises: A Novel Approach. International Journal of Environmental Research and Public Health, 17(18), 6882. https://doi.org/10.3390/ijerph17186882









