Water Environmental Capacity Calculated Based on Point and Non-Point Source Pollution Emission Intensity under Water Quality Assurance Rates in a Tidal River Network Area
Abstract
:1. Introduction
2. Methods
2.1. Response Relationship of Contaminant Concentration to Influencing Factors in the Control Section
2.2. Response of Various Pollution Sources to Control Section Pollutant Concentration
2.2.1. Plain River Network Water Flow Model
2.2.2. Water Quality Model of River Network
2.2.3. Time-Varying Pollution Factor Concentration
2.3. Correlation between Control Section Pollutant Concentration and Point Source Pollution Load
2.4. Calculation of Environmental Capacity
3. Application Case and Results
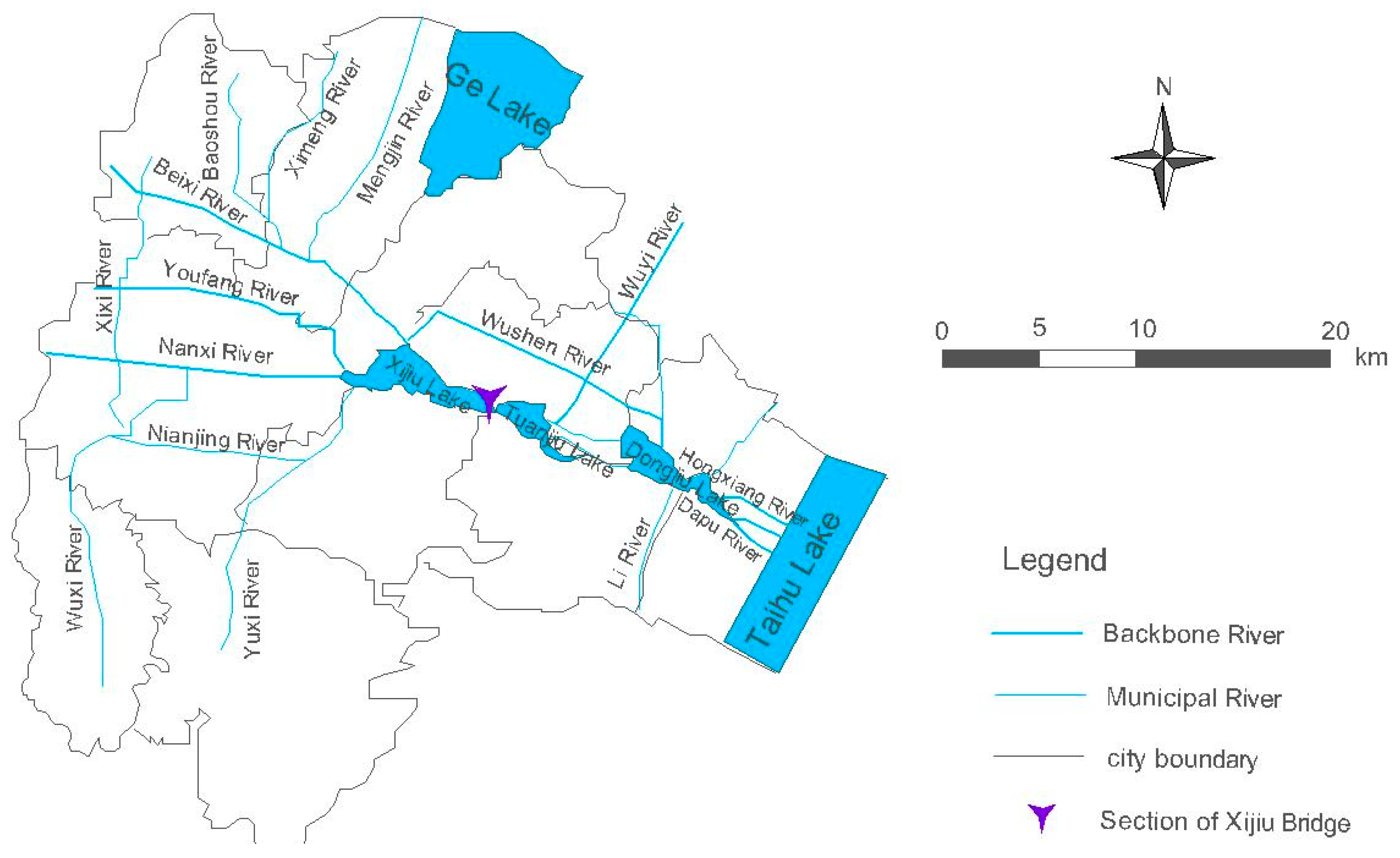
3.1. Overview of the Study Area
3.2. Establishment of the River Network Hydrodynamic Model
3.2.1. Boundary Conditions
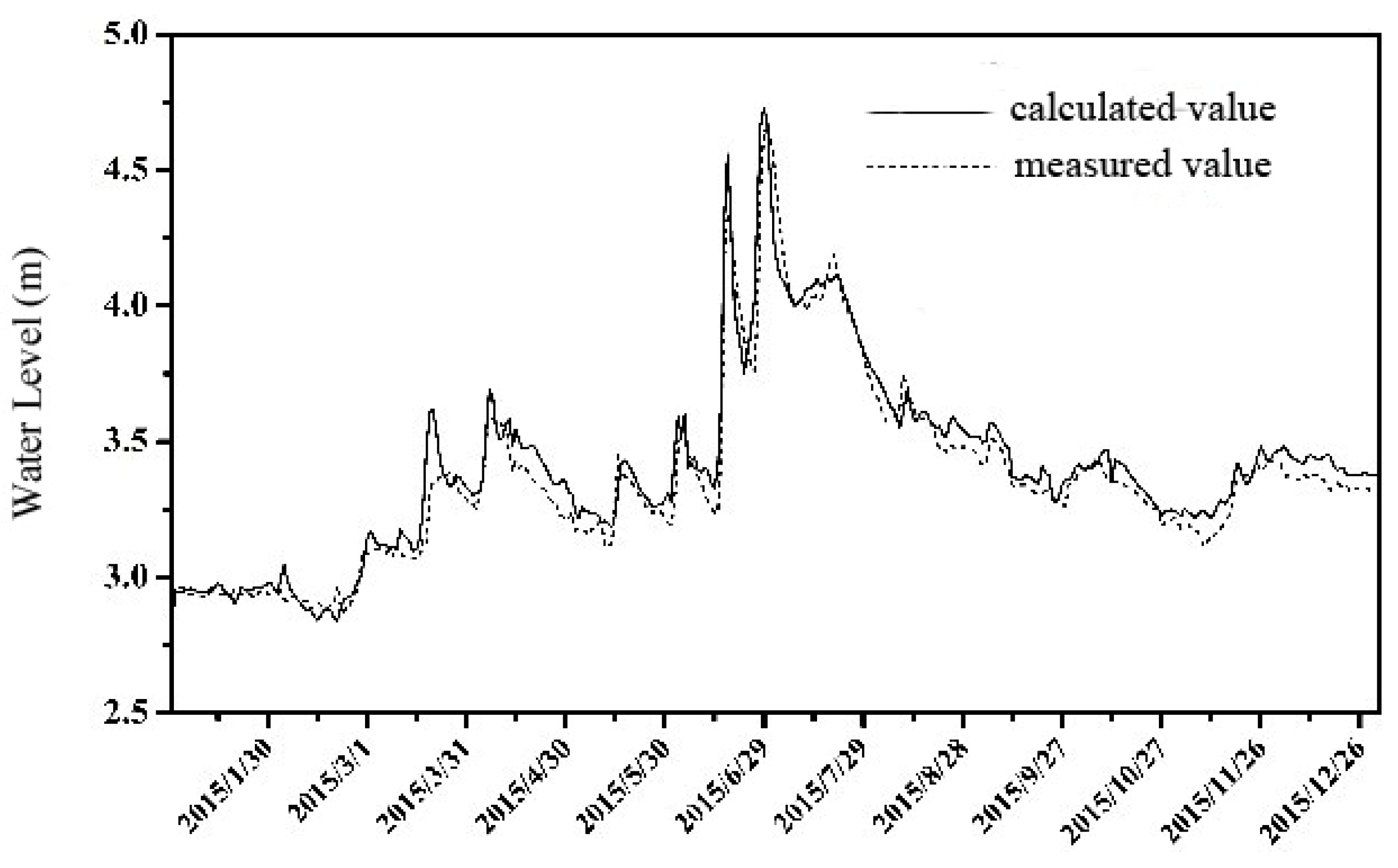
3.2.2. Parameterization and Validation of Water Model Verification
3.3. Establishment of River Network Water Quality Model
3.3.1. Boundary Conditions
3.3.2. Point and Non-Point Source Generalization
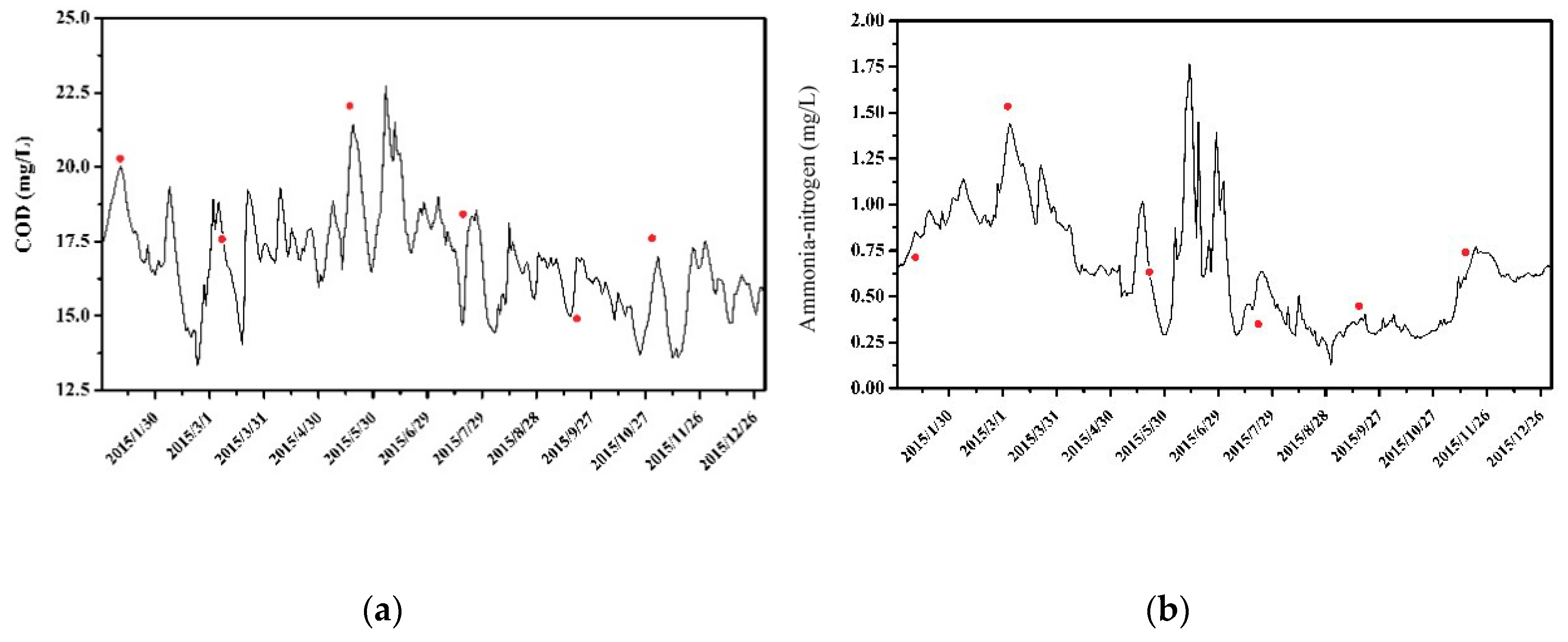
3.3.3. Parameters and Model Validation
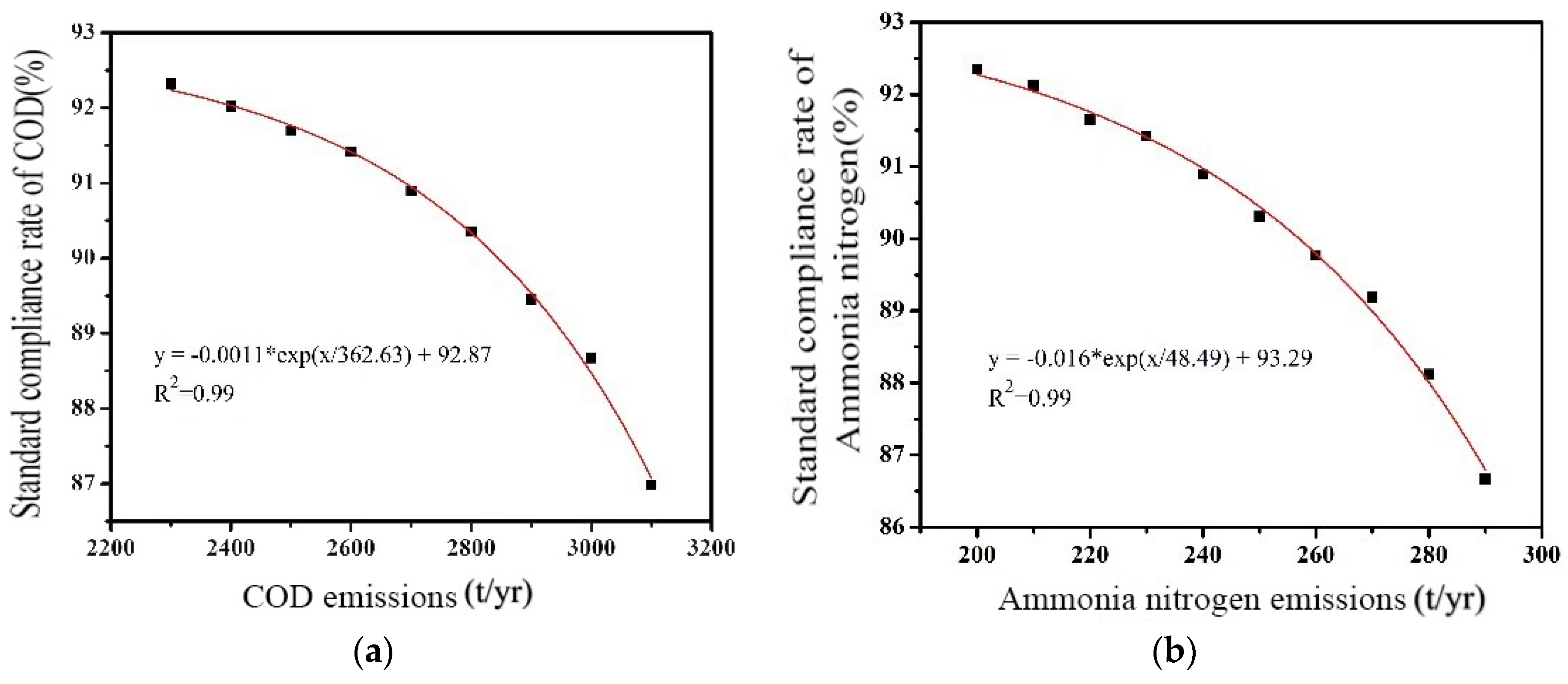
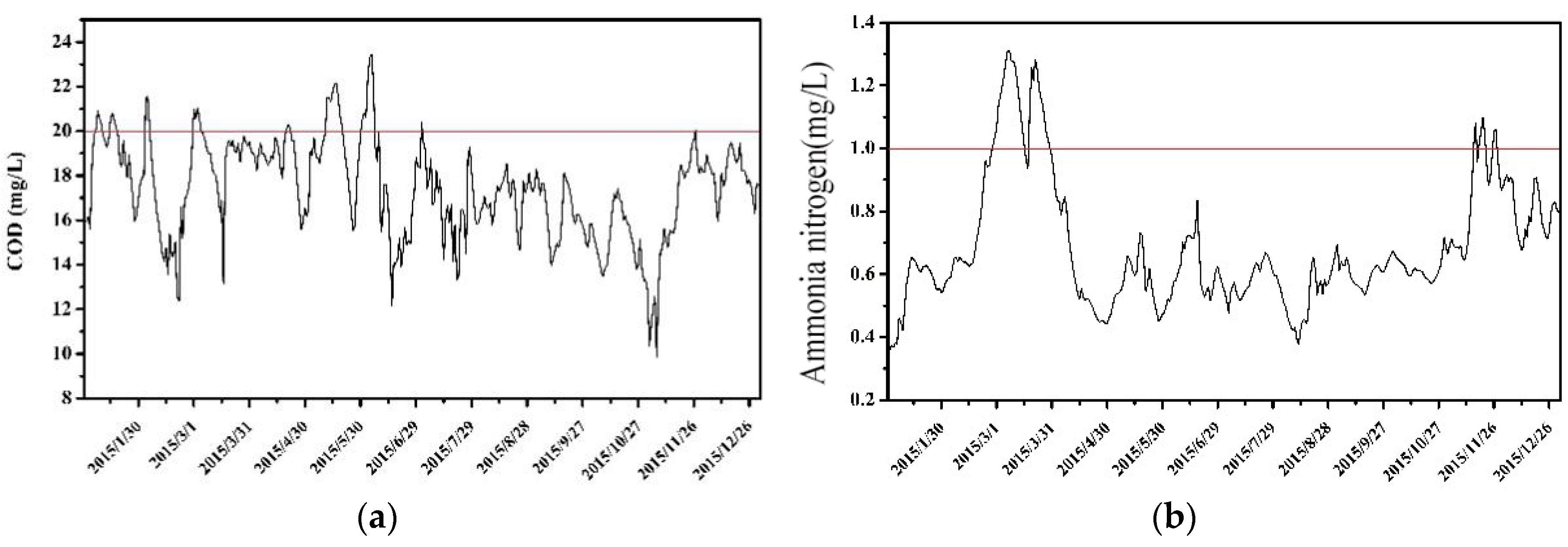
3.3.4. Water Environment Capacity and Water Quality Compliance Rate
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Xu, Z.-X.; Lu, S.-Q. Research on hydrodynamic and water quality model for tidal river networks. J. Hydrodyn. Ser. B Engl. Ed. 2003, 15, 64–70. [Google Scholar]
- Zheng, X.Y.; Zhu, J.D.; Zhu, W.B. Research on water environmental capacity of dynamic river system. Adv. Water Sci. 1997, 8, 25–31. [Google Scholar]
- Han, L.; Lu, D.; Ji, H. Study on the Concentration Response of Pollutant Concentration in the Inflow and Outflow Section of the Cross-type Mouth of Plain River Network. J. Sun Yat-Sen Univ. (Nat. Sci. Ed.) 2011, 50, 123–128. [Google Scholar]
- Han, L.; Lu, D. Prospect of numerical simulation study on water quality of plain river network. J. Hohai Univ. (Nat. Sci. Ed.) 2004, 32, 127–130. [Google Scholar]
- Yao, Y.; Yin, H.; Li, S. The computation approach for water environmental capacity in tidal river network. J. Hydrodyn. 2006, 18, 269–273. [Google Scholar] [CrossRef]
- Zhang, W. Study on Calculation of Water Environment Capacity in Huzhou Plain River Network Area. Environ. Dev. 2015, 27, 85–90. [Google Scholar]
- Ye, Z.; Chen, W. Study on water environment capacity of river channel in Jianghan Plain river network area. Environ. Sci. Technol. 2010, S1, 297–300. [Google Scholar]
- Zeng, S.; Xu, Y.; Zhang, T. Application of water quality model of annular river network in water pollution control planning. Prog. Water Sci. 2004, 15, 193–196. [Google Scholar]
- Jiang, X.; Xu, S.; Lian, J.; Meng, Q. Analysis and calculation of dynamic water environment capacity of northern rivers. J. Ecol. Rural Environ. 2013, 29, 409–414. [Google Scholar]
- Dong, Y.; Zhang, H.; Li, Z. Study on Water Environmental Capacity of Liaoyang Section of Taizi River Based on Linear Programming. Water Technol. Econ. 2016, 22, 12–14. [Google Scholar]
- Han, H.; Li, K.; Wang, X.; Shi, X.; Qiao, X.; Liu, J. Environmental capacity of nitrogen and phosphorus pollutions in Jiaozhou Bay, China: Modeling and assessing. Mar. Pollut. Bull. 2011, 63, 262–266. [Google Scholar] [CrossRef] [PubMed]
- Gou, T.; Feng, M.; Li, D. Study on Water Environment Capacity of Qinshui River Based on Blind Number Theory. J. Water Resour. Water Eng. 2015, 26, 77–82. [Google Scholar]
- Zhang, J.; Fu, Y.; Han, H. Study on hydrological conditions for dynamic water environmental capacity design in the Otta River Basin. China Rural Water and Hydropower 2017, 3, 75–80. [Google Scholar]
- United States Environmental Protection Agency (USEPA). Water Quality Guidance for the Great Lakes System: Supplementary Information Document (SID); USEPA: Washington, DC, USA, 1995.
- Han, L.; Zhu, D. Pollution source control method in water environment planning of river network area. J. Hydraul. Eng. 2001, 32, 28–31. [Google Scholar]
- Liu, Y.; Yang, P.; Hu, C.; Guo, H. Water quality modeling for load reduction under uncertainty: A Bayesian approach. Water Res. 2008, 42, 3305–3314. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.J.; Jun, L.U.; Yuan, S.F.; Jin, S.Q.; Shen, Y.N. Spatial and temporal variations of water quality in Cao-E River of eastern China. J. Environ. Sci. 2006, 18, 680–688. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Han, L.; Tan, J.; Zhou, M.; Sun, M.; Zhang, Y.; Chen, B.; Wang, C.; Liu, Z.; Fan, Y. Water Environmental Capacity Calculated Based on Point and Non-Point Source Pollution Emission Intensity under Water Quality Assurance Rates in a Tidal River Network Area. Int. J. Environ. Res. Public Health 2019, 16, 428. https://doi.org/10.3390/ijerph16030428
Chen L, Han L, Tan J, Zhou M, Sun M, Zhang Y, Chen B, Wang C, Liu Z, Fan Y. Water Environmental Capacity Calculated Based on Point and Non-Point Source Pollution Emission Intensity under Water Quality Assurance Rates in a Tidal River Network Area. International Journal of Environmental Research and Public Health. 2019; 16(3):428. https://doi.org/10.3390/ijerph16030428
Chicago/Turabian StyleChen, Lina, Longxi Han, Junyi Tan, Mengtian Zhou, Mingyuan Sun, Yi Zhang, Bo Chen, Chenfang Wang, Zixin Liu, and Yubo Fan. 2019. "Water Environmental Capacity Calculated Based on Point and Non-Point Source Pollution Emission Intensity under Water Quality Assurance Rates in a Tidal River Network Area" International Journal of Environmental Research and Public Health 16, no. 3: 428. https://doi.org/10.3390/ijerph16030428
APA StyleChen, L., Han, L., Tan, J., Zhou, M., Sun, M., Zhang, Y., Chen, B., Wang, C., Liu, Z., & Fan, Y. (2019). Water Environmental Capacity Calculated Based on Point and Non-Point Source Pollution Emission Intensity under Water Quality Assurance Rates in a Tidal River Network Area. International Journal of Environmental Research and Public Health, 16(3), 428. https://doi.org/10.3390/ijerph16030428



